Atmospheric Density and Temperature Vertical Profile Retrieval for Flight-Tests with a Rayleigh Lidar On-Board the French Advanced Test Range Ship Monge
Abstract
:1. Introduction
1.1. Temperature, Pressure and Density Methodology
1.2. Temperature, Pressure and Density Uncertainty
1.3. Measurement Goals and Requirements
2. Instrument Description
2.1. Optics and Lasers
2.2. Electronics and Signal Acquisition
3. Signal Characterisation
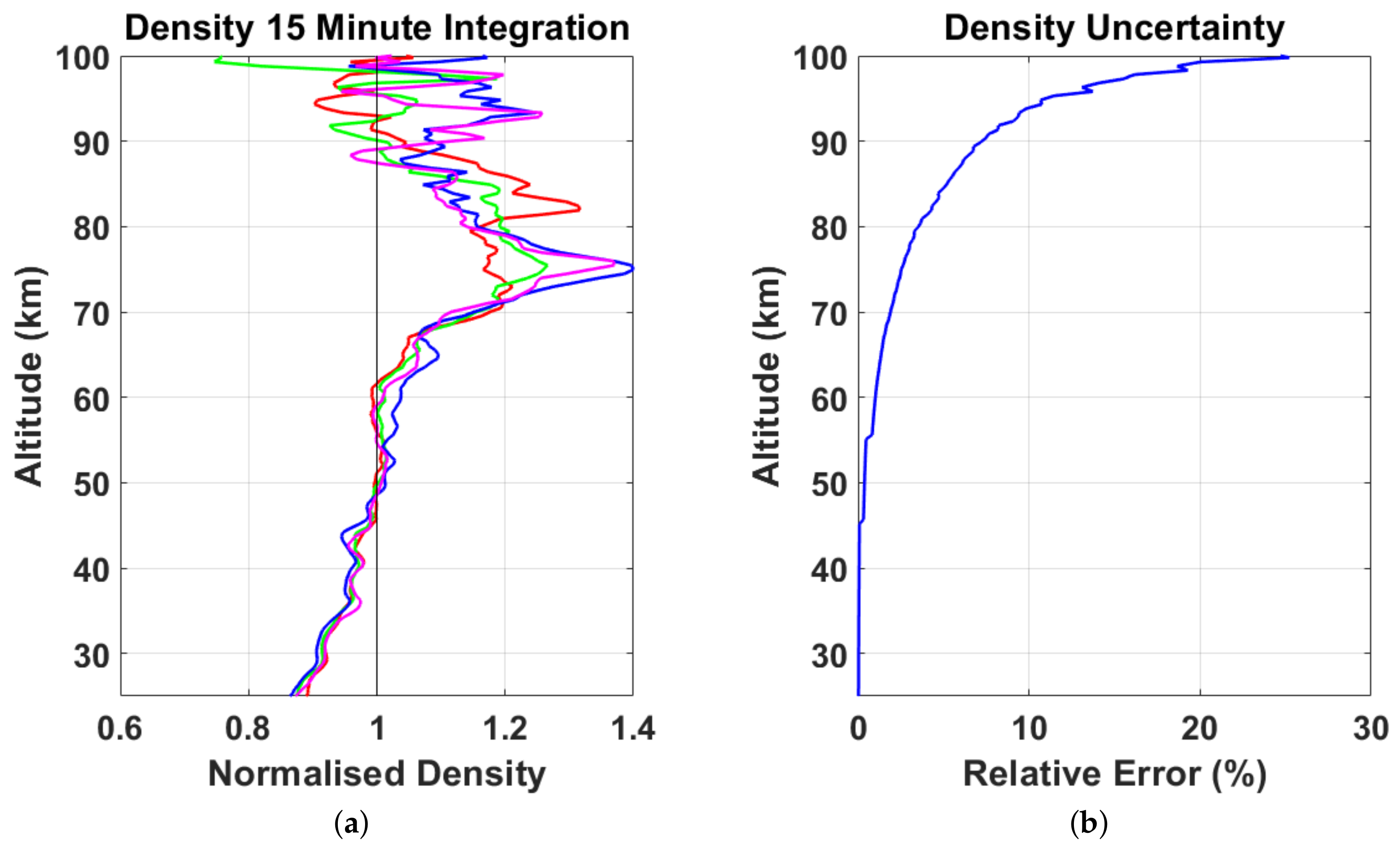
3.1. Density Characterisation
3.2. Temperature Characterisation
4. Gravity Wave Case Study
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bodilis, A. Le bâtiment d’essais et de mesures Monge. REE. Rev. De L’électricité Et De L’électronique 2001, 1, 84–89. [Google Scholar] [CrossRef]
- Lübken, F.J.; Baumgarten, G.; Hildebrand, J.; Schmidlin, F.J. Simultaneous and co-located wind measurements in the middle atmosphere by lidar and rocket-borne techniques. Atmos. Meas. Tech. 2016, 9, 3911–3919. [Google Scholar] [CrossRef] [Green Version]
- Schmidlin, F. Rocket techniques used to measure the neutral atmosphere. In International Council of Scientific Unions Handbook for MAP; (SEE N86-26725 17-46); SCOSTEP, Boston College: Chestnut Hill, MA, USA, 1986; Volume 19, 28p. [Google Scholar]
- Lübken, F.J.; Hillert, W.; Lehmacher, G.; Von Zahn, U.; Bittner, M.; Offermann, D.; Schmidlin, F.; Hauchecorne, A.; Mourier, M.; Czechowsky, P. Intercomparison of density and temperature profiles obtained by lidar, ionization gauges, falling spheres, datasondes and radiosondes during the DYANA campaign. J. Atmos. Terr. Phys. 1994, 56, 1969–1984. [Google Scholar] [CrossRef]
- Beig, G.; Keckhut, P.; Lowe, R.P.; Roble, R.G.; Mlynczak, M.G.; Scheer, J.; Fomichev, V.I.; Offermann, D.; French, W.J.R.; Shepherd, M.G.; et al. Review of mesospheric temperature trends. Rev. Geophys. 2003, 41. [Google Scholar] [CrossRef] [Green Version]
- Krueger, D.A.; She, C.Y.; Yuan, T. Retrieving mesopause temperature and line-of-sight wind from full-diurnal-cycle Na lidar observations. Appl. Opt. 2015, 54, 9469–9489. [Google Scholar] [CrossRef]
- Gelbwachs, J.A. Iron Boltzmann factor LIDAR: Proposed new remote-sensing technique for mesospheric temperature. Appl. Opt. 1994, 33, 7151–7156. [Google Scholar] [CrossRef]
- Von Zahn, U.; Höffner, J. Mesopause temperature profiling by potassium lidar. Geophys. Res. Lett. 1996, 23, 141–144. [Google Scholar] [CrossRef]
- Hauchecorne, A.; Chanin, M.L. Density and temperature profiles obtained by lidar between 35 and 70 km. Geophys. Res. Lett. 1980, 7, 565–568. [Google Scholar] [CrossRef]
- Keckhut, P.; Hauchecorne, A.; Chanin, M. A critical review of the database acquired for the long-term surveillance of the middle atmosphere by the French Rayleigh lidars. J. Atmos. Ocean. Technol. 1993, 10, 850–867. [Google Scholar] [CrossRef] [Green Version]
- Keckhut, P. Rayleigh temperature lidar applications: Tools and methods. J. Phys. (Proc.) 2006, 139, 337–360. [Google Scholar] [CrossRef]
- Hauchecorne, A.; Keckhut, P.; Chanin, M.L. Dynamics and transport in the middle atmosphere using remote sensing techniques from ground and space. In Infrasound Monitoring for Atmospheric Studies; Springer: Berlin/Heidelberg, Germany, 2010; pp. 665–683. [Google Scholar]
- Wing, R.; Hauchecorne, A.; Keckhut, P.; Godin-Beekmann, S.; Khaykin, S.; McCullough, E.M. Lidar temperature series in the middle atmosphere as a reference data set–Part 2: Assessment of temperature observations from MLS/Aura and SABER/TIMED satellites. Atmos. Meas. Tech. 2018, 11, 6703–6717. [Google Scholar] [CrossRef] [Green Version]
- Avdyushin, S.; Tulinov, G.; Ivanov, M.; Kuzmenko, B.; Mezhuev, I.; Nardi, B.; Hauchecorne, A.; Chanin, M.L. 1. Spatial and temporal evolution of the optical thickness of the Pinatubo aerosol cloud in the northern hemisphere from a network of ship-borne and stationary lidars. Geophys. Res. Lett. 1993, 20, 1963–1966. [Google Scholar] [CrossRef]
- Immler, F.; Schrems, O. Vertical profiles, optical and microphysical properties of Saharan dust layers determined by a ship-borne lidar. Atmos. Chem. Phys. 2003, 3, 1353–1364. [Google Scholar] [CrossRef] [Green Version]
- Picone, J.M.; Hedin, A.E.; Drob, D.P.; Aikin, A.C. NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues. J. Geophys. Res. Space Phys. 2002, 107. [Google Scholar] [CrossRef]
- Barton, D.L.; Wickwar, V.B.; Herron, J.P.; Sox, L.; Navarro, L.A. Variations in Mesospheric neutral densities from Rayleigh lidar observations at Utah State University. In EPJ Web of Conferences; EDP Sciences: Les Ulis, France, 2016; Volume 119, p. 13006. [Google Scholar]
- Argall, P. Upper altitude limit for Rayleigh lidar. Ann. Geophys. 2007, 25, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Donovan, D.P.; Whiteway, J.A.; Carswell, A.I. Correction for nonlinear photon-counting effects in lidar systems. Appl. Opt. 1993, 32, 6742–6753. [Google Scholar] [CrossRef]
- Khanna, J.; Bandoro, J.; Sica, R.J.; McElroy, C.T. New technique for retrieval of atmospheric temperature profiles from Rayleigh-scatter lidar measurements using nonlinear inversion. Appl. Opt. 2012, 51, 7945–7952. [Google Scholar] [CrossRef]
- Sica, R.; Haefele, A. Retrieval of temperature from a multiple-channel Rayleigh-scatter lidar using an optimal estimation method. Appl. Opt. 2015, 54, 1872–1889. [Google Scholar] [CrossRef]
- Jalali, A.; Sica, R.J.; Haefele, A. Improvements to a long-term Rayleigh-scatter lidar temperature climatology by using an optimal estimation method. Atmos. Meas. Tech. 2018, 11, 6043–6058. [Google Scholar] [CrossRef] [Green Version]
- Jalali, A.; Hicks-Jalali, S.; Sica, R.J.; Haefele, A.; Clarmann, T.v. A practical information-centered technique to remove a priori information from lidar optimal-estimation-method retrievals. Atmos. Meas. Tech. 2019, 12, 3943–3961. [Google Scholar] [CrossRef] [Green Version]
- Gallais, P. Atmospheric Re-Entry Vehicle Mechanics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Vincent, R.A.; Reid, I.M. HF Doppler Measurements of Mesospheric Gravity Wave Momentum Fluxes. J. Atmos. Sci. 1983, 40, 1321–1333. [Google Scholar] [CrossRef] [Green Version]
- Wilson, R.; Chanin, M.; Hauchecorne, A. Gravity waves in the middle atmosphere observed by Rayleigh lidar: 2. Climatology. J. Geophys. Res. Atmos. 1991, 96, 5169–5183. [Google Scholar] [CrossRef]
- Nakamura, T.; Tsuda, T.; Fukao, S.; Manson, A.; Meek, C.; Vincent, R.; Reid, I. Mesospheric gravity waves at Saskatoon (52 N), Kyoto (35 N), and Adelaide (35 S). J. Geophys. Res. Atmos. 1996, 101, 7005–7012. [Google Scholar] [CrossRef] [Green Version]
- Whiteway, J.; Duck, T.; Donovan, D.P.; Bird, J.; Pal, S.; Carswell, A. Measurements of gravity wave activity within and around the Arctic stratospheric vortex. Geophys. Res. Lett. 1997, 24, 1387–1390. [Google Scholar] [CrossRef] [Green Version]
- Pfenninger, M.; Liu, A.Z.; Papen, G.C.; Gardner, C.S. Gravity wave characteristics in the lower atmosphere at South Pole. J. Geophys. Res. Atmos. 1999, 104, 5963–5984. [Google Scholar] [CrossRef] [Green Version]
- Li, T.; Leblanc, T.; McDermid, I.S.; Wu, D.L.; Dou, X.; Wang, S. Seasonal and interannual variability of gravity wave activity revealed by long-term lidar observations over Mauna Loa Observatory, Hawaii. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Mzé, N.; Hauchecorne, A.; Keckhut, P.; Thétis, M. Vertical distribution of gravity wave potential energy from long-term Rayleigh lidar data at a northern middle-latitude site. J. Geophys. Res. Atmos. 2014, 119, 12–069. [Google Scholar] [CrossRef]
- Roberts, D.W.; Gimmestad, G.G.; Garrison, A.K.; Patterson, E.M.; Gimmestad, S.C.; Cathcart, J.M.; DuVarney, R.C.; Grams, G.W.; Servaites, J.M. Design and performance of a 100 inch lidar facility. Opt. Eng. 1991, 30, 79–88. [Google Scholar] [CrossRef]
- Keckhut, P.; Courcoux, Y.; Baray, J.L.; Porteneuve, J.; Vérèmes, H.; Hauchecorne, A.; Dionisi, D.; Posny, F.; Cammas, J.P.; Payen, G.; et al. Introduction to the Maïdo Lidar Calibration Campaign dedicated to the validation of upper air meteorological parameters. J. Appl. Remote Sens. 2015, 9, 094099. [Google Scholar] [CrossRef] [Green Version]
- Sica, R.J.; Sargoytchev, S.; Argall, P.S.; Borra, E.F.; Girard, L.; Sparrow, C.T.; Flatt, S. Lidar measurements taken with a large-aperture liquid mirror. 1. Rayleigh-scatter system. Appl. Opt. 1995, 34, 6925–6936. [Google Scholar] [CrossRef]
- Von Zahn, U.; Von Cossart, G.; Fiedler, J.; Fricke, K.; Nelke, G.; Baumgarten, G.; Rees, D.; Hauchecorne, A.; Adolfsen, K. The ALOMAR Rayleigh/Mie/Raman lidar: Objectives, configuration, and performance. In Annales Geophysicae; Springer: Berlin/Heidelberg, Germany, 2000; Volume 18, pp. 815–833. [Google Scholar]
- Sox, L.; Wickwar, V.B.; Yuan, T.; Criddle, N.R. Simultaneous Rayleigh-Scatter and Sodium Resonance Lidar Temperature Comparisons in the Mesosphere-Lower Thermosphere. J. Geophys. Res. Atmos. 2018, 123, 10–688. [Google Scholar] [CrossRef]








| 1992–2005 | 2005–2019 | |
|---|---|---|
| laser energy (mJ/pulse) | 800 | 4000–5000 @ 30 Hz |
| laser repetition rate (Hz) | 30 | 30, 60, 90, 180 |
| polarisation cubes | 0 | 3 |
| telescope area (m) | 1.57 | 1.57 |
| emission divergence (rad) | 50 | 33 |
| field of view (mrad) | 0.3 | 0.2 |
| telescope parallax (cm) | 67–95 | 67–95 |
| photomultipliers | R928 (water cooling) | R928/R9880U-20-TEC |
| Filter FWHM (nm) | 1 | 0.3 |
| Transient Recorder | SESO | Licel PR 20-160-P/PR10-160P |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wing, R.; Martic, M.; Hauchecorne, A.; Porteneuve, J.; Keckhut, P.; Courcoux, Y.; Yung, L.; Retailleau, P.; Cocuron, D. Atmospheric Density and Temperature Vertical Profile Retrieval for Flight-Tests with a Rayleigh Lidar On-Board the French Advanced Test Range Ship Monge. Atmosphere 2020, 11, 75. https://doi.org/10.3390/atmos11010075
Wing R, Martic M, Hauchecorne A, Porteneuve J, Keckhut P, Courcoux Y, Yung L, Retailleau P, Cocuron D. Atmospheric Density and Temperature Vertical Profile Retrieval for Flight-Tests with a Rayleigh Lidar On-Board the French Advanced Test Range Ship Monge. Atmosphere. 2020; 11(1):75. https://doi.org/10.3390/atmos11010075
Chicago/Turabian StyleWing, Robin, Milena Martic, Alain Hauchecorne, Jacques Porteneuve, Philippe Keckhut, Yann Courcoux, Laurent Yung, Patrick Retailleau, and Dorothee Cocuron. 2020. "Atmospheric Density and Temperature Vertical Profile Retrieval for Flight-Tests with a Rayleigh Lidar On-Board the French Advanced Test Range Ship Monge" Atmosphere 11, no. 1: 75. https://doi.org/10.3390/atmos11010075
APA StyleWing, R., Martic, M., Hauchecorne, A., Porteneuve, J., Keckhut, P., Courcoux, Y., Yung, L., Retailleau, P., & Cocuron, D. (2020). Atmospheric Density and Temperature Vertical Profile Retrieval for Flight-Tests with a Rayleigh Lidar On-Board the French Advanced Test Range Ship Monge. Atmosphere, 11(1), 75. https://doi.org/10.3390/atmos11010075






