A Fuzzy-Logic-Based Covariance Localization Method in Data Assimilation
Abstract
:1. Introduction
2. Assimilation Background
2.1. Ensemble Kalman Filter
2.2. Traditional Covariance Localization (CL)
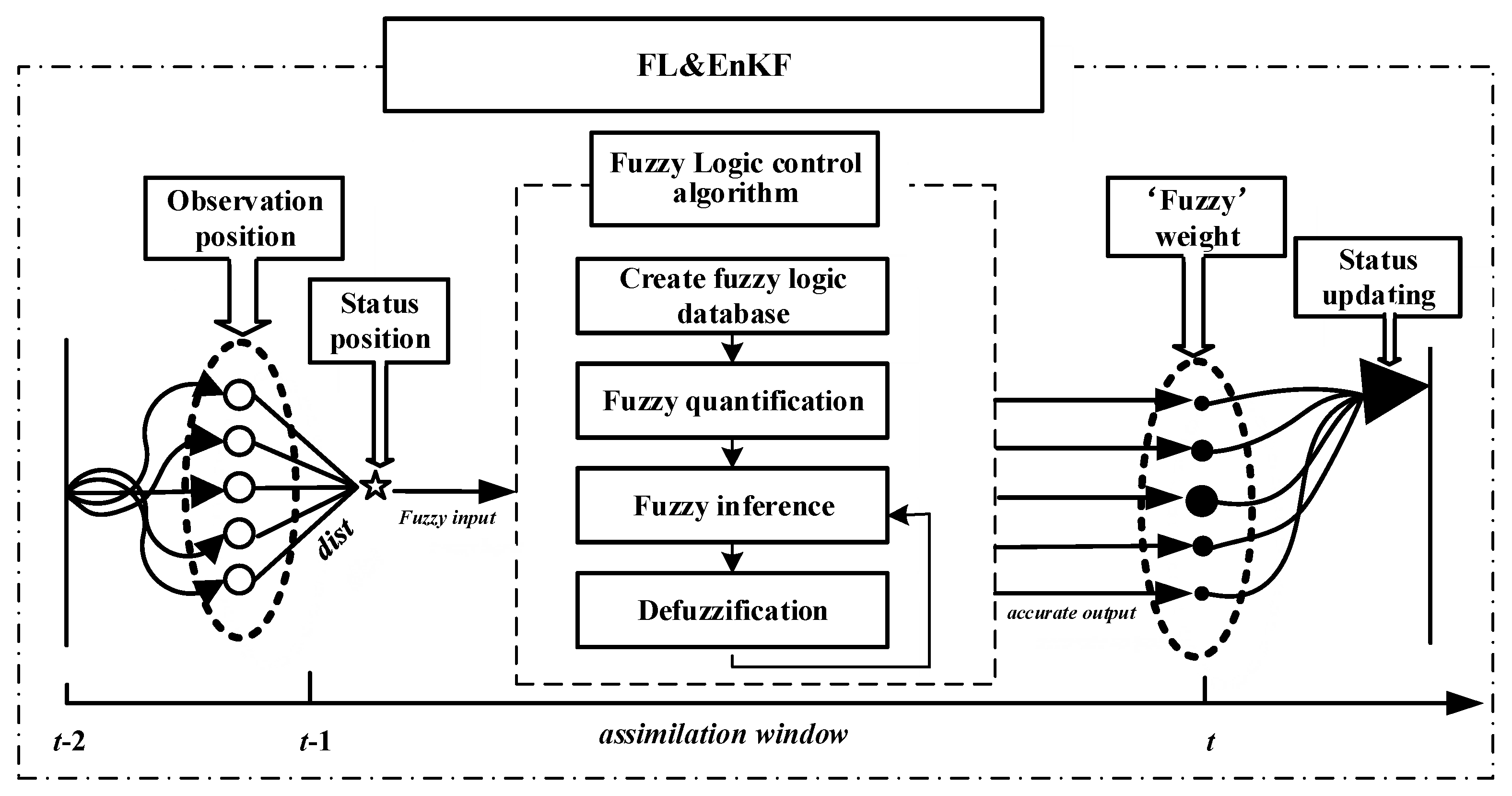
2.3. New Improved Covariance Localization Method: The CF Method
| Algorithm 1: A cycle of the EnKF assimilation method with localization algorithm |
| Require: is the assimilation step; initial background field matrix: , , , A, R; allocate space for observation data: y, HE, pos. m is the ensemble size. n is the state dimension. A is the ensemble anomalies. s is the scaled innovation vector. S is the scaled ensemble observation anomalies. dx is the ensemble mean correction. 1: for step = 1,… do 2: E = rk4step (@L40, dt, x, F) 3: 4: 5: 6: 7: 8: Localization: Algorithm 2 9: 10: 11: , and , 12: 13: 14: 15: 16: 17: 18: end for |
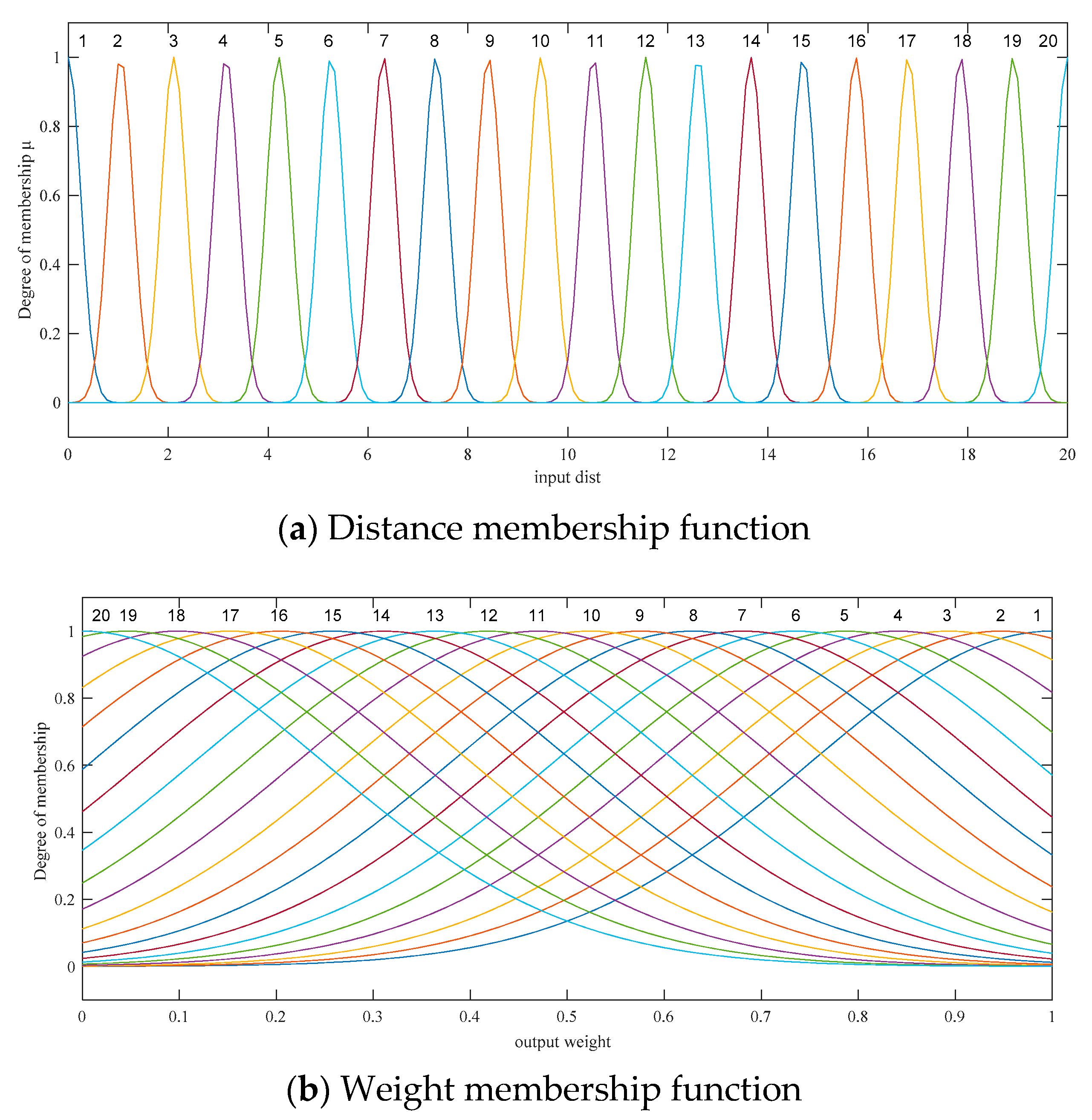
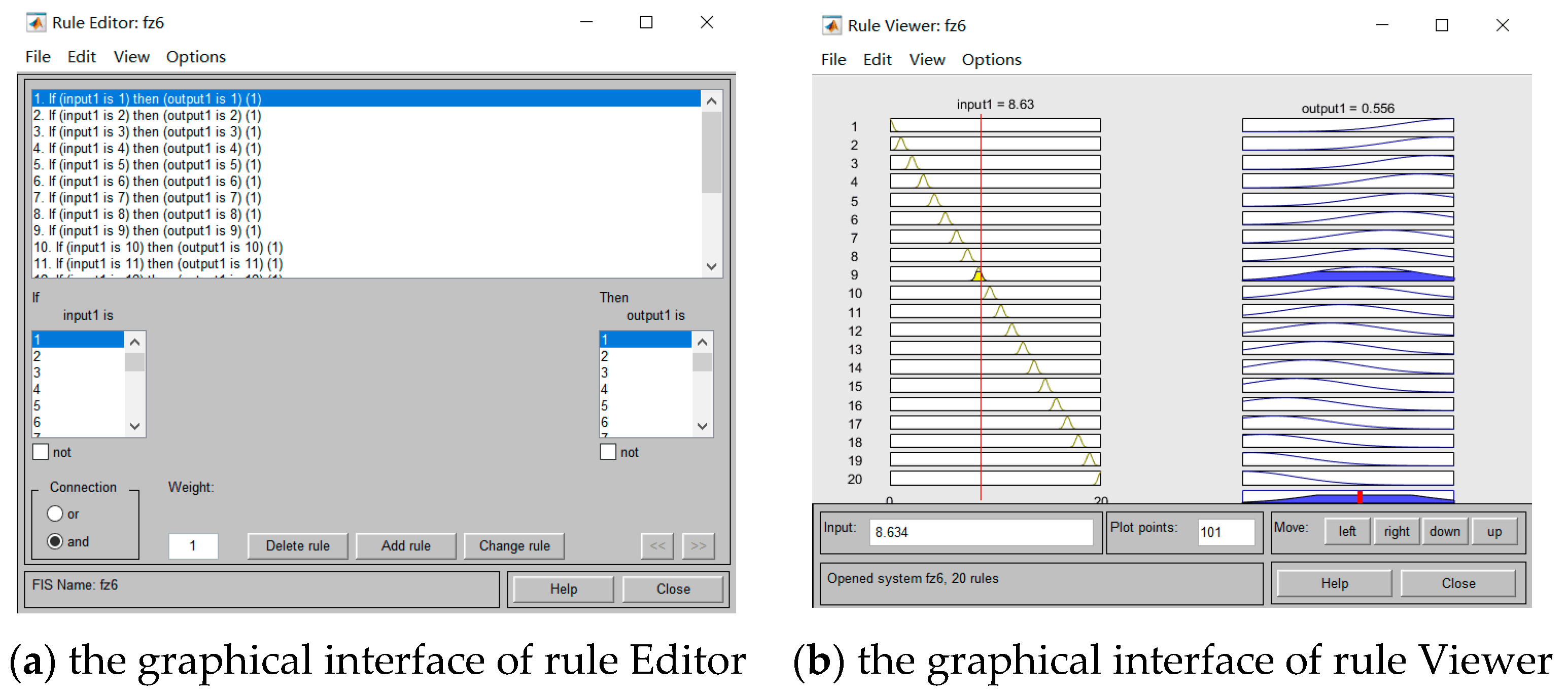
| Algorithm 2: Get localization coefficients coupled with fuzzy logic control algorithm |
| Require:d is the Euclidean distance between the observation point and the state update point. is the weight coefficient. and represent the center and width of the Gaussian membership function, respectively. is the position of the observation points. is the position of the state update points. nx is the model dimension. is the localization radius. is the scale range, . L is the fuzzy correlation coefficient matrix. is the so-called localization correlation matrix. denotes the elementwise product of matrices. /* abs is the absolute value function; hypot is the square root of sum of squares (hypotenuse). Gfuzzy refers to the local functions with fuzzy logic control; Gauss refers to the traditional Gaussian localization function; Gaspari_Cohn refers to the traditional Gaspari–Cohn (GC) localization function.*/ 1: if then 2: Lorenz 96: 3: else 4: QG model: 5: end if 6: switch tag 7: Case ‘Gfuzzy’ 8: 9: 10: 11: Case ‘Gauss’ 12: 13: Case ‘Gaspari_Cohn’ 14: if then 15: 16: else & 17: 18: … 19: end switch 20: 21: 22: 23: |
- (1)
- Create a fuzzy logic database
- (2)
- Fuzzy quantification
- (3)
- Define the membership function
- (4)
- Establish fuzzy control rules
- (5)
- Fuzzy inference and defuzzification
- (6)
- Model state updating
3. Configuration of Numerical Experiments
3.1. Experimental Model
- The Lorenz-96 model
- b
- The quasi-geostrophic (QG) model
3.2. Performance Index
- (1)
- The state variables and are generally obtained from the numerical solutions of differential equations. The RMSE of the analysis of the ensemble mean, at the specific time k, is defined as follows:where the symbol “” represents the norm of a vector, and and are the analysis and truth average values of the state variable, respectively. Normally, a better assimilation effect results in a smaller corresponding RMSE.
- (2)
- The power spectral density (PSD) is a probabilistic statistical value, the physical significance of which lies in the measure of the mean square value of random variables. Specifically, the area under the relation curve of the PSD–frequency value represents the variance, whereby a smaller area denotes better performance of the assimilation algorithm.
- (i)
- Given the forecast ensemble , the ensemble mean and the forecast ensemble anomalies are calculated; then, the forecast covariance matrix is calculated using Equation (6).
- (ii)
- The analysis ensemble is calculated using the Kalman analysis (see Equation (3)). Then, the analysis covariance matrix is calculated using Equation (5).
- (iii)
- The anomalies in the analysis ensemble and the Kalman gain are calculated.
- (iv)
- The eigenvalue of the PSD is calculated using the fast Fourier transform of the anomalies matrix for all ensembles , the analyzed anomalies , and the forecast anomalies .
3.3. Experimental Design and Preliminary Results
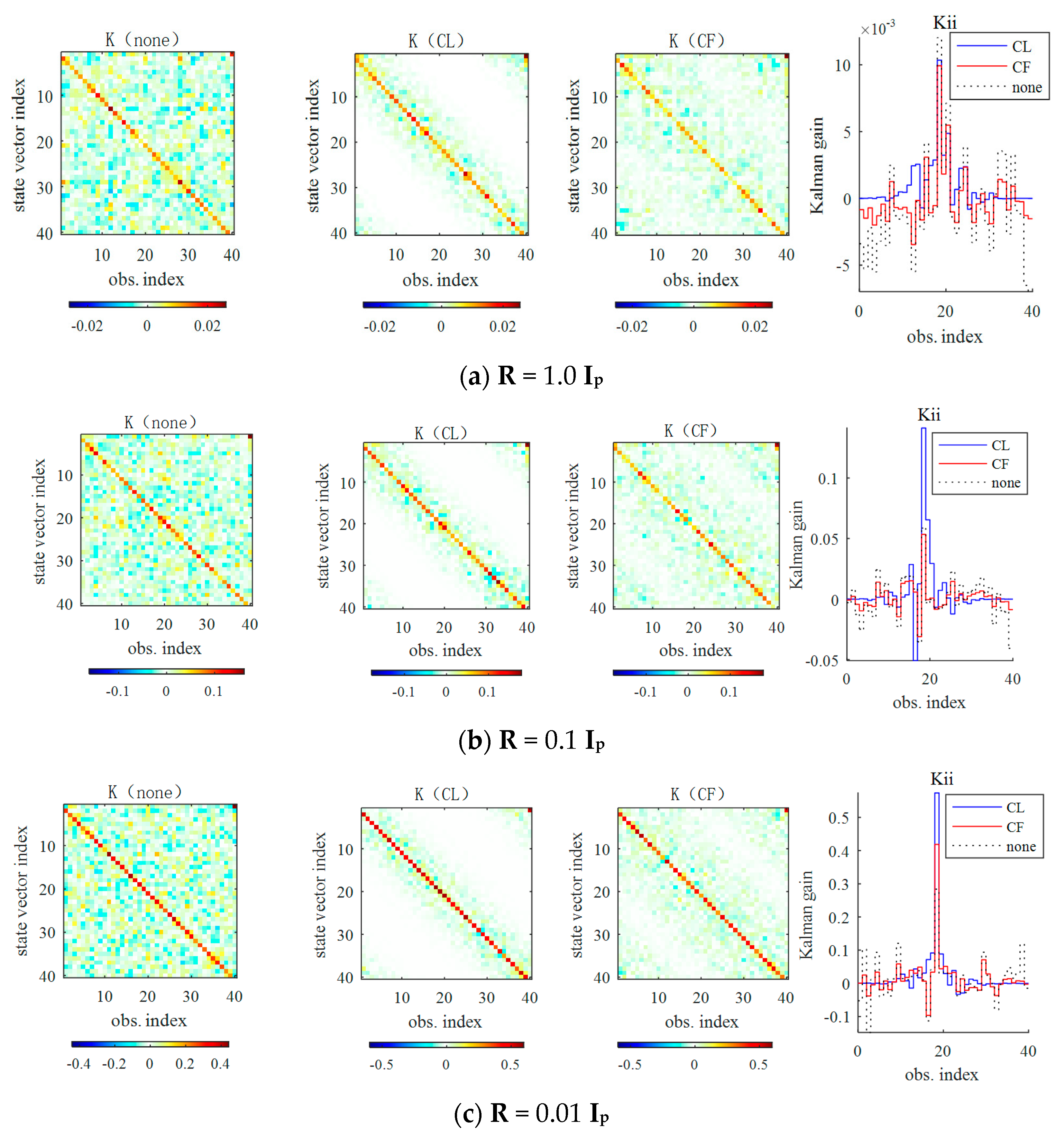
3.3.1. Influences of CL and CF on the Kalman Gain Matrix
3.3.2. Comparison of the Influence on the Two Localization Methods with Different Model Errors
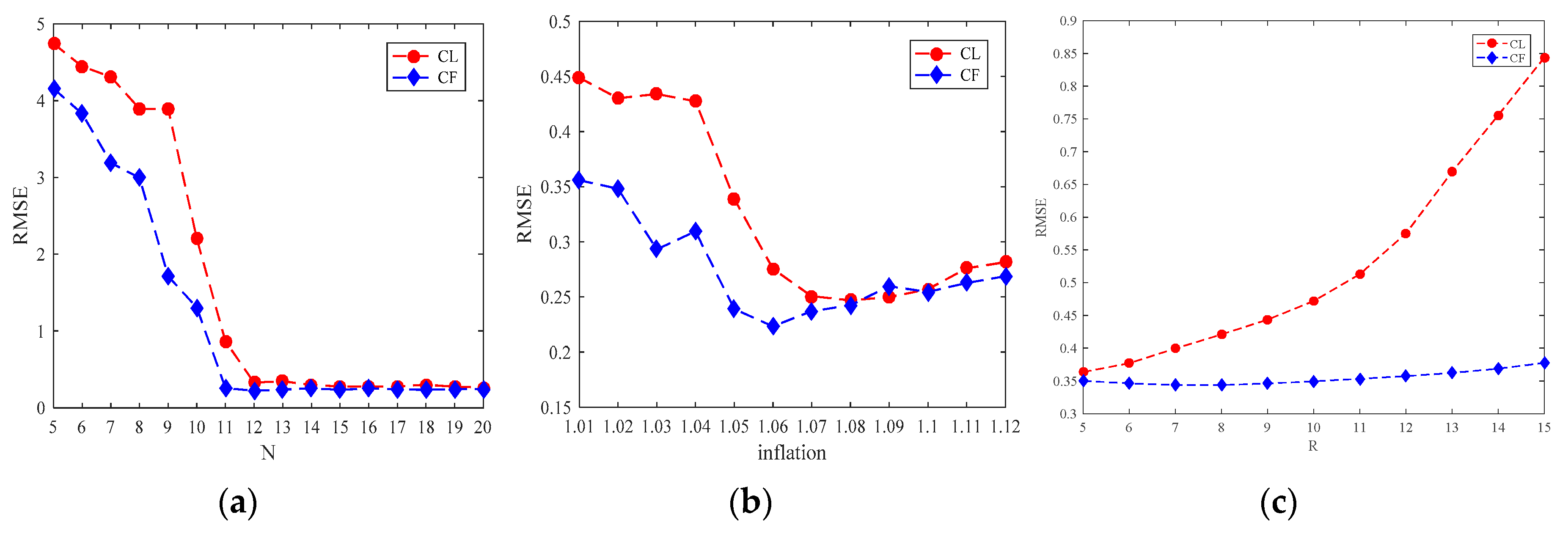
4. Localization Behavior Using the Lorenz-96 Model
4.1. Change in Ensemble Numbers
4.2. Change in Covariance Inflation Factors
4.3. Change in Localization Radius
4.4. Performance Index PSD
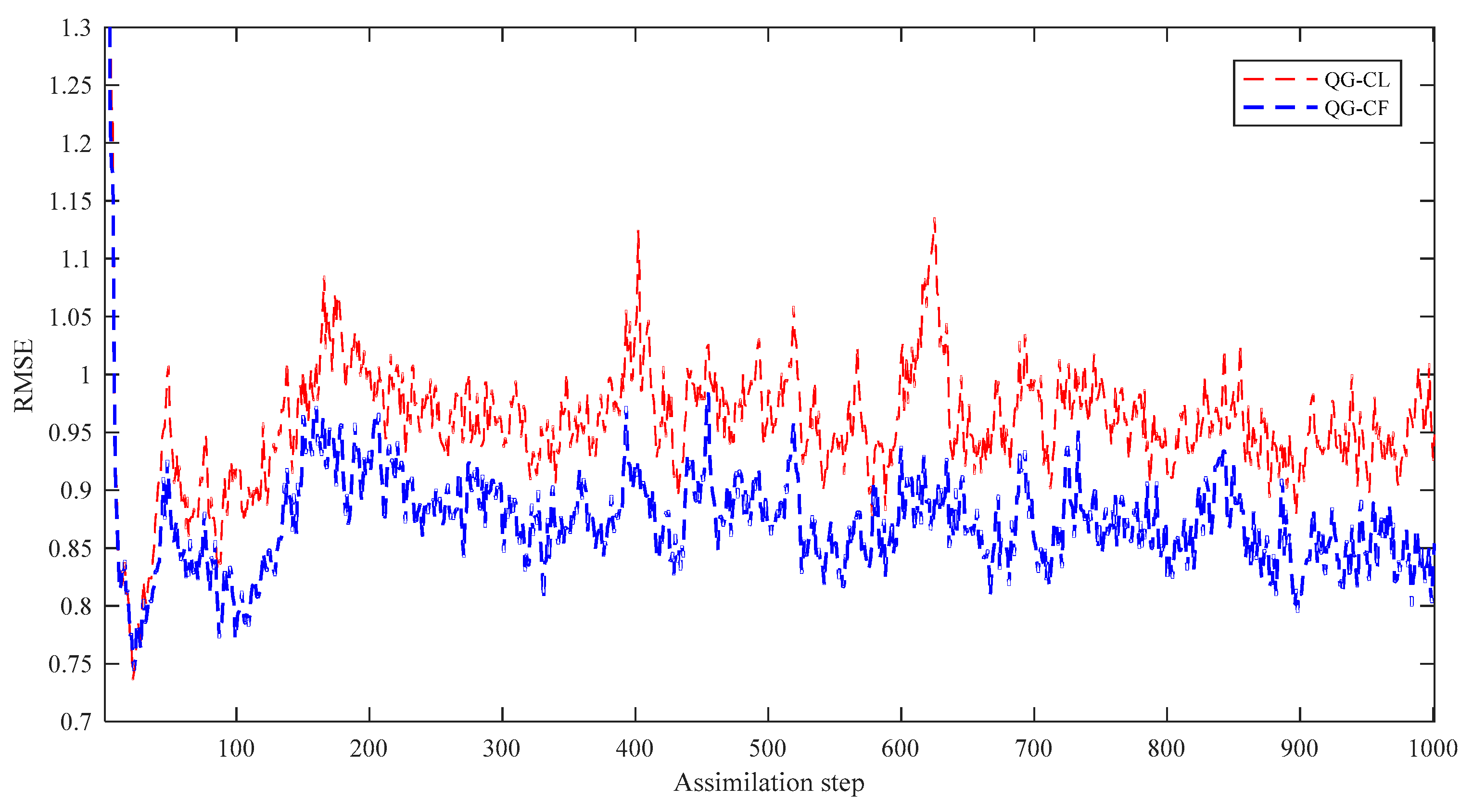
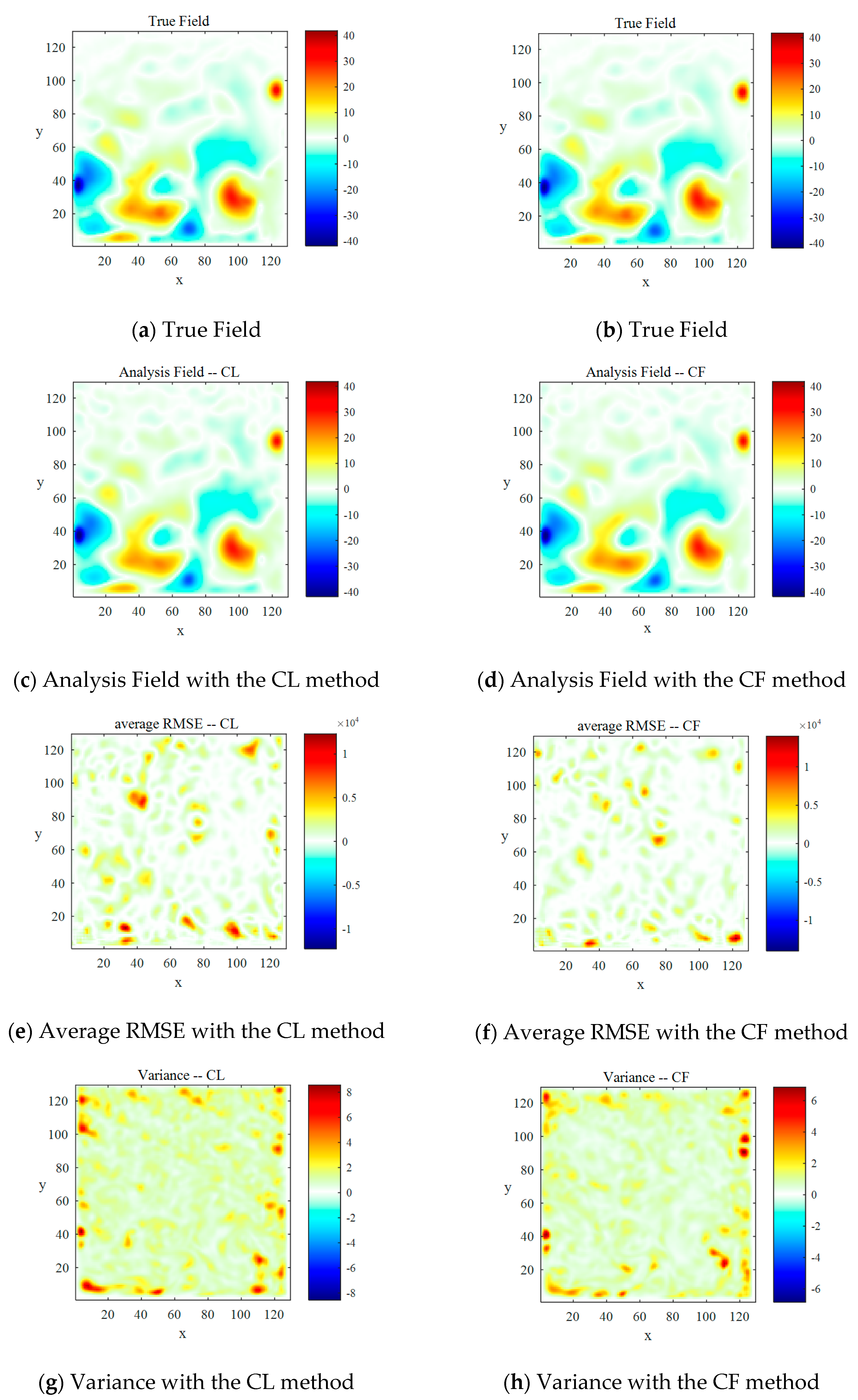
5. Localization Behavior Using the Quasi-Geostrophic (QG) Model
5.1. Comparison of Assimilation Performance of Two Localization Methods
5.2. Comparison of Spatial Distribution Characteristics between Two Localization Methods
6. Conclusions
- Effectiveness of the new algorithm
- b.
- Sensitivity and robustness of the new algorithm in experimental settings
- c.
- Applicability in real weather models
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Epstein, E.S. Stochastic dynamic prediction. Tellus Ser. A 1969, 21, 739–759. [Google Scholar] [CrossRef]
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. Geophys. Res. 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Miyoshi, T.; Kondo, K. A multi-scale localization approach to an ensemble Kalman filter. SOLA 2013, 9, 170–173. [Google Scholar] [CrossRef] [Green Version]
- Roh, S.; Genton, M.G.; Jun, M.; Szunyogh, I.; Hoteit, I. Observation quality control with a robust ensemble Kalman filter. Mon. Weather Rev. 2013, 141, 4414–4428. [Google Scholar] [CrossRef] [Green Version]
- Nerger, L. On serial observation processing in localized ensemble Kalman filters. Mon. Weather Rev. 2015, 143, 1554–1567. [Google Scholar] [CrossRef] [Green Version]
- Hamill, T.M.; Anderson, J.L.; Snyder, C. Comments on Sigma-point Kalman filter data assimilation methods for strongly nonlinear systems. J. Atmos. Sci. 2009, 66, 3498–3500. [Google Scholar] [CrossRef]
- Anderson, J.L. Localization and sampling error correction in ensemble Kalman filter data assimilation. Mon. Weather Rev. 2012, 140, 2359–2371. [Google Scholar] [CrossRef] [Green Version]
- Houtekamer, P.; Zhang, F. Review of the ensemble Kalman filter for atmospheric data assimilation. Mon. Weather Rev. 2016, 144, 4489–4532. [Google Scholar] [CrossRef]
- Yue, M. A multiscale alignment method for ensemble filtering with displacement errors. Mon. Weather Rev. 2019, 146, 543–560. [Google Scholar]
- Houtekamer, P.L.; Mitchell, H.L.; Pellerin, G.; Buehner, M.; Charron, M.; Spacek, L.; Hansen, B. Atmospheric data assimilation with an ensemble Kalman filter: Results with real observations. Mon. Weather Rev. 2005, 133, 604–620. [Google Scholar] [CrossRef] [Green Version]
- Anderson, J.L. Exploring the need for localization in ensemble data assimilation using a hierarchical ensemble filter. Phys. D Nonlinear Phenom. 2007, 230, 99–111. [Google Scholar] [CrossRef]
- Hamill, T.M.; Whitaker, J.S.; Snyder, C. Distance-dependent filtering of background error covariance estimates in an ensemble Kalman filter. Mon. Weather Rev. 2001, 129, 2776–2790. [Google Scholar] [CrossRef] [Green Version]
- Hamill, T.M.; Snyder, C. A hybrid ensemble Kalman filter/3D-variational analysis scheme. Mon. Weather Rev. 2000, 128, 2905–2919. [Google Scholar] [CrossRef]
- Luo, X.; Bhakta, T.; Nævdal, G. Correlation-based adaptive Localization for ensemble based history matching methods. SPE J. 2019, 23, 396–427. [Google Scholar] [CrossRef]
- Houtekamer, P.L.; Mitchell, H.L. A sequential ensemble Kalman filter for atmospheric data assimilation. Mon. Weather Rev. 2001, 129, 123–137. [Google Scholar] [CrossRef]
- Zhang, Y.; Oliver, D.S. Improving the ensemble estimate of the Kalman gain by bootstrap sampling. Math. Geosci. 2010, 42, 327–345. [Google Scholar] [CrossRef]
- Sakov, P.; Bertino, L. Relation between two common localisation methods for the EnKF. Comput. Geosci. 2011, 15, 225–237. [Google Scholar] [CrossRef]
- Gaspari, G.; Cohn, S.E. Construction of correlation functions in two and three dimensions. Q. J. R. Meteor. Soc. 1999, 125, 723–757. [Google Scholar] [CrossRef]
- Fertig, E.J.; Hunt, B.R.; Ott, E.; Szunyogh, I. Assimilating non-local observations with a local ensemble Kalman filter. Tellus A 2007, 59, 719–730. [Google Scholar] [CrossRef]
- Ott, E.; Hunt, B.; Szunyogh, I.; Zimin, A.; Kostelich, E.; Corazza, M.; Kalnay, E.; Patiland, D.; Yorke, J. A local ensemble Kalman filter for atmospheric data assimilation. Tellus A 2004, 56, 415–428. [Google Scholar] [CrossRef]
- Hunt, B.R.; Kostelich, E.J.; Szunyogh, I. Efficient data assimilation for spatiotemporal chaos: A local ensemble transform Kalman filter. Phys. D 2007, 230, 112–126. [Google Scholar] [CrossRef] [Green Version]
- Bishop, C.H.; Hodyss, D. Flow-adaptive moderation of spurious ensemble correlations and its use in ensemble-based data assimilation. Q. J. R. Meteor. Soc. 2007, 133, 2029–2044. [Google Scholar] [CrossRef]
- Chen, Y.; Oliver, D.S. Levenberg-Marquardt forms of the iterative ensemble smoother for efficient history matching and uncertainty quantification. Comput. Geosci. 2013, 17, 689–703. [Google Scholar] [CrossRef]
- De La Chevrotière, M.; Harlim, J. A data-driven method for improving the correlation estimation in serial ensemble Kalman filters. Mon. Weather Rev. 2017, 145, 985–1001. [Google Scholar] [CrossRef] [Green Version]
- Bocquet, M. Localization and the iterative ensemble Kalman smoother. Q. J. R. Meteor. Soc. 2016, 142, 1075–1089. [Google Scholar] [CrossRef]
- Bai, Y.; Lu, Y.; Guo, P.; Ma, Y.; Ma, B. Observation error handling methods for data assimilation Coupled with fuzzy control algorithms. In Fuzzy Systems and Data Mining III; IOS Press: Amsterdam, The Netherlands, 2017; Volume 10, pp. 152–159. [Google Scholar] [CrossRef]
- Sakov, P.; Evensen, G.; Bertino, L. Asynchronous data assimilation with the EnKF. Tellus A 2010, 62, 24–29. [Google Scholar] [CrossRef] [Green Version]
- Zadeh, L.A. A Theory of Approximate Reasoning; Halstead Press: New York, NY, USA, 1979; pp. 149–194. [Google Scholar]
- Zadeh, L.A. Is there a need for fuzzy logic? Inf. Sci. 2008, 178, 2751–2779. [Google Scholar] [CrossRef]
- Flowerdew, J. Towards a theory of optimal localisation. Tellus A 2015, 67, 252–257. [Google Scholar] [CrossRef]
- Perianez, A.; Reich, H.; Potthast, R. Optimal Localization for Ensemble Kalman Filter systems. J. Meteorol. Soc. Jpn. 2014, 92, 585–597. [Google Scholar] [CrossRef] [Green Version]
- Lorenc, A.C. Analysis methods for numerical weather prediction. Q. J. R. Meteor. Soc. 1986, 112, 1177–1194. [Google Scholar] [CrossRef]
- Ide, K.; Courtier, P.; Ghil, M.; Lorenc, A.C. Unified notation for data assimilation: Operational, sequential, and variational. J. Meteor. Soc. Jpn. 1997, 75, 181–189. [Google Scholar] [CrossRef] [Green Version]
- Burgers, G.; Peter, J.V.L.; Evensen, G. Analysis scheme in the ensemble Kalman filter. Mon. Weather Rev. 1998, 126, 1719–1724. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy logic and approximate reasoning. Syntheses 1975, 30, 407–428. [Google Scholar] [CrossRef]
- Passino, K.M.; Yurkovich, S. The Control Handbook. Fuzzy Control; CRC Press: Boca Raton, FL, USA, 1996; pp. 1001–1017. [Google Scholar]
- Siddique, N. Computational Intelligence: Synergies of Fuzzy Logic, Neural Networks and Evolutionary Computing; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Lorenz, E.N.; Emanuel, K.A. Optimal sites for supplementary weather observations: Simulation with a small model. Atmos. Sci. 1998, 55, 399–414. [Google Scholar] [CrossRef]
- Jelloul, M.B.; Huck, T. Basin-mode interactions and selection by the mean flow in a reduced-gravity quasigeostrophic model. J. Phys. Oceanogr. 2003, 33, 2320–2332. [Google Scholar] [CrossRef]
- Sakov, P.; Oke, P.R. A deterministic formulation of the ensemble Kalman filter: An alternative to ensemble square root filter. Tellus A 2008, 60, 361–371. [Google Scholar] [CrossRef] [Green Version]
- Tian, X.; Xie, Z.; Sun, Q. A POD-based ensemble four-dimensional variational assimilation method. Tellus A 2011, 63, 805–816. [Google Scholar] [CrossRef]
- Tian, X.; Zhang, H.; Feng, X.; Xie, Y. Nonlinear Least Squares En4DVar to 4DEnVar Methods for Data Assimilation: Formulation, Analysis, and Preliminary Evaluation. Mon. Weather Rev. 2018, 146, 77–93. [Google Scholar] [CrossRef]
- Bai, Y.; Li, X. Evolutionary Algorithm-Based Error Parameterization Methods for Data Assimilation. Mon. Weather Rev. 2011, 139, 2668–2685. [Google Scholar] [CrossRef] [Green Version]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Kalnay, E.; Li, H.; Miyoshi, T.; Yang, S.C.; Ballabera-Poy, J. 4DVar or ensemble Kalman filter? Tellus A 2007, 59, 758–773. [Google Scholar] [CrossRef] [Green Version]
- Miyoshi, T.; Yamane, S.; Enomoto, T. Localizing the Error Covariance by Physical Distances within a Local Ensemble Transform Kalman Filter (LETKF). SOLA 2007, 3, 89–92. [Google Scholar] [CrossRef] [Green Version]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Y.; Ma, X.; Ding, L. A Fuzzy-Logic-Based Covariance Localization Method in Data Assimilation. Atmosphere 2020, 11, 1055. https://doi.org/10.3390/atmos11101055
Bai Y, Ma X, Ding L. A Fuzzy-Logic-Based Covariance Localization Method in Data Assimilation. Atmosphere. 2020; 11(10):1055. https://doi.org/10.3390/atmos11101055
Chicago/Turabian StyleBai, Yulong, Xiaoyan Ma, and Lin Ding. 2020. "A Fuzzy-Logic-Based Covariance Localization Method in Data Assimilation" Atmosphere 11, no. 10: 1055. https://doi.org/10.3390/atmos11101055
APA StyleBai, Y., Ma, X., & Ding, L. (2020). A Fuzzy-Logic-Based Covariance Localization Method in Data Assimilation. Atmosphere, 11(10), 1055. https://doi.org/10.3390/atmos11101055




