A Review and Evaluation of Planetary Boundary Layer Parameterizations in Hurricane Weather Research and Forecasting Model Using Idealized Simulations and Observations
Abstract
:1. Introduction
2. Review of PBL Schemes in the Operational HWRF
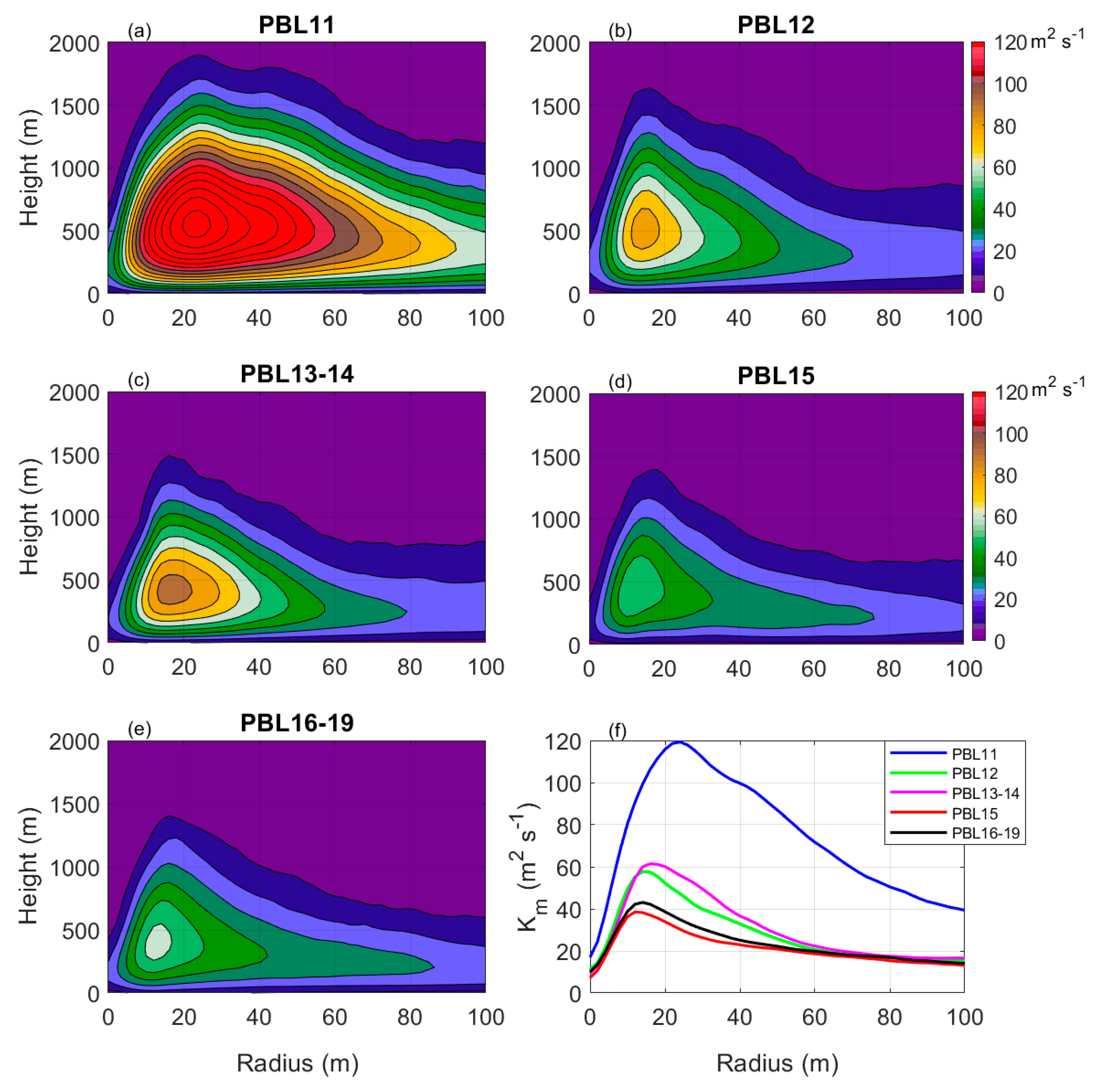
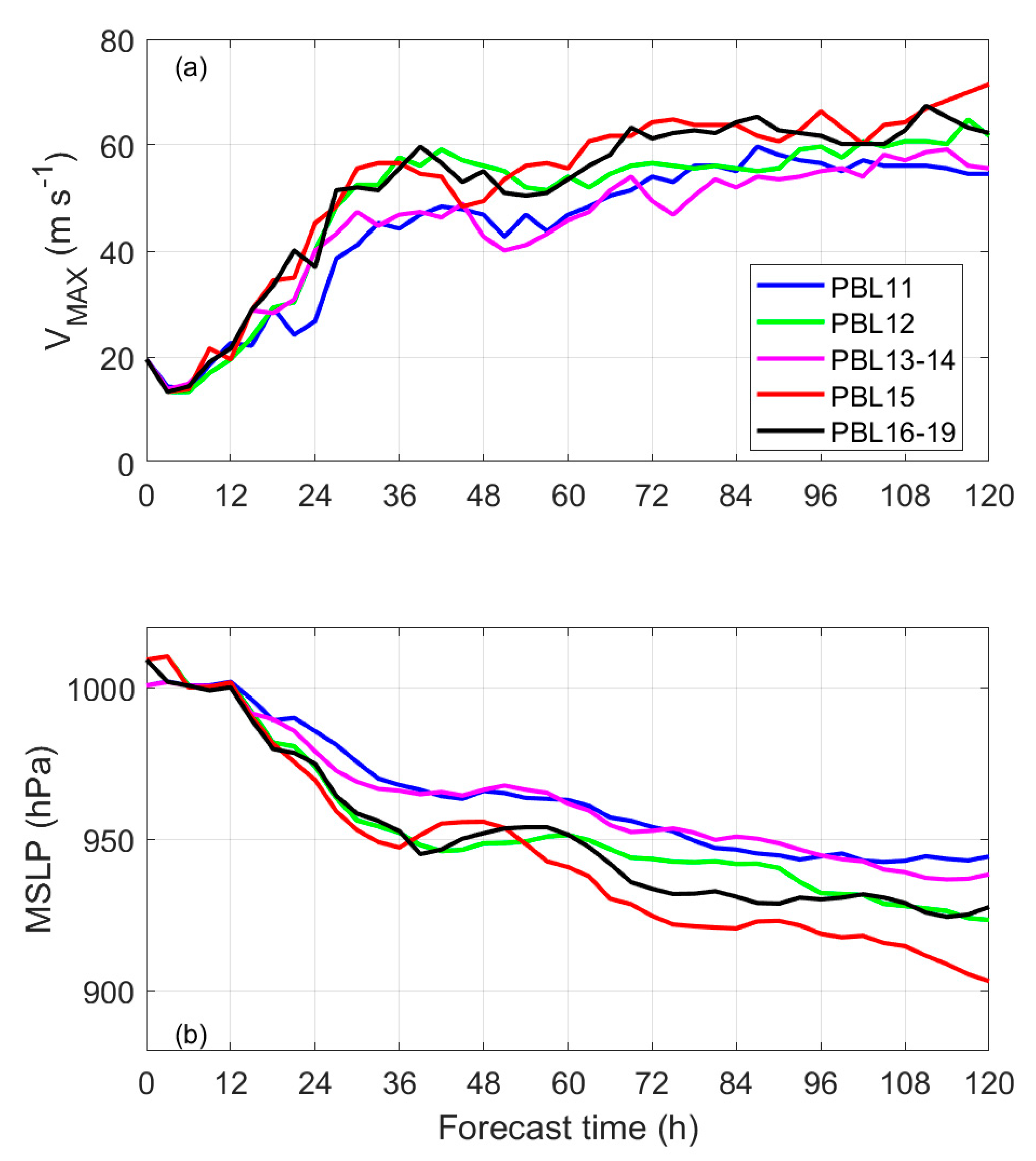
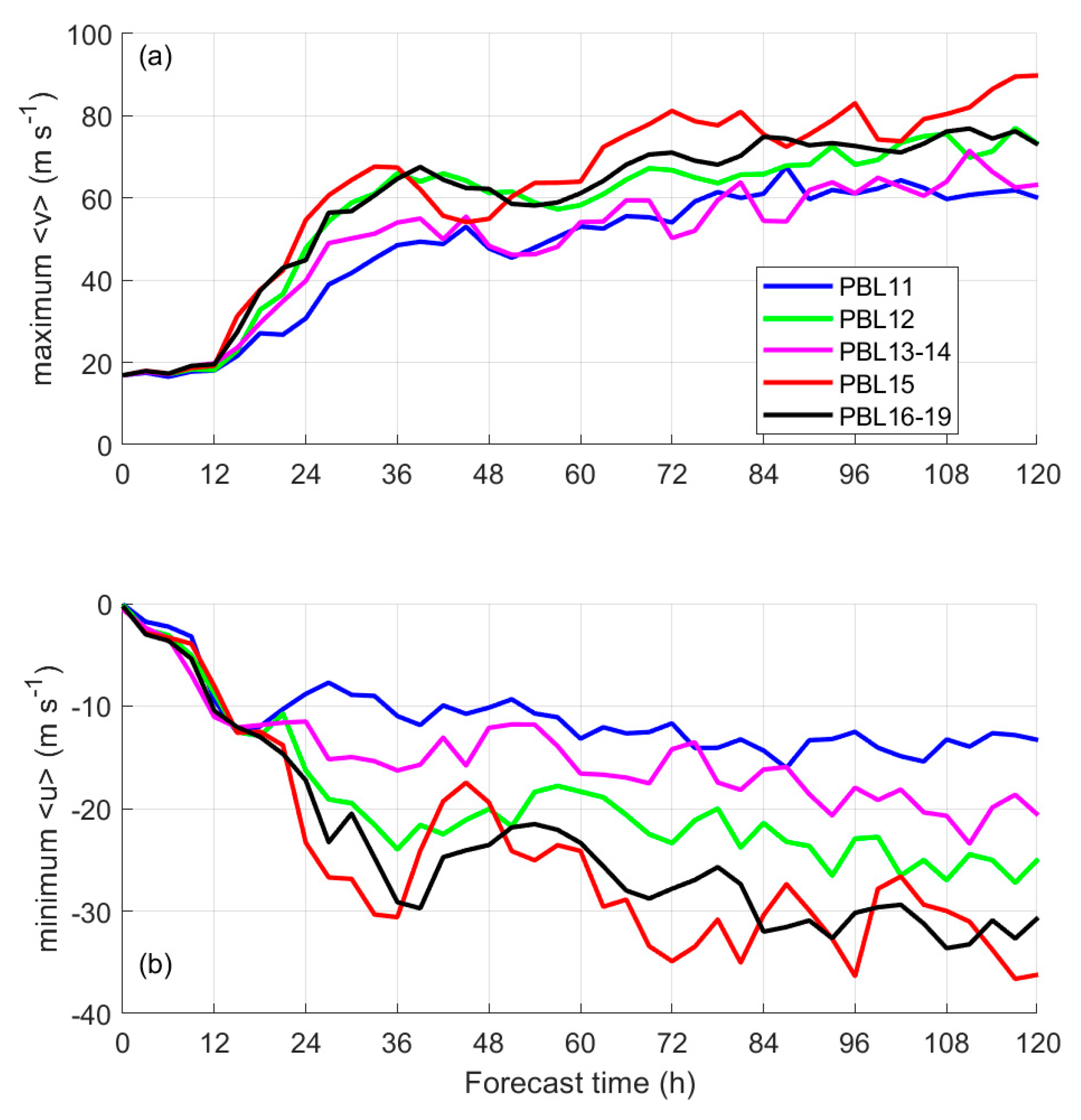
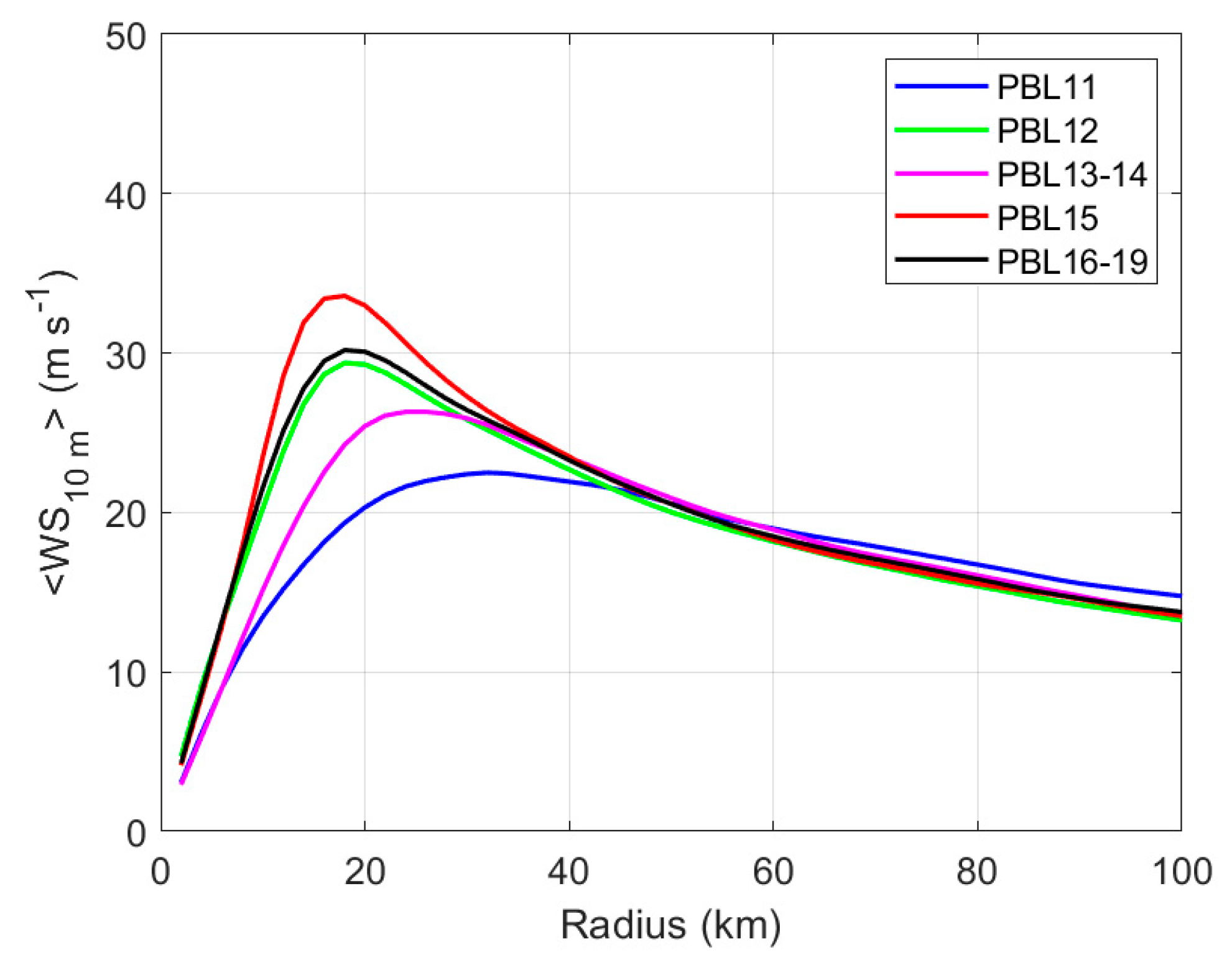
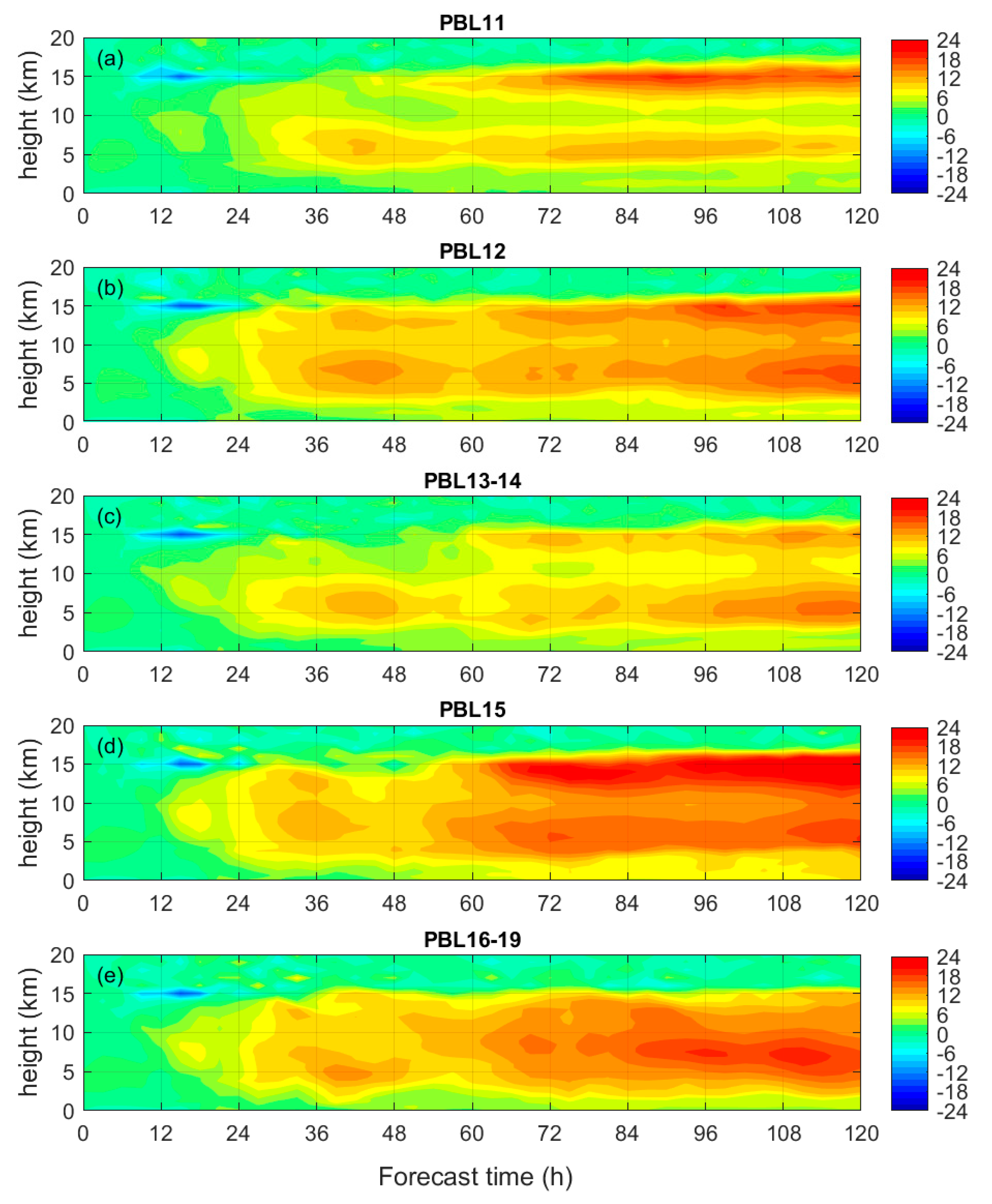
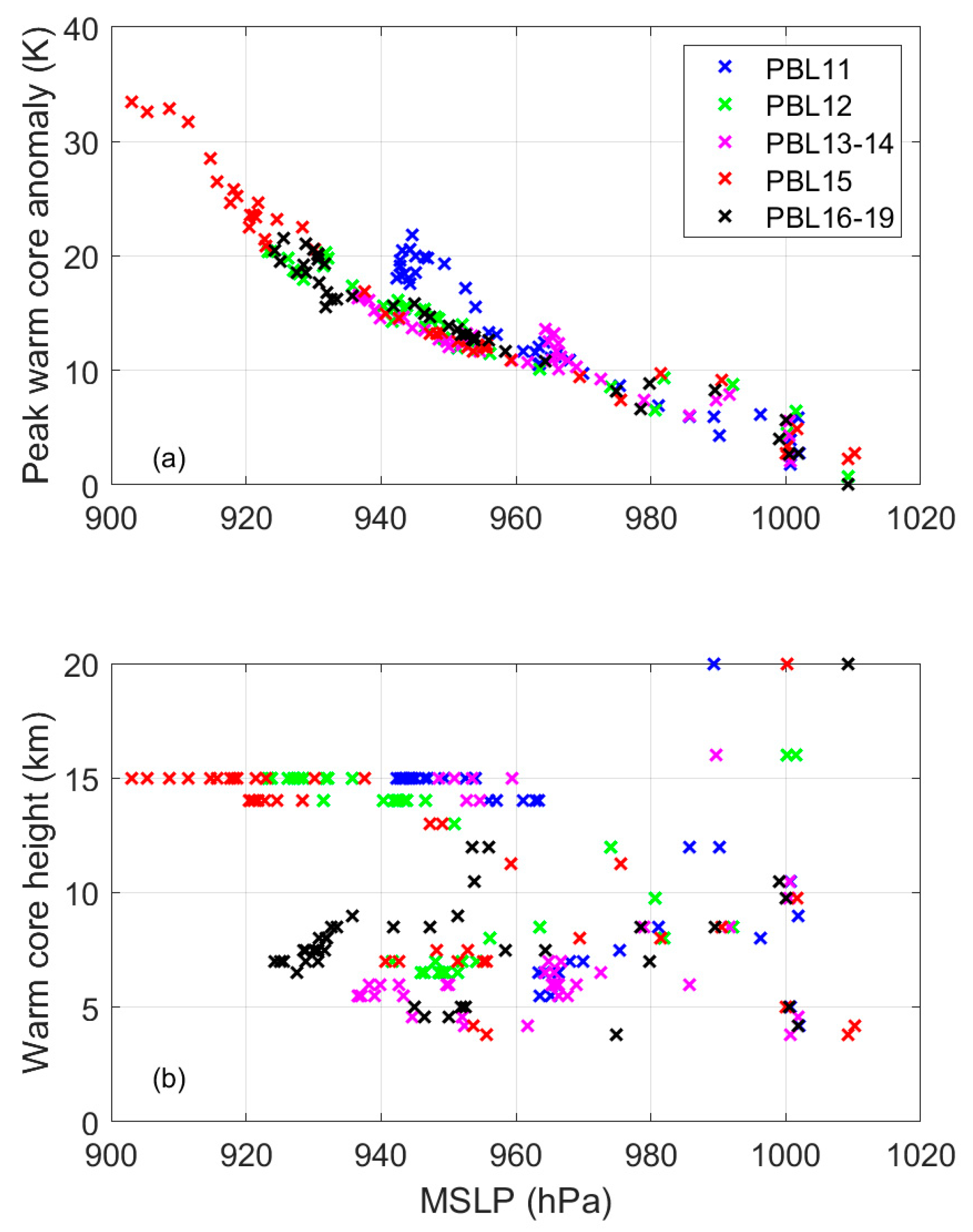
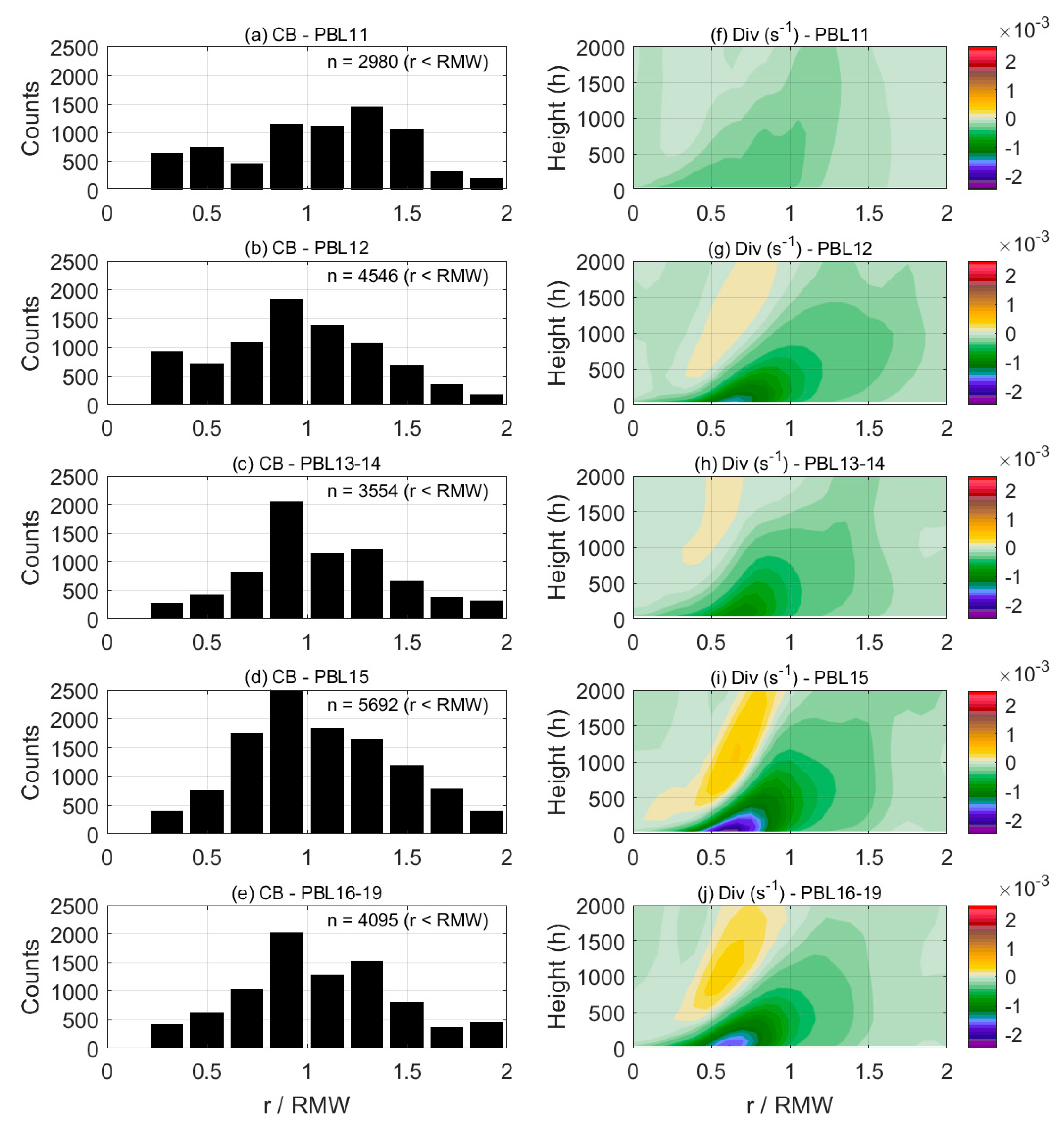
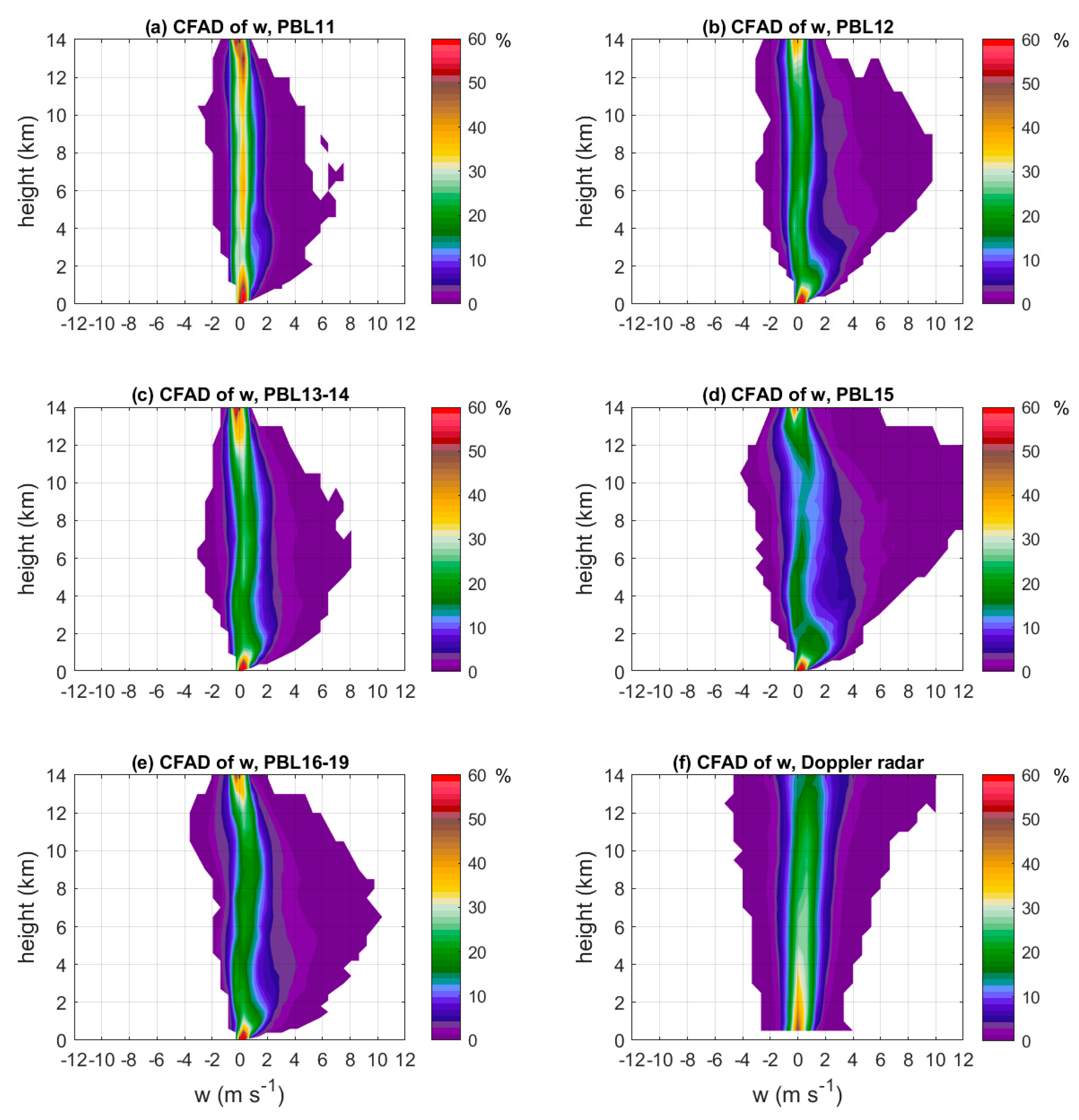
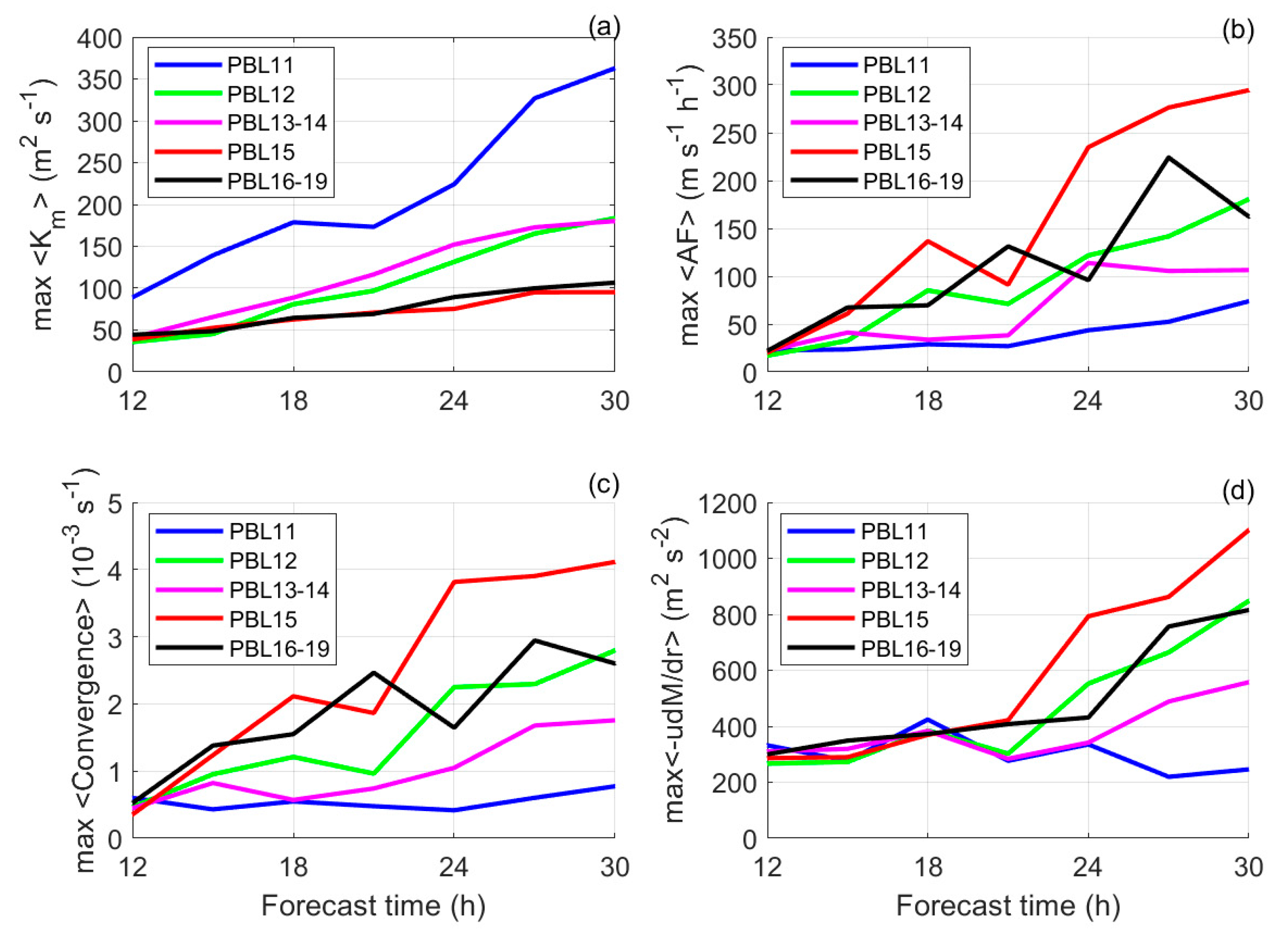
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Emanuel, K.A. An Air-Sea Interaction Theory for Tropical Cyclones. Part I: Steady-State Maintenance. J. Atmos. Sci. 1986, 43, 585–605. [Google Scholar] [CrossRef]
- Riemer, M.; Montgomery, M.T.; Nicholls, M.E. A new paradigm for intensity modification of tropical cyclones: Thermodynamic impact of vertical wind shear on the inflow layer. Atmos. Chem. Phys. 2010, 10, 3163–3188. [Google Scholar] [CrossRef] [Green Version]
- Cione, J.J.; Kalina, E.A.; Zhang, J.A.; Uhlhorn, E.W. Observations of Air–Sea Interaction and Intensity Change in Hurricanes. Mon. Weather Rev. 2013, 141, 2368–2382. [Google Scholar] [CrossRef]
- Montgomery, M.; Smith, R. Paradigms for tropical cyclone intensification. J. South. Hemisph. Earth Syst. Sci. 2014, 64, 37–66. [Google Scholar] [CrossRef]
- Montgomery, M.T.; Zhang, J.A.; Smith, R.K. An analysis of the observed low-level structure of rapidly intensifying and mature hurricane Earl (2010). Q. J. R. Meteorol. Soc. 2014, 140, 2132–2146. [Google Scholar] [CrossRef] [Green Version]
- Smith, R.K.; Montgomery, M.T.; Van Sang, N. Tropical cyclone spin-up revisited. Q. J. R. Meteorol. Soc. 2009, 135, 1321–1335. [Google Scholar] [CrossRef] [Green Version]
- Smith, R.K.; Zhang, J.A.; Montgomery, M.T. The dynamics of intensification in a Hurricane Weather and Research Forecast of Hurricane Earl (2010). Q. J. R. Meteorol. Soc. 2017, 143, 297–308. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.A.; Cione, J.J.; Kalina, E.A.; Uhlhorn, E.W.; Hock, T.; Smith, J.A. Observations of Infrared sea surface temperature and air-sea interaction in Hurricane Edouard (2014) using GPS dropsondes. J. Atmos. Ocean. Technol. 2017, 34, 1333–1349. [Google Scholar] [CrossRef]
- Nguyen, L.T.; Rogers, R.; Zawislak, J.; Zhang, J.A. Assessing the Influence of Convective Downdrafts and Surface Enthalpy Fluxes on Tropical Cyclone Intensity Change in Moderate Vertical Wind Shear. Mon. Weather Rev. 2019, 147, 3519–3534. [Google Scholar] [CrossRef]
- Ahern, K.; Bourassa, M.A.; Hart, R.E.; Zhang, J.A.; Rogers, R.F. Observed Kinematic and Thermodynamic Structure in the Hurricane Boundary Layer during Intensity Change. Mon. Weather. Rev. 2019, 147, 2765–2785. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, J.A.; Marks, F.D. A thermodynamic pathway leading to rapid intensification of tropical cyclones in shear. Geophys. Res. Lett. 2019, 46, 9241–9251. [Google Scholar] [CrossRef]
- Bryan, G.H.; Worsnop, R.P.; Lundquist, J.K.; Zhang, J.A. A simple method for simulating wind profiles in the boundary layer of tropical cyclones. Bound. Layer Meteor. 2017, 162, 475–502. [Google Scholar] [CrossRef] [Green Version]
- Worsnop, R.P.; Bryan, G.H.; Lundquist, J.K.; Zhang, J.A. Using Large-Eddy Simulations to define spectral and coherence characteristics of the hurricane boundary layer for wind-energy applications. Boundary Layer Meteor. 2017, 165, 55–86. [Google Scholar] [CrossRef]
- Worsnop, R.P.; Lundquist, J.K.; Bryan, G.H.; Damiani, R.; Musial, W. Gusts and shear within hurricane eyewalls can exceed offshore wind turbine design standards. Geophys. Res. Lett. 2017, 44, 6413–6420. [Google Scholar] [CrossRef] [Green Version]
- Donelan, M.A.; Haus, B.K.; Reul, N.; Plant, W.J.; Stiassnie, M.; Graber, H.C.; Brown, O.B.; Saltzman, E.S. On the limiting aerodynamic roughness of the ocean in very strong winds. Geophys. Res. Lett. 2014, 31, L18306. [Google Scholar] [CrossRef] [Green Version]
- Bell, M.M.; Montgomery, M.T.; Emanuel, K.A. Air–sea enthalpy and momentum exchange at major hurricane wind speeds observed during CBLAST. J. Atmos. Sci. 2012, 69, 3197–3222. [Google Scholar] [CrossRef]
- Braun, S.A.; Tao, W.K. Sensitivity of High-Resolution Simulations of Hurricane Bob (1991) to Planetary Boundary Layer Parameterizations. Mon. Weather. Rev. 2000, 128, 3941–3961. [Google Scholar] [CrossRef] [Green Version]
- Smith, R.K.; Thomsen, G.L. Dependence of tropical-cyclone intensification on the boundary-layer representation in a numerical model. Q. J. R. Meteorol. Soc. 2010, 136, 1671–1685. [Google Scholar] [CrossRef]
- Nolan, D.S.; Zhang, J.A.; Stern, D.P. Evaluation of planetary boundary layer parameterizations in tropical cyclones by comparison of in situ data and high-resolution simulations of Hurricane Isabel (2003). Part I: Initialization, maximum winds, and outer-core boundary layer structure. Mon. Weather Rev. 2009, 137, 3651–3674. [Google Scholar] [CrossRef]
- Zhu, P.; Menelaou, K.; Zhu, Z. Impact of subgrid-scale vertical turbulent mixing on eyewall asymmetric structures and mesovortices of hurricanes. Quart. J. Roy. Meteor. Soc. 2013, 140, 416–438. [Google Scholar] [CrossRef]
- Ming, J.; Zhang, J.A. Effects of surface flux parameterization on numerically simulated intensity and structure of Typhoon Morakot (2009). Advances Atmos. Sci. 2016, 33, 58–72. [Google Scholar] [CrossRef]
- Bryan, G.H. Effects of surface exchange coefficients and turbulence length scales on the intensity and structure of numerically simulated hurricanes. Mon. Wea. Rev. 2012, 140, 1125–1143. [Google Scholar] [CrossRef] [Green Version]
- Kilroy, G.; Smith, R.K.; Montgomery, M.T. Why do model tropical cyclones grow progressively in size and decay in intensity after reaching maturity? J. Atmos. Sci. 2016, 73, 487–503. [Google Scholar] [CrossRef]
- Kepert, J.D. Choosing a Boundary Layer Parameterization for Tropical Cyclone Modeling. Mon. Weather Rev. 2012, 140, 1427–1445. [Google Scholar] [CrossRef] [Green Version]
- Gall, R.; Franklin, J.; Marks, F.; Rappaport, E.N.; Toepfer, F. The Hurricane Forecast Improvement Project. Bull. Amer. Meteor. Soc. 2013, 94, 329–343. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.G.; Marks, F., Jr.; Zhang, J.A.; Zhang, X.; Bao, J.W.; Tallapragada, V. A study of the impacts of vertical diffusion on the structure and intensity of the tropical cyclones using the high-resolution HWRF system. J. Atmos. Sci. 2013, 70, 524–541. [Google Scholar] [CrossRef]
- Zhang, J.A.; Marks, F.D. Effects of horizontal eddy diffusivity on tropical cyclone intensity change and structure in idealized three-dimensional numerical simulations. Mon. Wea. Rev. 2015, 143, 3981–3995. [Google Scholar] [CrossRef]
- Bu, Y.P.; Fovell, R.G.; Corbosiero, K.L. The influences of boundary layer vertical mixing and cloud-radiative forcing on tropical cyclone size. J. Atmos. Sci. 2017, 74, 1273–1292. [Google Scholar] [CrossRef] [Green Version]
- Kieu, C.Q.; Tallapragada, V.; Hogsett, W. On the onset of the tropical cyclone rapid intensification in the HWRF model. Geophys. Res. Lett. 2014, 9, 3298–3306. [Google Scholar] [CrossRef]
- Tyner, B.; Zhu, P.; Zhang, J.A.; Gopalakrishnan, S.; Marks, F.M.; Tallapragada, V. A top-down pathway to secondary eyewall formation in simulated tropical cyclones. J. Geophys. Res. Atmos. 2017, 123, 174–197. [Google Scholar] [CrossRef]
- Leighton, H.; Gopalakrishnan, S.; Zhang, J.A.; Rogers, R.F.; Zhang, Z.; Tallapragada, V. Azimuthal distribution of deep convection, environmental factors and tropical cyclone rapid intensification: A perspective from HWRF ensemble forecasts of Hurricane Edouard (2014). J. Atmos. Sci. 2018, 75, 275–295. [Google Scholar] [CrossRef]
- Zhang, J.A.; Rogers, R.F. Effects of Parameterized Boundary Layer Structure on Hurricane Rapid Intensification in Shear. Mon. Weather Rev. 2019, 147, 853–871. [Google Scholar] [CrossRef]
- Biswas, M.K.; Zhang, J.A.; Grell, E.; Kalina, E.; Newman, K.; Bernardet, L.; Carson, L.; Frimel, J.; Grell, G. Evaluation of the Grell-Freitas convective scheme in the Hurricane Weather Research and Forecasting (HWRF) model. Weather Forecast. 2020, 35, 1017–1033. [Google Scholar] [CrossRef] [Green Version]
- Zhu, P.; Tyner, B.; Zhang, J.A.; Aligo, E.; Gopalakrishnan, S.; Marks, F.D.; Mehra, A.; Tallapragada, V. Role of eyewall and rainband eddy forcing in tropical cyclone intensification. Atmos. Chem. Phys. 2019, 19, 14289–14310. [Google Scholar] [CrossRef] [Green Version]
- Troen, I.B.; Mahrt, L. A simple model of the atmospheric boundary layer; sensitivity to surface evaporation. Bound. Layer Meteorol. 1986, 37, 129–148. [Google Scholar] [CrossRef]
- Han, J.; Pan, H.-L. Revision of convection and vertical diffusion schemes in the ncep global forecast system. Weather Forcasting 2011, 26, 520–533. [Google Scholar] [CrossRef]
- Zhang, J.A.; Gopalakrishnan, S.; Marks, F.D.; Rogers, R.F.; Tallapragada, V. A developmental framework for improving hurricane model physical parameterization using aircraft observations. Trop. Cyclone Res. Rev. 2012, 1, 419–429. [Google Scholar]
- Tallapragada, V.; Kieu, C.; Kwon, Y.; Trahan, S.; Liu, Q.; Zhang, Z.; Kwon, I. Evaluation of storm structure from the operational HWRF during 2012 implementation. Mon. Wea. Rev. 2014, 142, 4308–4325. [Google Scholar] [CrossRef]
- Zhang, J.A.; Nolan, D.S.; Rogers, R.F.; Tallapragada, V. Evaluating the Impact of Improvements in the Boundary Layer Parameterization on Hurricane Intensity and Structure Forecasts in HWRF. Mon. Wea. Rev. 2015, 143, 3136–3155. [Google Scholar] [CrossRef]
- Bu, Y.P.; Fovell, R.G.; Corbosiero, K.L. Influence of cloud-radiative forcing on tropical cyclone structure. J. Atmos. Sci. 2014, 71, 1644–1662. [Google Scholar] [CrossRef] [Green Version]
- Han, J.; Witek, M.L.; Teixeira, J.; Sun, R.; Pan, H.; Fletcher, J.K.; Bretherton, C.S. Implementation in the ncep gfs of a hybrid eddy-diffusivity mass-flux (EDMF) boundary layer parameterization with dissipative heating and modified stable boundary layer mixing. Weather Forcasting 2016, 31, 341–352. [Google Scholar] [CrossRef]
- Wang, W.; Sippel, J.A.; Abarca, S.; Zhu, L.; Liu, B.; Zhang, Z.; Mehra, A.; Tallapragada, V. Improving ncep hwrf simulations of surface wind and inflow angle in the eyewall area. Weather Forecasting 2018, 33, 887–898. [Google Scholar] [CrossRef]
- Biswas, M.K. Hurricane Weather Research and Forecasting (HWRF) Model: 2017 Scientific Documentation. NCAR Technical Notes, NCAR/TN-544+STR. 2018. Available online: https://opensky.ucar.edu/islandora/object/technotes:563 (accessed on 4 October 2020).
- Gray, W.; Ruprecht, E.; Phelps, R. Relative humidity in tropical weather systems. Mon. Weather Rev. 1975, 103, 685–690. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y. An inverse balance equation in sigma coordinates for model initialization. Mon. Weather Rev. 1995, 123, 482–488. [Google Scholar] [CrossRef] [Green Version]
- Aligo, E.; Ferrier, B.; Thompson, G.; Carley, J.R.; Rogers, E.; Dimego, J. The New-Ferrier-Aligo Microphysics in the NCEP 3-km NAM Nest. In Proceedings of the 97th AMS Annual Meeting, Seattle, WA, USA, 21–26 January 2017. [Google Scholar]
- Grell, G.A.; Freitas, S.R. A scale and aerosol aware stochastic convective parameterization for weather and air quality modeling. Atmos. Chem. Phys. 2014, 14, 5233–5250. [Google Scholar] [CrossRef] [Green Version]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Edson, J.B. Coauthors On the exchange of momentum over the open ocean. J. Phys. Oceanogr. 2013, 43, 1589–1610. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.A.; Rogers, R.F.; Nolan, D.S.; Marks, F.D., Jr. On the Characteristic Height Scales of the Hurricane Boundary Layer. Mon. Weather Rev. 2011, 139, 2523–2535. [Google Scholar] [CrossRef]
- Nolan, D.S.; Atlas, R.A.; Bhatia, K.T.; Bucci, L.R. Development and validation of a hurricane nature run using the joint OSSE nature run and the WRF model. J. Adv. Model. Earth Sys. 2013, 5, 382–405. [Google Scholar] [CrossRef]
- Kepert, J.D.; Schwendike, J.; Ramsay, H. Why is the tropical cyclone boundary layer not “well mixed”? J. Atmos. Sci. 2016, 73, 957–973. [Google Scholar] [CrossRef]
- Gao, K.; Ginis, I. On the generation of roll vortices due the inflection point instability of the hurricane boundary layer flow. J. Atmos. Sci. 2014, 71, 4292–4307. [Google Scholar] [CrossRef] [Green Version]
- Cione, J.J.; Bryan, G.H.; Dobosy, R.; Zhang, J.A.; de Boer, G.; Aksoy, A.; Wadler, J.B.; Kalina, E.A.; Dahl, B.A.; Neuhaus, K.R.J.; et al. Eye of the storm: Observing hurricanes with a small unmanned aircraft system. Bull. Am. Meteor. Soc. 2020, 101, E186–E205. [Google Scholar] [CrossRef]
- Stern, D.P.; Nolan, D.S. On the Height of the Warm Core in Tropical Cyclones. J. Atmos. Sci. 2012, 69, 1657–1680. [Google Scholar] [CrossRef]
- Stern, D.P.; Zhang, F. How Does the Eye Warm? Part I: A Potential Temperature Budget Analysis of an Idealized Tropical Cyclone. J. Atmos. Sci. 2013, 70, 73–90. [Google Scholar] [CrossRef]
- Kieu, C.Q.; Tallapragada, V.; Zhang, D.; Moon, Z. On the Development of Double Warm-Core Structures in Intense Tropical Cyclones. J. Atmos. Sci. 2016, 73, 4487–4506. [Google Scholar] [CrossRef]
- Zhang, D.-L.; Chen, H. Importance of the upper-level warm core in the rapid intensification of a tropical cyclone. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Gopalakrishnan, S. A study on the asymmetric rapid intensification of Hurricane Earl (2010) using the HWRF system. J. Atmos. Sci. 2015, 72, 531–550. [Google Scholar] [CrossRef]
- Rogers, R.F. Convective-scale structure and evolution during a high-resolution simulation of tropical cyclone rapid intensification. J. Atmos. Sci. 2010, 67, 44–70. [Google Scholar] [CrossRef]
- Schubert, W.H.; Hack, J.J. Inertial stability and tropical cyclone development. J. Atmos. Sci. 1982, 39, 1687–1697. [Google Scholar] [CrossRef]
- Nolan, D.S.; Moon, Y.; Stern, D.P. Tropical cyclone intensification from asymmetric convection: Energetics and efficiency. J. Atmos. Sci. 2007, 64, 3377–3405. [Google Scholar] [CrossRef]
- Rogers, R.F.; Reasor, P.; Lorsolo, S. Airborne Doppler observations of the inner-core structural differences between intensifying and steady-state tropical cyclones. Mon. Weather Rev. 2013, 141, 2970–2991. [Google Scholar] [CrossRef]
- Smith, R.K.; Montgomery, M.T. The efficiency of diabatic heating and tropical cyclone intensification. Quart. J. Roy. Meteor. Soc. 2016, 142, 2081–2086. [Google Scholar] [CrossRef]
- Yuter, S.E.; Houze, R.A., Jr. Three-dimensional kinematic and microphysical evolution of Florida cumulonimbus. Part III: Vertical mass transport, mass divergence, and synthesis. Mon. Weather Rev. 1995, 123, 1964–1983. [Google Scholar] [CrossRef] [Green Version]
- Rogers, R.F.; Black, M.L.; Chen, S.S.; Black, R.A. An evaluation of microphysics fields from mesoscale model simulations of tropical cyclones, Part I: Comparisons with observations. J. Atmos. Sci. 2007, 64, 1811–1834. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.A.; Rogers, R.F.; Tallapragada, V. Impact of parameterized boundary layer structure on tropical cyclone rapid intensification forecasts in HWRF. Mon. Weather Rev. 2017, 145, 1413–1426. [Google Scholar] [CrossRef]


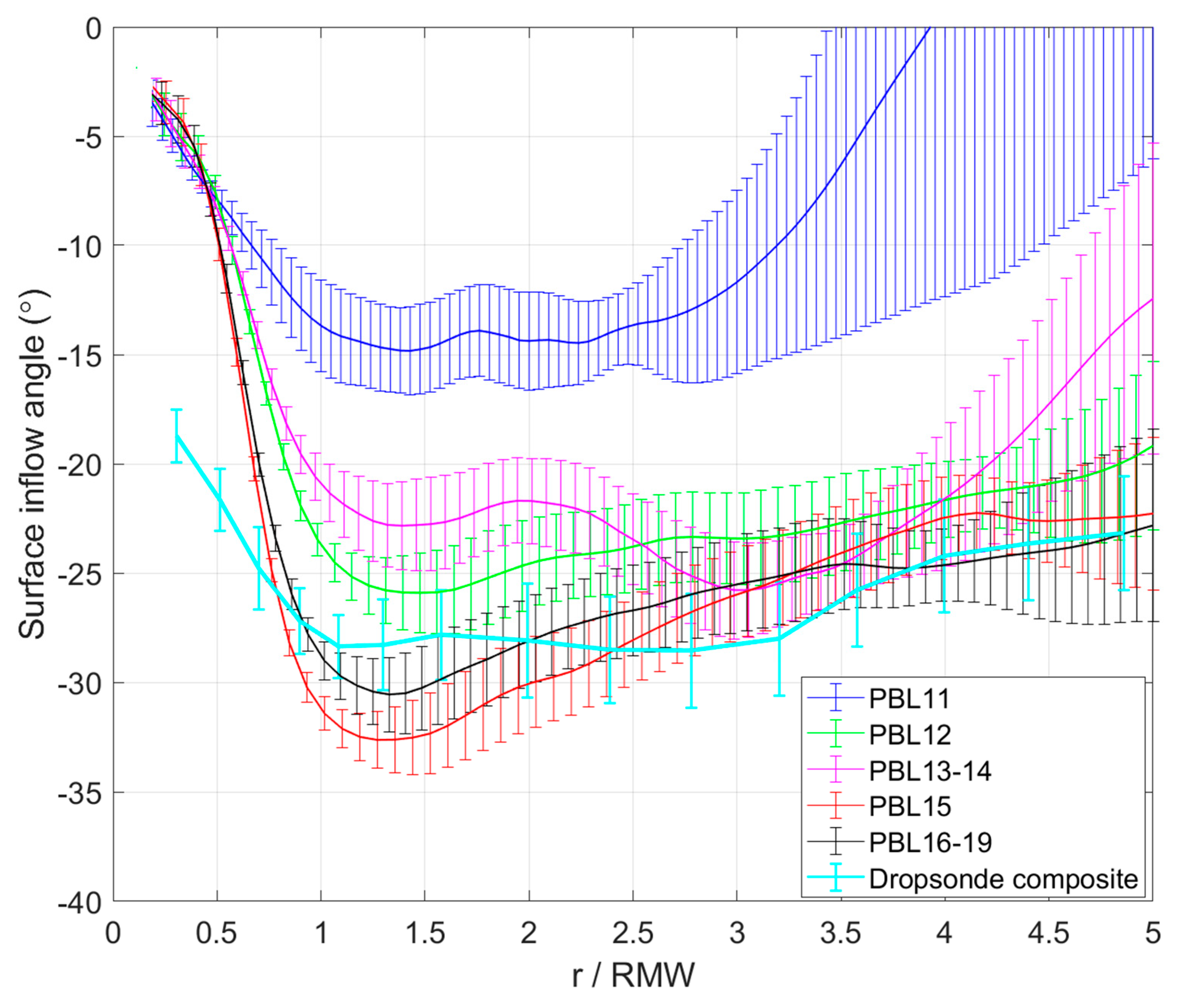
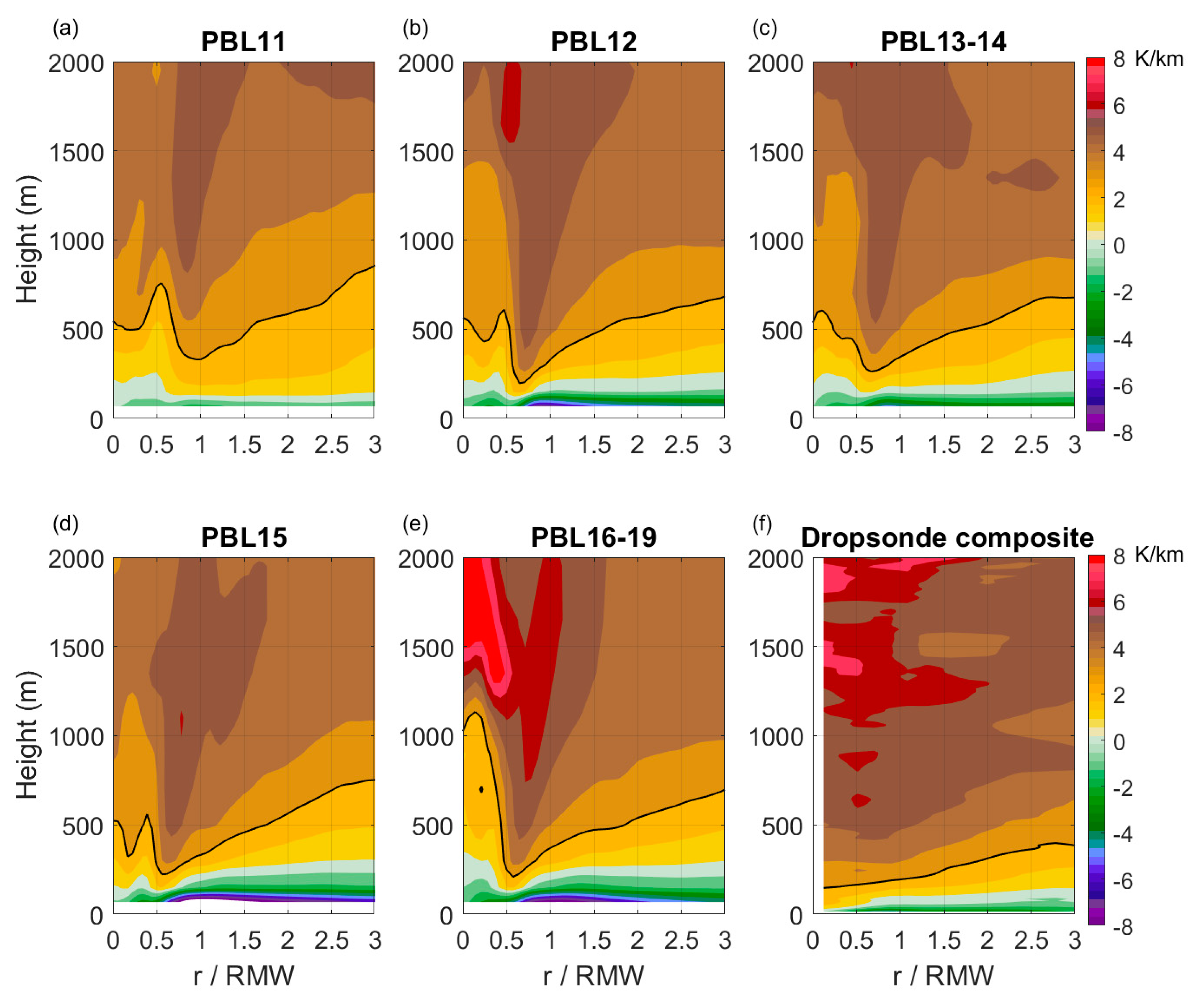
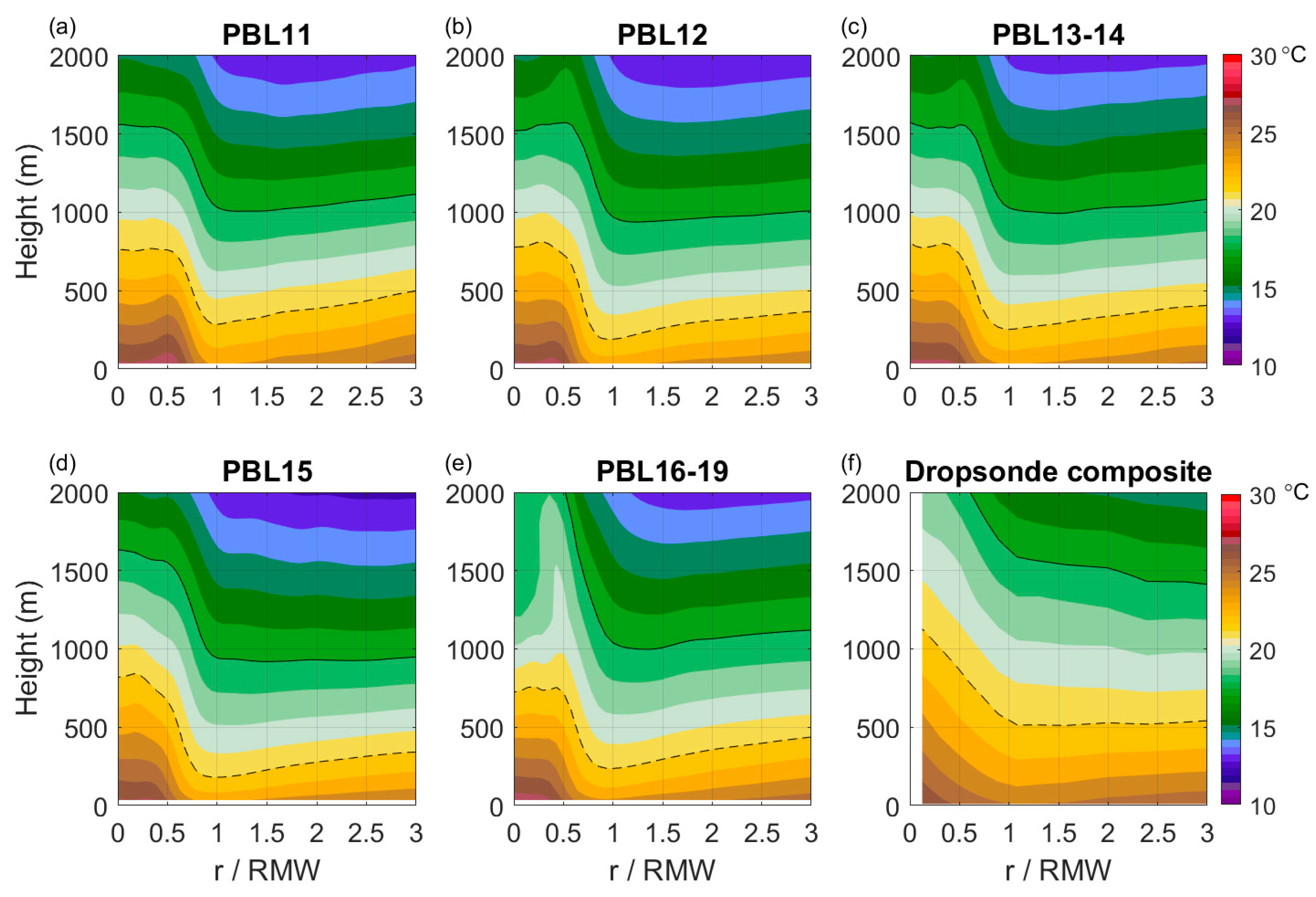
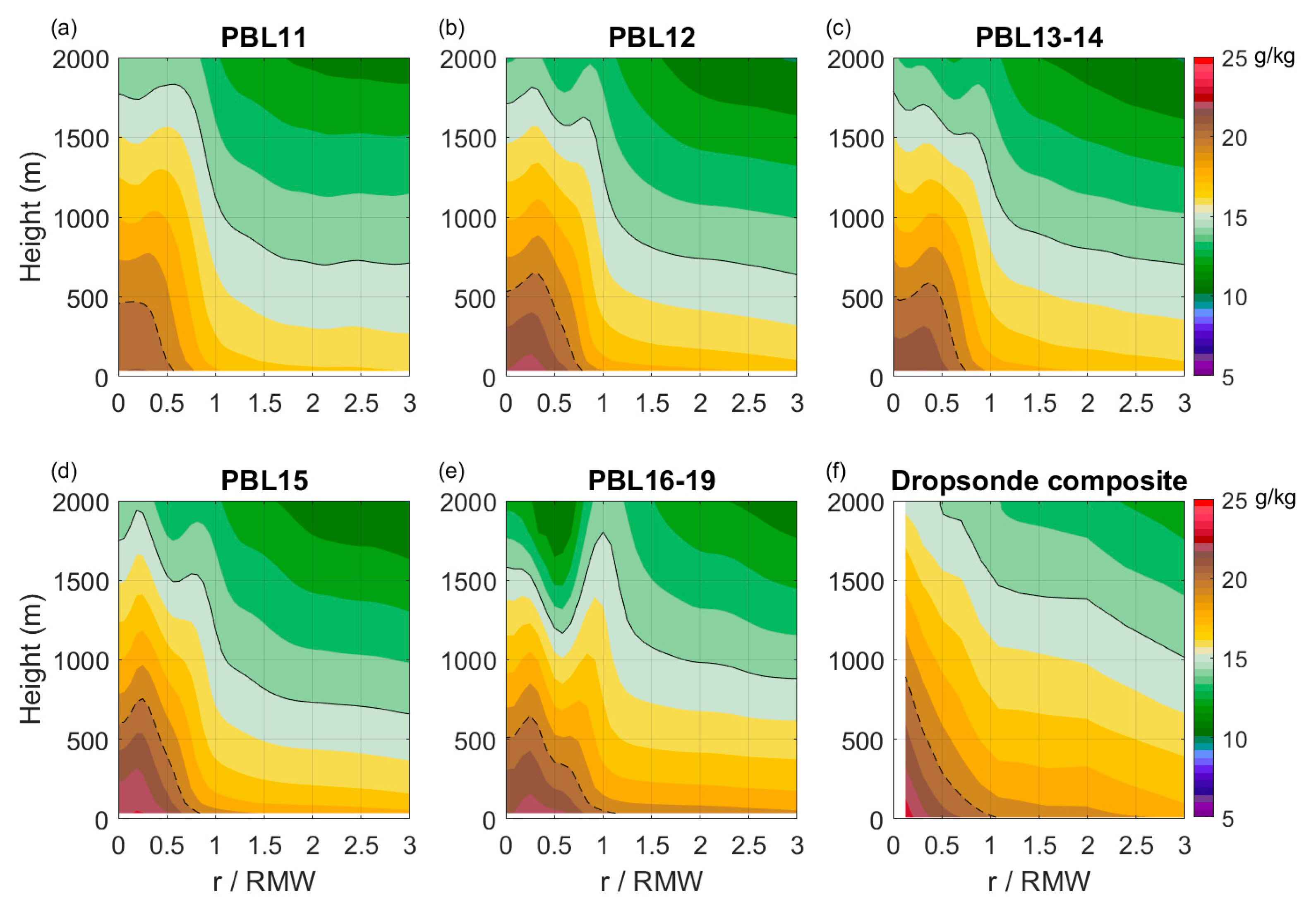
| HWRF Version | Year | PBL Scheme | Alpha Parameter | Critical Richardson Number | Referred to as |
|---|---|---|---|---|---|
| 3.3a | 2011 | GFS | 1.0 | 0.5 | PBL11 |
| 3.4a | 2012 | GFS | 0.5 | 0.25 | PBL12 |
| 3.5a 3.6a | 2013 2014 | GFS | 0.7 | Varies with Rossby number | PBL13–14 |
| 3.7a | 2015 | GFS | Varies with wind speed | Varies with Rossby number | PBL15 |
| 3.8a 3.9a 4.0a | 2016 2017 2018 2019 | GFS EDMF | Varies with wind speed and height | Varies with Rossby number | PBL16–19 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.A.; Kalina, E.A.; Biswas, M.K.; Rogers, R.F.; Zhu, P.; Marks, F.D. A Review and Evaluation of Planetary Boundary Layer Parameterizations in Hurricane Weather Research and Forecasting Model Using Idealized Simulations and Observations. Atmosphere 2020, 11, 1091. https://doi.org/10.3390/atmos11101091
Zhang JA, Kalina EA, Biswas MK, Rogers RF, Zhu P, Marks FD. A Review and Evaluation of Planetary Boundary Layer Parameterizations in Hurricane Weather Research and Forecasting Model Using Idealized Simulations and Observations. Atmosphere. 2020; 11(10):1091. https://doi.org/10.3390/atmos11101091
Chicago/Turabian StyleZhang, Jun A., Evan A. Kalina, Mrinal K. Biswas, Robert F. Rogers, Ping Zhu, and Frank D. Marks. 2020. "A Review and Evaluation of Planetary Boundary Layer Parameterizations in Hurricane Weather Research and Forecasting Model Using Idealized Simulations and Observations" Atmosphere 11, no. 10: 1091. https://doi.org/10.3390/atmos11101091
APA StyleZhang, J. A., Kalina, E. A., Biswas, M. K., Rogers, R. F., Zhu, P., & Marks, F. D. (2020). A Review and Evaluation of Planetary Boundary Layer Parameterizations in Hurricane Weather Research and Forecasting Model Using Idealized Simulations and Observations. Atmosphere, 11(10), 1091. https://doi.org/10.3390/atmos11101091







