Wind and Wind Power Ramp Variability over Northern Mexico
Abstract
:1. Introduction
2. Data and Method
2.1. Weather Stations
2.2. Forecast Models
2.3. Method
2.3.1. Weather Station Groups
2.3.2. Model Verification
3. Results and Discussion
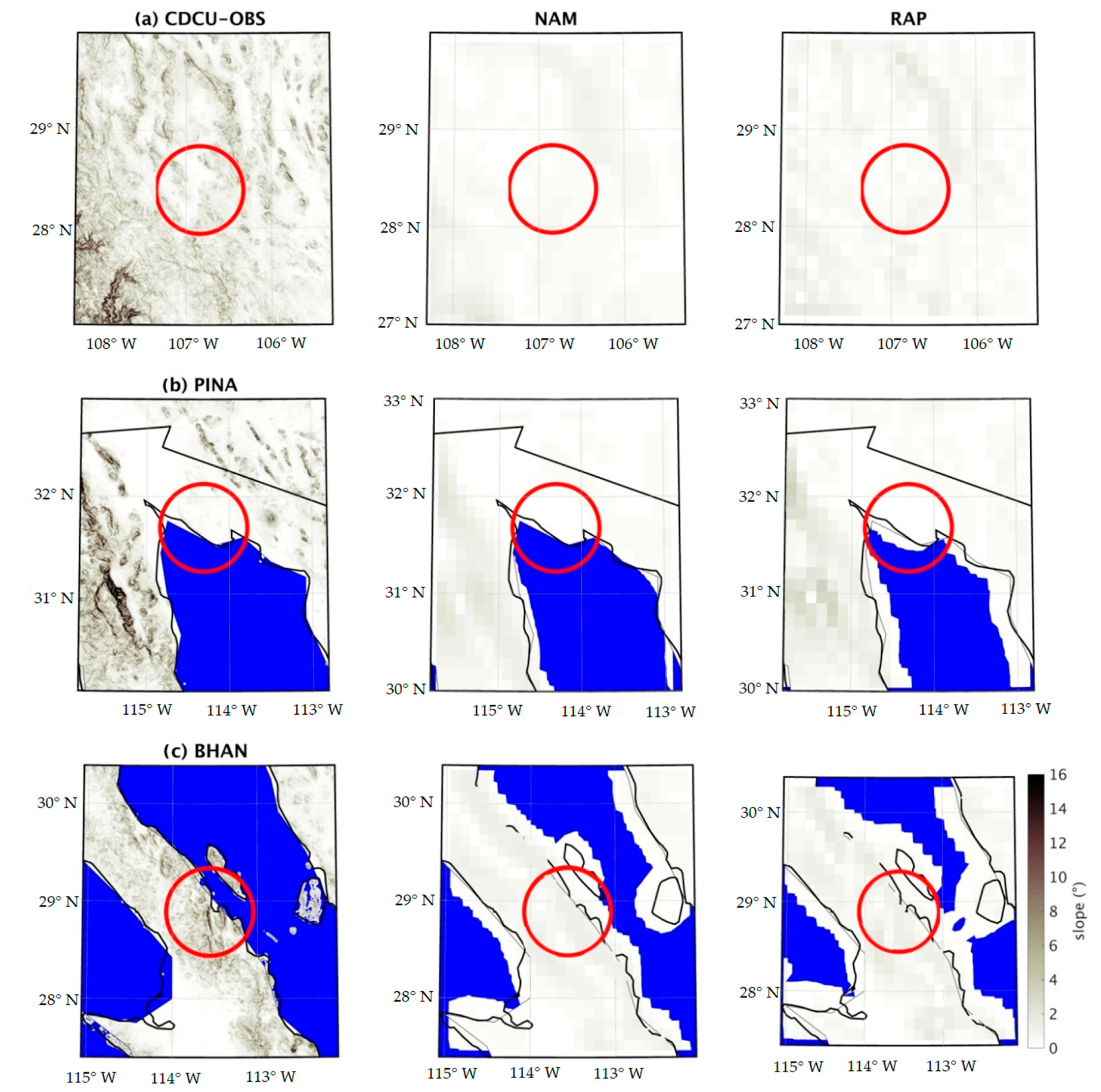
3.1. Study Regions
3.2. Wind Power Variability
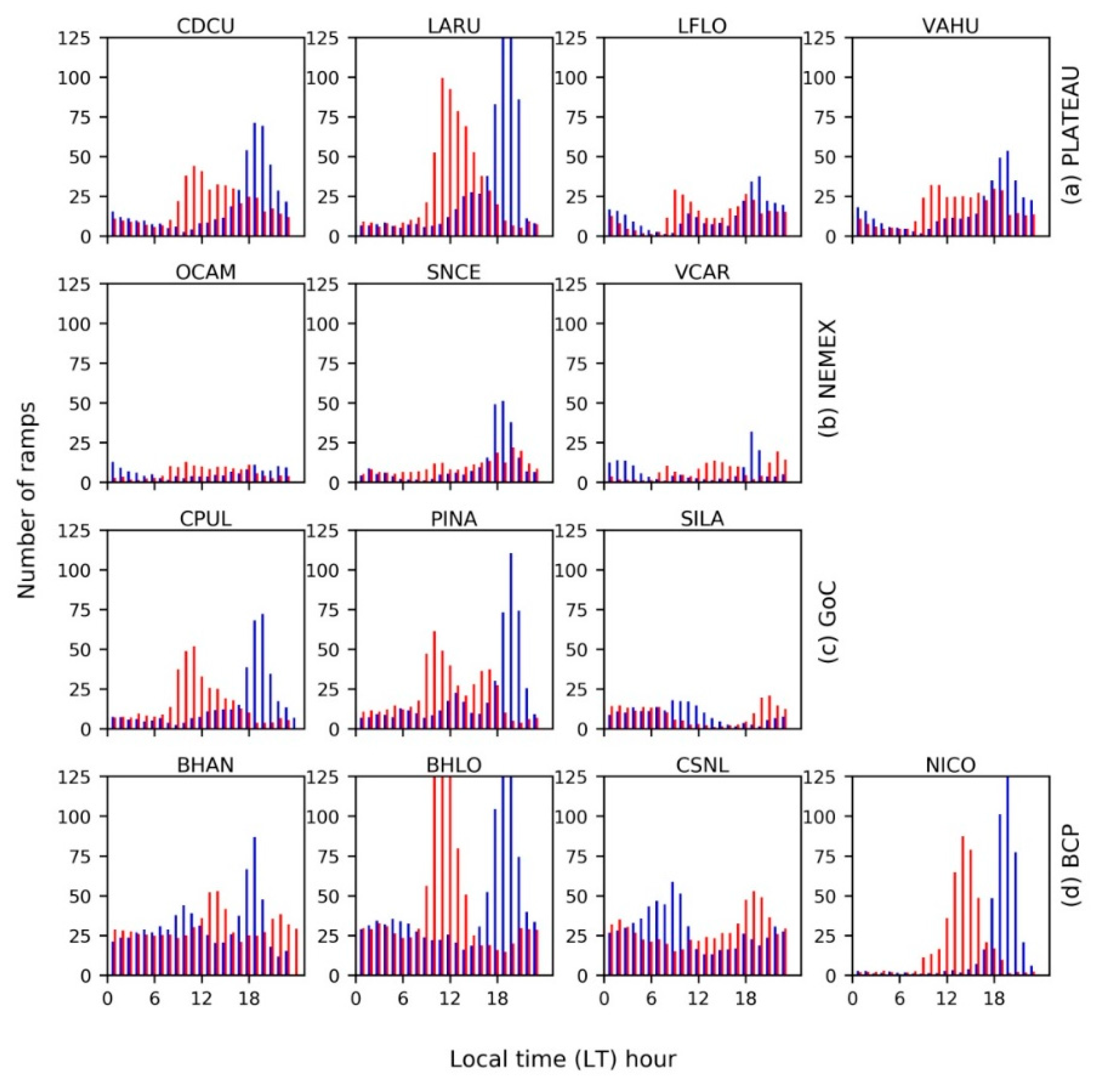
3.2.1. Wind Power Ramp Characterization
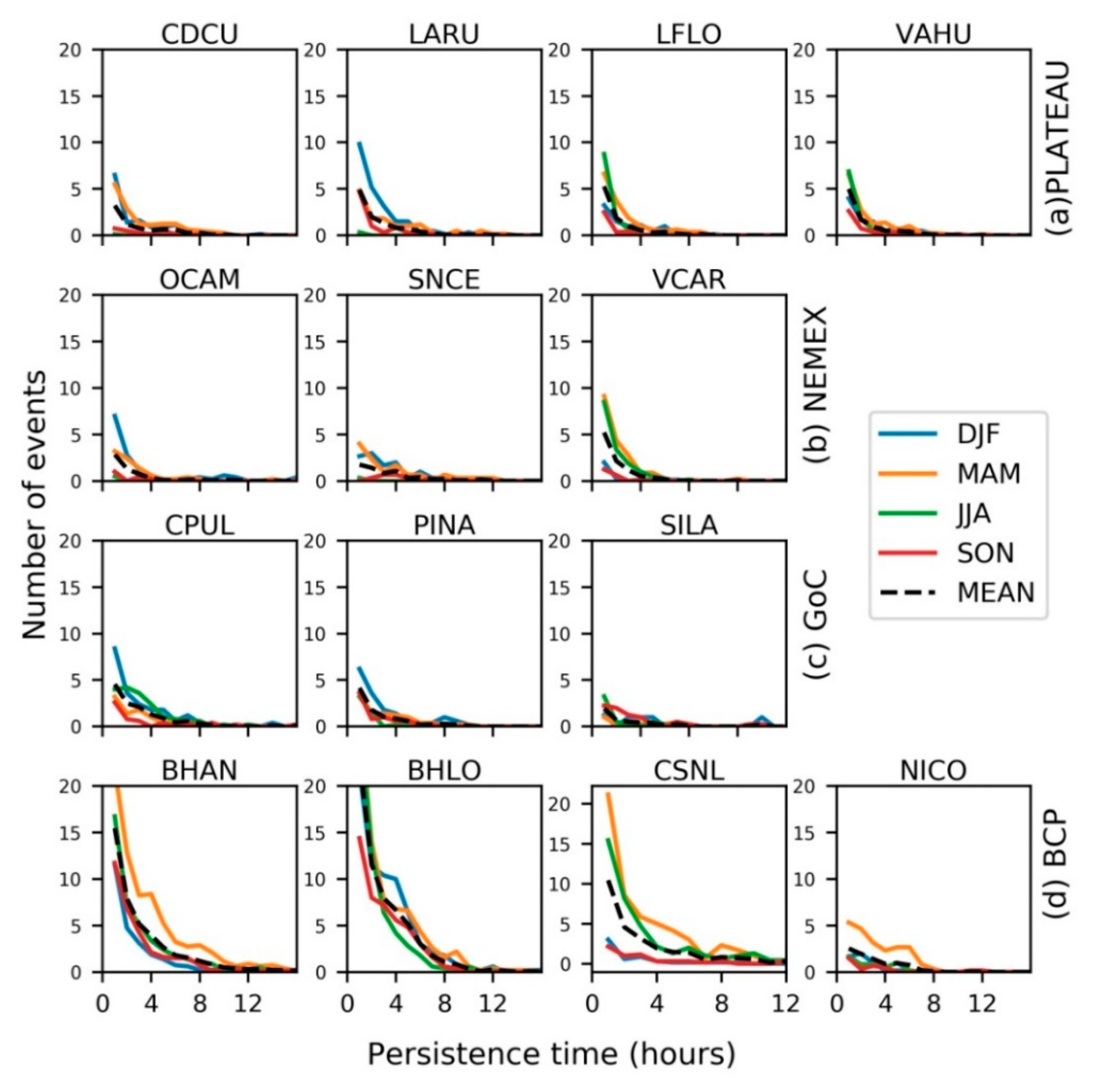
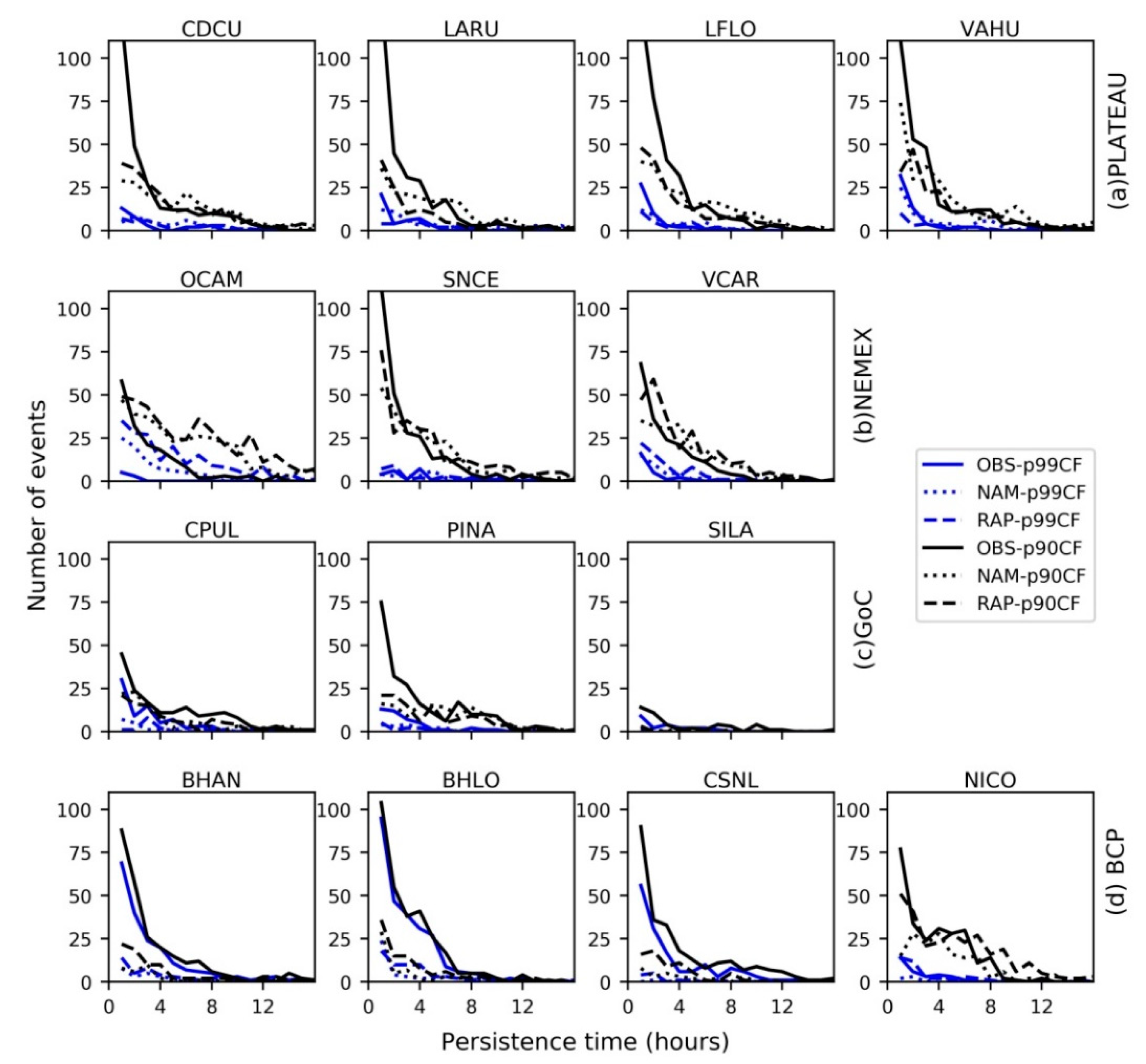
3.2.2. Persistent High and Low Wind Power Generation Events
3.2.3. Weather Systems Underlying Wind Ramps
3.3. NAM and RAP Wind Forecasting
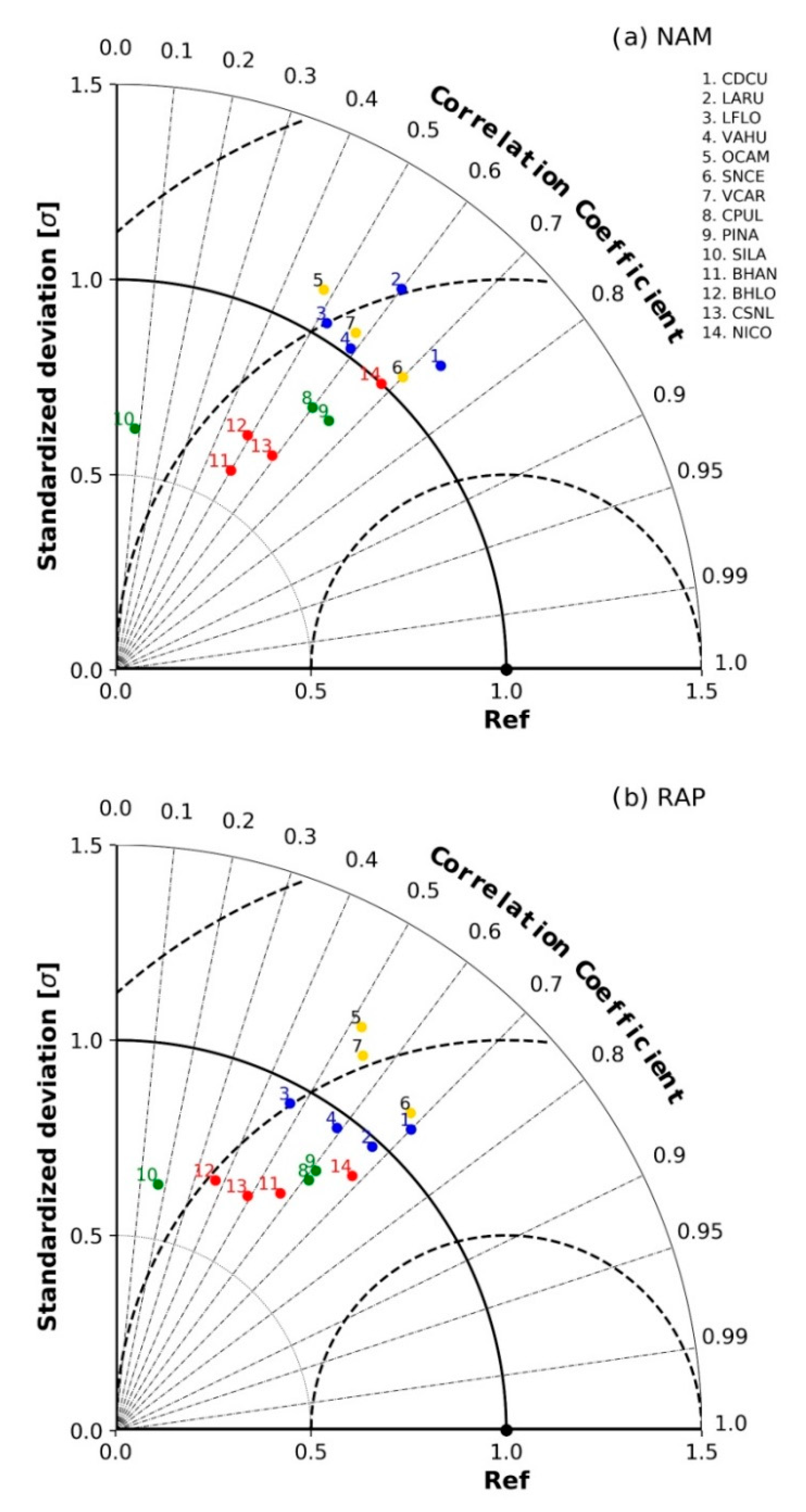
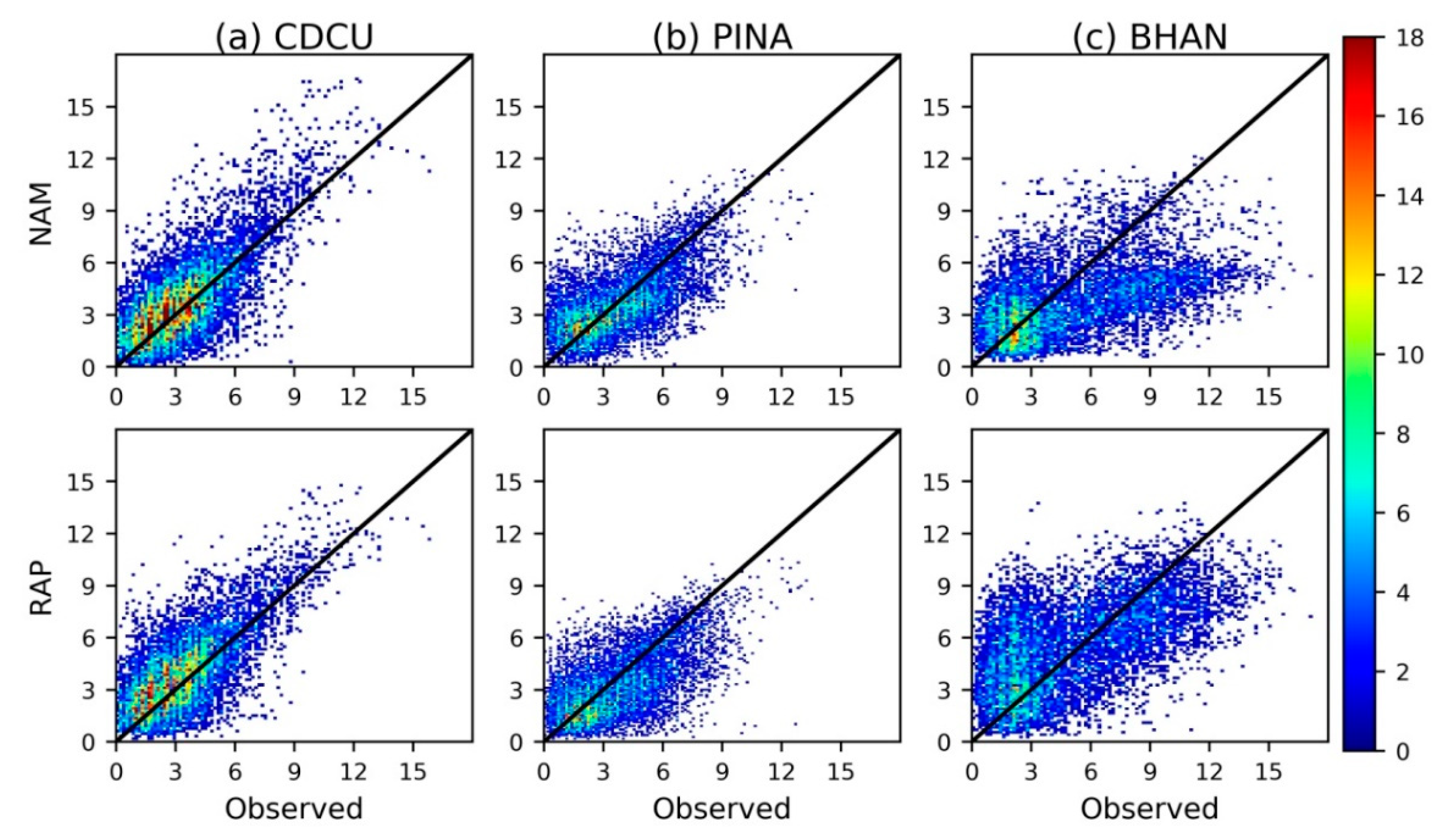
3.3.1. Model Verification
3.3.2. Ramp Indices
3.3.3. Forecast of High Generation Events
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- SENER. Programa de Desarrollo del Sistema Eléctrico Nacional 2015–2029; Secretaría de Energía: Ciudad de México, México, 2015; Available online: https://www.gob.mx/sener/acciones-y-programas/programa-de-desarrollo-del-sistema-electrico-nacional-33462 (accessed on 24 September 2020).
- DeCesaro, J.; Porter, K.; Milligan, M. Wind energy and power system operations: A review of wind integration studies to date. Electr. J. 2009, 22, 34–43. [Google Scholar] [CrossRef] [Green Version]
- Greaves, B.; Collins, J.; Parkes, J.; Tindal, A. Temporal forecast uncertainty for ramp events. Wind. Eng. 2009, 33, 309–319. [Google Scholar] [CrossRef]
- Gallego-Castillo, C.; Cuerva-Tejero, A.; Lopez-Garcia, O. A review on the recent history of wind power ramp forecasting. Renew. Sustain. Energy Rev. 2015, 52, 1148–1157. [Google Scholar] [CrossRef] [Green Version]
- Cutler, N.; Kay, M.; Jacka, K.; Nielsen, T.S. Detecting, categorizing and forecasting large ramps in wind farm power output using meteorological observations and WPPT. Wind. Energy 2007, 10, 453–470. [Google Scholar] [CrossRef]
- Bossavy, A.; Girard, R.; Kariniotakis, G. Forecasting Uncertainty Related to Ramps of Wind Power Production. In Proceedings of the European Wind Energy Conference and Exhibition 2010 (EWEC 2010), Warsaw, Poland, 20–23 April 2010; Curran Associates: Reed Hook, NY, USA, 2010; Volume 2, p. 9, ISBN 9781617823107. hal-00765885. [Google Scholar]
- Kamath, C. Associating weather conditions with ramp events in wind power generation. In Proceedings of the 2011 IEEE/PES Power Systems Conference and Exposition, Phoenix, AZ, USA, 20–23 March 2011; pp. 1–8. [Google Scholar] [CrossRef]
- Yang, Q.; Berg, L.K.; Pekour, M.; Fast, J.D.; Newsom, R.K.; Stoelinga, M.; Finley, C. Evaluation of WRF-predicted near-hub-height winds and ramp events over a Pacific Northwest site with complex terrain. J. Appl. Meteorol. Clim. 2013, 52, 1753–1763. [Google Scholar] [CrossRef]
- Gallego, C.; Cuerva, A.; Costa, A. Detecting and characterising ramp events in wind power time series. J. Physics: Conf. Ser. 2014, 555, 012040. [Google Scholar] [CrossRef] [Green Version]
- Cui, M.; Zhang, J.; Florita, A.R.; Hodge, B.-M.; Ke, D.; Sun, Y. An optimized swinging door algorithm for identifying wind ramping events. IEEE Trans. Sustain. Energy 2016, 7, 150–162. [Google Scholar] [CrossRef]
- Bianco, L.; Djalalova, I.V.; Wilczak, J.M.; Cline, J.; Calvert, S.; Konopleva-Akish, E.; Finley, C.; Freedman, J. A wind energy ramp tool and metric for measuring the skill of numerical weather prediction models. Weather. Forecast. 2016, 31, 1137–1156. [Google Scholar] [CrossRef]
- Smith, N.H.; Ancell, B.C. Variations in parametric sensitivity for wind ramp events in the Columbia river basin. Mon. Weather. Rev. 2019, 147, 4633–4651. [Google Scholar] [CrossRef]
- Siuta, D.; West, G.; Stull, R. WRF Hub-height wind forecast sensitivity to PBL scheme, grid length, and initial condition choice in complex terrain. Weather. Forecast. 2017, 32, 493–509. [Google Scholar] [CrossRef]
- Deppe, A.J.; Gallus, W.A.; Takle, E.S. A WRF Ensemble for improved wind speed forecasts at turbine height. Weather. Forecast. 2013, 28, 212–228. [Google Scholar] [CrossRef]
- Benjamin, S.G.; Weygandt, S.S.; Brown, J.M.; Hu, M.; Alexander, C.R.; Smirnova, T.G.; Olson, J.B.; James, E.P.; Dowell, D.C.; Grell, G.A.; et al. A North American hourly assimilation and model forecast cycle: The rapid refresh. Mon. Weather. Rev. 2016, 144, 1669–1694. [Google Scholar] [CrossRef]
- Archer, C.L.; Colle, B.A.; Monache, L.D.; Dvorak, M.J.; Lundquist, J.K.; Bailey, B.H.; Beaucage, P.; Churchfield, M.J.; Fitch, A.C.; Kosovic, B.; et al. Meteorology for coastal/offshore wind energy in the united states: Recommendations and research needs for the next 10 years. Bull. Am. Meteorol. Soc. 2014, 95, 515–519. [Google Scholar] [CrossRef]
- Cannon, D.; Brayshaw, D.; Methven, J.; Coker, P.; Lenaghan, D. Using reanalysis data to quantify extreme wind power generation statistics: A 33 year case study in Great Britain. Renew. Energy 2015, 75, 767–778. [Google Scholar] [CrossRef] [Green Version]
- Musilek, P.; Li, Y. Forecasting of wind ramp events-Analysis of cold front detection. In Proceedings of the 31st International Symposium on Forecasting, Prague, Czech Republic, 26–29 June 2011. [Google Scholar]
- Ohba, M.; Kadokura, S.; Nohara, D. Impacts of synoptic circulation patterns on wind power ramp events in East Japan. Renew. Energy 2016, 96, 591–602. [Google Scholar] [CrossRef] [Green Version]
- Sherry, M.; Rival, D.E. Meteorological phenomena associated with wind-power ramps downwind of mountainous terrain. J. Renew. Sustain. Energy 2015, 7, 033101. [Google Scholar] [CrossRef] [Green Version]
- Walton, R.A.; Gallus, W.A.; Takle, E.S. Wind ramp events at turbine height-spatial consistency and causes at two Iowa wind farms. In Proceedings of the 4th Conference Weather, Climate, New Energy Economy, Austin, TX, USA, 5–10 January 2013; pp. 1–7. [Google Scholar]
- Colle, B.A.; Mass, C.F. The structure and evolution of cold surges east of the Rocky Mountains. Mon. Weather. Rev. 1995, 123, 2577–2610. [Google Scholar] [CrossRef] [Green Version]
- Fitzjarrald, D.R. Slope wind in Veracruz. J. Clim. Appl. Meteorol. 1986, 25, 133–144. [Google Scholar] [CrossRef] [Green Version]
- Carvalho, D.; Rocha, A.; Gómez-Gesteira, M.; Santos, C.S. A sensitivity study of the WRF model in wind simulation for an area of high wind energy. Environ. Model. Softw. 2012, 33, 23–34. [Google Scholar] [CrossRef] [Green Version]
- Carvalho, D.; Rocha, A.M.A.C.; Gómez-Gesteira, M.; Santos, C.S. Sensitivity of the WRF model wind simulation and wind energy production estimates to planetary boundary layer parameterizations for onshore and offshore areas in the Iberian Peninsula. Appl. Energy 2014, 135, 234–246. [Google Scholar] [CrossRef]
- Draxl, C.; Hahmann, A.N.; Peña, A.; Giebel, G. Evaluating winds and vertical wind shear from Weather Research and Forecasting model forecasts using seven planetary boundary layer schemes. Wind. Energy 2014, 17, 39–55. [Google Scholar] [CrossRef]
- Rogers, E.; DiMego, G.; Black, T.; Ek, M.; Ferrier, B.; Gayno, G.; Janjic, Z.; Lin, Y.; Pyle, M.; Wong, V. The NCEP North American mesoscale modeling system: Recent changes and future plans. In Proceedings of the 23rd Conference on Weather Analysis and Forecasting and 19th Conference on Numerical Weather Prediction, Omaha, NE, USA, 1–5 June 2009; p. 2A.4. [Google Scholar]
- Hernandez-Escobedo, Q.; Manzano-Agugliaro, F.; Zapata-Sierra, A. The wind power of Mexico. Renew. Sustain. Energy Rev. 2010, 14, 2830–2840. [Google Scholar] [CrossRef]
- James, E.P.; Benjamin, S.G.; Marquis, M. A unified high-resolution wind and solar dataset from a rapidly updating numerical weather prediction model. Renew. Energy 2017, 102, 390–405. [Google Scholar] [CrossRef] [Green Version]
- Li, A.K.; Paek, H.; Yu, J.-Y. The changing influences of the AMO and PDO on the decadal variation of the Santa Ana winds. Environ. Res. Lett. 2016, 11, 64019. [Google Scholar] [CrossRef] [Green Version]
- Bingoel, F. Complex Terrain and Wind Lidars. Ph.D. Thesis, Technical University of Denmark, Risoe National Laboratory for Sustainable Energy, Roskilde, DK, USA, 2019. [Google Scholar]
- USGS 30 ARC-second Global Elevation Data, GTOPO30 1997; USGS: Reston, VA, USA, 1997. [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.Y.; Wang, W.; Powers, J.G. A description of the advanced research WRF Version 3, mesoscale and microscale meteorology division. Natl. Cent. Atmos. Res. Boulder Color. USA 2008, 88, 7–25. [Google Scholar]
- Wu, W.-S.; Purser, R.J.; Parrish, D.F. Three-dimensional variational analysis with spatially inhomogeneous covariances. Mon. Weather. Rev. 2002, 130, 2905–2916. [Google Scholar] [CrossRef] [Green Version]
- Henry, W.K. Some aspects of the fate of cold fronts in the gulf of Mexico. Mon. Weather. Rev. 1979, 107, 1078–1082. [Google Scholar] [CrossRef] [Green Version]
- Perez, E.P.; Magana, A.V.; Caetano, E.; Kusunoki, S. Cold surge activity over the Gulf of Mexico in a warmer climate1. Front. Earth Sci. 2014, 2. [Google Scholar] [CrossRef] [Green Version]
- Dominguez, C.; Done, J.M.; Bruyère, C.L. Easterly wave contributions to seasonal rainfall over the tropical Americas in observations and a regional climate model. Clim. Dyn. 2019, 54, 191–209. [Google Scholar] [CrossRef] [Green Version]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Monin, A.S.; Obukhov, A.M. Basic Laws of Turbulent Mixing in the Atmosphere near the Ground. Tr. Akad. Nauk SSSR Geofiz. Inst. 1954, 24, 163–187. [Google Scholar]
- Stull, R. An Introduction to Boundary Layer, 1st ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2013; p. 666. [Google Scholar]
- International Electrotechnical Commission. Wind Turbines-Part. 1: Design Requirements, IEC 614001, 3rd ed.; International Electrotechnical Commission: Geneva, Switzerland, 2005. [Google Scholar]
- Hernández-Escobedo, Q.; Saldaña-Flores, R.; Rodríguez-García, E.; Manzano-Agugliaro, F. Wind energy resource in Northern Mexico. Renew. Sustain. Energy Rev. 2014, 32, 890–914. [Google Scholar] [CrossRef]
- Kamath, C. Understanding wind ramp events through analysis of historical data. In Proceedings of the IEEE PES T&D 2010, Sao Paolo, Brazil, 8–10 November 2010; pp. 1–6. [Google Scholar]
- Bradford, K.T.; Carpenter, R.L.; Shaw, B.L. Forecasting southern plains wind ramp events using the WRF Model At 3-Km. In Proceedings of the 9th Annual Student Conference of the American Meteorological Society, Atlanta, GA, USA, 16 January 2010; pp. 1–10. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Science, 2nd ed.; Elsevier: Burlington, MA, USA, 2006; ISBN 0-12-064490-8. [Google Scholar]
- Magaña, V.; Amador, J.A.; Medina, S. The midsummer drought over Mexico and Central America. J. Clim. 1999, 12, 1577–1588. [Google Scholar] [CrossRef]
- Schultz, D.M.; Bracken, W.E.; Bosart, L.F. Planetary-and synoptic-scale signatures associated with Central American cold surges. Mon. Weather. Rev. 1998, 126, 5–27. [Google Scholar] [CrossRef]
- Manzanilla, A.V. Mesoscale convective systems in NW Mexico during the strong ENSO events of 1997–1999. Atmósfera 2015, 28, 143–148. [Google Scholar] [CrossRef] [Green Version]
- Manzanilla, A.V.; Vázquez, M.C.; Francisco, J.J.P. Un estudio explorativo de los Sistemas Convectivos de Mesoescala de Mexico. Investig. Geográficas 2012, 26. [Google Scholar] [CrossRef]
- Badan-Dangon, A.; Dorman, C.E.; Merrifield, M.A.; Winant, C.D. The lower atmosphere over the Gulf of California. J. Geophys. Res. Space Phys. 1991, 96, 16877–16896. [Google Scholar] [CrossRef]
- Zhang, S.; Solari, G.; De Gaetano, P.; Burlando, M.; Repetto, M.P. A refined analysis of thunderstorm outflow characteristics relevant to the wind loading of structures. Probabilistic Eng. Mech. 2018, 54, 9–24. [Google Scholar] [CrossRef]
- Parzen, E. On Estimation of a probability density function and mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Martinez-Sanchez, J.; Cavazos, T. Eastern Tropical Pacific hurricane variability and landfalls on Mexican coasts. Clim. Res. 2014, 58, 221–234. [Google Scholar] [CrossRef]
- Morales-Acuña, E.; Torres, C.R.; Linero-Cueto, J.R. Surface wind characteristics over Baja California Peninsula during summer. Reg. Stud. Mar. Sci. 2019, 29, 100654. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Space Phys. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Dudhia, J. Improving the representation of resolved and unresolved topographic effects on surface wind in the WRF model. J. Appl. Meteorol. Clim. 2012, 51, 300–316. [Google Scholar] [CrossRef] [Green Version]
- Parker, D.J. Mesoescale meteorology overview. Encycl. Atmos. Sci. 2015, 316–322. [Google Scholar] [CrossRef]
- Zardi, D.; Whiteman, C.D. Diurnal mountain wind systems. In Mountain Weather Research and Forecasting; Chow, F., De Wekker, S., Snyder, B., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 35–119. ISBN 978-94-007-4098-3. [Google Scholar]
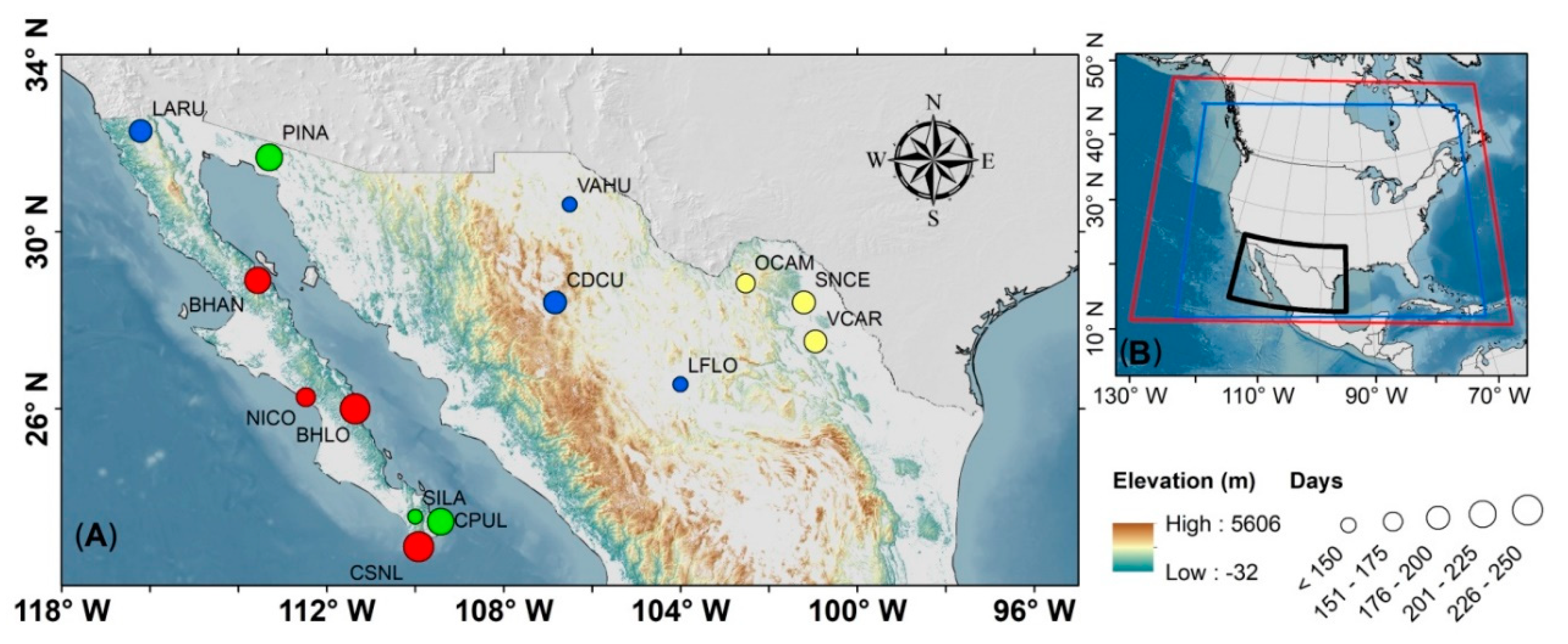
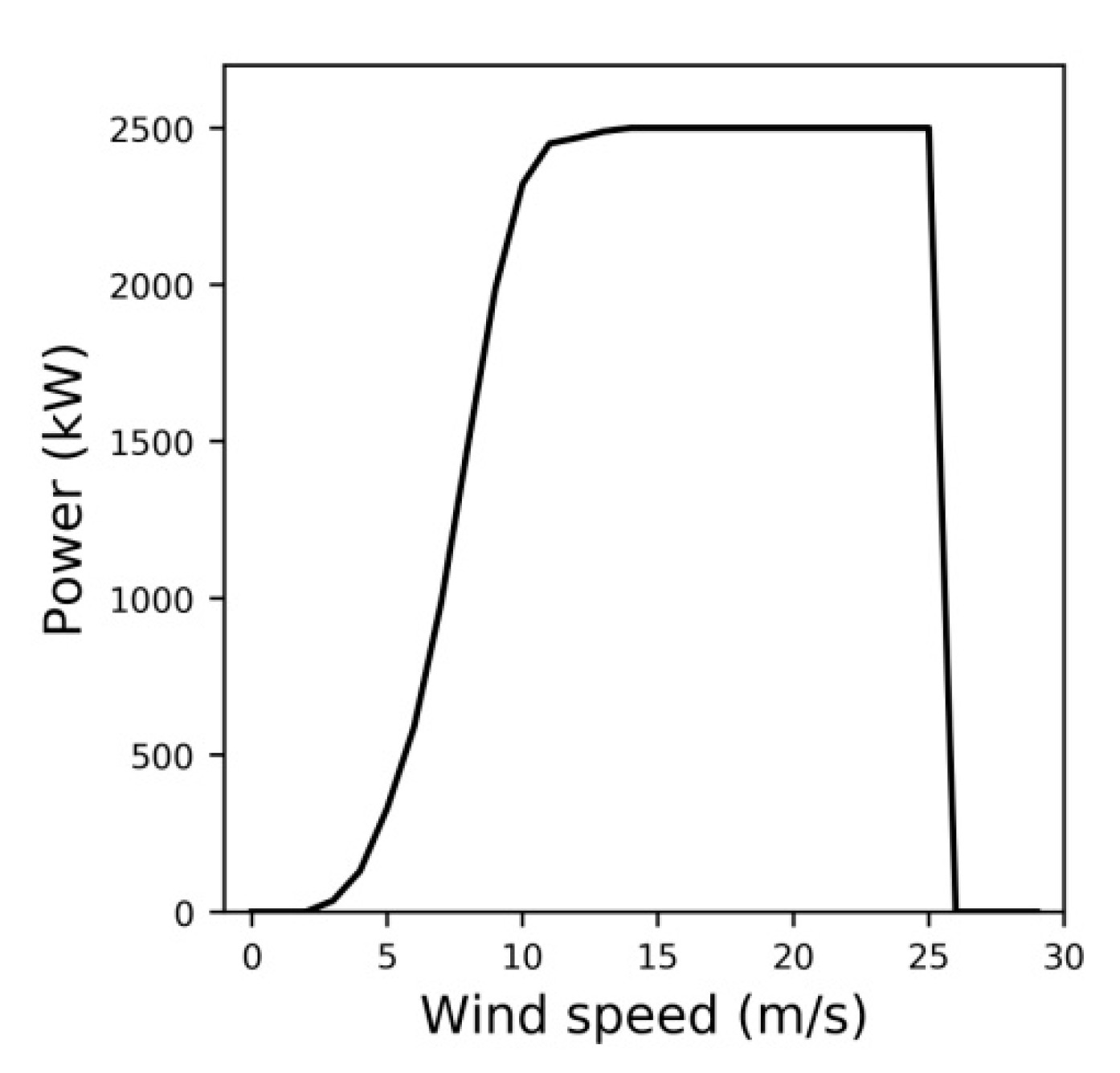
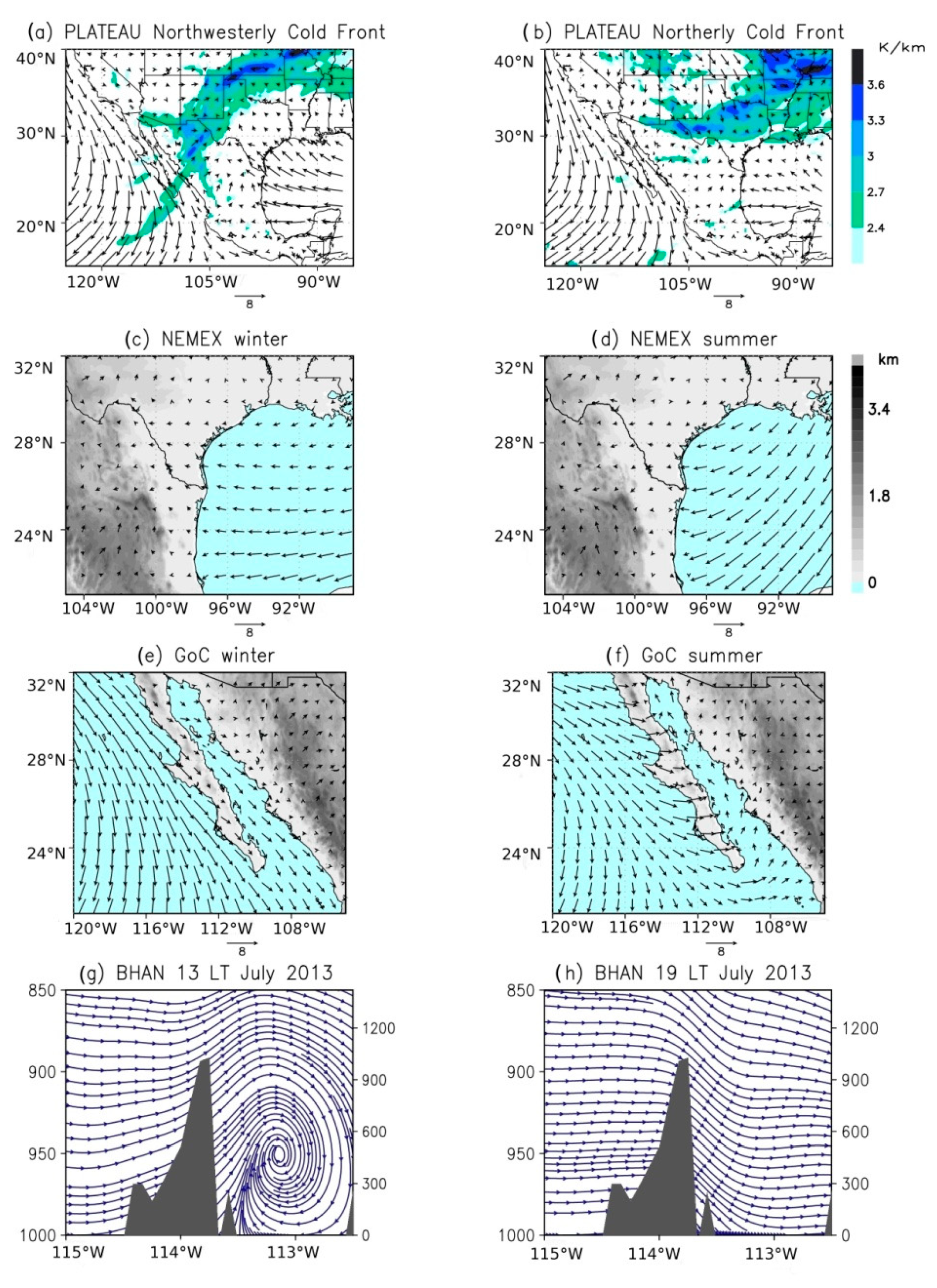
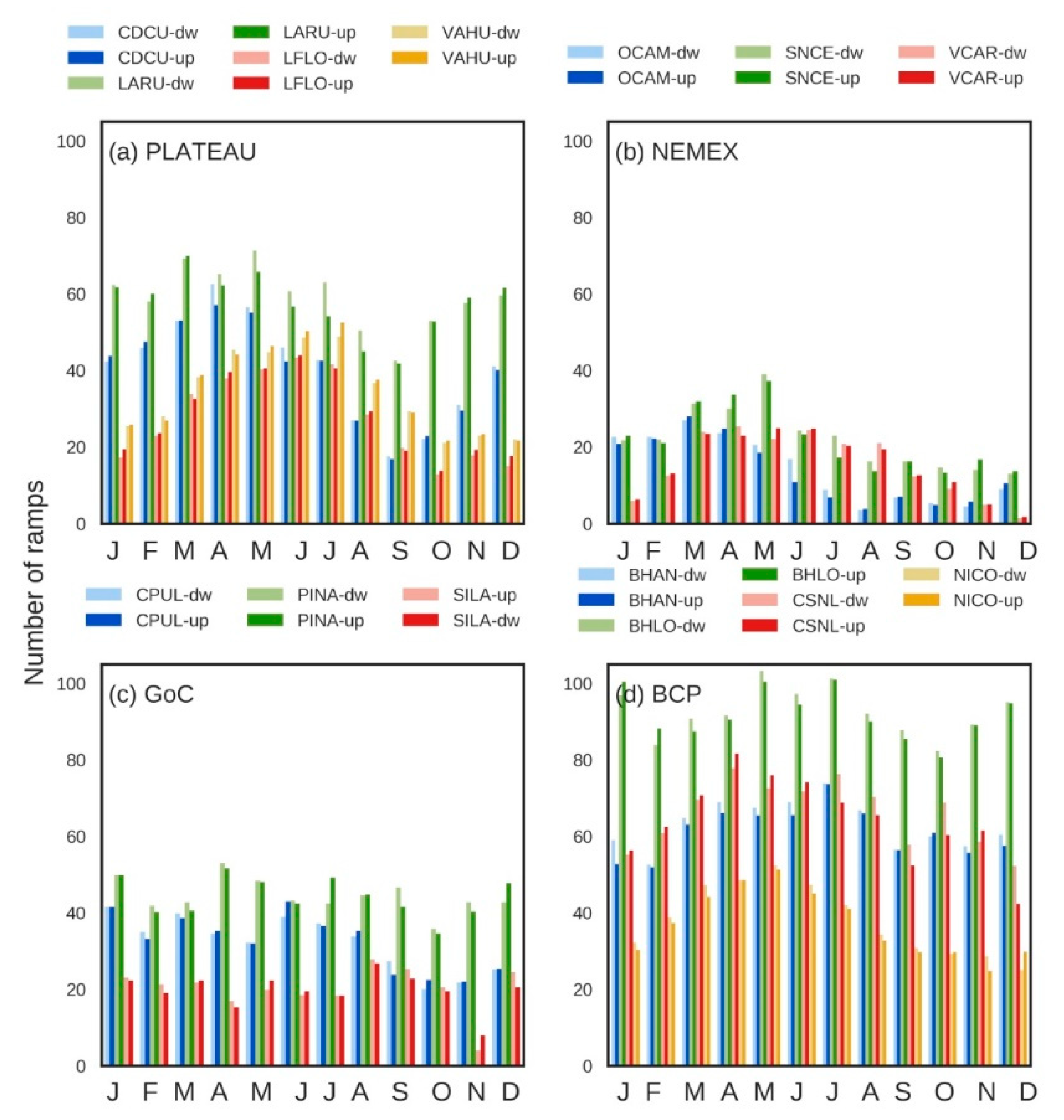



| Region | Weather Station | ID Weather Station | Topography | Dry Season | Wet Season | Record Period |
|---|---|---|---|---|---|---|
| PLATEAU | Ciudad Cuauhtemoc | CDCU | MC | MLS | LC | 2010–2017 |
| La Flor | LFLO | MC | MLS-LC | LC | 2010–2017 | |
| La Rumorosa | LARU | MC | MLS | LC | 2010–2015 | |
| Villa Ahumada | VAHU | MC | MLS | TC | 2010–2017 | |
| NEMEX | Ocampo | OCAM | MC | MLS | TC | 2013–2017 |
| Santa Cecilia | SNCE | MC | MLS | TC | 2013–2015 | |
| Venustiano Carranza | VCAR | MC | MLS | TC | 2010–2017 | |
| GoC | Cabo Pulmo | CPUL | MC | MLS | MLS | 2013–2017 |
| Pinacate | PINA | LC | MLS | MLS | 2013–2017 | |
| Sierra la Laguna | SILA | HC | LC | LC | 2013–2017 * | |
| BCP | Bahia de los Angeles | BHAN | C | LC | LC | 2010–2017 |
| Bahia de Loreto | BHLO | MC | LC | LC | 2013–2017 * | |
| Cabo San Lucas | CSNL | C | LC | LC | 2010–2017 | |
| San Juanico | NICO | MC | LC-MLS | LC-MLS | 2010–2015 |
| Forecast Verification | ||
|---|---|---|
| Metric | Definition | Formula |
| Mean Absolute Error (MAE) | Typical magnitude for the forecast error in a given verification data set. The MAE is the arithmetic average of the absolute values of the differences between the n pairs of forecasts ( and observations (). | |
| Correlation Coefficient (r) | It is a measure of the linear correlation between forecast and observations . Ratio of observation and forecast covariance ( and the product of their standard deviations | |
| Bias | The averaged difference between the forecast () and observation pairs. | |
| Contingency Table Derived Indices | ||
| Probability of detection (POD) | The ratio between the number of true positives and the number of observed positives, which indicates the fraction of observed YES events that are actually forecast. | |
| Critical Success Index (CSI) | The score is the number of correct YES events divided by the total number of occasions in which that event was forecast and/or observed. | |
| Frequency bias score (FBIAS) | The index measures the ratio of the frequency of forecast YES events to the frequency of observed YES events. The ramp forecasting system tends to underforecast when FBIAS < 1. | |
| False Alarm Rate (FAR) | This index measures the fraction of predicted YES events that did not occur. | |
| Region | Station | NAM | RAP | ||||
|---|---|---|---|---|---|---|---|
| MAE (m/s) | BIAS (m/s) | MAE (m/s) | BIAS (m/s) | ||||
| PLATEAU | CDCU | 1.3 | 0.5 | 37.1 | 1.4 | 0.6 | 0.7 |
| LARU | 1.5 | 0.5 | −3.2 | 1.2 | -0.1 | 6.2 | |
| LFLO | 1.3 | −0.2 | 0.8 | 1.3 | −0.3 | 7.2 | |
| VAHU | 1.3 | 0.2 | −38.6 | 1.3 | 0.2 | −55.9 | |
| NEMEX | OCAM | 1.4 | 0.9 | 235.4 | 2.0 | 1.8 | 200.1 |
| SNCE | 1.1 | 0.5 | 42.4 | 1.2 | 0.5 | 71.3 | |
| VCAR | 1.3 | −0.2 | 683.4 | 1.4 | 0.1 | 695.5 | |
| GoC | CPUL | 1.8 | 0.2 | −28.8 | 1.8 | 0.1 | −70.0 |
| PINA | 1.3 | −0.1 | −93.41 | 1.4 | −0.5 | −72.0 | |
| SLAG | 1.7 | −0.8 | 1224.9 | 1.6 | −0.2 | 1104.4 | |
| BCP | BHAN | 2.5 | −1.2 | −339.9 | 2.3 | 0.3 | −315.3 |
| BHLO | 2.0 | −0.9 | −156.1 | 2.2 | −0.2 | −84.4 | |
| CSNL | 2.0 | −1.3 | 161.2 | 2.0 | −0.3 | 41.3 | |
| NICO | 1.2 | −0.2 | −31.0 | 1.4 | 0.9 | −2.3 | |
| Region | Station | Critical Success Index (CSI) [RAP/NAM] | |||
|---|---|---|---|---|---|
| DJF (1 h) | JJA (1 h) | DEF (3 h) | JJA (3 h) | ||
| PLATEAU | CDCU | 0.09/0.14 | 0.05/0.04 | 0.28/0.34 | 0.17/0.20 |
| LARU | 0.05/0.08 | 0.08/0.06 | 0.17/0.20 | 0.43/0.32 | |
| LFLO | 0.09/0.06 | 0.04/0.01 | 0.21/0.21 | 0.12/0.11 | |
| VAHU | 0.12/0.07 | 0.08/0.09 | 0.23/0.18 | 0.18/0.16 | |
| NEMEX | OCAM | 0.03/0.02 | 0.01/0.01 | 0.10/0.09 | 0.08/0.05 |
| SNCE | 0.13/0.08 | 0.03/0.04 | 0.29/0.25 | 0.21/0.22 | |
| VCAR | 0.06/0.01 | 0.05/0.01 | 0.21/0.06 | 0.11/0.05 | |
| GoC | CPUL | 0.07/0.04 | 0.08/0.05 | 0.21/0.13 | 0.21/0.24 |
| PINA | 0.05/0.02 | 0.12/0.11 | 0.16/0.11 | 0.34/0.33 | |
| SILA | 0.02/0.01 | 0.01/0.01 | 0.05/0.01 | 0.03/0.01 | |
| BCP | BHAN | 0.08/0.06 | 0.03/0.02 | 0.19/0.20 | 0.09/0.04 |
| BHLO | 0.04/0.04 | 0.07/0.07 | 0.18/0.13 | 0.24/0.24 | |
| CSNL | 0.03/0.03 | 0.05/0.04 | 0.11/0.08 | 0.13/0.12 | |
| NICO | 0.09/0.06 | 0.07/0.10 | 0.29/0.24 | 0.28/0.24 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pereyra-Castro, K.; Caetano, E.; Martínez-Alvarado, O.; Quintanilla-Montoya, A.L. Wind and Wind Power Ramp Variability over Northern Mexico. Atmosphere 2020, 11, 1281. https://doi.org/10.3390/atmos11121281
Pereyra-Castro K, Caetano E, Martínez-Alvarado O, Quintanilla-Montoya AL. Wind and Wind Power Ramp Variability over Northern Mexico. Atmosphere. 2020; 11(12):1281. https://doi.org/10.3390/atmos11121281
Chicago/Turabian StylePereyra-Castro, Karla, Ernesto Caetano, Oscar Martínez-Alvarado, and Ana L. Quintanilla-Montoya. 2020. "Wind and Wind Power Ramp Variability over Northern Mexico" Atmosphere 11, no. 12: 1281. https://doi.org/10.3390/atmos11121281
APA StylePereyra-Castro, K., Caetano, E., Martínez-Alvarado, O., & Quintanilla-Montoya, A. L. (2020). Wind and Wind Power Ramp Variability over Northern Mexico. Atmosphere, 11(12), 1281. https://doi.org/10.3390/atmos11121281





