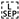Innovative Trend Analysis of Precipitation in the Lake Issyk-Kul Basin, Kyrgyzstan
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data Sources
3. Methodology
- Use of the ITA method [26] to detect details about the trends of monthly precipitation and temporal trends.
3.1. The Mann-Kendall Monotonic Trend Test
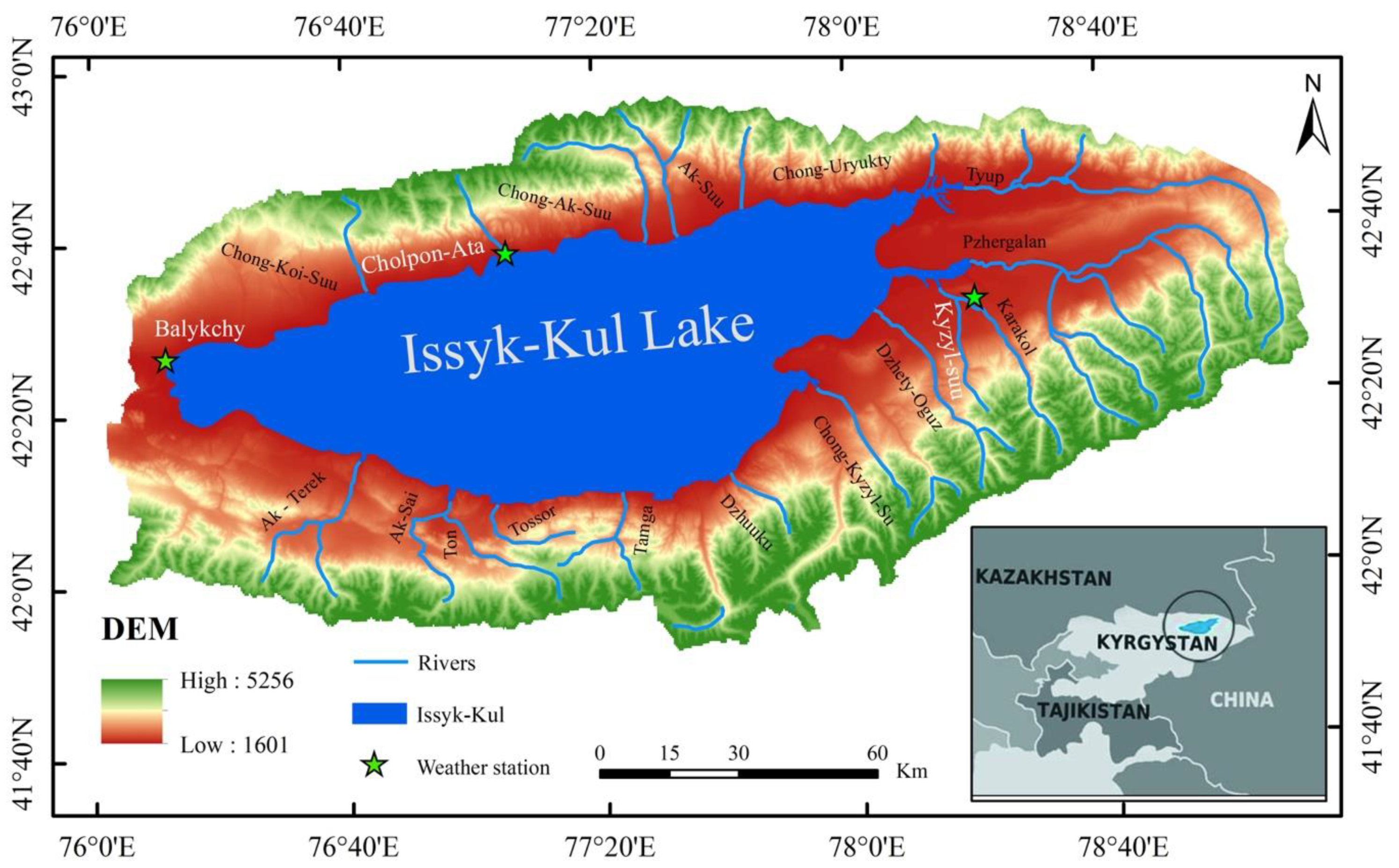
3.2. The Method for Innovative Trend Analysis ![Atmosphere 11 00332 i001]()
4. Results and Analysis
4.1. The Mann-Kendall Trend Test for Analyzing the Temporal Precipitation Dynamics in the Lake Issyk-Kul Basin
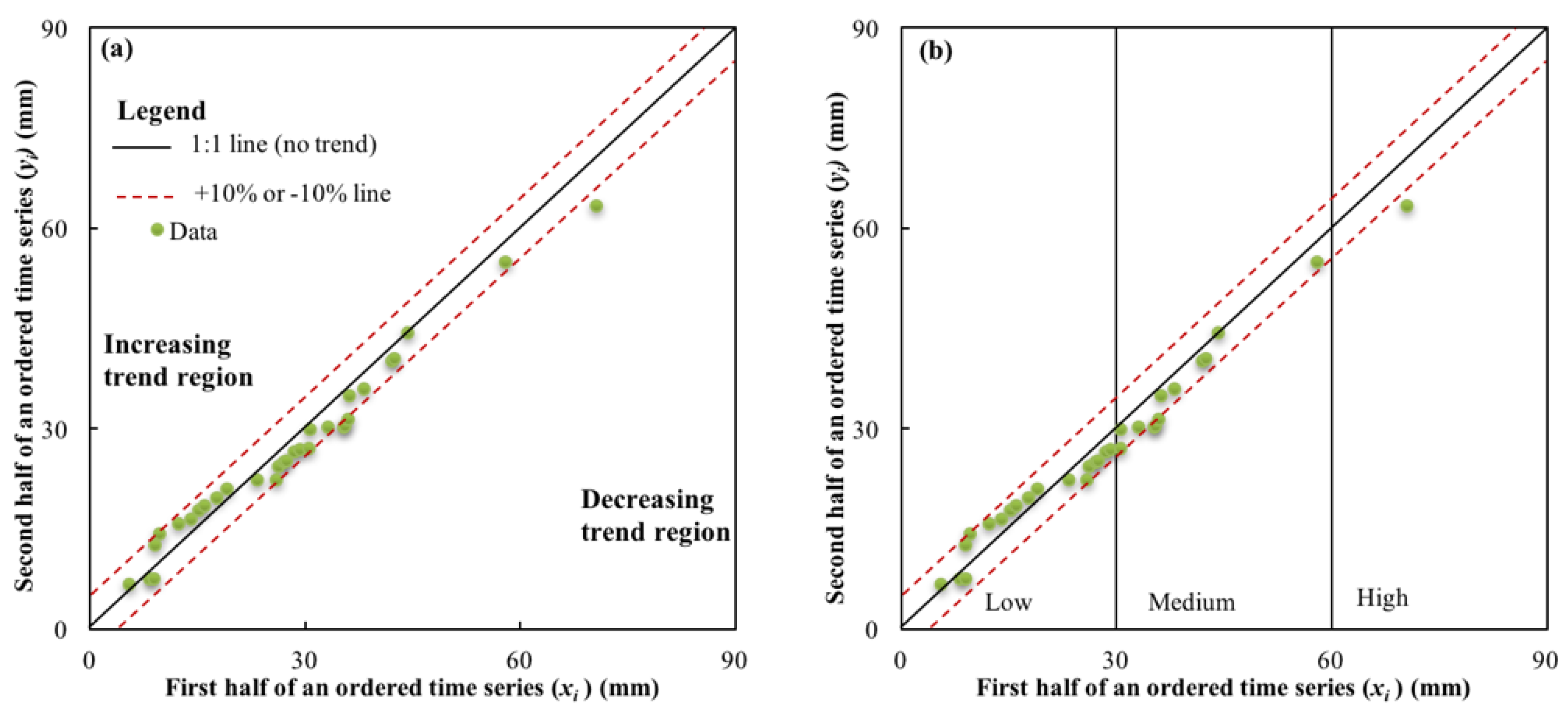
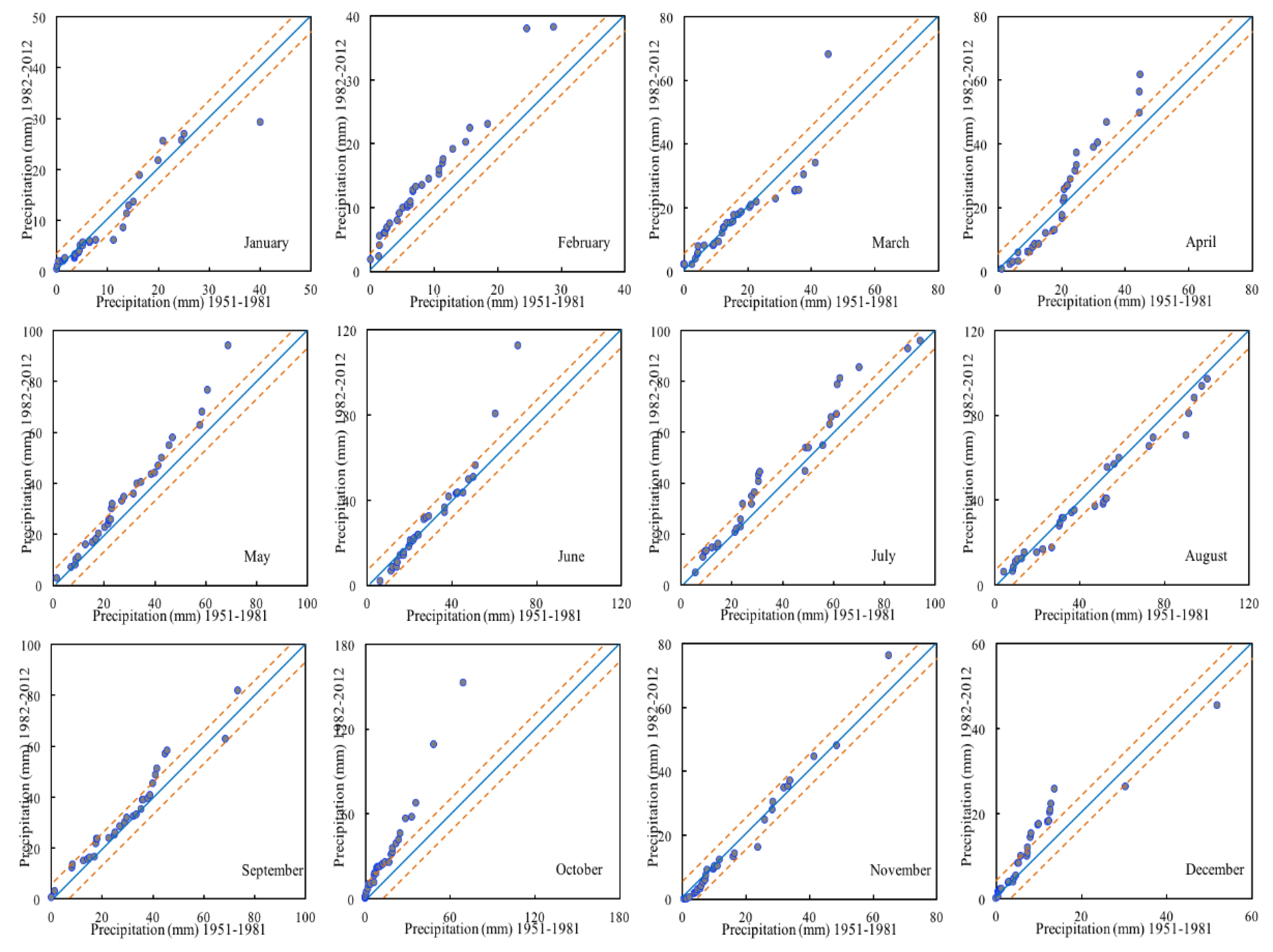
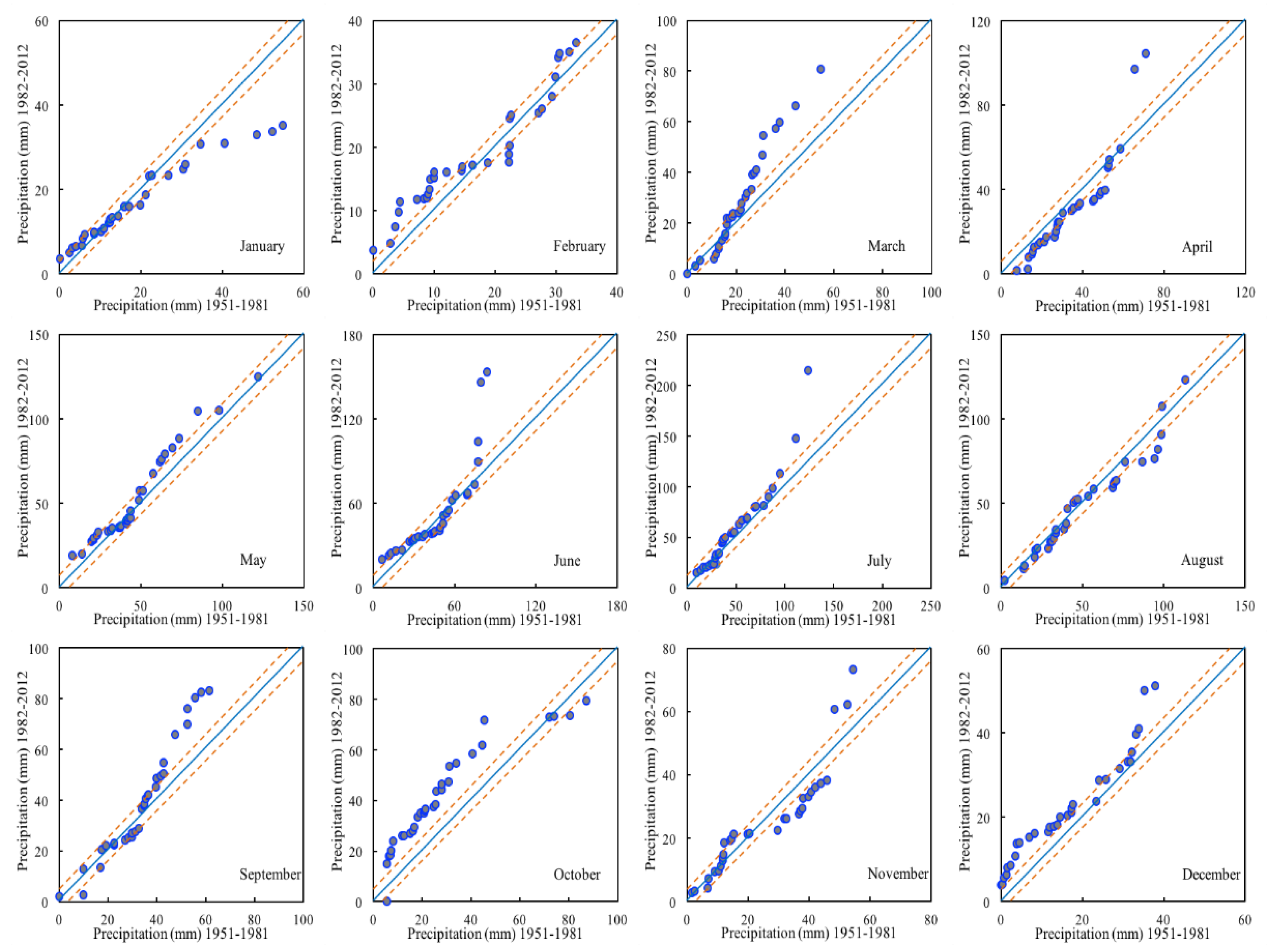
4.2. The ITA Method for Analyzing the Temporal Precipitation Dynamics in the Lake Issyk-Kull Basin
4.3. Comparison of the Mann-Kendall Trend Test and the ITA Method for Analyzing the Temporal Precipitation Dynamics in the Lake Issyk-Kul Basin
5. Discussion
6. Conclusions
- (1)
- The Mann-Kendall monotonic trend test and ITA method give different trends for the precipitation variables, which provide us with the complexity of the trend phenomena. According to the Mann-Kendall trend test, precipitation in all months at the Balykchy station shows a positive trend (except in January (Zc = −0.784) and July (Zc = 0.079)), and these in February and October (Zc = 2.769 and 3.912 > Z0.01 = 2.58) were significant at the 99% confidence level, and in December (Zc = 1.786 > Z0.10 = 1.645) at the 90% confidence level. At the Cholpon-Ata and Kyzyl-Suu stations, monthly precipitation also indicated a decreasing trend in January (Zc = -0.619 and 0.079), June (Zc = −0.134 and 0.249), August (Zc = −0.966 and −1.033), and November (Zc = −0.298 and −0.449). Meanwhile, precipitation at the two meteorological stations showed distinct differences in other months. At the monthly scale, significant increasing trends were detected in February (Zc = 2.381 and 1.871 > Z0.10 = 1.645) and October (Zc = 2.223 and 2.600 > Z0.05 = 1.96).
- (2)
- The ITA method allows a comprehensive investigation of the monthly variation of precipitation in this study, the results of which indicated that increasing trends were seen in 16 out of 36 months at the three stations, while six months showed decreasing patterns for “high” monthly precipitation. According to the “low” monthly precipitations, 14 months had an increasing trend, and four months showed a decreasing trend. Through the application of the ITA method (for January, March, and August at Balykchy, December at Cholpon-Ata, and July and December at Kyzyl-Suu), some data showed a significant increasing trend. However, with the Mann-Kendall test, no meaningful patterns were found.
- (3)
- Compared with the classical Mann-Kendall test, the ITA method has some advantages. This approach allows more detailed interpretations about trend detection, which is of benefit for identifying hidden variation trends of precipitation. These cannot be discovered by applying traditional methods, nor can the trend variability of extreme events—such as “high” and “low” values of monthly precipitation—be graphically illustrated by such methods. Besides, in the results from the two methods, the significant trend occupies 19.4% in the Mann-Kendall test and 36.1% in the ITA method, which indicates that the ITA method displays a more definite significant pattern than the Mann–Kendall Zc.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Arnell, N.W.; Gosling, S.N. The impacts of climate change on river flow regimes at the global scale. J. Hydrol. 2013, 486, 351–364. [Google Scholar] [CrossRef]
- Gosling, S.N.; Taylor, R.G.; Arnell, N.; Todd, M.C. A comparative analysis of projected impacts of climate change on river runoff from global and catchment-scale hydrological models. Hydrol. Earth Syst. Sci. 2011, 15, 279–294. [Google Scholar] [CrossRef] [Green Version]
- Van Vliet, M.T.H.; Franssen, W.H.P.; Yearsley, J.R.; Ludwig, F.; Haddeland, I.; Lettenmaier, D.P.; Kabat, P. Global river discharge and water temperature under climate change. Glob. Environ. Chang.-Hum. Policy Dimens. 2013, 23, 450–464. [Google Scholar] [CrossRef]
- Zhan, C.S.; Niu, C.W.; Song, X.M.; Xu, C.Y. The impacts of climate variability and human activities on streamflow in Bai River basin, northern China. Hydrol. Res. 2013, 44, 875–885. [Google Scholar] [CrossRef]
- Bronstert, A.; Niehoff, D.; Burger, G. Effects of climate and land-use change on storm runoff generation: Present knowledge and modelling capabilities. Hydrol. Processes 2002, 16, 509–529. [Google Scholar] [CrossRef]
- Karlsson, I.B.; Sonnenborg, T.O.; Refsgaard, J.C.; Trolle, D.; Børgesen, C.D.; Olesen, J.E.; Jeppesen, E.; Jensen, K.H. Combined effects of climate models, hydrological model structures and land use scenarios on hydrological impacts of climate change. J. Hydrol. 2016, 535, 301–317. [Google Scholar] [CrossRef]
- Xu, C.; Chen, Y.; Chen, Y.; Zhao, R.; Ding, H. Responses of Surface Runoff to Climate Change and Human Activities in the Arid Region of Central Asia: A Case Study in the Tarim River Basin, China. Environ. Manag. 2013. [Google Scholar] [CrossRef]
- Lioubimtseva, E.; Henebry, G.M. Climate and environmental change in arid Central Asia: Impacts, vulnerability, and adaptations. J. Arid Environ. 2009, 73, 963–977. [Google Scholar] [CrossRef]
- Deng, H.; Chen, Y.N.; Wang, H.J.; Zhang, S.H. Climate change with elevation and its potential impact on water resources in the tianshan mountains, central Asia. Glob. Planetary Chang. 2015, 135, 28–37. [Google Scholar] [CrossRef]
- White, C.J.; Tanton, T.W.; Rycroft, D.W. The Impact of Climate Change on the Water Resources of the Amu Darya Basin in Central Asia. Water Resour. Manag. 2014, 28, 5267–5281. [Google Scholar] [CrossRef]
- Jianqing, Z.; Mingjin, Z.; Buda, S. The Interpretation of Freshwater Resources in the Fifth Assessment Report of IPCC. Progress. Inquisitiones DE Mutat. Clim. 2014, 2014. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.Y.; Shi, Y.Y.; Guo, Y.Z.; Zheng, Y.X. Temporal and spatial variation of annual mean air temperature in arid and semiarid region in northwest China over a recent 46 year period. J. Arid Land 2010, 2, 87–97. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, C.-Y.; Yang, T. Scaling properties of the runoff variations in the arid and semi-arid regions of China: A case study of the Yellow River basin. Stoch. Environ. Res. Risk Assess. 2009, 23, 1103–1111. [Google Scholar] [CrossRef]
- Balocchi, F.; Pizarro, R.; Meixner, T.; Urbina, F. Annual and monthly runoff analysis in the Elqui River, Chile, a semi-arid snow-glacier fed basin. Tecnologia Y Ciencias Del Agua 2017, 8, 23–35. [Google Scholar] [CrossRef]
- Alifujiang, Y.; Abuduwaili, J.; Ma, L.; Samat, A.; Groll, M. System Dynamics Modeling of Water Level Variations of Lake Issyk-Kul, Kyrgyzstan. Water 2017, 9, 989. [Google Scholar] [CrossRef] [Green Version]
- Alymkulova, B.; Abuduwaili, J.; Issanova, G.; Nahayo, L. Consideration of Water Uses for Its Sustainable Management, the Case of Issyk-Kul Lake, Kyrgyzstan. Water 2016, 8, 298. [Google Scholar] [CrossRef] [Green Version]
- Gocic, M.; Trajkovic, S. Analysis of changes in meteorological variables using Mann-Kendall and Sen’s slope estimator statistical tests in Serbia. Glob. Planetary Chang. 2013, 100, 172–182. [Google Scholar] [CrossRef]
- Rahman, M.A.; Yunsheng, L.; Sultana, N. Analysis and prediction of rainfall trends over Bangladesh using Mann–Kendall, Spearman’s rho tests and ARIMA model. Meteorol. Atmos. Phys. 2016. [Google Scholar] [CrossRef]
- He, X.; Guan, H.D.; Zhang, X.P.; Simmons, C.T. A wavelet-based multiple linear regression model for forecasting monthly rainfall. Int. J. Climatol. 2014, 34, 1898–1912. [Google Scholar] [CrossRef]
- Eslami-Andargoli, L.; Dale, P.; Sipe, N.; Chaseling, J. Mangrove expansion and rainfall patterns in Moreton Bay, Southeast Queensland, Australia. Estuar. Coast. Shelf Sci. 2009, 85, 292–298. [Google Scholar] [CrossRef] [Green Version]
- Sang, Y.-F.; Wang, Z.; Liu, C. Comparison of the MK test and EMD method for trend identification in hydrological time series. J. Hydrol. 2014, 510, 293–298. [Google Scholar] [CrossRef]
- Zhao, X.; Li, Z.; Zhu, Q.; Zhu, D.; Liu, H. Climatic and drought characteristics in the loess hilly-gully region of China from 1957 to 2014. PLoS ONE 2017, 12, e0178701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adarsh, S.; Reddy, M.J. Trend analysis of rainfall in four meteorological subdivisions of southern India using nonparametric methods and discrete wavelet transforms. Int. J. Climatol. 2015, 35, 1107–1124. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E. Application of the Innovative Trend Analysis Method for the Trend Analysis of Rainfall Anomalies in Southern Italy. Water Resour. Manag. 2018. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Y.; Tabari, H.; Jie, W. Innovative trend analysis of annual and seasonal rainfall in the Yangtze River Delta, eastern China. Atmos. Res. 2020, 231. [Google Scholar] [CrossRef]
- Şen, Z. Innovative Trend Analysis Methodology. J. Hydrol. Eng. 2012, 17, 1042–1046. [Google Scholar] [CrossRef]
- Kisi, O. An innovative method for trend analysis of monthly pan evaporations. J. Hydrol. 2015, 527, 1123–1129. [Google Scholar] [CrossRef]
- Tabari, H.; Taye, M.T.; Onyutha, C.; Willems, P. Decadal Analysis of River Flow Extremes Using Quantile-Based Approaches. Water Resour. Manag. 2017, 31, 3371–3387. [Google Scholar] [CrossRef]
- Caloiero, T. Evaluation of rainfall trends in the South Island of New Zealand through the innovative trend analysis (ITA). Theor. Appl. Climatol. 2019, 139, 493–504. [Google Scholar] [CrossRef]
- Li, J.; Wu, W.; Ye, X.; Jiang, H. Innovative trend analysis of main agriculture natural hazards in China during 1989–2014. Nat. Hazards 2018. [Google Scholar] [CrossRef]
- Saplıoğlu, K.; Kilit, M.; Yavuz, B.K. Trend analysis of streams in the Western Mediterranean Basin of Turkey. Fresenius Environ. Bull. 2014, 23, 313–324. [Google Scholar]
- Wu, H.; Qian, H. Innovative trend analysis of annual and seasonal rainfall and extreme values in Shaanxi, China, since the 1950s. Int. J. Climatol. 2017, 37, 2582–2592. [Google Scholar] [CrossRef]
- Alashan, S. An improved version of innovative trend analyses. Arab. J. Geosci. 2018, 11. [Google Scholar] [CrossRef]
- Dean, J.F.; Webb, J.A.; Jacobsen, G.E.; Chisari, R.; Dresel, P.E. A groundwater recharge perspective on locating tree plantations within low-rainfall catchments to limit water resource losses. Hydrol. Earth Syst. Sci. 2015, 19, 1107–1123. [Google Scholar] [CrossRef] [Green Version]
- García-Garizábal, I. Rainfall variability and trend analysis in coastal arid Ecuador. Int. J. Climatol. 2017. [Google Scholar] [CrossRef]
- Karthe, D.; Chalov, S.; Borchardt, D. Water Resources and Their Management in Central Asia in the Early 21st Century: Status, Challenges and Future Prospects. Environ. Earth Sci. 2014, 73, 487–499. [Google Scholar] [CrossRef]
- Mathis, M.; Sorrel, P.; Klotz, S.; Huang, X.; Oberhänsli, H. Regional vegetation patterns at lake Son Kul reveal Holocene climatic variability in central Tien Shan (Kyrgyzstan, Central Asia). Quat. Sci. Rev. 2014, 89, 169–185. [Google Scholar] [CrossRef]
- Junli, L.I.; Müller, J.P.; Schneider, J.F. Spatio-temporal Analysis of Recent Changes of Lake Area and Lake Water Level at High Mountains in Central Asia. Resour. Sci. 2011, 33, 1839–1846. [Google Scholar]
- Aizen, V.B.; Aizen, E.; Glazirin, G.; Loaiciga, H. Simulation of daily runoff in Central Asian alpine watersheds. J. Hydrol. 2000, 238, 15–34. [Google Scholar] [CrossRef]
- Kakahaji, H.; Banadaki, H.D.; Kakahaji, A.; Kakahaji, A. Prediction of Urmia Lake Water-Level Fluctuations by Using Analytical, Linear Statistic and Intelligent Methods. Water Resour. Manag. 2013, 27, 4469–4492. [Google Scholar] [CrossRef]
- Romanovsky, V.V. Water Level Variations and Water Balance of Lake Issyk-Kul. In Lake Issyk-Kul: Its Natural Environment; Springer: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Salamat, A.U.; Abuduwaili, J.; Shaidyldaeva, N. Impact of climate change on water level fluctuation of Issyk-Kul Lake. Arab. J. Geosci. 2015, 8, 5361–5371. [Google Scholar] [CrossRef]
- Romanovsky, V.V.; Tashbaeva, S.; Cretaux, J.; Calmant, S. The closed Lake Issyk-Kul as an indicator of global warming in Tien-Shan. Nat. Sci. 2013, 5, 608–623. [Google Scholar] [CrossRef] [Green Version]
- Ferronskii, V.I.; Polyakov, V.A.; Brezgunov, V.S.; Vlasova, L.S.; Karpychev, Y.A.; Bobkov, A.F.; Romaniovskii, V.V.; Johnson, T.; Ricketts, D.; Rasmussen, K. Variations in the Hydrological Regime of Kara-Bogaz-Gol Gulf, Lake Issyk-Kul, and the Aral Sea Assessed Based on Data of Bottom Sediment Studies. Water Resour. 2003, 30, 252–259. [Google Scholar] [CrossRef]
- Shabunin, G.D.; Shabunin, A.G. Climate and Physical Properties of Water in Lake Issyk-Kul. In Lake Issyk-Kul: Its Natural Environment; Springer: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Mann, H.B. Nonparametric Tests against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. A new measure of rank correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Miao, C.Y.; Ni, J.R.; Borthwick, A.G.L. Recent changes of water discharge and sediment load in the Yellow River basin, China. Progress Phys. Geogr. 2010, 34, 541–561. [Google Scholar] [CrossRef] [Green Version]
- Farlie, D.J.G. Rank Correlation Methods—Kendall, Mg. J. R. Stat. Soc. Ser. General 1971, 134, 682. [Google Scholar] [CrossRef]
- Şen, Z. Innovative trend significance test and applications. Theor. Appl. Climatol. 2015, 127, 1–9. [Google Scholar] [CrossRef]
- Dorjsuren, B.; Yan, D.H.; Wang, H.; Sonomdagva, C.; Enkhbold, A.; Xu, Y.; Girma, A.; Gedefaw, M.; Abiyu, A. Observed Trends of Climate and River Discharge in Mongolia’s Selenga Sub-Basin of the Lake Baikal Basin. Water 2018, 10, 1436. [Google Scholar] [CrossRef] [Green Version]
- Malik, A.; Kumar, A.; Guhathakurta, P.; Kisi, O. Spatial-temporal trend analysis of seasonal and annual rainfall (1966–2015) using innovative trend analysis method with significance test. Arab. J. Geosci. 2019, 12, 328. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, L.; Lin, A.; Zhang, M.; Niu, Z. Innovative trend analysis of solar radiation in China during 1962–2015. Renew. Energy 2018, 119, 675–689. [Google Scholar] [CrossRef]
- Sonali, P.; Kumar, D.N. Review of trend detection methods and their application to detect temperature changes in India. J. Hydrol. 2013, 476, 212–227. [Google Scholar] [CrossRef]
- Şen, Z. Innovative Trend Methodologies in Science and Engineering; Springer: Berlin, Germany, 2017. [Google Scholar] [CrossRef]
- Lacombe, G.; McCartney, M.; Forkuor, G. Drying Climate in Ghana over the Period 1960–2005: Evidence from the Resampling-Based Mann-Kendall Test at Local and Regional Levels. Hydrologic. Sci. J. 2012, 8. [Google Scholar] [CrossRef] [Green Version]
| Precipitation | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Station | mm | mm | mm | mm | mm | mm | mm | mm | mm | mm | mm | mm | mm |
| Balykchy | 1.2 | 1.4 | 3.7 | 6.8 | 23.6 | 27.1 | 29.2 | 26.1 | 10.7 | 4.5 | 1.3 | 1.2 | 136.7 |
| Cholpon-Ata | 8.9 | 10.7 | 16.8 | 20.7 | 32.0 | 30.8 | 39.3 | 41.5 | 30.4 | 23.2 | 16.3 | 9.9 | 280.6 |
| Kyzyl-Suu | 17.7 | 17.8 | 24.7 | 32.9 | 49.1 | 49.6 | 54.4 | 50.4 | 36.5 | 34.7 | 25.3 | 19.1 | 412.2 |
| Average | 9.27 | 9.97 | 15.07 | 20.13 | 34.90 | 35.83 | 40.97 | 39.33 | 25.87 | 20.80 | 14.30 | 10.07 | 276.50 |
| Stations | Balykchy | Cholpon-Ata | Kyzyl-Suu | |||
|---|---|---|---|---|---|---|
| Z Month | Mann-Kendall Test Statistics (S) | Zc [H0] Values per Month | Mann-Kendall Test Statistics (S) | Zc [H0] Values per Month | Mann-Kendall Test Statistics (S) | Zc [H0] Values per Month |
| Jan | −169 | −0.784[A] | −103 | −0.619[A] | −14 | −0.079[A] |
| Feb | 409 | 2.769[R] *** | 393 | 2.381[R] ** | 309 | 1.871[A] * |
| Mar | 187 | 1.476[A] | −44 | −0.018[A] | 120 | 0.723[A] |
| Apr | 27 | 0.516[A] | −4 | 0.172[A] | −203 | −1.227[A] |
| May | −3 | 0.352[A] | 71 | 0.425[A] | −41 | −0.243[A] |
| Jun | −17 | 0.267[A] | −23 | −0.134[A] | −42 | −0.249[A] |
| Jul | −76 | −0.079[A] | 108 | 0.650[A] | 87 | 0.522[A] |
| Aug | −12 | 0.292[A] | −160 | −0.966[A] | −171 | −1.033[A] |
| Sep | −20 | 0.243[A] | 253 | 1.531[A] | 241 | 1.458[A] |
| Oct | −594 | 3.912[R] *** | 367 | 2.223[R] ** | 429 | 2.600[R] *** |
| Nov | 226 | 1.604[A] | −50 | −0.298[A] | −75 | −0.449[A] |
| Dec | 262 | 1.786[A] * | 126 | 0.759[A] | 200 | 1.209[A] |
| Balykchy Station | Cholpon-Ata Station | Kyzyl-Suu Station | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Month | MK Test | ITA Method | MK Test | ITA Method | MK Test | ITA Method | |||
| Low | High | Low | High | Low | High | ||||
| Jan Feb | No | No | No | No | No | No | No | No | Yes (-) |
| Yes (+) | Yes (+) | Yes (+) | Yes (+) | Yes (+) | Yes (+) | Yes (+) | Yes (+) | No | |
| Mar Apr | No | No | Yes (+) | No | No | No | No | No | Yes (+) |
| No | No | No | No | Yes (-) | Yes (+) | No | Yes (-) | Yes (+) | |
| May Jun | No | No | Yes (-) | No | Yes (+) | Yes (+) | No | No | Yes (+) |
| No | No | Yes (-) | No | No | Yes (+) | No | No | Yes (+) | |
| Jul Aug | No | No | Yes (-) | No | Yes (+) | Yes (+) | No | No | Yes (+) |
| No | Yes (+) | No | No | No | Yes (-) | No | No | No | |
| Sep Oct | No | Yes (-) | No | No | Yes (+) | No | No | No | Yes (+) |
| Yes (+) | Yes (+) | No | Yes (+) | Yes (+) | Yes (+) | Yes (+) | Yes (+) | No | |
| Nov Dec | No | No | No | No | Yes (-) | No | No | Yes (+) | No |
| Yes (+) | Yes (+) | Yes (+) | No | Yes (+) | Yes (-) | No | Yes (+) | Yes (+) | |
| Month | Balykchy | Cholpon-Ata | Kyzyl-Suu | |||
|---|---|---|---|---|---|---|
| Slope b | ITA (D) | Slope b | ITA (D) | Slope b | ITA (D) | |
| Jan Feb | 0.01 | 6.09 ** | −0.03 | −0.49 | −0.02 | −1.14 |
| 0.04 | 26.94 ** | 0.13 | 6.16 ** | 0.06 | 3.15 ** | |
| Mar Apr | 0.04 | 6.54 ** | −0.03 | −0.23 | 0.10 | 1.36 |
| 0.01 | 0.27 | 0.04 | 1.14 | −0.11 | −0.87 | |
| May Jun | 0.04 | −0.12 | 0.08 | 1.88 | 0.04 | 1.27 |
| 0.004 | −0.37 | −0.01 | 0.53 | 0.13 | 1.43 | |
| Jul Aug | 0.001 | −0.24 | 0.10 | 1.36 | 0.22 | 2.07 * |
| 0.02 | 1.97 * | −0.20 | −0.99 | −0.24 | −0.42 | |
| Sep Oct | 0.03 | −0.95 | 0.22 | 1.07 | 0.17 | 1.71 |
| 0.09 | 4.96 ** | 0.27 | 10.46 ** | 0.32 | 4.29 ** | |
| Nov Dec | 0.01 | −1.01 | 0.01 | −0.16 | −0.08 | −0.17 |
| 0.04 | 29.29 ** | 0.02 | 3.82 ** | 0.16 | 3.43 ** | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alifujiang, Y.; Abuduwaili, J.; Maihemuti, B.; Emin, B.; Groll, M. Innovative Trend Analysis of Precipitation in the Lake Issyk-Kul Basin, Kyrgyzstan. Atmosphere 2020, 11, 332. https://doi.org/10.3390/atmos11040332
Alifujiang Y, Abuduwaili J, Maihemuti B, Emin B, Groll M. Innovative Trend Analysis of Precipitation in the Lake Issyk-Kul Basin, Kyrgyzstan. Atmosphere. 2020; 11(4):332. https://doi.org/10.3390/atmos11040332
Chicago/Turabian StyleAlifujiang, Yilinuer, Jilili Abuduwaili, Balati Maihemuti, Bilal Emin, and Michael Groll. 2020. "Innovative Trend Analysis of Precipitation in the Lake Issyk-Kul Basin, Kyrgyzstan" Atmosphere 11, no. 4: 332. https://doi.org/10.3390/atmos11040332