Fast Camera Analysis of Plasma Instabilities in Hall Effect Thrusters Using a POD Method under Different Operating Regimes
Abstract
:1. Introduction
2. Materials and Methods
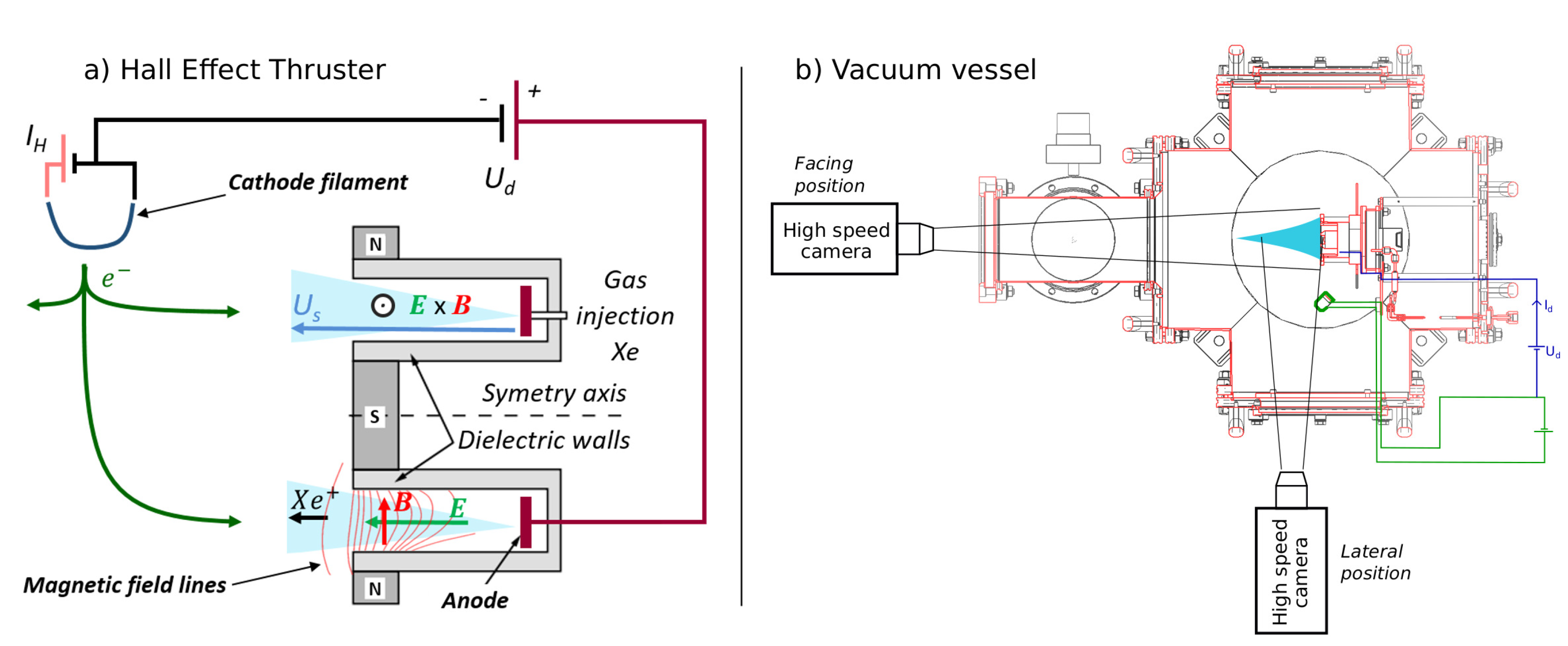
2.1. The Hall Effect Thruster
2.2. Vacuum Chamber
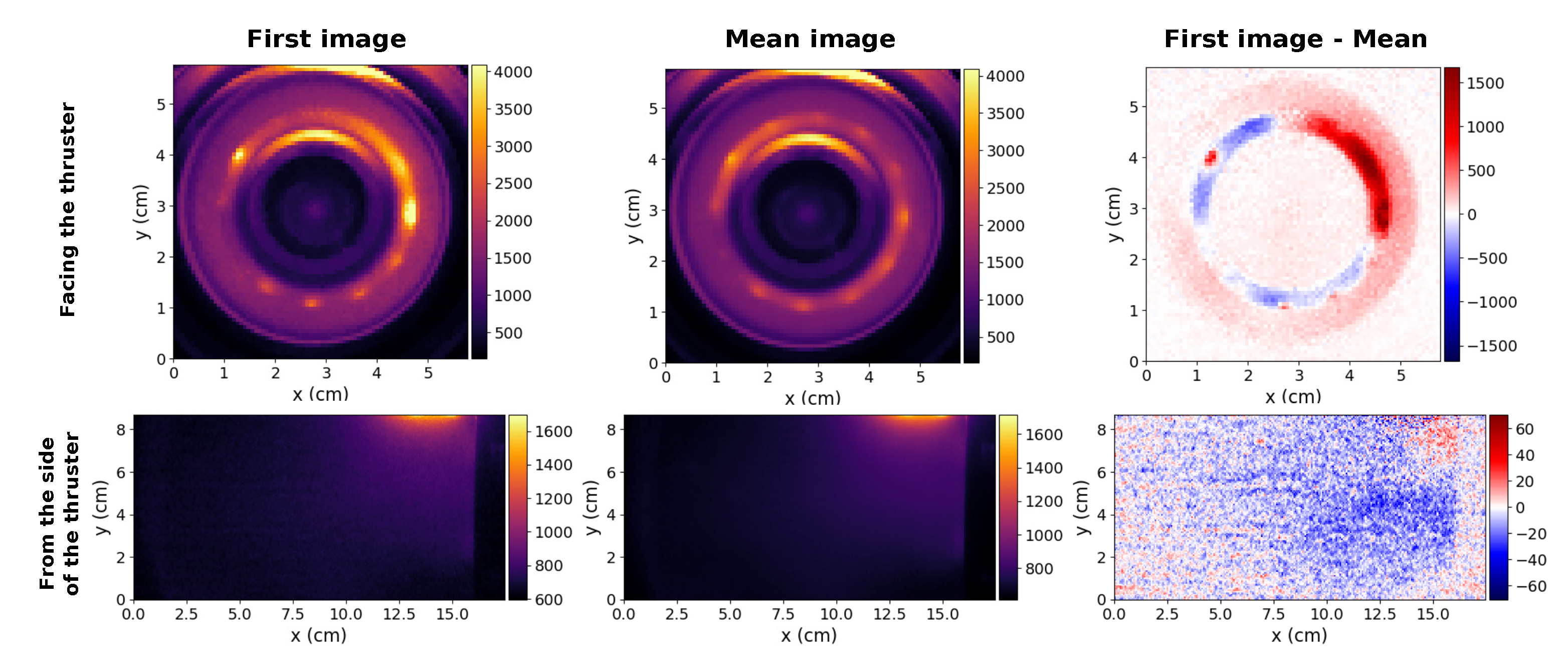
2.3. Fast Frame Camera, Data Acquisition
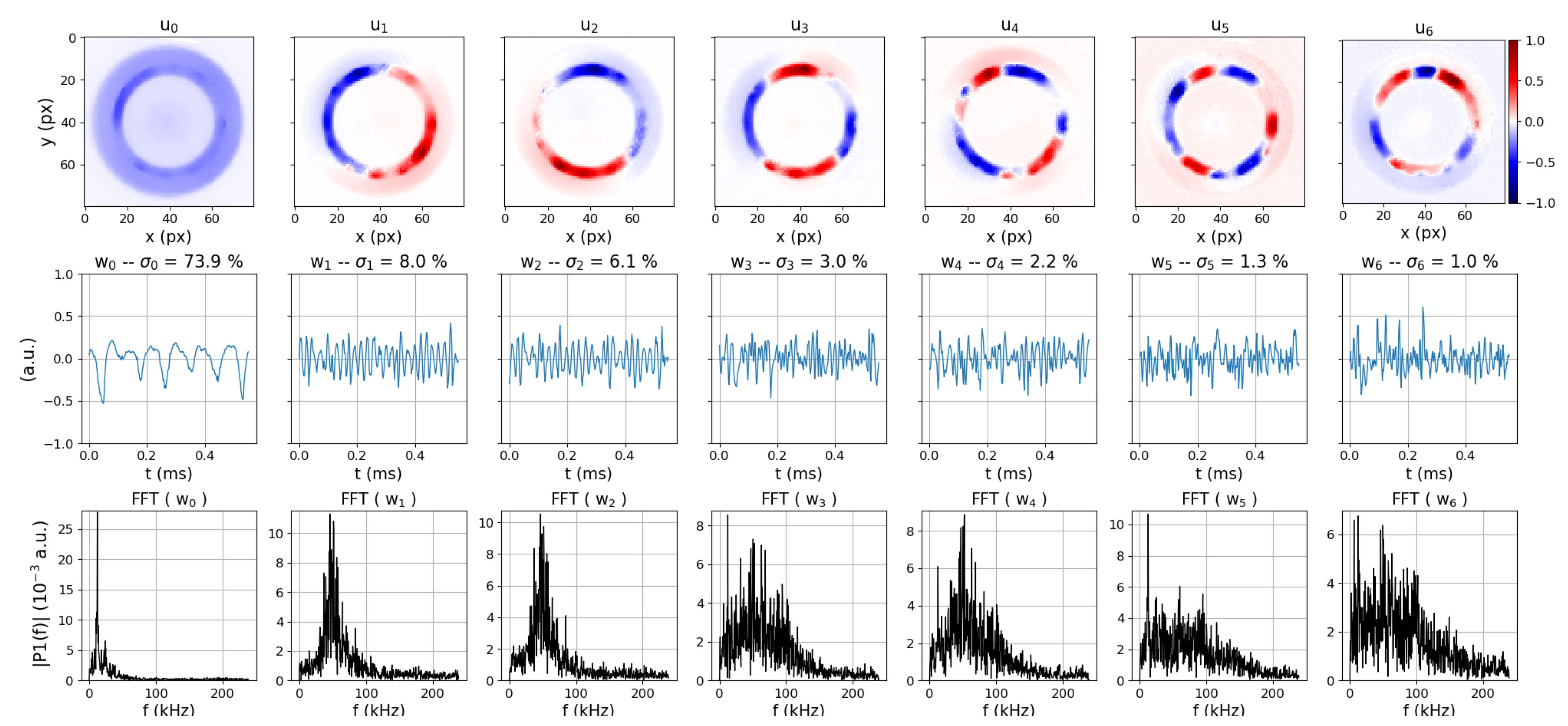
2.4. POD Analysis Routine
3. Results
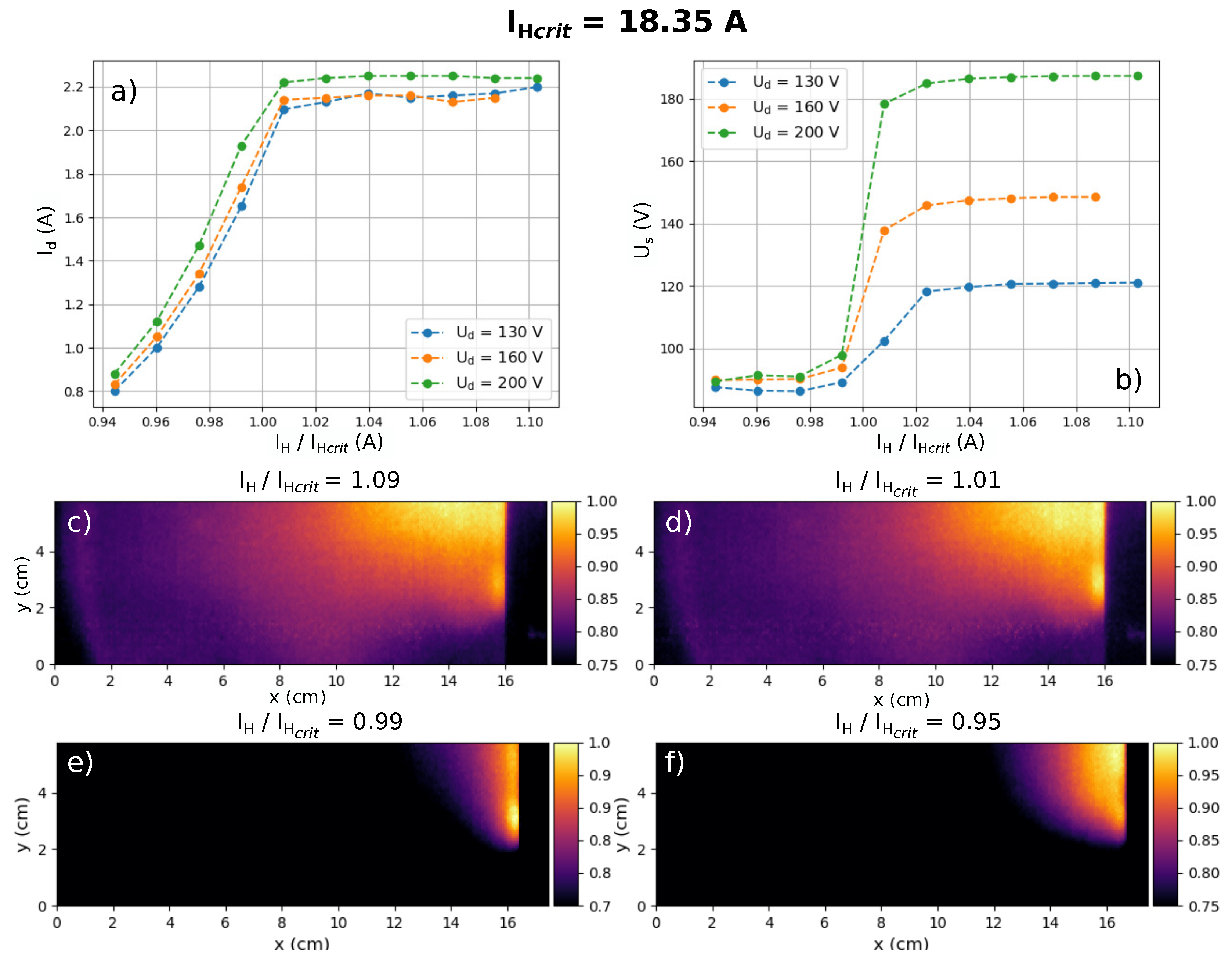
3.1. Cathode Emissivity and Thruster Operating Regime
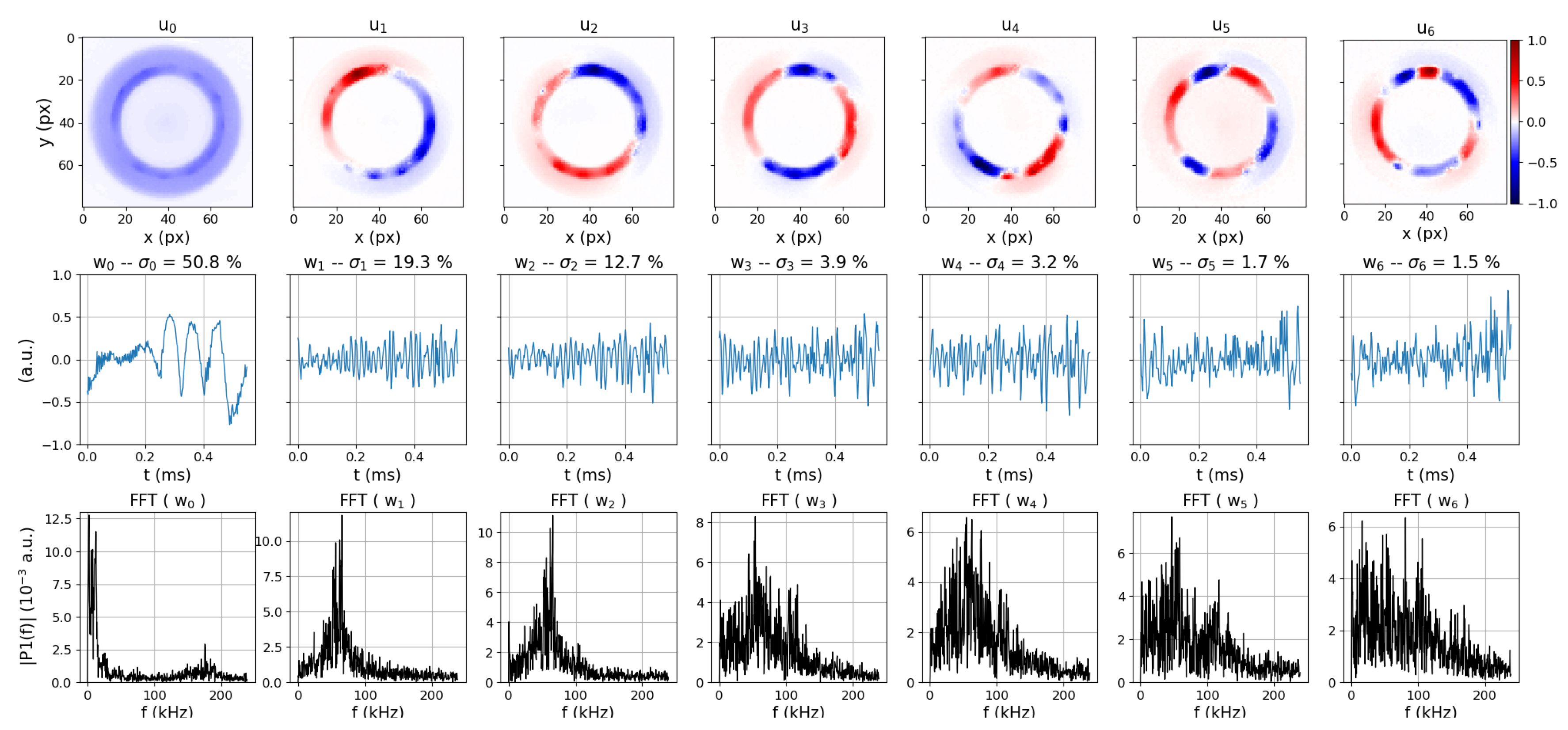
3.2. Analysis of the Oscillatory Phenomenon through the Regime Transition
3.2.1. The Nominal Regime
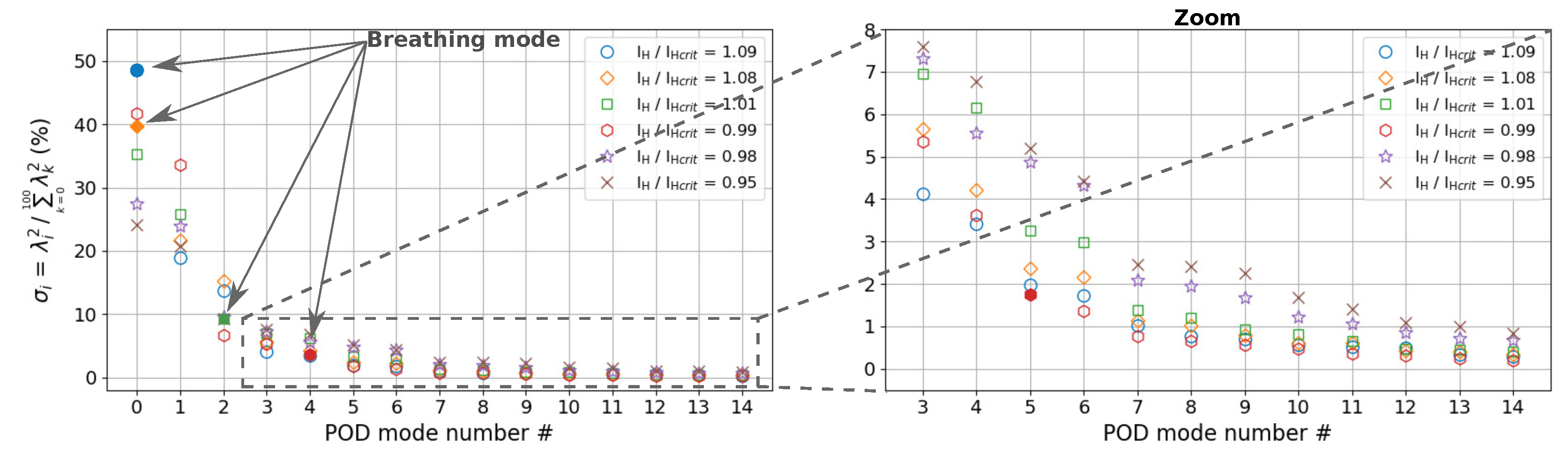
The Breathing Mode
The Rotating Modes
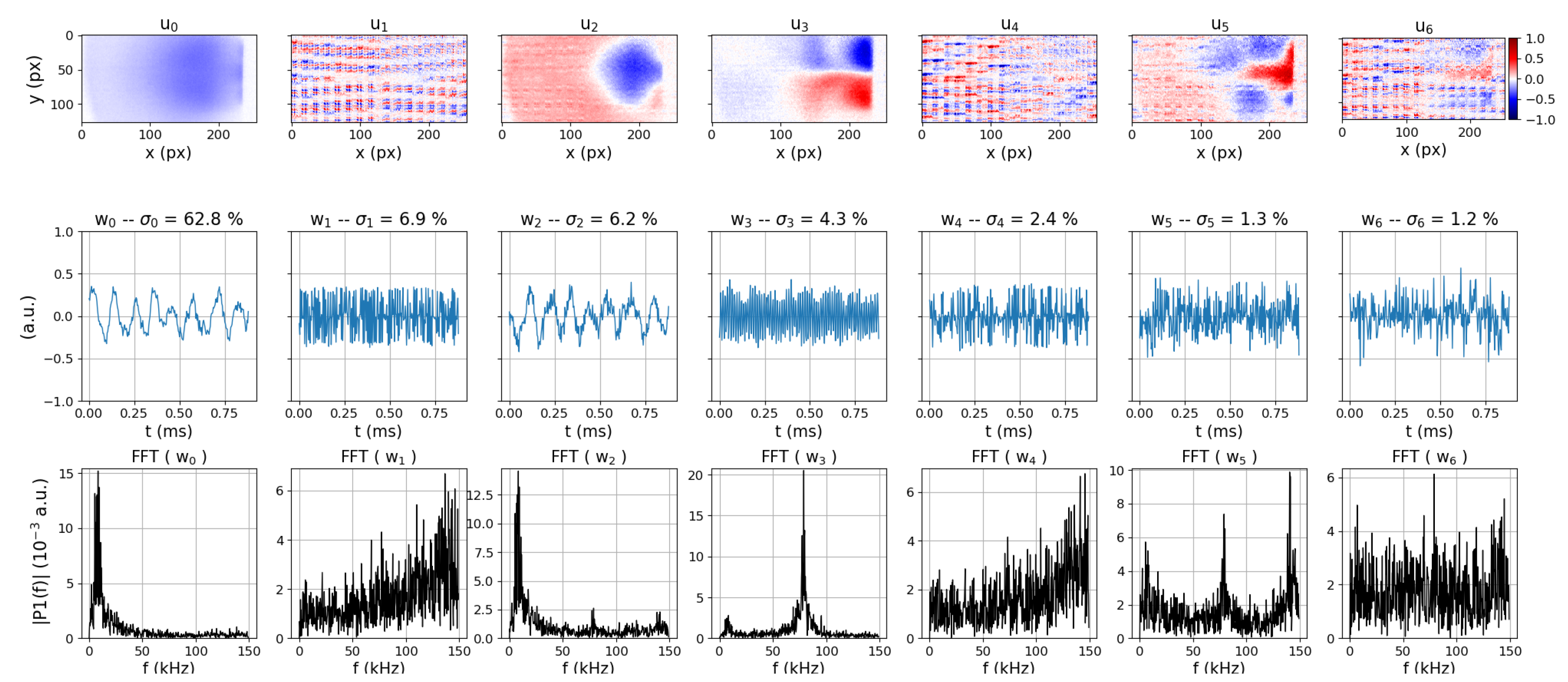
3.2.2. The under-Emissive Regime
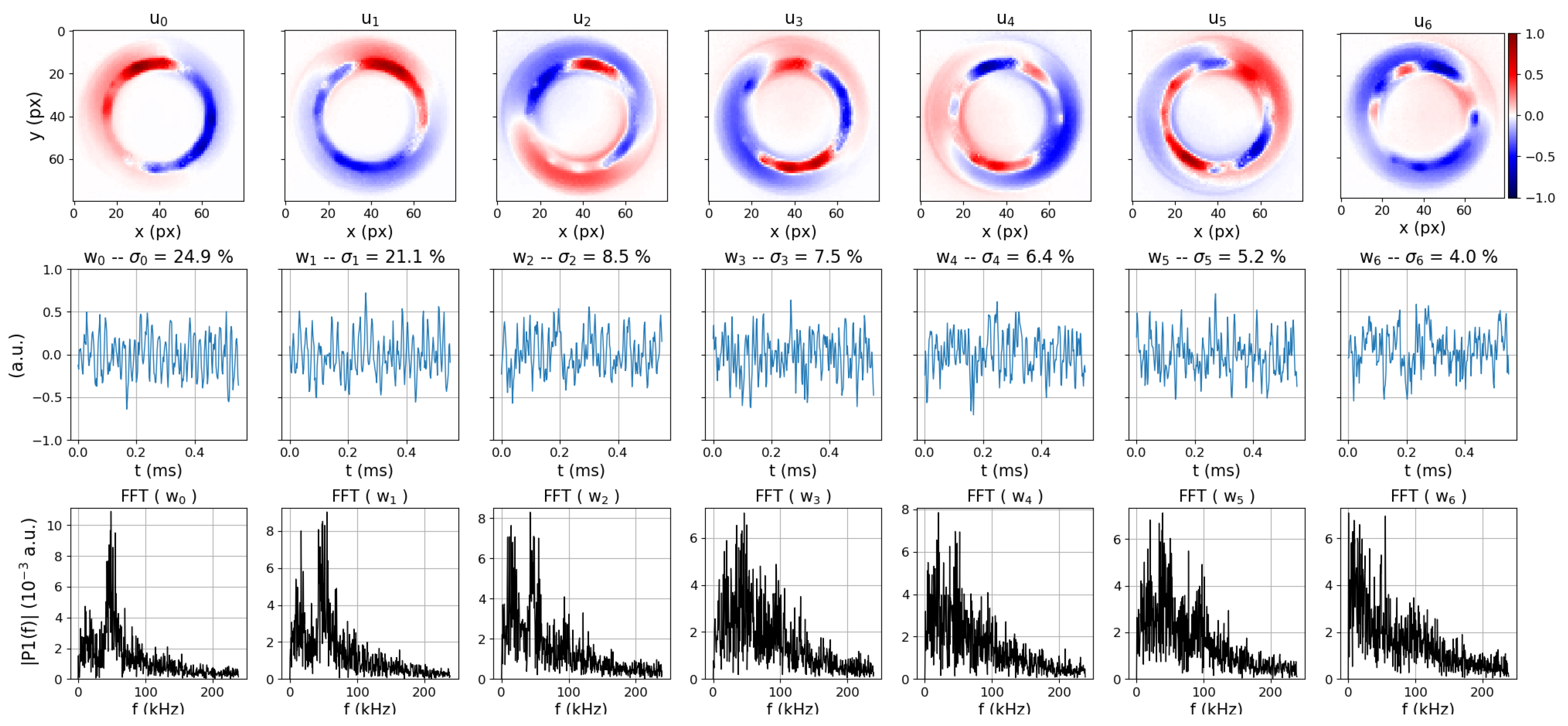
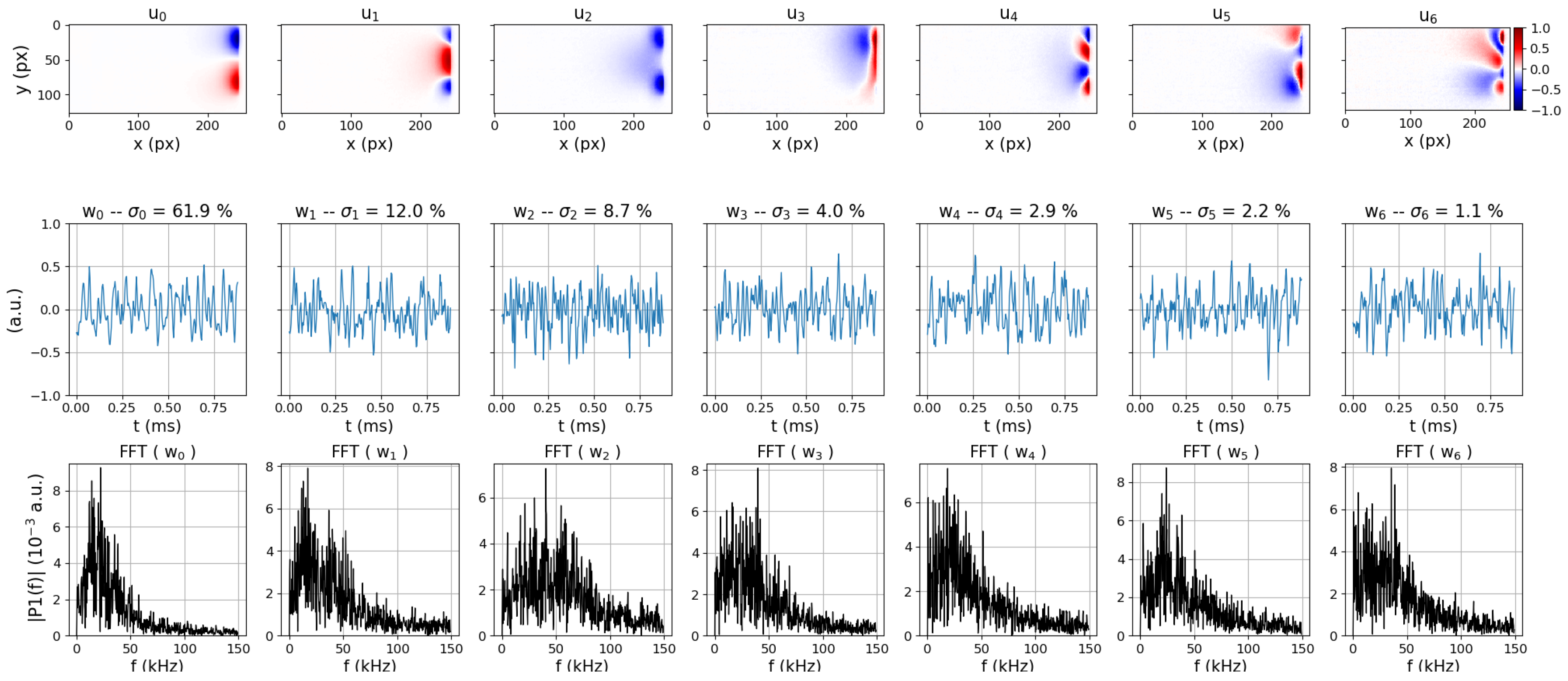
3.2.3. The Transition
4. Discussion
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| HET | Hall Effect Thruster |
| PIC | Particle-In-Cell |
| POD | Proper Orthogonal Decomposition |
| SVD | Singular Value Decomposition |
References
- Goebel, D.; Katz, I. Fundamentals of Electric Propulsion: Ion and Hall Thrusters; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Lev, D.; Myers, R.M.; Lemmer, K.M.; Kolbeck, J.; Koizumi, H.; Polzin, K. The technological and commercial expansion of electric propulsion. Acta Astronaut. 2019, 159, 213–227. [Google Scholar] [CrossRef]
- Adam, J.C.; Boeuf, J.P.; Dubuit, N.; Dudeck, M.; Garrigues, L.; Gresillon, D.; Heron, A.; Hagelaar, G.; Kulaev, V.; Lemoine, N.; et al. Physics, simulation and diagnostics of Hall effect thrusters. Plasma Phys. Control. Fusion 2008, 50, 124041. [Google Scholar] [CrossRef]
- Mazouffre, S. Electric propulsion for satellites and spacecraft: Established technologies and novel approaches. Plasma Sources Sci. Technol. 2016, 25, 033002. [Google Scholar] [CrossRef]
- Boeuf, J.P. Tutorial: Physics and modeling of Hall thrusters. J. Appl. Phys. 2017, 121, 011101. [Google Scholar] [CrossRef]
- Morozov, A.I.; Savelyev, V. Fundamentals of Stationary Plasma Thruster Theory. Rev. Plasma Phys. 2000, 21, 203–391. [Google Scholar]
- Morozov, A.I. The conceptual development of stationary plasma thrusters. Plasma Phys. Rep. 2003, 29, 235–250. [Google Scholar] [CrossRef]
- Choueiri, E. Plasma oscillations in Hall thrusters. Phys. Plasmas 2001, 8, 1411. [Google Scholar] [CrossRef] [Green Version]
- Smolyakov, A.; Chapurin, O.; Frias Pombo, W.; Koshkarov, O.; Romadanov, I.; Tang, T.; Umansky, M.; Raitses, Y.; Kaganovich, I.; Lakhin, V. Fluid theory and simulations of instabilities, turbulent transport and coherent structures in partially-magnetized plasmas of E × B discharges. Plasma Phys. Control Fusion 2017, 59, 014041. [Google Scholar] [CrossRef]
- Chesta, E.; Lam, C.M.; Meezan, N.B.; Schmidt, D.P.; Cappelli, M.A. A characterization of plasma fluctuations within a Hall discharge. IEEE Trans. Plasma Sci. 2001, 29, 582–591. [Google Scholar] [CrossRef]
- Litvak, A.A.; Raitses, Y.; Fisch, N.J. Experimental studies of high-frequency azimuthal waves in Hall thrusters. Phys. Plasmas 2004, 11, 1701–1705. [Google Scholar] [CrossRef]
- Tsikata, S.; Lemoine, N.; Pisarev, V.; Grésillon, D.M. Dispersion relations of electron density fluctuations in a Hall thruster plasma, observed by collective light scattering. Phys. Plasmas 2009, 16, 033506. [Google Scholar] [CrossRef]
- Lobbia, R.B. A Time-resolved Investigation of the Hall Thruster Breathing Mode. Ph.D. Thesis, The University of Michigan, Ann Arbor, MI, USA, 2010. [Google Scholar]
- Brown, Z.A.; Jorns, B.A. Spatial evolution of small wavelength fluctuations in a Hall Thruster. Phys. Plasmas 2019, 26, 113504. [Google Scholar] [CrossRef]
- Fife, J.M. Hybrid-PIC Modeling and Electrostatic Probe Survey of Hall Thrusters. Ph.D. Thesis, Massachussets Instititute of Technology, Cambridge, MA, USA, 1998. [Google Scholar]
- Lafleur, T.; Chabert, P. The role of instability-enhanced friction on ‘anomalous’ electron and ion transport in Hall-effect thrusters. Plasma Sources Sci. Technol. 2018, 27, 015003. [Google Scholar] [CrossRef]
- Hara, K. An overview of discharge plasma modeling for Hall effect thrusters. Plasma Sources Sci. Technol. 2019, 28, 044001. [Google Scholar] [CrossRef]
- Cavalier, J.; Lemoine, N.; Bonhomme, G.; Tsikata, S.; Honore, C.; Gresillon, D. Hall thruster plasma fluctuations identified as the E × B electron drift instability: Modeling and fitting on experimental data. Phys. Plasmas 2013, 20, 082107. [Google Scholar] [CrossRef]
- Hara, K.; Sekerak, M.J.; Boyd, I.D.; Gallimore, A.D. Perturbation analysis of ionization oscillations in Hall effect thrusters. Phys. Plasmas 2014, 21, 122103. [Google Scholar] [CrossRef]
- Lafleur, T.; Baalrud, S.D.; Chabert, P. Theory for the anomalous electron transport in Hall effect thrusters. II. Kinetic model. Phys. Plasmas 2016, 23, 053503. [Google Scholar] [CrossRef] [Green Version]
- Joncquieres, V. Modélisation et simulation numérique des moteurs à effet Hall. Ph.D. Thesis, Institut National Polytechnique de Toulouse, Toulouse, France, 2019. [Google Scholar]
- Mikellides, I.G.; Jorns, B.; Katz, I.; Lopez Ortega, A. Hall2De Simulations with a First-principles Electron Transport Model Based on the Electron Cyclotron Drift Instability. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference. American Institute of Aeronautics and Astronautics, Salt Lake City, UT, USA, 25–27 July 2016. [Google Scholar]
- Martorelli, R.; Lafleur, T.; Bourdon, A.; Chabert, P. Comparison between ad-hoc and instability-induced electron anomalous transport in a 1D fluid simulation of Hall-effect thruster. Phys. Plasmas 2019, 26, 083502. [Google Scholar] [CrossRef]
- Katz, I.; Ortega, A.L.; Jorns, B.; Mikellides, I. Growth and Saturation of Ion Acoustic Waves in Hall Thrusters. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, USA, 25–27 July 2016. [Google Scholar]
- Croes, V. Modélisation bidimensionnelle de la décharge plasma dans un propulseur de Hall. Ph.D. Thesis, Université Paris-Saclay, Saint-Aubin, France, 2018. [Google Scholar]
- Tavant, A. Plasma-Wall Interaction and Electron Transport in Hall Effect Thrusters. Ph.D. Thesis, Université Paris-Saclay, Saint-Aubin, France, 2019. [Google Scholar]
- Charoy, T.; Boeuf, J.P.; Bourdon, A.; Carlsson, J.A.; Chabert, P.; Cuenot, B.; Eremin, D.; Garrigues, L.; Hara, K.; Kaganovich, I.D.; et al. 2D axial-azimuthal particle-in-cell benchmark for low-temperature partially magnetized plasmas. Plasma Sources Sci. Technol. 2019, 28, 105010. [Google Scholar] [CrossRef] [Green Version]
- Mikellides, I.G.; Ortega, A.L. Challenges in the development and verification of first-principles models in Hall-effect thruster simulations that are based on anomalous resistivity and generalized Ohm’s law. Plasma Sources Sci. Technol. 2019, 28, 014003. [Google Scholar] [CrossRef]
- Tichý, M.; Pétin, A.; Kudrna, P.; Horký, M.; Mazouffre, S. Electron energy distribution function in a low-power Hall thruster discharge and near-field plume. Phys. Plasmas 2018, 25, 061205. [Google Scholar] [CrossRef]
- Mazouffre, S.; Grimaud, L.; Tsikata, S.; Matyash, K.; Schneider, R. Rotating spoke instabilities in a wall-less Hall thruster: Experiments. Plasma Sources Sci. Technol. 2019, 28, 054002. [Google Scholar] [CrossRef]
- Holmes, P.; Lumley, J.; Berkooz, G.; Rowley, C. Turbulence, Coherent Structures, Dynamical Systems and Symmetry, 2nd ed.; Cambridge Monographs on Mechanics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Boeuf, J.P.; Garrigues, L. Low frequency oscillations in a stationary plasma thruster. J. Appl. Phys. 1998, 84, 3541–3554. [Google Scholar] [CrossRef]
- Barral, S.; Ahedo, E. Low-frequency model of breathing oscillations in Hall discharges. Phys. Rev. E 2009, 79, 046401. [Google Scholar] [CrossRef] [Green Version]
- Kawashima, R.; Hara, K.; Komurasaki, K. Numerical analysis of azimuthal rotating spokes in a crossed-field discharge plasma. Plasma Sources Sci. Technol. 2017, 27, 035010. [Google Scholar] [CrossRef] [Green Version]
- Rodríguez, E.; Skoutnev, V.; Raitses, Y.; Powis, A.; Kaganovich, I.; Smolyakov, A. Boundary-induced effect on the spoke-like activity in E × B plasma. Phys. Plasmas 2019, 26, 053503. [Google Scholar] [CrossRef] [Green Version]
- Janes, G.S.; Lowder, R.S. Anomalous Electron Diffusion and Ion Acceleration in a Low Density Plasma. Phys. Fluids 1966, 9, 1115. [Google Scholar] [CrossRef]
- Morozov, A.I.; Epsinchuc, Y.; Kapulkin, A.M. Effect of the magnetic field a closed-electron-drift accelerator. Sov. Phys. Tech. Phys. 1972, 17, 482. [Google Scholar]
- Tilinin, G.N. High-frequency plasma waves in a Hall accelerator with an extended acceleration zone. Sov. Phys. Tech. Phys. 1977, 22, 974. [Google Scholar]
- Hara, K.; Sekerak, M.; Boyd, I.; Gallimore, A. Mode transition of a Hall thruster discharge plasma. J. Appl. Phys. 2014, 115, 203304. [Google Scholar] [CrossRef]
- Sekerak, M.; Gallimore, A.D.; Brown, D.L.; Hofer, R.; Polk, J. Mode Tansitions in Hall-Effect Thrusters Induced by Variable Magnetic Field Strength. J. Propuls. Power 2016, 32, 903–917. [Google Scholar] [CrossRef] [Green Version]
- Khmelevskoi, I.; Lovtsov, A.; Tomilin, D. Study of two Different Discharge Modes in Hall Thruster. In Proceedings of the 36th International Electric Propulsion Conference, Vienna, Austria, 15–20 September 2019; p. 387. [Google Scholar]
- Klinger, T.; Latten, A.; Piel, A.; Bonhomme, G.; Pierre, T. Chaos and turbulence studies in low-β plasmas. Plasma Phys. Control Fusion 1997, 39, B145–B156. [Google Scholar] [CrossRef]
- Brandt, C.; Grulke, O.; Klinger, T.; Negrete, J.; Bousselin, G.; Brochard, F.; Bonhomme, G.; Oldenbürger, S. Spatiotemporal mode structure of nonlinearly coupled drift wave modes. Phys. Rev. E 2011, 84, 056405. [Google Scholar] [CrossRef] [PubMed]
- Thakur, S.C.; Brandt, C.; Cui, L.; Gosselin, J.J.; Light, A.D.; Tynan, G.R. Multi-instability plasma dynamics during the route to fully developed turbulence in a helicon plasma. Plasma Sources Sci. Technol. 2014, 23, 0440006. [Google Scholar] [CrossRef]
- Lucken, R.; Bourdon, A.; Lieberman, M.A.; Chabert, P. Instability-enhanced transport in low temperature magnetized plasma. Phys. Plasmas 2019, 26, 070702. [Google Scholar] [CrossRef] [Green Version]
- Karabadzhak, G.F.; Chiu, Y.H.; Dressler, R.A. Passive optical diagnostic of Xe propelled Hall thrusters. II. Collisional-radiative model. J. Appl. Phys. 2006, 99, 113304. [Google Scholar] [CrossRef] [Green Version]
- Mazouffre, S.; Tsikata, S.; Vaudolon, J. Development and experimental characterization of a wall-less Hall thruster. J. Appl. Phys. 2014, 116, 243302. [Google Scholar] [CrossRef]
- McDonald, M.S.; Gallimore, A.D. Parametric Investigation of the Rotating Spoke Instability in Hall Thrusters. In Proceedings of the 32nd International Electric Propulsion Conference, Weisbaden, Germany, 11–15 September 2011; p. 242. [Google Scholar]
- Diamant, K.; Liang, R.; Corey, R. The Effect of Background Pressure on SPT-100 Hall Thruster Performance. ARC 2014. [Google Scholar] [CrossRef]
- Oldenbürger, S.; Brandt, C.; Brochard, F.; Lemoine, N.; Bonhomme, G. Spectroscopic interpretation and velocimetry analysis of fluctuations in a cylindrical plasma recorded by a fast camera. Rev. Sci. Instrum. 2010, 81, 063505. [Google Scholar] [CrossRef]
- Zweben, S.J.; Terry, J.L.; Stotler, D.P.; Maqueda, R.J. Invited Review Article: Gas puff imaging diagnostics of edge plasma turbulence in magnetic fusion devices. Rev. Sci. Instrum. 2017, 88, 041101. [Google Scholar] [CrossRef] [Green Version]
- Pearson, K. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef] [Green Version]
- Kosambi, D. Statistics in function space. J. Ind. Math. Soc. 1943. [Google Scholar] [CrossRef]
- Lumley, J.L. The structure of inhomogeneous turbulence. In Atmospheric Turbulence and Wave Propagation; Yaglom, A.M., Tatarski, V.I., Eds.; Nauka: Moscow, Russia, 1967; pp. 166–178. [Google Scholar]
- Sirovich, L. Turbulence and the Dynamics of Coherent Structures, Part I: Coherent Structures. Q. Appl. Math. 1987, 45, 561–571. [Google Scholar] [CrossRef] [Green Version]
- Demmel, J. Singular Value Decomposition. In Templates for the Solution of Algebraic Eigenvalue Problems; Software; Environments and Tools, Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2000; pp. 135–147. [Google Scholar] [CrossRef] [Green Version]
- Richardson, O.W. Electron Emission from Metals as a Function of Temperature. Phys. Rev. 1924, 23, 153. [Google Scholar] [CrossRef]
- Granstedt, E.M.; Raitses, Y.; Fisch, N.J. Cathode effects in cylindrical Hall thrusters. J. Appl. Phys. 2008, 104, 103302. [Google Scholar] [CrossRef] [Green Version]
- Darnon, F.; Garrigues, L.; Boeuf, J.P.; Bouchoule, A.; Lyszyk, M. Spontaneous Oscillations in a Hall Thruster. IEEE Trans. Plasm Sci. 1999, 27, 98–99. [Google Scholar] [CrossRef]
- Bouchoule, A.; Philippe-Kadlec, C.; Prioul, M.; Darnon, F.; Lyszyk, M.; Magne, L.; Pagon, D.; Roche, S.; Touzeau, M.; Béchu, S.; et al. Transient phenomena in closed electron drift plasma thrusters: Insights obtained in a French cooperative program. Plasma Sources Sci. Technol. 2001, 10, 364. [Google Scholar] [CrossRef]
- Matyash, K.; Schneider, R.; Mazouffre, S.; Tsikata, S.; Grimaud, L. Rotating spoke instabilities in a wall-less Hall thruster: Simulations. Plasma Sources Sci. Technol. 2019, 28, 044002. [Google Scholar] [CrossRef] [Green Version]
- Horton, W. Drift waves and transport. Rev. Mod. Phys. 1999, 71, 735. [Google Scholar] [CrossRef] [Green Version]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Désangles, V.; Shcherbanev, S.; Charoy, T.; Clément, N.; Deltel, C.; Richard, P.; Vincent, S.; Chabert, P.; Bourdon, A. Fast Camera Analysis of Plasma Instabilities in Hall Effect Thrusters Using a POD Method under Different Operating Regimes. Atmosphere 2020, 11, 518. https://doi.org/10.3390/atmos11050518
Désangles V, Shcherbanev S, Charoy T, Clément N, Deltel C, Richard P, Vincent S, Chabert P, Bourdon A. Fast Camera Analysis of Plasma Instabilities in Hall Effect Thrusters Using a POD Method under Different Operating Regimes. Atmosphere. 2020; 11(5):518. https://doi.org/10.3390/atmos11050518
Chicago/Turabian StyleDésangles, Victor, Sergey Shcherbanev, Thomas Charoy, Noé Clément, Clarence Deltel, Pablo Richard, Simon Vincent, Pascal Chabert, and Anne Bourdon. 2020. "Fast Camera Analysis of Plasma Instabilities in Hall Effect Thrusters Using a POD Method under Different Operating Regimes" Atmosphere 11, no. 5: 518. https://doi.org/10.3390/atmos11050518
APA StyleDésangles, V., Shcherbanev, S., Charoy, T., Clément, N., Deltel, C., Richard, P., Vincent, S., Chabert, P., & Bourdon, A. (2020). Fast Camera Analysis of Plasma Instabilities in Hall Effect Thrusters Using a POD Method under Different Operating Regimes. Atmosphere, 11(5), 518. https://doi.org/10.3390/atmos11050518




