Investigation of the Weather Conditions During the Collapse of the Morandi Bridge in Genoa on 14 August 2018 Using Field Observations and WRF Model
Abstract
:1. Introduction
2. Data and Numerical Simulations
2.1. Meteorological Data
2.2. WRF Model Setup
3. Results and Discussion: Observations
3.1. Weather Conditions at Large Scales
3.2. Local Observations
3.3. Lidar Gust Front Detection and Analysis
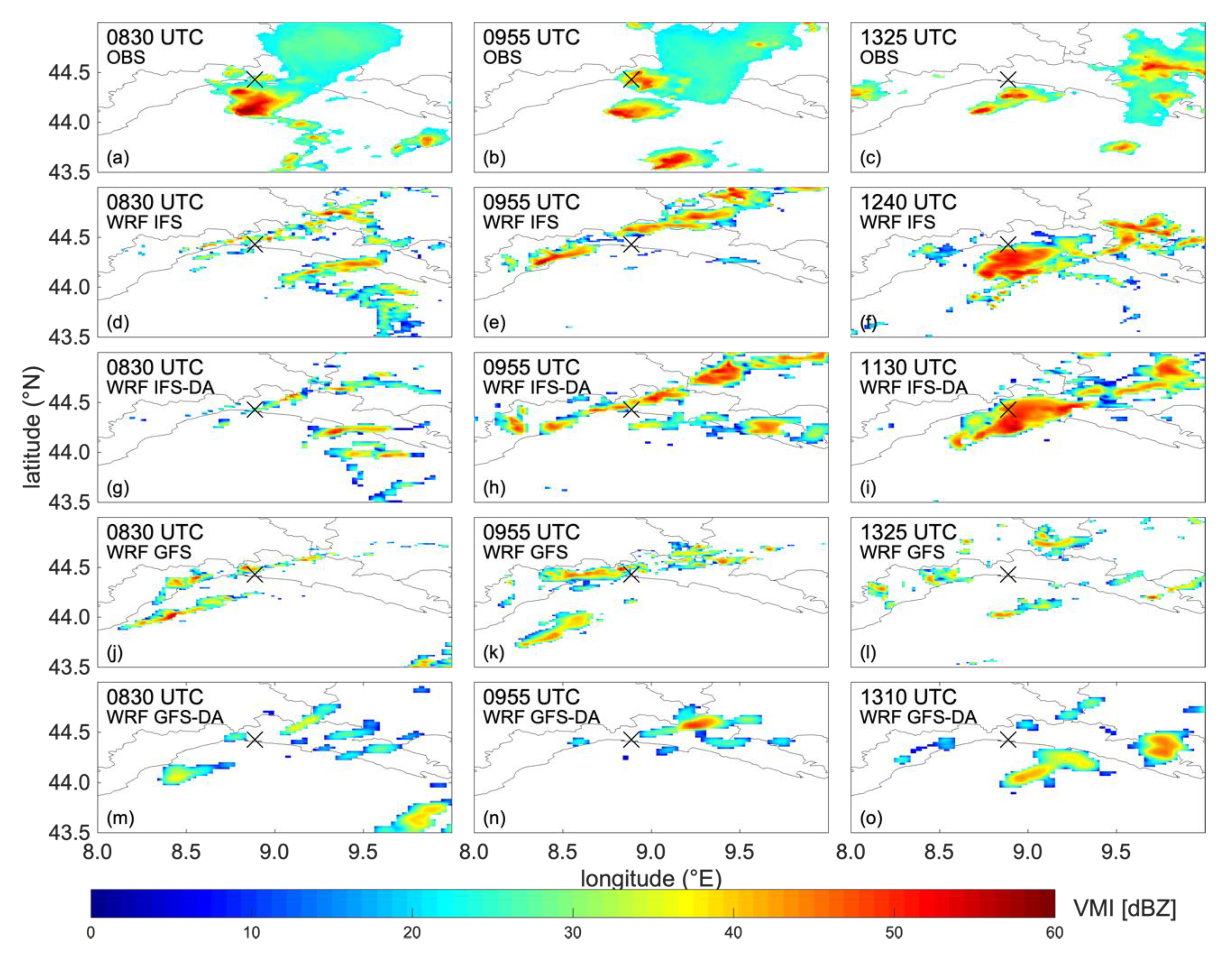
4. Results and Discussion: WRF Numerical Simulations
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- NSSL. Thunderstorm Basics. Available online: http://www.nssl.noaa.gov/education/svrwx101/thunderstorms/ (accessed on 27 June 2019).
- Burlando, M.; Romanić, D.; Solari, G.; Hangan, H.; Zhang, S. Field data analysis and weather scenario of a downburst event in Livorno, Italy, on 1 October 2012. Mon. Weather Rev. 2017, 145, 3507–3527. [Google Scholar] [CrossRef]
- Radinović, D. Mediterranean Cyclones and Their Influence on the Weather and Climate; WMO: Geneva, Switzerland, 1987. [Google Scholar]
- Maheras, P.; Flocas, H.A.; Patrikas, I.; Anagnostopoulou, C. A 40 year objective climatology of surface cyclones in the Mediterranean region: Spatial and temporal distribution. Int. J. Clim. 2001, 21, 109–130. [Google Scholar] [CrossRef]
- Trigo, I.F.; Bigg, G.R.; Davies, T.D. Climatology of Cyclogenesis Mechanisms in the Mediterranean. Mon. Weather Rev. 2002, 130, 549–569. [Google Scholar] [CrossRef]
- Flocas, H.A.; Simmonds, I.; Kouroutzoglou, J.; Keay, K.; Hatzaki, M.; Bricolas, V.; Asimakopoulos, D. On Cyclonic Tracks over the Eastern Mediterranean. J. Clim. 2010, 23, 5243–5257. [Google Scholar] [CrossRef]
- Kouroutzoglou, J.; Flocas, H.A.; Keay, K.; Simmonds, I.; Hatzaki, M. Climatological aspects of explosive cyclones in the Mediterranean. Int. J. Clim. 2011, 31, 1785–1802. [Google Scholar] [CrossRef]
- Drobinski, P.; Ducrocq, V.; Alpert, P.; Anagnostou, E.; Béranger, K.; Borga, M.; Braud, I.; Chanzy, A.; Davolio, S.; Delrieu, G.; et al. HyMeX: A 10-year multidisciplinary program on the Mediterranean water cycle. Bull. Am. Meteor. Soc. 2013, 95, 1063–1082. [Google Scholar] [CrossRef]
- Romanić, D.; Ćurić, M.; Lompar, M.; Jovičić, I. Contributing factors to Koshava wind characteristics. Int. J. Clim. 2016, 36, 956–973. [Google Scholar] [CrossRef]
- Zolt, S.D.; Lionello, P.; Nuhu, A.; Tomasin, A. The disastrous storm of 4 November 1966 on Italy. Nat. Hazards Earth Syst. Sci. 2006, 6, 861–879. [Google Scholar] [CrossRef] [Green Version]
- Parodi, A.; Lagasio, M.; Maugeri, M.; Turato, B.; Gallus, W. Observational and Modelling Study of a Major Downburst Event in Liguria: The 14 October 2016 Case. Atmosphere 2019, 10, 788. [Google Scholar] [CrossRef] [Green Version]
- Fujita, T.T. Downbursts: Meteorological features and wind field characteristics. J. Wind Eng. Ind. Aerodyn. 1990, 36, 75–86. [Google Scholar] [CrossRef]
- McDonald, J.R.; Mehta, K.C.; Mani, S. A Recommendation for an Enhanced Fujita Scale (EF-Scale); Wind Science and Engineering Center, Texas Tech University: Lubbock, TX, USA, 2006; p. 111. [Google Scholar]
- De Gaetano, P.; Repetto, M.P.; Repetto, T.; Solari, G. Separation and classification of extreme wind events from anemometric records. J. Wind Eng. Ind. Aerodyn. 2014, 126, 132–143. [Google Scholar] [CrossRef]
- Burlando, M.; Zhang, S.; Solari, G. Monitoring, cataloguing, and weather scenarios of thunderstorm outflows in the northern Mediterranean. Nat. Hazards Earth Syst. Sci. 2018, 18, 2309–2330. [Google Scholar] [CrossRef] [Green Version]
- Solari, G. Emerging issues and new frameworks for wind loading on structures in mixed climates. Wind Struct. 2014, 19, 295–320. [Google Scholar] [CrossRef]
- Shehata, A.Y.; El Damatty, A.A.; Savory, E. Finite element modeling of transmission line under downburst wind loading. Finite Elem. Anal. Des. 2005, 42, 71–89. [Google Scholar] [CrossRef]
- Solari, G. Wind Science and Engineering: Origins, Developments, Fundamentals and Advancements, 1st ed.; Springer International Publishing: Basel, Switzerland, 2019; ISBN 978-3-030-18814-6. [Google Scholar]
- Biron, D.; De Leonibus, L.; Zauli, F. The lightning network LAMPINET of the Italian Air Force Meteorological Service. In Proceedings of the 19th International Lightning Detection Conference, Tucson, AZ, USA, 24–25 April 2006. [Google Scholar]
- Biron, D. LAMPINET—Lightning Detection in Italy. In Lightning: Principles, Instruments and Applications: Review of Modern Lightning Research; Betz, H.D., Schumann, U., Laroche, P., Eds.; Springer: Dordrecht, The Netherlands, 2009; ISBN 978-1-4020-9079-0. [Google Scholar]
- De Leonibus, L.; Biron, D.; Sist, M.; Labate, D.; Zauli, F.; Melfi, D. Wind intensity reconstruction over Italy through lampinet lightning data. In Proceedings of the 21st International Lighting Detection Conference, Orlando, FL, USA, 19–20 April 2010. [Google Scholar]
- Solari, G.; Burlando, M.; Repetto, M.P. Detection, simulation, modelling and loading of thunderstorm outflows to design wind-safer and cost-efficient structures. J. Wind Eng. Ind. Aerodyn. 2020, 200, 104142. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.; Huang, X.-Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; National Center for Atmospheric Research: Boulder, CO, USA, 2008; p. 113. [Google Scholar]
- Ide, K.; Courtier, P.; Ghil, M.; Lorenc, A.C. Unified notation for data assimilation: Operational, sequential and variational. J. Meteorol. Soc. Jpn. Ser. II 1997, 75, 181–189. [Google Scholar] [CrossRef] [Green Version]
- Lagasio, M.; Silvestro, F.; Campo, L.; Parodi, A. Predictive capability of a high-resolution hydrometeorological forecasting framework coupling WRF cycling 3DVAR and continuum. J. Hydrometeor. 2019, 20, 1307–1337. [Google Scholar] [CrossRef]
- Fiori, E.; Ferraris, L.; Molini, L.; Siccardi, F.; Kranzlmueller, D.; Parodi, A. Triggering and evolution of a deep convective system in the Mediterranean Sea: Modelling and observations at a very fine scale. Q. J. R. Meteorol. Soc. 2017, 143, 927–941. [Google Scholar] [CrossRef]
- Lagasio, M.; Parodi, A.; Procopio, R.; Rachidi, F.; Fiori, E. Lightning Potential Index performances in multimicrophysical cloud-resolving simulations of a back-building mesoscale convective system: The Genoa 2014 event. J. Geophys. Res. Atmos. 2017, 122, 4238–4257. [Google Scholar] [CrossRef]
- Paulson, C.A. The mathematical representation of wind speed and temperature profiles in the unstable atmospheric surface layer. J. Appl. Meteor. 1970, 9, 857–861. [Google Scholar] [CrossRef]
- Dyer, A.J.; Hicks, B.B. Flux-gradient relationships in the constant flux layer. Q. J. R. Meteorol. Soc. 1970, 96, 715–721. [Google Scholar] [CrossRef]
- Webb, E.K. Profile relationships: The log-linear range, and extension to strong stability. Q. J. R. Meteorol. Soc. 1970, 96, 67–90. [Google Scholar] [CrossRef]
- Beljaars, A.C.M. The parametrization of surface fluxes in large-scale models under free convection. Q. J. R. Meteorol. Soc. 1995, 121, 255–270. [Google Scholar] [CrossRef]
- Smirnova, T.G.; Brown, J.M.; Benjamin, S.G. Performance off different soil model configurations in simulating ground surface temperature and surface fluxes. Mon. Weather Rev. 1997, 125, 1870–1884. [Google Scholar] [CrossRef]
- Smirnova, T.G.; Brown, J.M.; Benjamin, S.G.; Kim, D. Parameterization of cold-season processes in the MAPS land-surface scheme. J. Geophys. Res. Atmos. 2000, 105, 4077–4086. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef] [Green Version]
- Noh, Y.; Cheon, W.G.; Hong, S.Y.; Raasch, S. Improvement of the K-profile model for the planetary boundary layer based on large eddy simulation data. Bound.-Layer Meteorol. 2003, 107, 401–427. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.-Y.; Lim, J.-O.J. The WRF single-moment 6-class microphysics scheme (WSM6). J. Korean Meteorol. Soc. 2006, 42, 129–151. [Google Scholar]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Ćurić, M.; Janc, D.; Vujović, D.; Vučković, V. The effects of a river valley on an isolated cumulonimbus cloud development. Atmos. Res. 2003, 66, 123–139. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002; ISBN 978-0-201-18075-6. [Google Scholar]
- Zhang, S.; Solari, G.; De Gaetano, P.; Burlando, M.; Repetto, M.P. A refined analysis of thunderstorm outflow characteristics relevant to the wind loading of structures. Probabilistic Eng. Mech. 2018, 54, 9–24. [Google Scholar] [CrossRef]
- Pantillon, F.; Adler, B.; Corsmeier, U.; Knippertz, P.; Wieser, A.; Hansen, A. Formation of wind gusts in an extratropical cyclone in light of Doppler lidar observations and large-eddy simulations. Mon. Weather Rev. 2019, 148, 353–375. [Google Scholar] [CrossRef]
- Charba, J. Application of gravity current model to analysis of squall-line gust front. Mon. Weather Rev. 1974, 102, 140–156. [Google Scholar] [CrossRef] [Green Version]
- Wakimoto, R.M. The life cycle of thunderstorm gust fronts as viewed with Doppler radar and rawinsonde data. Mon. Weather Rev. 1982, 110, 1060–1082. [Google Scholar] [CrossRef] [Green Version]
- Mueller, C.K.; Carbone, R.E. Dynamics of a thunderstorm outflow. J. Atmos. Sci. 1987, 44, 1879–1898. [Google Scholar] [CrossRef] [Green Version]
- Droegemeier, K.K.; Wilhelmson, R.B. Numerical simulation of thunderstorm outflow dynamics. Part I: Outflow sensitivity experiments and turbulence dynamics. J. Atmos. Sci. 1987, 44, 1180–1210. [Google Scholar] [CrossRef] [Green Version]
- Lompar, M.; Ćurić, M.; Romanic, D. Implementation of a gust front head collapse scheme in the WRF numerical model. Atmos. Res. 2018, 203, 231–245. [Google Scholar] [CrossRef]
- Lawrence, M.G. The relationship between relative humidity and the dewpoint temperature in moist air: A simple conversion and applications. Bull. Am. Meteor. Soc. 2005, 86, 225–234. [Google Scholar] [CrossRef]
- Alduchov, O.A.; Eskridge, R.E. Improved Magnus form approximation of saturation vapor pressure. J. Appl. Meteor. 1996, 35, 601–609. [Google Scholar] [CrossRef]
- Von Kármán, T. The engineer grapples with nonlinear problems. Bull. Am. Math. Soc. 1940, 46, 615–683. [Google Scholar] [CrossRef] [Green Version]
- Middleton, G.V. Experiments on density and turbidity currents: I. Motion of the head. Can. J. Earth Sci. 1966, 3, 523–546. [Google Scholar] [CrossRef]
- Daly, B.J.; Pracht, W.E. Numerical study of density-current surges. Phys. Fluids 1968, 11, 15–30. [Google Scholar] [CrossRef]
- Seitter, K.L. The effect of arc cloud generation on thunderstorm gust front motion. In Proceedings of the Preprints, 13th Conference on Severe Local Storms, Boston, MA, USA, 17–20 October 1983; pp. 249–252. [Google Scholar]
- Goff, R.C. Vertical structure of thunderstorm outflows. Mon. Weather Rev. 1976, 104, 1429–1440. [Google Scholar] [CrossRef]
- Hjelmfelt, M.R. Structure and life cycle of microburst outflows observed in Colorado. J. Appl. Meteor. 1988, 27, 900–927. [Google Scholar] [CrossRef]
- Britter, R.E.; Simpson, J.E. Experiments on the dynamics of a gravity current head. J. Fluid Mech. 1978, 88, 223–240. [Google Scholar] [CrossRef]
- Pryor, K.L. Progress and Developments of Downburst Prediction Applications of GOES. Weather Forecast. 2015, 30, 1182–1200. [Google Scholar] [CrossRef]
- Caracena, F.; Maier, M.W. Analysis of a microburst in the face meteorological mesonetwork in southern Florida. Mon. Weather Rev. 1987, 115, 969–985. [Google Scholar] [CrossRef] [Green Version]
- Burlando, M.; Romanic, D. The ground-breaking contributions to downburst monitoring, modelling, and detection. In Oxford Handbook on Non-Synoptic Wind Storms; Oxford University Press: Oxford, UK, 2020. [Google Scholar]
- Lompar, M.; Ćurić, M.; Romanic, D. Simulation of a severe convective storm using a numerical model with explicitly incorporated aerosols. Atmos. Res. 2017, 194, 164–177. [Google Scholar] [CrossRef]
- Chen, F.; Kusaka, H.; Bornstein, R.; Ching, J.; Grimmond, C.S.B.; Grossman-Clarke, S.; Loridan, T.; Manning, K.W.; Martilli, A.; Miao, S.; et al. The integrated WRF/urban modelling system: Development, evaluation, and applications to urban environmental problems. Int. J. Clim. 2011, 31, 273–288. [Google Scholar] [CrossRef]
- Solari, G.; Repetto, M.P.; Burlando, M.; De Gaetano, P.; Pizzo, M.; Tizzi, M.; Parodi, M. The wind forecast for safety management of port areas. J. Wind Eng. Ind. Aerodyn. 2012, 104–106, 266–277. [Google Scholar] [CrossRef]
- Burlando, M.; Carassale, L.; Georgieva, E.; Ratto, C.F.; Solari, G. A simple and efficient procedure for the numerical simulation of wind fields in complex terrain. Bound.-Layer Meteorol. 2007, 125, 417–439. [Google Scholar] [CrossRef]
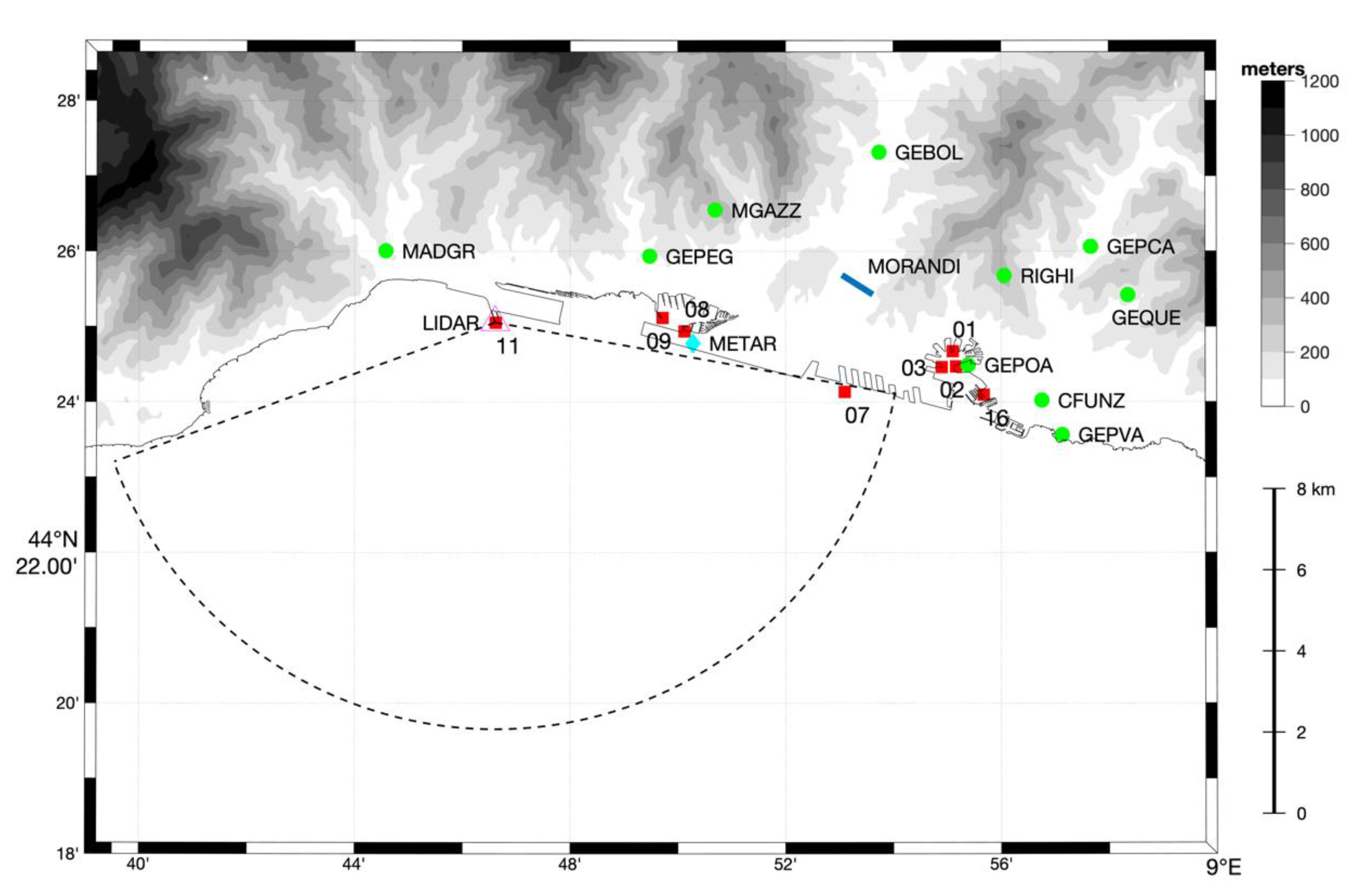

















| Station ID | Coordinates (Lon ° E, Lat ° N, Altitude m ASL) | Parameters 1 |
|---|---|---|
| GEBOL | (8.89561, 44.45530, 47) | T, PR |
| RIGHI | (8.93433, 44.42797, 360) | T, PR, W |
| CFUNZ | (8.94591, 44.40035, 30) | P, T, R, PR, RAD |
| GEPCA | (8.96109, 44.43439, 30) | PR |
| GEPEG | (8.82460, 44.43227, 69) | T, PR |
| GEQUE | (8.97260, 44.42367, 200) | T, RH, PR |
| MADGR | (8.74299, 44.43344, 104) | T, RH, PR |
| MGAZZ | (8.84485, 44.44247, 310) | T, PR |
| GEPOA | (8.92317, 44.40816, 25) | W |
| GEPVA | (8.95222, 44.39278, 10) | W |
| Station ID | Coordinates (Lon ° E, Lat ° N, Altitude m ASL) | Data Coverage 14 August 2018 | Data Coverage 09:00–10:00 UTC |
|---|---|---|---|
| 01 | (8.91838, 44.41119, 16) | 66.6 | 78.8 |
| 02 | (8.91939, 44.40780, 17) | 64.9 | 81.6 |
| 03 | (8.91501, 44.40771, 15) | 72.4 | 79.8 |
| 07 | (8.88499, 44.40220, 15) | 84.4 | 85.7 |
| 08 | (8.83541, 44.41562, 16) | 66.5 | 90.8 |
| 09 | (8.82859, 44.41862, 15) | 65.9 | 87.9 |
| 11 | (8.77698, 44.41754, 25) | 62.7 | 88.0 |
| 16 | (8.92797, 44.40157, 18) | 72.4 | 78.0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burlando, M.; Romanic, D.; Boni, G.; Lagasio, M.; Parodi, A. Investigation of the Weather Conditions During the Collapse of the Morandi Bridge in Genoa on 14 August 2018 Using Field Observations and WRF Model. Atmosphere 2020, 11, 724. https://doi.org/10.3390/atmos11070724
Burlando M, Romanic D, Boni G, Lagasio M, Parodi A. Investigation of the Weather Conditions During the Collapse of the Morandi Bridge in Genoa on 14 August 2018 Using Field Observations and WRF Model. Atmosphere. 2020; 11(7):724. https://doi.org/10.3390/atmos11070724
Chicago/Turabian StyleBurlando, Massimiliano, Djordje Romanic, Giorgio Boni, Martina Lagasio, and Antonio Parodi. 2020. "Investigation of the Weather Conditions During the Collapse of the Morandi Bridge in Genoa on 14 August 2018 Using Field Observations and WRF Model" Atmosphere 11, no. 7: 724. https://doi.org/10.3390/atmos11070724






