A Weighting Scheme in A Multi-Model Ensemble for Bias-Corrected Climate Simulation
Abstract
:1. Introduction
2. Data and Simulation Models
- : future value
- : bias corrected value in the future
- : observed value in the reference period
- : historical value in the reference period
3. Preliminary Methods
3.1. Generalized Extreme Value Distribution
3.2. Bayesian Model Averaging
3.3. Bias Correction by Quantile Mapping
4. Proposed Method
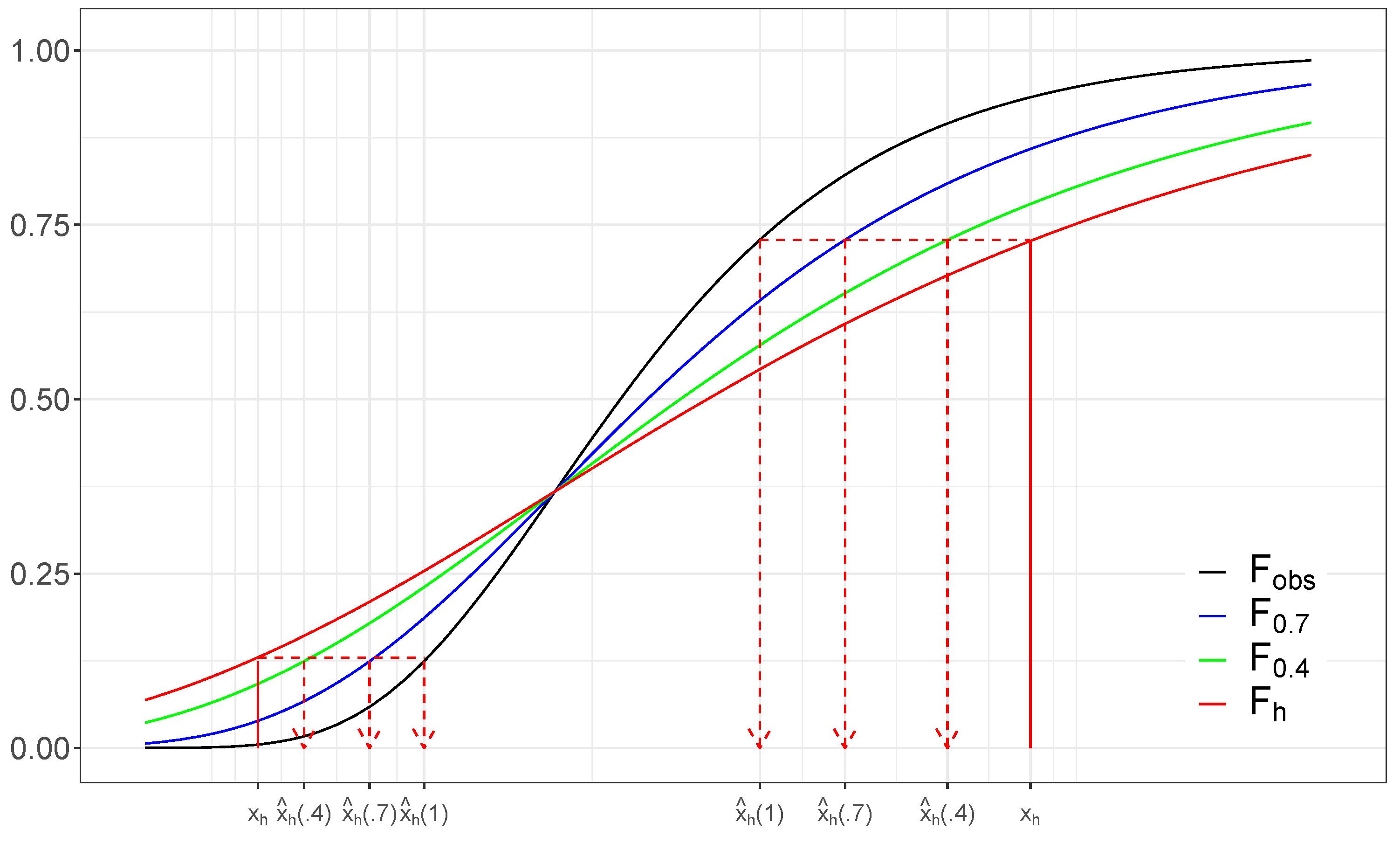
4.1. -Correction
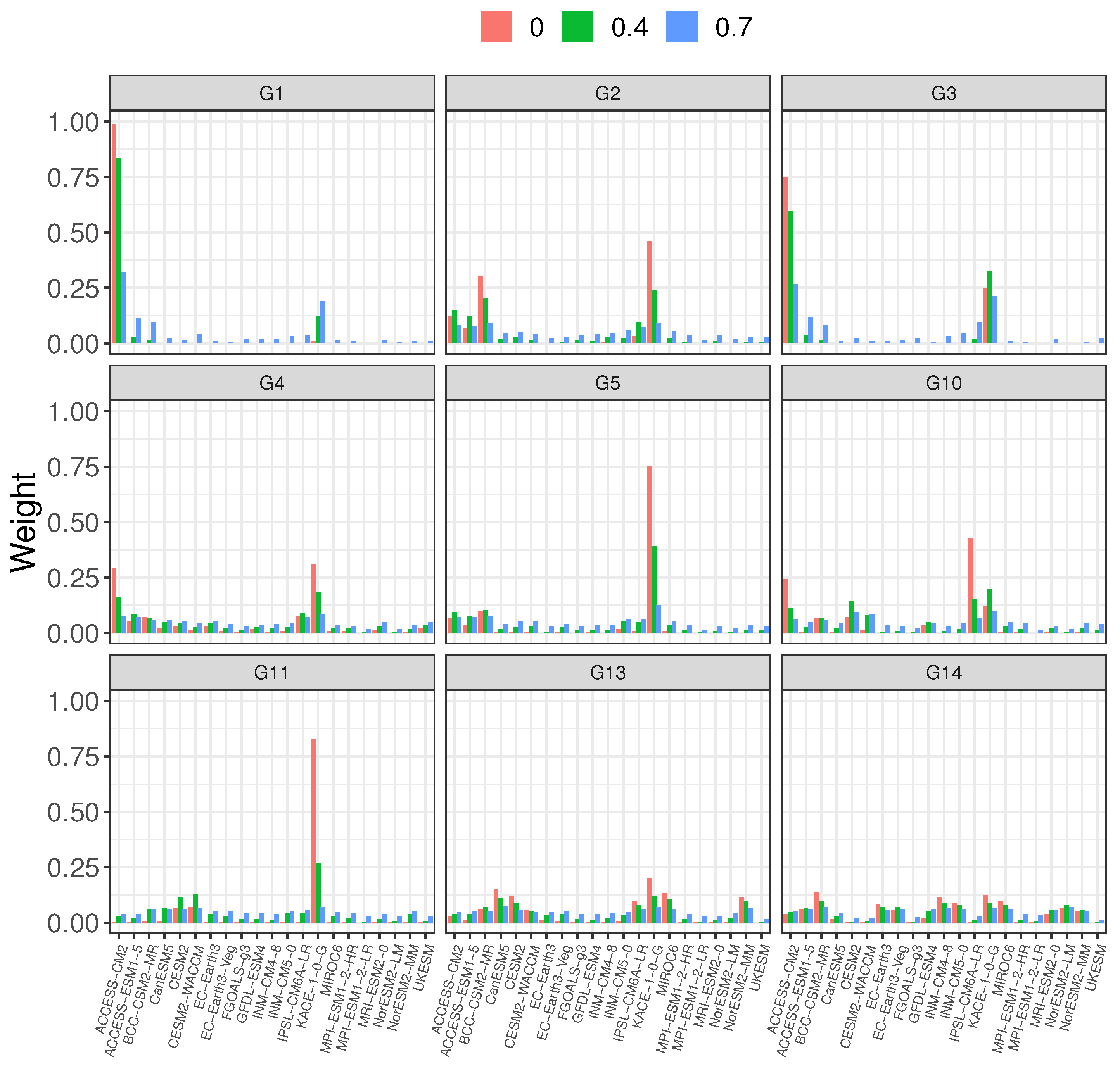
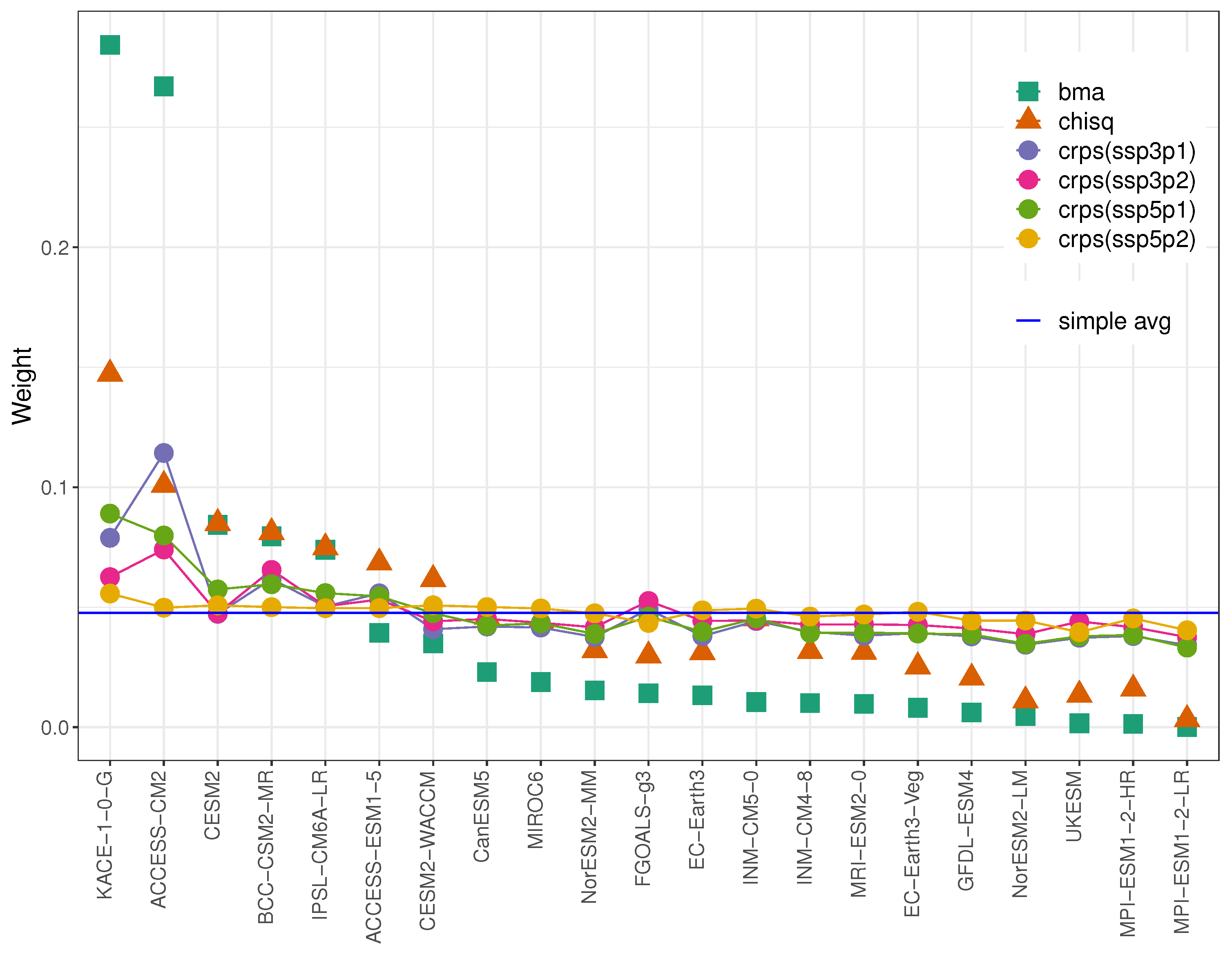
4.2. -Weights
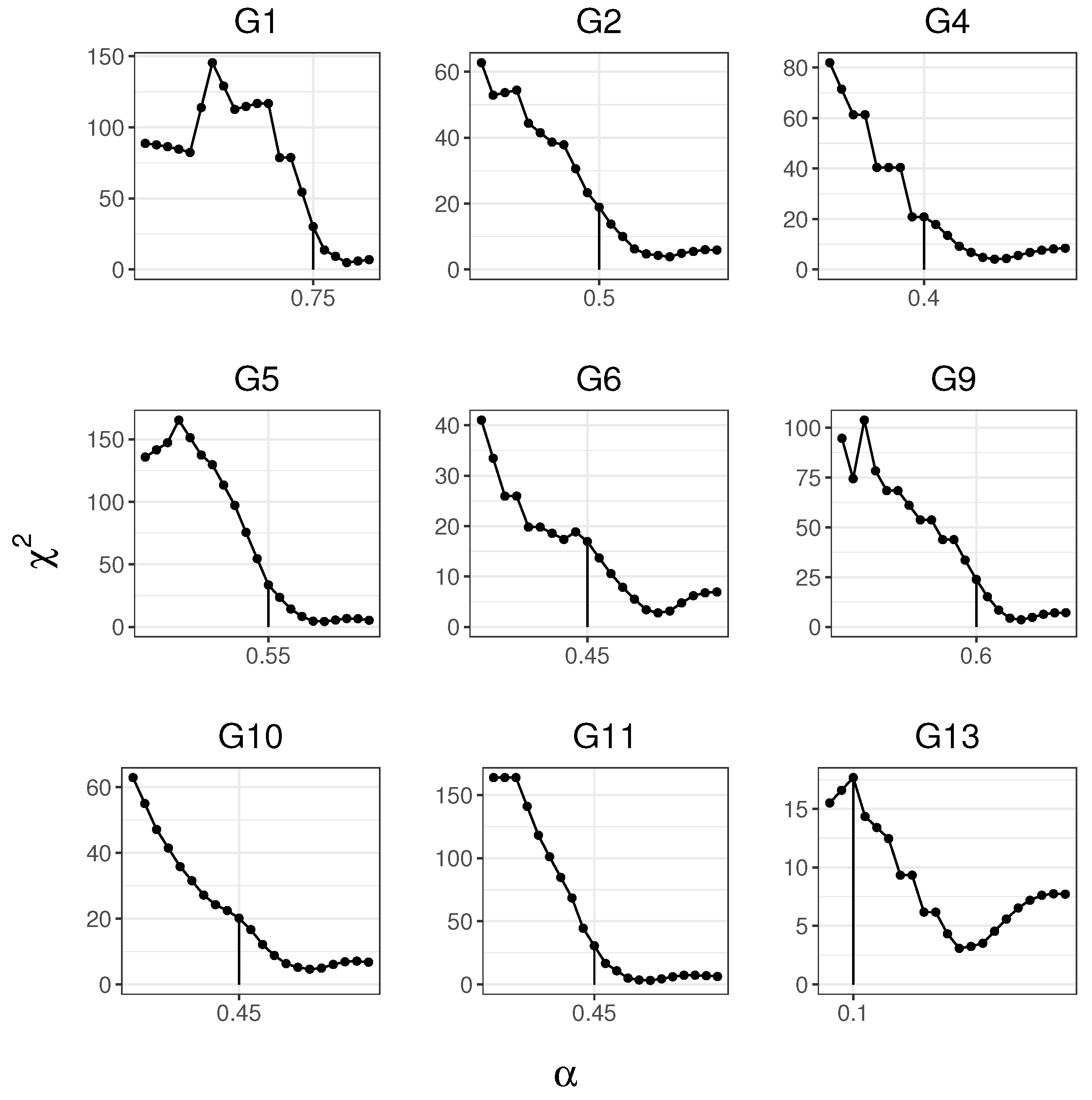
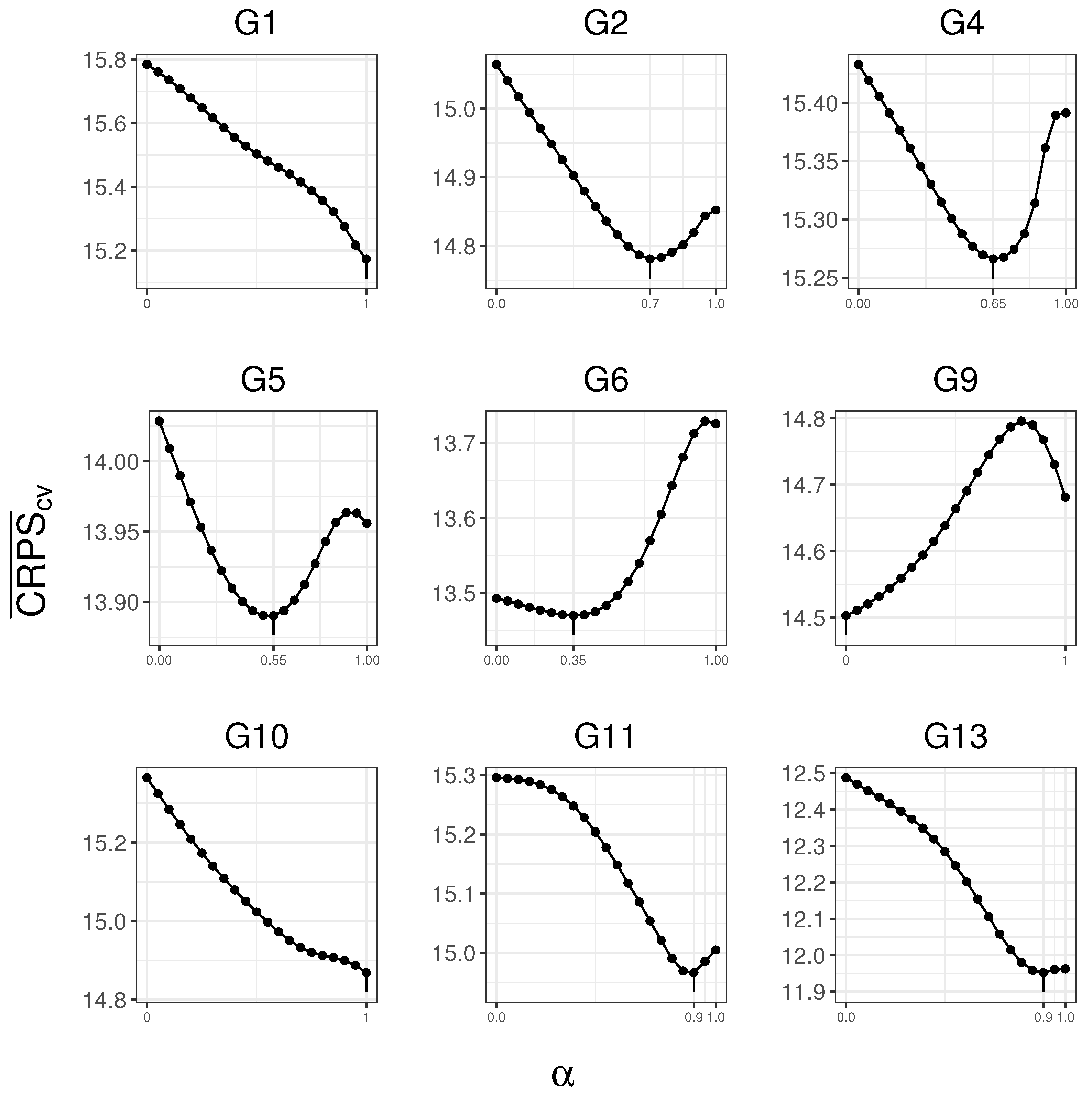
4.3. Selection of the Correction Rate
5. Comparison of Weighting Schemes
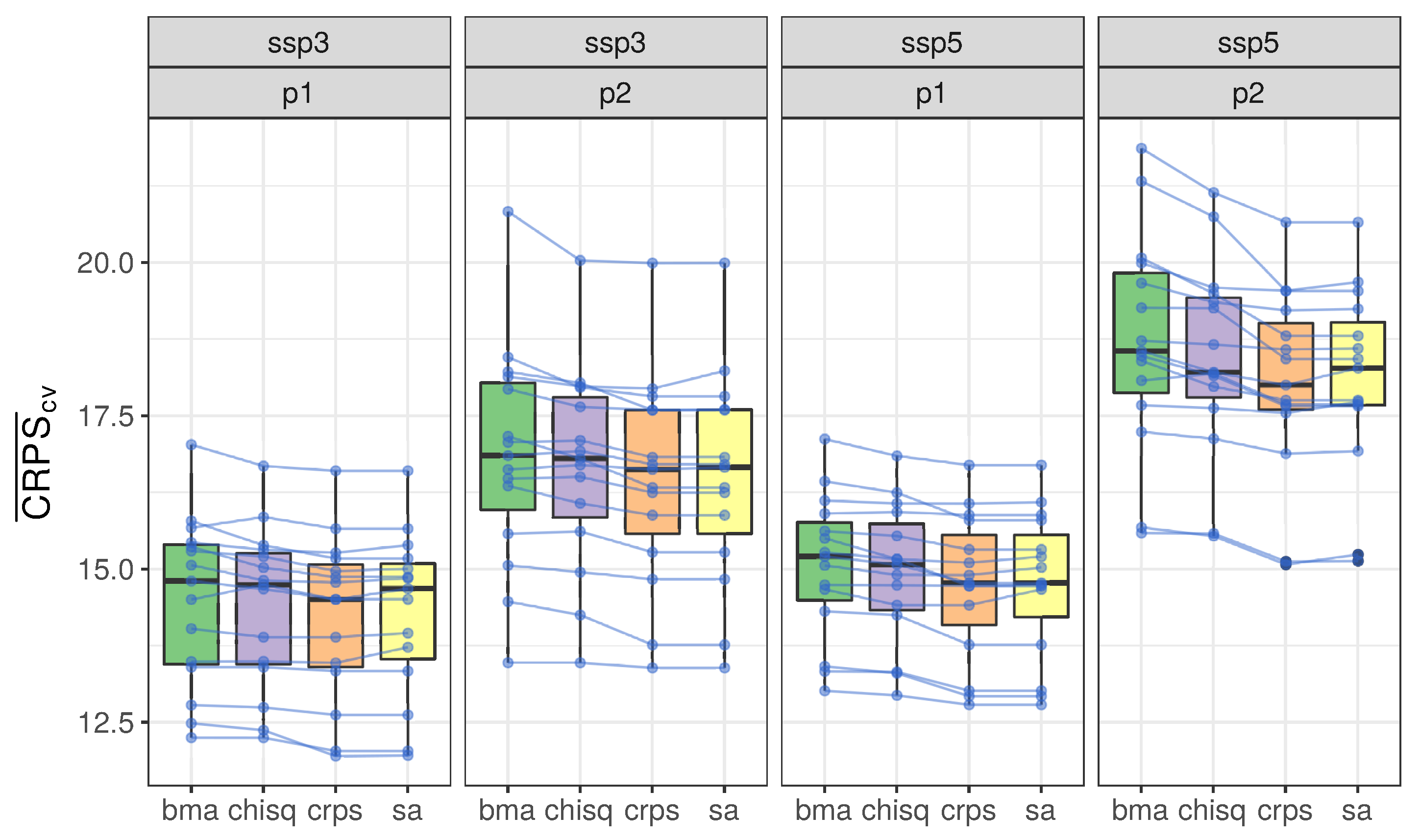
5.1. Leave-One-Model-Out Validation
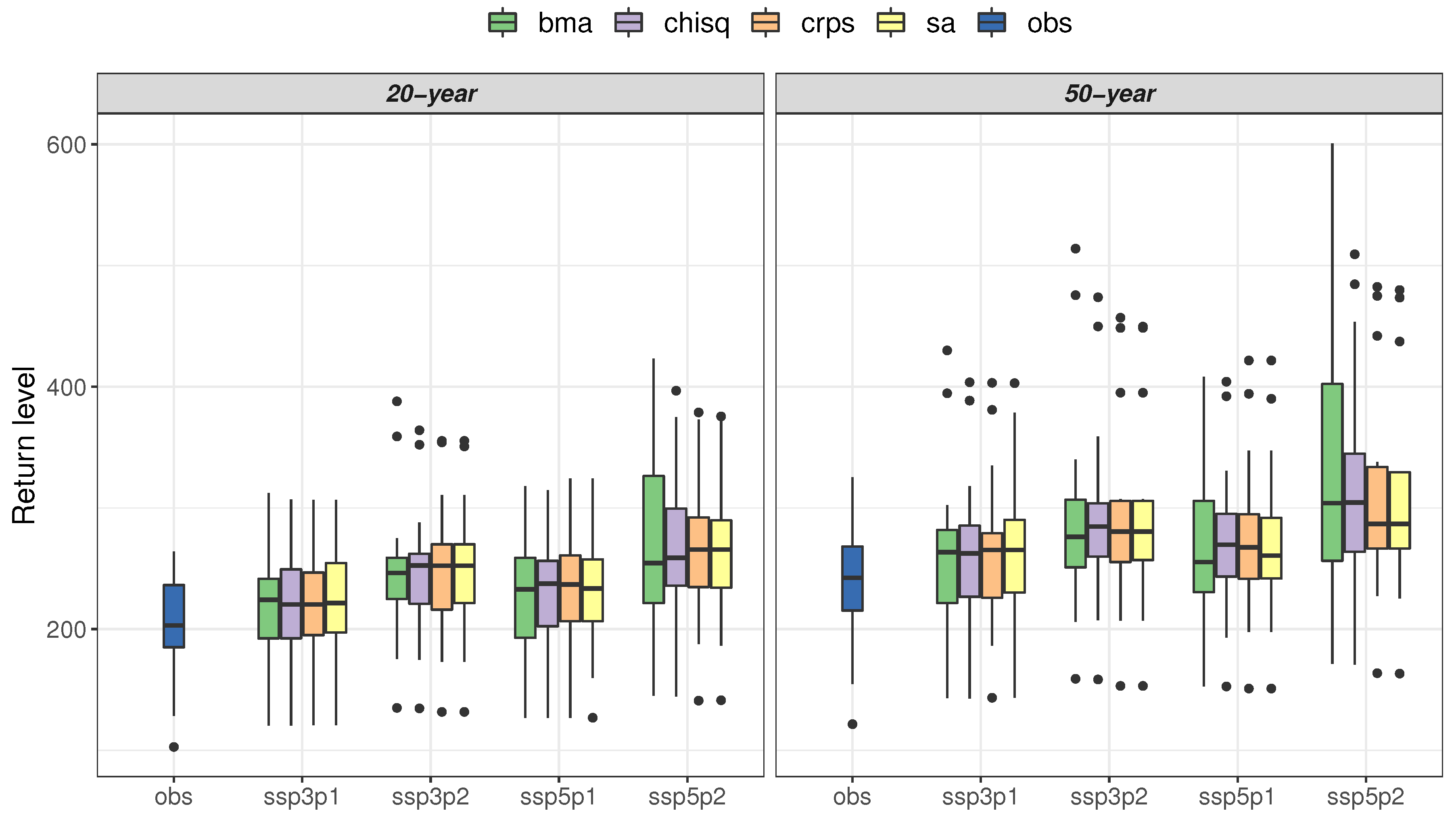
5.2. Quantile Estimation
6. Discussion
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Georgi, F.; Mearns, L.O. Calculation of average, uncertainty range and reliability of regional climate changes from AOGCM simulations via the ‘Reliability Ensemble Averaging (REA)’ method. J. Clim. 2002, 15, 1141–1158. [Google Scholar] [CrossRef]
- Tebaldi, C.; Knutti, R. The use of multi-model ensemble in probabilistic climate projections. Phil. Trans. R. Soc. A 2007, 365, 2053–2075. [Google Scholar] [CrossRef] [PubMed]
- Smith, R.L.; Tebaldi, C.; Nychka, D.; Mearns, L.O. Bayesian modeling of uncertainty in ensembles of climate models. J. Am. Stat. Assoc. 2009, 104, 97–116. [Google Scholar] [CrossRef]
- Coppola, E.; Giorgi, F.; Rauscher, S.; Piani, C. Model weighting based on mesoscale structures in precipitation and temperature in an ensemble of regional climate models. Clim. Res. 2010, 44, 121–134. [Google Scholar] [CrossRef] [Green Version]
- Sanderson, B.M.; Knutti, R.; Caldwell, P. A representative democracy to reduce interderpendency in a multimodel ensemble. J. Clim. 2015, 28, 5171–5194. [Google Scholar] [CrossRef] [Green Version]
- Knutti, R.; Sedlacek, J.; Sanderson, B.M.; Lorenz, R.; Fischer, E.M.; Eyring, V. A climate model projection weighting scheme accounting for performance and independence. Geophys. Res. Lett. 2017, 44, 1909–1918. [Google Scholar]
- Hoeting, J.A.; Madigan, D.; Raftery, A.E.; Volinsky, C.T. Bayesian model averaging: A tutorial. Stat. Sci. 1999, 14, 382–417. [Google Scholar]
- Raftery, A.E.; Gneiting, T.; Balabdaoui, F.; Polakowski, M. Using Bayesian model averaging to calibrate forecast ensembles. Mon. Weather Rev. 2005, 133, 1155–1174. [Google Scholar] [CrossRef] [Green Version]
- Sloughter, J.M.; Raftery, A.E.; Gneiting, T.; Fraley, C. Probabilistic quantitative precipitation forecasting using Bayesian model averaging. Mon. Weather Rev. 2007, 135, 3209–3220. [Google Scholar] [CrossRef]
- Darbandsari, P.; Coulibaly, P. Inter-comparison of different Bayesian model averaging modifications in streamflow simulation. Water 2019, 11, 1707. [Google Scholar] [CrossRef] [Green Version]
- Sanderson, B.M.; Knutti, R.; Caldwell, P. Addressing interdependency in a multimodel ensemble by interpolation of model properties. J. Clim. 2015, 28, 5150–5170. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modelling of Extreme Values; Springer: New York, NY, USA, 2001; p. 224. [Google Scholar]
- Zhu, J.; Forsee, W.; Schumer, R.; Gautam, M. Future projections and uncertainty assessment of extreme rainfall intensity in the United States from an ensemble of climate models. Clim. Chang. 2013, 118, 469–485. [Google Scholar] [CrossRef]
- Maraun, D.; Widmann, M. Statistical Downscaling and Bias Correction for Climate Research; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Wehner, M.F.; Easterling, D.R.; Lawrimore, J.H.; Heim, R.R., Jr.; Vose, R.S.; Santer, B. Projections of future drought in the continental United States and Mexico. J. Hydrometeorol. 2011, 12, 1359–1377. [Google Scholar] [CrossRef]
- Cannon, A.J. Multivariate quantile mapping bias correction: An N-dimensional probability density function transform for climate model simulations of multiple variables. Clim. Dyn. 2018, 50, 31–49. [Google Scholar] [CrossRef] [Green Version]
- Brekke, L.D.; Barsugli, J.J. Uncertainties in projections of future changes in extremes. In Extremes in a Changing Climate: Detection, Analysis and Uncertainty; AghaKouchak, A., Eatering, D., Hsu, K., Schubert, S., Sorooshian, S., Eds.; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Annan, J.D.; Hargreaves, J.C. Reliability of the CMIP5 ensemble. Geophys. Res. Lett. 2010, 37, L02703. [Google Scholar] [CrossRef]
- Wang, H.M.; Chen, J.; Xu, C.Y.; Chen, H.; Guo, S.; Xie, P.; Li, X. Does the weighting of climate simulation result in a better quantification of hydrological impacts? Hydrol. Earth Syst. Sci. 2019, 23, 4033–4050. [Google Scholar] [CrossRef] [Green Version]
- Stainforth, D.A.; Allen, M.R.; Tredger, E.R.; Smith, L.A. Confidence, uncertainty and decision-support relevance in climate predictions. Philos. Trans. R. Soc. A 2007, 365, 2145–2161. [Google Scholar] [CrossRef]
- Knutti, R. The end of model democracy? Clim. Chang. 2010, 102, 394–404. [Google Scholar] [CrossRef]
- Massoud, E.C.; Espinoza, V.; Guan, B.; Waliser, D.E. Global Climate Model Ensemble Approaches for Future Projections of Atmospheric Rivers. Earth’s Future 2019, 7, 1136–1151. [Google Scholar] [CrossRef] [Green Version]
- Wenzel, S.; Cox, P.M.; Eyring, V.; Friedlingstein, P. Emergent constraints on climate-carbon cycle feedbacks in the CMIP5 Earth system models. J. Geophys. Res. Biogeosci. 2014, 119, 794–807. [Google Scholar] [CrossRef] [Green Version]
- Eyring, V.; Cox, P.M.; Flato, G.M.; Gleckler, P.J.; Abramowitz, G.; Caldwell, P.; Collins, W.D.; Gier, B.K.; Hall, A.D.; Hoffman, F.M.; et al. Taking climate model evaluation to the next level. Nat. Clim. Chang. 2019, 9, 102–110. [Google Scholar] [CrossRef] [Green Version]
- Lee, Y.; Shin, Y.G.; Park, J.S.; Boo, K.O. Future projections and uncertainty assessment of precipitation extremes in the Korean peninsula from the CMIP5 ensemble. Atmos. Sci. Lett. 2020, e954. [Google Scholar] [CrossRef] [Green Version]
- Xu, D.; Ivanov, V.; Kim, J.; Fatichi, S. On the use of observations in assessment of multi-model climate ensemble. Stoch. Environ. Res. Risk Assess. 2019, 33, 1923–1937. [Google Scholar] [CrossRef]
- Brunner, L.; Lorenz, R.; Zumwald, M.; Knutti, R. Quantifying uncertainty in European climate projections using combined performance-independence weighting. Environ. Res. Lett. 2019, 14, 124010. [Google Scholar] [CrossRef]
- Abramowitz, G.; Gupta, H. Toward a model space and model independence metric. Geophy. Res. Lett. 2008, 35, L05705. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, R.; Herger, N.; Sedlacek, J.; Eyring, V.; Fischer, E.M.; Knutti, R. Prospects and caveats of weighting climate models for summer maximum temperature projections over North America. J. Geophys. Res. Atmos. 2018, 123, 4509–4526. [Google Scholar] [CrossRef]
- Herger, N.; Abramowitz, G.; Sherwood, S.; Knutti, R.; Angelil, O.; Sisson, S. Ensemble optimisation, multiple constrints and overconfidence: A case study with future Australian precipitation change. Clim. Dyn. 2019. [Google Scholar] [CrossRef]
- O’Neill, B.C.; Kriegler, E.; Riahi, K.; Ebi, K.L.; Hallegatte, S.; Carter, T.R.; Mathur, R.; van Vuuren, D.P. A new scenario framework for climate change research: The concept of Shared Socioeconomic Pathways. Clim. Chang. 2014, 122, 387–400. [Google Scholar] [CrossRef] [Green Version]
- Koch, S.E.; DesJardins, M.; Kocin, P.J. An interactive Barnes objective map analysis scheme for use with satellite and conventional data. J. Clim. Appl. Meteorol. 1983, 22, 1487–1503. [Google Scholar] [CrossRef]
- Maddox, R.A. An objective technique for separating macroscale and mesoscale features in meteorological data. Mon. Weather Rev. 1980, 108, 1108–1121. [Google Scholar] [CrossRef] [Green Version]
- Kuleshov, Y.; de Hoedt, G.; Wright, W.; Brewster, A. Thunderstorm distribution and frequency in Australia. Aust. Meteorol. Mag. 2002, 51, 145–154. [Google Scholar]
- Garcia-Pintado, J.; Barbera, G.G.; Erena, M.; Castillo, V.M. Rainfall estimation by rain gauge-radar combination: A concurrent multiplicative-additive approach. Water Resour. Res. 2009, 45, W01415. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Abramowitz, G.; Bishop, C.H. Climate model dependence and the ensemble dependence transformation of CMIP projections. J. Clim. 2015, 28, 2332–2348. [Google Scholar] [CrossRef]
- Wilks, D. Statistical Methods in the Atmospheric Sciences, 3rd ed.; Academic Press: New York, NY, USA, 2011. [Google Scholar]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997; p. 244. [Google Scholar]
- Hosking, J.R.M. L-Moments. R Package, Version 2.8. 2019. Available online: https://CRAN.R-project.org/package=lmom (accessed on 28 May 2020).
- Niu, X.; Wang, S.; Tang, J.; Lee, D.K.; Gutowsky, W.; Dairaku, K.; McGregor, J.; Katzfey, J.; Gao, X.; Wu, J.; et al. Ensemble evaluation and projection of climate extremes in China using RMIP models. Int. J. Climatol. 2018, 38, 2039–2055. [Google Scholar] [CrossRef]
- Qi, H.; Zhi, X.; Peng, T.; Bai, Y.; Lin, C. Comparative Study on Probabilistic Forecasts of Heavy Rainfall in Mountainous Areas of the Wujiang River Basin in China Based on TIGGE Data. Atmosphere 2019, 10, 608. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Yang, Y.; Wu, R.; Gui, D.; Xue, J.; Liu, Y.; Yan, D. Improving Estimation of Cropland Evapotranspiration by the Bayesian Model Averaging Method with Surface Energy Balance Models. Atmosphere 2019, 10, 188. [Google Scholar] [CrossRef] [Green Version]
- Rojas, R.; Feyen, L.; Dassargues, A. Conceptual model uncertainty in groundwater modeling: Combining generalized likelihood uncertainty estimation and Bayesian model averaging. Water Resour. Res. 2008, 44, W12418. [Google Scholar] [CrossRef] [Green Version]
- Christensen, J.H.; Boberg, F.; Christensen, O.B.; Lucas-Picher, P. On the need for bias correction of regional climate change projections of temperature and precipitation. Geophys. Res. Lett. 2008, 35, L20709. [Google Scholar] [CrossRef]
- Vrac, M.; Friederichs, P. Multivariate-intervariable, spatial, and temporal-bias correction. J. Clim. 2015, 28, 218–237. [Google Scholar] [CrossRef]
- Panofsky, H.; Brier, G. Some Applications of Statistics to Meteorology; Pennsylvania State University: University Park, PA, USA, 1968; p. 224. [Google Scholar]
- Switanek, M.B.; Troch, P.A.; Castro, C.L.; Leuprecht, A.; Chang, H.I.; Mukherjee, R.; Demaria, E. Scaled distribution mapping: A bias correction method that preserves raw climate model projected changes. Hydrol. Earth Syst. Sci. 2015, 21, 2649–2666. [Google Scholar] [CrossRef] [Green Version]
- Pierce, D.W.; Cayan, D.R.; Maurer, E.P.; Abatzoglou, J.T.; Hegewisch, K.C. Improved bias correction techniques for hydrological simulations of climate change. J. Hydrometeorol. 2015, 16, 2421–2442. [Google Scholar] [CrossRef]
- Hersbach, H. Decomposition of the continous ranked probability score for ensemble prediction systems. Weather Forecast 2000, 15, 559–570. [Google Scholar] [CrossRef]
- Jordan, A.; Krüger, F.; Lerch, S. Evaluating probabilistic forecasts with scoringRules. J. Stat. Softw. 2018, 90, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Calaway, R.; Ooi, H.; Weston, S. Package ‘Foreach’. R Program Repository CRAN. 2020. Available online: https://github.com/RevolutionAnalytics/foreach (accessed on 28 May 2020).
- Scott, P.A.; Kettleborough, J.A. Origins and estimates of uncertainty in predictions of twenty-first century temperature rise. Nature 2002, 416, 723–726. [Google Scholar]
- Boe, J.L.; Hall, A.; Qu, X. September sea-ice cover in the Arctic Ocean projected to vanish by 2100. Nat. Geosci. 2009, 2, 341–343. [Google Scholar] [CrossRef]
- Smith, I.; Chandler, E. Refining rainfall projections for the Murray Darling Basin of south-east Australia–the effect of sampling model results based on performance. Clim. Chang. 2010, 102, 377–393. [Google Scholar] [CrossRef]

| Model Name | Institution | Resolution (Lon × Lat Level#) |
|---|---|---|
| MIROC6 | JAMSTEC, AORI, NIES, R-CCS, Japan (MIROC) | 256 × 128 L81 (T85) |
| BCC-CSM2-MR | Beijing Climate Center, Beijing, China (BCC) | 320 × 160 L46 (T106) |
| CanESM5 | Canadian Centre for Climate Modelling & Analysis, Enviro & Climate Change Canada, Victoria, BC, Canada (CCCma) | 128 × 64 L49 (T63) |
| MRI-ESM2.0 | Meteoro Res Inst, Tsukuba, Ibaraki, Japan (MRI) | 320 × 160 L80 (TL159) |
| CESM2-WACCM | National Center for Atmos Res, Climate & Global Dynamics Lab, Boulder, CO, USA (NCAR) | 288 × 192 L70 |
| CESM2 | National Center for Atmos Res, Climate & Global Dynamics Lab, Boulder, CO, USA (NCAR) | 288 × 192 L32 |
| KACE1.0-GLOMAP | National Inst of Meteoro Sciences/Meteoro Admin, Climate Res Division, Seogwipo, Republic of Korea (NIMS-KMA) | 192 × 144 L85 |
| UKESM1-0-N96ORCA1 | UK (MOHC & NERC), Republic of Korea (NIMS-KMA), New Zealand (NIWA) | 192 × 144 L85 |
| MPI-ESM1.2-LR | Max Planck Inst for Meteoro, Hamburg, Germany (MPI-M) | 192 × 96 L47 (T63) |
| MPI-ESM1.2-HR | Max Planck Inst for Meteoro, Hamburg, Germany (MPI-M) | 384 × 192 L95 (T127) |
| INM-CM5-0 | Inst for Numerical Math, Russian Academy of Science, Moscow, Russia (INM) | 180 × 120 L73 |
| INM-CM4-8 | Inst for Numerical Math, Russian Academy of Science, Moscow, Russia (INM) | 180 × 120 L21 |
| IPSL-CM6A-LR | Institut Pierre Simon Laplace, Paris, France (IPSL) | 144 × 143 L79 |
| NorESM2-LM | NorESM Climate modeling Consortium of CICERO, MET-Norway, NERSC, NILU, UiB, UiO and UNI, Norway | 144 × 96 L32 |
| NorESM2-MM | NorESM Climate modeling Consortium of CICERO, MET-Norway, NERSC, NILU, UiB, UiO and UNI, Norway | 288 × 192 L32 |
| EC-Earth3-Veg | EC-Earth consortium, Rossby Center, Swedish Meteoro & Hydro Inst/SMHI, Norrkoping, Sweden (EC-Earth-Consortium) | 512 × 256 L91 (TL255) |
| EC Earth 3.3 | EC-Earth consortium, Rossby Center, Swedish Meteoro & Hydro Inst/SMHI, Norrkoping, Sweden (EC-Earth-Consortium) | 512 × 256 L91 (TL255) |
| ACCESS-CM2 | CSIRO (Australia), ARCCSS (Australian Res Council Centre of Excellence for Climate System Science) (CSIRO-ARCCSS) | 192 × 144 L85 |
| ACCESS-ESM1-5 | Commonwealth Scientific & Industrial Res Organisation, Victoria, Australia (CSIRO) | 192 × 145 L38 |
| GFDL-ESM4 | National Oceanic & Atmospheric Admi, Geophy Fluid Dynamics Lab, Princeton, NJ, USA (NOAA-GFDL) | 360 × 180 L49 |
| FGOALS-g3 | Chinese Academy of Sciences, Beijing, China (CAS) | 180 × 80 L26 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, Y.; Lee, Y.; Park, J.-S. A Weighting Scheme in A Multi-Model Ensemble for Bias-Corrected Climate Simulation. Atmosphere 2020, 11, 775. https://doi.org/10.3390/atmos11080775
Shin Y, Lee Y, Park J-S. A Weighting Scheme in A Multi-Model Ensemble for Bias-Corrected Climate Simulation. Atmosphere. 2020; 11(8):775. https://doi.org/10.3390/atmos11080775
Chicago/Turabian StyleShin, Yonggwan, Youngsaeng Lee, and Jeong-Soo Park. 2020. "A Weighting Scheme in A Multi-Model Ensemble for Bias-Corrected Climate Simulation" Atmosphere 11, no. 8: 775. https://doi.org/10.3390/atmos11080775
APA StyleShin, Y., Lee, Y., & Park, J.-S. (2020). A Weighting Scheme in A Multi-Model Ensemble for Bias-Corrected Climate Simulation. Atmosphere, 11(8), 775. https://doi.org/10.3390/atmos11080775





