Limits of Predictability of a Global Self-Similar Routing Model in a Local Self-Similar Environment
Abstract
1. Introduction
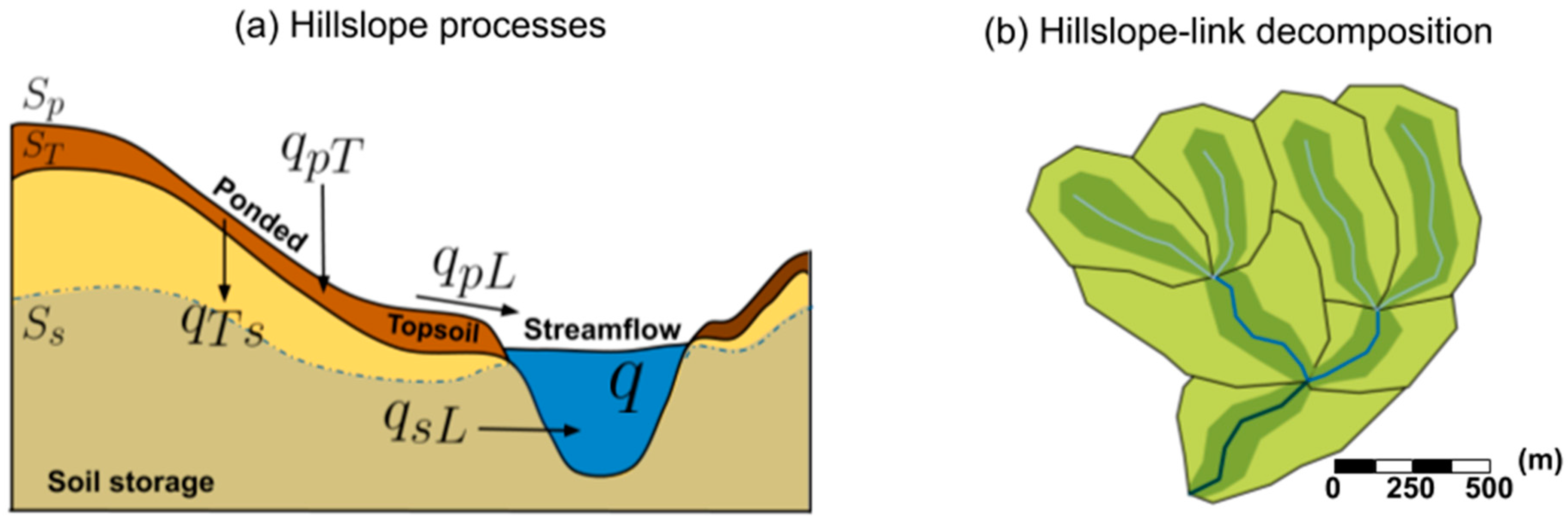
2. Preliminaries
3. Methodology
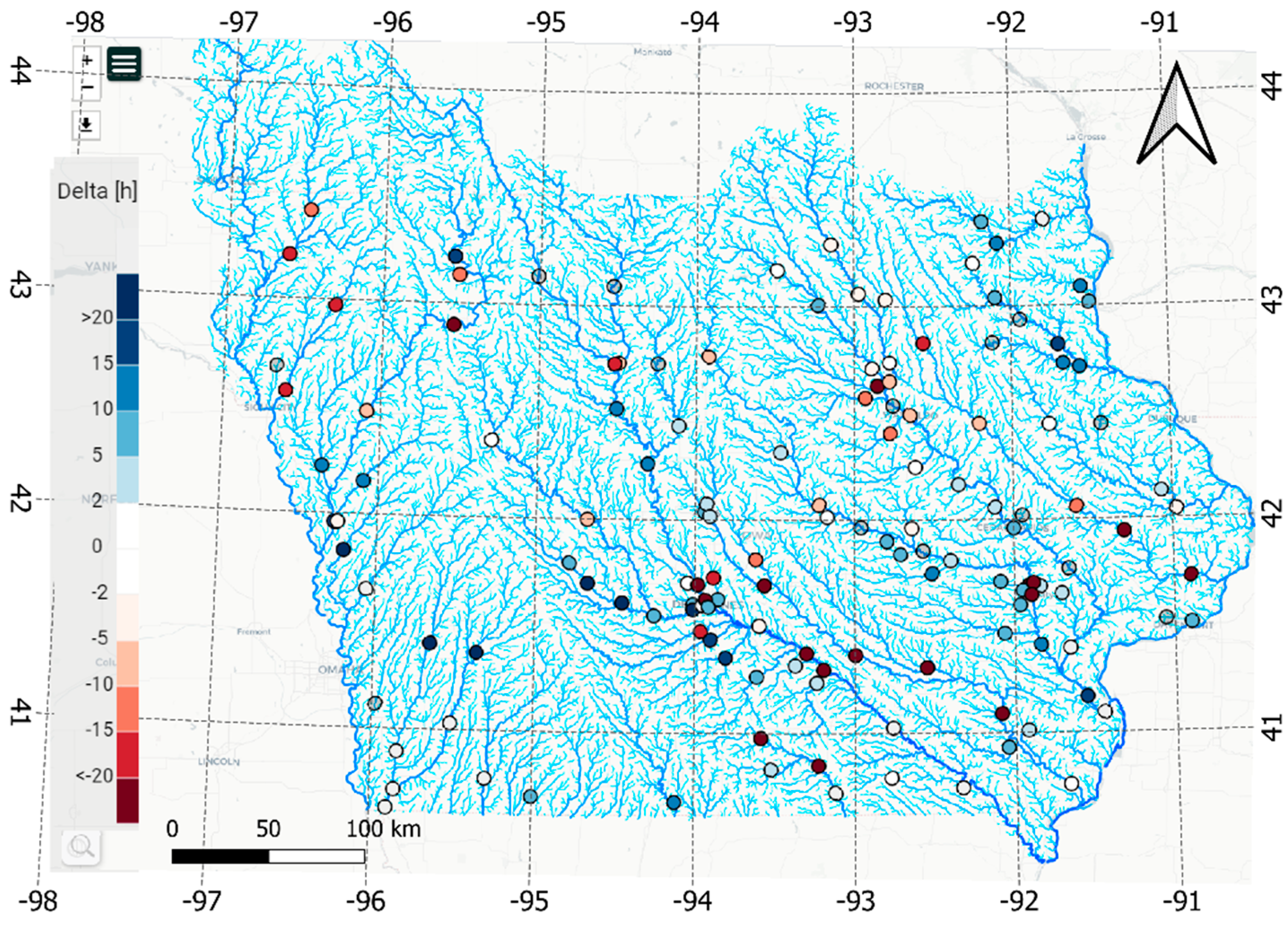
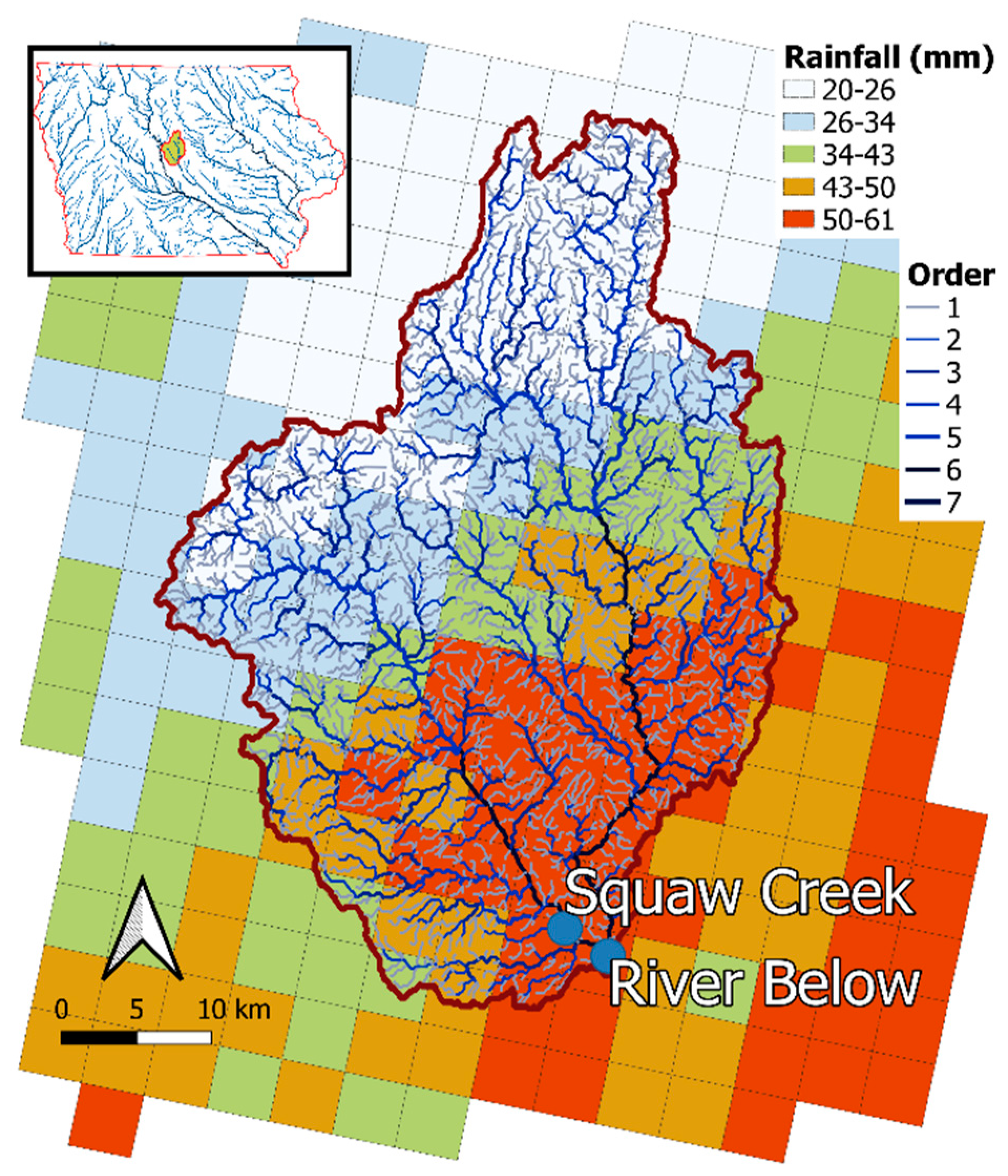
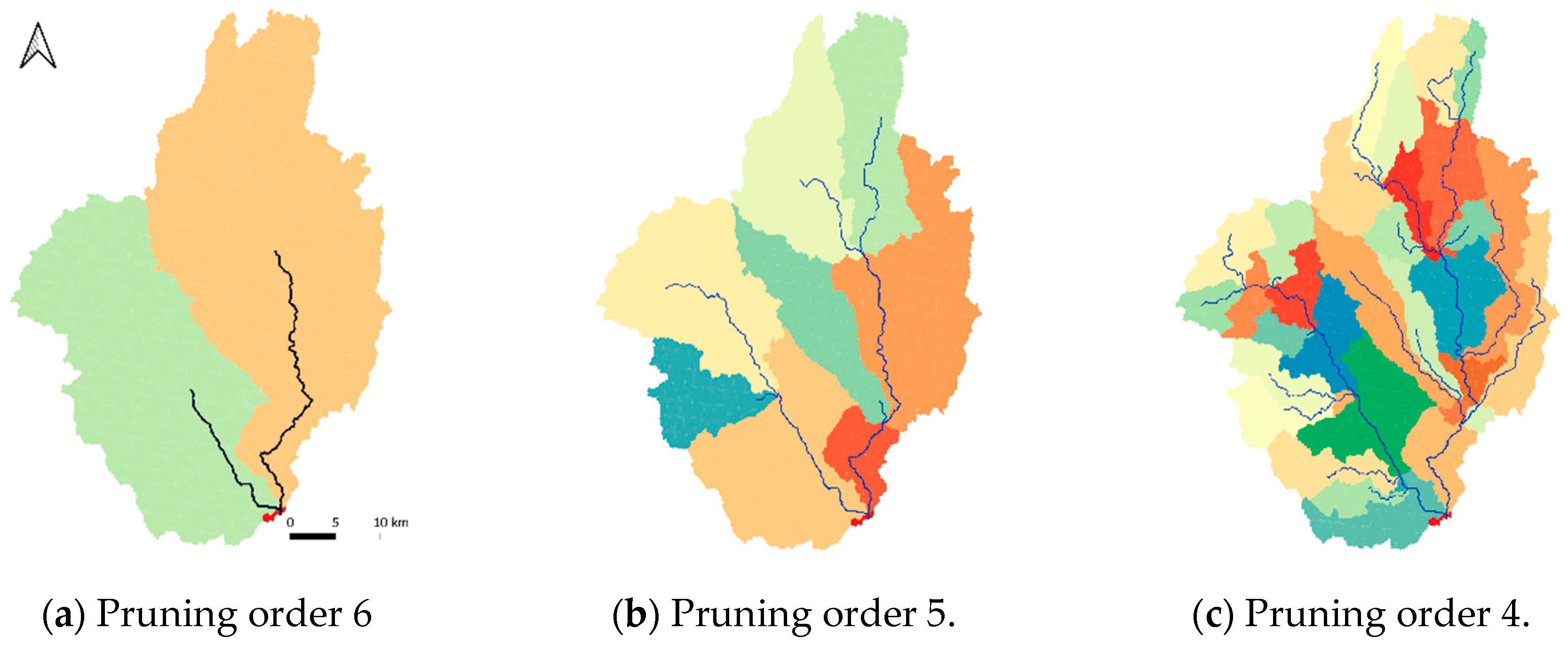
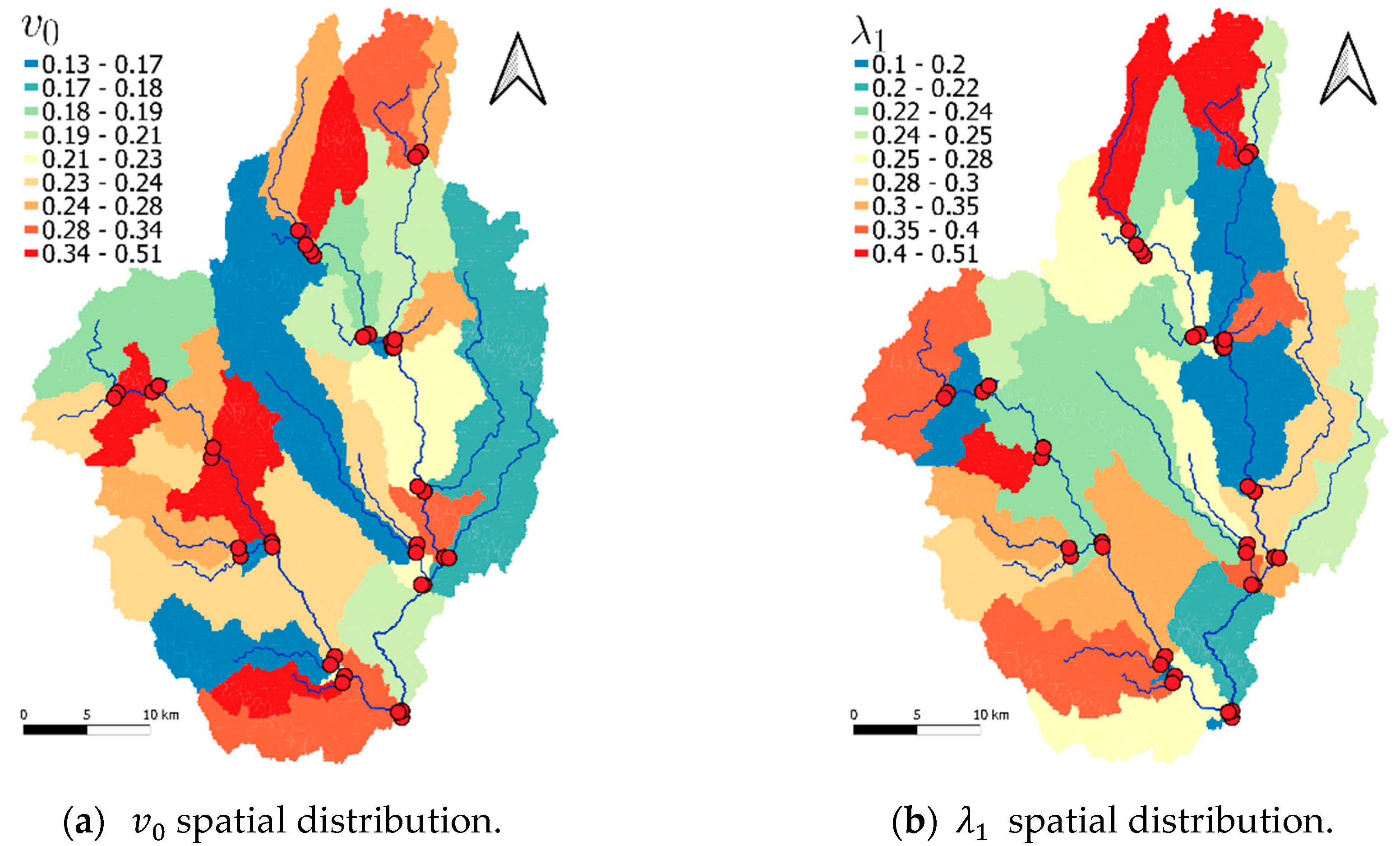
3.1. Study Catchment and Reference Scenario
3.2. Comparison Scenarios
3.3. Hydrological Modeling Setup
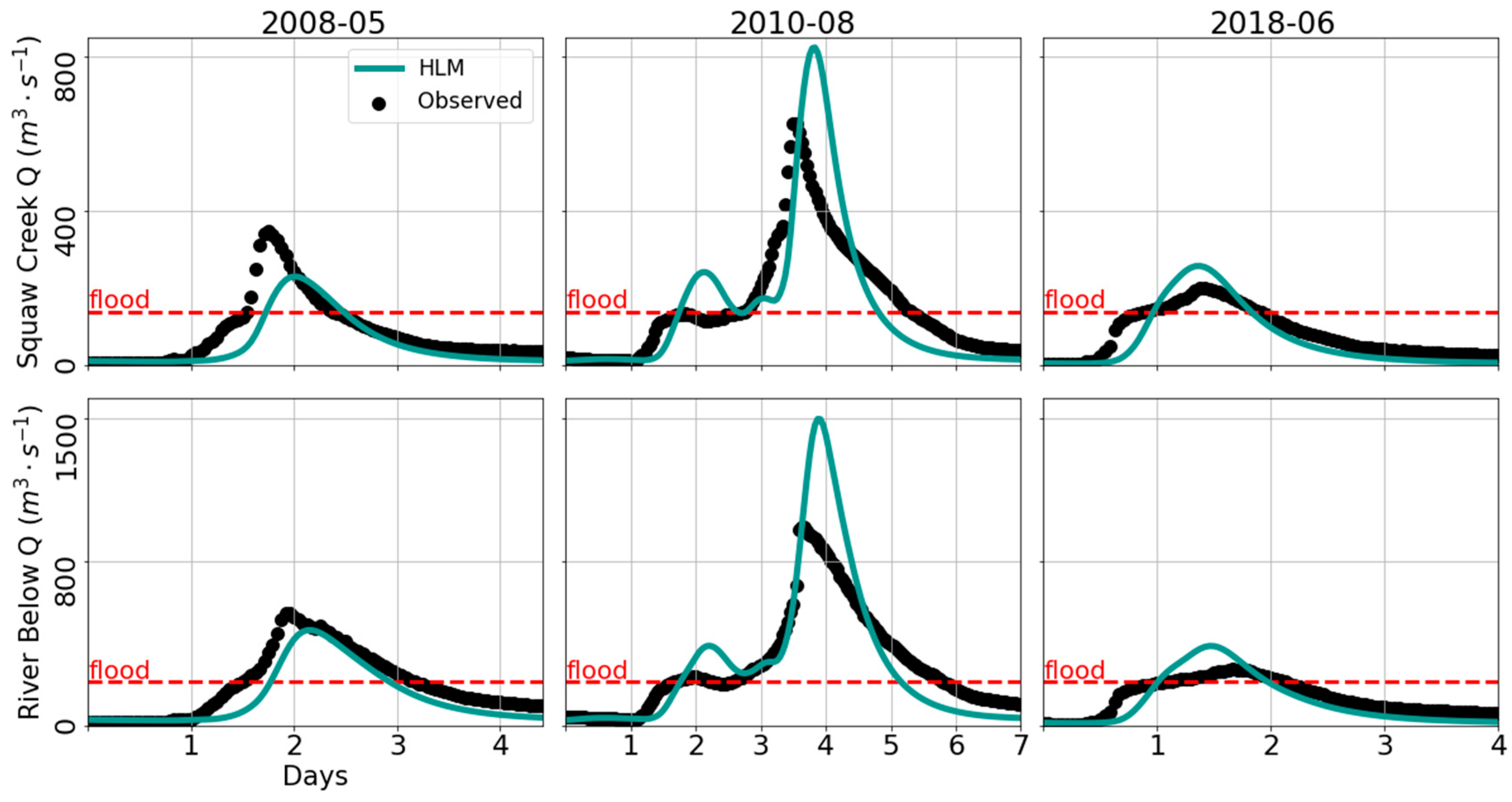
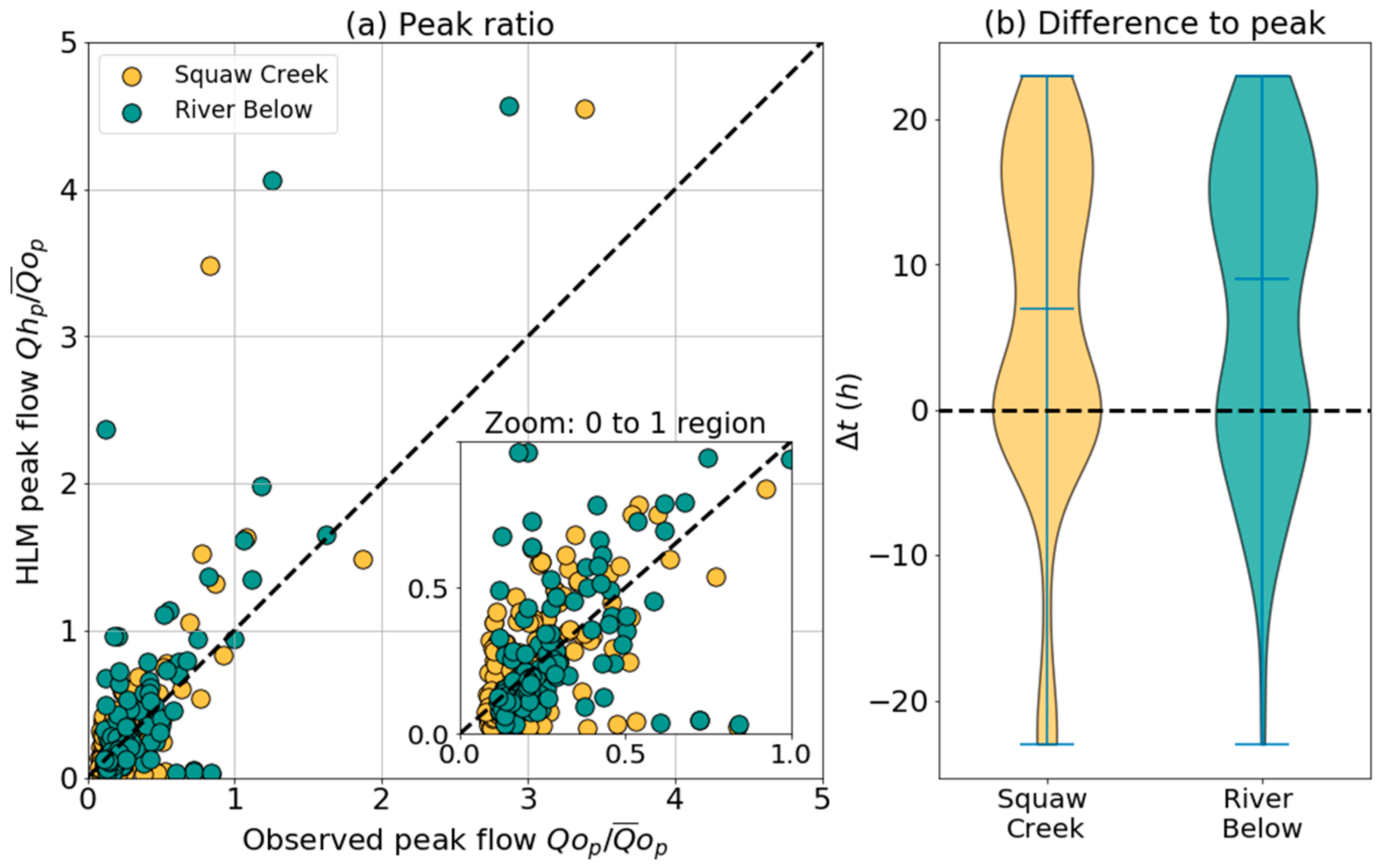
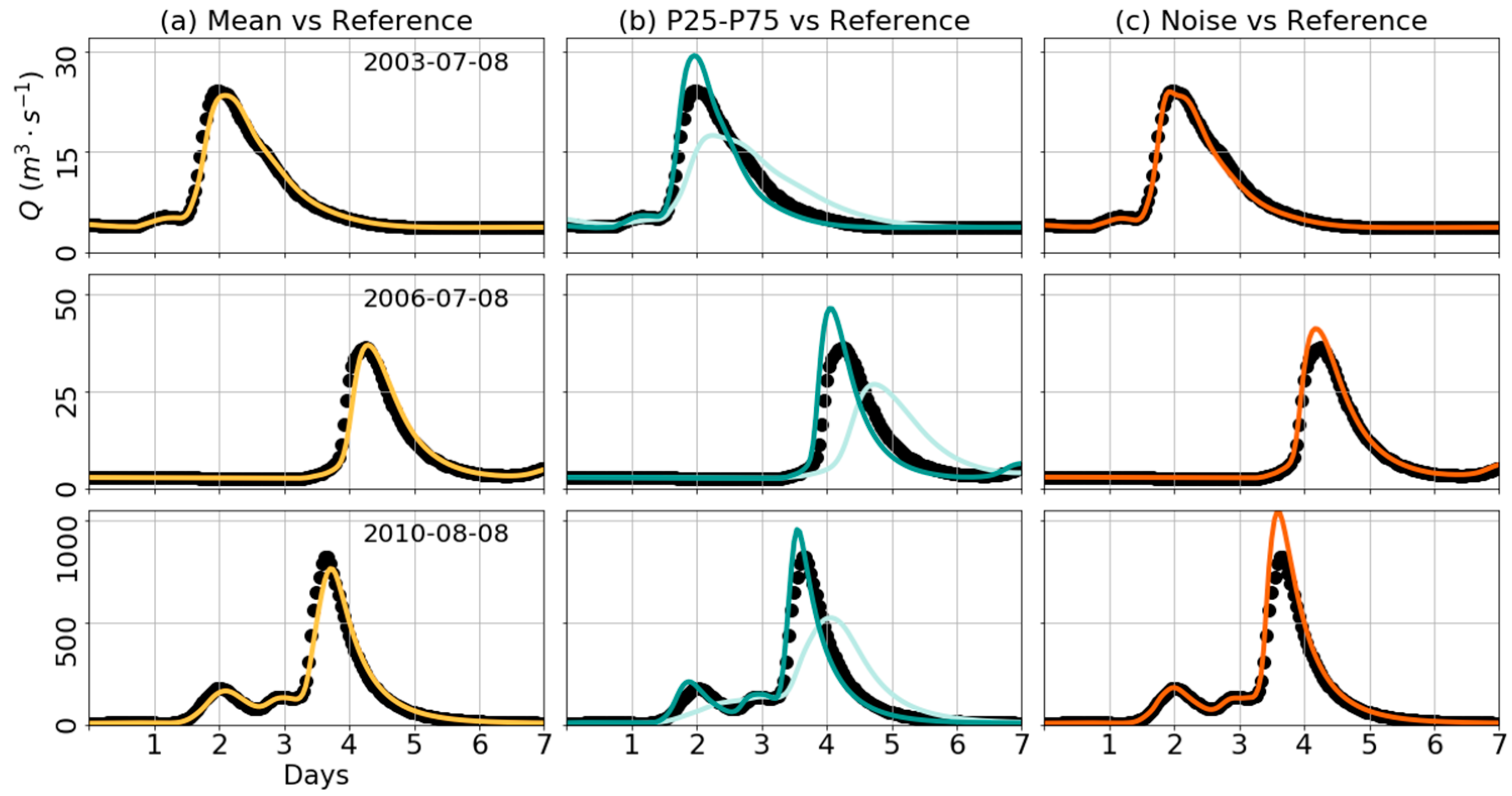
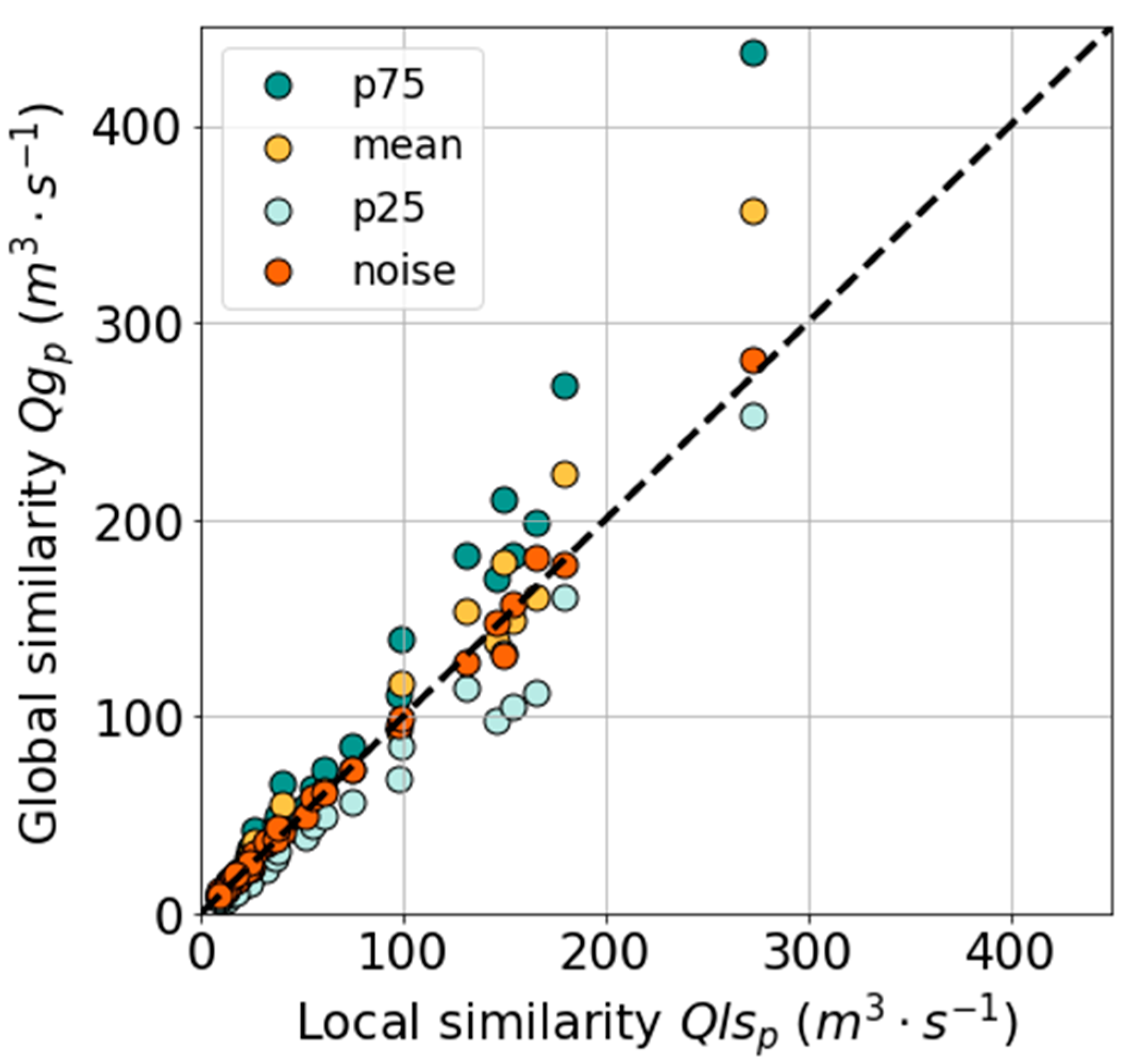
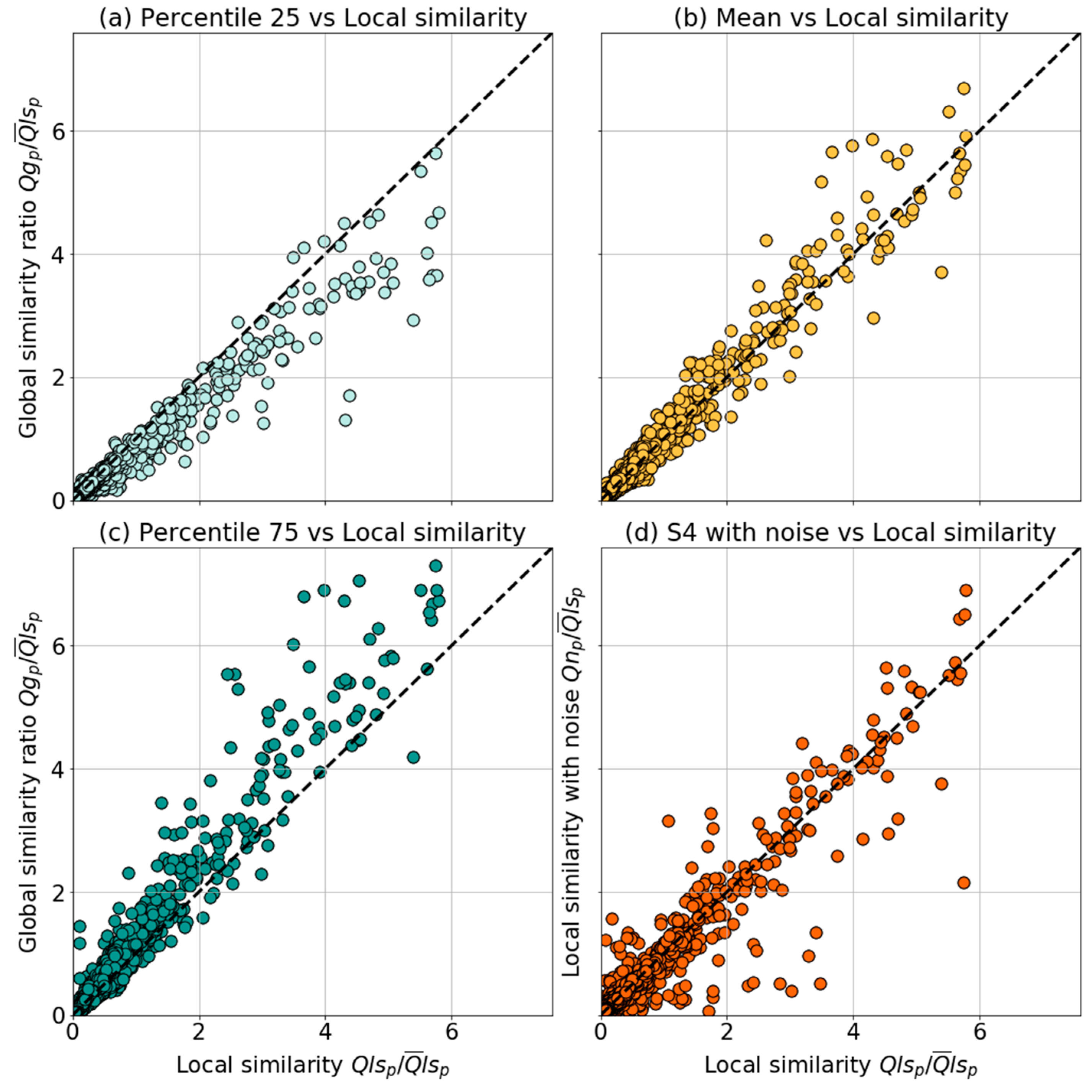
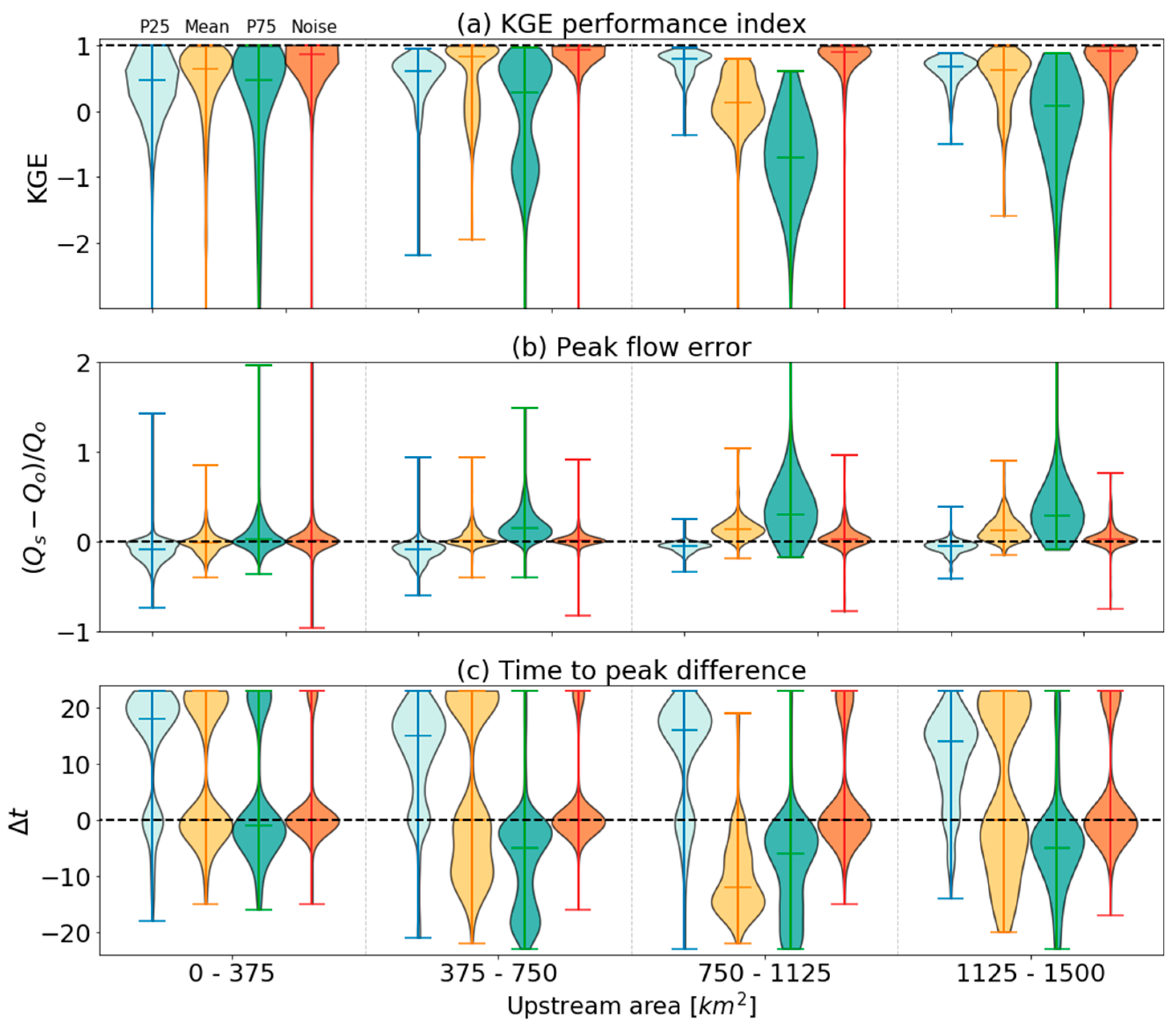
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Krajewski, W.F.; Smith, J.A. Radar hydrology: Rainfall estimation. Adv. Water Resour. 2002, 25, 1387–1394. [Google Scholar] [CrossRef]
- Berne, A.; Krajewski, W.F. Radar for hydrology: Unfulfilled promise or unrecognized potential? Adv. Water Resour. 2013, 51, 357–366. [Google Scholar] [CrossRef]
- Thomas, E.; Karsten, A.-N.; Claudia, G.; Niels, -E.J.; Markus, Q.; Guido, V.; Baxter, V. Towards a roadmap for use of radar rainfall data in urban drainage. J. Hydrol. 2004, 299, 186–202. [Google Scholar] [CrossRef]
- Wood, E.F.; Roundy, J.K.; Troy, T.J.; Van Beek, L.P.H.; Bierkens, M.F.; Blyth, E.; de Roo, A.; Döll, P.; Mike, E.; James, F. Hyperresolution global land surface modeling: Meeting a grand challenge for monitoring Earth’s terrestrial water. Water Resour. Res. 2011, 47, 1–10. [Google Scholar] [CrossRef]
- Carpenter, T.M.; Georgakakos, K.P.; Sperfslagea, J.A. On the parametric and NEXRAD-radar sensitivities of a distributed hydrologic model suitable for operational use. J. Hydrol. 2001, 253, 169–193. [Google Scholar] [CrossRef]
- Cole, S.J.; Moore, R.J. Distributed hydrological modelling using weather radar in gauged and ungauged basins. Adv. Water Resour. 2009, 32, 1107–1120. [Google Scholar] [CrossRef]
- Thorndahl, S.; Einfalt, T.; Willems, P.; Nielsen, J.E.; ten Veldhuis, M.-C.; Arnbjerg-Nielsen, K.; Rasmussen, M.R.; Molnar, P. Weather radar rainfall data in urban hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 1359–1380. [Google Scholar] [CrossRef]
- Grimaldi, S.; Schumann, G.J.-P.; Shokri, A.; Walker, J.P.; Pauwels, V.R.N. Challenges, opportunities, and pitfalls for global coupled hydrologic-hydraulic modeling of floods. Water Resour. Res. 2019, 55, 5277–5300. [Google Scholar] [CrossRef]
- Pathiraja, S.; Westra, S.; Sharma, A. Why continuous simulation? The role of antecedent moisture in design flood estimation. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Bates, P.D.; Neal, J.; Sampson, C.; Smith, A.; Trigg, M. Chapter 9-progress toward hyperresolution models of global flood hazard. In Risk Modeling for Hazards and Disasters; Michel, G., Ed.; Elsevier: Amsterdam, The Nederlands, 2018; pp. 211–232. [Google Scholar]
- Mantilla, R.; Gupta, V.K. A GIS numerical framework to study the process basis of scaling statistics in river networks. IEEE Geosci. Remote. Sens. Lett. 2005, 2, 404–408. [Google Scholar] [CrossRef]
- Gupta, V.K.; Waymire, E.C. Spatial variability and scale invariance in hydrologic regionalization. In Scale Dependence and Scale Invariance in Hydrology; Sposito, G., Ed.; Cambridge University Press: Cambridge, UK, 1998; pp. 88–135. [Google Scholar]
- Mantilla, R. Physical Basis of Statistical Scaling in Peak Flows and Stream Flow Hydrographs for Topologic and Spatially Embedded Random Self-similar Channel Networks; University of Colorado at Boulder: Boulder, CO, USA, 2007. [Google Scholar]
- Quintero, F.; Krajewski, W.F.; Seo, B.C.; Mantilla, R. Improvement and evaluation of the Iowa Flood Center Hillslope Link Model (HLM) by calibration-free approach. J. Hydrol. 2020, 584, 124686. [Google Scholar] [CrossRef]
- Quintero, F.; Krajewski, W.F.; Mantilla, R.; Small, S.; Seo, B.C. A spatial-dynamical framework for evaluation of satellite rainfall products for flood prediction. J. Hydrometeorol. 2016, 17, 2137–2154. [Google Scholar] [CrossRef]
- Jadidoleslam, N.; Goska, R.; Mantilla, R.; Krajewski, W.F. Hydrovise: A non-proprietary open-source software for hydrologic model and data visualization and evaluation. Environ. Model. Softw. 2020. Sumbbited. [Google Scholar]
- Leopold, L.B.; Maddock, T.J. The Hydraulic Geometry of Stream Channels and Some Physiographic Implications (USGS Numbered Series No. 252); US Government Printing Office: Washington, DC, USA, 1953. [Google Scholar]
- Ibbitt, R.P. Evaluation of optimal channel network and river basin heterogeneity concepts using measured flow and channel properties. J. Hydrol. 1997, 196, 119–138. [Google Scholar] [CrossRef]
- Ibbitt, R.P.; McKerchar, A.I.; Duncan, M.J. Taieri river data to test channel network and river basin heterogeneity concepts. Water Resour. Res. 1998, 34, 2085–2088. [Google Scholar] [CrossRef]
- Ibbitt, R.P.; Willgoose, G.R.; Duncan, M.J. Channel network simulation models compared with data from the Ashley River, New Zealand. Water Resour. Res. 1999, 35, 3875–3890. [Google Scholar] [CrossRef]
- Pitlick, J.; Cress, R. Downstream changes in the channel geometry of a large gravel bed river. Water Resour. Res. 2002, 38, 11–34. [Google Scholar] [CrossRef]
- Parker, G.; Wilcock, P.R.; Paola, C.; Dietrich, W.E.; Pitlick, J. Physical basis for quasi-universal relations describing bankfull hydraulic geometry of single-thread gravel bed rivers. J. Geophys. Res. Earth Surf. 2007, 112. [Google Scholar] [CrossRef]
- Palutikof, J.P.; Street, B.R.; Gardiner, E.P. Decision support platforms for climate change adaptation: An overview and introduction. Clim. Chang. 2019, 153, 459–476. [Google Scholar] [CrossRef]
- Wohl, E. 9.1 treatise on fluvial geomorphology. In Treatise on Geomorphology; Shroder, J.F., Ed.; Academic Press: San Diego, CA, USA, 2013; pp. 1–5. [Google Scholar]
- GCIP/EOP Surface: Precipitation NCEP/EMC 4KM Gridded Data (GRIB) Stage IV Data. Available online: https://doi.org/10.5065/D6PG1QDD (accessed on 15 July 2020).
- Ghimire, G.R.; Krajewski, W.F.; Mantilla, R. A power law model for river flow velocity in Iowa Basins. J. Am. Water Resour. Assoc. 2018, 54, 1055–1067. [Google Scholar] [CrossRef]
- Velasquez, N.; Mantilla, R.I.; Krajewski, W.; Quintero, F. Identifying streamflow routing parameters for the HLM hydrological model in Iowa. J. Hydrol. 2020, in press. [Google Scholar]
- Beven, K. Rainfall-Runoff Modelling: The Primer, 2nd ed.; John Wiley & Sons: Chichester, UK, 2012. [Google Scholar]
- Collier, C.G. Flash flood forecasting: What are the limits of predictability? J. Atmos. Sci. Appl. Meteorol. Phys. Oceanogr. 2007, 133, 3–23. [Google Scholar] [CrossRef]
- Singh, V.P.; Asce, F.; Woolhiser, D.A.; Asce, M. Mathematical modeling of watershed hydrology. J. Hydrol. Eng. 2002, 7, 270–292. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Gupta, H.V.; Bouten, W.; Sorooshian, S. A Shuffled Complex Evolution Metropolis algorithm for optimization and uncertainty assessment of hydrologic model parameters. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Rodriguez-Rincon, J.P.; Pedrozo-Acuna, A.; Berena-Naranjo, J. Propagation of hydro-meteorological uncertainty in a model cascade. Hydrol. Earth Syst. Sci. 2015, 19, 2981–2998. [Google Scholar] [CrossRef]
- Mejia, A.I.; Reed, S.M. Evaluating the effects of parameterized cross section shapes and simplified routing with a coupled distributed hydrologic and hydraulic model. J. Hydrol. 2011, 409, 512–524. [Google Scholar] [CrossRef]
- Villarini, G.; Mandapaka, P.V.; Krajewski, W.F.; Moore, R.J. Rainfall and sampling uncertainties: A rain gauge perspective. J. Geophys. Res. Atmos. 2008, 113, 1–12. [Google Scholar] [CrossRef]
- Yang, D.; Koike, T.; Tanizawa, H. Application of a distributed hydrological model and weather radar observations for flood management in the upper Tone River of Japan. Hydrol. Process. 2004, 18, 3119–3132. [Google Scholar] [CrossRef]
- Ibbitt, R.P.; Clark, M.P.; Woods, R.A.; Zheng, X.; Slater, A.G.; Rupp, D.E.; Schmidt, J.; Uddstrom, M. Hydrological data assimilation with the ensemble Kalman filter: Use of streamflow observations to update states in a distributed hydrological model. Adv. Water Resour. 2008, 31, 1309–1324. [Google Scholar] [CrossRef]
- Hamilton, A.S.; Moore, R.D. Quantifying uncertainty in streamflow records. Can. Water Resour. J./Rev. Can. Des. Ressour. Hydr. 2012, 37, 3–21. [Google Scholar] [CrossRef]
- Quintero, F.; Krajewski, W.F. Mapping outlets of iowa flood center and national water center river networks for hydrologic model comparison. J. Am. Water Resour. Assoc. 2018, 54, 28–39. [Google Scholar] [CrossRef]
- Strahler, A.N. Quantitative analysis of watershed geomorphology. Eos Trans. Am. Geophys. Union 1957, 38, 913–920. [Google Scholar] [CrossRef]
- Horton, R.E. Erosional Development of Streams and Their Drainage Basins; Hydrophysical Approach to Quantitative Morphology. GSA Bull. 1945, 56, 275–370. [Google Scholar] [CrossRef]
- Duda, J.D.; Gallus, W.A. Spring and summer midwestern severe weather reports in supercells compared to other morphologies. Weather Forecast. 2010, 25, 190–206. [Google Scholar] [CrossRef]
- Therrell, M.D.; Bialecki, M.B. A multi-century tree-ring record of spring flooding on the Mississippi River. J. Hydrol. 2015, 529, 490–498. [Google Scholar] [CrossRef]
- MODIS/Terra Net Evapotranspiration 8-Day L4 Global 500 m SIN Grid. Available online: https://doi.org/10.5067/MODIS/MOD16A2.006 (accessed on 15 July 2020).
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]

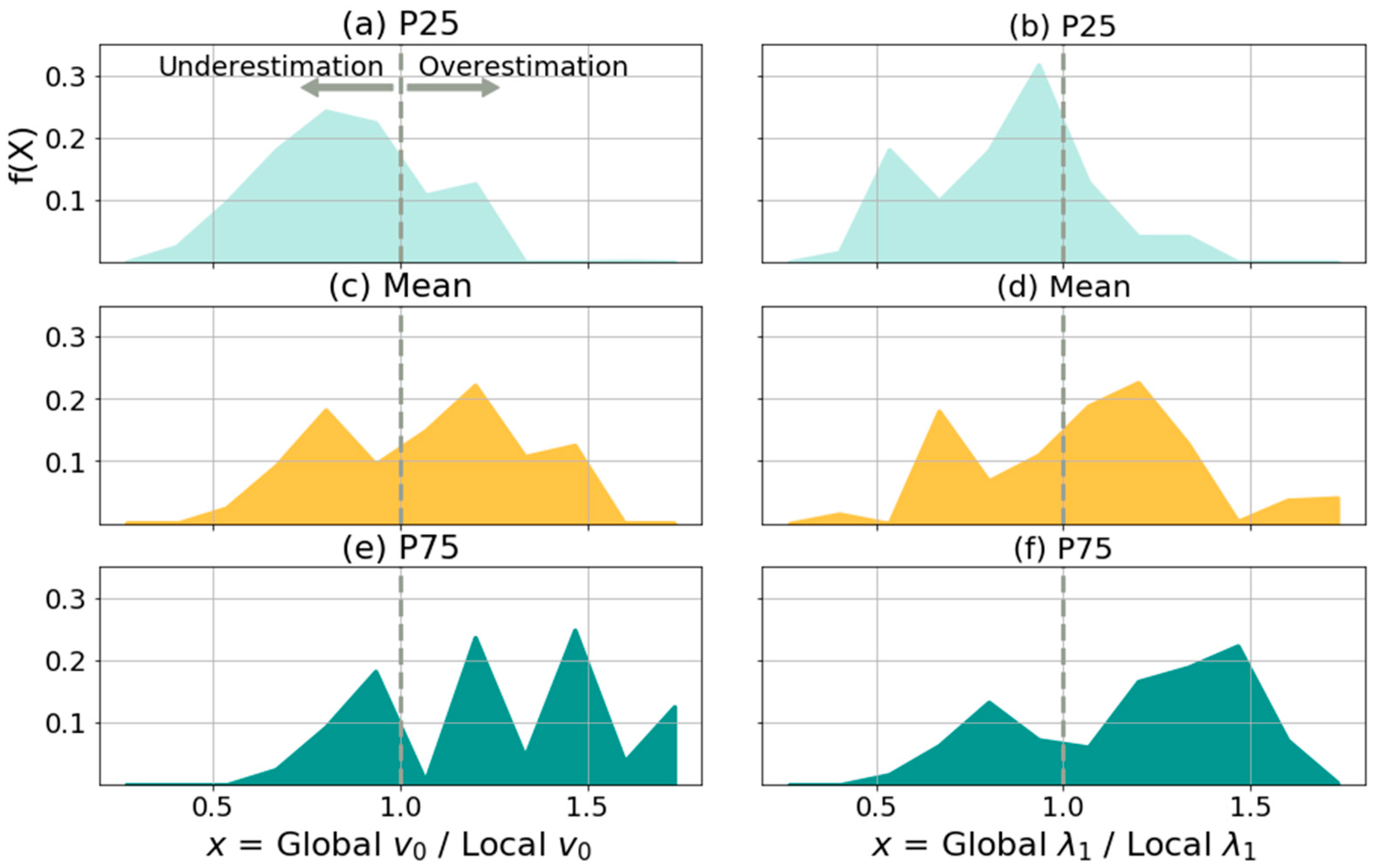
| and Distribution | Setup Name | Setup Use | Value | Value | Rainfall |
|---|---|---|---|---|---|
| Local self-similarity | Local | Reference | Distributed | Distributed | Stage IV |
| Noise | Comparison | Distributed | Distributed | Stage IV + noise | |
| Global self-similarity | Mean | Comparison | 0.29 | 0.23 | Stage IV |
| P25 | Comparison | 0.23 | 0.18 | Stage IV | |
| P75 | Comparison | 0.34 | 0.27 | Stage IV |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velasquez, N.; Mantilla, R. Limits of Predictability of a Global Self-Similar Routing Model in a Local Self-Similar Environment. Atmosphere 2020, 11, 791. https://doi.org/10.3390/atmos11080791
Velasquez N, Mantilla R. Limits of Predictability of a Global Self-Similar Routing Model in a Local Self-Similar Environment. Atmosphere. 2020; 11(8):791. https://doi.org/10.3390/atmos11080791
Chicago/Turabian StyleVelasquez, Nicolas, and Ricardo Mantilla. 2020. "Limits of Predictability of a Global Self-Similar Routing Model in a Local Self-Similar Environment" Atmosphere 11, no. 8: 791. https://doi.org/10.3390/atmos11080791
APA StyleVelasquez, N., & Mantilla, R. (2020). Limits of Predictability of a Global Self-Similar Routing Model in a Local Self-Similar Environment. Atmosphere, 11(8), 791. https://doi.org/10.3390/atmos11080791






