Prediction Skill of Extended Range 2-m Maximum Air Temperature Probabilistic Forecasts Using Machine Learning Post-Processing Methods
Abstract
:1. Introduction
2. Data
3. Post-Processing and Verification Methods
3.1. Ensemble Model Output Statistics
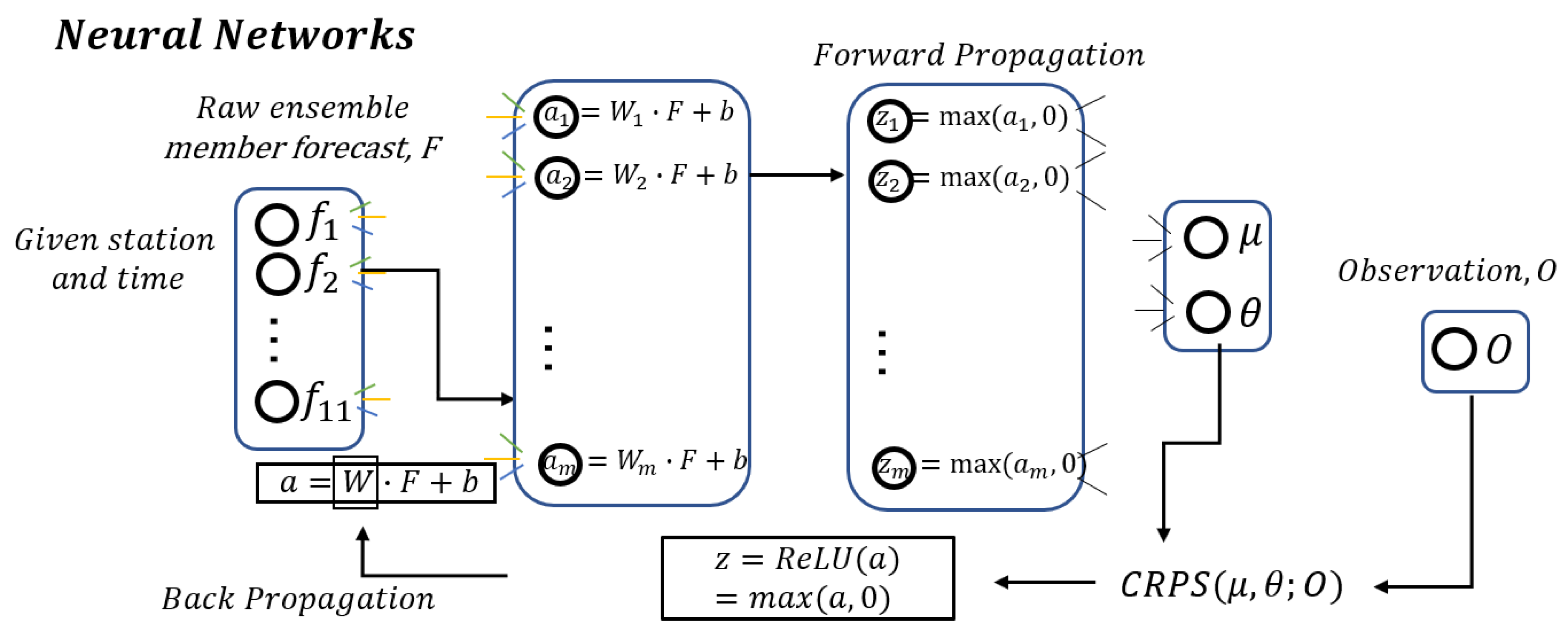
3.2. Neural Networks
3.3. Natural Gradient Boosting
3.4. Verification Methods
4. Results
4.1. Overall Performance of EMOS, the Neural Network and NGBoost
4.2. Spatiotemporal Characteristics
5. Conclusions
6. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- DelSole, T.; Trenary, L.; Tippett, M.K.; Pegion, K. Predictability of week-3–4 average temperature and precipitation over the contiguous United States. J. Clim. 2017, 30, 3499–3512. [Google Scholar] [CrossRef]
- Black, J.; Johnson, N.C.; Baxter, S.; Feldstein, S.B.; Harnos, D.S.; L’Heureux, M.L. The predictors and forecast skill of Northern Hemisphere teleconnection patterns for lead times of 3–4 weeks. Mon. Weather Rev. 2017, 145, 2855–2877. [Google Scholar] [CrossRef]
- National Research Council. Assessment of Intraseasonal to Interannual Climate Prediction and Predictability; The National Academies Press: Washington, DC, USA, 2010; ISBN 978-0-309-15183-2. [Google Scholar]
- Brunet, G.; Shapiro, M.; Hoskins, B.; Moncrieff, M.; Dole, R.; Kiladis, G.N.; Kirtman, B.; Lorenc, A.; Mills, B.; Morss, R.; et al. Collaboration of the Weather and Climate Communities to Advance Subseasonal-to-Seasonal Prediction. Bull. Amer. Meteorol. Soc. 2010, 91, 1397–1406. [Google Scholar] [CrossRef]
- The National Academies of Sciences, Engineering, Medicine. Next Generation Earth System Prediction: Strategies for Subseasonal to Seasonal Forecasts; The National Academies Press: Washington, DC, USA, 2016; ISBN 978-0-309-38880-1. [Google Scholar]
- Mariotti, A.; Ruti, P.M.; Rixen, M. Progress in subseasonal to seasonal prediction through a joint weather and climate community effort. npj Clim. Atmos. Sci. 2018, 1, 4. [Google Scholar] [CrossRef]
- Pegion, K.; Sardeshmukh, P.D. Prospects for improving subseasonal predictions. Mon. Weather Rev. 2011, 139, 3648–3666. [Google Scholar] [CrossRef]
- Li, S.; Robertson, A.W. Evaluation of Submonthly Precipitation Forecast Skill from Global Ensemble Prediction Systems. Mon. Weather Rev. 2015, 143, 2871–2889. [Google Scholar] [CrossRef]
- Pegion, K.; Kirtman, B.P.; Becker, E.; Collins, D.C.; Lajoie, E.; Burgman, R.; Bell, R.; Delsole, T.; Min, D.; Zhu, Y.; et al. The subseasonal experiment (SUBX). Bull. Amer. Meteorol. Soc. 2019, 100, 2043–2060. [Google Scholar] [CrossRef]
- Raftery, A.E.; Gneiting, T.; Balabdaoui, F.; Polakowski, M. Using Bayesian model averaging to calibrate forecast ensembles. Mon. Weather Rev. 2005, 133, 1155–1174. [Google Scholar] [CrossRef] [Green Version]
- Gneiting, T.; Raftery, A.E.; Westveld, A.H.; Goldman, T. Calibrated probabilistic forecasting using ensemble model output statistics and minimum CRPS estimation. Mon. Weather Rev. 2005, 133, 1098–1118. [Google Scholar] [CrossRef]
- Krishnamurti, T.N.; Kishtawal, C.M.; LaRow, T.E.; Bachiochi, D.R.; Zhang, Z.; Williford, C.E.; Gadgil, S.; Surendran, S. Improved weather and seasonal climate forecasts from multimodel superensemble. Science 1999, 285, 1548–1550. [Google Scholar] [CrossRef] [Green Version]
- Zhi, X.; Qi, H.; Bai, Y.; Lin, C. A comparison of three kinds of multimodel ensemble forecast techniques based on the TIGGE data. Acta Meteorol. Sin. 2012, 26, 41–51. [Google Scholar] [CrossRef]
- He, C.; Zhi, X.; You, Q.; Song, B.; Fraedrich, K. Multi-model ensemble forecasts of tropical cyclones in 2010 and 2011 based on the Kalman Filter method. Meteorol. Atmos. Phys. 2015, 127, 467–479. [Google Scholar] [CrossRef]
- Ji, L.; Zhi, X.; Simmer, C.; Zhu, S.; Ji, Y. Multimodel Ensemble Forecasts of Precipitation Based on an Object-Based Diagnostic Evaluation. Mon. Weather Rev. 2020, 148, 2591–2606. [Google Scholar] [CrossRef]
- Ji, L.; Zhi, X.; Zhu, S.; Fraedrich, K. Probabilistic precipitation forecasting over East Asia using Bayesian model averaging. Weather Forecast. 2019, 34, 377–392. [Google Scholar] [CrossRef]
- Neapolitan, R.E.; Neapolitan, R.E. Neural Networks and Deep Learning. Artif. Intell. 2018, 389–411. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Angermueller, C.; Pärnamaa, T.; Parts, L.; Stegle, O. Deep learning for computational biology. Mol. Syst. Biol. 2016, 12, 878. [Google Scholar] [CrossRef]
- Goh, G.B.; Hodas, N.O.; Vishnu, A. Deep learning for computational chemistry. J. Comput. Chem. 2017, 38, 1291–1307. [Google Scholar] [CrossRef] [Green Version]
- Chao, Z.; Pu, F.; Yin, Y.; Han, B.; Chen, X. Research on real-time local rainfall prediction based on MEMS sensors. J. Sens. 2018, 2018, 1–9. [Google Scholar] [CrossRef]
- Shi, X.; Gao, Z.; Lausen, L.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Deep learning for precipitation nowcasting: A benchmark and a new model. In Proceedings of the neural information processing systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 5617–5627. [Google Scholar]
- Akbari Asanjan, A.; Yang, T.; Hsu, K.; Sorooshian, S.; Lin, J.; Peng, Q. Short-Term Precipitation Forecast Based on the PERSIANN System and LSTM Recurrent Neural Networks. J. Geophys. Res. Atmos. 2018, 123, 12543–12563. [Google Scholar] [CrossRef]
- Rasp, S.; Lerch, S. Neural networks for postprocessing ensemble weather forecasts. Mon. Weather Rev. 2018, 146, 3885–3900. [Google Scholar] [CrossRef] [Green Version]
- Duan, T.; Avati, A.; Ding, D.Y.; Thai, K.K.; Basu, S.; Ng, A.Y.; Schuler, A. NGBoost: Natural Gradient Boosting for Probabilistic Prediction. Available online: https://arxiv.org/abs/1910.03225 (accessed on 9 June 2020).
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Ren, L.; Sun, G.; Wu, J. RoNGBa: A Robustly Optimized Natural Gradient Boosting Training Approach with Leaf Number Clipping. Available online: https://arxiv.org/abs/1912.02338 (accessed on 9 June 2020).
- Fan, Y.; van den Dool, H. A global monthly land surface air temperature analysis for 1948–present. J. Geophys. Res. Atmos. 2008, 113, D01103. [Google Scholar] [CrossRef]
- Glahn, H.R.; Lowry, D.A. The Use of Model Output Statistics (MOS) in Objective Weather Forecasting. J. Appl. Meteorol. 1972, 11, 1203–1211. [Google Scholar] [CrossRef] [Green Version]
- Hamill, T.M.; Wilks, D.S. A probabilistic forecast contest and the difficulty in assessing short-range forecast uncertainty. Weather Forecast. 1995, 10, 620–631. [Google Scholar] [CrossRef] [Green Version]
- Stefanova, L.; Krishnamurti, T.N. Interpretation of seasonal climate forecast using Brier skill score, the Florida State University Superensemble, and the AMIP-I dataset. J. Clim. 2002, 15, 537–544. [Google Scholar] [CrossRef]
- Jordan, A.; Krüger, F.; Lerch, S. Evaluating probabilistic forecasts with scoringRules. J. Stat. Softw. 2019, 90, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR 2015), San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Amari, S. Natural Gradient Works Efficiently in Learning. Neural Comput. 1998, 10, 251–276. [Google Scholar] [CrossRef]
- Martens, J. New insights and perspectives on the natural gradient method. Available online: https://arxiv.org/abs/1412.1193 (accessed on 9 June 2020).
- Gneiting, T.; Raftery, A.E. Strictly Proper Scoring Rules, Prediction, and Estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- Gebetsberger, M.; Messner, J.W.; Mayr, G.J.; Zeileis, A. Estimation Methods for Nonhomogeneous Regression Models: Minimum Continuous Ranked Probability Score versus Maximum Likelihood. Mon. Weather Rev. 2018, 146, 4323–4338. [Google Scholar] [CrossRef]
- Gneiting, T.; Balabdaoui, F.; Raftery, A.E. Probabilistic and sharpness forecasts, calibration. J. R. Stat. Soc. Ser. B-Stat. Methodol. 2013, 69, 243–268. [Google Scholar] [CrossRef] [Green Version]
- Anderson, J.L. A Method for Producing and Evaluating Proababilistic Forecasts from ensemble Model Integrations. J. Clim. 1996, 9, 1518–1530. [Google Scholar] [CrossRef]
- Hamill, T.M.; Colucci, S.J. Verification of Eta–RSM Short-Range Ensemble Forecasts. Mon. Weather Rev. 1997, 125, 1312–1327. [Google Scholar] [CrossRef]
- Talagrand, O.; Vautard, R.; Strauss, B. Evaluation of probabilistic prediction systems. In Proceedings of the Workshop on Predictability, Reading, UK, 20–22 October 1997; p. 12555. [Google Scholar]
- Hamill, T.M. Interpretation of Rank Histograms for Verifying Ensemble Forecasts. Mon. Weather Rev. 2001, 129, 550–560. [Google Scholar] [CrossRef]
- Hersbach, H. Decomposition of the Continuous Ranked Probability Score for Ensemble Prediction Systems. Weather Forecast. 2000, 15, 559–570. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhou, X.; Li, W.; Hou, D.; Melhauser, C.; Sinsky, E.; Peña, M.; Fu, B.; Guan, H.; Kolczynski, W.; et al. Toward the Improvement of Subseasonal Prediction in the National Centers for Environmental Prediction Global Ensemble Forecast System. J. Geophys. Res. Atmos. 2018, 123, 6732–6745. [Google Scholar] [CrossRef]







| Week 1 | Week 2 | Week 3 | Week 4 | Week 5 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | |
| ENS | 2.91 | 3.52 | 3.12 | 3.80 | 3.31 | 4.05 | 3.49 | 4.30 | 3.64 | 4.50 |
| EMOS | 2.20 | 2.84 | 2.49 | 3.21 | 2.78 | 3.57 | 3.05 | 3.90 | 3.26 | 4.17 |
| NGB | 2.05 | 2.63 | 2.30 | 2.93 | 2.54 | 3.24 | 2.77 | 3.53 | 2.97 | 3.77 |
| NN | 2.05 | 2.64 | 2.28 | 2.92 | 2.52 | 3.22 | 2.75 | 3.50 | 2.93 | 3.73 |
| Week 1 | Week 2 | Week 3 | Week 4 | Week 5 | |
|---|---|---|---|---|---|
| CRPS | |||||
| ENS | 2.40 | 2.51 | 2.61 | 2.71 | 2.80 |
| EMOS | 1.60 | 1.81 | 2.02 | 2.21 | 2.36 |
| NGB | 1.48 | 1.65 | 1.82 | 1.98 | 2.12 |
| NN | 1.49 | 1.66 | 1.83 | 1.98 | 2.11 |
| Coverage at 88.33% Prediction Interval | |||||
| ENS | 41.73 | 47.73 | 52.45 | 55.99 | 58.28 |
| EMOS | 67.88 | 67.76 | 67.91 | 67.99 | 67.94 |
| NGB | 80.30 | 80.06 | 79.98 | 79.94 | 79.71 |
| NN | 76.43 | 76.92 | 77.48 | 78.51 | 78.78 |
| Average Width at 88.33% Prediction Interval | |||||
| ENS | 2.16 | 2.75 | 3.29 | 3.77 | 4.12 |
| EMOS | 2.87 | 3.27 | 3.68 | 4.06 | 4.34 |
| NGB | 3.52 | 3.94 | 4.38 | 4.78 | 5.10 |
| NN | 3.35 | 3.76 | 4.19 | 4.64 | 4.95 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, T.; Zhi, X.; Ji, Y.; Ji, L.; Tian, Y. Prediction Skill of Extended Range 2-m Maximum Air Temperature Probabilistic Forecasts Using Machine Learning Post-Processing Methods. Atmosphere 2020, 11, 823. https://doi.org/10.3390/atmos11080823
Peng T, Zhi X, Ji Y, Ji L, Tian Y. Prediction Skill of Extended Range 2-m Maximum Air Temperature Probabilistic Forecasts Using Machine Learning Post-Processing Methods. Atmosphere. 2020; 11(8):823. https://doi.org/10.3390/atmos11080823
Chicago/Turabian StylePeng, Ting, Xiefei Zhi, Yan Ji, Luying Ji, and Ye Tian. 2020. "Prediction Skill of Extended Range 2-m Maximum Air Temperature Probabilistic Forecasts Using Machine Learning Post-Processing Methods" Atmosphere 11, no. 8: 823. https://doi.org/10.3390/atmos11080823
APA StylePeng, T., Zhi, X., Ji, Y., Ji, L., & Tian, Y. (2020). Prediction Skill of Extended Range 2-m Maximum Air Temperature Probabilistic Forecasts Using Machine Learning Post-Processing Methods. Atmosphere, 11(8), 823. https://doi.org/10.3390/atmos11080823




