Road Traffic Dynamic Pollutant Emissions Estimation: From Macroscopic Road Information to Microscopic Environmental Impact
Abstract
1. Introduction
- The proposed modeling framework is able to estimate time-varying and microscopic road traffic emissions by only using easily obtainable macroscopic topographic and traffic information on any given geographical area;
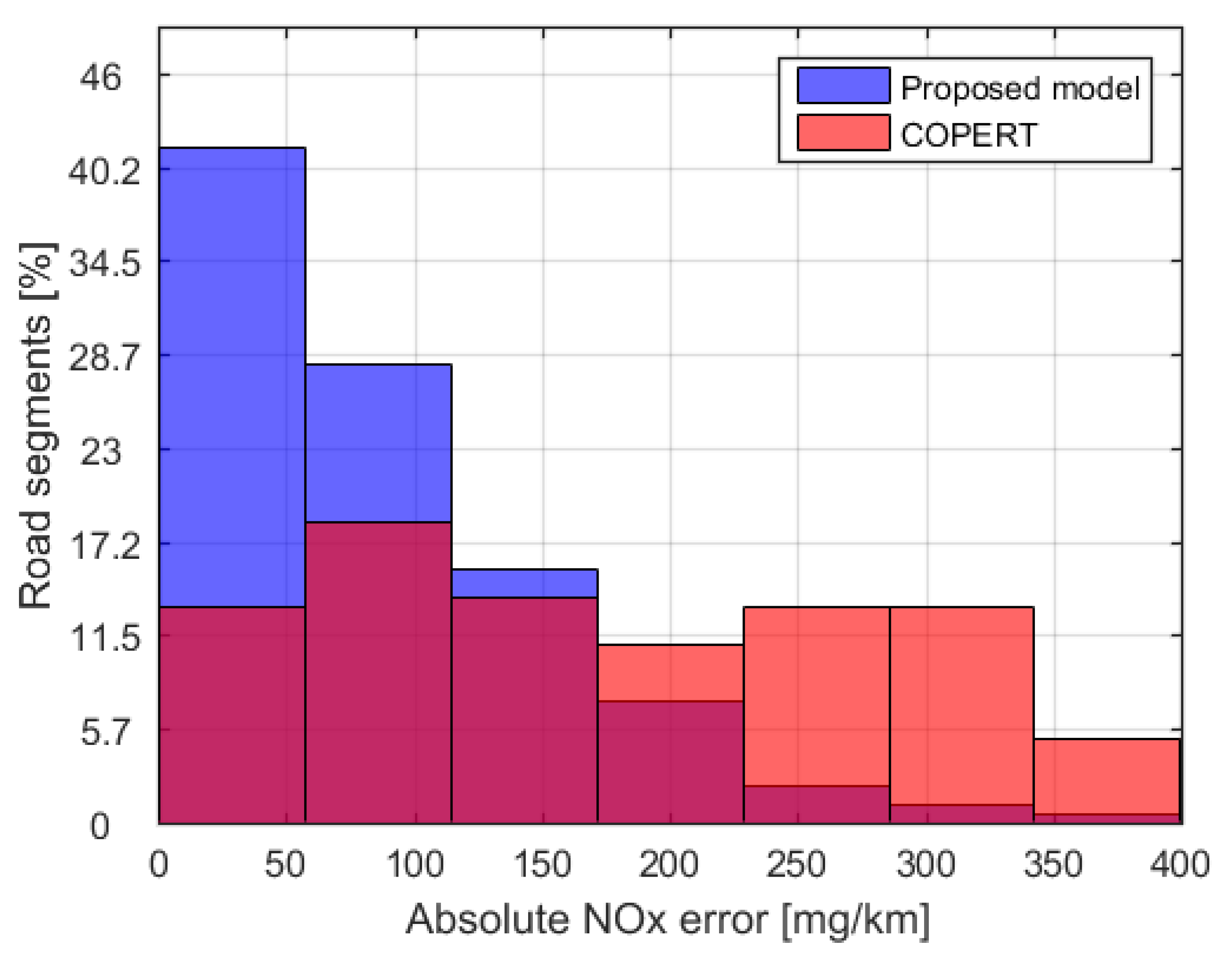
- A thorough model validation is able to highlight the model accuracy and the drastic emissions estimation error when compared to well-established macroscopic emissions models, such as COPERT [32]. In addition, our model is able to identify critical road links in terms of pollutant emissions at a very high spatial resolution. Such a precision is very valuable to understand what road segments should need careful investigation and perhaps infrastructure modification, as well as to feed atmospheric dispersion and air quality models with high-resolution emission sources.
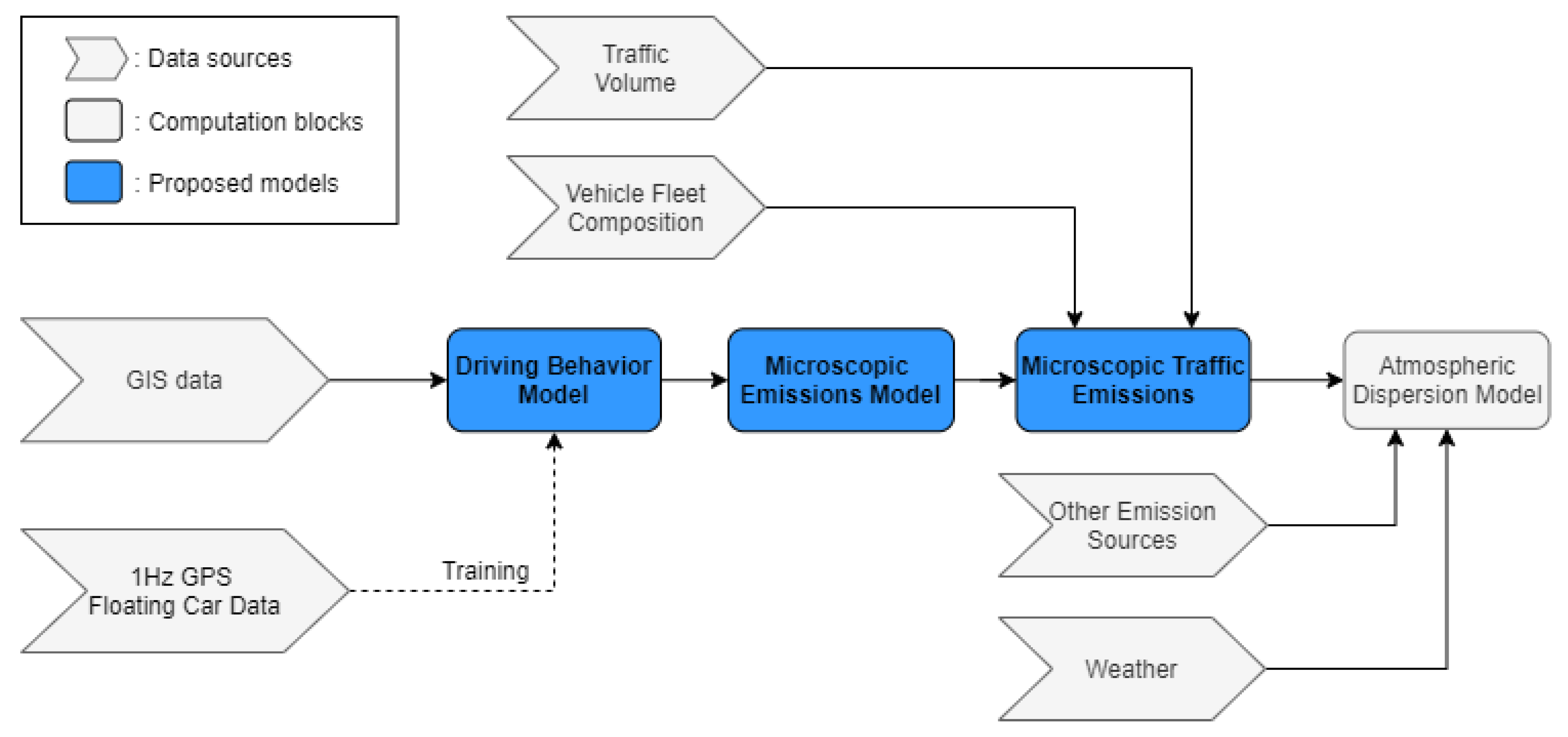
2. Materials and Methods
2.1. Driving Behavior Model
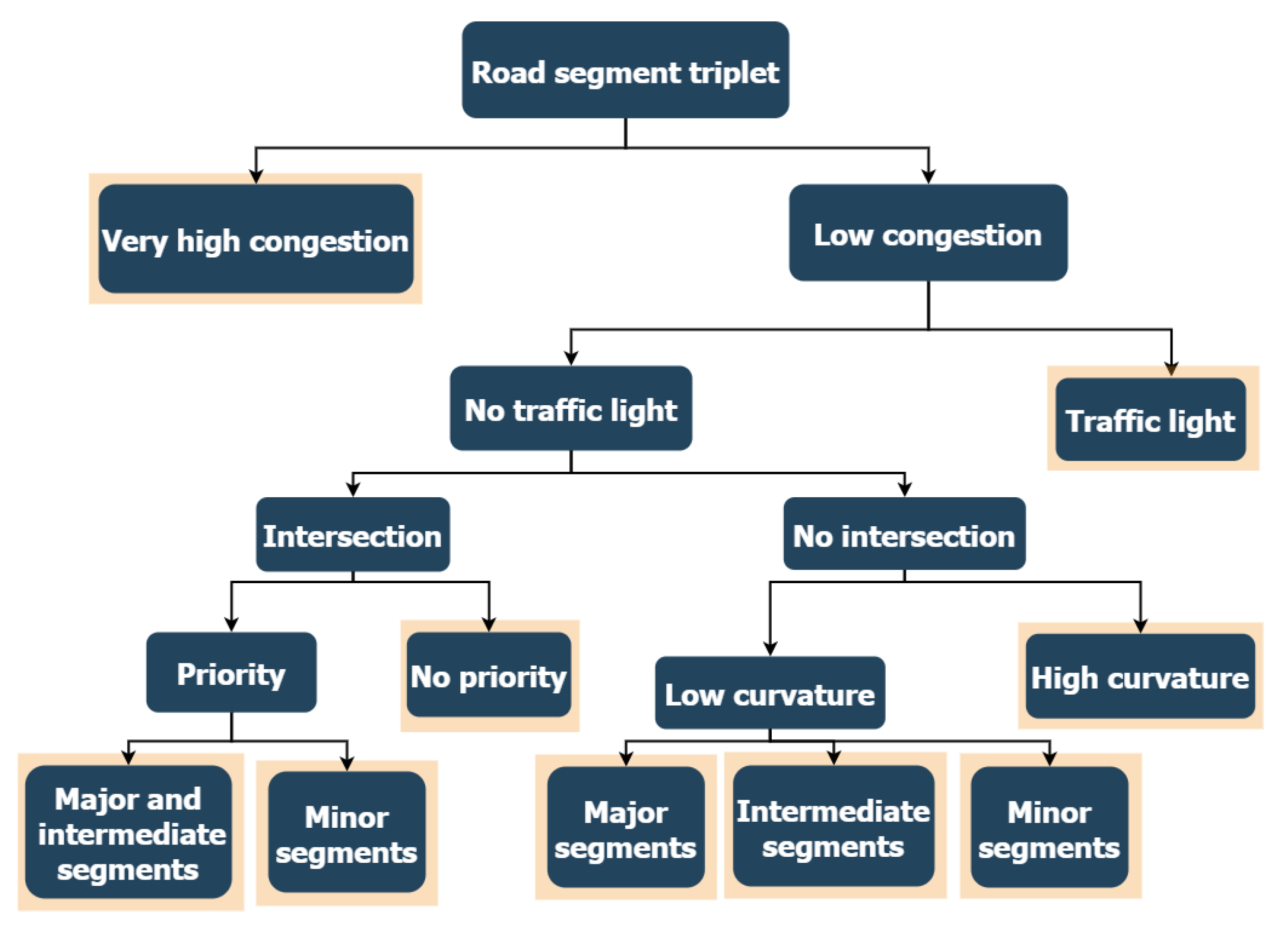
2.1.1. Road Network Segmentation
2.1.2. Driving Behavior Categorization
- Very high congestion: The congestion level, which is the ratio between the traffic speed and the free-flow speed, is below a defined threshold.
- Traffic light: Traffic light presence in the middle road link of the triplet.
- No priority: Existence of stop or yield sign in the middle road link of the triplet. It is also the case if the destination road link has lower functional importance than the other downstream road links.
- Priority—Major and intermediate segments: The destination road link has more functional importance than the other downstream road links. The triplet is a motorway, a major road link, or a secondary road link with high volume traffic.
- Priority—Minor segments: The destination road link has more functional importance than the other downstream road links. The triplet is a minor road link with low volume traffic and low-speed limitation.
- High curvature: The triplet curvature is above a defined threshold.
- Low curvature: The triplet curvature is below a defined threshold. Then, three categories are defined based on their functional importance within the Transportation Network.
2.1.3. Clustering of Driving Styles
2.1.4. Driving Characteristics Extraction
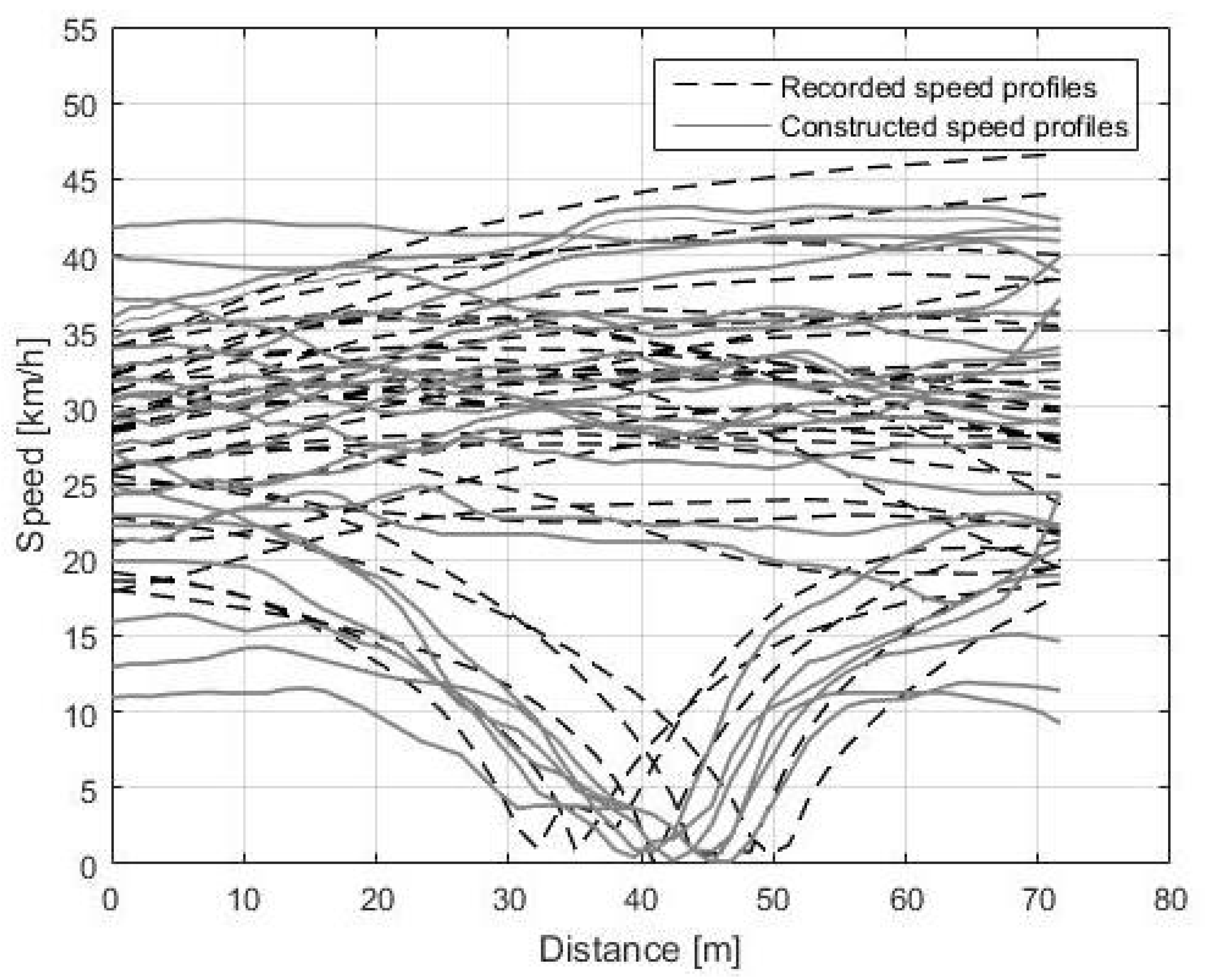
2.1.5. Stochastic Speed Construction
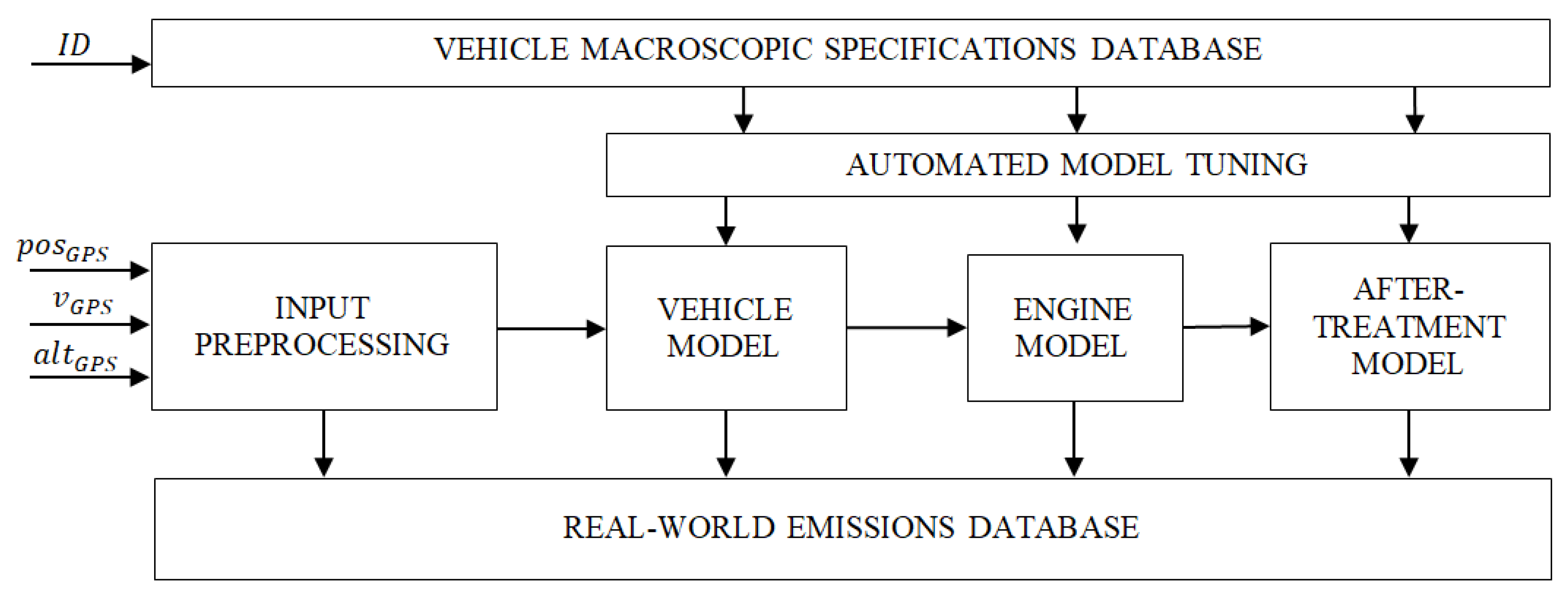
2.2. Microscopic Emissions Model
2.2.1. Vehicle Model
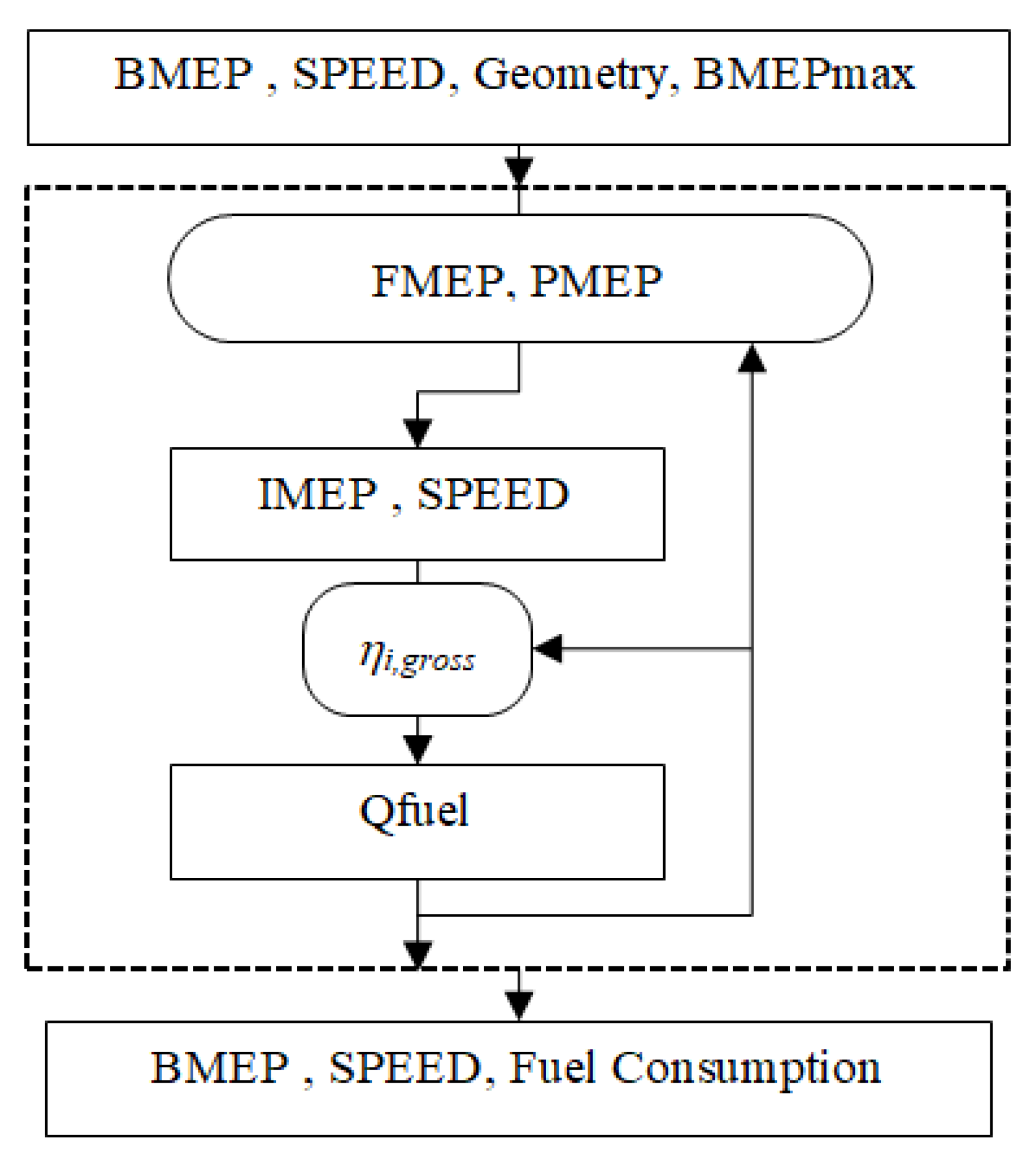
2.2.2. Engine Fuel Consumption Model
- Maximum torque curve and air-path architecture are known for the engine;
- Generic law for the friction mean effective pressure (FMEP), as a function of engine speed;
- Constant gross indicated efficiency;
- Fuel air equivalence ratio equal to 1 in spark-ignition engines (except at high load where it increases linearly with load), and varying between two values for compression–ignition engines;
- The exhaust gas recirculation (EGR) fraction is known for each point of the engine map.
- The engine coolant temperature is modeled using a simple heat exchange model. This model takes into account the heat produced by the combustion which is assumed to be a function of the engine operating point and the ambient heat exchange. Cold start effect on fuel consumption is then modeled with a coefficient function of the coolant temperature.
2.2.3. Engine-Out Emissions Model
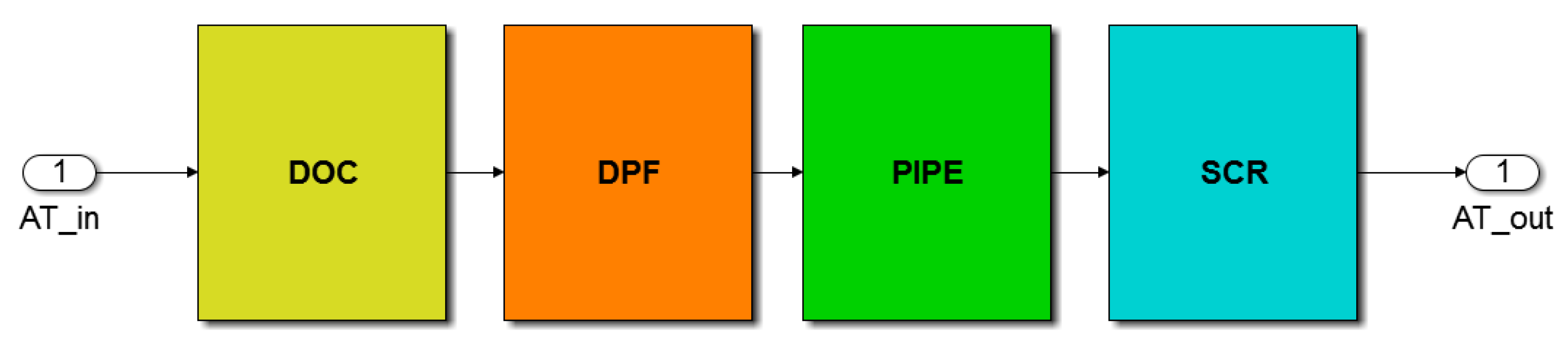
2.2.4. After-Treatment Model
2.3. Microscopic Traffic Emissions
3. Results
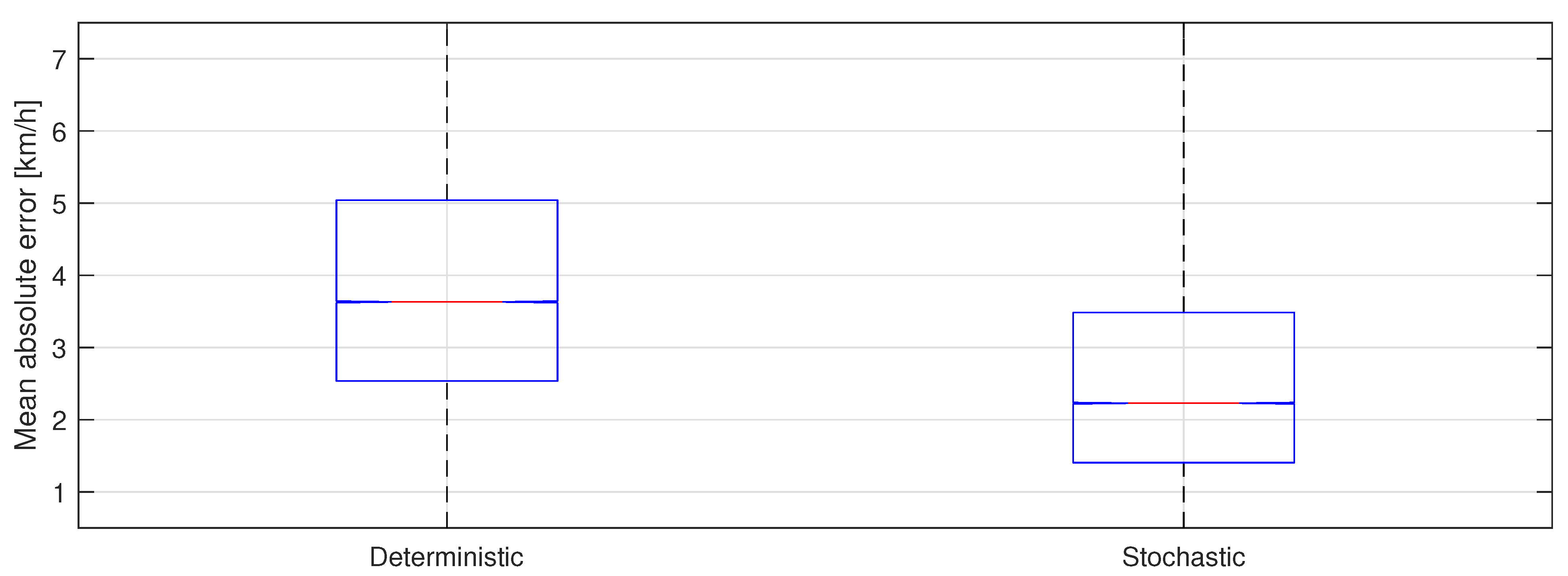
3.1. Driving Behavior Model Validation
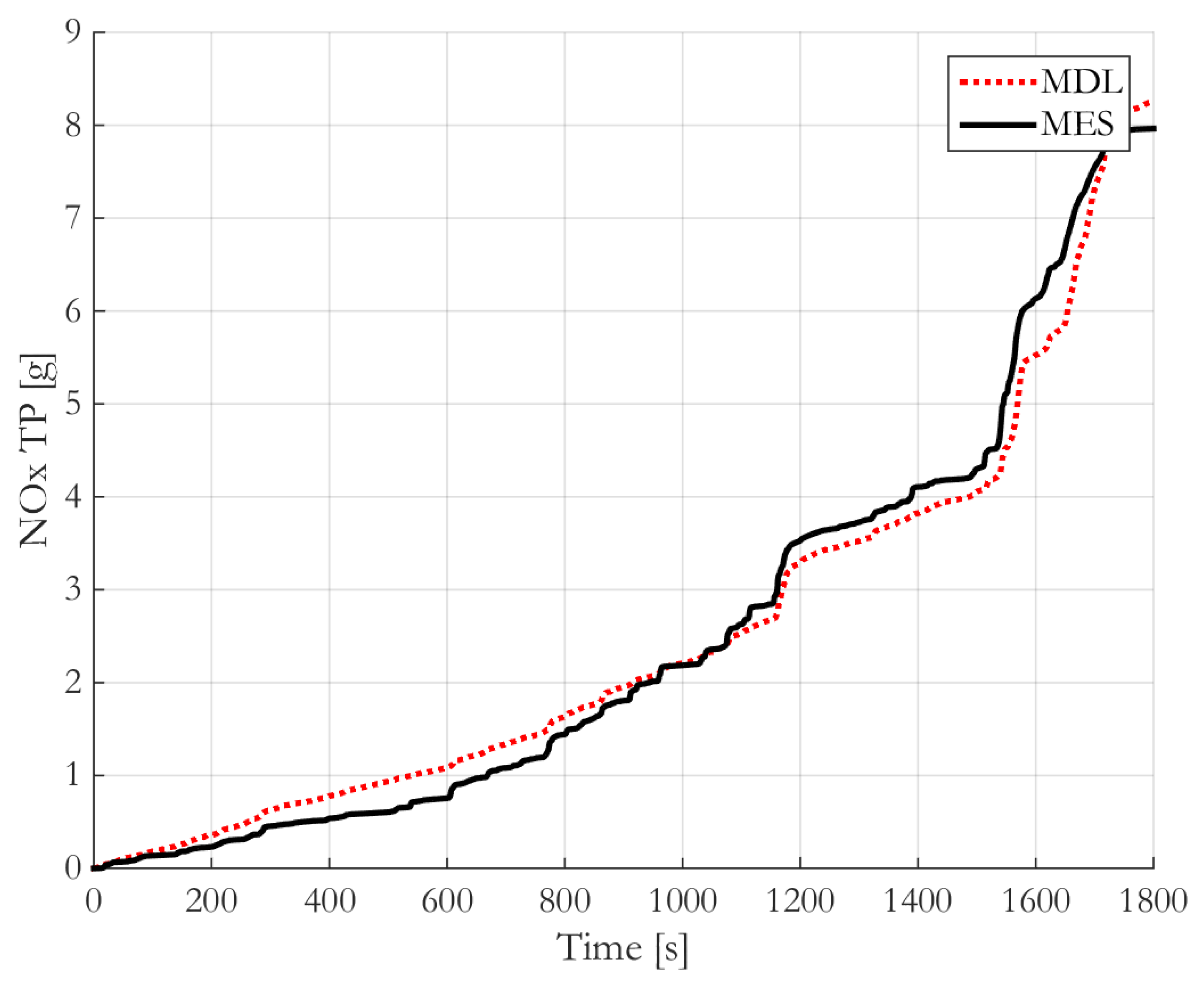
3.2. Microscopic Emissions’ Model Validation
3.2.1. Impact of the Driving Behavior
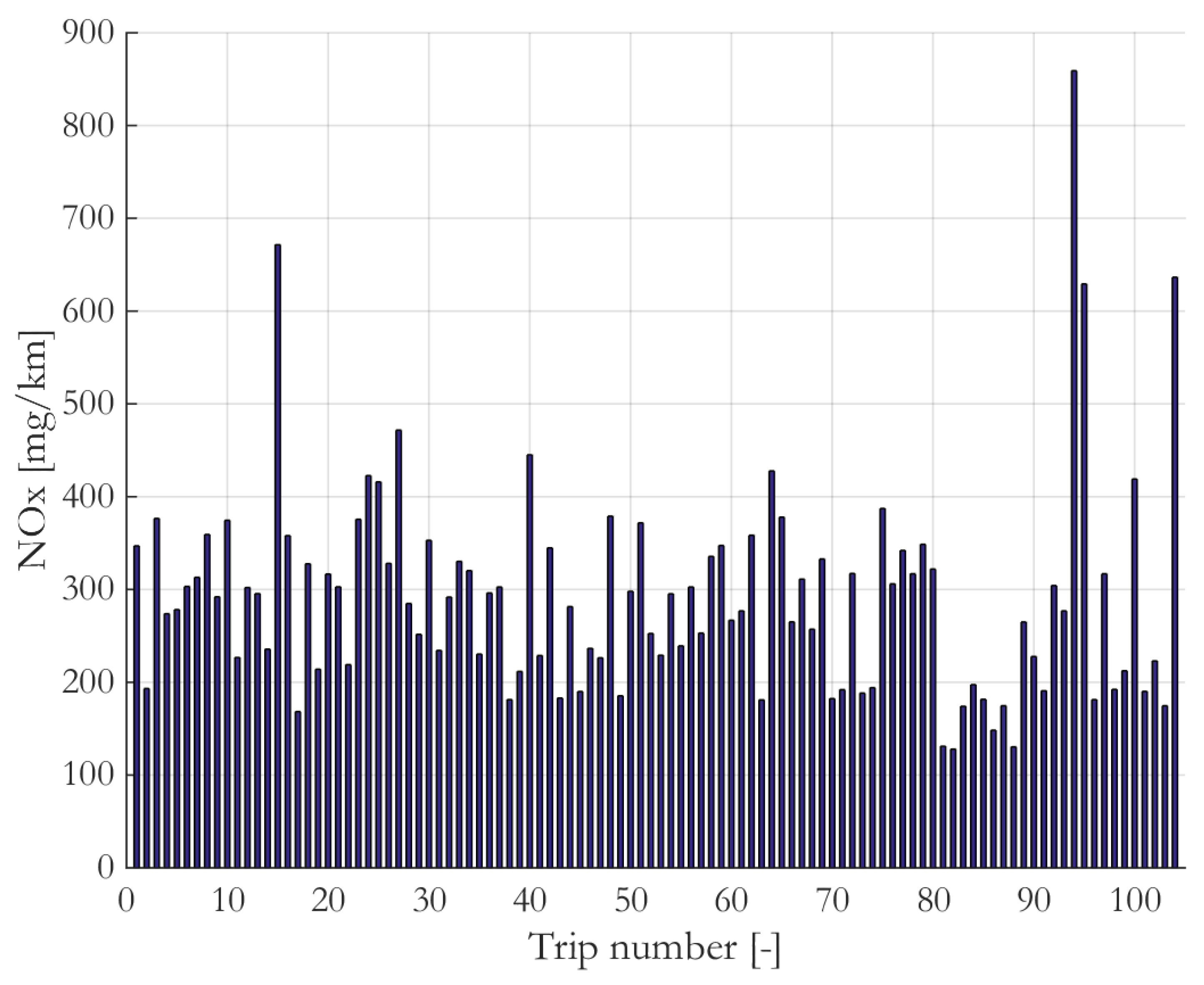
3.2.2. Impact of the Trip
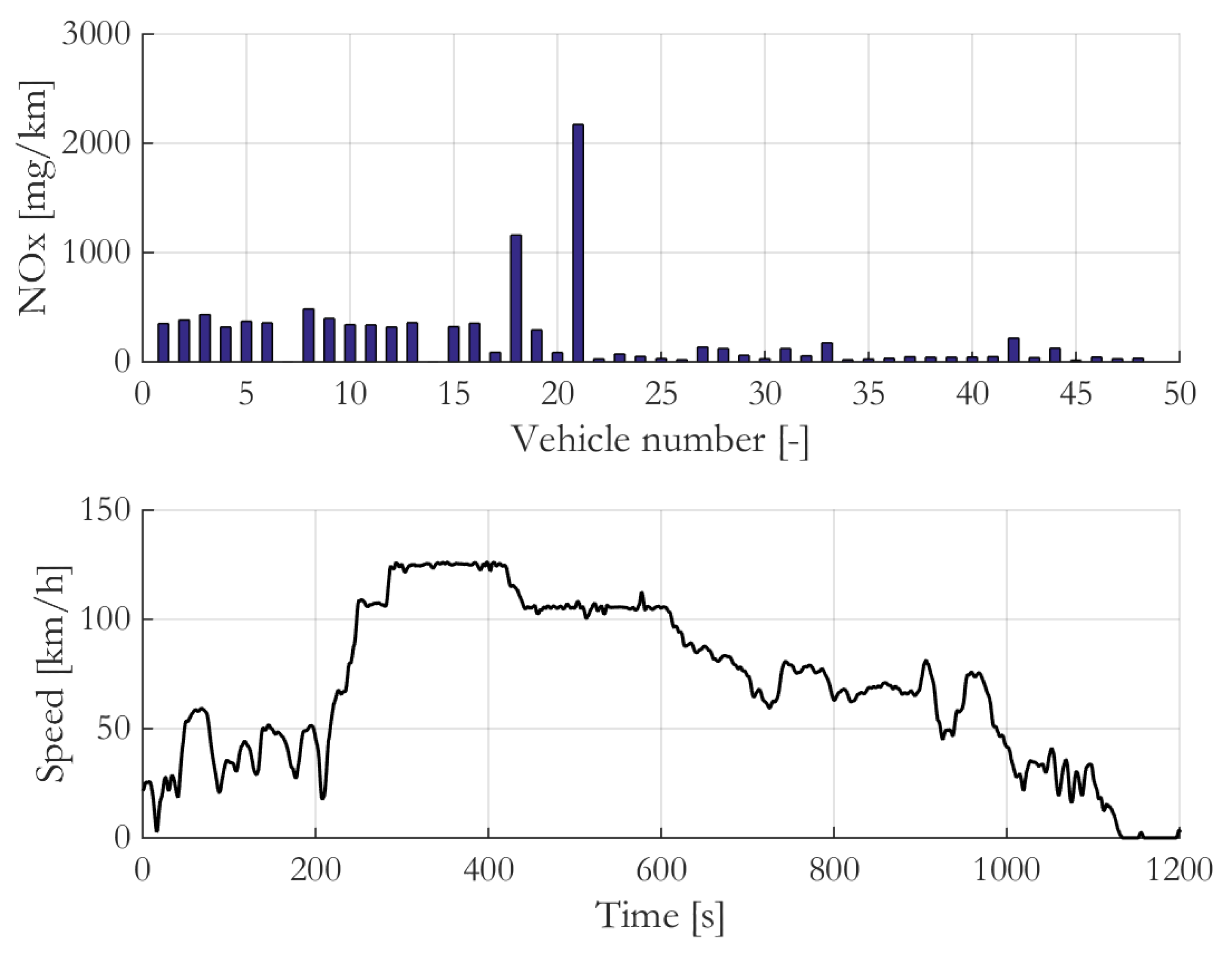
3.2.3. Impact of the Vehicle
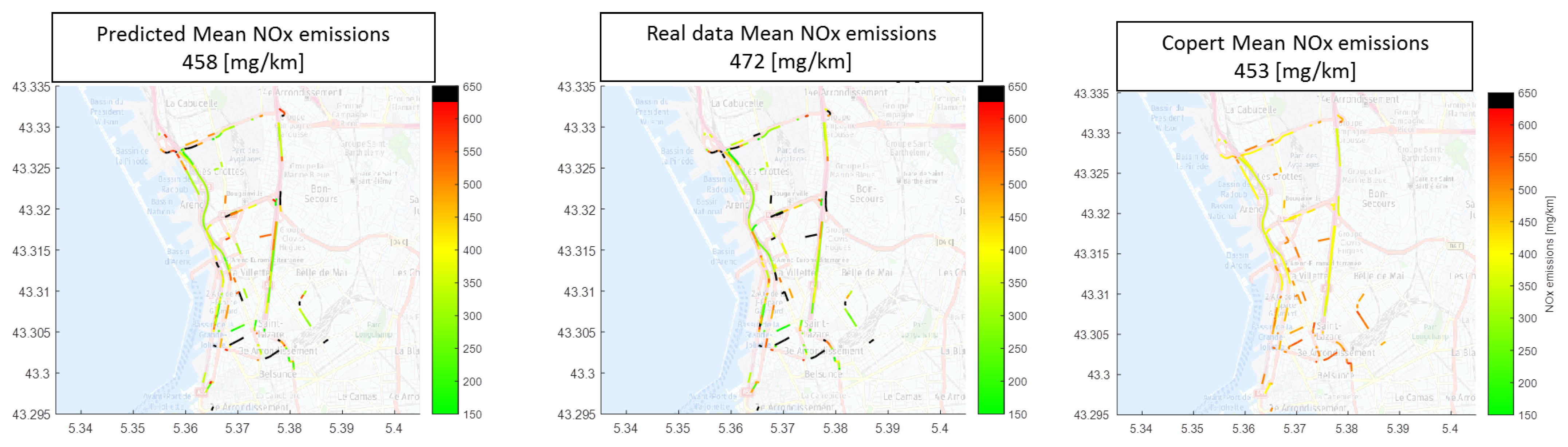
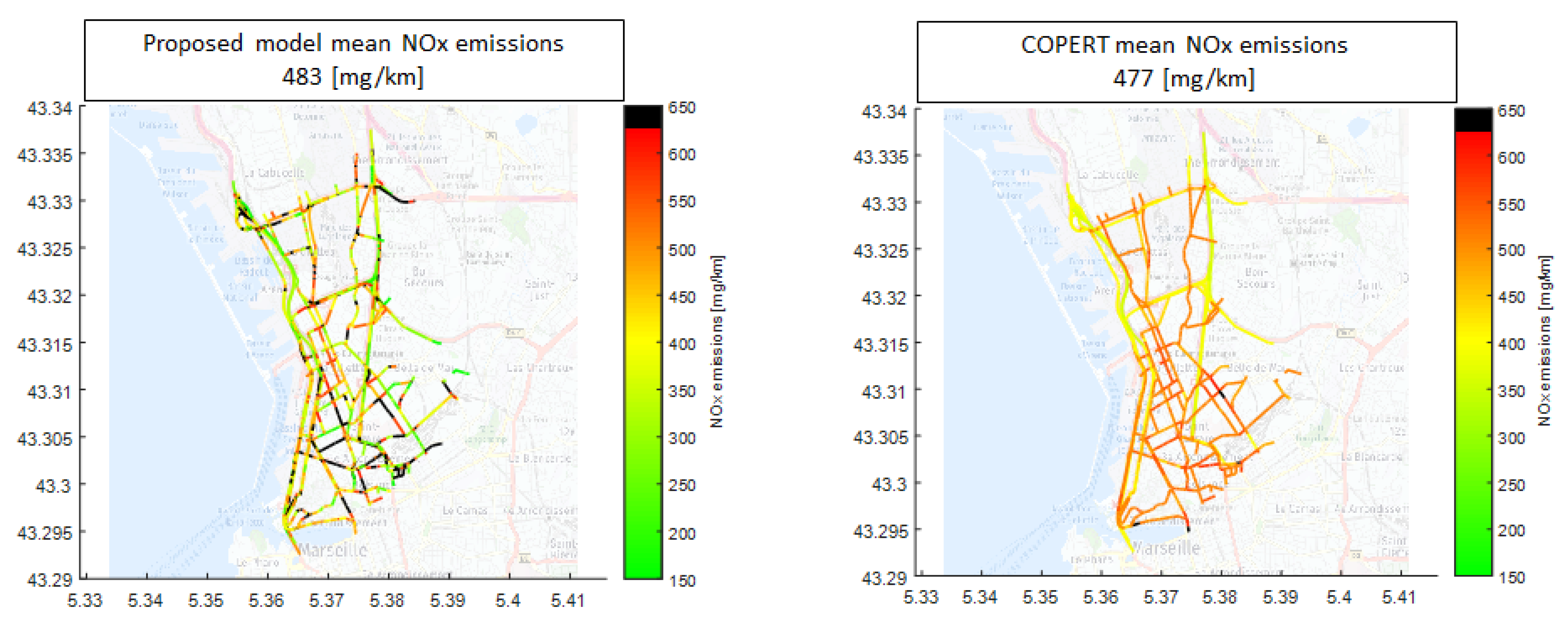
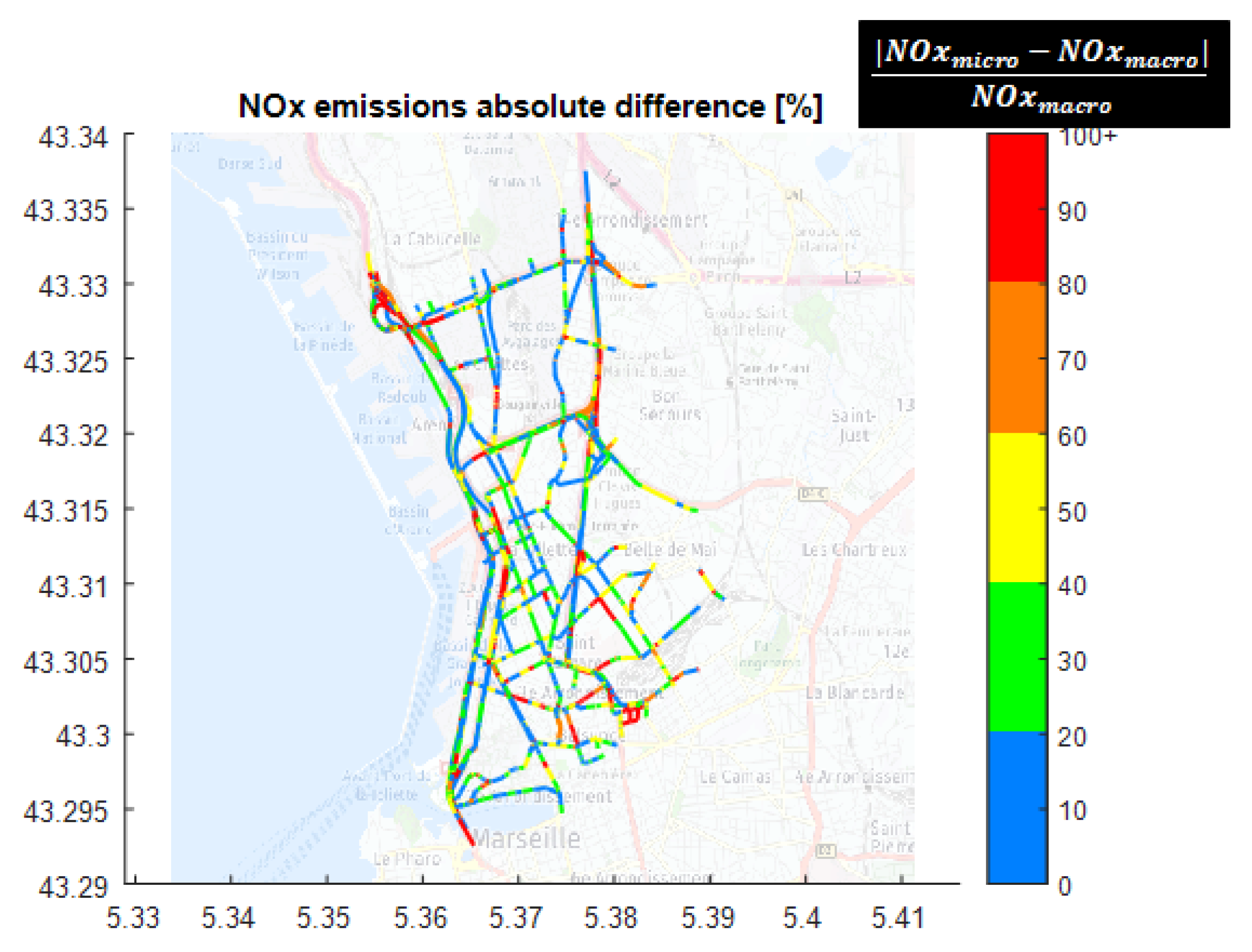
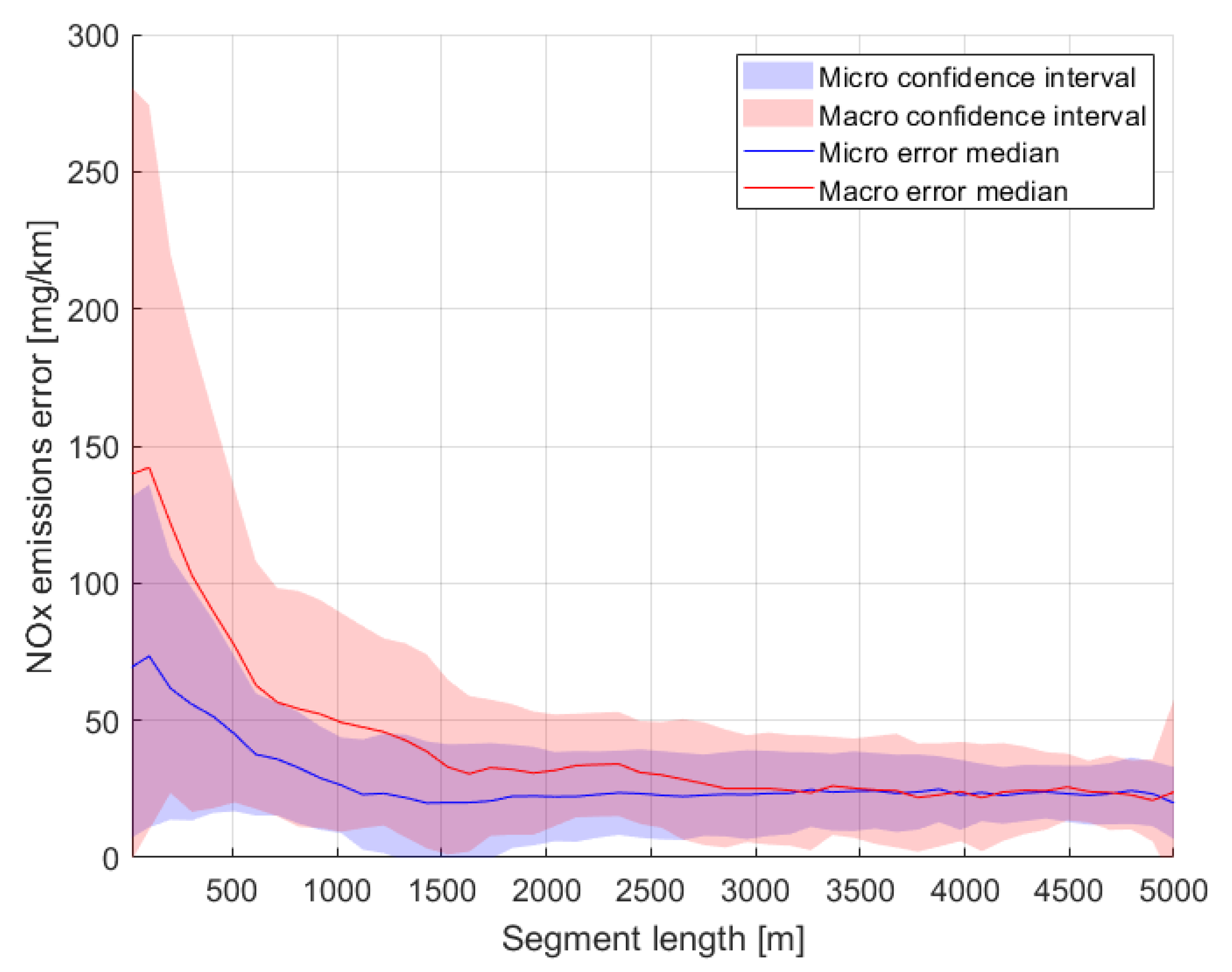
3.3. Microscopic Traffic Emissions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- CITEPA. Gaz à effet de Serre et Polluants Atmosphériques. Bilan des émissions en France de 1990 à 2018; Technical Report; CITEPA: Paris, France, 2020. [Google Scholar]
- Dalton, G.; de la Peña, E.; Vassallo, J.M.; Acciaro, M. Transport Infrastructure; Technical Report; European Commission: Brussels, Belgium, 2017. [Google Scholar]
- Höglund, P.G.; Niittymäki, J. Estimating vehicle emissions and air pollution related to driving patterns and traffic calming. In Submitted Paper for the Conference Urban Transport Systems, Lund, Sweden; Lund University: Lund, Sweden, 1999; Volume 7. [Google Scholar]
- Van Lint, J.; Van der Zijpp, N. Improving a travel-time estimation algorithm by using dual loop detectors. Transp. Res. Rec. 2003, 1855, 41–48. [Google Scholar] [CrossRef]
- Treiber, M.; Helbing, D. An adaptive smoothing method for traffic state identification from incomplete information. In Interface and Transport Dynamics; Springer: Berlin/Heidelberg, Germany, 2003; pp. 343–360. [Google Scholar]
- Chu, L.; Oh, S.; Recker, W. Adaptive Kalman filter based freeway travel time estimation. In Proceedings of the 84th TRB Annual Meeting, Washington, DC, USA, 9–13 January 2005. [Google Scholar]
- Min, W.; Wynter, L. Real-time road traffic prediction with spatio-temporal correlations. Transp. Res. Part C Emerg. Technol. 2011, 19, 606–616. [Google Scholar] [CrossRef]
- Newell, G.F. A simplified theory of kinematic waves in highway traffic, part I: General theory. Transp. Res. Part B Methodol. 1993, 27, 281–287. [Google Scholar] [CrossRef]
- Smulders, S. Control of freeway traffic flow by variable speed signs. Transp. Res. Part B Methodol. 1990, 24, 111–132. [Google Scholar] [CrossRef]
- Fellendorf, M.; Vortisch, P. Microscopic traffic flow simulator VISSIM. In Fundamentals of Traffic Simulation; Springer: Berlin/Heidelberg, Germany, 2010; pp. 63–93. [Google Scholar]
- Yang, Q.; Koutsopoulos, H.N. A microscopic traffic simulator for evaluation of dynamic traffic management systems. Transp. Res. Part C Emerg. Technol. 1996, 4, 113–129. [Google Scholar] [CrossRef]
- Effa, R.C.; Larsen, L. Development of real-world driving cycles for estimating facility-specific emissions from light-duty vehicles. In Proceedings of the Air and Waste Management Association Annual Specialty Conference Emission Inventory: Perception and Reality, Pasadena, CA, USA, 18–20 October 1993. [Google Scholar]
- Lin, J.; Niemeier, D.A. Estimating regional air quality vehicle emission inventories: Constructing robust driving cycles. Transp. Sci. 2003, 37, 330–346. [Google Scholar] [CrossRef][Green Version]
- Andrieu, C. Modélisation Fonctionnelle de Profils de Vitesse en lien Avec l’infrastructure et méthodologie de Construction d’un profil agrégé. Ph.D. Thesis, Paul Sabatier University, Toulouse, France, 6 January 2013. [Google Scholar]
- Wolfermann, A.; Alhajyaseen, W.K.; Nakamura, H. Modeling speed profiles of turning vehicles at signalized intersections. In Proceedings of the 3rd International Conference on Road Safety and Simulation RSS2011, Transportation Research Board TRB, Indianapolis, IN, USA, 14–16 September 2011. [Google Scholar]
- Minett, C.F.; Salomons, A.M.; Daamen, W.; Van Arem, B.; Kuijpers, S. Eco-routing: Comparing the fuel consumption of different routes between an origin and destination using field test speed profiles and synthetic speed profiles. In Proceedings of the 2011 IEEE Forum on Integrated and Sustainable Transportation Systems, Vienna, Austria, 29 June–1 July 2011; pp. 32–39. [Google Scholar]
- De Nunzio, G.; Thibault, L.; Sciarretta, A. Model-based eco-routing strategy for electric vehicles in large urban networks. In Comprehensive Energy Management—eco Routing & Velocity Profiles; Springer: Berlin/Heidelberg, Germany, 2017; pp. 81–99. [Google Scholar]
- Laureshyn, A.; Åström, K.; Brundell-Freij, K. From speed profile data to analysis of behaviour: Classification by pattern recognition techniques. IATSS Res. 2009, 33, 88–98. [Google Scholar] [CrossRef]
- Laraki, M.; De Nunzio, G.; Thibault, L. Vehicle speed trajectory estimation using road traffic and infrastructure information. In Proceedings of the IEEE 23rd International Conference on Intelligent Transportation Systems, Rhodes, Greece, 20–23 September 2020. [Google Scholar]
- Pelkmans, L.; Debal, P. Comparison of on-road emissions with emissions measured on chassis dynamometer test cycles. Transp. Res. Part D Transp. Environ. 2006, 11, 233–241. [Google Scholar] [CrossRef]
- Real-Time on-road Vehicle Exhaust Gas Modular Flowmeter and Emissions Reporting System. U.S. Patent 6,148,656, 21 November 2000.
- Gao, J.; Tian, G.; Sorniotti, A.; Karci, A.E.; Di Palo, R. Review of thermal management of catalytic converters to decrease engine emissions during cold start and warm up. Appl. Therm. Eng. 2019, 147, 177–187. [Google Scholar] [CrossRef]
- Gao, J.; Chen, H.; Dave, K.; Chen, J.; Jia, D. Fuel economy and exhaust emissions of a diesel vehicle under real traffic conditions. Energy Sci. Eng. 2020, 8, 1781–1792. [Google Scholar] [CrossRef]
- Liu, H.; Chen, X.; Wang, Y.; Han, S. Vehicle Emission and Near-Road Air Quality Modeling for Shanghai, China: Based on Global Positioning System Data from Taxis and Revised MOVES Emission Inventory. Transp. Res. Rec. 2013, 2340, 38–48. [Google Scholar] [CrossRef]
- Sentoff, K.M.; Aultman-Hall, L.; Holmén, B.A. Implications of driving style and road grade for accurate vehicle activity data and emissions estimates. Transp. Res. Part D Transp. Environ. 2015, 35, 1756188. [Google Scholar] [CrossRef]
- Ma, X.; Lei, W.; Andréasson, I.; Chen, H. An Evaluation of Microscopic Emission Models for Traffic Pollution Simulation Using On-board Measurement. Environ. Model. Assess. 2012, 17, 375–387. [Google Scholar] [CrossRef]
- Chen, K.; Yu, L. Microscopic Traffic-Emission Simulation and Case Study for Evaluation of Traffic Control Strategies. J. Transp. Syst. Eng. Inf. Technol. 2007, 7, 93–99. [Google Scholar] [CrossRef]
- Badin, A.L.; Clavel, A.; Vittoz, T.; Sorand, C.; Lejri, D.; Leclercq, L.; Olny, X. Combining microscopic traffic modelling and 3 pollutant emission modellings to assess modifications of traffic supply and demand. J. Earth Sci. Geotech. Eng. 2017, 7, 175–190. [Google Scholar]
- Nam, E.K.; Gierczak, C.A.; Butler, J.W. A Comparison of Real-World and Modeled Emissions Under Conditions of Variable Driver Aggressiveness. 2003. Available online: https://silo.tips/download/a-comparison-of-real-world-and-modeled-emissions-under-conditions-of-variable-dr (accessed on 30 November 2020).
- Hausberger, S. Simulation of Real World Vehicle Exhaust Emissions; VKM-THD Mitteilungen Technical University Graz: Graz, Austria, 2003; Volume 82. [Google Scholar]
- Geco Air. Available online: https://www.gecoair.fr/home_en/ (accessed on 30 November 2020).
- Ntziachristos, L.; Gkatzoflias, D.; Kouridis, C.; Samaras, Z. COPERT: A European road transport emission inventory model. In Information Technologies in Environmental Engineering; Springer: Berlin/Heidelberg, Germany, 2009; pp. 491–504. [Google Scholar]
- HERE Maps. Available online: https://www.here.com/ (accessed on 30 November 2020).
- Van Hieu, D.; Meesad, P. Fast K-Means Clustering for Very Large Datasets Based onMapReduce Combined with a New Cutting Method. Available online: http://link.springer.com/chapter/10.1007%2F978-3-319-11680-8_23 (accessed on 30 November 2020).
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: An Introduction to Cluster Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 344. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Bengio, Y.; Grandvalet, Y. No unbiased estimator of the variance of k-fold cross-validation. J. Mach. Learn. Res. 2004, 5, 1089–1105. [Google Scholar]
- Alix, G.; Dabadie, J.; Font, G. An ICE Map Generation Tool Applied to the Evaluation of the Impact of Downsizing on Hybrid Vehicle Consumption.; SAE International: Warrendale, PA, USA, 2015. [Google Scholar]
- Gärtner, U.; Hohenberg, G.; Daudel, C.; Oelschlegel, H. Development and Application of a Semi-Empirical NOx Model to Various HD Diesel Engines. In Thermo- and Fluid Dynamic Processes in Diesel Engines 2; Springer: Berlin/Heidelberg, Germany, 2004; pp. 285–312. [Google Scholar]
- Depcik, C.; Assanis, D. One-dimensional automotive catalyst modeling. Prog. Energy Combust. Sci. 2005, 31, 308–369. [Google Scholar] [CrossRef]


| Feature Description |
|---|
| Congestion level |
| Traffic light |
| Stop sign |
| Yield sign |
| Road network hierarchy |
| Road link curvature |
| Feature Description |
|---|
| Mean speed |
| Percentage of null speed |
| 75% percentile of speed |
| Minimum speed |
| Sum of positive acceleration |
| Sum of negative acceleration |
| Difference between initial and final speed |
| Feature | Description |
|---|---|
| Number of lanes in the road link | |
| Origin road link traffic speed | |
| Center road link traffic speed | |
| Destination road link traffic speed | |
| Nominal speed | |
| road link length | |
| Slope angle | |
| Curvature angle | |
| Number of adjacent origin road links | |
| Number of adjacent destination road links |
| Error | |||
|---|---|---|---|
| Mean absolute error | 2.22 km/h | 2.26 km/h | 2.32 km/h |
| Relative error | 8 % | 8.5 % | 9 % |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Nunzio, G.; Laraki, M.; Thibault, L. Road Traffic Dynamic Pollutant Emissions Estimation: From Macroscopic Road Information to Microscopic Environmental Impact. Atmosphere 2021, 12, 53. https://doi.org/10.3390/atmos12010053
De Nunzio G, Laraki M, Thibault L. Road Traffic Dynamic Pollutant Emissions Estimation: From Macroscopic Road Information to Microscopic Environmental Impact. Atmosphere. 2021; 12(1):53. https://doi.org/10.3390/atmos12010053
Chicago/Turabian StyleDe Nunzio, Giovanni, Mohamed Laraki, and Laurent Thibault. 2021. "Road Traffic Dynamic Pollutant Emissions Estimation: From Macroscopic Road Information to Microscopic Environmental Impact" Atmosphere 12, no. 1: 53. https://doi.org/10.3390/atmos12010053
APA StyleDe Nunzio, G., Laraki, M., & Thibault, L. (2021). Road Traffic Dynamic Pollutant Emissions Estimation: From Macroscopic Road Information to Microscopic Environmental Impact. Atmosphere, 12(1), 53. https://doi.org/10.3390/atmos12010053






