The Increased Likelihood in the 21st Century for a Tropical Cyclone to Rapidly Intensify When Crossing a Warm Ocean Feature—A Simple Model’s Prediction

Abstract

A warm ocean feature (WOF) is a blob of the ocean’s surface where the sea-surface temperature (SST) is anomalously warmer than its adjacent ambient SST. Examples are warm coastal seas in summer, western boundary currents, and warm eddies. Several studies have suggested that a WOF may cause a crossing tropical cyclone (TC) to undergo rapid intensification (RI). However, testing the “WOF-induced RI” hypothesis is difficult due to many other contributing factors that can cause RI. The author develops a simple analytical model with ocean feedback to estimate TC rapid intensity change across a WOF. It shows that WOF-induced RI is unlikely in the present climate when the ambient SST is ≲29.5 °C and the WOF anomaly is ≲+1 °C. This conclusion agrees well with the result of a recent numerical ensemble experiment. However, the simple model also indicates that RI is very sensitive to the WOF anomaly, much more so than the ambient SST. Thus, as coastal seas and western boundary currents are warming more rapidly than the adjacent open oceans, the model suggests a potentially increased likelihood in the 21st century of WOF-induced RIs across coastal seas and western boundary currents. Particularly vulnerable are China’s and Japan’s coasts, where WOF-induced RI events may become more common.

1. Introduction

A tropical cyclone (TC) is said to undergo rapid intensification (RI) when its maximum 10-m wind increases by more than 15.4 m/s in 1 day [1]. RI may be due to TC internal dynamics, environmental factors, and a combination [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. Often, storms that have undergone RI develop into major storms (Category 3 and above) [17,18]. They are therefore of interest to researchers and forecasters.

By supplying heat and moisture to the atmosphere, ocean, and coupled ocean feedback play a significant role in TC intensity change [19,20,21]. Some studies suggested that RI may be triggered when a TC crosses a warm ocean feature (WOF) [12,22,23,24,25,26,27,28,29]. The WOF may be a warm eddy, a western boundary current, or a summertime coastal shelf sea. It has an anomalously warmer sea-surface temperature (SST) than the ambient sea. We define WOF-induced RI when the RI triggered as a TC crosses a WOF. In practice, however, isolating and identifying WOF-induced RI is challenging due to the simultaneous existence of other factors cited above. Oey and Huang [30] designed numerical ensemble experiments to eliminate other potential RI-causing environmental factors and isolate the WOF-induced intensity change. They conducted twin experiments and showed statistically indistinguishable RI occurrences between the experiments with and without the WOF. They then used a strip-down version of the analytical model presented here to support their numerical findings.

In this manuscript, we extend and provide complete details of the analytical model. The analytical model includes ocean feedback and estimates the WOF-induced intensity change and RI. The model shows that ocean feedback decreases intensity change, necessitating a warmer WOF anomaly for a TC to develop RI. We provide observations and conclude that WOF-induced RI is unlikely under the present background and WOF SSTs in the tropics and subtropics. However, WOFs can potentially play an increasingly significant role in triggering RIs as these SSTs, particularly the WOF SST, continue to rise in a warming climate.

2. The Model

2.1. The Problem

A tropical cyclone (TC) translates westward along the negative x-axis at a constant speed U_h. Across x = 0, the SST (T) changes by δT_W due to a WOF:

$$\begin{array}{lll}\mathrm{T}& ={\mathrm{T}}_0& \mathrm{x}\ge 0,\\ & ={\mathrm{T}}_0+\mathsf{\delta }{\mathrm{T}}_{\mathrm{w}}& \mathrm{x}<0,\end{array}$$

(1)

where T₀ is the ambient or background sea-surface temperature before the WOF (Figure 1). (For convenience, the variables are defined both in the text and in the Appendix A). The TC crosses onto the WOF where δT_W > 0. We focus on the redpoint shortly after the crossing under the direct path of the storm’s core or eyewall, where SST changes, and ocean feedback can most influence intensity [19,31,32]. The goal is to calculate the change in the maximum wind (δV_m) and estimate the (δT_W, T₀)-combination where a WOF-induced RI is possible. The analysis is independent of where the redpoint is, provided it is in the WOF and the direct path of the storm’s core.

2.2. Intensity Change Due to the WOF: The WOF-Induced RI

The TC experiences a warmer SST as it crosses x = 0. The warmer SST increases the wind, which we can estimate using the maximum potential intensity (MPI) theory [19]. We use the empirical form given by DeMaria and Kaplan [33]:

V_m = A + B e^C(T-30).

(2)

Here, V_m (m/s) is the maximum wind, the SST T is in °C, and A, B, and C are empirical coefficients. DeMaria and Kaplan [33] limit the applicability of Equation (2) to T ≤ 30 °C. However, later extensions using higher-resolution data suggest no such limit [6,34,35]. The change in the maximum wind, δV_m, due to a change in SST, δT, i.e., the WOF-induced intensity change, is:

$$\mathsf{\delta }{\mathrm{V}}_{\mathrm{m}}=\mathrm{s}\mathsf{\delta }\mathrm{T}+\mathrm{s}\mathrm{C}\mathsf{\delta }{\mathrm{T}}^2/2+0\left(\mathsf{\delta }{\mathrm{T}}^3\right);\mathrm{s}\left(\mathrm{T}\right)=\left(\partial {\mathrm{V}}_{\mathrm{m}}/\partial \mathrm{T}\right){|}_0,$$

(3)

where (..)|₀ means evaluation at the ambient state T₀, and s is the slope of V_m in the T-space. Partial derivatives are a reminder that (A, B, C) may not depend on T alone. We assume the increased intensity occurs within one day of the storm crossing x = 0 and define WOF-induced RI when δV_m ≥ 15.4 m/s. The vast majority (85%) of RI events occur in storms that translate faster than ~3 m/s [36]. The assumption is reasonable since the time for the TC core to cross a WOF of typical size 100–200 km [30] is one day or less. By definition, V₀ ≲ V_m, where V₀ is the maximum wind of the TC approaching the WOF. We will see that δV₀ ≲ δV_m (see Section 2.3.6 below). Therefore, the above RI criterion “δV_m ≥ 15.4 m/s” is more easily satisfied than the conventional RI criterion “δV₀ ≥ 15.4 m/s”. In other words, if the model predicts RI to be unlikely in the present climate, as will be shown to be the case, using the conventional criterion leads to the same conclusion.

2.3. Ocean Feedback

The increased δV_m in the WOF (the red point) increases ocean mixing and upwelling [37,38], hence SST cooling, δT₀ < 0, which reduces δV_m. The reduced δV_m modifies the amount of cooling, which further changes the δV_m, in a coupled manner.

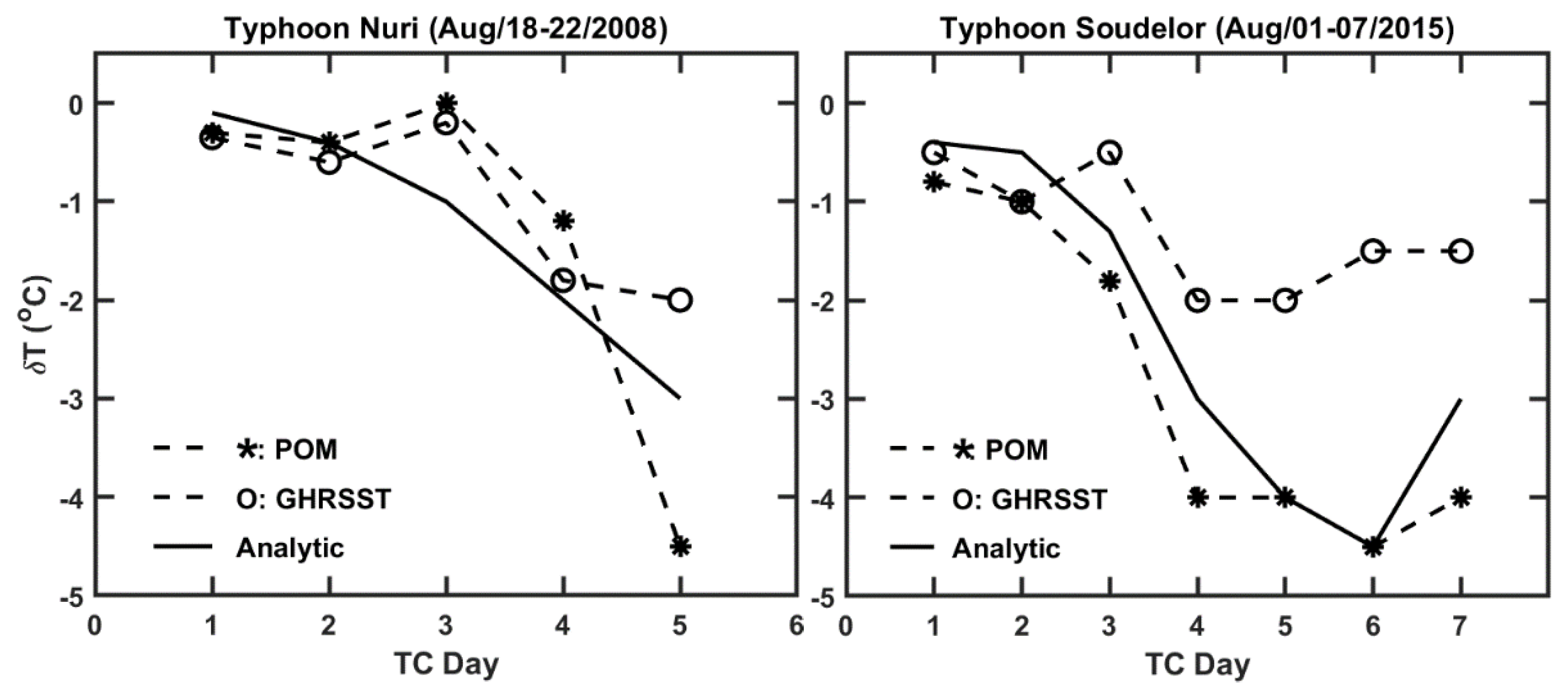
2.3.1. Assumptions

We assume an ocean with no horizontal variation. For example, the SST front at x = 0 is fixed and has no dynamics. Vertical mixing then predominantly controls the SST cooling under super-critically translating storms when U_h/c > 1, where c is the ocean’s mode-1 baroclinic phase speed [39]. In the tropical and subtropical oceans, c ≈ 2.5 ~ 3 m/s [40,41]. Thus, we require that U_h exceeds ~3 m/s. Then we may neglect the contribution to SST cooling from horizontal processes, such as upwelling and mixing due to breaking near-inertial internal waves [42]. For U_h ≥ 3 m/s and a typical TC core’s diameter of 100–200 km (e.g., ref. [43]), a point in the storm’s path remains influenced by the maximum wind stress curl for at most 8–18 hours. This time is less than the inertial time > 1 day (for latitudes < 28^°) required for wind curl-driven upwelling to establish and contribute significantly to SST cooling [39,44]. It is also less than the time required for near-inertial internal waves to develop and contribute to mixing [45,46]. As mentioned before, global TC observations also show that most RI events occur in storms with U_h > 3 m/s [6,36], providing a further incentive to focus on these storms. The one-dimensional model underestimates cooling for slow storms with U_h ≲ 3 m/s. Additional SST cooling due to horizontal processes mentioned above can be more significant for slow storms. However, as will become apparent, any additional cooling can only weaken the TC intensity and not change our conclusions. The one-dimensional model then provides an upper-bound intensity change.

2.3.2. Two-Layer Ocean

We divide the ocean into two active layers of thicknesses, h₁ and h₂. Layer 1 consists of warm water of a uniform temperature T₁ and density ρ₁ from sea-surface z = 0 to z = −h₁. Layer 2 consists of cooler water of uniform temperature T₂ (< T₁) and density ρ₂ (> ρ₁) from z = −h₁ to z = −(h₁ + h₂) (a third layer below extending to the ocean bottom is assumed to be inactive). Suppose the wind adiabatically mixes the two layers into a single layer, the uniform density and temperature after mixing (subscript ’mix’) are weighted averages of layers 1 and 2:

ρ_mix = (ρ₂ h₂ + ρ₁ h₁)/(h₁ + h₂),     T_mix = (T₂ h₂ + T₁ h₁)/(h₁ + h₂),

(4)

expressing mass and heat conservations. The SST after mixing is:

T_mix = T₁ + δT,    δT = −[h₂/(h₁ + h₂)] ΔT,

(5)

where ΔT = T₁ − T₂ (> 0) is the differenced temperature of the two original layers. The corresponding differenced density Δρ = ρ₁ − ρ₂ (< 0):

Δρ/ρ₀ = −α ΔT,

(6)

where ρ₀ is the reference seawater density ≈ 1025 kg/m³, and α = (∂ρ/∂T)/ρ₀ is the thermal expansion coefficient of seawater, ≈ 3×10⁻⁴ K⁻¹ at the sea surface with SST ≈ 28 °C and salinity ≈35 psu.

2.3.3. Potential Energy

Wind work raises the potential energy (PE) of the fluid by mixing it. Equating the raised PE = PE|_mix − PE|_2layers to wind work yields a formula relating the wind to density (and temperature). Thus, since

$${\mathrm{PE}}_{2\mathrm{layers}}={{\displaystyle \int }}_{-{\mathrm{h}}_1}^0{\mathsf{\rho }}_1\mathrm{g}\mathrm{zd}{\mathrm{z}}^{\prime }+{{\displaystyle \int }}_{-{\mathrm{h}}_1-{\mathrm{h}}_2}^{-{\mathrm{h}}_1}{\mathsf{\rho }}_2\mathrm{g}\mathrm{zd}{\mathrm{z}}^{\prime },$$

(7)

and

$${\mathrm{PE}}_{\mathrm{mix}}={{\displaystyle \int }}_{-{\mathrm{h}}_1-{\mathrm{h}}_2}^0{\mathsf{\rho }}_{\mathrm{mix}}\mathrm{g}\mathrm{zd}{\mathrm{z}}^{\prime },$$

(8)

we obtain

PE = −(g/2) ∆ρ h₂ h₁ = (g/2) α ρ₀ ∆T h₂ h₁   (J/m²).

(9)

2.3.4. Wind Energy

The wind power on the ocean is ρ_aC_dV³ in J/(m²∙s), the scalar product of the surface drag ρ_aC_d|V|V and wind V, neglecting the ocean current. Here, ρ_a is the air density, C_d is the drag coefficient, and V = |V| the wind speed. Due to the TC’s size, the redpoint (Figure 1) experiences the wind and SST cooling hours or days before the storm arrives, depending on U_h. Oey et al. [37] observed this ahead-of-storm SST cooling in buoy measurements in the Caribbean Sea before the arrival of Hurricane Wilma (2005). Therefore the wind energy for mixing at the redpoint is:

$$\mathrm{WE}=\mathsf{\gamma }{{\displaystyle \int }}_0^{\mathrm{P}}{\mathsf{\rho }}_{\mathrm{a}}{\mathrm{C}}_{\mathrm{d}}{\mathrm{V}}^3\mathrm{dt}(\mathrm{J}/{\mathrm{m}}^2).$$

(10)

Here, the mixing efficiency γ takes into account that only a fraction of the wind work goes into mixing, and P = L/U_h, where L ≈ storm’s radius. The integral is from t = 0 when the outer-most circle of weak TC wind influences the redpoint to t = P when the TC center arrives (one could formally transform the integral by setting x = −U_h t + L + x_redpoint but thinking in “t” is more straightforward). We neglect the contribution from the generally even weaker, non-TC wind before the TC’s outer-most circle arrives. We also assume that after time t = P, SST cooling at the redpoint will not affect intensity. For t > P, the TC center has passed the redpoint. Thus, ignoring the short distance across the back half of the eye, ocean cooling in the TC’s wake has a minor further impact on intensity.

2.3.5. Wind-Induced SST Cooling

Set PE = WE, and use (5) to yield:

$${\mathrm{T}}_{\mathrm{mix}}={\mathrm{T}}_1-\left\{\left[\mathsf{\gamma }{{\displaystyle \int }}_0^{\mathrm{P}}{\mathsf{\rho }}_{\mathrm{a}}{\mathrm{C}}_{\mathrm{d}}{\mathrm{V}}^3\mathrm{dt}\right]/\left[\left(\frac{\mathrm{g}}{2}\right)\mathsf{\alpha }{\mathsf{\rho }}_0{\mathrm{h}}_2{\mathrm{h}}_1\right]\right\}\left[\frac{{\mathrm{h}}_2}{{\mathrm{h}}_2+{\mathrm{h}}_1}\right].$$

(11)

Piecewise continuous formulae of V are available [43] to evaluate the integral. To obtain simple formulae, we choose to model V as a simple rise and fall as the TC passes the point:

V = V₀ sin[πt/(2P)],   V₀ = maximum wind,

(12)

Thus, ignoring the rapid wind change with two maxima as the TC center passes. Because of integration, the exact form is not crucial. Using Equation (12) in Equation (11), we obtain:

$${\mathrm{T}}_{\mathrm{mix}}={\mathrm{T}}_1-\left[\left(\frac{4}{3\mathsf{\pi }}\right)\left(\frac{\mathrm{L}}{{\mathrm{U}}_{\mathrm{h}}}\right)\left(\frac{{\mathsf{\rho }}_{\mathrm{a}}}{{\mathsf{\rho }}_0}\right)\left(\mathsf{\gamma }{\mathrm{C}}_{\mathrm{d}}{\mathrm{V}}_0^3\right)\right]/\left[\left(\frac{\mathrm{g}}{2}\right){\mathsf{\alpha }\mathrm{h}\mathrm{h}}_1\right],$$

(13)

where h = h₁ + h₂. Equation (13) gives the cooled SST the arriving TC sees at a point ahead of the TC path, including the redpoint. The SST cooling (= T_mix − T₁) is inversely related to U_h and h₁. It shows that a slower storm sees a cooler SST than a faster one, and a thicker upper warm layer is less susceptible to cooling than a thinner one.

2.3.6. Coupling

Focusing on the redpoint, as the TC crosses into the WOF, we assume that its maximum wind V₀ changes while its temporal functional form remains unchanged:

δV ≈ δV₀ sin[πt/(2P)].

(14)

This is a good approximation since the redpoint is only a short distance into the WOF. We can then use Equation (11) to relate the change in SST due to a change in the wind. Taking δ of Equation (11) and evaluating the integral (or taking δ of Equation (13)):

$${\mathsf{\delta }\mathrm{T}}_0=-{\mathsf{\delta }\mathrm{V}}_0{\mathrm{F}}_{\mathrm{T}}$$

(15)

$${\mathrm{F}}_{\mathrm{T}}=\left[\left(\frac{8}{\mathsf{\pi }}\right)\left(\frac{\mathrm{L}}{{\mathrm{U}}_{\mathrm{h}}}\right)\left(\frac{{\mathsf{\rho }}_{\mathrm{a}}}{{\mathsf{\rho }}_0}\right)\left({\mathrm{C}}_{\mathrm{d}}{\mathrm{V}}_0^2\right)\right]/\left[{\mathrm{g}\mathsf{\alpha }\mathrm{h}\mathrm{h}}_1\right].$$

(16)

The special notation δT₀ (with subscript ‘o’) is used instead of δT_mix, as a reminder that it is the ocean cooling caused by increased δV₀ as the TC crosses into the WOF. At the redpoint, the total SST change is the sum of the warmer SST due to the WOF and cooling due to ocean mixing:

δT_redpoint = δT_W + δT₀.

(17)

The V₀ refers to the incoming TC that translates into the WOF. To close the model (i.e., to couple), one needs to relate δV₀ to δV_m, where δV_m depends on SST from Equation (3). A reasonable assumption is that δV₀/δV_m is proportional to V₀/V_m, and we set the proportionality to one for simplicity. The assumption is equivalent to letting V₀ be proportional to V_m, such that their ratio is approximately invariant, as the data and analysis of [6,33,34,35] suggest. Thus:

δV₀ = μ δV_m, μ = V₀/V_m ≤ 1.

(18)

The μ is ≲0.5 for V₀ ≲ 50 m/s and tropical/subtropical SST ≳ 28 °C (Figure 2) (in Oey and Huang [30], we set δV₀ = δV_m, i.e., μ =1, which overestimates the cooling, although their conclusions remain unchanged).

Setting δT = δT_redpoint and using Equations (15)–(18) in Equation (3) yields a quadratic equation for δV_m. Both roots are positive, but the smaller root is physically plausible:

$${\mathsf{\delta }\mathrm{V}}_{\mathrm{m}}=[{\mathsf{\mu }}_2-\sqrt{{\mathsf{\mu }}_2^2-4{\mathsf{\mu }}_1{\mathsf{\mu }}_3}]/[2{\mathsf{\mu }}_1]$$

(19)

$$\begin{array}{l}{\mathsf{\mu }}_1=\mathrm{sC}{\left({\mathsf{\mu }\mathrm{F}}_{\mathrm{T}}\right)}^2/2,{\mathsf{\mu }}_2=1+\left(1+{\mathrm{C}\mathsf{\delta }\mathrm{T}}_{\mathrm{W}}\right){\mathrm{s}\mathsf{\mu }\mathrm{F}}_{\mathrm{T}},\\ {\mathsf{\mu }}_3={\mathrm{s}\mathsf{\delta }\mathrm{T}}_{\mathrm{W}}\left(1+{\mathrm{C}\mathsf{\delta }\mathrm{T}}_{\mathrm{W}}/2\right).\end{array}$$

Taylor’s expansion in small F_T shows that the solution tends to Equation (3) without ocean cooling as F_T ~ 0.

Although Equation (19) will be used in the plots, we can more easily see the effect of ocean feedback by dropping the O(δT²) term in Equation (3). The solution is:

$${\mathsf{\delta }\mathrm{V}}_{\mathrm{m}}=\mathrm{s}\left({\mathrm{T}}_0\right){\mathsf{\delta }\mathrm{T}}_{\mathrm{W}}/\left[1+\mathrm{s}({\mathrm{T}}_0\right){\mathsf{\mu }\mathrm{F}}_{\mathrm{T}}],$$

(20)

where s(T₀) is a reminder that it depends on the ambient SST T₀.

2.3.7. Values of Parameters

We use the following values of the model parameters:

• A = 15.69 (2758) m/s, B = 98.03 (74.03) m/s, and C = 0.1806 (0.1903) °C⁻¹ for western North Pacific (North Atlantic), from Zeng et al. [6] (Xu et al. [35]), see Equation (2);
• L = 200 km, the TC’s radial scale (roughly to ~18 m/s) [40];
• ρ_a/ρ₀ = 10⁻³, the ratio of air to seawater densities;
• γ = 0.02, see below;
• C_d = 2 × 10⁻³, the drag coefficient at high wind speeds [47];
• g = 10 m/s², the Earth’s gravity;
• α = 3 × 10⁻⁴ K⁻¹, seawater’s thermal expansion coefficient [39];
• h₁ and h₂ are chosen to be from the surface to the 26 °C isotherm z = −z₂₆, and from z = −z₂₆ to the 20 °C isotherm z = −z₂₀. The h₁ ≈ h₂ ≈ 100 m in the RI region (10~25 ^°N) in the tropical and subtropical western North Pacific (Figure 3).

Choosing γ:

Given Z₂₆ and Z₂₀ as a slowly-varying background ocean state, one can calculate the SST cooling δT(Z₂₆, Z₂₀, U_h, V₀; γ) (Equation (13)) along a storm’s track with γ serving as a parameter. Here we use the EN4 data as the ocean state given as monthly analysis from 1900 to the present [48]. We calculate U_h and V₀ at a track location using the average of the present and previous day’s values. We then choose γ to yield SST cooling that reasonably matches the observed and full ocean model’s cooling in two TCs: Typhoon Nuri (2008) and Typhoon Soudelor (2015). We previously conducted detailed analyses and SST cooling simulations for these typhoons using the Princeton ocean model (POM) [16,49,50]. We find that γ = 0.02 gives reasonably good agreements between δT and SST cooling from GHRSST observation and POM (Figure 4). The γ = 0.02 is within the range cited in the literature for strong boundary stirring at high buoyancy Reynolds number [51,52,53,54].

3. Results

We describe the modeled WOF-induced intensity change δV_m, focusing first on the western North Pacific’s typhoons since these have the largest intensity changes. Then, however, we will comment on the North Atlantic’s hurricanes.

3.1. δV_m with No Ocean Feedback

Figure 5 (color shading) shows δV_m without ocean feedback as a function of δT_W and T₀. Mathematically, it is equivalent to the maximum possible increased intensity as the storm enters the WOF at an infinite translation speed U_h. There is then little time for ocean mixing by the wind to cool the sea surface. It is also the δV_m when the TC crosses onto a shallow warm sea where the entire water column is well-mixed. The white line shows the corresponding δV_m = 15.4 m/s separating the (δT_W, T₀) on the upper right where a WOF-induced RI is possible from the lower-left where RI is unlikely. Figure 5 uses V₀ = 30 m/s as a representative example. Most observed RIs develop when the TC is in the tropical storm (TS) or Categories 1–2 stages [15,17,18,30,36]. However, the δV_m = 15.4 m/s line in this plot and Figure 6, hence the inferences derived from it are independent of V₀ since the line is for the asymptotic limit of zero ocean cooling. The present climatological SST (T₀) in the RI region is 28–29.5 °C (Figure 3). The composite (1993–2015) mean eddy’s SST anomaly is +0.3 °C [55], but δT_W in individual WOFs can reach +1 °C [15,16,24,27]. For reference, white dashed lines indicate the present climate’s (δT_W, T₀) = (1, 29) °C. As the majority (~85%) of RIs occur for U_h ≲ 7 m/s [6,36], the result suggests that RIs triggered by the WOF alone are unlikely to be frequent occurrences in the present climate. In other words, factors other than WOF alone more likely trigger the RIs observed in the present climate. See Section 3.3.

3.2. δV_m with Ocean Feedback

In Equation (20), the “s × δT_W” is the MPI estimate of the WOF-induced intensification. The “s × μF_T” (> 0) is the coupling term that includes the contribution (F_T) from ocean cooling caused by the mixing of surface and subsurface water by the translating storm. The formula shows that ocean cooling always reduces δV_m. Since F_T is inversely related to U_h and h₁ (see Equation (16)), the ocean cools more for slower storms, a thinner upper warm layer, or both, which then reduces δV_m. For very deep h₁, F_T ~ 0, and ocean feedback is negligible. Ocean feedback is also weak for very fast storms since there is little time for the wind to mix the upper ocean, and the feedback to the storm is negligible. In either case, the intensification is due to the WOF alone and becomes the upper-bound MPI estimate: δV_m = s × δT_W.

The blue dashed lines in Figure 5 show the δVm = 15.4 m/s contours obtained from the solution with ocean feedback for different U_h. (The plot is for the solution 19, although the quadratic correction is small: 5–10% less cooling). Ocean cooling at finite U_h shifts the 15.4 m/s line rightward and upward, meaning ocean feedback makes it even harder for WOF-induced RI to develop under the present climate.

3.3. Observed RIs in the Present Climate

Figure 5 plots the (δT_W, T₀) points of nine TCs whose RIs may be related to WOFs (source references in the caption). We only include Tropical Cyclone Bansi for comparison since the empirical MPI used is not for the South Indian Ocean. The magenta line shows the 15.4 m/s using Xu et al.’s [35] empirical MPI coefficients for the North Atlantic. We use it to assess the four Atlantic hurricanes (E, H, Mw, and O). The magenta line shifts slightly rightward and upward relative to the western North Pacific line (white) because the Atlantic’s slope ∂V_m/∂T is less steep (roughly 0.8:1). The 9-TCs’ mean (δT_W, T₀) are (0.87, 28.8) °C (red asterisk), and the mean U_h is 5.2 m/s. The plot shows that none of the TCs’ rapid intensifications was WOF-induced. Typhoon Soudelor is the only storm that crosses the white 15.4 m/s-line. However, ocean cooling at U_h = 5.5 m/s would also render a WOF-induced RI unlikely in Soudelor. Instead, Oey and Lin [16] argued that weakened environmental vertical wind shear < 4 m/s contributes to the storm’s RI [5]. They also suggested that weak vertical wind shears may have contributed to the RIs in Hurricane Opal [57] and Typhoon Maemi [16]. These results show that for WOF-induced RIs to develop, the WOF and ambient SST would have to be warmer than the present-day T₀ ≈ 28–29.5 °C and δT_W ≲ 1 °C. Thus, as stated before, RIs triggered by the WOF alone are unlikely to be frequent occurrences in the present climate. Oey and Huang [30] arrived at this same conclusion in numerical experiments designed to isolate the WOF-induced intensity change. They found that although WOF increases intensity, the intensification is insufficient to trigger more RIs. Consequently, the number of RIs is not statistically significantly different between ensemble simulations with and without the WOF included in the model.

4. Discussion

Three of the four listed typhoons in Figure 5 are close to the white 15.4 m/s-line. Thus, they are close to a “tipping point or line”, meaning that slight increases in T₀ or δT_W or both may potentially foster more RIs. We use the simple model to project how WOF-induced RIs may evolve as the Earth’s climate warms. The SST trend is +0.1 °C per decade in the western North Pacific, but two times higher in the Philippines Sea (latitudes ≲ 20 ^°N) [58,59,60]. Similar warming trends occur in the Atlantic. At these rates and assuming that SST continues to rise [61], T₀ would reach 30–31 °C near the end of the 21st century.

SSTs in coastal seas and western boundary currents show higher rates of warming trends [60,62]. Along the western North Pacific rim and US southern and eastern shelves, coastal SST trends reach +0.4 °C per decade in summer [62], approximately two times higher than the adjacent open seas. The value is consistent with a recent estimate of |∇SST| trends of more than +0.2 °C/100 km/decade) across China’s and Japan’s coastal shelves, the northern Gulf of Mexico, the US south-mid-Atlantic, as well as across the Kuroshio and the Gulf Stream [60]. At these rates, the corresponding δT_W|_Coast and δT_W|_WBC would reach 1.2–1.8 °C or more near the end of the 21st century. The trend of δT_W|_Eddy for mesoscale eddies is harder to estimate. In the western North Pacific, Martínez-Moreno et al. [60] show an increasing |∇SST| trend of +0.02 °C/(100 km/decade) for eddies north of 20 °N, but a decreasing trend of −0.04 °C/(100 km/decade) south of 20 °N. The trends in tropical and subtropical North Atlantic are similarly weakly decreasing. However, these values for δT_W|_Eddy are weaker with larger uncertainty than the trends of δT_W|_Coast or δT_W|_WBC.

Figure 6 (color shading) shows δV_m as a function of U_h and h₁ for T₀ = 29.5 °C and δT_W = 1 °C near their upper limits in the western North Pacific in the present climate. The white line shows the corresponding δV_m = 15.4 m/s separating the (U_h, h₁) space on the upper right where a WOF-induced RI is possible from the lower-left where RI is unlikely. Ocean cooling is inversely related to h₁ or U_h (Equations (15) and (16)). There is more (less) cooling as the upper layer gets thinner (thicker), or the storm translates slower (faster), or both. As a result, the atmospheric response is a weaker (stronger) δV_m (Equation (3)). The white dashed box encloses the RI region’s Z₂₆ range (60–120 m; Figure 3) and the U_h range (3–7 m/s; [36]), where the majority of RI events occur. Thus, as discussed before, one sees that WOF-induced RIs in the present climate T₀ ≲ 29.5 °C and δT_W = 1 °C are unlikely.

Blue dashed lines show the sensitivity of intensity change to ambient SST at a fixed δT_W = 1 °C. These 15.4 m/s lines shift left and down as the T₀ increases, sweeping across the white dashed box. For example, for a future T₀ = 30 °C, WOF-induced RIs can occur over the small northeast corner of the box U_h > 5.5 m/s and Z₂₆ > 95 m. When T₀ = 31 (32) °C, the likelihood for WOF-induced RIs substantially increases as the region where δV_m > 15.4 m/s now occupies 60% (95%) of the box.

Black lines show the sensitivity of intensity change to WOF’s anomaly at a fixed T₀ = 29.5 °C. Note that the dependency of δV_m on h₁ or U_h is unchanged, and one can always find T₀ and δT_W pair for which the blue dashed and black lines coincide. However, from Equation (20), $\left(\frac{\partial {\mathsf{\delta }\mathrm{V}}_{\mathrm{m}}}{\partial {\mathsf{\delta }\mathrm{T}}_{\mathrm{W}}}\right)/\left(\frac{\partial {\mathsf{\delta }\mathrm{V}}_{\mathrm{m}}}{\partial {\mathrm{T}}_0}\right)\approx 1/\left({\mathsf{\delta }\mathrm{T}}_{\mathrm{W}}\mathrm{C}\right)+0\left({\mathrm{s}\mathsf{\mu }\mathrm{F}}_{\mathrm{T}}\right)$, where C ≈ 0.18 °C⁻¹ (see Section 2.2). Thus, δV_m is ~5 times more sensitive to δT_W than T₀ (the sensitivity difference is somewhat reduced by ocean feedback (the O(sμF_T) term) especially when h₁ or U_h or both are small). Thus a 1 °C change in T₀ takes only ~0.2 °C change in δT_W to effect the same intensity change. For example, Figure 6 shows that a 0.3 °C (0.5 °C) change of δT_W from 1 to 1.3 °C (1.5 °C) increases the likelihood for WOF-induced RIs as the region where δV_m > 15.4 m/s sweeps across more than 60% (95%) of the box. The effect is the same as a 1.5 °C (2.5 °C) change in T₀ from 29.5 to 31 (32) °C.

One may question the suitability of using the empirical MPI relationship (Equation (2)) based on present climate’s data to make future inferences. In the absence of data, it is, of course, impossible to address this with absolute certainty. However, we can make some reasonable deductions that the empirical relation will remain valid, at least into the 21st century. First, the theoretical MPI critically depends on the saturation mixing ratio, which varies exponentially with SST according to the Clausius–Clapeyron relationship [63,64]. Thus, the exponential form of the empirical MPI relationship is likely to remain valid in the future. Second, any numerical change in the empirical MPI is likely to be ‘slow’. Evidence of the slow change is that the exponent coefficient C remains stable despite the different periods and regions in the four cited studies. In the North Atlantic, C = 0.1813, 0.1813, and 0.1903 for the data from 1962–1992, 1981–2003, and 1988–2014, respectively [33,34,35], while C = 0.1806 for the 1981–2003 data for the western North Pacific [6]. Zeng et al. [34] made a similar argument when noting that the C they obtained was identical to DeMaria and Kaplan’s [33] using an earlier dataset. Finally, in the simple model, the most critical parameter is the slope s on the T-space. Based on the three analysis periods for the North Atlantic hurricanes [33,34,35], s appears to be increasing. The s = 10.12, 11.71, and 14.09 m/s °C⁻¹ for the 1962–1992, 1981–2003, and 1988–2014 data. We do not know the statistical significance of this increase. However, as long as this parameter is non-decreasing with time, the model would not overpredict WOF-induced RIs.

Rapid intensifications may become more frequent and storms more powerful as the planet warms [65]. Our simple model also predicts this as the likelihood for RI increases with increased ambient SST. Moreover, the greater sensitivity of RI to WOF anomaly suggests more powerful landfalling TCs as storms cross warmer coastal seas and western boundary currents. The simple model indicates that Western North Pacific coastlines: China and Japan, are particularly vulnerable. Wada [12] already suggests such a possibility with Typhoon Manyi crossing the warm Kuroshio south of Japan.

5. Conclusions

This study presents a simple analytical model with ocean feedback of tropical cyclones’ rapid intensity change induced by warm ocean features (WOF). The model indicates that WOF-induced rapid intensification (RI) is unlikely in the present climate. We provide evidence of this inference using observations from nine TCs that developed RIs. We show that the observed RIs have parameters below the model’s RI threshold. In other words, in the present climate, other environmental and internal dynamical factors likely contributed to the RIs observed in these TCs. The inference is in excellent agreement with the conclusion of a recent numerical study [30].

On the other hand, the simple model shows that WOF-induced RI is very sensitive to the WOF’s anomalous amplitude, five times more sensitive than the background SST. Thus, as coastal seas and western boundary currents continue to warm in the 21st century, the model suggests an increased likelihood for RIs near the coasts, China and Japan in particular. Future work may seek to show evidence of this prediction by analyzing landfalling TCs. This model prediction that WOF-induced RI by increased δT_W|_Coast or δT_W|_WBC