Multi-Radar Analysis of the 20 May 2013 Moore, Oklahoma Supercell through Tornadogenesis and Intensification
Abstract
:1. Introduction
- Understanding the characteristics of debris lofting in a pre-tornadic mesocyclone and differences in debris detectability between radar wavelengths (S- and X-bands);
- Exploring the structural evolution of the hook echo and associated changes in microphysical characteristics during momentum surges;
- Examining how the characteristics of supercell polarimetric signatures relate to hail, DSS, and updrafts evolve through tornadogenesis and tornado intensification.
2. Data and Methods
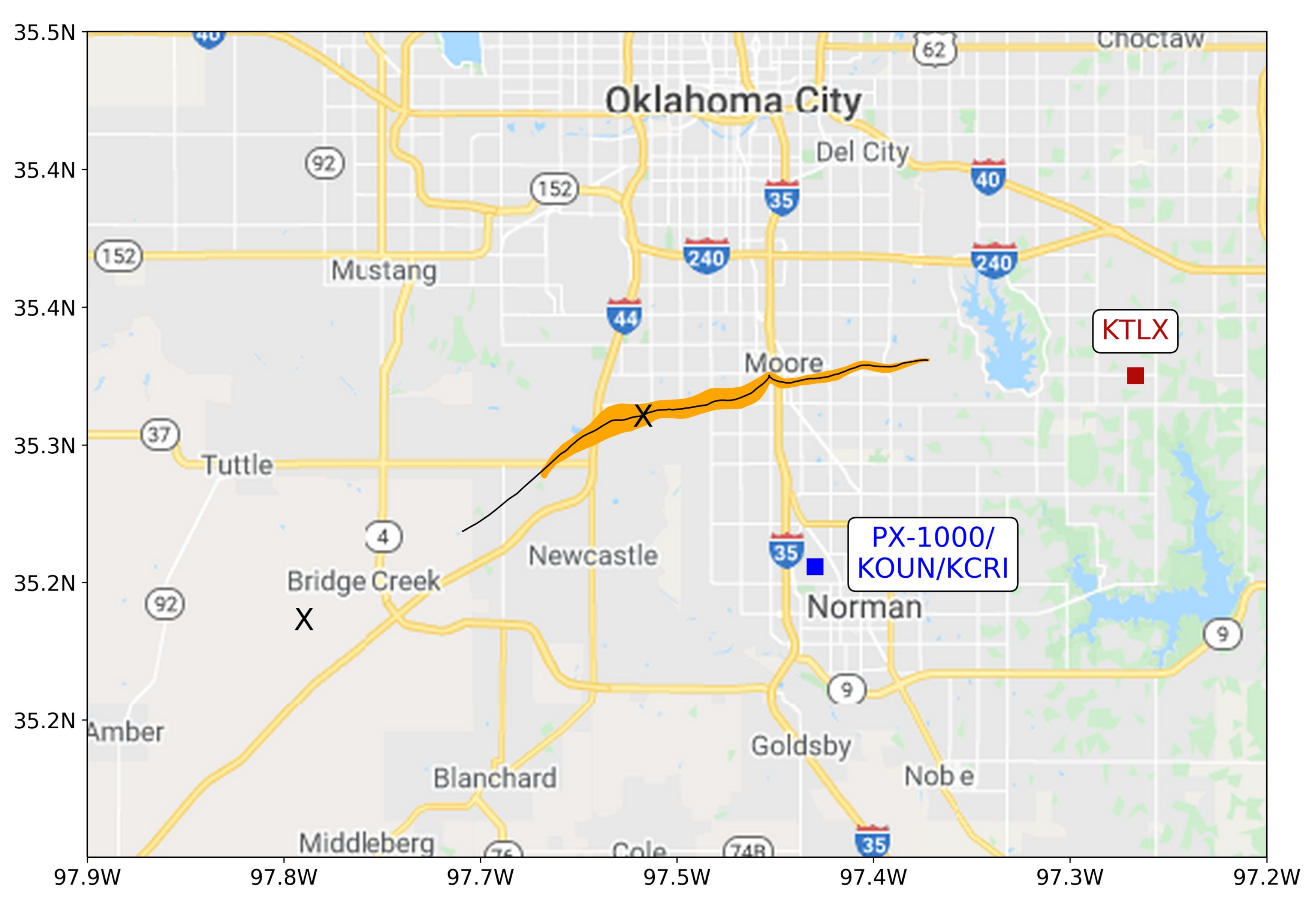
2.1. Radar Specifications
2.2. Hydrometeor Classification Algorithm
2.3. and Detection
3. Results
3.1. Microphysical Properties and Characteristics within the Hook Echo
3.1.1. Evolution of the Low-Level Mesocyclone and Tornado
3.1.2. Multi-Wavelength Comparison of HCA for Hydrometeors and Debris
3.1.3. Evolution of Momentum Surges
3.2. and Signatures
3.2.1. Arc and Foot
3.2.2. and Columns
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Isom, B.; Palmer, R.; Kelley, R.; Meier, J.; Bodine, D.; Yeary, M.; Cheong, B.L.; Zhang, Y.; Yu, T.Y.; Biggerstaff, M.I. The Atmospheric Imaging Radar: Simultaneous volumetric observations using a Phased Array Weather Radar. J. Atmos. Ocean. Technol. 2013, 30, 655–675. [Google Scholar] [CrossRef] [Green Version]
- Pazmany, A.L.; Mead, J.B.; Bluestein, H.B.; Snyder, J.C.; Houser, J.B. A mobile rapid-scanning X-band polarimetric (RaXPol) Doppler radar system. J. Atmos. Ocean. Technol. 2013, 30, 1398–1413. [Google Scholar] [CrossRef]
- Kurdzo, J.M.; Nai, F.; Bodine, D.J.; Bonin, T.A.; Palmer, R.D.; Cheong, B.L.; Lujan, J.; Mahre, A.; Byrd, A.D. Observations of severe local storms and tornadoes with the Atmospheric Imaging Radar. Bull. Am. Meteorol. Soc. 2017, 98, 915–935. [Google Scholar] [CrossRef]
- Weber, M.E.; Cho, J.Y.N.; Herd, J.S.; Flavin, J.M.; Benner, W.E.; Torok, G.S. The next-generation multimission U.S. surveillance radar network. Bull. Am. Meteorol. Soc. 2007, 88, 1739–1751. [Google Scholar] [CrossRef] [Green Version]
- Zrnic, D.S.; Kimpel, J.F.; Forsyth, D.E.; Shapiro, A.; Crain, G.; Ferek, R.; Heimmer, J.; Benner, W.; McNellis, F.T.J.; Vogt, R.J. Agile-beam phased array radar for weather observations. Bull. Am. Meteorol. Soc. 2007, 88, 1753–1766. [Google Scholar] [CrossRef]
- Yoshikawa, E.; Ushio, T.; Kawasaki, Z.; Yoshida, S.; Morimoto, T.; Mizutani, F.; Wada, W. MMSE beam forming on fast-scanning phased array weather radar. IEEE Trans. Geosci. Remote Sens. 2012, 51, 3077–3088. [Google Scholar] [CrossRef]
- Bluestein, H.B.; Rauber, R.M.; Burgess, D.W.; Albrecht, B.; Ellis, S.M.; Richardson, Y.P.; Jorgensen, D.P.; Frasier, S.; Chilson, P.; Palmer, R.D.; et al. Radar in atmospheric sciences and related research: Current systems, emerging technology, and future needs. Bull. Am. Meteorol. Soc. 2014, 95, 1850–1861. [Google Scholar] [CrossRef]
- Markowski, P.M. Hook echoes and rear-flank downdrafts: A review. Mon. Weather Rev. 2002, 130, 852–876. [Google Scholar] [CrossRef]
- Grzych, M.L.; Lee, B.D.; Finley, C.A. Thermodynamic analysis of supercell rear-flank downdrafts from Project ANSWERS. Mon. Weather Rev. 2007, 135, 240–246. [Google Scholar] [CrossRef]
- Hirth, B.D.; Schroeder, J.L.; Weiss, C.C. Surface analysis of the rear-flank downdraft outflow in two tornadic supercells. Mon. Weather Rev. 2008, 136, 2344–2363. [Google Scholar] [CrossRef]
- Lee, B.D.; Finley, C.A.; Karstens, C.D. The Bowdle, South Dakota, cyclic tornadic supercell of 22 May 2010: Surface analysis of rear-flank downdraft evolution and multiple internal surges. Mon. Weather Rev. 2012, 140, 3419–3441. [Google Scholar] [CrossRef]
- Atkins, N.T.; Butler, K.M.; Flynn, K.R.; Wakimoto, R.M. An integrated damage, visual, and radar analysis of the 2013 Moore, Oklahoma EF5 tornado. Bull. Am. Meteorol. Soc. 2014, 95, 1549–1561. [Google Scholar] [CrossRef]
- Skinner, P.S.; Weiss, C.C.; French, M.M.; Bluestein, H.B.; Markowski, P.M.; Richardson, Y.P. VORTEX2 observations of a low-level mesocyclone with multiple internal rear-flank downdraft momentum surges in the 18 May 2010 Dumas, Texas, supercell. Mon. Weather Rev. 2014, 142, 2935–2960. [Google Scholar] [CrossRef]
- Adlerman, E.J. Numerical Simulations of Cyclic Storm Behavior: Mesocylogenesis and Tornadogenesis. Ph.D. Thesis, University of Oklahoma, Norman, OK, USA, 2003. [Google Scholar]
- Mashiko, W.; Niino, H.; Kato, T. Numerical simulation of tornadogenesis in an outer-rainband minisupercell of Typhoon ShanShan on 17 September 2006. Mon. Weather Rev. 2009, 137, 4238–4260. [Google Scholar] [CrossRef]
- Schenkman, A.D.; Xue, M.; Hu, M. Tornadogenesis in a high-resolution simulation of the 8 May 2003 Oklahoma City supercell. J. Atmos. Sci. 2014, 71, 130–154. [Google Scholar] [CrossRef]
- Dahl, J.M.L.; Parker, M.D.; Wicker, L.J. Imported and storm-generated near-ground vertical vorticity in a simulated supercell. J. Atmos. Sci. 2014, 71, 3027–3051. [Google Scholar] [CrossRef]
- Adlerman, E.J.; Droegemeier, K.K.; Davies-Jones, R. A numerical simulation of cyclic mesocyclogenesis. J. Atmos. Sci. 1999, 56, 2045–2069. [Google Scholar] [CrossRef]
- Finley, C.A.; Lee, B.D. High-resolution mobile mesonet observations of RFD surges in the June 9 Basset, Nebraska supercell during Project ANSWERS 2003. In Proceedings of the 22nd Conference on Severe Local Storms, Hyannis, MA, USA, 7 October 2004. [Google Scholar]
- Adlerman, E.J.; Droegemeier, K.K. The dependence of numerically simulated cyclic mesocyclogenesis upon environmental vertical wind shear. Mon. Weather Rev. 2005, 133, 3595–3623. [Google Scholar] [CrossRef] [Green Version]
- Kumjian, M.R.; Ryzhkov, A.V. Polarimetric signatures in supercell thunderstorms. J. Appl. Meteorol. Climatol. 2008, 48, 1940–1961. [Google Scholar] [CrossRef]
- Van Den Broeke, M.S.; Straka, J.M.; Rasmussen, E.N. Polarimetric radar observations at low levels during tornado life cycles in a small sample of classic southern Plains supercells. J. Appl. Meteorol. Climatol. 2008, 47, 1232–1247. [Google Scholar] [CrossRef] [Green Version]
- Van Den Broeke, M.S. Polarimetric radar metrics related to tornado life cycles and intensity in supercell storms. Mon. Weather Rev. 2017, 145, 3671–3686. [Google Scholar] [CrossRef]
- Van Den Broeke, M.S. Disdrometer, polarimetric radar, and condensation nuclei observations of supercell and multicell storms on 11 June 2018 in eastern Nebraska. Atmosphere 2020, 11, 770. [Google Scholar] [CrossRef]
- Kumjian, M.R.; Picca, J.C.; Ganson, S.M.; Ryzhkov, A.V.; Krause, J. Polarimetric radar characteristics of large hail. In Proceedings of the 25th Conference on Severe Local Storms, Denver, CO, USA, 13 October 2010. [Google Scholar]
- Dawson, D.T.; Mansell, E.R.; Jung, Y.; Wicker, L.J.; Kumjian, M.R.; Xue, M. Low-level ZDR Signatures in Supercell Forward Flanks: The role of size sorting and melting of hail. J. Atmos. Sci. 2014, 71, 276–299. [Google Scholar] [CrossRef]
- Romine, G.S.; Burgess, D.W.; Wilhelmson, R.B. A dual-polarization-radar-based assessment of the 8 May 2003 Oklahoma City tornado supercell. Mon. Weather Rev. 2008, 136, 2849–2870. [Google Scholar] [CrossRef]
- Palmer, R.D.; Bodine, D.; Kumjian, M.; Cheong, B.; Zhang, G.; Cao, Q.; Bluestein, H.B.; Ryzhkov, A.; Yu, T.Y.; Wang, Y. The 10 May 2010 tornado outbreak in central Oklahoma: Potential for new science with high-resolution polarimetric radar. Bull. Am. Meteorol. Soc. 2011, 92, 871–891. [Google Scholar] [CrossRef] [Green Version]
- Crowe, C.C.; Schultz, C.J.; Kumjian, M.; Carey, L.D.; Petersen, W.A. Use of dual-polarization signatures in diagnosing tornado potential. Electron. J. Oper. Meteorol. 2012, 13, 57–78. [Google Scholar]
- Loeffler, S.D.; Kumjian, M.R. Quantifying the separation of enhanced ZDR and KDP regions in nonsupercell tornadic storms. Weather Forecast. 2018, 33, 1143–1157. [Google Scholar] [CrossRef]
- Loeffler, S.D.; Kumjian, M.R.; Jurewicz, M.; French, M.M. Differentiating between tornadic and nontornadic supercells using polarimetric radar signatures of hydrometeor size sorting. Geophys. Res. Lett. 2020, 47, e2020GL088242. [Google Scholar] [CrossRef]
- Hall, M.M.; Cherry, S.M.; Goddard, J.F. Identification of hydrometeors and other targets by dual-polarization radar. Radio Sci. 1984, 19, 132–140. [Google Scholar] [CrossRef]
- Illingworth, A.J.; Caylor, I.J. Identification of precipitation using dual-polarization radar. In Proceedings of the Tenth International Cloud Physics Conference, Bad Homburg, Germany, 15–20 August 1988; pp. 372–377. Available online: https://apps.dtic.mil/sti/citations/ADA196726 (accessed on 20 February 2021).
- Conway, J.W.; Zrnić, D.S. A study of embryo production and hail growth using dual-Doppler and multiparameter radars. Mon. Weather Rev. 1993, 121, 2511–2528. [Google Scholar] [CrossRef] [Green Version]
- Brandes, E.A.; Vivekanandan, J.; Tuttle, J.D.; Kessinger, C.J. A study of thunderstorm microphysics with multiparameter radar and aircraft observations. Mon. Weather Rev. 1995, 123, 3129–3143. [Google Scholar] [CrossRef] [Green Version]
- Zrnić, D.S.; Ryzhkov, A.V. Polarimetry for weather surveillance radars. Bull. Am. Meteorol. Soc. 1999, 80, 389–406. [Google Scholar] [CrossRef]
- Loney, M.L.; Zrnić, D.S.; Straka, J.M.; Ryzhkov, A.V. Enhanced polarimetric radar signatures above the melting level in a supercell storm. J. Appl. Meteorol. 2002, 41, 1179–1194. [Google Scholar] [CrossRef]
- Kumjian, M.; Ryzhkov, A.V.; Melnikov, V.M.; Schuur, T.J. Rapid-scan super-resolution observations of a cyclic supercell with a dual-polarization WSR-88D. Mon. Weather Rev. 2010, 138, 3762–3786. [Google Scholar] [CrossRef]
- Kumjian, M.R.; Khain, A.P.; Benmoshe, N.; Ilotoviz, E.; Ryzhkov, A.V.; Phillips, V.T.J. The anatomy and physics of ZDR columns: Investigating a polarimetric radar signature with a spectral bin microphysical model. J. Appl. Meteorol. Climatol. 2014, 53, 1820–1843. [Google Scholar] [CrossRef]
- Homeyer, C.R.; Kumjian, M.R. Microphysical characteristics of overshooting convection from polarimetric radar observations. J. Atmos. Sci. 2015, 72, 870–891. [Google Scholar] [CrossRef]
- Snyder, J.C.; Bluestein, H.B.; Dawson, D.T., II; Jung, Y. Simulations of polarimetric, X-band radar signatures in supercells. Part II: ZDR columns and rings and KDP columns. J. Appl. Meteorol. Climatol. 2017, 56, 2001–2026. [Google Scholar] [CrossRef]
- Hubbert, J.; Bringi, V.N.; Carey, L.D. CSU-CHILL polarimetric measurements from a severe hailstorm in eastern Colorado. J. Appl. Meteorol. 1998, 37, 749–755. [Google Scholar] [CrossRef] [Green Version]
- Snyder, J.C.; Bluestein, H.B.; Venkatesh, V.; Frasier, S.J. Observations of polarimetric signatures in supercells by an X-band mobile Doppler radar. Mon. Weather Rev. 2013, 141, 3–29. [Google Scholar] [CrossRef]
- Snyder, J.C.; Kumjian, M.R.; Khain, A.P.; Picca, J. A ZDR Column detection algorithm to examine convective storm updrafts. Weather Forecast. 2015, 30, 1819–1844. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Schuur, T.J.; Burgess, D.W.; Zrnić, D.S. Polarimetric tornado detection. J. Appl. Meteorol. 2005, 44, 557–570. [Google Scholar] [CrossRef]
- Bluestein, H.B.; French, M.M.; Tanamachi, R.L.; Frasier, S.; Hardwick, K.; Junyent, F.; Pazmany, A. Close-range observations of tornadoes in supercells made with a dual-polarization, X-band, mobile Doppler radar. Mon. Weather Rev. 2007, 135, 1522–1543. [Google Scholar] [CrossRef]
- Bodine, D.; Kumjian, M.R.; Palmer, R.D.; Heinselman, P.L.; Ryzhkov, A.V. Tornado damage estimation using polarimetric radar. Weather Forecast. 2013, 28, 139–158. [Google Scholar] [CrossRef]
- Bodine, D.J.; Palmer, R.D.; Zhang, G. Dual-wavelength polarimetric radar analyses of tornadic debris signatures. J. Appl. Meteorol. Climatol. 2014, 53, 242–261. [Google Scholar] [CrossRef]
- Snyder, J.C.; Ryzhkov, A.V. Automated detection of polarimetric tornadic debris signatures using a hydrometeor classification algorithm. J. Appl. Meteorol. Climatol. 2015, 54, 1861–1870. [Google Scholar] [CrossRef]
- Cheong, B.L.; Bodine, D.J.; Fulton, C.J.; Torres, S.M.; Maruyama, T.; Palmer, R.D. SimRadar: A polarimetric radar time-series simulator for tornadic debris studies. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2858–2870. [Google Scholar] [CrossRef]
- Van Den Broeke, M.S.; Jauernic, S.T. Spatial and Temporal Characteristics of Polarimetric Tornadic Debris Signatures. J. Appl. Meteorol. Climatol. 2014, 53, 2217–2231. [Google Scholar] [CrossRef] [Green Version]
- Saari, M.D.W.; Lawton, R.M.; Schultz, C.J.; Carey, L.D. Early characteristics of the polarimetric tornadic debris signature associated with the 20 May 2013 Newcastle-Moore, Oklahoma, tornado. J. Oper. Meteorol. 2014, 2, 110–114. [Google Scholar] [CrossRef]
- Broeke, M.S.V.D.; Broeke, C.A.V.D. Polarimetric radar observations from a waterspout-producing thunderstorm. Weather Forecast. 2015, 30, 329–348. [Google Scholar] [CrossRef]
- Broeke, M.S.V.D. Potential tornado warning improvement resulting from utilization of the TDS in the warning decision process. J. Oper. Meteorol. 2017, 5, 121–133. [Google Scholar] [CrossRef]
- Ortega, K.; Burgess, D.; Garfield, G.; Karstens, C.; LaDue, J.; Marshall, T.; Meyer, T.; Smith, B.; Smith, R.; Spegeher, D.; et al. Damage survey and analysis of the 20 May 2013 Newcastle-Moore EF-5 tornado. In Special Sym. on Severe Local Storms: The Current State of the Science and Understanding Impacts; American Meteorological Society: Atlanta, GA, USA, 2014. [Google Scholar]
- Kurdzo, J.M.; Bodine, D.J.; Cheong, B.L.; Palmer, R.D. High-temporal resolution polarimetric X-band Doppler radar observations of the 20 May 2013 Moore, Oklahoma tornado. Mon. Weather Rev. 2015, 143, 2711–2735. [Google Scholar] [CrossRef] [Green Version]
- Satrio, C.N. Multi-Radar Analysis of the 20 May 2013 Moore, Oklahoma Supercell through Tornadogenesis and Intensification. Ph.D. Thesis, University of Oklahoma, Norman, OK, USA, 2019. [Google Scholar]
- Burgess, D.; Ortega, K.; Stumpf, G.; Garfield, G.; Karstens, C.; Meyer, T.; Smith, B.; Speheger, D.; Ladue, J.; Smith, R.; et al. 20 May 2013 Moore, Oklahoma tornado: Damage survey and analysis. Weather Forecast. 2014, 29, 1229–1237. [Google Scholar] [CrossRef]
- Kurdzo, J.M.; Cheong, B.L.; Palmer, R.D.; Zhang, G.; Meier, J.B. A pulse compression waveform for improved-sensitivity weather radar observations. J. Atmos. Ocean. Technol. 2014, 31, 2713–2731. [Google Scholar] [CrossRef] [Green Version]
- Cheong, B.L.; Kelley, R.; Palmer, R.D.; Zhang, Y.; Yeary, M.; Yu, T.Y. PX-1000: A solid-state polarimetric X-band weather radar and time–frequency multiplexed waveform for blind range mitigation. IEEE Trans. Instr. Meas. 2013, 62, 3064–3072. [Google Scholar] [CrossRef]
- Lei, L.; Zhang, G.; Doviak, R.J.; Palmer, R.; Cheong, B.L.; Xue, M.; Cao, Q.; Li, Y. Multilag correlation estimators for polarimetric radar measurements in the presence of noise. J. Atmos. Ocean. Technol. 2012, 29, 772–795. [Google Scholar] [CrossRef] [Green Version]
- Bringi, V.N.; Chandrasekar, V.; Balakrishnan, N.; Zrnić, D.S. An examination of propagation effects in rainfall at microwave frequencies. J. Atmos. Ocean. Technol. 1990, 7, 829–840. [Google Scholar] [CrossRef]
- Snyder, J.C.; Bluestein, H.B.; Zhang, G.; Frasier, S.J. Attenuation correction and hydrometeor classification of high-resolution, X-band, dual-polarized mobile radar measurements in severe convective storms. J. Atmos. Ocean. Technol. 2010, 27, 1979–2001. [Google Scholar] [CrossRef]
- Picca, J.C.; Ryzhkov, A.V. A dual-wavelength polarimetric analysis of the 16 May 2010 Oklahoma City extreme hailstorm. Mon. Weather Rev. 2012, 140, 1385–1403. [Google Scholar] [CrossRef] [Green Version]
- Wilson, M.B.; Broeke, M.S.V.D. An Automated Python Algorithm to Quantify ZDR Arc and KDP-ZDR Separation Signatures in Supercells. J. Atmos. Ocean. Technol. 2020, 38, 371–386. [Google Scholar] [CrossRef]
- Weaver, H.J. Applications of Discrete and Continuous Fourier Analysis; J. Wiley and Sons: Hoboken, NJ, USA, 1983; p. 582. [Google Scholar]
- Trapp, R.J.; Doswell, C.A. Radar data objective analysis. J. Atmos. Ocean. Technol. 2000, 17, 105–120. [Google Scholar] [CrossRef] [Green Version]
- Cressman, G.P. An operational objective analysis system. Mon. Weather Rev. 1959, 87, 367–374. [Google Scholar] [CrossRef]
- Barnes, S.L. A technique for maximizing details in numerical weather map analysis. J. Appl. Meteorol. 1964, 3, 396–409. [Google Scholar] [CrossRef] [Green Version]
- Schuur, T.J.; Ryzhkov, A.V.; Heinselman, P.L. Observations and Classification of Echoes with the Polarimetric WSR-88D Radar; Technical Report; NOAA/National Severe Storms Laboratory: Norman, OK, USA, 2003. [Google Scholar]
- Park, H.S.; Ryzhkov, A.V.; Zrnić, D.S.; Kim, K. The hydrometeor classification algorithm for the polarimetric WSR-88D: Description and application to an MCS. Weather Forecast. 2009, 24, 730–748. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Kumjian, M.R.; Ganson, S.M.; Zhang, P. Polarimetric radar characteristics of melting hail. Part II: Practical implications. J. Appl. Meteorol. Climatol. 2013, 52, 2871–2886. [Google Scholar] [CrossRef]
- Kumjian, M.R.; Ryzhkov, A.V. Storm-relative helicity revealed from polarimetric radar measurements. J. Atmos. Sci. 2009, 66, 667–685. [Google Scholar] [CrossRef] [Green Version]
- Van Den Broeke, M.S. Polarimetric Variability of classic supercell storms as a function of environment. J. Appl. Meteorol. Climatol. 2016, 55, 1907–1925. [Google Scholar] [CrossRef]
- Markowski, P.M.; Rasmussen, E.N.; Straka, J.M. The occurence of tornadoes in supercells interacting with boundaries during VORTEX-95. Weather Forecast. 1998, 13, 852–859. [Google Scholar] [CrossRef]
- Rasmussen, E.N.; Richardson, S.; Straka, J.M.; Markowski, P.M.; Blanchard, D.O. The association of significant tornadoes with a baroclinic boundary on 2 June 1995. Mon. Weather Rev. 2000, 128, 174–191. [Google Scholar] [CrossRef]
- Houston, A.L.; Wilhelmson, R.B. Observational analysis of the 27 May 1997 central Texas tornadic event. Part II: Tornadoes. Mon. Weather Rev. 2007, 135, 727–735. [Google Scholar] [CrossRef]
- Honda, T.; Kawano, T. A possible mechanism of tornadogenesis associated with the interaction between a supercell and an outflow boundary without horizontal shear. J. Atmos. Sci. 2016, 73, 1273–1292. [Google Scholar] [CrossRef]
- Marquis, J.; Richardson, Y.; Markowski, P.; Dowell, D.; Wurman, J. Tornado maintenance investigated with high-resolution dual-Doppler and EnKF analysis. Mon. Weather Rev. 2012, 140, 3–27. [Google Scholar] [CrossRef] [Green Version]
- Kosiba, K.A.; Wurman, J.; Richardson, Y.; Markowski, P.; Robinson, P.; Marquis, J. Genesis of the Goshen County, Wyoming, tornado on 5 June 2009 during VORTEX2. Mon. Weather Rev. 2013, 141, 1157–1181. [Google Scholar] [CrossRef]
- French, M.M.; Bluestein, H.B.; PopStefanija, I.; Baldi, C.A.; Bluth, R.T. Reexamining the Vertical Development of Tornadic Vortex Signatures in Supercells. Mon. Weather Rev. 2013, 141, 4576–4601. [Google Scholar] [CrossRef]
- Griffin, C.B.; Bodine, D.J.; Kurdzo, J.M.; Mahre, A.; Palmer, R.D. High-temporal resolution observations of the 27 May 2015 Canadian, Texas, tornado using the Atmospheric Imaging Radar. Mon. Weather Rev. 2019, 147, 873–891. [Google Scholar] [CrossRef]
- Mahre, A.; Kurdzo, J.M.; Bodine, D.J.; Griffin, C.B.; Palmer, R.D.; Yu, T. Analysis of the 16 May 2015 Tipton, Oklahoma, EF-3 Tornado at High Spatiotemporal Resolution Using the Atmospheric Imaging Radar. Mon. Weather Rev. 2018, 146, 2103–2124. [Google Scholar] [CrossRef]
- Huuskonen, A.; Saltikoff, E.; Holleman, I. The operational weather radar network in Europe. Bull. Am. Meteorol. Soc. 2014, 95, 897–907. [Google Scholar] [CrossRef]
- McLaughlin, D.; Pepyne, D.; Chandrasekar, V.; Philips, B.; Kurose, J.; Zink, M.; Droegemeier, K.; Cruz-Pol, S.; Junyent, F.; Brotzge, J.; et al. Short-wavelength technology and the potential for distributed networks of small radar systems. Bull. Am. Meteorol. Soc. 2009, 90, 1797–1818. [Google Scholar] [CrossRef]
- Bodine, D.J.; Palmer, R.D.; Maruyama, T.; Fulton, C.J.; Zhu, Y.; Cheong, B.L. Simulated Frequency Dependence of Radar Observations of Tornadoes. J. Atmos. Ocean. Technol. 2016, 33, 1825–1842. [Google Scholar] [CrossRef]
- Davies-Jones, R. Can a descending rain curtain in a supercell instigate tornadogenesis barotropically? J. Atmos. Sci. 2008, 65, 2469–2497. [Google Scholar] [CrossRef] [Green Version]
- Kumjian, M. Precipitation properties of supercell hook echoes. E J. Sev. Storms Meteorol. 2011, 6, 1–21. [Google Scholar]
- Karstens, C.D.; Gallus, W.A., Jr.; Lee, B.D.; Finley, C.A. Analysis of tornado-induced tree fall using aerial photography from the Joplin, Missouri, and Tuscaloosa–Birmingham, Alabama, tornadoes of 2011. J. Appl. Meteorol. Climatol. 2013, 52, 1049–1068. [Google Scholar] [CrossRef] [Green Version]
- Straka, J.M.; Rasmussen, E.N.; Davies-Jones, R.P.; Markowski, P.M. An observational and idealized numerical examination of low-level counter-rotating vortices towards the rear flank of supercells. E J. Sev. Storms Meteorol. 2007, 2, 1–22. [Google Scholar]
- Markowski, P.M.; Straka, J.M.; Rasmussen, E.N.; Davies-Jones, R.P.; Richardson, Y.; Trapp, J. Vortex lines within low-level mesocyclones obtrained from psuedo-dual-Doppler radar observations. Mon. Weather Rev. 2008, 136, 3513–3535. [Google Scholar] [CrossRef] [Green Version]
- Markowski, P.M.; Richardson, Y.P. The influence of environmental low-level shear and cold pools on tornadogenesis: Insights from toy simulations. J. Atmos. Sci. 2014, 71, 243–275. [Google Scholar] [CrossRef]
- Coffer, B.E.; Parker, M.D.; Dahl, J.M.L.; Wicker, L.J.; Clark, A.J. Volatility of tornadogenesis: An ensemble of simulated nontornadic and tornadic supercells in VORTEX2 environments. Mon. Weather Rev. 2017, 145, 4605–4625. [Google Scholar] [CrossRef]
- Orf, L.; Wilhelmson, R.; Lee, B.; Finley, C.; Houston, A. Evolution of a long-track violent tornado within a simulated supercell. Bull. Am. Meteorol. Soc. 2017, 98, 45–68. [Google Scholar] [CrossRef]
- Yokota, S.; Niino, H.; Seko, H.; Kunii, M.; Yamauchi, H. Important factors for tornadogenesis as revealed by high-resolution ensemble forecasts of the Tsukuba supercell tornado of 6 May 2012 in Japan. Mon. Weather Rev. 2018, 146, 1109–1132. [Google Scholar] [CrossRef]
- Martinaitis, S.M. Radar observations of tornado-warned convection associated with tropical cyclones over Florida. Weather Forecast. 2017, 32, 165–186. [Google Scholar] [CrossRef]
- Tanamachi, R.L.; Heinselman, P.L. Rapid-scan, polarimetric observations of central Oklahoma severe storms on 31 May 2013. Weather Forecast. 2016, 31, 19–42. [Google Scholar] [CrossRef]
- Picca, J.C.; Snyder, J.C.; Ryzhkov, A.V. An observational analysis of ZDR column trends in tornadic supercells. In Proceedings of the 37th Conference on Radar Meteorology, Norman, OK, USA, 15 September 2015. [Google Scholar]
- Dalman, D.M.; Tanamachi, R.L.; Saunders, P.E.; Cheong, B.L.; Bodine, D.; Bluestein, H.B.; Weinhoff, Z.B. Cataloging rapid-scan observations of ZDR columns in supercells. In Proceedings of the 29th Conference on Severe Local Storms, Stowe, VT, USA, 23 October 2018. [Google Scholar]
- Brandes, E.A. Mesocyclone evolution and tornadogenesis: Some observations. Mon. Weather Rev. 1978, 106, 995–1011. [Google Scholar] [CrossRef] [Green Version]
- Lemon, L.R.; Doswell, C.A. Severe Thunderstorm Evolution and Mesocyclone Structure as Related to Tornadogenesis. Mon. Weather Rev. 1979, 107, 1184–1197. [Google Scholar] [CrossRef]
- Trapp, R.J.; Mitchell, E.D.; Tipton, G.A.; Effertz, D.W.; Watson, A.I.; Andra, D.L.; Magsig, M.A. Descending and nondescending tornadic vortex signatures detected by WSR-88Ds. Weather Forecast. 1999, 14, 625–639. [Google Scholar] [CrossRef]
















| PX-1000 | KTLX | KOUN | KCRI | |
|---|---|---|---|---|
| Temporal Resolution | 20 s | 4–5 min | 2–3 min | 4–5 min |
| Azimuthal Resolution () | 1 | 0.5 * | 0.5 * | 0.5 * |
| Beamwidth () | 1.8 | 0.9 | 0.9 | 0.9 |
| Range Resolution (m) | 30 | 250 | 250 | 250 |
| Elevation Angles () | 2.6 | 0.5–19.5 | 0.5–10.0 | 0.5–19.5 |
| Analysis Period (UTC) | 1930–2008 | 1929–2008 | 1947–2007 | 1949–2008 |
| Beam Height (km) | 1.1/0.75/0.6 | 0.48/0.35/0.28 | 0.18/0.15/0.13 | 0.17/0.16/0.12 |
| Range (km) | 24.3/16.3/13.1 | 42.6/32.8/27.2 | 18.7/15.9/13.6 | 17.8/16.4/13.1 |
| GC | BD | RA | HR | RH | SH | LH | GH | TDS | |
|---|---|---|---|---|---|---|---|---|---|
| (dBZ) | |||||||||
| 15 | 24 | 5 | 40 | 45 | 45 | 54 | 54 | 30 | |
| 20 | 29 | 10 | 47 | 55 | 49 | 59 | 64 | 35 | |
| 70 | 49 | 37 | 57 | 65 | 59 | 64 | 74 | 70 | |
| 80 | 54 | 42 | 62 | 75 | 64 | 69 | 80 | 75 | |
| (dB) | |||||||||
| −4 | 1 | 0.4 | 0 | −2.5 | |||||
| −2 | 1.5 | 0.9 | 0.5 | −1.5 | |||||
| 1 | 2.5 | 1.9 | 1.5 | 1.5 | |||||
| 2 | 4 | 3.5 | 2 | 2.5 | |||||
| 0.5 | 0.92 | 0.95 | 0.92 | 0.80 | 0.94 | 0.88 | 0.8 | 0 | |
| 0.6 | 0.93 | 0.96 | 0.94 | 0.85 | 0.96 | 0.92 | 0.88 | 0.01 | |
| 0.9 | 1 | 1 | 1 | 0.95 | 0.98 | 0.98 | 0.96 | 0.85 | |
| 0.95 | 1.01 | 1.01 | 1.01 | 1.01 | 0.99 | 0.99 | 0.98 | 0.92 | |
| Weights | |||||||||
| 0.2 | 0.8 | 1 | 1 | 1 | 1 | 1 | 1 | 0.6 | |
| 0.4 | 1 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | |
| 1 | 0.6 | 0.6 | 0.6 | 0.6 | 0.6 | 0.6 | 0.6 | 1 | |
| Abbreviation | Classifier |
|---|---|
| GC | Ground Clutter/Anomalous Propagation |
| BD | Big Drops |
| RA | Rain |
| HR | Heavy Rain |
| RH | Rain/Hail |
| SH | Small Hail |
| LH | Large Hail |
| GH | Giant Hail |
| TDS | Tornado Debris Signature |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Satrio, C.N.; Bodine, D.J.; Palmer, R.D.; Kuster, C.M. Multi-Radar Analysis of the 20 May 2013 Moore, Oklahoma Supercell through Tornadogenesis and Intensification. Atmosphere 2021, 12, 313. https://doi.org/10.3390/atmos12030313
Satrio CN, Bodine DJ, Palmer RD, Kuster CM. Multi-Radar Analysis of the 20 May 2013 Moore, Oklahoma Supercell through Tornadogenesis and Intensification. Atmosphere. 2021; 12(3):313. https://doi.org/10.3390/atmos12030313
Chicago/Turabian StyleSatrio, Clarice N., David J. Bodine, Robert D. Palmer, and Charles M. Kuster. 2021. "Multi-Radar Analysis of the 20 May 2013 Moore, Oklahoma Supercell through Tornadogenesis and Intensification" Atmosphere 12, no. 3: 313. https://doi.org/10.3390/atmos12030313
APA StyleSatrio, C. N., Bodine, D. J., Palmer, R. D., & Kuster, C. M. (2021). Multi-Radar Analysis of the 20 May 2013 Moore, Oklahoma Supercell through Tornadogenesis and Intensification. Atmosphere, 12(3), 313. https://doi.org/10.3390/atmos12030313






