Tephra4D: A Python-Based Model for High-Resolution Tephra Transport and Deposition Simulations—Applications at Sakurajima Volcano, Japan
Abstract
:1. Introduction
2. Model Description
2.1. The Advection-Diffusion Model Tephra2 and Its Modifications
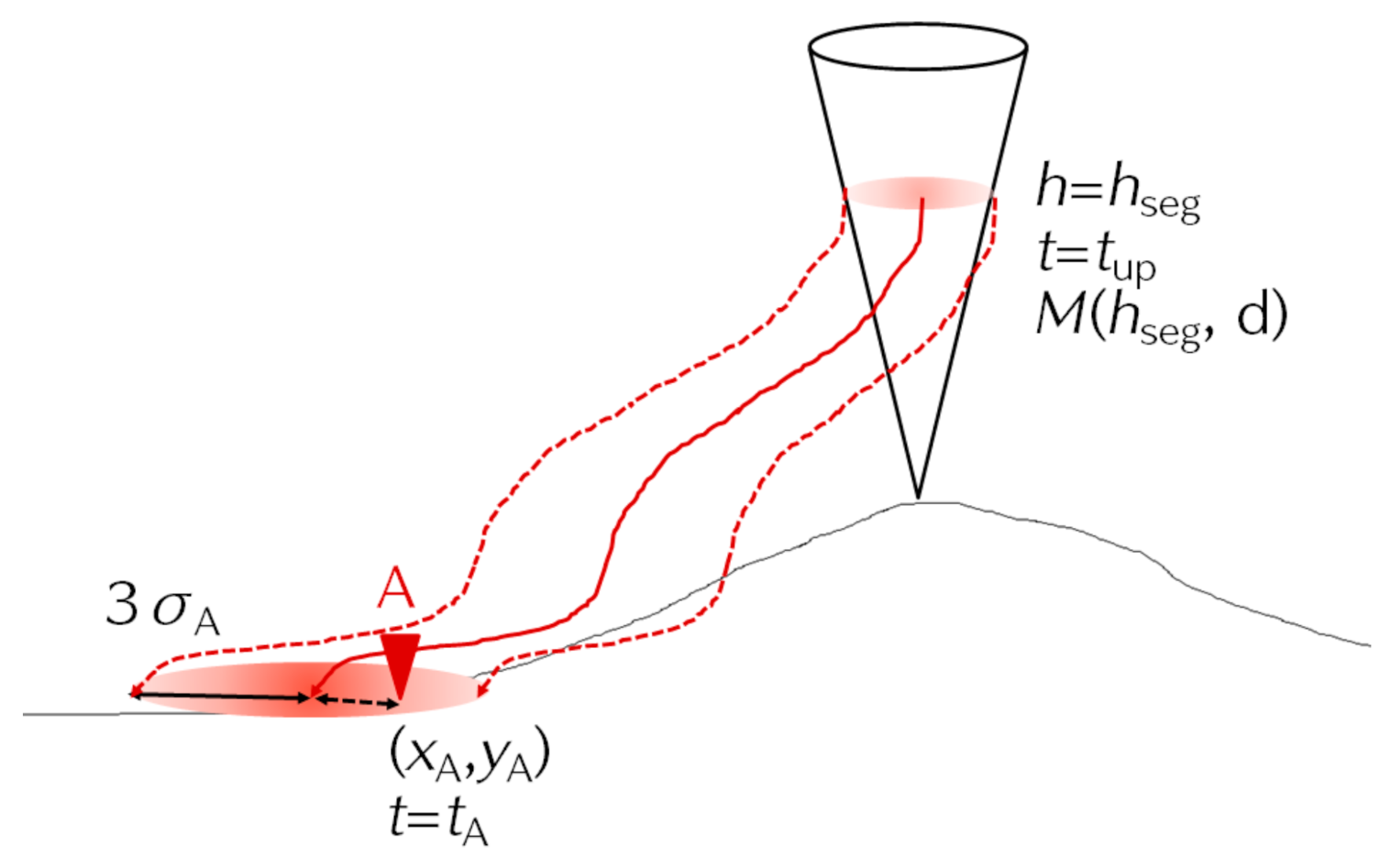
2.2. The Trajectory Calculation
2.3. Wind Field and Atmospheric Density
2.4. The Settling Velocity of Pyroclastic Particles
2.5. Tephra Segregation Profile
3. Benchmarking
3.1. The Eruptions Studied
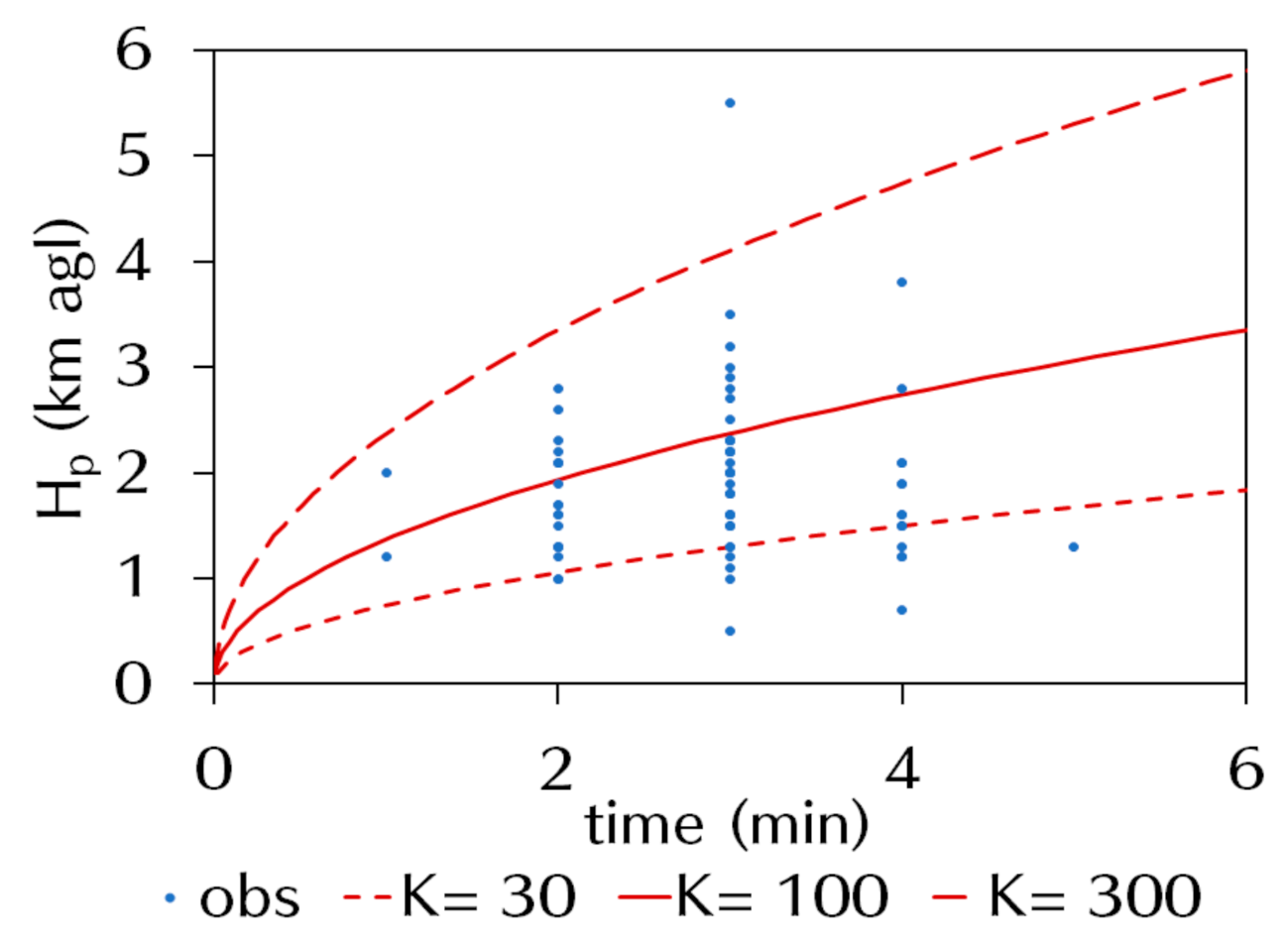
3.2. Model Setup
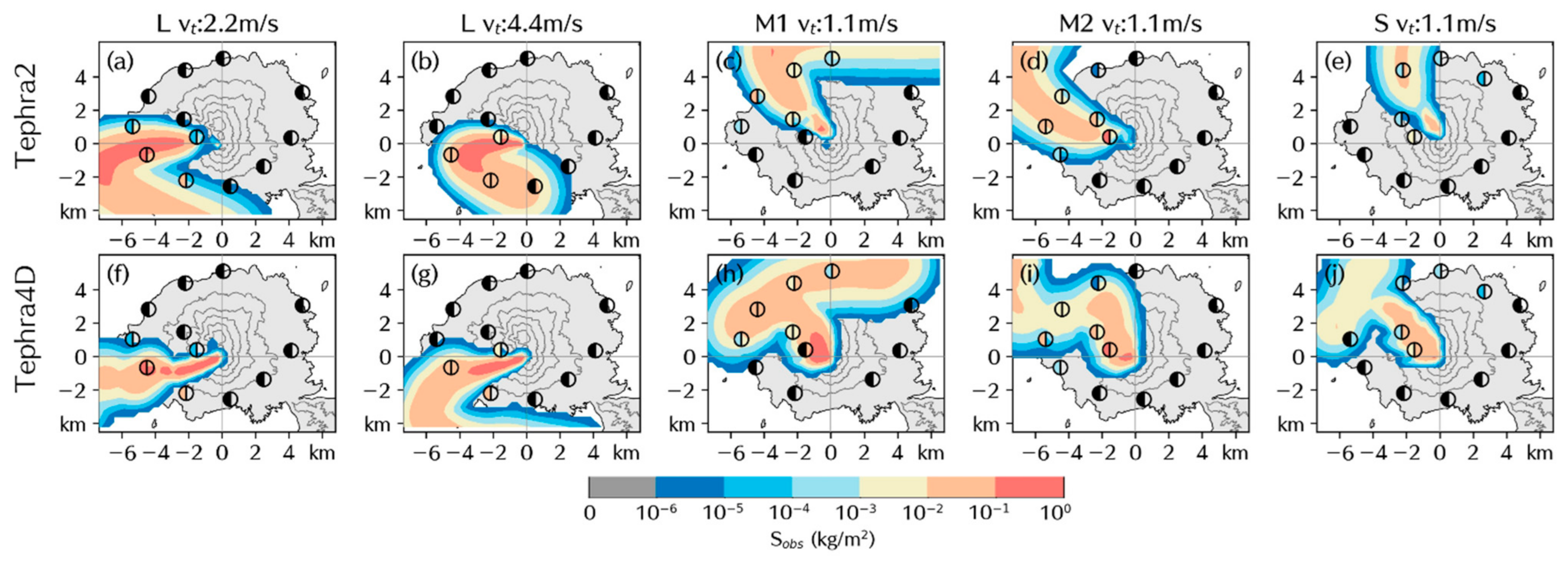
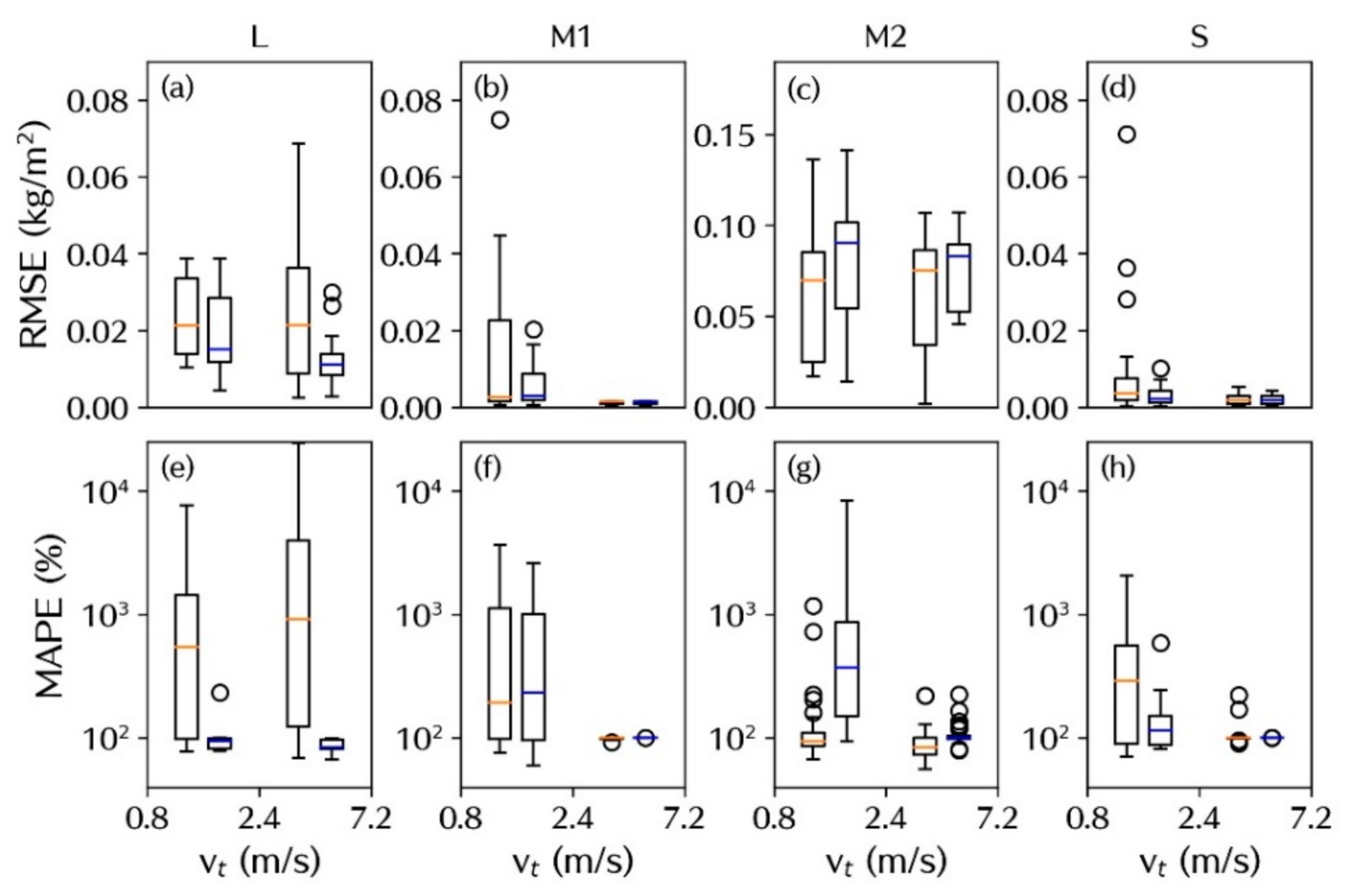
3.3. Results Comparison
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
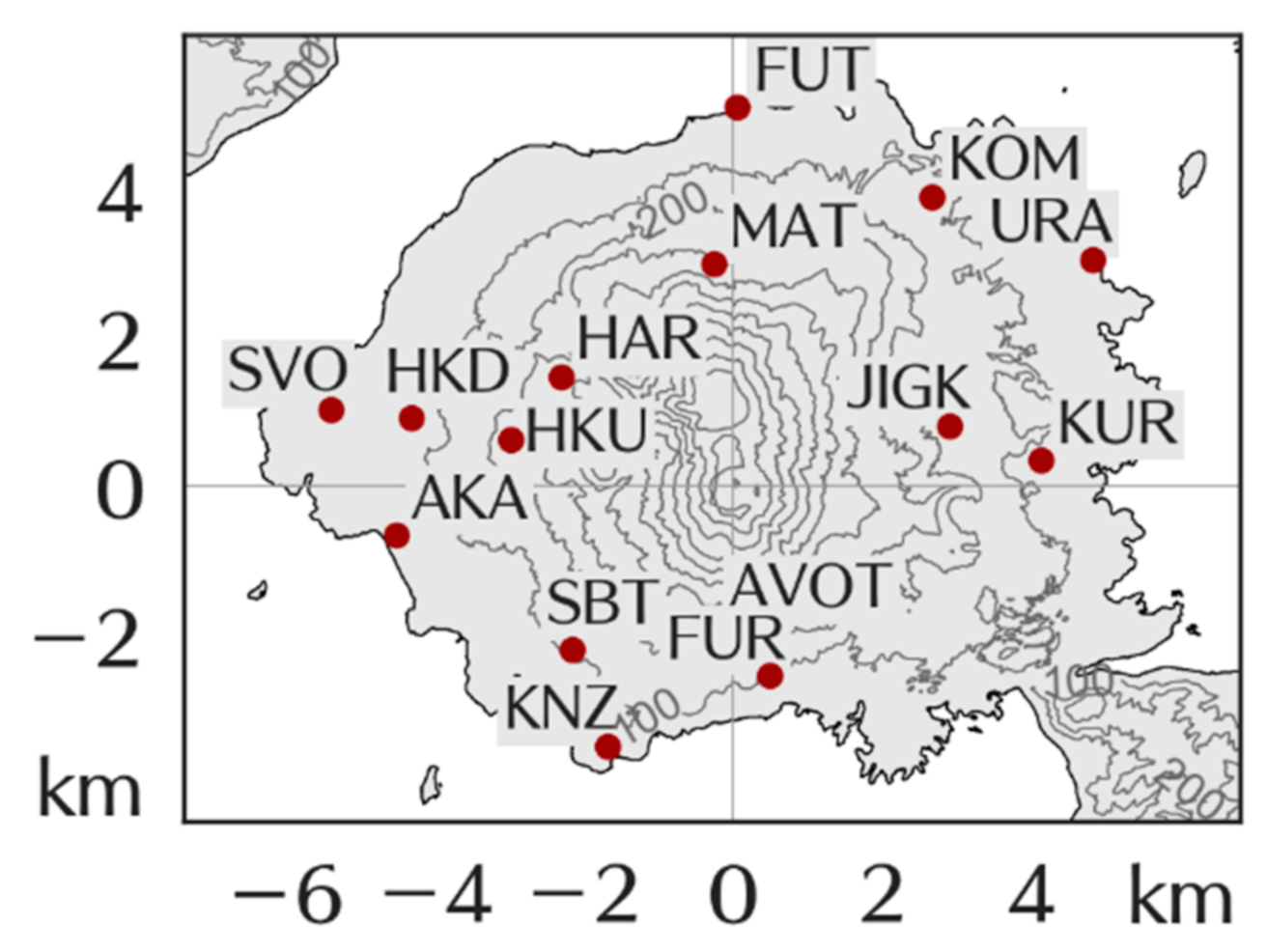
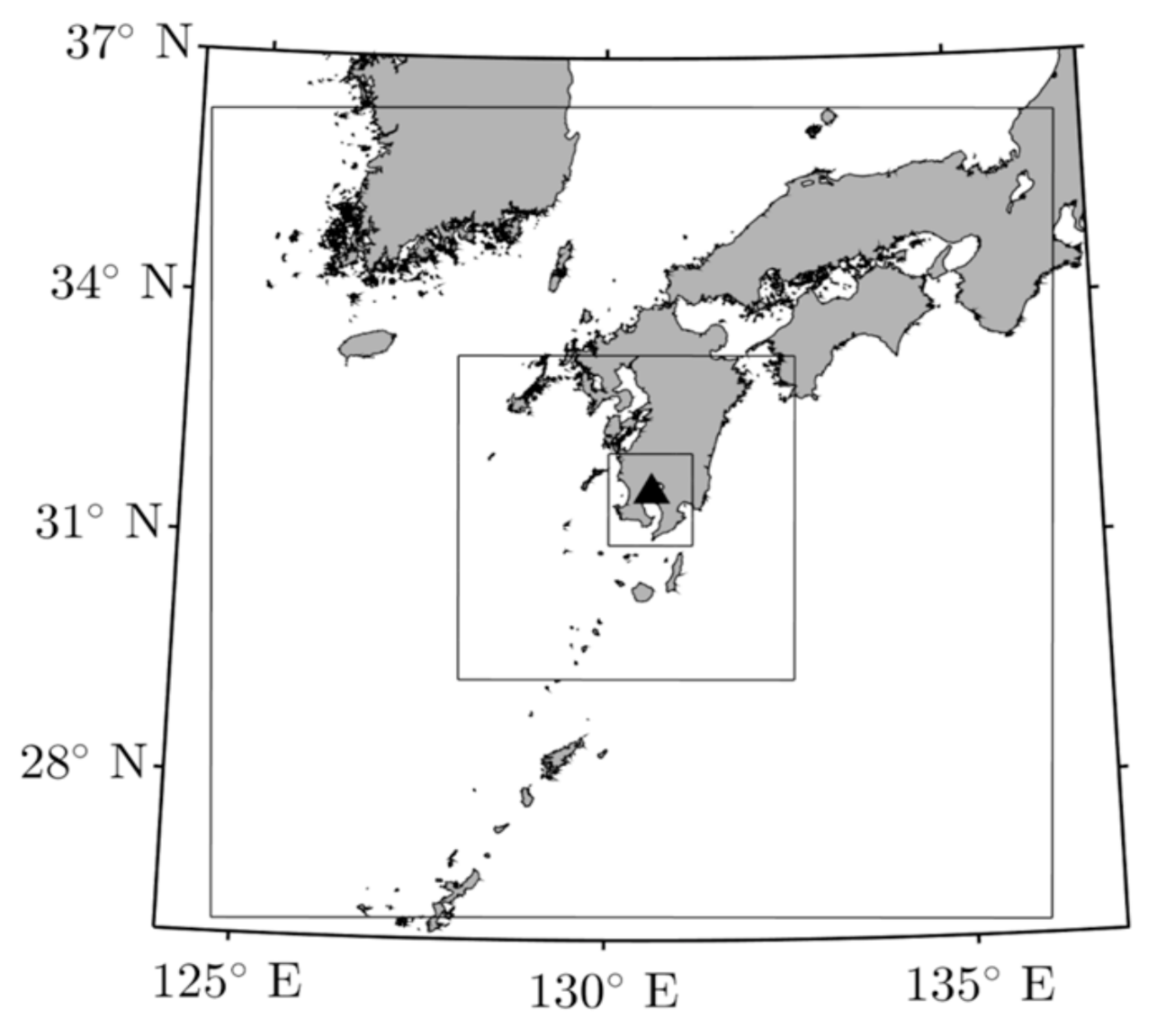
Appendix A. Sakurajima


Appendix B. Tephra Load Observation Using the Disdrometer


Appendix C. WRF Setup
References
- Langmann, B.; Folch, A.; Hensch, M.; Matthias, V. Volcanic ash over Europe during the eruption of Eyjafjallajökull on Iceland, April-May 2010. Atmos. Environ. 2012, 48, 1–8. [Google Scholar] [CrossRef]
- Folch, A. A review of tephra transport and dispersal models: Evolution, current Status, and future perspectives. J. Volcanol. Geotherm. Res. 2012, 235–236, 96–115. [Google Scholar] [CrossRef]
- Bonadonna, C.; Connor, C.B.; Houghton, B.F.; Connor, L.; Byrne, M.; Laing, A.; Hincks, T.K. Probabilistic modeling of tephra dispersal: Hazard assessment of a multiphase rhyolitic eruption at Tarawera, New Zealand. J. Geophys. Res. Solid Earth 2005, 110, 1–21. [Google Scholar] [CrossRef]
- Fero, J.; Carey, S.N.; Merrill, J.T. Simulating the dispersal of tephra from the 1991 Pinatubo eruption: Implications for the formation of widespread ash layers. J. Volcanol. Geotherm. Res. 2009, 186, 120–131. [Google Scholar] [CrossRef]
- Mannen, K. Particle segregation of an eruption plume as revealed by a comprehensive analysis of tephra dispersal: Theory and application. J. Volcanol. Geotherm. Res. 2014, 284, 61–78. [Google Scholar] [CrossRef]
- Suzuki, T. A theoretical model for dispersion of tephra. In Arc Volcanism Phys. Tecton.; Shimozuru, D., Yokoyama, I., Eds.; Terra Scientific Publishing Company (TERRAPUB): Tokyo, Japan, 1983; pp. 95–113. [Google Scholar]
- Del Bello, E.; Taddeucci, J.; Michieli Vitturi, M.; Scarlato, P.; Andronico, D.; Scollo, S.; Kueppers, U.; Ricci, T. Effect of particle volume fraction on the settling velocity of volcanic ash particles: Insights from joint experimental and numerical simulations. Sci. Rep. 2017, 7, 39620. [Google Scholar] [CrossRef] [Green Version]
- Freret-Lorgeril, V.; Gilchrist, J.; Donnadieu, F.; Jellinek, A.M.; Delanoë, J.; Latchimy, T.; Vinson, J.P.; Caudoux, C.; Peyrin, F.; Hervier, C.; et al. Ash sedimentation by fingering and sediment thermals from wind-affected volcanic plumes. Earth Planet. Sci. Lett. 2020, 534, 116072. [Google Scholar] [CrossRef]
- Mannen, K.; Hasenaka, T.; Higuchi, A.; Kiyosugi, K.; Miyabuchi, Y. Simulations of tephra fall deposits from a bending eruption plume and the optimum model for particle release. J. Geophys. Res. Solid Earth 2020, 125, 1–29. [Google Scholar] [CrossRef]
- Poulidis, A.P.; Takemi, T.; Iguchi, M.; Renfrew, I.A. Orographic effects on the transport and deposition of volcanic ash: A case study of mount Sakurajima, Japan. J. Geophys. Res. Atmos. 2017, 122, 9332–9350. [Google Scholar] [CrossRef]
- Poulidis, A.P.; Takemi, T.; Iguchi, M. The effect of wind and atmospheric stability on the morphology of volcanic plumes from vulcanian eruptions. J. Geophys. Res. Solid Earth 2019, 124, 8013–8029. [Google Scholar] [CrossRef]
- Ganser, G.H. A rational approach to drag prediction of spherical and nonspherical particles. Powder Technol. 1993, 77, 143–152. [Google Scholar] [CrossRef]
- Bonadonna, C.; Mayberry, G.C.; Calder, E.S.; Sparks, R.S.J.; Choux, C.; Jackson, P.; Lejeune, A.M.; Loughlin, S.C.; Norton, G.E.; Rose, W.I.; et al. Tephra fallout in the eruption of Soufrière Hills Volcano, Montserrat. Geol. Soc. Lond. Mem. 2002, 21, 483–516. [Google Scholar] [CrossRef]
- Kozono, T.; Iguchi, M.; Miwa, T.; Maki, M.; Maesaka, T.; Miki, D. Characteristics of tephra fall from eruptions at Sakurajima volcano, revealed by optical disdrometer measurements. Bull. Volcanol. 2019, 81. [Google Scholar] [CrossRef]
- Suh, S.H.; Maki, M.; Iguchi, M.; Lee, D.I.; Yamaji, A.; Momotani, T. Free-fall experiments of volcanic ash particles using a 2-D video disdrometer. Atmos. Meas. Tech. 2019, 12, 5363–5379. [Google Scholar] [CrossRef] [Green Version]
- Connor, C.B.; Hill, B.E.; Winfrey, B.; Franklin, N.M.; Femina, P.C. Estimation of volcanic hazards from tephra fallout. Nat. Hazards Rev. 2001, 2, 33–42. [Google Scholar] [CrossRef]
- Kunii, D.; Levenspiel, O. Entrapment and elutriation from fludized beds. J. Chem. Eng. Japan 1969, 2, 84–88. [Google Scholar] [CrossRef] [Green Version]
- Haruyama, M.; Shimokawa, E.; Inoue, T. Geotechnical properties of the volcanic ash and sand in Sakurajima volcano. Bull. Kagoshima Univ. For. 1977, 5, 65–92. [Google Scholar]
- Sparks, R.S.J.; Wilson, L. Explosive volcanic eruptions—V. Observations of plume dynamics during the 1979 Soufrière eruption, St Vincent. Geophys. J. Int. 1982, 69, 551–570. [Google Scholar] [CrossRef] [Green Version]
- Sakurajima Live Camera. Available online: https://373news.com/_sakucap/ (accessed on 5 January 2021).
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Zhiquan, L.; Berner, J.; Wang, W.; Powers, J.G.; Duda, M.G.; Barker, D.M.; et al. A Description of the Advanced Research WRF Model Version 4 (No. NCAR/TN-556+STR); National Center for Atmospheric Research: Boulder, CO, USA, 2019. [Google Scholar] [CrossRef]
- Smith, R.B. Linear theory of stratified hydrostatic flow past an isolated mountain. Tellus 1980, 32, 348–364. [Google Scholar] [CrossRef] [Green Version]
- Freret-Lorgeril, V.; Donnadieu, F.; Eychenne, J.; Soriaux, C.; Latchimy, T. In situ terminal settling velocity measurements at Stromboli volcano: Input from physical characterization of ash. J. Volcanol. Geotherm. Res. 2019, 374, 62–79. [Google Scholar] [CrossRef] [Green Version]
- Iguchi, M.; Nakamichi, H.; Tanaka, H.; Ohta, Y.; Shimizu, A.; Miki, D. Integrated monitoring of volcanic ash and forecasting at Sakurajima volcano, japan. J. Disaster Res. 2019, 14, 798–809. [Google Scholar] [CrossRef]
- Poulidis, A.P.; Shimizu, A.; Nakamichi, H.; Iguchi, M. A computational methodology for the calibration of tephra transport nowcasting at Sakurajima volcano, Japan. Atmosphere 2021, 12, 104. [Google Scholar] [CrossRef]
- Iguchi, M. Method for real-time evaluation of discharge rate of volcanic ash—Case study on intermittent eruptions at the Sakurajima volcano, Japan. J. Disaster Res. 2016, 11, 4–14. [Google Scholar] [CrossRef]
- Watt, S.F.L.; Gilbert, J.S.; Folch, A.; Phillips, J.C.; Cai, X.M. An example of enhanced tephra deposition driven by topographically induced atmospheric turbulence. Bull. Volcanol. 2015, 77. [Google Scholar] [CrossRef] [Green Version]
- Klawonn, M.; Wolfe, C.J.; Frazer, L.N.; Houghton, B.F. Novel inversion approach to constrain plume sedimentation from tephra deposit data: Application to the 17 June 1996 eruption of Ruapehu volcano, New Zealand. J. Geophys. Res. Solid Earth 2012, 117, B05205. [Google Scholar] [CrossRef] [Green Version]
- Scollo, S.; Del Carlo, P.; Coltelli, M. Tephra fallout of 2001 Etna flank eruption: Analysis of the deposit and plume dispersion. J. Volcanol. Geotherm. Res. 2007, 160, 147–164. [Google Scholar] [CrossRef]
- Iguchi, M.; Yakiwara, H.; Tameguri, T.; Hendrasto, M.; Hirabayashi, J. Mechanism of explosive eruption revealed by geophysical observations at the Sakurajima, Suwanosejima and Semeru volcanoes. J. Volcanol. Geotherm. Res. 2008, 178, 1–9. [Google Scholar] [CrossRef]
- Poulidis, A.P.; Takemi, T.; Iguchi, M. Experimental high-resolution forecasting of volcanic ash hazard at Sakurajima, Japan. J. Disaster Res. 2019, 14, 786–797. [Google Scholar] [CrossRef] [Green Version]
- The Volcanic Plume Echo of Sakurajima Eruption on Jun. 4, 2020 Observed by Meteorological Radar. 2020. Available online: https://www.mri-jma.go.jp/Topics/R02/020714/020714_oshirase.html (accessed on 4 March 2021).
- Tephra Deposit Load around Sakurajima Since 2008. Available online: http://www.pref.kagoshima.jp/aj01/bosai/sonae/sakurajima/sakurajimakouhairyou2.html (accessed on 5 January 2021).
- Marti, A.; Folch, A. Volcanic ash modeling with the NMMB-MONARCH-ASH model: Quantification of offline modeling errors. Atmos. Chem. Phys. 2018, 18, 4019–4038. [Google Scholar] [CrossRef] [Green Version]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Shin, H.H.; Hong, S.Y. Representation of the subgrid-scale turbulent transport in convective boundary layers at gray-zone resolutions. Mon. Weather Rev. 2015, 143, 250–271. [Google Scholar] [CrossRef]
- Wyngaard, J.C. Toward numerical modeling in the “Terra Incognita”. J. Atmos. Sci. 2004, 61, 1816–1826. [Google Scholar] [CrossRef]
- Kessler, E. On the Distribution and Continuity of Water Substance in Atmospheric Circulations; American Meteorological Society: Boston, MA, USA, 1969; pp. 1–84. [Google Scholar]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the aer radiative transfer models. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Dudhia, J.; González-Rouco, J.F.; Navarro, J.; Montávez, J.P.; García-Bustamante, E. A revised scheme for the WRF surface layer formulation. Mon. Weather Rev. 2012, 140, 898–918. [Google Scholar] [CrossRef] [Green Version]
- Dudhia, J. A Multi-Layer Soil Temperature Model for MM5. In Proceedings of the Preprints, the Sixth PSU/NCAR Mesoscale Model Users’ Workshop, Bouilder, CO, USA, 22–24 July 1996; pp. 22–24. [Google Scholar]









| Parameters | Tephra2 | Tephra2PY | Tephra4D |
|---|---|---|---|
| Δhx (km) | - | - | ≈0.3 |
| Δt (min) | - | - | 10 |
| Continuity of σ at t = FTT | - | Equation (4) | Equation (4) |
| Plume bending | - | - | Equations (7) and (8) |
| vt distribution | Calculated from d | Directly substituted | Directly substituted |
| Wind below vent | Equation (10) | Equation (10) | Same as above vent (WRF) |
| ρa (h) | Equation (11) | Equation (11) | WRF |
| Settling velocity | [17] | [17] | Equation (15) |
| TSP | Equation (20) | Equations (17)–(20) | Equations (17)–(20) |
| Language | C | Python3 | Python3 |
| Symbol | Definition |
|---|---|
| z = z0, z1 | The lower and the higher surface of the hexahedron. |
| A(x10, y10, z0), B(x11, y11, z0),C(x00, y00, z0), D(x01, y01, z0) | The coordinate of vertices of the lower surface. |
| (xn, yn, zn) | The coordinate of a particle inside a hexahedron. |
| (un, vn, wn) | The wind vector in the hexahedron. |
| vtn | The terminal velocity of the particle. |
| tn | Time to start. |
| Δtx, Δty, Δt𝑧 | Time for the particle to reach the interface almost vertical to the x-, y-, and z-axis. |
| id | Eruption Start | Plume Height (m agl) | Direction | Stations | Detected Sites | Ejecta (t) |
|---|---|---|---|---|---|---|
| L | 2018/6/16 7:19 | 4700 | W | 12 | 4 | 22,000 |
| M1 | 2018/5/29 3:34 | 2500 | T | 11 | 5 | 8100 |
| M2 | 2018/6/9 21:27 | 2500 | T | 12 | 6 | 10,100 |
| S | 2018/11/27 9:01 | 1500 | NE | 12 | 5 | 3200 |
| Parameters | Tephra2PY | Tephra4D |
|---|---|---|
| Δhz (km) | 0.1 | 0.1 |
| hvent (m asl) | 1000 | 1000 |
| ρa(0) (kg/m3) | 1.205 | 1.205 |
| K, C (m2/s, m2/s2.5) | 100, 1.2 × 10−3 | 100, 1.2 × 10−3 |
| FTT (s) | 3600 | 3600 |
| ηa (Pa s) | 1.8 × 10−5 | 1.8 × 10−5 |
| 0–0.8 m/s | 0.8–2.4 m/s | 2.4–7.2 m/s | 7.2–22.4 m/s | |
|---|---|---|---|---|
| N > 0 | 78 | 96 | 75 | 15 |
| N’ > 0 (Tephra2PY) | 16 | 96 | 59 | 12 |
| N’ > 0 (Tephra4D) | 58 | 96 | 43 | 3 |
| Observation/Model | L | M1 | M2 | S |
|---|---|---|---|---|
| Disdrometer | 0.15–7.6 | 0.25–4.4 | 0.05–12 | 0.35–3.8 |
| Tephra2PY | 0.85–7.6 | 0.65–3 | 0.45–12 | 0.75–3 |
| Tephra4D | 0.35–7.6 | 0.45–2.6 | 0.15–4.4 | 0.35–2.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takishita, K.; Poulidis, A.P.; Iguchi, M. Tephra4D: A Python-Based Model for High-Resolution Tephra Transport and Deposition Simulations—Applications at Sakurajima Volcano, Japan. Atmosphere 2021, 12, 331. https://doi.org/10.3390/atmos12030331
Takishita K, Poulidis AP, Iguchi M. Tephra4D: A Python-Based Model for High-Resolution Tephra Transport and Deposition Simulations—Applications at Sakurajima Volcano, Japan. Atmosphere. 2021; 12(3):331. https://doi.org/10.3390/atmos12030331
Chicago/Turabian StyleTakishita, Kosei, Alexandros P. Poulidis, and Masato Iguchi. 2021. "Tephra4D: A Python-Based Model for High-Resolution Tephra Transport and Deposition Simulations—Applications at Sakurajima Volcano, Japan" Atmosphere 12, no. 3: 331. https://doi.org/10.3390/atmos12030331
APA StyleTakishita, K., Poulidis, A. P., & Iguchi, M. (2021). Tephra4D: A Python-Based Model for High-Resolution Tephra Transport and Deposition Simulations—Applications at Sakurajima Volcano, Japan. Atmosphere, 12(3), 331. https://doi.org/10.3390/atmos12030331







