Introducing a New Detailed Long-Term COSMO-CLM Hindcast for the Russian Arctic and the First Results of Its Evaluation
Abstract
:1. Introduction
2. Data and Methods
2.1. Model Description
2.2. Experimental Design
2.2.1. Model Setup
2.2.2. Final Long-Term Experiments Scheme
3. Results
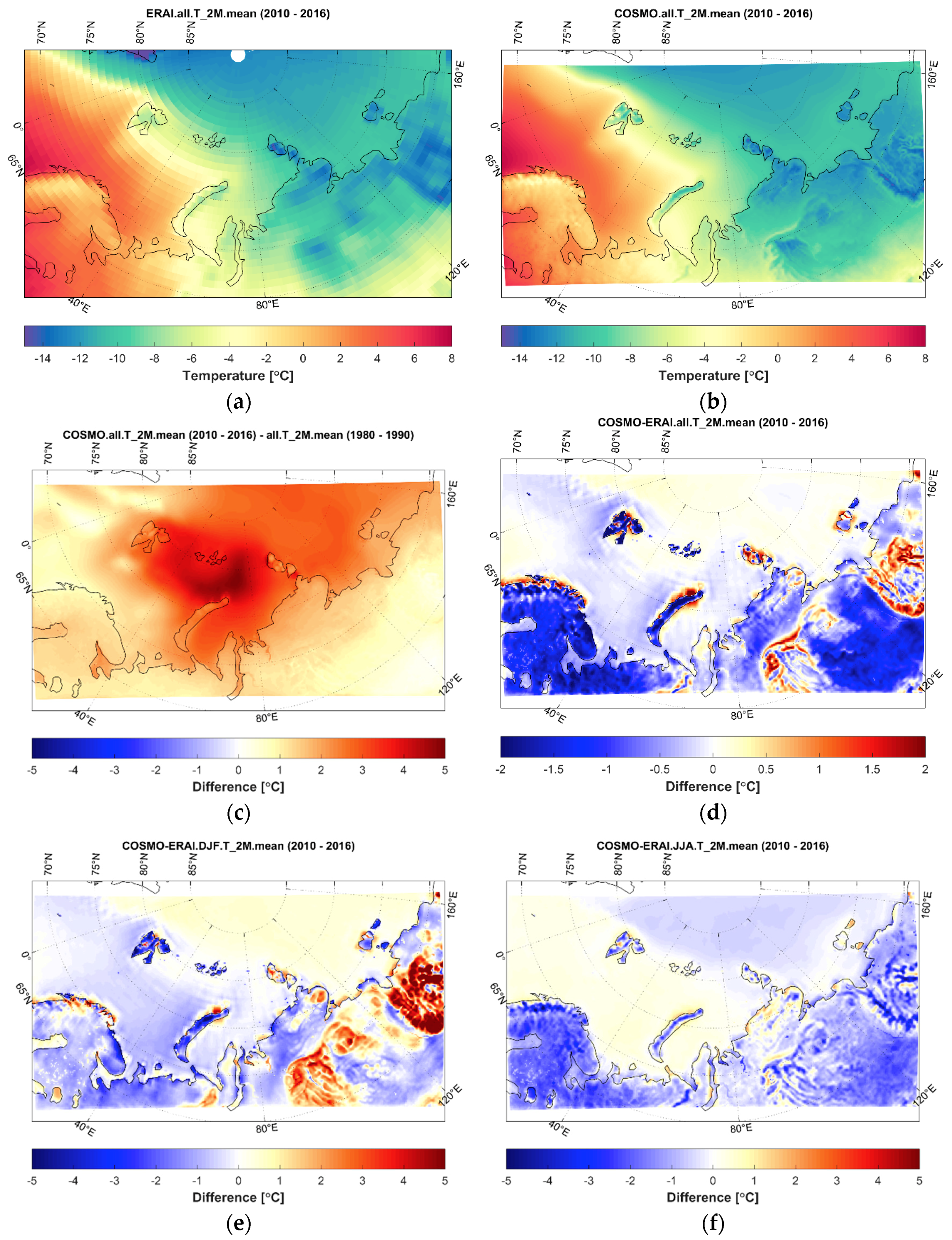
3.1. Long-Term Dataset
3.2. Added Value of the COSMO-CLM Hindcast
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Experiment Acronym | Model Version | Forcing Data | Spin Up | Spectral Nudging | Turbulence Scheme Correction (tkhmin = tkmmin = 0.1) |
|---|---|---|---|---|---|
| COSMO_erai | 5.0 | ERA-Interim | No | No | Standard |
| COSMO_erai_long | 5.0 | ERA-Interim | Yes | No | Standard |
| COSMO_era5 | 5.0 | ERA5 | No | Yes | Standard |
| COSMO_erai_sn | 5.0 | ERA-Interim | No | Yes | Standard |
| COSMO_era5_sn | 5.0 | ERA5 | No | Yes | Standard |
| COSMO_erai_turb | 5.0 | ERA-Interim | No | No | Corrected |
| COSMO_era5_turb | 5.0 | ERA5 | No | Yes | Corrected |
| COSMO_erai_turb_sn | 5.0 | ERA-Interim | No | Yes | Corrected |
| COSMO_erai_turb_sn_long | 5.0 | ERA-Interim | Yes | Yes | Corrected |
| COSMO_era5_turb_sn | 5.0 | ERA5 | No | Yes | Corrected |
| COSMO_era5_sn_v505 | 5.05 | ERA5 | No | Yes | Standard |
| COSMO_erai_sn_v505 | 5.05 | ERA-Interim | No | Yes | Standard |
| COSMO_erai_v505_long | 5.05 | ERA-Interim | Yes | No | Standard |
| COSMO_erai_sn_v505_long | 5.05 | ERA-Interim | No | No | Standard |
Appendix B
| Variable Acronyms | Variable Full Names | Dimensions (2D—Surface/3D—Model Levels) |
|---|---|---|
| U, V, W, T, FI, TKE, POT_VORTIC, H_SNOW, RHO_SNOW, W_SNOW, RELHUM, QV | Zonal, meridional, and vertical velocities, temperature, geopotential, turbulence kinetic energy, Ertel potential vorticity, snow height, density, water content, relative and specific humidity | 3D |
| U_10M, V_10M, VMAX_10M, VABSMX_10M | Zonal, meridional, maximal velocities, and wind gusts on 10 m | 2D |
| T_2M, TMAX_2M, TMIN_2M, TD_2M, TWATER | 2 m temperature, maximal and minimal, 2 m dew point, water temperature | 2D |
| PMSL, HPBL | Sea level pressure, planetary boundary layer height | 2D |
| T_S, T_SNOW, T_SO, T_ICE | Surface, snow, soil, ice temperatures | 2D |
| TQC, TQI, TQR, TQS, TQG, TQV, | Vertical integrated cloud water, ice, rain, snow, graupel, precipitable water, total water content | 2D |
| CLCM, CLCH, CLCL, CLCT, CLDEPTH | Medium, high, low, total, convective cloud cover, cloud depth | 2D |
| CLC_CON | Convective cloud area fraction | 3D |
| LHFL_S, SHFL_S | Latent and sensible heat fluxes | 2D |
| SWDIRS_RAD, SWDIFDS_RAD, THDS_RAD, THUS_RAD, SOBS_RAD, THBS_RAD, SWDIFUS_RAD, ALB_RAD | Surface radiation components: shortwave direct and diffuse, longwave downward and upward, net shortwave and longwave radiation, reflected, albedo | 2D |
| RELHUM_2M, QV_2M | Relative and specific humidity at 2 m | 2D |
| FRESHSNW, SNOW_MELT | Freshness of snow, snow melt | 2D |
| TOT_PREC, SNOW_CON, SNOW_GSP, RAIN_CON, RAIN_GSP, RUNOFF_S, RUNOFF_G | Total precipitation, convective and grid-scale snow, convective and grid-scale rain, surface and subsurface runoff | 2D |
| CAPE_MU, CIN_MU, CAPE_ML, CIN_ML | Convective Available Potential Energy (CAPE) and Convective Inhibition (CIN) indexes of most unstable (MU) parcel, and mean surface layer parcel (ML) | 2D |
Appendix C
References
- Stocker, T.F.; Qin, D.; Plattner, G.-K.; Tignor, M.M.B.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M.; et al. Climate Change 2013: The Physical Science Basis; Contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 1535. [Google Scholar]
- Johannessen, O.M.; Kuzmina, S.; Bobylev, L.P.; Miles, M.W. Surface air temperature variability and trends in the Arctic: New amplification assessment and regionalization. Tellus 2016, 68A, 28234. [Google Scholar] [CrossRef] [Green Version]
- Walsh, J.E. Intensified warming of the Arctic: Causes and impacts on middle latitudes. Glob. Plan. Chang. 2014, 117, 52–63. [Google Scholar] [CrossRef]
- Mori, M.; Watanabe, M.; Shiogama, H.; Inoue, J.; Kimoto, M. Robust Arctic sea-ice influence on the frequent Eurasian cold winters in past decades. Nat. Geosci. 2014, 7, 869–873. [Google Scholar] [CrossRef]
- Overland, J.; Francis, J.A.; Hall, R.; Hanna, E.; Kim, S.J.; Vihma, T. The melting Arctic and midlatitude weather patterns: Are they connected? J. Clim. 2015, 28, 7917–7932. [Google Scholar] [CrossRef] [Green Version]
- Vihma, T. Effects of Arctic sea ice decline on weather and climate: A review. Surv. Geophys. 2014, 35, 1175–1214. [Google Scholar] [CrossRef] [Green Version]
- Bekryaev, R.V.; Polyakov, I.V.; Alexeev, V.A. Role of polar amplification in long-term surface air temperature variations and modern Arctic warming. J. Clim. 2010, 23, 3888–3906. [Google Scholar] [CrossRef]
- Barnes, E.A. Revisiting the evidence linking Arctic amplification to extreme weather in midlatitudes. Geophys. Res. Lett. 2013, 40, 4734–4739. [Google Scholar] [CrossRef]
- Ivanov, V.; Alexeev, V.A.; Koldunov, N.V.; Repina, I.A.; Sandø, A.B.; Smedsrud, L.H.; Smirnov, A. Is the “Atlantification” of the Arctic Ocean extending? In AGU Fall Meeting Abstracts; AGU: San Francisco, CA, USA, 2015; p. GC11G-1092. [Google Scholar]
- Orlanski, I. A rational subdivision of scales for atmospheric processes. Bull. Am. Meteorol. Soc. 1975, 56, 527–530. [Google Scholar]
- Vihma, T.; Pirazzini, R.; Fer, I.; Renfrew, I.A.; Sedlar, J.; Tjernstrom, M.; Lüpkes, C.; Nygård, T.; Notz, D.; Weiss, J.; et al. Advances in understanding and parameterization of small-scale physical processes in the marine Arctic climate system: A review. Atmos. Chem. Phys. 2014, 14, 9403–9450. [Google Scholar] [CrossRef] [Green Version]
- Tjernström, M.; Mauritsen, T. Mesoscale Variability in the Summer Arctic Boundary Layer. Bound. Layer Meteorol. 2009, 130, 383–406. [Google Scholar] [CrossRef]
- Ivanov, V.; Smirnov, A.; Alexeev, V.; Koldunov, N.; Repina, I.; Semenov, V. Contribution of convection-induced heat flux to winter ice decay in the western Nansen Basin. J. Geophys. Res. 2018, 123, C013995. [Google Scholar] [CrossRef]
- Stoll, P.J.; Graversen, R.G.; Noer, G.; Hodges, K. An objective global climatology of polar lows based on reanalysis data. Q. J. R. Meteorol. Soc. 2018, 144, 2099–2117. [Google Scholar] [CrossRef] [Green Version]
- Shestakova, A.A. Novaya Zemlya bora: The lee characteristics and the oncoming flow’s structure. Arct. Antarct. 2016, 2, 11–22. (In Russian) [Google Scholar] [CrossRef]
- Moore, G.W.K.; Renfrew, I.A. Tip jets and barrier winds: A QuikSCAT climatology of high wind speed events around Greenland. J. Clim. 2005, 18, 3713–3725. [Google Scholar] [CrossRef]
- Knol, M.; Arbo, P.; Duske, P.; Gerland, S.; Lamers, M.; Pavlova, O.; Doksæter Sivle, A.; Tronstad, S. Making the Arctic predictable: The changing information infrastructure of Arctic weather and sea ice services. Polar Geogr. 2018, 41. [Google Scholar] [CrossRef] [Green Version]
- Ludwig, V.; Spreen, G.; Pedersen, L.T. Evaluation of a New Merged Sea-Ice Concentration Dataset at 1 km Resolution from Thermal Infrared and Passive Microwave Satellite Data in the Arctic. Remote Sens. 2020, 12, 3183. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef] [Green Version]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef] [PubMed]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Pan, H.-L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP climate forecast system reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015. [Google Scholar] [CrossRef]
- Bromwich, D.; Kuo, Y.H.; Serreze, M.; Walsh, J.; Bai, L.S.; Barlage, M.; Hines, K.; Slater, A. Arctic system reanalysis: Call for community involvement. Eos Trans. AGU 2010, 91, 13–14. [Google Scholar] [CrossRef] [Green Version]
- Bromwich, D.; Wilson, A.B.; Bai, L.; Liu, Z.; Barlage, M.; Shih, C.-F.; Maldonado, S.; Hines, K.M.; Wang, S.-H.; Woollen, J.; et al. The Arctic System Reanalysis, Version 2. Bull. Am. Meteorol. Soc. 2018, 99, 805–828. [Google Scholar] [CrossRef]
- Hines, K.M.; Bromwich, D.H. Development and testing of Polar WRF. Part I: Greenland ice sheet meteorology. Mon. Weather Rev. 2008, 136, 1971–1989. [Google Scholar] [CrossRef] [Green Version]
- Varentsov, M.I.; Verezemskaya, P.S.; Zabolotskikh, E.V.; Repina, I.A. Quality estimation of polar lows reproduction based on reanalysis data and regional climate modelling. Sovrem. Probl. Distantsionnogo Zondirovaniya Zemli iz Kosm. 2016, 13, 168–191. [Google Scholar] [CrossRef]
- Sedlar, J.; Tjernström, M.; Rinke, A.; Orr, A.; Cassano, J.; Fettweis, X.; Heinemann, G.; Seefeldt, M.; Solomon, A.; Matthes, H.; et al. Confronting Arctic troposphere, clouds, and surface energy budget representations regional climate models with observations. J. Geophys. Res. 2020, 124. [Google Scholar] [CrossRef]
- Akperov, M.; Rinke, A.; Mokhov, I.; Matthes, H.; Semenov, V.; Adakudlu, M.; Cassano, J.; Christensen, J.; Dembitskaya, M.; Dethloff, K.; et al. Cyclone activity in the Arctic from an ensemble of regional climate models (Arctic CORDEX). J. Geophys. Res. Atm. 2018, 123, 2537–2554. [Google Scholar] [CrossRef]
- Zhou, X.; Matthes, H.; Rinke, A.; Huang, B.; Yang, K.; Dethloff, K. Simulating Arctic 2-m air temperature and its linear trends using the HIRHAM5 regional climate model. Atmos. Res. 2019, 217, 137–149. [Google Scholar] [CrossRef]
- Gutjahr, O.; Heinemann, G. A model-based comparison of extreme winds in the Arctic and around Greenland. Int. J. Climatol. 2018, 38, 5272–5292. [Google Scholar] [CrossRef] [Green Version]
- Kohnemann, S.H.E.; Heinemann, G.; Bromwich, D.H.; Gutjahr, O. Extreme Warming in the Kara Sea and Barents Sea during the Winter Period 2000–16. J. Clim. 2017, 30, 8913–8927. [Google Scholar] [CrossRef]
- Cohen, J.; Pfeiffer, K.; Francis, J.A. Warm Arctic episodes linked with increased frequency of extreme winter weather in the United States. Nat. Commun. 2018, 9, 1–12. [Google Scholar] [CrossRef]
- Hansen, B.B.; Isaksen, K.; Benestad, R.E.; Kohler, J.; Pedersen, Å.Ø.; Loe, L.E.; Coulson, S.J.; Larsen, J.O.; Varpe, Ø. Warmer and wetter winters: Characteristics and implications of an extreme weather event in the High Arctic. Environ. Res. Lett. 2014, 9, 114021. [Google Scholar] [CrossRef]
- Information about CLM-Community. Available online: https://wiki.coast.hzg.de/clmcom (accessed on 25 October 2020).
- Böhm, U.; Kücken, M.; Ahrens, W.; Block, A.; Hauffe, D.; Keuler, K.; Rockel, B.; Will, A. CLM—The Climate Version of LM: Brief Description and Long-Term Applications. COSMO Newsl. 2006, 6, 225–235. [Google Scholar]
- Rockel, B.; Geyer, B. The performance of the regional climate model CLM in different climate regions, based on the example of precipitation. Meteorol. Z. 2008, 17, 487–498. [Google Scholar] [CrossRef]
- Arakawa, A.; Lamb, V.R. Computational design of the basic dynamical processes of the UCLA general circulation model. Methods Comput. Phys. 1977, 17, 173–265. [Google Scholar]
- Gal-Chen, T.; Somerville, R.C.J. On the use of a coordinate transformation for the solution of the Navier-Stokes equations. J. Comput. Phys. 1975, 17, 209–228. [Google Scholar] [CrossRef]
- Schär, C.; Leuenberger, D.; Fuhrer, O.; Lüthi, D.; Girard, C. A new terrain-following vertical coordinate formulation for atmospheric prediction models. Mon. Weather Rev. 2002, 130, 2459–2480. [Google Scholar] [CrossRef]
- Von Storch, H.; Langenberg, H.; Feser, F. A spectral nudging technique for dynamical downscaling purposes. Mon. Weather Rev. 2000, 128, 3664–3673. [Google Scholar] [CrossRef]
- Feser, F.; Barcikowska, M. The influence of spectral nudging on typhoon formation in regional climate models. Environ. Res. Lett. 2012, 7, 014024. [Google Scholar] [CrossRef]
- Miguez-Macho, G.; Stenchikov, G.L.; Robock, A. Spectral nudging to eliminate the effects of domain position and geometry in regional climate model simulations. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef] [Green Version]
- Ritter, B.; Geleyn, J.F. A comprehensive radiation scheme for numerical weather prediction models with potential applications in climate simulations. Mon. Weather Rev. 1992, 120, 303–325. [Google Scholar] [CrossRef] [Green Version]
- Tiedtke, M. A comprehensive mass flux scheme for cumulus parameterization in large-scale models. Mon. Weather Rev. 1989, 117, 1779–1800. [Google Scholar] [CrossRef] [Green Version]
- Herzog, H.-J.; Vogel, G.; Schubert, U. LLM—A nonhydrostatic model applied to high-resolving simulations of turbulent fluxes over heterogeneous terrain. Theor. Appl. Clim. 2002, 73, 67–86. [Google Scholar] [CrossRef]
- Heise, E.; Ritter, B.; Schrodin, R. Operational implementation of the multilayer soil model. COSMO Tech. Rep. 2006, 9, 19. [Google Scholar]
- Schulz, J.-P.; Vogel, G.; Becker, C.; Kothe, S.; Rummel, U.; Ahrens, B. Evaluation of the ground heat flux simulated by a multi-layer land surface scheme using high quality observations at grass land and bare soil. Meteorol. Z. 2016, 25, 607–620. [Google Scholar] [CrossRef]
- Mironov, D.; Heise, E.; Kourzeneva, E.; Ritter, B.; Schneider, N.; Terzhevik, A. Implementation of the lake parameterisation scheme FLake into the numerical weather prediction model COSMO. Boreal Environ. Res. 2010, 15, 218–230. [Google Scholar]
- Core Documentation of the COSMO Model. Available online: http://www.cosmo-model.org/content/model/documentation/core/default.htm (accessed on 25 October 2020).
- Asensio, H.; Messmer, M.; Lüthi, D.; Osterried, K. External Parameters for Numerical Weather Prediction and Climate Application EXTPAR v5_0. User and Implementation Guide. Available online: http://www.cosmo-model.org/content/support/software/ethz/EXTPAR_user_and_implementation_ manual_202003.pdf (accessed on 16 November 2018).
- Bontemps, S.; Defourny, P.; Van Bogaert, E.; Arino, O.; Kalogirou, V.; Perez, J.R. GLOBCOVER 2009 Products Description and Validation Report. ESA Bull. 2011, 136, 53, hdl:10013/epic.39884.d016. [Google Scholar]
- Silva, N.P.; Camargo, R. Impact of wave number choice in spectral nudging applications during a South Atlantic Convergence Zone event. Front. Earth Sci. 2018, 6, 232. [Google Scholar] [CrossRef] [Green Version]
- Gómez, B.; Miguez-Macho, G. The impact of wave number selection and spin-up time in spectral nudging. Q. J. R. Meteorol. Soc. 2017, 143, 1772–1786. [Google Scholar] [CrossRef]
- Radu, R.; Déqué, M.; Somot, S. Spectral nudging in a spectral regional climate model. Tellus A Dyn. Meteorol. Ocean. 2008, 60, 898–910. [Google Scholar] [CrossRef]
- Kislov, A.V.; Rivin, G.S.; Platonov, V.S.; Varentsov, M.I.; Rozinkina, I.A.; Nikitin, M.A.; Chumakov, M.M. Mesoscale Atmospheric Modeling of Extreme Velocities over the Sea of Okhotsk and Sakhalin. Izv. Atmos. Ocean. Phys. 2018, 54, 322–326. [Google Scholar] [CrossRef]
- Varentsov, M.; Wouters, H.; Platonov, V.; Konstantinov, P. Megacity-Induced Mesoclimatic Effects in the Lower Atmosphere: A Modeling Study for Multiple Summers over Moscow, Russia. Atmosphere 2018, 9, 50. [Google Scholar] [CrossRef] [Green Version]
- Zängl, G.; Reinert, D.; Rípodas, P.; Baldauf, M. The ICON (ICOsahedral Non-hydrostatic) modelling framework of DWD and MPI-M: Description of the non-hydrostatic dynamical core. Q. J. R. Meteorol. Soc. 2015, 141, 563–579. [Google Scholar] [CrossRef]
- Giorgetta, M.A.; Brokopf, R.; Crueger, T.; Esch, M.; Fiedler, S.; Helmert, J.; Hohenegger, C.; Kornblueh, L.; Köhler, M.; Manzini, E.; et al. ICON-A, the Atmosphere Component of the ICON Earth System Model: I. Model Description. J. Adv. Model. Earth Syst. 2018, 10, 1613–1637. [Google Scholar] [CrossRef]
- Neske, S. Towards an improved Turbulence Closure Scheme by analyzing ICON Model Simulations. Ph.D. Thesis, Universität Köln, Köln, Germany, 2017. [Google Scholar]
- Rivin, G.S.; Rozinkina, I.A.; Vil’fand, R.M.; Kiktev, D.B.; Tudrii, K.O.; Blinov, D.V.; Varentsov, M.I.; Zakharchenko, D.I.; Samsonov, T.E.; Repina, I.A.; et al. Development of the High-Resolution Operational System for Numerical Prediction of Weather and Severe Weather Events for the Moscow Region. Russ. Meteorol. Hydrol. 2020, 45, 455–465. [Google Scholar] [CrossRef]
- Garbero, V.; Milelli, M.; Bucchignani, E.; Mercogliano, P.; Varentsov, M.; Rozinkina, I.; Rivin, G.; Blinov, D.; Wouters, H.; Schulz, J.-P.; et al. Evaluating the Urban Canopy Scheme TERRA_URB in the COSMO Model for Selected European Cities. Atmosphere 2021, 12, 237. [Google Scholar] [CrossRef]
- Different Configurations for the COSMO-ICON Physics. Available online: http://www.cosmo-model.org/content/model/releases/cosmo-icon-physics.htm (accessed on 15 January 2021).
- Heinemann, G. Assessment of regional climate model simulations of the katabatic boundary layer structure over Greenland. Atmosphere 2020, 11, 571. [Google Scholar] [CrossRef]
- Cerenzia, I.; Tampieri, F.; Tesini, M.S. Diagnosis of Turbulence Schema in Stable Atmospheric Conditions and Sensitivity Tests. COSMO Newsl. 2014, 14, 28–36. [Google Scholar]
- Platonov, V.; Varentsov, M. Creation of the long-term high-resolution hydrometeorological archive for Russian Arctic: Methodology and first results. IOP Conf. Series Earth Environ. Sci. 2019, 386. [Google Scholar] [CrossRef]
- Cerenzia, I. Challenges and Critical Aspects in Stable Boundary Layer Representation in Numerical Weather Prediction Modeling: Diagnostic Analyses and Proposals for Improvement. Dottorato di ricerca in Geofisica, 29 Ciclo. Alma Mater. Studiorum Univ. Bologna 2017. [Google Scholar] [CrossRef]
- Buzzi, M.; Rotach, M.W.; Holtslag, M.; Holtslag, A.A.M. Evaluation of the COSMO-SC turbulence scheme in a shear-driven stable boundary layer. Meteorol. Z. 2011, 20, 335–350. [Google Scholar] [CrossRef]
- Kislov, A.V.; Varentsov, M.I.; Tarasova, L.L. Role of spring soil moisture in the formation of large-scale droughts in the East European Plain in 2002 and 2010. Izv. Atmos. Ocean. Phys. 2015, 51, 405–411. [Google Scholar] [CrossRef]
- Schlemmer, L.; Schär, C.; Lüthi, D.; Strebel, L. A Groundwater and Runoff Formulation for Weather and Climate Models. J. Adv. Model. Earth Syst. 2018, 10, 1809–1832. [Google Scholar] [CrossRef]
- Voevodin, V.; Antonov, A.; Nikitenko, D.; Shvets, P.; Sobolev, S.; Sidorov, I.; Stefanov, K.; Voevodin, V.; Zhumatiy, S. Supercomputer Lomonosov-2: Large Scale, Deep Monitoring and Fine Analytics for the User Community. Supercomp. Front. Innov. 2019, 6, 4–11. [Google Scholar] [CrossRef] [Green Version]
- Platonov, V.; Varentsov, M. Russian Arctic COSMO-CLM hindcast over 1980–2016 period. figshare. Collection 2020. [Google Scholar] [CrossRef]
- Davies, H.C. A lateral boundary formulation for multi-level prediction models. Q. J. R. Meteorol. Soc. 1976, 102, 405–418. [Google Scholar] [CrossRef]
- Doms, G. A Description of the Nonhydrostatic Regional COSMO-Model. Part I: Dynamics and Numerics; Deutscher Wetterdienst: Offenbach, Germany, 2011; p. 147. [Google Scholar]
- Paeth, H.; Mannig, B. On the added value of regional climate modeling in climate change assessment. Clim. Dyn. 2013, 41, 1057–1066. [Google Scholar] [CrossRef]
- Lenz, C.J.; Früh, B.; Adalatpanah, F.D. Is there potential added value in COSMO–CLM forced by ERA reanalysis data? Clim. Dyn. 2017, 49, 4061–4074. [Google Scholar] [CrossRef] [Green Version]
- Souverijns, N.; Gossart, A.; Demuzere, M.; Lenaerts, J.T.M.; Medley, B.; Gorodetskaya, I.V.; Vanden Broucke, S.; van Lipzig, N.P.M. A New Regional Climate Model for POLAR-CORDEX: Evaluation of a 30-Year Hindcast with COSMO-CLM2 over Antarctica. J. Geophys. Res. Atm. 2019, 124, 1405–1427. [Google Scholar] [CrossRef] [Green Version]
- Kelemen, F.D.; Primo, C.; Feldmann, H.; Ahrens, B. Added Value of Atmosphere-Ocean Coupling in a Century-Long Regional Climate Simulation. Atmosphere 2019, 10, 537. [Google Scholar] [CrossRef] [Green Version]
- Efimov, V.V.; Komarovskaya, O.I. The Novaya Zemlya bora: Analysis and numerical modeling. Izv. Atm. Ocean. Phys. 2018, 54, 73–85. [Google Scholar] [CrossRef]
- Shestakova, A.A.; Myslenkov, S.A.; Kuznetsova, A.M. Influence of Novaya Zemlya Bora on Sea Waves: Satellite Measurements and Numerical Modeling. Atmosphere 2020, 11, 726. [Google Scholar] [CrossRef]
- Wetzel, C.; Brümmer, B. An Arctic inversion climatology based on the European Centre Reanalysis ERA-40. Meteorol. Z. 2011, 20, 589–600. [Google Scholar] [CrossRef] [PubMed]
- Christakos, K.; Furevik, B.R.; Aarnes, O.J.; Breivik, Ø.; Tuomi, L.; Byrkjedal, Ø. The importance of wind forcing in fjord wave modelling. Ocean Dyn. 2020, 70, 57–75. [Google Scholar] [CrossRef] [Green Version]
- Noer, G.; Saetra, Ø.; Lien, T.; Gusdal, Y. A climatological study of polar lows in the Nordic Seas. Q. J. R. Meteorol. Soc. 2011, 137, 1762–1772. [Google Scholar] [CrossRef]
- Hallerstig, M.; Magnusson, L.; Kolstad, E.W.; Mayer, S. How grid-spacing and convection representation affected the wind speed forecasts of four polar lows. Q. J. R. Meteorol. Soc. 2021, 147, 150–165. [Google Scholar] [CrossRef]
- Smirnova, J.; Golubkin, P. Comparing polar lows in atmospheric reanalyses: Arctic System Reanalysis versus ERA-Interim. Mon. Weather Rev. 2017, 145, 2375–2383. [Google Scholar] [CrossRef]
- Zappa, G.; Shaffrey, L.; Hodges, K. Can polar lows be objectively identified and tracked in the ECMWF operational analysis and the ERA-Interim reanalysis? Mon. Weather Rev. 2014, 142, 2596–2608. [Google Scholar] [CrossRef]
- Orimolade, A.P.; Furevik, B.R.; Noer, G.; Gudmestad, O.T.; Samelson, R.M. Waves in polar lows. J. Geophys. Res. Ocean. 2016, 121, 6470–6481. [Google Scholar] [CrossRef]
- Revokatova, A.; Nikitin, M.; Rivin, G.; Rozinkina, I.; Nikitin, A.; Tatarinovich, E. High-Resolution Simulation of Polar Lows over Norwegian and Barents Seas Using the COSMO-CLM and ICON Models for the 2019–2020 Cold Season. Atmosphere 2021, 12, 137. [Google Scholar] [CrossRef]
- Morice, C.P.; Kennedy, J.J.; Rayner, N.A.; Jones, P.D. Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: The HadCRUT4 dataset. J. Geophys. Res. 2012, 117, D08101. [Google Scholar] [CrossRef]
- Adler, R.F.; Huffman, G.J.; Chang, A.; Ferraro, R.; Xie, P.; Janowiak, J.; Rudolf, B.; Schneider, U.; Curtis, S.; Bolvin, D.; et al. The Version 2 Global Precipitation Climatology Project (GPCP) Monthly Precipitation Analysis (1979-Present). J. Hydrometeor. 2003, 4, 1147–1167. [Google Scholar] [CrossRef]
- Pichel, W.G.; Monaldo, F.M.; Jackson, C.h.R.; Sapper, J.; Hatteberg, R. NOAA high resolution sea surface winds data from Synthetic Aperture Radar (SAR) on the RADARSAT-2 satellite. NOAA National Centers for Environmental Information. Dataset 2015. [Google Scholar] [CrossRef]
- SeaPAC. QuikSCAT Level 2B Ocean Wind Vectors in 12.5km Slice Composites Version 4.0; PO.DAAC: Pasadena, CA, USA, 2018; Ver. 4.0. [Google Scholar] [CrossRef]
- Kummerow, C.; Ferraro, R.; Randel, D. AMSR-E/AMSR2 Unified L2B Global Swath Surface Precipitation, Version 1; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2020. [Google Scholar] [CrossRef]






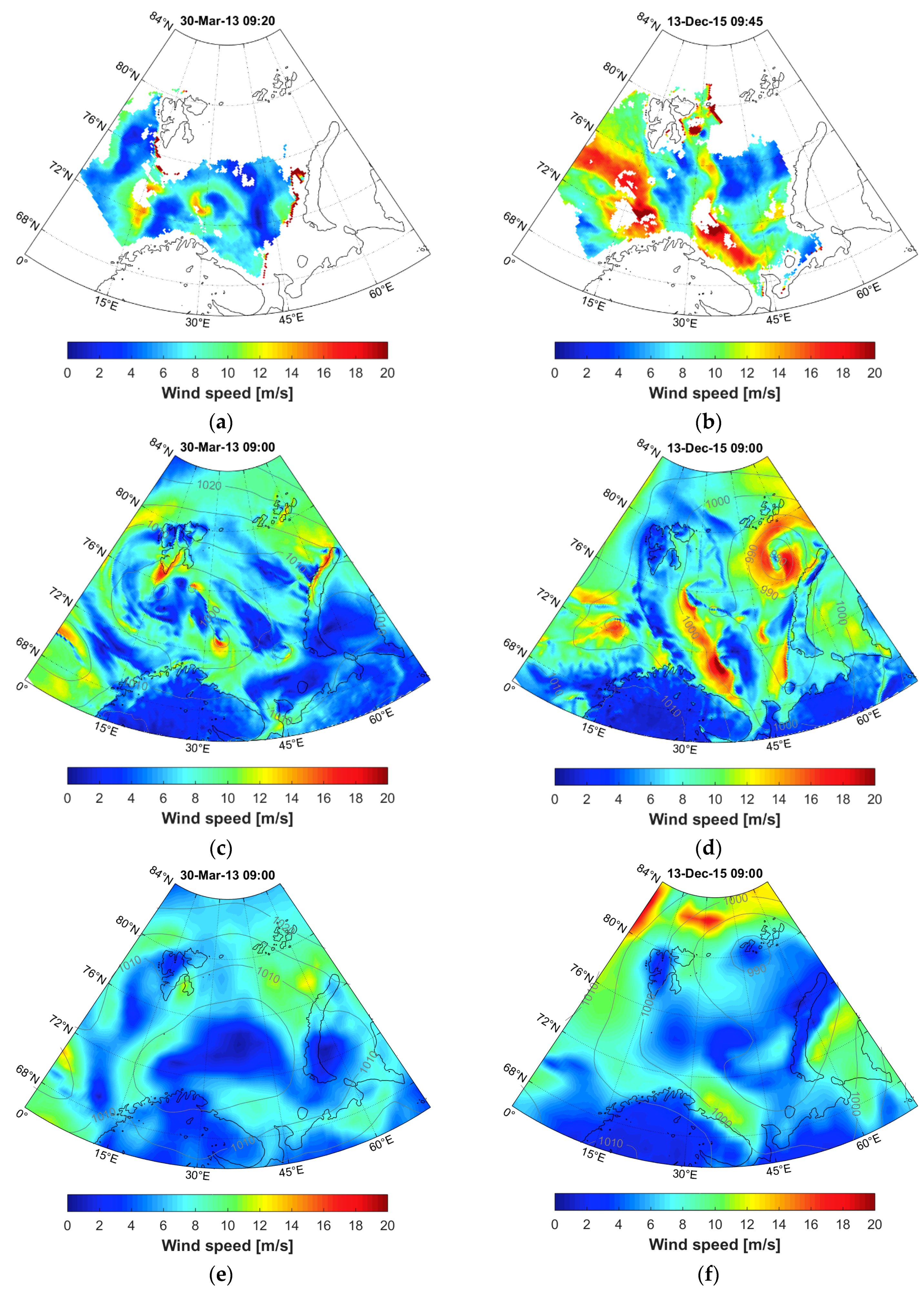
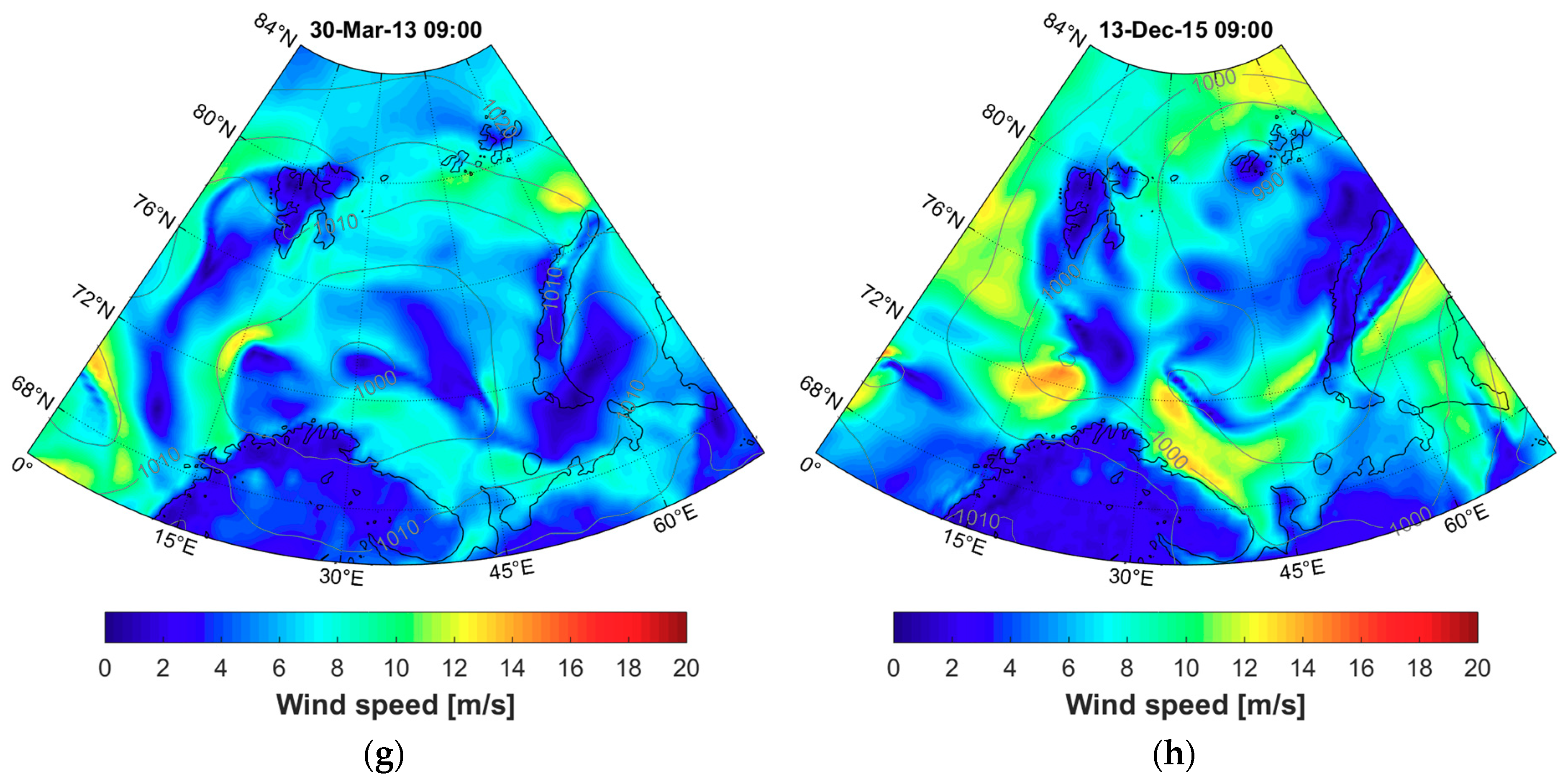
| Model Set Up | December–January 2012–2013 | August–September 2015 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T_2M | V_10M | PMSL | T_2M | V_10M | PMSL | |||||||
| RMSE | R | RMSE | R | RMSE | R | RMSE | R | RMSE | R | RMSE | R | |
| COSMO_erai | 4.22 | 0.76 | 2.30 | 0.55 | 2.98 | 0.96 | 2.38 | 0.77 | 2.02 | 0.65 | 1.87 | 0.99 |
| COSMO_era5 | 4.19 | 0.76 | 2.30 | 0.57 | 2.77 | 0.97 | 2.34 | 0.79 | 2.00 | 0.67 | 1.70 | 0.99 |
| COSMO_erai_sn | 3.69 | 0.83 | 2.12 | 0.65 | 2.01 | 0.99 | 2.89 | 0.79 | 1.89 | 0.70 | 1.53 | 1.00 |
| COSMO_era5_sn | 3.70 | 0.83 | 2.10 | 0.66 | 2.13 | 0.99 | 2.29 | 0.81 | 1.87 | 0.71 | 1.42 | 1.00 |
| COSMO_erai_turb_sn | 3.38 | 0.84 | 2.12 | 0.65 | 2.08 | 0.99 | 2.35 | 0.79 | 1.89 | 0.69 | 1.57 | 1.00 |
| COSMO_era5_turb_sn | 3.37 | 0.85 | 2.09 | 0.66 | 2.18 | 0.99 | 2.35 | 0.81 | 1.88 | 0.70 | 1.45 | 1.00 |
| COSMO_erai_sn_v505 | 3.34 | 0.85 | 2.22 | 0.65 | 1.69 | 0.99 | 2.10 | 0.81 | 1.97 | 0.70 | 1.40 | 1.00 |
| COSMO_era5_sn_v505 | 3.33 | 0.85 | 2.24 | 0.67 | 1.63 | 0.99 | 2.16 | 0.82 | 1.97 | 0.70 | 1.34 | 1.00 |
| Variable, Period | Mean Difference, Whole Domain | Mean Difference, Land Grids | Mean Difference, Sea Grids | First Percentile of Difference, Whole Domain | 99th Percentile of Difference, Whole Domain |
|---|---|---|---|---|---|
| VEL_10M, 1980–1990 | 0.13 | 0.34 | −0.14 | −1.63 | 2.22 |
| VEL_10M, 2010–2016 | 0.14 | 0.37 | −0.13 | −1.63 | 2.19 |
| VEL_10M, 1980–1990 (DJF) | 0.03 | 0.37 | −0.38 | −2.25 | 2.47 |
| VEL_10M, 2010–2016 (DJF) | 0.06 | 0.42 | −0.38 | −2.14 | 2.47 |
| VEL_10M, 1980–1990 (JJA) | 0.23 | 0.24 | 0.23 | −1.06 | 2.15 |
| VEL_10M, 2010–2016 (JJA) | 0.25 | 0.24 | 0.26 | −1.12 | 2.14 |
| T_2M, 1980–1990 | −0.03 | 0.10 | −0.19 | −1.67 | 1.72 |
| T_2M, 2010–2016 | −0.24 | 0.01 | −0.56 | −1.87 | 1.39 |
| T_2M, 1980–1990 (DJF) | 0.30 | 0.16 | 0.48 | −2.18 | 4.81 |
| T_2M, 2010–2016 (DJF) | 0.04 | 0.08 | 0.00 | −2.51 | 4.85 |
| T_2M, 1980–1990 (JJA) | −0.37 | −0.05 | −0.76 | −2.70 | 1.31 |
| T_2M, 2010–2016 (JJA) | −0.42 | −0.07 | −0.85 | −2.61 | 1.14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Platonov, V.; Varentsov, M. Introducing a New Detailed Long-Term COSMO-CLM Hindcast for the Russian Arctic and the First Results of Its Evaluation. Atmosphere 2021, 12, 350. https://doi.org/10.3390/atmos12030350
Platonov V, Varentsov M. Introducing a New Detailed Long-Term COSMO-CLM Hindcast for the Russian Arctic and the First Results of Its Evaluation. Atmosphere. 2021; 12(3):350. https://doi.org/10.3390/atmos12030350
Chicago/Turabian StylePlatonov, Vladimir, and Mikhail Varentsov. 2021. "Introducing a New Detailed Long-Term COSMO-CLM Hindcast for the Russian Arctic and the First Results of Its Evaluation" Atmosphere 12, no. 3: 350. https://doi.org/10.3390/atmos12030350







