Atmosphere Driven Mass-Balance Sensitivity of Halji Glacier, Himalayas
Abstract
:1. Introduction
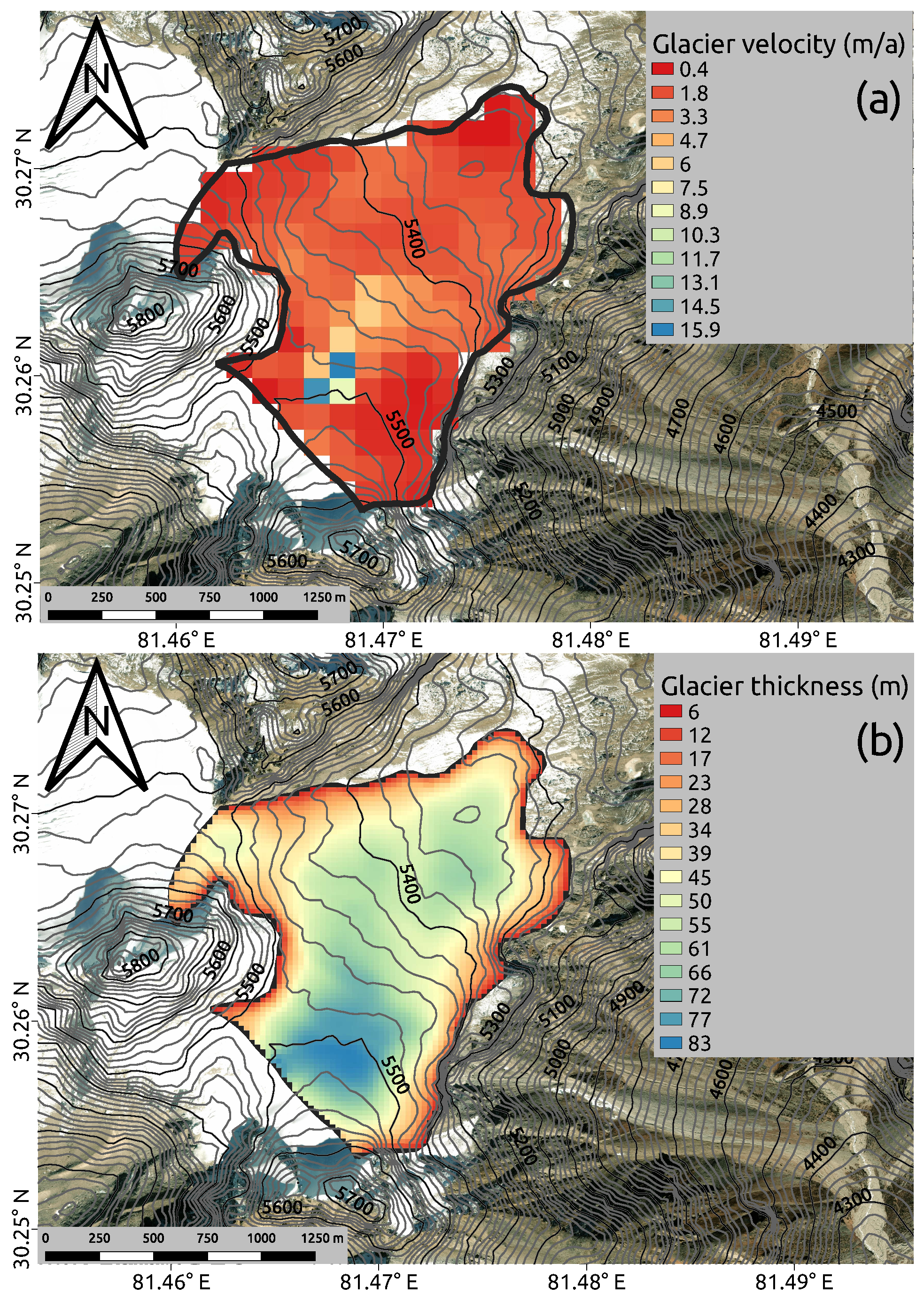
2. Halji Glacier

3. Data and Methods
3.1. COSIPY
3.2. Climate Forcing Model Input
3.2.1. Automatic Weather Station Measurements
3.2.2. Downscaling ERA5-L
3.2.3. Comparison of Downscaled ERA5-L to Automatic Weather Station Measurements
3.3. COSIPY Simulations
3.4. Sensitivity Studies and Large Scale Teleconnections
4. Results
4.1. Sensitivity to Climate Forcing Input Variables
4.2. Temperature and Total Precipitation Perturbations and Seasonal Sensitivity Characteristic
4.3. Index Correlations
5. Discussion
5.1. Uncertainties
5.1.1. Forcing Data Uncertainties
5.1.2. COSIPY Simulation Uncertainties
5.2. Glacier-Wide Climatic Mass Balance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AMI | Australian Monsoon Index |
| AMO | Atlantic Multi-decadal Oscillation |
| AO | Arctic Oscillation index |
| AWS | automatic weather station |
| COSIPY | COupled Snowpack and Ice surface energy and mass balance model in PYthon |
| DEM | digital elevation model |
| EA | East Atlantic index |
| EATL/WRUS | East Atlantic/West Russia index |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| ERA5 | ECMWF Reanalysis fifth generation |
| ERA5-L | ECMWF Reanalysis fifth generation-Land |
| GDAL | Geospatial Data Abstraction Library |
| GGP | glacier grid point |
| GLOF | glacial lake outburst flood |
| H-TESSEL | Hydrology revised Tiled ECMWF Scheme for Surface Exchanges over Land |
| HMA | High Mountain Asia |
| HPCC | High-Performance Computing Cluster |
| IOD | Indian Ocean Dipol index |
| ISM | Indian Summer Monsoon index |
| MB | mass balance |
| MB-year | mass-balance year |
| MBE | mean bias error |
| MEI | Multivariate ENSO Index |
| NAO | North Atlantic Oscillation |
| Nino1+2 | Nino 1+2 index |
| Nino34 | Nino 3.4 index |
| Nino4 | Nino 4 index |
| ONI | Oceanic Nino Index |
| PDO | Pacific Decadal Oscillation |
| PNA | Pacific/North American index |
| POL | Polar/Eurasia index |
| RGI6 | Randolph Glacier Inventory 6.0 |
| RMSE | root mean square error |
| SCAND | Scandinavia index |
| SEB | surface energy balance |
| SOI | Southern Oscillation Index |
| SRTM | Shuttle Radar Topography Mission |
| SSC | seasonal sensitivity characteristic |
| TNI | Trans-Niño Index |
| WNPM | Western North Pacific Monsoon index |
| WP | West Pacific index |
| WYM | Webster and Yang Monsoon index |
| Symbol | Description | Unit | Default Value |
| M | average molar mass of air | mol−1 | 0.02897 |
| R | gas constant | kg m (s mol K) | 8.314462 |
| melting point temperature | 273.16 | ||
| g | gravitational acceleration | −2 | 9.80665 |
| Symbol | Description | Unit |
| annual glacier-wide climatic mass balance | ||
| glacier-wide cumulative climatic mass balance | ||
| glacier-wide climatic mass balance | ||
| latent heat flux | W m−2 | |
| glacier heat flux | W m−2 | |
| sensible heat flux | W m−2 | |
| available melt energy | W m−2 | |
| sensible heat flux of rain | W m−2 | |
| incoming longwave radiation | W m−2 | |
| net longwave radiation | W m−2 | |
| outgoing longwave radiation | W m−2 | |
| incoming shortwave radiation | W m−2 | |
| net shortwave radiation | W m−2 | |
| relative humidity at 2 | % | |
| accumulated snowfall | ||
| specific humidity at 2 | −1 | |
| total precipitation | ||
| air temperature at reference height | ||
| layer temperature | ||
| surface temperature | ||
| air temperature at 2 | ||
| dewpoint temperature at 2 | ||
| wind speed at 2 | −1 | |
| wind speed at 10 | −1 | |
| snow/ice albedo | - | |
| internal ablation | ||
| surface ablation | ||
| a | thermal gradient | −1 |
| annual climatic mass balance | ||
| cumulative climatic mass balance | ||
| climatic mass balance | ||
| internal mass balance | ||
| surface mass balance | ||
| internal accumulation | ||
| surface accumulation | ||
| h | height difference | |
| atmospheric pressure at reference height | ||
| surface pressure | ||
| p-value | p-value | - |
| coefficient of determination | - | |
| Spearman’s rank correlation coefficient | - | |
| surface roughness |
Appendix A


| Index | Description | Temporal Resolution and Coverage |
|---|---|---|
| AMI [109] | Australian Monsoon Index | Seasonal (DJF), 1948–2014 |
| http://apdrc.soest.hawaii.edu/projects/monsoon/seasonal-monidx.html, accessed on 22 March 2021 | ||
| AMO [110] | Atlantic Multi-decadal Oscillation | Annual, 1870–2010 |
| https://climatedataguide.ucar.edu/climate-data/atlantic-multi-decadal-oscillation-amo, accessed on 22 March 2021 | ||
| AO [111] | Arctic Oscillation index | Monthly, January 1950–April 2020 |
| https://www.cpc.ncep.noaa.gov/products/precip/CWlink/daily_ao_index/ao.shtml, accessed on 22 March 2021 | ||
| EA [80] | East Atlantic index | Monthly, January 1950–April 2020 |
| https://www.cpc.ncep.noaa.gov/data/teledoc/ea.shtml, accessed on 22 March 2021 | ||
| EATL/WRUS [80] | East Atlantic/West Russia index | Monthly, January 1950–April 2020 |
| https://www.cpc.ncep.noaa.gov/data/teledoc/eawruss.shtml, accessed on 22 March 2021 | ||
| IOD [112] | Indian Ocean Dipol index | Monthly, January 1870–December 2018 |
| http://www.bom.gov.au/climate/enso/indices/about.shtml, accessed on 22 March 2021 | ||
| ISM [113,114] | Indian Summer Monsoon index | Seasonal (JJAS), 1948–2015 |
| http://apdrc.soest.hawaii.edu/projects/monsoon/seasonal-monidx.html, accessed on 22 March 2021 | ||
| MEI [115] | Multivariate ENSO Index | Monthly, January 1979–December 2019 |
| https://psl.noaa.gov/enso/mei/, accessed on 22 March 2021 | ||
| NAO [116] | North Atlantic Oscillation | Monthly, January 1899–February 2020 |
| https://climatedataguide.ucar.edu/climate-data/hurrell-north-atlantic-oscillation-nao-index-pc-based, accessed on 22 March 2021 | ||
| Nino1+2 [117] | Nino 1+2 index | Monthly, January 1950–June 2020 |
| https://climatedataguide.ucar.edu/climate-data/nino-sst-indices-nino-12-3-34-4-oni-and-tni, accessed on 22 March 2021 | ||
| Nino34 [117] | Nino 3.4 index | Monthly, January 1950–June 2020 |
| https://climatedataguide.ucar.edu/climate-data/nino-sst-indices-nino-12-3-34-4-oni-and-tni, accessed on 22 March 2021 | ||
| Nino4 [117] | Nino 4 index | Monthly, January 1950–June 2020 |
| https://climatedataguide.ucar.edu/climate-data/nino-sst-indices-nino-12-3-34-4-oni-and-tni, accessed on 22 March 2021 | ||
| ONI [117] | Oceanic Nino Index | Monthly, January 1950–May 2020 |
| https://climatedataguide.ucar.edu/climate-data/nino-sst-indices-nino-12-3-34-4-oni-and-tni, accessed on 22 March 2021 | ||
| PDO [118] | Pacific Decadal Oscillation | Monthly, January 1854–February 2020 |
| https://www.ncdc.noaa.gov/teleconnections/pdo/, accessed on 22 March 2021 | ||
| PNA [119] | Pacific/North American index | Monthly, January 1950–April 2020 |
| https://www.cpc.ncep.noaa.gov/data/teledoc/pna.shtml, accessed on 22 March 2021 | ||
| POL [80] | Polar/Eurasia index | Monthly, January 1950–April 2020 |
| https://www.cpc.ncep.noaa.gov/data/teledoc/poleur.shtml, accessed on 22 March 2021 | ||
| SCAND [80] | Scandinavia index | Monthly, January 1950–June 2020 |
| https://www.cpc.ncep.noaa.gov/data/teledoc/scand.shtml, accessed on 22 March 2021 | ||
| SOI [120] | Southern Oscillation Index | Monthly, January 1951–December 2019 |
| https://www.ncdc.noaa.gov/teleconnections/enso/indicators/soi/, accessed on 22 March 2021 | ||
| TNI [117] | Trans-Niño Index | Monthly, January 1948–April 2020 |
| https://climatedataguide.ucar.edu/climate-data/nino-sst-indices-nino-12-3-34-4-oni-and-tni, accessed on 22 March 2021 | ||
| WNPM [113,114] | Western North Pacific Monsoon index | Seasonal (JJAS), 1948–2015 |
| http://apdrc.soest.hawaii.edu/projects/monsoon/seasonal-monidx.html, accessed on 22 March 2021 | ||
| WP [80,119] | West Pacific index | Monthly, January 1950–April 2020 |
| https://www.cpc.ncep.noaa.gov/data/teledoc/wp.shtml, accessed on 22 March 2021 | ||
| WYM [40] | Webster and Yang Monsoon index | Seasonal (JJAS), 1948–2015 |
| http://apdrc.soest.hawaii.edu/projects/monsoon/seasonal-monidx.html, accessed on 22 March 2021 | ||

References
- Bolch, T.; Pieczonka, T.; Benn, D.I. Multi-decadal mass loss of glaciers in the Everest area (Nepal Himalaya) derived from stereo imagery. Cryosphere 2011, 5, 349–358. [Google Scholar] [CrossRef] [Green Version]
- Lei, Y.; Yao, T.; Yi, C.; Wang, W.; Sheng, Y.; Li, J.; Joswiak, D. Glacier mass loss induced the rapid growth of Linggo Co on the central Tibetan Plateau. J. Glaciol. 2012, 58, 177–184. [Google Scholar] [CrossRef] [Green Version]
- Neckel, N.; Kropáček, J.; Bolch, T.; Hochschild, V. Glacier mass changes on the Tibetan Plateau 2003–2009 derived from ICESat laser altimetry measurements. Environ. Res. Lett. 2014, 9, 014009. [Google Scholar] [CrossRef]
- Kang, S.; Wang, F.; Morgenstern, U.; Zhang, Y.; Grigholm, B.; Kaspari, S.; Schwikowski, M.; Ren, J.; Yao, T.; Qin, D.; et al. Dramatic loss of glacier accumulation area on the Tibetan Plateau revealed by ice core tritium and mercury records. Cryosphere 2015, 9, 1213–1222. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Jiang, L.; Jiang, H.; Wang, H.; Ma, N.; Xu, H. Accelerated glacier mass loss (2011–2016) over the Puruogangri ice field in the inner Tibetan Plateau revealed by bistatic InSAR measurements. Remote Sens. Environ. 2019, 231, 111241. [Google Scholar] [CrossRef]
- Liu, L.; Jiang, L.; Zhang, Z.; Wang, H.; Ding, X. Recent Accelerating Glacier Mass Loss of the Geladandong Mountain, Inner Tibetan Plateau, Estimated from ZiYuan-3 and TanDEM-X Measurements. Remote Sens. 2020, 12, 472. [Google Scholar] [CrossRef] [Green Version]
- Shean, D.E.; Bhushan, S.; Montesano, P.; Rounce, D.R.; Arendt, A.; Osmanoglu, B. A Systematic, Regional Assessment of High Mountain Asia Glacier Mass Balance. Front. Earth Sci. 2020, 7, 363. [Google Scholar] [CrossRef] [Green Version]
- Rounce, D.R. Glacier Mass Change in High Mountain Asia Through 2100 Using the Open-Source Python Glacier Evolution Model (PyGEM). Front. Earth Sci. 2020, 7, 20. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Zhang, M.; Wang, B.; Sun, M.; Li, X. Recent changes in daily extremes of temperature and precipitation over the western Tibetan Plateau, 1973–2011. Quat. Int. 2013, 313–314, 110–117. [Google Scholar] [CrossRef]
- Wei, Y.; Fang, Y. Spatio-Temporal Characteristics of GlobalWarming in the Tibetan Plateau during the Last 50 Years Based on a Generalised Temperature Zone—Elevation Model. PLoS ONE 2013, 8, e60044. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schiemann, R.; Lüthi, D.; Schär, C. Seasonality and interannual variability of the westerly jet in the Tibetan Plateau region. J. Clim. 2009, 22, 2940–2957. [Google Scholar] [CrossRef]
- Mölg, T.; Maussion, F.; Scherer, D. Mid-latitude westerlies as a driver of glacier variability in monsoonal High Asia. Nat. Clim. Chang. 2013, 4, 68–73. [Google Scholar] [CrossRef]
- Xu, X.; Zhao, T.; Lu, C.; Guo, Y.; Chen, B.; Liu, R.; Li, Y.; Shi, X. An important mechanism sustaining the atmospheric “water tower” over the Tibetan Plateau. Atmos. Chem. Phys. 2014, 14, 11287–11295. [Google Scholar] [CrossRef] [Green Version]
- Curio, J.; Maussion, F.; Scherer, D. A 12-year high-resolution climatology of atmospheric water transport over the Tibetan Plateau. Earth Syst. Dyn. 2015, 6, 109–124. [Google Scholar] [CrossRef] [Green Version]
- Curio, J.; Scherer, D. Seasonality and spatial variability of dynamic precipitation controls on the Tibetan Plateau. Earth Syst. Dyn. 2016, 7, 767–782. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Lu, M.; Chen, H.; Pan, M.; Hong, Y. Atmospheric moisture transport versus precipitation across the Tibetan Plateau: A mini-review and current challenges. Atmos. Res. 2018, 209, 50–58. [Google Scholar] [CrossRef]
- Li, S.; Yao, T.; Yang, W.; Yu, W.; Zhu, M. Glacier Energy and Mass Balance in the Inland Tibetan Plateau: Seasonal and Interannual Variability in Relation to Atmospheric Changes. J. Geophys. Res. Atmos. 2018, 123, 6390–6409. [Google Scholar] [CrossRef]
- Wang, X.; Pang, G.; Yang, M. Precipitation over the Tibetan Plateau during recent decades: A review based on observations and simulations: PRECIPITATION ON THE TIBETAN PLATEAU. Int. J. Climatol. 2018, 38, 1116–1131. [Google Scholar] [CrossRef]
- Yao, T.; Thompson, L.; Yang, W.; Yu, W.; Gao, Y.; Guo, X.; Yang, X.; Duan, K.; Zhao, H.; Xu, B.; et al. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Chang. 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Gardelle, J.; Berthier, E.; Arnaud, Y.; Kääb, A. Region-wide glacier mass balances over the Pamir-Karakoram-Himalaya during 1999–2011. Cryosphere 2013, 7, 1263–1286. [Google Scholar] [CrossRef] [Green Version]
- Bonekamp, P.N.J.; de Kok, R.J.; Collier, E.; Immerzeel, W.W. Contrasting Meteorological Drivers of the Glacier Mass Balance Between the Karakoram and Central Himalaya. Front. Earth Sci. 2019, 7, 107. [Google Scholar] [CrossRef]
- Farinotti, D.; Huss, M.; Fürst, J.J.; Landmann, J.; Machguth, H.; Maussion, F.; Pandit, A. A consensus estimate for the ice thickness distribution of all glaciers on Earth. Nat. Geosci. 2019, 12, 168–173. [Google Scholar] [CrossRef] [Green Version]
- Ageta, Y.; Higuchi, K. Estimation of Mass Balance Components of a Summer-Accumulation Type Glacier in the Nepal Himalaya. Geogr. Annaler. Ser. A Phys. Geogr. 1984, 66, 249. [Google Scholar] [CrossRef]
- Maussion, F.; Scherer, D.; Mölg, T.; Collier, E.; Curio, J.; Finkelnburg, R. Precipitation Seasonality and Variability over the Tibetan Plateau as Resolved by the High Asia Reanalysis*. J. Clim. 2014, 27, 1910–1927. [Google Scholar] [CrossRef] [Green Version]
- Naito, N. Summer Accumulation Type Glaciers. In Encyclopedia of Snow, Ice and Glaciers; Singh, V.P., Singh, P., Haritashya, U.K., Eds.; Encyclopedia of Earth Sciences Series; Springer: Dordrecht, The Netherlands, 2011; pp. 1107–1108. [Google Scholar] [CrossRef]
- Qu, X.; Hall, A. What Controls the Strength of Snow-Albedo Feedback? J. Clim. 2007, 20, 3971–3981. [Google Scholar] [CrossRef] [Green Version]
- Qu, X.; Hall, A. On the persistent spread in snow-albedo feedback. Clim. Dyn. 2014, 42, 69–81. [Google Scholar] [CrossRef]
- Ghatak, D.; Sinsky, E.; Miller, J. Role of snow-albedo feedback in higher elevation warming over the Himalayas, Tibetan Plateau and Central Asia. Environ. Res. Lett. 2014, 9, 114008. [Google Scholar] [CrossRef]
- Wang, X.; Siegert, F.; Zhou, A.G.; Franke, J. Glacier and glacial lake changes and their relationship in the context of climate change, Central Tibetan Plateau 1972–2010. Glob. Planet. Chang. 2013, 111, 246–257. [Google Scholar] [CrossRef]
- Treichler, D.; Kääb, A.; Salzmann, N.; Xu, C.Y. Recent glacier and lake changes in High Mountain Asia and their relation to precipitation changes. Cryosphere 2019, 13, 2977–3005. [Google Scholar] [CrossRef] [Green Version]
- Haeberli, W. Frequency and Characteristics of Glacier Floods in the Swiss Alps. Ann. Glaciol. 1983, 4, 85–90. [Google Scholar] [CrossRef] [Green Version]
- Björnsson, H. Jökulhlaups in Iceland: Prediction, characteristics and simulation. Ann. Glaciol. 1992, 16, 95–106. [Google Scholar] [CrossRef] [Green Version]
- Huggel, C.; Kääb, A.; Haeberli, W.; Teysseire, P.; Paul, F. Remote sensing based assessment of hazards from glacier lake outbursts: A case study in the Swiss Alps. Can. Geotech. J. 2002, 39, 316–330. [Google Scholar] [CrossRef] [Green Version]
- Veh, G.; Korup, O.; von Specht, S.; Roessner, S.; Walz, A. Unchanged frequency of moraine-dammed glacial lake outburst floods in the Himalaya. Nat. Clim. Chang. 2019, 9, 379–383. [Google Scholar] [CrossRef]
- Wester, P.; Mishra, A.; Mukherji, A.; Shrestha, A.B. (Eds.) The Hindu Kush Himalaya Assessment: Mountains, Climate Change, Sustainability and People; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar] [CrossRef] [Green Version]
- Hovden, A. Who were the sponsors? Reflections on recruitment and ritual economy in three Himalayan village monasteries. In Tibetans Who Escaped the Historians Net: Studies in the Social History of Tibetan Societies; Ram ble, C., Schwieger, P., Travers, A., Eds.; Vajra Publications: Kathmandu, Nepal, 2013; pp. 209–230. [Google Scholar]
- Diemberger, H.; Hovden, A.; Yeh, E.T. The honour of the snow-mountains is the snow: Tibetan livelihoods in a changing climate. In The High-Mountain Cryosphere: Environmelt Changes and Human Risks; Huggel, C., Carey, M., Clague, J.J., Kaab, A., Eds.; Cambridge University Press: Cambridge, UK, 2015; pp. 249–271. [Google Scholar] [CrossRef]
- Kropáček, J.; Neckel, N.; Tyrna, B.; Holzer, N.; Hovden, A.; Gourmelen, N.; Schneider, C.; Buchroithner, M.; Hochschild, V. Repeated glacial lake outburst flood threatening the oldest Buddhist monastery in north-western Nepal. Nat. Hazards Earth Syst. Sci. 2015, 15, 2425–2437. [Google Scholar] [CrossRef] [Green Version]
- Benn, D.I.; Owen, L.A. The role of the Indian summer monsoon and the mid-latitude westerlies in Himalayan glaciation: Review and speculative discussion. J. Geol. Soc. 1998, 155, 353–363. [Google Scholar] [CrossRef] [Green Version]
- Webster, P.J.; Magaña, V.O.; Palmer, T.N.; Shukla, J.; Tomas, R.A.; Yanai, M.; Yasunari, T. Monsoons: Processes, predictability, and the prospects for prediction. J. Geophys. Res. Ocean. 1998, 103, 14451–14510. [Google Scholar] [CrossRef]
- Copernicus. Climate Data Store ERA5-Land Reanalysis. 2019. Available online: https://cds.climate.copernicus.eu/cdsapp#!/home (accessed on 11 January 2021).
- Sauter, T.; Arndt, A.; Schneider, C. COSIPY v1.3—An open-source coupled snowpack and ice surface energy and mass balance model. Geosci. Model Dev. 2020, 13, 5645–5662. [Google Scholar] [CrossRef]
- Oerlemans, J.; Reichert, B. Relating glacier mass balance to meteorological data by using a seasonal sensitivity characteristic. J. Glaciol. 2000, 46, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Earth Resources Observation And Science (EROS) Center. Shuttle Radar Topography Mission (SRTM) 1 Arc-Second Global; U.S. Geological Survey: Reston, VA, USA, 2017. [CrossRef]
- Consortium, R.G.I. Randolph Glacier Inventory 6.0; NSIDC: Boulder, CO, USA, 2017. [Google Scholar] [CrossRef]
- Farinotti, D. A consensus estimate for the ice thickness distribution of all glaciers on Earth—Dataset. In Medium: Txt/Plain, Application/Zip, Image/Tiff, 12.48 GB; ETH: Zurich, Switzerland, 2019. [Google Scholar] [CrossRef]
- Dehecq, A.; Gourmelen, N.; Trouve, E. Deriving large-scale glacier velocities from a complete satellite archive: Application to the Pamir–Karakoram–Himalaya. Remote Sens. Environ. 2015, 162, 55–66. [Google Scholar] [CrossRef] [Green Version]
- Dehecq, A.; Gourmelen, N.; Trouvé, E. High Mountain Asia Glacier Velocities 2013–2015 (Landsat 8); Zenodo: Geneva, Switzerland, 2019. [Google Scholar] [CrossRef]
- Shean, D.; Bhushan, S. Zenodo, Geneva, Switzerland. Type: Dataset; 2020; Available online: https://zenodo.org/record/3600624#.YF1M_twRXIU (accessed on 22 March 2021). [CrossRef]
- Ye, Q.; Yao, T.; Kang, S.; Chen, F.; Wang, J. Glacier variations in the Naimona’nyi region, western Himalaya, in the last three decades. Ann. Glaciol. 2006, 43, 385–389. [Google Scholar] [CrossRef] [Green Version]
- Racoviteanu, A.S.; Bajracharya, S.A. GLIMS Glacier Database; NSIDC: Boulder, CO, USA, 2008. [Google Scholar] [CrossRef]
- Sakai, A.S.; Sakai, A.A. GLIMS Glacier Database; NSIDC: Boulder, CO, USA, 2018. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Lea, J.M. The Google Earth Engine Digitisation Tool (GEEDiT) and the Margin change Quantification Tool (MaQiT) – simple tools for the rapid mapping and quantification of changing Earth surface margins. Earth Surf. Dyn. 2018, 6, 551–561. [Google Scholar] [CrossRef] [Green Version]
- Microsoft. Bing Maps; Microsoft: Redmond, WA, USA, 2020. [Google Scholar]
- Terrestris GmbH & Co. KG. TOPOGRAPHIC WMS. 2021. Available online: https://www.terrestris.de/de/topographic-wms/ (accessed on 11 January 2021).
- Oerlemans, J.; Knap, W.H. A 1 year record of global radiation and albedo in the ablation zone of Morteratschgletscher, Switzerland. J. Glaciol. 1998, 44, 231–238. [Google Scholar] [CrossRef] [Green Version]
- Mölg, T.; Maussion, F.; Yang, W.; Scherer, D. The footprint of Asian monsoon dynamics in the mass and energy balance of a Tibetan glacier. Cryosphere 2012, 6, 1445–1461. [Google Scholar] [CrossRef] [Green Version]
- Mazumder, S. Numerical Methods for Partial Differential Equations: Finite Difference and Finite Volume Methods; OCLC: ocn913556966; Academic Press: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Bintanja, R.; Van Den Broeke, M.R. The Surface Energy Balance of Antarctic Snow and Blue Ice. J. Appl. Meteorol. 1995, 34, 902–926. [Google Scholar] [CrossRef]
- Anderson, E.A. A Point Energy and Mass Balance Model of a Snow Cover; Technical Report; National Weather Service (NWS): Silver Spring, MD, USA, 1976.
- Boone, A. Description du Schema de Neige ISBA-ES (Explicit Snow); Technical Report; Updated in November, 2009; Centre National de Recherches Météorologiques, Météo-France: Toulouse, France, 2004. [Google Scholar]
- Cogley, J.G.; Hock, R.; A Rasmussen, L.; Arendt, A.; Bauder, A.; J Braithwaite, R.; Jansson, P.; Kaser, G.; Möller, M.; Nicholson, L.; et al. Glossary of glacier mass balance and related terms. Int. Assoc. Cryospheric Sci. 2011. [Google Scholar] [CrossRef]
- Kaser, G.; Fountain, A.; Jansson, P. A Manual for Monitoring the Mass Balance of Mountain Glaciers; IHP-VI, Technical Documents in Hydrology No. 59; UNESCO: Paris, France, 2003. [Google Scholar]
- Neckel, N.; Kropáček, J.; Schröter, B.; Scherer, D. Effects of Cyclone Hudhud captured by a high altitude Automatic Weather Station in northwestern Nepal. Weather 2015, 70, 208–210. [Google Scholar] [CrossRef]
- ECMWF. ERA5-Land: Data Documentation; ECMWF: Reading, UK, 2020. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020. [Google Scholar] [CrossRef]
- Wohlfahrt, G.; Hammerle, A.; Niedrist, G.; Scholz, K.; Tomelleri, E.; Zhao, P. On the energy balance closure and net radiation in complex terrain. Agric. For. Meteorol. 2016, 226–227, 37–49. [Google Scholar] [CrossRef] [Green Version]
- Lente, G.; Ősz, K. Barometric formulas: Various derivations and comparisons to environmentally relevant observations. ChemTexts 2020, 6, 13. [Google Scholar] [CrossRef] [Green Version]
- Gudmundsson, L.; Bremnes, J.B.; Haugen, J.E.; Engen-Skaugen, T. Technical Note: Downscaling RCM precipitation to the station scale using statistical transformations—A comparison of methods. Hydrol. Earth Syst. Sci. 2012, 16, 3383–3390. [Google Scholar] [CrossRef] [Green Version]
- ECMWF. IFS Documentation CY41R2—Part IV: Physical Processes. 2016. Available online: https://www.ecmwf.int/node/16648 (accessed on 9 December 2020).
- ECMWF. ERA5-Land: Data Documentation; ECMWF: Reading, UK, 2021. [Google Scholar]
- Stull, R.B. (Ed.) An Introduction to Boundary Layer Meteorology; Springer: Dordrecht, The Netherlands, 1988. [Google Scholar] [CrossRef]
- Brock, B.W.; Willis, I.C.; Sharp, M.J. Measurement and parameterization of aerodynamic roughness length variations at Haut Glacier d’Arolla, Switzerland. J. Glaciol. 2006, 52, 281–297. [Google Scholar] [CrossRef] [Green Version]
- Gromke, C.; Manes, C.; Walter, B.; Lehning, M.; Guala, M. Aerodynamic Roughness Length of Fresh Snow. Bound. Layer Meteorol. 2011, 141, 21–34. [Google Scholar] [CrossRef] [Green Version]
- GDAL/OGR Contributors. GDAL/OGR Geospatial Data Abstraction Software Library; Open Source Geospatial Foundation: DE, USA, 2020. [Google Scholar]
- Zwillinger, D.; Kokoska, S. CRC Standard Probability and Statistics Tables and Formulae; Chapman & Hall/CRC: Boca Raton, FL, USA, 2000. [Google Scholar]
- Reichert, B.K.; Bengtsson, L.; Oerlemans, J. Midlatitude Forcing Mechanisms for Glacier Mass Balance Investigated Using General Circulation Models. J. Clim. 2001, 14, 18. [Google Scholar] [CrossRef]
- Webster, P.J.; Yang, S. Monsoon and Enso: Selectively Interactive Systems. Q. J. R. Meteorol. Soc. 1992, 118, 877–926. [Google Scholar] [CrossRef]
- Barnston, A.G.; Livezey, R.E. Classification, Seasonality and Persistence of Low-Frequency Atmospheric Circulation Patterns. Mon. Weather Rev. 1987, 115, 1083–1126. [Google Scholar] [CrossRef]
- Gao, N.; Bueh, C.; Xie, Z.; Gong, Y. A Novel Identification of the Polar/Eurasia Pattern and Its Weather Impact in May. J. Meteorol. Res. 2019, 33, 810–825. [Google Scholar] [CrossRef]
- Lin, Z. Intercomparison of the impacts of four summer teleconnections over Eurasia on East Asian rainfall. Adv. Atmos. Sci. 2014, 31, 1366–1376. [Google Scholar] [CrossRef]
- Gao, T.; Yu, J.y.; Paek, H. Impacts of four northern-hemisphere teleconnection patterns on atmospheric circulations over Eurasia and the Pacific. Theor. Appl. Climatol. 2017, 129, 815–831. [Google Scholar] [CrossRef] [Green Version]
- Carturan, L.; Cazorzi, F.; De Blasi, F.; Dalla Fontana, G. Air temperature variability over three glaciers in the Ortles—Cevedale (Italian Alps): Effects of glacier fragmentation, comparison of calculation methods, and impacts on mass balance modeling. Cryosphere 2015, 9, 1129–1146. [Google Scholar] [CrossRef] [Green Version]
- Sauter, T.; Möller, M.; Finkelnburg, R.; Grabiec, M.; Scherer, D.; Schneider, C. Snowdrift modelling for the Vestfonna ice cap, north-eastern Svalbard. Cryosphere 2013, 7, 1287–1301. [Google Scholar] [CrossRef] [Green Version]
- Groot Zwaaftink, C.D.; Cagnati, A.; Crepaz, A.; Fierz, C.; Macelloni, G.; Valt, M.; Lehning, M. Event-driven deposition of snow on the Antarctic Plateau: Analyzing field measurements with SNOWPACK. Cryosphere 2013, 7, 333–347. [Google Scholar] [CrossRef] [Green Version]
- Olson, M.; Rupper, S. Impacts of topographic shading on direct solar radiation for valley glaciers in complex topography. Cryosphere 2019, 13, 29–40. [Google Scholar] [CrossRef] [Green Version]
- Olson, M.; Rupper, S.; Shean, D.E. Terrain Induced Biases in Clear-Sky Shortwave Radiation Due to Digital Elevation Model Resolution for Glaciers in Complex Terrain. Front. Earth Sci. 2019, 7, 216. [Google Scholar] [CrossRef] [Green Version]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; van Dijk, A.I.J.M.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling. Hydrol. Earth Syst. Sci. 2017, 21, 6201–6217. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.Y.; Kim, J.; Boo, K.O.; Shim, S.; Kim, Y. Intercomparison of precipitation datasets for summer precipitation characteristics over East Asia. Clim. Dyn. 2019, 52, 3005–3022. [Google Scholar] [CrossRef] [Green Version]
- Immerzeel, W.W.; Wanders, N.; Lutz, A.F.; Shea, J.M.; Bierkens, M.F.P. Reconciling high altitude precipitation in the upper Indus Basin with glacier mass balances and runoff. Hydrol. Earth Syst. Sci. Discuss. 2015, 12, 4755–4784. [Google Scholar] [CrossRef] [Green Version]
- Hamm, A.; Arndt, A.; Kolbe, C.; Wang, X.; Thies, B.; Boyko, O.; Reggiani, P.; Scherer, D.; Bendix, J.; Schneider, C. Intercomparison of Gridded Precipitation Datasets over a Sub-Region of the Central Himalaya and the Southwestern Tibetan Plateau. Water 2020, 12, 3271. [Google Scholar] [CrossRef]
- Wang, X.; Tolksdorf, V.; Otto, M.; Scherer, D. WRF-based dynamical downscaling of ERA5 reanalysis data for High Mountain Asia: Towards a new version of the High Asia Refined analysis. Int. J. Climatol. 2020. [Google Scholar] [CrossRef]
- Hopkinson, C.; Chasmer, L.; Munro, S.; Demuth, M.N. The influence of DEM resolution on simulated solar radiation-induced glacier melt. Hydrol. Process. 2010, 24, 775–788. [Google Scholar] [CrossRef]
- Thiel, K.; Arndt, A.; Wang, P.; Li, H.; Li, Z.; Schneider, C. Modeling of Mass Balance Variability and Its Impact on Water Discharge from the Urumqi Glacier No. 1 Catchment, Tian Shan, China. Water 2020, 12, 3297. [Google Scholar] [CrossRef]
- Gut, A. Probability: A Graduate Course; OCLC: 56096548; Springer: New York, NY, USA, 2005. [Google Scholar]
- Klok, E.; Oerlemans, J. Model study of the spatial distribution of the energy and mass balance of Morteratschgletscher, Switzerland. J. Glaciol. 2002, 48, 505–518. [Google Scholar] [CrossRef] [Green Version]
- Hock, R.; Holmgren, B. A distributed surface energy-balance model for complex topography and its application to Storglaciären, Sweden. J. Glaciol. 2005, 51, 25–36. [Google Scholar] [CrossRef] [Green Version]
- Machguth, H.; Paul, F.; Hoelzle, M.; Haeberli, W. Distributed glacier mass-balance modelling as an important component of modern multi-level glacier monitoring. Ann. Glaciol. 2006, 43, 335–343. [Google Scholar] [CrossRef] [Green Version]
- Reijmer, C.H.; Hock, R. Internal accumulation on Storglaciären, Sweden, in a multi-layer snow model coupled to a distributed energy-and mass-balance model. J. Glaciol. 2008, 54, 61–72. [Google Scholar] [CrossRef] [Green Version]
- Sicart, J.E.; Hock, R.; Ribstein, P.; Litt, M.; Ramirez, E. Analysis of seasonal variations in mass balance and meltwater discharge of the tropical Zongo Glacier by application of a distributed energy balance model. J. Geophys. Res. 2011, 116, D13105. [Google Scholar] [CrossRef]
- Van Pelt, W.J.J.; Oerlemans, J.; Reijmer, C.H.; Pohjola, V.A.; Pettersson, R.; van Angelen, J.H. Simulating melt, runoff and refreezing on Nordenskiöldbreen, Svalbard, using a coupled snow and energy balance model. Cryosphere 2012, 6, 641–659. [Google Scholar] [CrossRef] [Green Version]
- Yao, T.D.; Pu, J.C.; Tian, L.D.; Yang, W.; Duan, K.Q.; Ye, Q.H.; Thompson, L.G. Recent Rapid Retreat of the Naimona’nyi Glacier in Southwestern Tibetan Plateau. J. Glaciol. Geocryol. 2007, 29, 503–508. [Google Scholar]
- Zhu, D.; Tian, L.; Wang, J.; Wang, Y.; Cui, J. Rapid glacier retreat in the Naimona’Nyi region, western Himalayas, between 2003 and 2013. J. Appl. Remote Sens. 2014, 8, 083508. [Google Scholar] [CrossRef] [Green Version]
- Priya, P.; Krishnan, R.; Mujumdar, M.; Houze, R.A. Changing monsoon and midlatitude circulation interactions over the Western Himalayas and possible links to occurrences of extreme precipitation. Clim. Dyn. 2017, 49, 2351–2364. [Google Scholar] [CrossRef]
- Bothe, O.; Fraedrich, K.; Zhu, X. Tibetan Plateau summer precipitation: Covariability with circulation indices. Theor. Appl. Climatol. 2012, 108, 293–300. [Google Scholar] [CrossRef]
- Liu, W.; Wang, L.; Chen, D.; Tu, K.; Ruan, C.; Hu, Z. Large-scale circulation classification and its links to observed precipitation in the eastern and central Tibetan Plateau. Clim. Dyn. 2016, 46, 3481–3497. [Google Scholar] [CrossRef]
- Palazzi, E.; von Hardenberg, J.; Provenzale, A. Precipitation in the Hindu-Kush Karakoram Himalaya: Observations and future scenarios: PRECIPITATION IN HINDU-KUSH KARAKORAM HIMALAYA. J. Geophys. Res. Atmos. 2013, 118, 85–100. [Google Scholar] [CrossRef]
- Kajikawa, Y.; Wang, B.; Yang, J. A multi-time scale Australian monsoon index: A MULTI-TIME SCALE AUSTRALIAN MONSOON INDEX. Int. J. Climatol. 2010, 30, 1114–1120. [Google Scholar] [CrossRef]
- Enfield, D.B.; Mestas-Nuñez, A.M.; Trimble, P.J. The Atlantic Multidecadal Oscillation and its relation to rainfall and river flows in the continental U.S. Geophys. Res. Lett. 2001, 28, 2077–2080. [Google Scholar] [CrossRef] [Green Version]
- Thompson, D.W.J.; Wallace, J.M. The Arctic oscillation signature in the wintertime geopotential height and temperature fields. Geophys. Res. Lett. 1998, 25, 1297–1300. [Google Scholar] [CrossRef] [Green Version]
- Bureau of Meteorology, Commonwealth of Australia. About ENSO and IOD Indices; Online Resources (2021): Bureau of Meteorology, Commonwealth of Australia. Available online: http://www.bom.gov.au/climate/enso/indices/about.shtml (accessed on 22 March 2021).
- Wang, B.; Fan, Z. Choice of South Asian Summer Monsoon Indices*. Bull. Am. Meteorol. Soc. 1999, 80, 629–638. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Wu, R.; Lau, K.M. Interannual Variability of the Asian Summer Monsoon: Contrasts between the Indian and the Western North Pacific–East Asian Monsoons*. J. Clim. 2001, 14, 4073–4090. [Google Scholar] [CrossRef]
- Zhang, T.; Hoell, A.; Perlwitz, J.; Eischeid, J.; Murray, D.; Hoerling, M.; Hamill, T.M. Towards Probabilistic Multivariate ENSO Monitoring. Geophys. Res. Lett. 2019, 46, 10532–10540. [Google Scholar] [CrossRef]
- Hurrell, J.W. Decadal Trends in the North Atlantic Oscillation: Regional Temperatures and Precipitation. Science 1995, 269, 676–679. [Google Scholar] [CrossRef] [Green Version]
- Trenberth, K.E.; Stepaniak, D.P. Indices of El Niño Evolution. J. Clim. 2001, 14, 1697–1701. [Google Scholar] [CrossRef] [Green Version]
- Mantua, N.J.; Hare, S.R. The Pacific Decadal Oscillation. J. Oceanogr. 2002, 58, 35–44. [Google Scholar] [CrossRef]
- Wallace, J.M.; Gutzler, D.S. Teleconnections in the Geopotential Height Field during the Northern Hemisphere Winter. Mon. Weather Rev. 1981, 109, 784–812. [Google Scholar] [CrossRef]
- National Oceanic and Atmospheric Administration. Southern Oscillation Index (SOI); Online Resources (2021): National Oceanic and Atmospheric Administration. Available online: https://www.ncdc.noaa.gov/teleconnections/enso/indicators/soi/ (accessed on 22 March 2021).









| Variable | Instrument | Measuring Range | Nominal Accuracy |
|---|---|---|---|
| Surface pressure | Lufft WS501-UMB | 300 … 1200 | |
| Air temperature at 2 | Lufft WS501-UMB | –50 … 60 | |
| Total precipitation | Lufft WS100 Radar | 0.01 … 200 mm h−1 | mm or * |
| Relative humidity at 2 | Lufft WS501-UMB | 0 … 100 | % |
| Wind speed at 2 | Lufft WS501-UMB | 0 … 75 s−1 | |
| Variable | AWS | Downscaling | Interpolation |
|---|---|---|---|
| Surface pressure () | yes | Barometric formula | Barometric formula |
| Air temperature at 2 () | yes | Quantile mapping | Lapse rate |
| Relative humidity at 2 RH2 (%) | yes | Lapse rate | - |
| Incoming shortwave radiation (W m−2) | yes | - | Radiation modelling [68] |
| Incoming longwave radiation (W m−2) | no | - | - |
| Wind speed at 2 (m s−1) | yes | Scale factor of 5 | - |
| Total precipitation TP (mm) | yes | Scale factor of 2 | - |
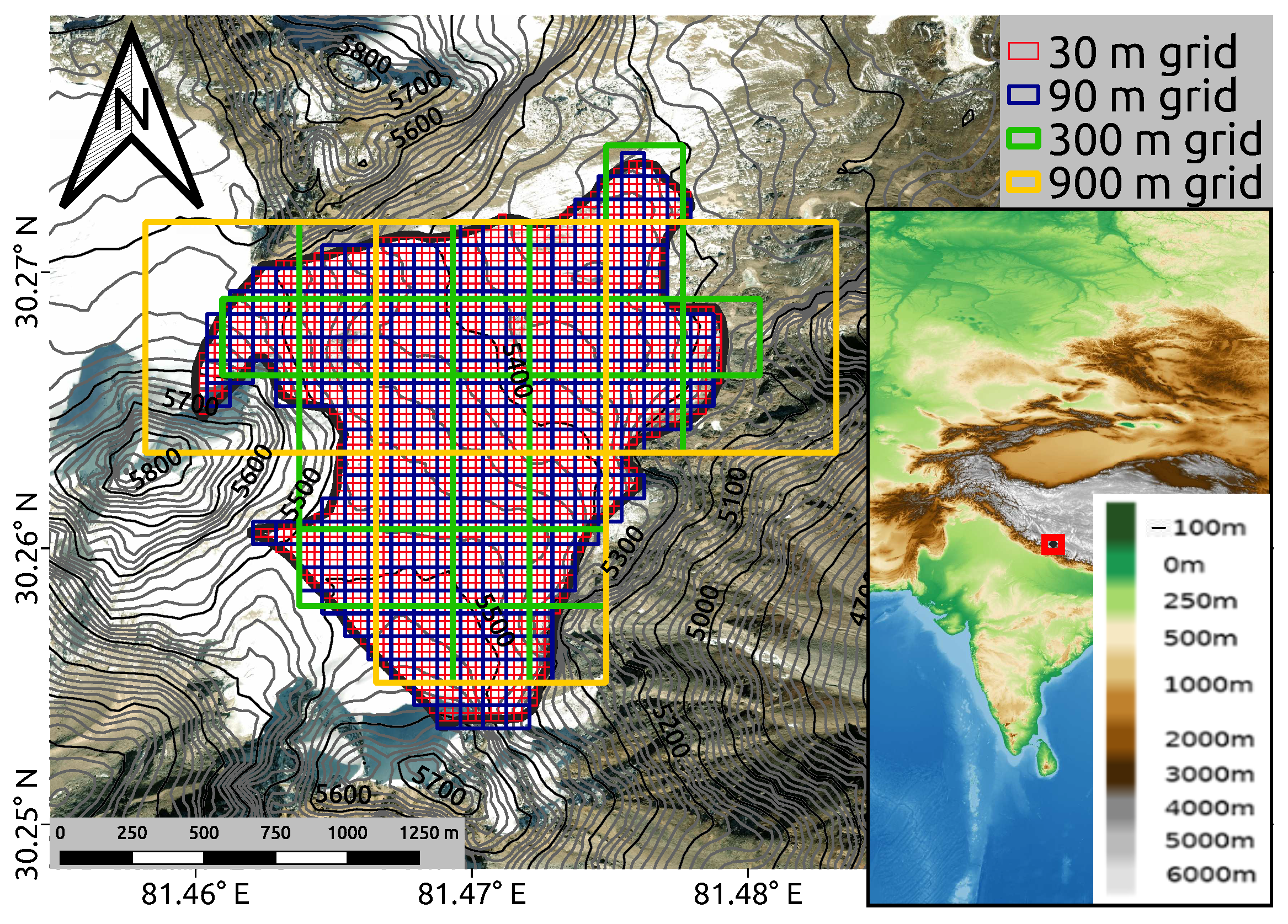
| Resolution in Arcseconds () | 1.0 | 2.0 | 3.0 | 3.33 | 5.0 | 6.67 | 10.00 | 16.67 | 30.0 | 33.33 | 50.0 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Resolution in ∼m | 30 | 60 | 90 | 100 | 150 | 200 | 300 | 500 | 900 | 1000 | 1500 |
| Resulting GGPs | 2735 | 688 | 303 | 248 | 110 | 59 | 28 | 11 | 4 | 2 | 1 |
| Variable | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Metric | mean | mean | mean | mean | sum | sum | mean | mean | mean | mean | mean |
| Type | f | f | f | f | f | i | f | i | f | i | i |
| Annual | −0.42 | −0.07 | 0.36 | −0.45 | 0.42 | 0.54 | 0.17 | −0.81 | −0.32 | 0.09 | 0.8 |
| September before | −0.31 | −0.09 | 0.26 | −0.28 | 0.43 | 0.47 | −0.15 | −0.16 | 0.04 | 0.14 | 0.14 |
| October | −0.49 | −0.3 | 0.43 | −0.21 | 0.36 | 0.36 | −0.0 | −0.44 | −0.05 | 0.32 | 0.44 |
| November | −0.32 | −0.16 | 0.32 | −0.37 | −0.06 | 0.08 | 0.21 | −0.37 | −0.04 | 0.28 | 0.37 |
| December | −0.06 | −0.02 | 0.19 | −0.17 | 0.16 | 0.19 | −0.03 | −0.14 | 0.1 | 0.13 | 0.14 |
| January | −0.21 | 0.06 | −0.11 | 0.18 | 0.33 | 0.29 | 0.0 | −0.08 | −0.0 | 0.06 | 0.09 |
| February | −0.55 | −0.2 | −0.09 | −0.2 | 0.18 | 0.24 | 0.05 | −0.01 | −0.35 | −0.07 | 0.05 |
| March | 0.13 | 0.17 | 0.21 | 0.06 | −0.15 | −0.23 | 0.02 | 0.2 | 0.11 | 0.04 | −0.21 |
| April | −0.12 | −0.04 | −0.05 | −0.08 | 0.04 | 0.12 | 0.16 | −0.03 | −0.17 | −0.08 | 0.04 |
| May | −0.39 | −0.31 | 0.09 | −0.06 | 0.03 | 0.0 | 0.25 | −0.02 | −0.36 | −0.24 | 0.08 |
| June | −0.68 | −0.19 | 0.51 | −0.55 | 0.03 | 0.35 | 0.22 | −0.27 | −0.36 | −0.24 | 0.31 |
| July | −0.46 | 0.16 | 0.04 | −0.26 | 0.12 | 0.32 | 0.14 | −0.82 | −0.16 | −0.12 | 0.86 |
| August | −0.3 | 0.01 | 0.13 | −0.37 | 0.11 | 0.31 | −0.11 | −0.9 | −0.0 | 0.01 | 0.91 |
| September | 0.02 | −0.17 | 0.01 | −0.15 | 0.06 | −0.02 | −0.12 | −0.74 | 0.01 | 0.14 | 0.75 |
| Index | Annual | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | JJA | JJA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| POL | 0.48 | 0.29 | 0.41 | –0.03 | –0.05 | –0.22 | 0.56 | 0.23 | 0.06 | 0.17 | ||
| WYM | –0.42 | –0.43 | –0.35 | –0.33 | –0.17 | –0.44 | –0.43 |
| Mass-Balance Year | COSIPY | Kropáček et al. [38] | Shean et al. ([7], Dataset: [49]) |
|---|---|---|---|
| 1982–2019 | −0.48 | - | - |
| 2001–2013 | −0.35 | −0.40 ± 30 | - |
| 2001–2018 | −0.53 | - | −0.70 ± 15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arndt, A.; Scherer, D.; Schneider, C. Atmosphere Driven Mass-Balance Sensitivity of Halji Glacier, Himalayas. Atmosphere 2021, 12, 426. https://doi.org/10.3390/atmos12040426
Arndt A, Scherer D, Schneider C. Atmosphere Driven Mass-Balance Sensitivity of Halji Glacier, Himalayas. Atmosphere. 2021; 12(4):426. https://doi.org/10.3390/atmos12040426
Chicago/Turabian StyleArndt, Anselm, Dieter Scherer, and Christoph Schneider. 2021. "Atmosphere Driven Mass-Balance Sensitivity of Halji Glacier, Himalayas" Atmosphere 12, no. 4: 426. https://doi.org/10.3390/atmos12040426
APA StyleArndt, A., Scherer, D., & Schneider, C. (2021). Atmosphere Driven Mass-Balance Sensitivity of Halji Glacier, Himalayas. Atmosphere, 12(4), 426. https://doi.org/10.3390/atmos12040426






