The Signal to Noise Ratio and the Completeness Magnitude: The Effect of the COVID-19 Lockdown
Abstract
:1. Introduction
2. Data and Methods
- Istituto Nazionale di Geofisica e Vulcanologia terremoti.ingv.it/search (accessed on 20 April 2021)
- Southern California Earthquake Data Center scedc.caltech.edu/data/alt-2011-dd-hauksson-yang-shearer.html (accessed on 20 April 2021)
- University of Athens geophysics.geol.uoa.gr/stations/gmapv3db/index.php?lang=en (accessed on 20 April 2021)
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Marzorati, S.; Bindi, D. Ambient noise levels in north central Italy. Geochem. Geophys. Geosyst. 2006, 7. [Google Scholar] [CrossRef]
- Marzorati, S.; Bindi, D. Characteristics of Ambient Noise Cross Correlations in Northern Italy within the Frequency Range of 0.1–0.6 Hz. Bull. Seismol. Soc. Am. 2008, 98, 1389–1398. [Google Scholar] [CrossRef]
- Li, H.; Bernardi, F.; Michelini, A. Surface wave dispersion measurements from ambient seismic noise analysis in Italy. Geophys. J. Int. 2010, 180, 1242–1252. [Google Scholar] [CrossRef] [Green Version]
- Vassallo, M.; Festa, G.; Bobbio, A. Seismic Ambient Noise Analysis in Southern Italy. Bull. Seismol. Soc. Am. 2012, 102, 574–586. [Google Scholar] [CrossRef]
- McNamara, D.E.; Buland, R.P. Ambient Noise Levels in the Continental United States. Bull. Seismol. Soc. Am. 2004, 94, 1517–1527. [Google Scholar] [CrossRef]
- Rydelek, P.A.; Sacks, I.S. Testing the completeness of earth- quake catalogs and the hypothesis of self-similarity. Nature 1989, 337, 251–253. [Google Scholar] [CrossRef]
- Wiemer, S.; Giardini, D.; Fäh, D.; Deichmann, N.; Sellami, S. Probabilistic seismic hazard assessment of Switzerland: Best estimates and uncertainties. J. Seismol. 2009, 13, 449–478. [Google Scholar] [CrossRef] [Green Version]
- Wiemer, S.; Schorlemmer, D. ALM: An Asperity-based Likelihood Model for California. Seismol. Res. Lett. 2007, 78, 134–140. [Google Scholar] [CrossRef]
- Mignan, A. Retrospective on the Accelerating Seismic Release (ASR) hypothesis: Controversy and new horizons. Tectonophysics 2011, 505, 1–16. [Google Scholar] [CrossRef]
- Scholz, C. The frequency-magnitude relation of microfracturing in rock and its relation to earthquakes. Bull. Seism. Soc. Am. 1968, 58, 399–415. [Google Scholar]
- Xiao, H.; Eilon, Z.C.; Ji, C.; Tanimoto, T. COVID-19 Societal Response Captured by Seismic Noise in China and Italy. Seismol. Res. Lett. 2020, 91, 2757–2768. [Google Scholar] [CrossRef]
- Marzorati, S. Riduzione dei Livelli di Rumore Sismico Ambientale Nelle Città Italiane e Stima Dell’Effetto Sulla Capacità di Rilevamento Della Rete Sismica Nazionale a Seguito Delle Misure Restrittive COVID-19 del Febbraio-Marzo 2020; Open File Report; Istituto Nazionale di Geofisica e Vulcanologia—Osservatorio Nazionale Terremoti: Rome, Italy, 2020. [Google Scholar]
- Lecocq, T.; Hicks, S.P.; Van Noten, K.; van Wijk, K.; Koelemeijer, P.; De Plaen, R.S.M.; Massin, F.; Hillers, G.; Anthony, R.E.; Apoloner, M.T.; et al. Global quieting of high-frequency seismic noise due to COVID-19 pandemic lockdown measures. Science 2020, 369, 1338–1343. [Google Scholar] [CrossRef]
- Yabe, S.; Imanishi, K.; Nishida, K. Two-step seismic noise reduction caused by COVID-19 induced reduction in social activity in metropolitan Tokyo, Japan. Earth Planets Space 2020, 72, 1880–5981. [Google Scholar] [CrossRef]
- Mavroulis, S.; Mavrouli, M.; Lekkas, E. Geological and hydrometeorological hazards and related disasters amid COVID-19 pandemic in Greece: Post-disaster trends and factors affecting the COVID-19 evolution in affected areas. Saf. Sci. 2021, 138, 105236. [Google Scholar] [CrossRef]
- Roy, K.S.; Sharma, J.; Kumar, S.; Kumar, M.R. Effect of coronavirus lockdowns on the ambient seismic noise levels in Gujarat, northwest India. Sci. Rep. 2021, 11, 7148. [Google Scholar] [CrossRef] [PubMed]
- Salvage, R.O.; Eaton, D.W. Unprecedented quiescence in resource development area allows detection of long-lived latent seismicity. Solid Earth 2021, 12, 765–783. [Google Scholar] [CrossRef]
- Piccinini, D.; Giunchi, C.; Olivieri, M.; Frattini, F.; Di Giovanni, M.; Prodi, G.; Chiarabba, C. COVID-19 lockdown and its latency in Northern Italy: Seismic evidence and socio-economic interpretation. Sci. Rep. 2020, 10, 16487. [Google Scholar] [CrossRef] [PubMed]
- Godano, C. A new method for the estimation of the completeness magnitude. Phys. Earth Planet. Inter. 2017, 263, 7–11. [Google Scholar] [CrossRef]
- Wiemer, S.; Wyss, M. Minimum Magnitude of Completeness in Earthquake Catalogs: Examples from Alaska, the Western United States, and Japan. Bull. Seismol. Soc. Am. 2000, 90, 859–869. [Google Scholar] [CrossRef]
- Aki, K. Maximum likelihood estimate of b in the formula logN = a − bM and its confidence limits. Bull. Earthq. Res. Inst. Univ. Tokyo 1965, 43, 237–239. [Google Scholar]
- Shi, Y.; Bolt, B.A. The standard error of the magnitude-frequency b value. Bull. Seismol. Soc. Am. 1982, 72, 1677–1687. Available online: http://xxx.lanl.gov/abs/http://www.bssaonline.org/content/72/5/1677.full.pdf+html (accessed on 20 April 2021).
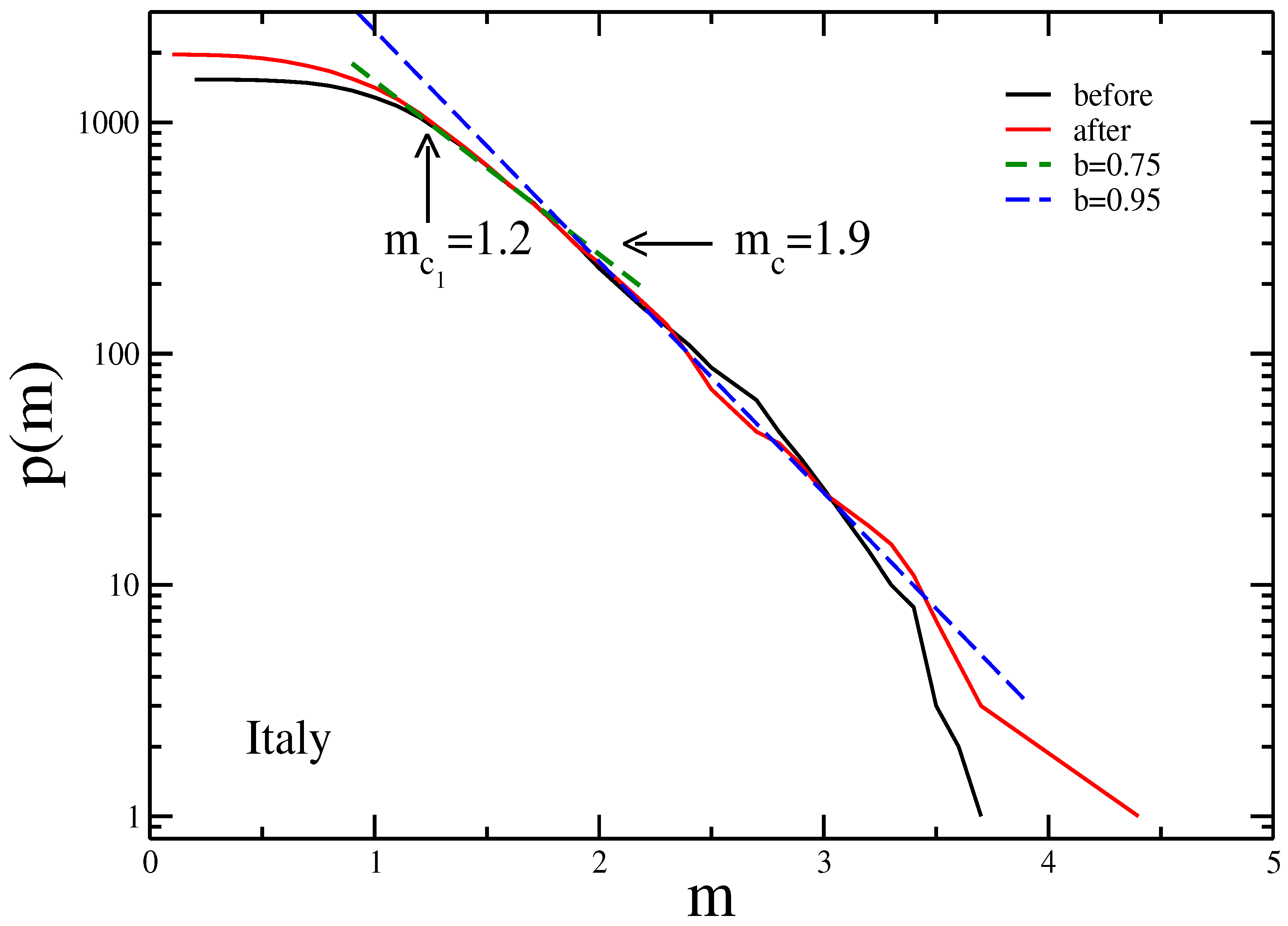
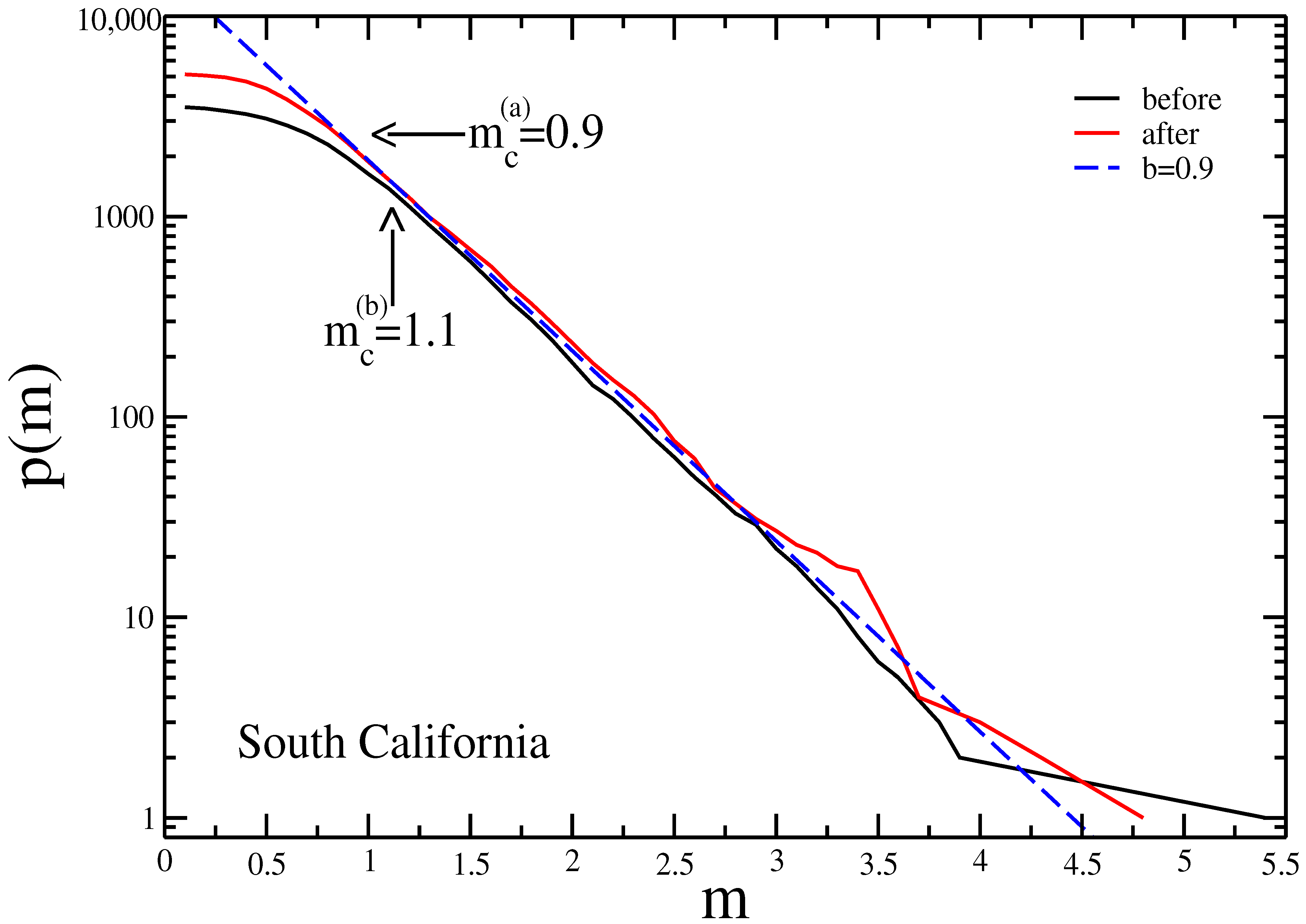
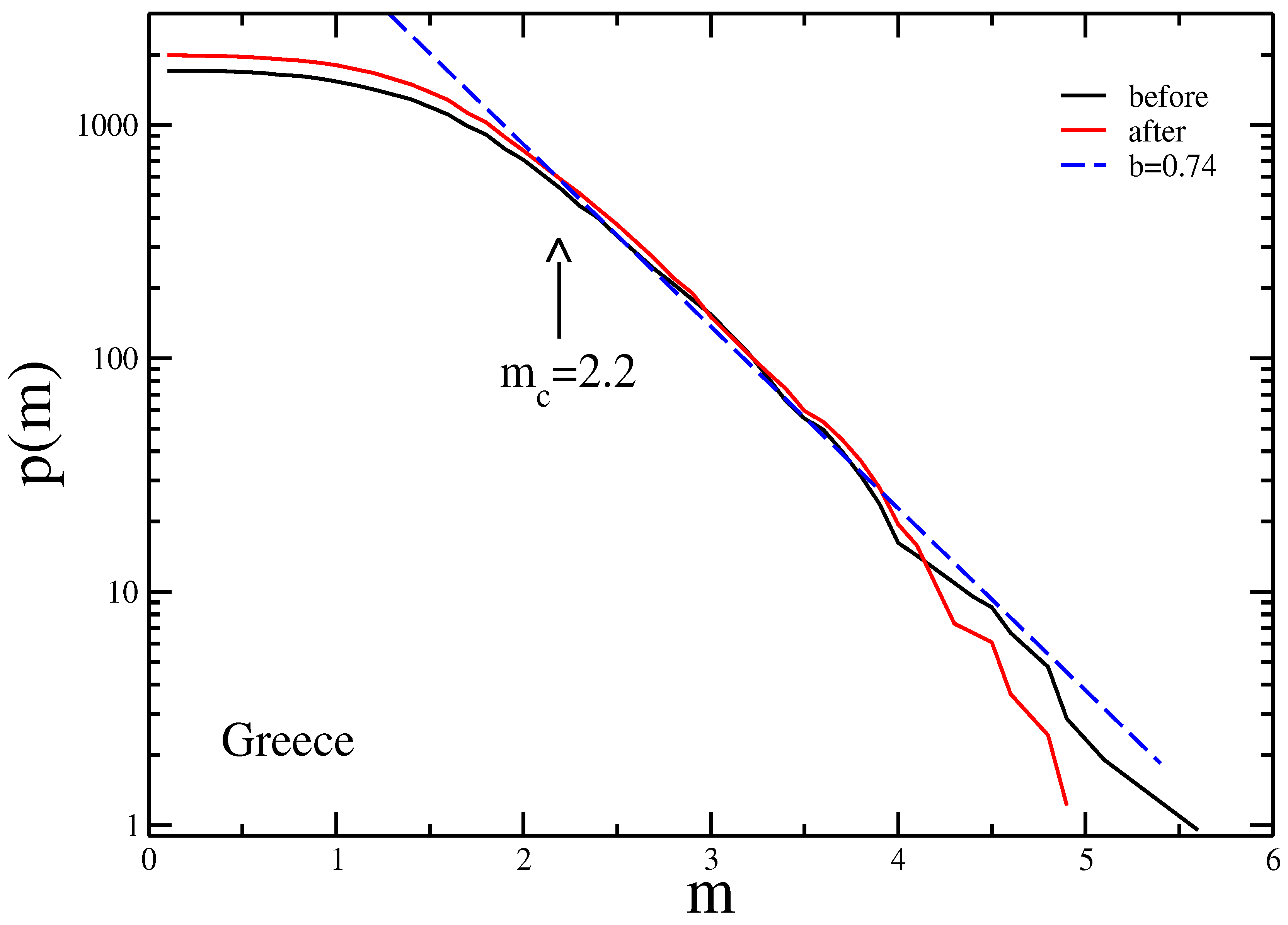
| Area | Before | After | ||
|---|---|---|---|---|
| Analysed Period | Analysed Period | |||
| Italy | 25 January–9 March | 1533 | 10 March–22 April | 1967 |
| South California | 2 February–18 March | 3622 | 19 March–27 April | 5254 |
| Greece | 10 February–21 March | 1636 | 22 March–2 May | 1796 |
| Area | Before | After | ||||
|---|---|---|---|---|---|---|
| Italy | 1.9 | 0.95 | 4.9 | 1.9 | 0.95 | 5 |
| South California | 1.1 | 0.91 | 2 | 0.9 | 0.88 | 1.6 |
| Greece | 2.2 | 0.73 | 2.8 | 2.2 | 0.74 | 2.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Godano, C.; Convertito, V.; Pino, N.A. The Signal to Noise Ratio and the Completeness Magnitude: The Effect of the COVID-19 Lockdown. Atmosphere 2021, 12, 525. https://doi.org/10.3390/atmos12050525
Godano C, Convertito V, Pino NA. The Signal to Noise Ratio and the Completeness Magnitude: The Effect of the COVID-19 Lockdown. Atmosphere. 2021; 12(5):525. https://doi.org/10.3390/atmos12050525
Chicago/Turabian StyleGodano, Cataldo, Vincenzo Convertito, and Nicola Alessandro Pino. 2021. "The Signal to Noise Ratio and the Completeness Magnitude: The Effect of the COVID-19 Lockdown" Atmosphere 12, no. 5: 525. https://doi.org/10.3390/atmos12050525
APA StyleGodano, C., Convertito, V., & Pino, N. A. (2021). The Signal to Noise Ratio and the Completeness Magnitude: The Effect of the COVID-19 Lockdown. Atmosphere, 12(5), 525. https://doi.org/10.3390/atmos12050525







