On the u??U Relationship in the Stable Atmospheric Boundary Layer over Arctic Sea Ice
Abstract
:1. Introduction
2. Observations and Models
2.1. SHEBA Observations
2.2. Surface-Layer MOST
2.3. Single-Column RANS Model
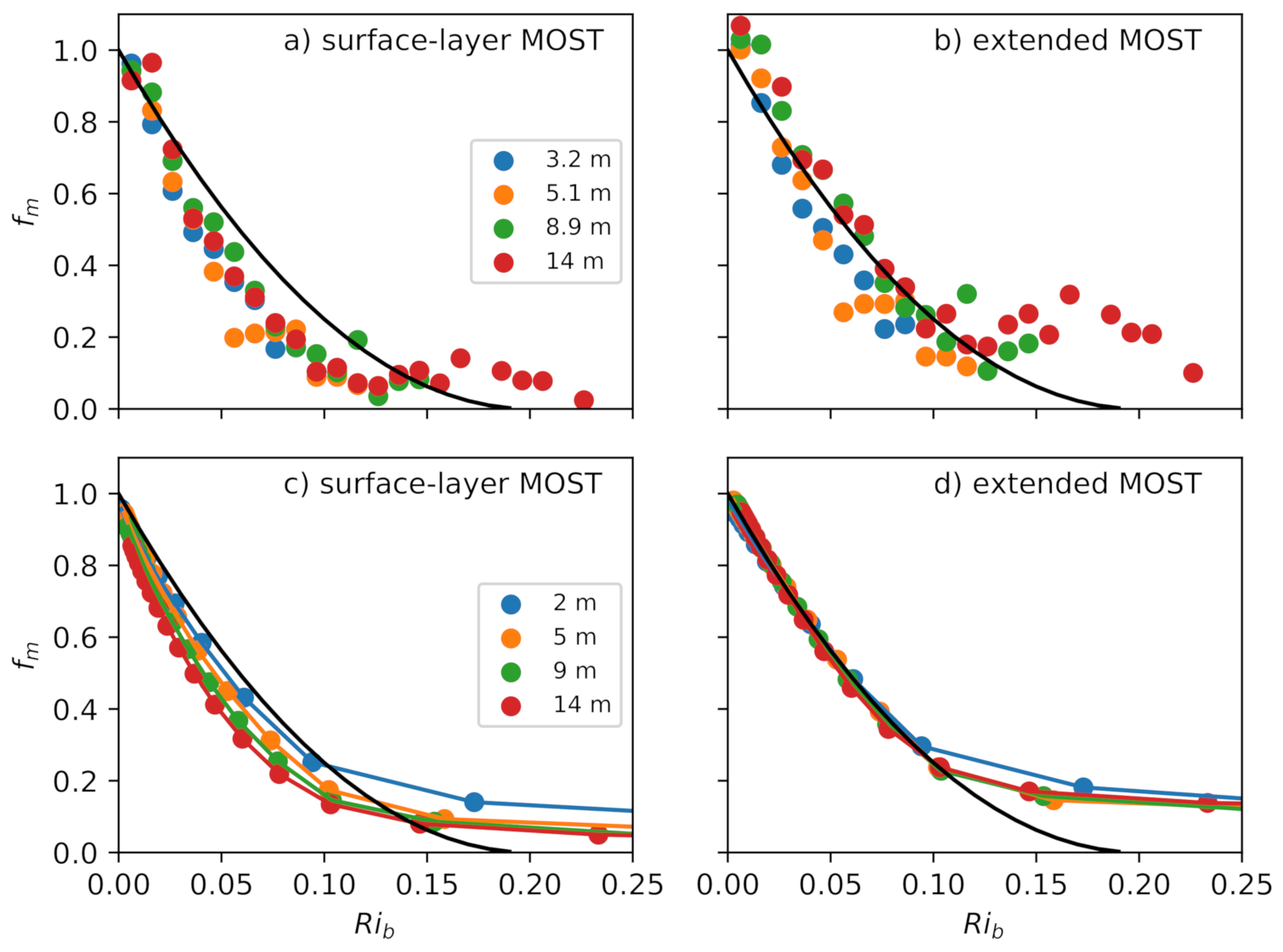
3. Results
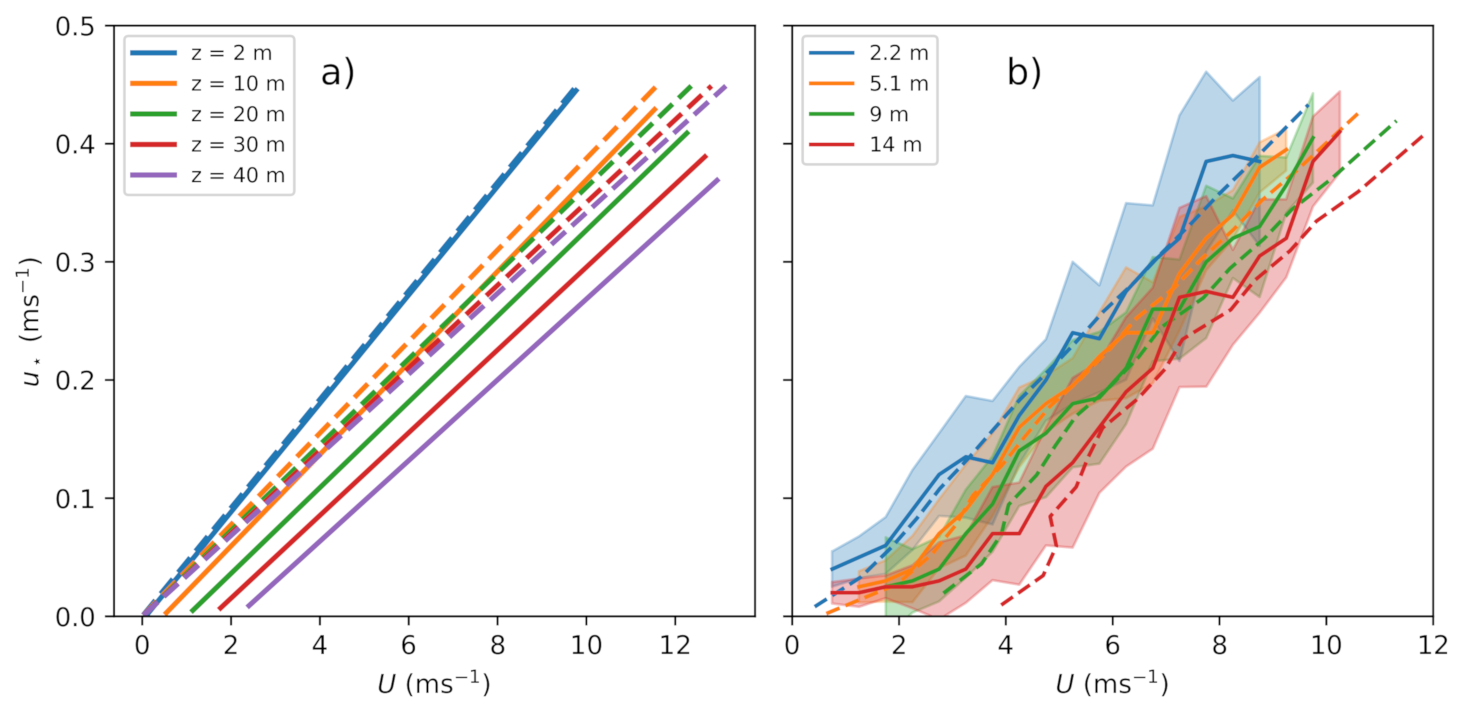
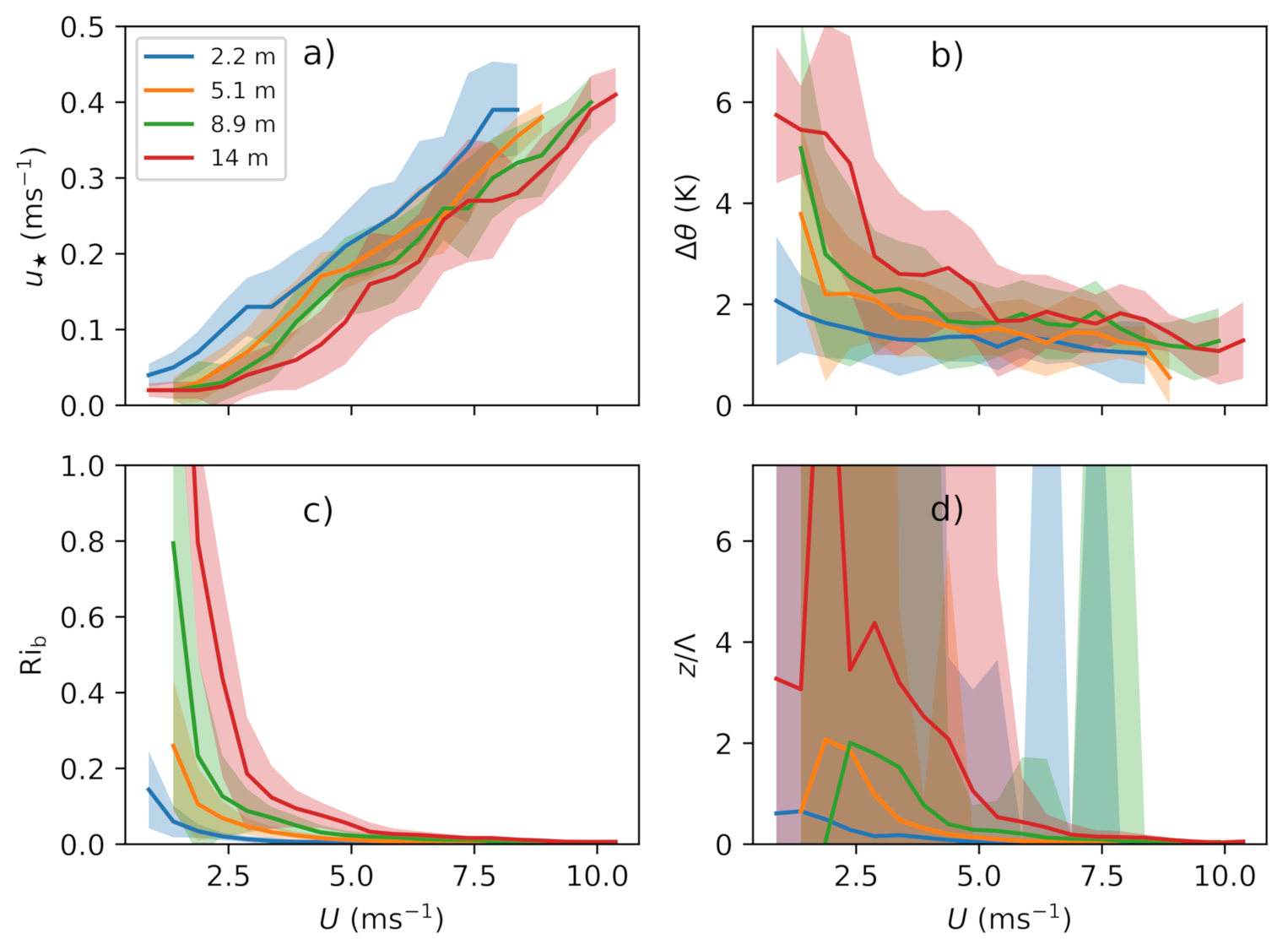
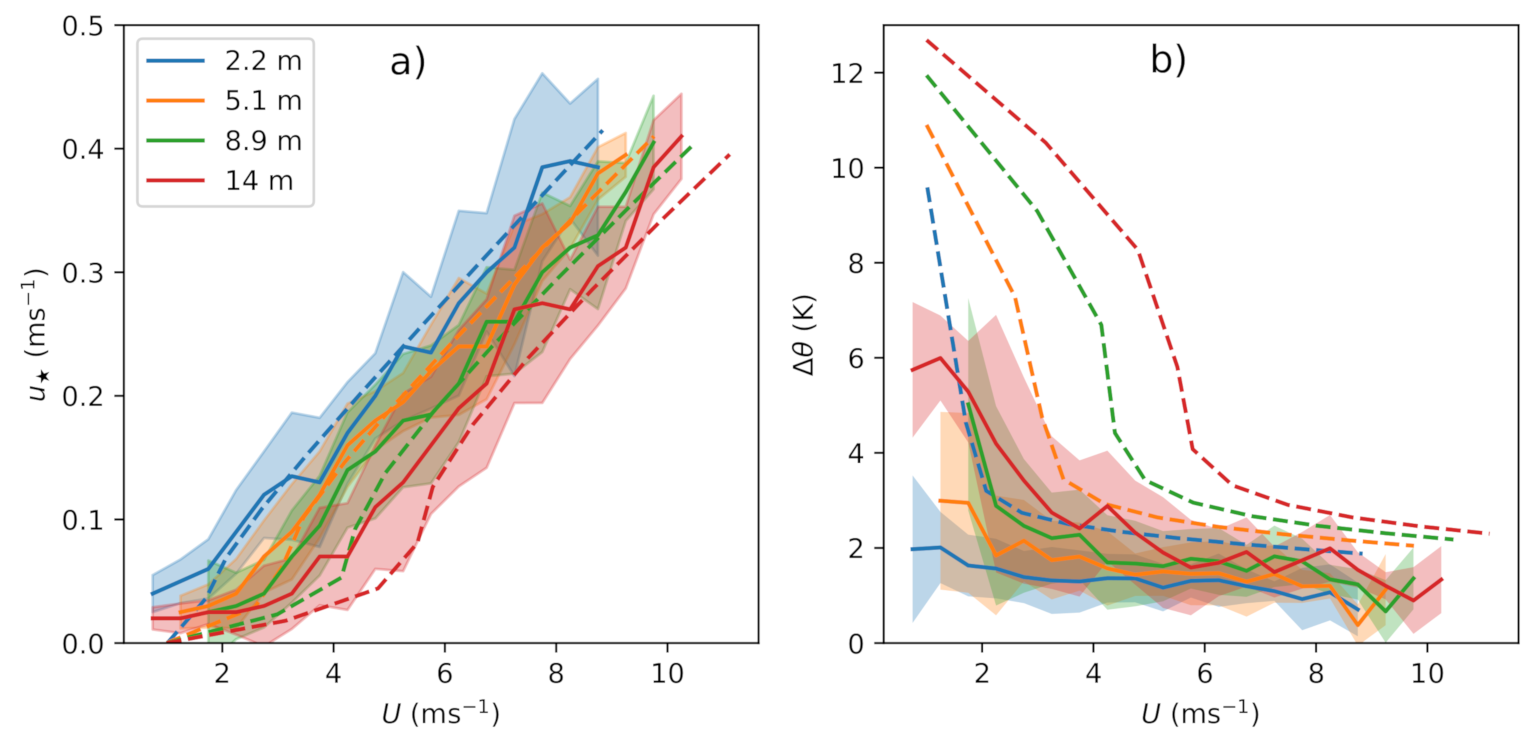
3.1. Observations
3.2. Classical MOST Using Scaling with Surface Fluxes
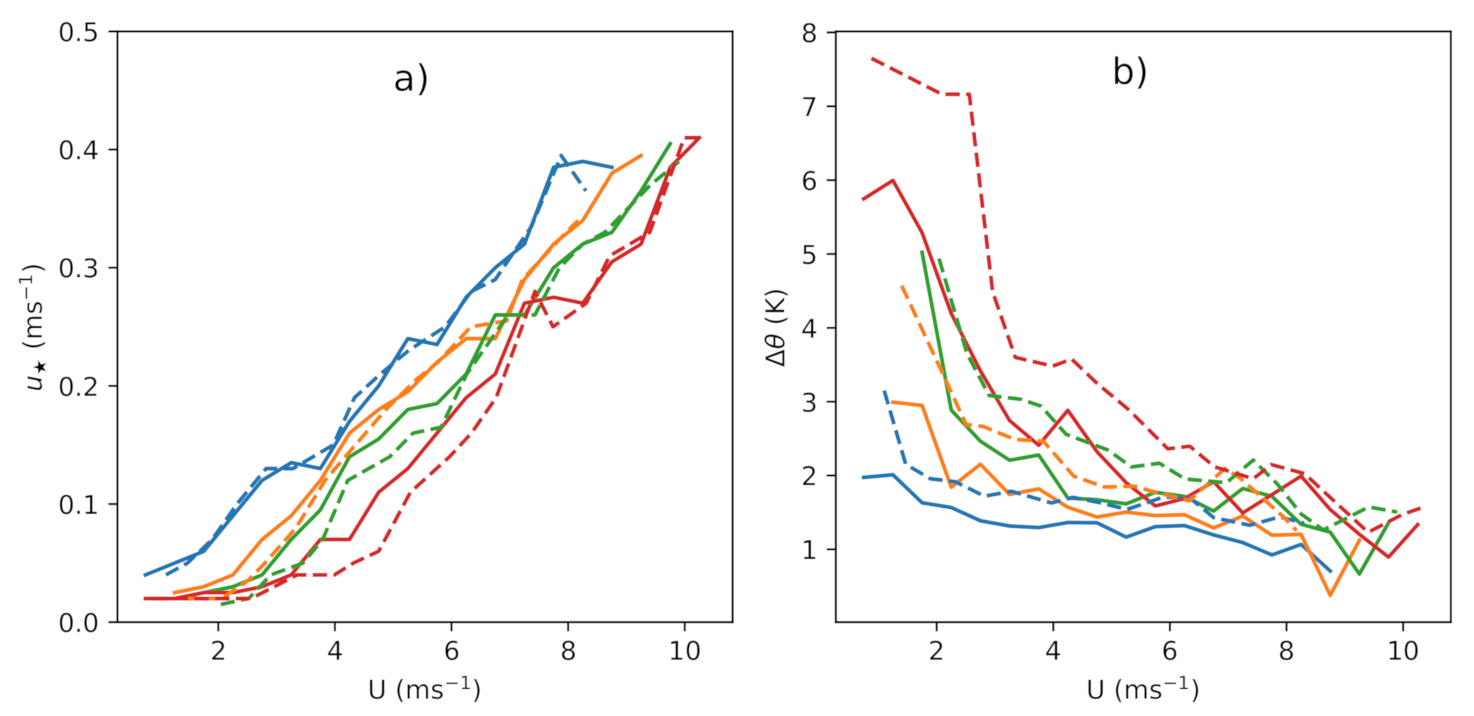
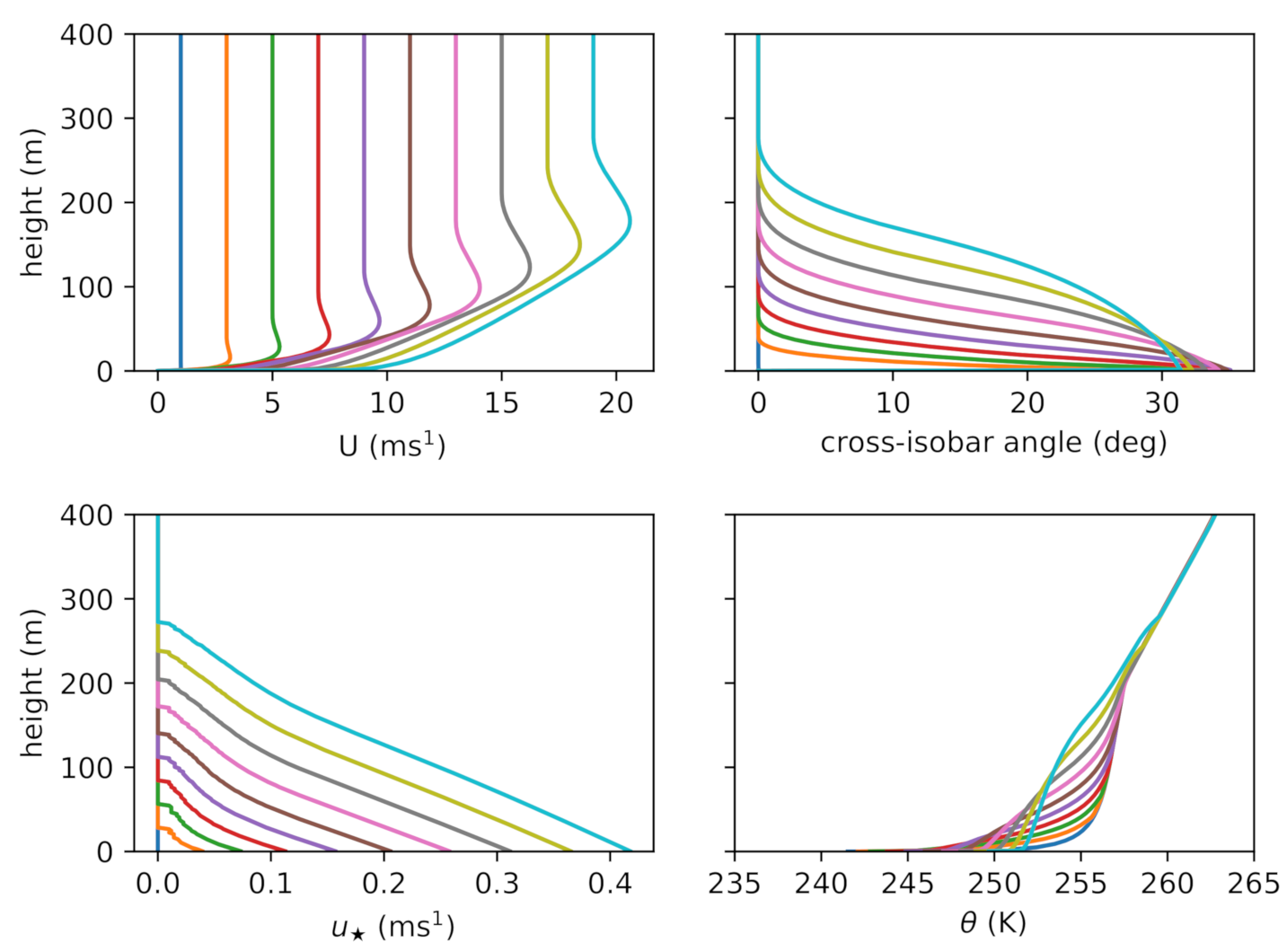
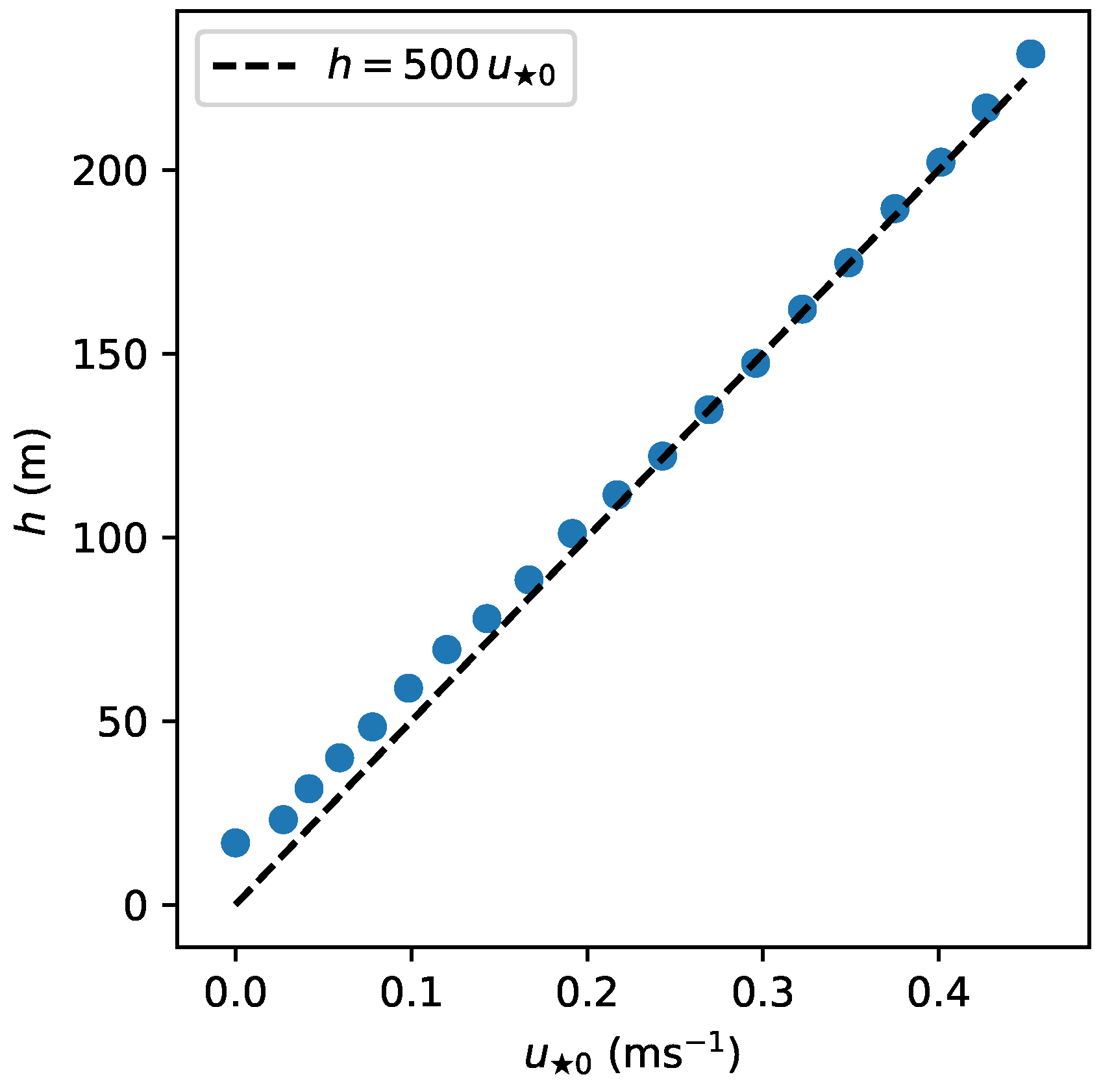
3.3. Single-Column Modeling
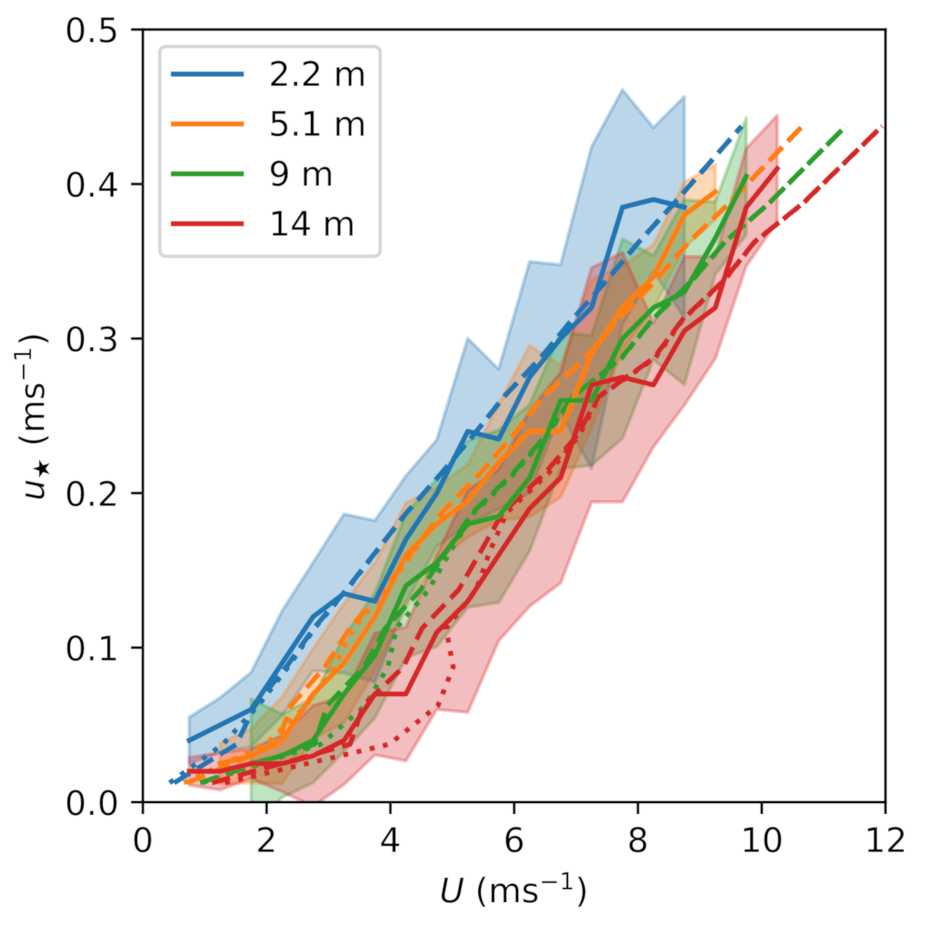
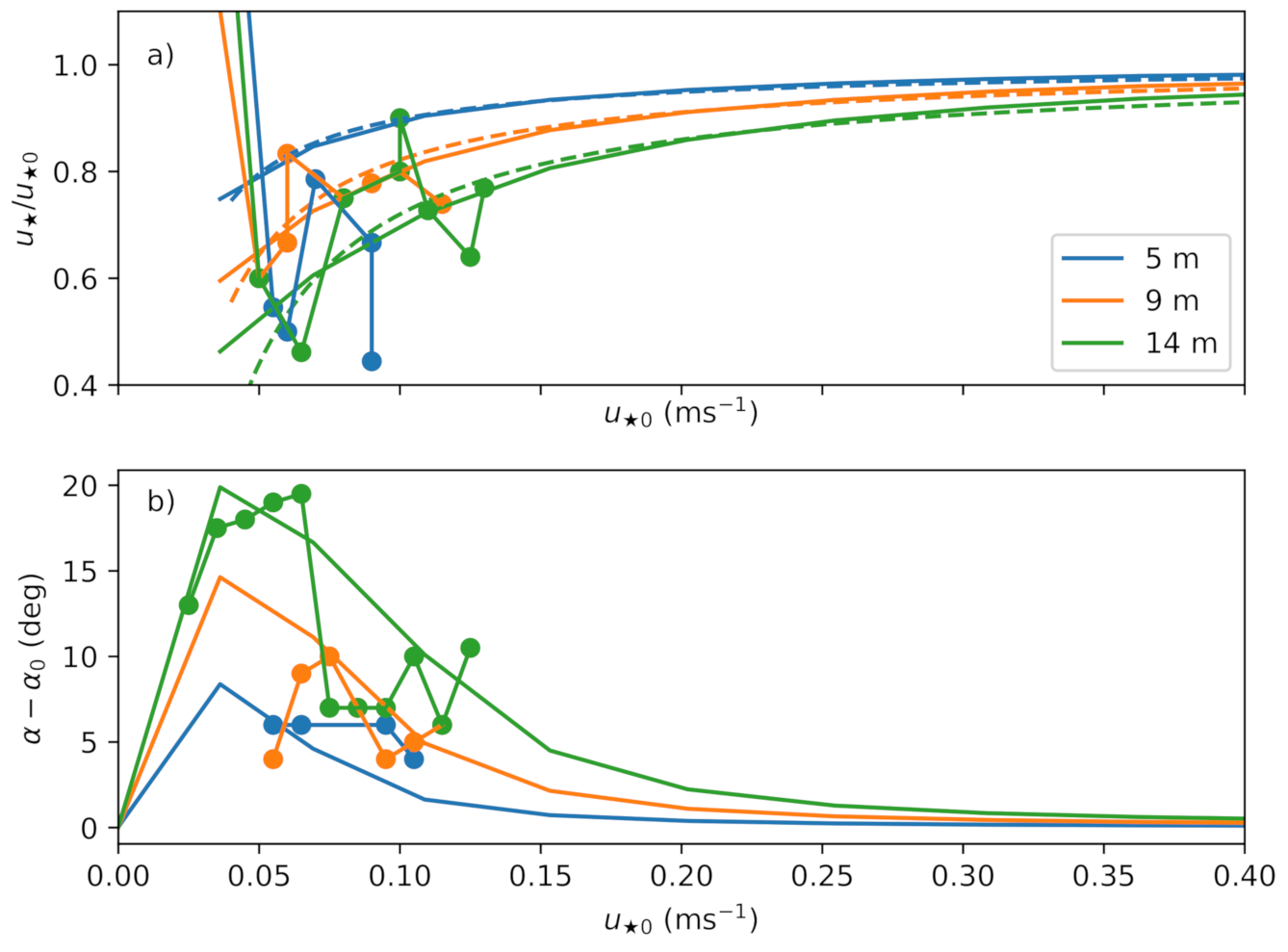
4. Extended MOST
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Vihma, T.; Pirazzini, R.; Fer, I.; Renfrew, I.A.; Sedlar, J.; Tjernström, M.; Lüpkes, C.; Nygård, T.; Notz, D.; Weiss, J.; et al. Advances in understanding and parameterization of small-scale physical processes in the marine Arctic climate system: A review. Atmos. Chem. Phys. 2014, 14, 9403–9450. [Google Scholar] [CrossRef] [Green Version]
- Zilitinkevich, S.S.; Esau, I.N. Resistance and heat-transfer laws for stable and neutral planetary boundary layers: Old theory advanced and re-evaluated. Q. J. R. Meteorol. Soc. 2005, 131, 1863–1892. [Google Scholar] [CrossRef] [Green Version]
- Chechin, D.G.; Makhotina, I.A.; Lüpkes, C.; Makshtas, A.P. Effect of Wind Speed and Leads on Clear-Sky Cooling over Arctic Sea Ice during Polar Night. J. Atmos. Sci. 2019, 76, 2481–2503. [Google Scholar] [CrossRef]
- De Wiel, B.J.H.V.; Moene, A.F.; Jonker, H.J.J.; Baas, P.; Basu, S.; Donda, J.M.M.; Sun, J.; Holtslag, A.A.M. The Minimum Wind Speed for Sustainable Turbulence in the Nocturnal Boundary Layer. J. Atmos. Sci. 2012, 69, 3116–3127. [Google Scholar] [CrossRef] [Green Version]
- De Wiel, B.J.H.V.; Vignon, E.; Baas, P.; van Hooijdonk, I.G.S.; van der Linden, S.J.A.; van Hooft, J.A.; Bosveld, F.C.; de Roode, S.R.; Moene, A.F.; Genthon, C. Regime Transitions in Near-Surface Temperature Inversions: A Conceptual Model. J. Atmos. Sci. 2017, 74, 1057–1073. [Google Scholar] [CrossRef] [Green Version]
- Vignon, E.; van de Wiel, B.J.H.; van Hooijdonk, I.G.S.; Genthon, C.; van der Linden, S.J.A.; van Hooft, J.A.; Baas, P.; Maurel, W.; Traullé, O.; Casasanta, G. Stable boundary layer regimes at Dome C, Antarctica: Observation and analysis. Q. J. R. Meteorol. Soc. 2017, 143, 1241–1253. [Google Scholar] [CrossRef]
- Nieuwstadt, F.T.M. The Turbulent Structure of the Stable, Nocturnal Boundary Layer. J. Atmos. Sci. 1984, 41, 2202–2216. [Google Scholar] [CrossRef]
- Nieuwstadt, F.T.M. Some aspects of the turbulent stable boundary layer. Bound.-Layer Meteorol. 1984, 30, 31–55. [Google Scholar] [CrossRef]
- Basu, S.; Porté-agel, F.; Foufoula-Georgiou, E.; Vinuesa, J.F.; Pahlow, M. Revisiting the Local Scaling Hypothesis in Stably Stratified Atmospheric Boundary-Layer Turbulence: An Integration of Field and Laboratory Measurements with Large-Eddy Simulations. Bound.-Layer Meteorol. 2006, 119, 473–500. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Mahrt, L.; Banta, R.M.; Pichugina, Y.L. Turbulence Regimes and Turbulence Intermittency in the Stable Boundary Layer during CASES-99. J. Atmos. Sci. 2012, 69, 338–351. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Lenschow, D.H.; LeMone, M.A.; Mahrt, L. The Role of Large-Coherent-Eddy Transport in the Atmospheric Surface Layer Based on CASES-99 Observations. Bound.-Layer Meteorol. 2016, 160, 83–111. [Google Scholar] [CrossRef]
- Sun, J.; Takle, E.S.; Acevedo, O.C. Understanding Physical Processes Represented by the Monin–Obukhov Bulk Formula for Momentum Transfer. Bound.-Layer Meteorol. 2020, 177, 69–95. [Google Scholar] [CrossRef]
- Grisogono, B.; Sun, J.; Belušić, D. A note on MOST and HOST for turbulence parametrization. Q. J. R. Meteorol. Soc. 2020, 146, 1991–1997. [Google Scholar] [CrossRef]
- Chenge, Y.; Brutsaert, W. Flux-profile Relationships for Wind Speed and Temperature in the Stable Atmospheric Boundary Layer. Bound.-Layer Meteorol. 2005, 114, 519–538. [Google Scholar] [CrossRef]
- Uttal, T.; Curry, J.A.; McPhee, M.G.; Perovich, D.K.; Moritz, R.E.; Maslanik, J.A.; Guest, P.S.; Stern, H.L.; Moore, J.A.; Turenne, R.; et al. Surface Heat Budget of the Arctic Ocean. Bull. Am. Meteorol. Soc. 2002, 83, 255–276. [Google Scholar] [CrossRef] [Green Version]
- Grachev, A.A.; Fairall, C.W.; Persson, P.O.G.; Andreas, E.L.; Guest, P.S. Stable Boundary-Layer Scaling Regimes: The Sheba Data. Bound.-Layer Meteorol. 2005, 116, 201–235. [Google Scholar] [CrossRef]
- Grachev, A.A.; Andreas, E.L.; Fairall, C.W.; Guest, P.S.; Persson, P.O.G. The Critical Richardson Number and Limits of Applicability of Local Similarity Theory in the Stable Boundary Layer. Bound.-Layer Meteorol. 2013, 147, 51–82. [Google Scholar] [CrossRef] [Green Version]
- Andreas, E.; Fairall, C.; Guest, P.; Persson, O. Tower, 5-Level Hourly Measurements Plus Radiometer and Surface Data at Met City (ASFG); Version 1.0; UCAR/NCAR-Earth Observing Laboratory: Boulder, CO, USA, 2007. [Google Scholar] [CrossRef]
- Persson, P.O.G.; Fairall, C.W.; Andreas, E.L.; Guest, P.S.; Perovich, D.K. Measurements near the Atmospheric Surface Flux Group tower at SHEBA: Near-surface conditions and surface energy budget. J. Geophys. Res. Ocean. 2002, 107, SHE 21-1–SHE 21-35. [Google Scholar] [CrossRef] [Green Version]
- Stramler, K.; Genio, A.D.D.; Rossow, W.B. Synoptically Driven Arctic Winter States. J. Clim. 2011, 24, 1747–1762. [Google Scholar] [CrossRef]
- Makhotina, I.A.; Makshtas, A.P.; Chechin, D.G. Meteorological winter conditions in the Central Arctic according to the drifting stations “North Pole 35–40”. IOP Conf. Ser. Earth Environ. Sci. 2019, 231, 012031. [Google Scholar] [CrossRef] [Green Version]
- Gryanik, V.M.; Lüpkes, C.; Grachev, A.; Sidorenko, D. New Modified and Extended Stability Functions for the Stable Boundary Layer based on SHEBA and Parametrizations of Bulk Transfer Coefficients for Climate Models. J. Atmos. Sci. 2020, 77, 2687–2716. [Google Scholar] [CrossRef]
- Businger, J.A.; Wyngaard, J.C.; Izumi, Y.; Bradley, E.F. Flux-Profile Relationships in the Atmospheric Surface Layer. J. Atmos. Sci. 1971, 28, 181–189. [Google Scholar] [CrossRef]
- Dyer, A.J. A review of flux-profile relationships. Bound.-Layer Meteorol. 1974, 7, 363–372. [Google Scholar] [CrossRef]
- Grachev, A.A.; Andreas, E.L.; Fairall, C.W.; Guest, P.S.; Persson, P.O.G. SHEBA flux–profile relationships in the stable atmospheric boundary layer. Bound.-Layer Meteorol. 2007, 124, 315–333. [Google Scholar] [CrossRef]
- Vihma, T.; Hartmann, J.; Lüpkes, C. A Case Study of An On-Ice Air Flow Over The Arctic Marginal Sea-Ice Zone. Bound.-Layer Meteorol. 2003, 107, 189–217. [Google Scholar] [CrossRef]
- Therry, G.; Lacarrère, P. Improving the Eddy Kinetic Energy model for planetary boundary layer description. Bound.-Layer Meteorol. 1983, 25, 63–88. [Google Scholar] [CrossRef]
- England, D.E.; McNider, R.T. Stability functions based upon shear functions. Bound.-Layer Meteorol. 1995, 74, 113–130. [Google Scholar] [CrossRef]
- Savijärvi, H.; Kauhanen, J. High resolution numerical simulations of temporal and vertical variability in the stable wintertime boreal boundary layer: A case study. Theor. Appl. Climatol. 2001, 70, 97–103. [Google Scholar] [CrossRef]
- Cuxart, J.; Holtslag, A.A.M.; Beare, R.J.; Bazile, E.; Beljaars, A.; Cheng, A.; Conangla, L.; Ek, M.; Freedman, F.; Hamdi, R.; et al. Single-Column Model Intercomparison for a Stably Stratified Atmospheric Boundary Layer. Bound.-Layer Meteorol. 2006, 118, 273–303. [Google Scholar] [CrossRef] [Green Version]
- Gryanik, V.M.; Lüpkes, C. An Efficient Non-iterative Bulk Parametrization of Surface Fluxes for Stable Atmospheric Conditions Over Polar Sea-Ice. Bound.-Layer Meteorol. 2018, 166, 301–325. [Google Scholar] [CrossRef]
- Chou, M.D.; Suarez, M.J.; Liang, X.J.; Yan, M.H. A Thermal Infrared Parameterization for Atmospheric Studies; NASA Tech. Rep. Series on Global Modeling and Data Assimilation NASA/TM-2001-104606; Goddard Space Flight Center: Greenbelt, MD, USA, 2001; Volume 19.
- Savijärvi, H. Stable boundary layer: Parametrizations for local and larger scales. Q. J. R. Meteorol. Soc. 2009, 135, 914–921. [Google Scholar] [CrossRef]
- Baas, P.; van de Wiel, B.J.H.; van Meijgaard, E.; Vignon, E.; Genthon, C.; van der Linden, S.J.A.; de Roode, S.R. Transitions in the wintertime near-surface temperature inversion at Dome C, Antarctica. Q. J. R. Meteorol. Soc. 2019, 145, 930–946. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sorbjan, Z.; Grachev, A.A. An Evaluation of the Flux–Gradient Relationship in the Stable Boundary Layer. Bound.-Layer Meteorol. 2010, 135, 385–405. [Google Scholar] [CrossRef]
- Mahrt, L.; Sun, J.; Stauffer, D. Dependence of Turbulent Velocities on Wind Speed and Stratification. Bound.-Layer Meteorol. 2015, 155, 55–71. [Google Scholar] [CrossRef] [Green Version]
- Van Hooijdonk, I.G.S.; Donda, J.M.M.; Clercx, H.J.H.; Bosveld, F.C.; van de Wiel, B.J.H. Shear Capacity as Prognostic for Nocturnal Boundary Layer Regimes. J. Atmos. Sci. 2015, 72, 1518–1532. [Google Scholar] [CrossRef] [Green Version]
- Svensson, G.; Holtslag, A.A.M. Analysis of Model Results for the Turning of the Wind and Related Momentum Fluxes in the Stable Boundary Layer. Bound.-Layer Meteorol. 2009, 132, 261–277. [Google Scholar] [CrossRef]
- Sorbjan, Z. A Study of the Stable Boundary Layer Based on a Single-Column K-Theory Model. Bound.-Layer Meteorol. 2012, 142, 33–53. [Google Scholar] [CrossRef] [Green Version]
- Sterk, H.A.M.; Steeneveld, G.J.; Holtslag, A.A.M. The role of snow-surface coupling, radiation, and turbulent mixing in modeling a stable boundary layer over Arctic sea ice. J. Geophys. Res. Atmos. 2013, 118, 1199–1217. [Google Scholar] [CrossRef]
- Zilitinkevich, S.; Mironov, D.V. A multi-limit formulation for the equilibrium depth of a stably stratified boundary layer. Bound.-Layer Meteorol. 1996, 81, 325–351. [Google Scholar] [CrossRef]
- Zilitinkevich, S.; Baklanov, A. Calculation of the height of the stable boundary layer in practical applications. Bound.-Layer Meteorol. 2002, 105, 389–409. [Google Scholar] [CrossRef]
- Vickers, D.; Mahrt, L. Evaluating Formulations of Stable Boundary Layer Height. J. Appl. Meteorol. 2004, 43, 1736–1749. [Google Scholar] [CrossRef] [Green Version]
- Steeneveld, G.J.; van de Wiel, B.J.H.; Holtslag, A.A.M. Diagnostic Equations for the Stable Boundary Layer Height: Evaluation and Dimensional Analysis. J. Appl. Meteorol. Climatol. 2007, 46, 212–225. [Google Scholar] [CrossRef]
- Rossby, C.G.; Montgomery, R.B. The Layer of Frictional Influence in Wind and Ocean Currents; Massachusetts Institute of Technology and Woods Hole Oceanographic Institution: Cambridge, MA, USA, 1935. [Google Scholar]
- Pollard, R.T.; Rhines, P.B.; Thompson, R.O. The deepening of the wind-mixed layer. Geophys. Fluid Dyn. 1973, 4, 381–404. [Google Scholar] [CrossRef]
- Kitaigorodskii, S.; Joffre, S.M. In search of a simple scaling for the height of the stratified atmospheric boundary layer. Tellus A 1988, 40, 419–433. [Google Scholar] [CrossRef]
- Gryning, S.E.; Batchvarova, E.; Brümmer, B.; Jørgensen, H.; Larsen, S. On the extension of the wind profile over homogeneous terrain beyond the surface boundary layer. Bound.-Layer Meteorol. 2007, 124, 251–268. [Google Scholar] [CrossRef]
- Grachev, A.A.; Fairall, C.W. Dependence of the Monin–Obukhov Stability Parameter on the Bulk Richardson Number over the Ocean. J. Appl. Meteorol. 1997, 36, 406–414. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chechin, D. On the u??U Relationship in the Stable Atmospheric Boundary Layer over Arctic Sea Ice. Atmosphere 2021, 12, 591. https://doi.org/10.3390/atmos12050591
Chechin D. On the u??U Relationship in the Stable Atmospheric Boundary Layer over Arctic Sea Ice. Atmosphere. 2021; 12(5):591. https://doi.org/10.3390/atmos12050591
Chicago/Turabian StyleChechin, Dmitry. 2021. "On the u??U Relationship in the Stable Atmospheric Boundary Layer over Arctic Sea Ice" Atmosphere 12, no. 5: 591. https://doi.org/10.3390/atmos12050591
APA StyleChechin, D. (2021). On the u??U Relationship in the Stable Atmospheric Boundary Layer over Arctic Sea Ice. Atmosphere, 12(5), 591. https://doi.org/10.3390/atmos12050591