Applications of Radar Data Assimilation with Hydrometeor Control Variables within the WRFDA on the Prediction of Landfalling Hurricane IKE (2008)

Abstract

The impact of assimilating radar radial velocity and reflectivity on the analyses and forecast of Hurricane IKE is investigated within the framework of the WRF (Weather Research and Forecasting) model and its three-dimensional variational (3DVar) data assimilation system, including the hydrometeor control variables. Hurricane IKE in the year 2008 was chosen as the study case. It was found that assimilating radar data is able to effectively improve the small-scale information of the hurricane vortex area in the model background. Radar data assimilation experiments yield significant cyclonic wind increments in the inner-core area of the hurricane, enhancing the intensity of the hurricane in the model background. On the other hand, by extending the traditional control variables to include the hydrometeor control variables, the assimilation of radar reflectivity can effectively adjust the water vapor and hydrometeors of the background, further improving the track and intensity forecast of the hurricane. The precipitation forecast skill is also enhanced to some extent with the radar data assimilation, especially with the extended hydrometeor control variables.

1. Introduction

Tropical cyclones (TC) have become one of the most important natural disasters in the world because of their great destructive power. The accurate forecast of TC track and intensity can greatly reduce unnecessary economic losses. In the past 20 years, some achievements have been made in the prediction of TC track, but there are still many works to be further done in terms of TC intensity prediction (Dong and Xue [1] (2013)). For a large number of TCs, most of their lifespan is in the open ocean, and their movement and development are often influenced by the large-scale steering flow and the underlying surface. Therefore, the improvement of TC prediction mainly depends on numerical weather prediction (NWP). With the development of the NWP model, the accuracy of the initial condition (IC) has become a vital factor in determining the forecast skills of the TC systems.

Generally, conventional observation data are relatively scarcely distributed in the open ocean with relatively low temporal resolution. Thus, it is highly essential to introduce unconventional observation data (such as radar observations, satellite observations, etc.) to improve the ICs of the NWP model. As one of the most outstanding observing systems, Doppler weather radar is able to provide multi-dimensional thermal and dynamic observations [2,3]. Radar radial velocity and reflectivity can provide information on wind field and hydrometeors, respectively. How to effectively use radar observations to initialize the NWP model becomes a notable issue.

In the past decades, experts and scholars have done a lot of research on radar data assimilation. Xiao et al. [4] (2007) developed a direct assimilation scheme of radar reflectivity using total hydrometeors as the control variable, which used the warm rain scheme to refine total hydrometeors into water vapor, cloud rain, and rain phase states. Gao et al. [5] (2012) used the background temperature field of the NWP model to divide the hydrometeors, introduced the ice phase hydrometeors, and improved the analysis and prediction of storms; Wang et al. [6] (2013) used an indirect radar reflectivity assimilation scheme to improve the prediction of local precipitation by introducing a new observation operator based on the z-qr (reflectivity-rain) equation to avoid the linearization error of the observation operator. Several studies have focused on TC initialization based on radar data assimilation, among which most researches mainly focused on radar radial velocity observations [7,8,9,10,11]. However, the assimilation of radar reflectivity data, especially those with multiple hydrometeor control variables, obviously need more detailed investigation.

The control variable is the key component of the variational data assimilation technique in terms of optimizing the meteorological state by minimizing the cost function. Generally, the state control variables of the NWP model, including [12]: (1) momentum related control variables (e.g., stream function ψ and velocity potential χ); (2) unbalanced temperature (${\mathrm{T}}_{\mathrm{u}}$); (3) unbalanced surface pressure (${\mathrm{P}}_{\mathrm{s},\mathrm{u}}$); and (4) humidity related control variables (e.g., pseudo relative humidity ($\mathrm{R}{\mathrm{H}}_{\mathrm{s}}$)), are adjusted or expanded to better optimize the analysis. Sun et al. [13] (2016) used horizontal wind components as control variables for improving the convective scale analysis. Multivariable correlation methods are proposed by Michel et al. (2011) and Descombes et al. (2015), which consider hydrometeors for the control variables to improve the analysis [14,15]. Meng et al. [16] (2018) adopted the EnVar method to include hydrometeors variable to effectively improve the simulation of the convective available potential energy and humidity of a convective system, leading to improvement in the prediction for the spatial distribution and intensity of the precipitation. Zhao et al. [17] (2008) updated the hydrometers in the NWP model directly by applying general analytic relationship when assimilating the radar reflectivity in two storm cases with promising results. As far as the authors know, there is very few published work with radar reflectivity within the framework of WRFDA with UV control variables (Li et al., (2016) [18], Sun et al., (2016) [13]). The control variables related to hydrometeors have become one of the key technologies to effectively assimilate hydrometeor-related observations, such as radar reflectivity. However, up to now, there are not many researches on radar data assimilation technology based on the control variables of hydrometeors, and there are few researches on radar reflectivity assimilation for landing TCs in America. Therefore, this study will discuss the impact of assimilation of radar reflectivity on the analysis and prediction of Hurricane IKE (2008) by using control variables from hydrometeors based on the WRF model and its assimilation system.

2. Methodology

2.1. WRFDA 3DVar Data Assimilation System

Data assimilation aims to obtain optimized initial conditions of the NWP model by analyzing multi-source observations [19,20]. The typical three-dimensional variational DA technique in WRFDA specific formula is as follows:

$$J={(x-x_b)}^T{B}^{-1}(x-x_b)+{(y^o-H(x))}^T{R}^{-1}(y^o-H(x))$$

(1)

where vectors x and x_b represent the atmospheric state and background state [21], y⁰ represents the observation vector. H is the observation operator. B and R are background error covariance matrix, and observation error covariance matrix, respectively.

In this study, the NMC (National Meteorological Center) method [22] is used to estimate the background error covariance. The differences in the forecasts valid at the same time but with different forecast lengths (24 h forecast and 12 h forecast) are taken as the approximation of the forecast error. The forecasts are launched twice a day from 1 September to 20 September 2008 to provide a large number of prediction samples for the estimation of background error covariance. According to the differences between samples, estimate the covariance matrix of background error [18], as follows:

$$B\approx \overline{(x^{24}-x^{12})(x^{24}-x^{12}{)}^{\mathrm{T}}}$$

(2)

Among them, $x^{24}$ and $x^{12}$ are 24 h and 12 h forecasts, respectively. It should be pointed out that both prediction fields have errors and are expressed as follows:

$$x^{24}{=x}^{\mathrm{truth}}{+\mathsf{\epsilon }}^{24}{+\mathrm{b}}^{24}$$

(3)

$$x^{12}=x^{\mathrm{truth}}+{\mathsf{\epsilon }}^{12}+b^{12}$$

(4)

Here, $x^{\mathrm{truth}}$ represents the real value. $b^{24}$ and $b^{12}$ are the biases in each prediction. ${\mathsf{\epsilon }}^{24}$ and ${\mathsf{\epsilon }}^{12}$ are random errors. Suppose that the prediction of 24 h and 12 h is unbiased, or the deviation is constant in time, because $b^{24}$ = $b^{12}$, the prediction difference is expressed as:

$$x^{\mathrm{diff}}={\mathsf{\epsilon }}^{24}-{\mathsf{\epsilon }}^{12}$$

(5)

B matrix can be expressed by formula (6):

$$B\approx \overline{(x^{\mathrm{diff}}){(x^{\mathrm{diff}})}^{\mathrm{T}}}=\overline{({\mathsf{\epsilon }}^{24}-{\mathsf{\epsilon }}^{12}){({\mathsf{\epsilon }}^{24}-{\mathsf{\epsilon }}^{12})}^{\mathrm{T}}},$$

(6)

In the data assimilation system, due to the large dimension of the background error covariance matrix, it is difficult to conduct the minimum. Generally, the B matrix is decomposed into $B=U{U}^T$, and the following preprocessing process can be formed through decomposition $Uv=x-x_b$. $\delta x=x-x_b$ stands for the analysis increment and $v$ represents the control variable. One approximation is applied as:

$$y^o-\mathit{H}(x)\approx y^o-\mathit{H}(x_b)-H(x-x_b),$$

(7)

where H is the linearized observation operator of H. The final format of the cost function of 3DVAR is:

$$J=\frac{1}{2}{v}^{T}v+\frac{1}{2}{(d-HUv)}^T{R}^{-1}(d-HUv),$$

(8)

where $d=y^o-H(x_b)$ is the innovation.

There are two types of momentum control variables in WRFDA-3DVar. The default option in WRFDA-3DVar is the CV5 scheme. The control variables include the stream function ψ, the unbalanced velocity potential x_u, the unbalanced temperature T_u, and the unbalanced surface pressure ${\mathrm{P}}_{\mathrm{su}}$ and pseudo relative humidity RH_s. Another option is the CV7 scheme in which velocity component (U, V) is used as a dynamic control variable. Other control variables include total temperature (T), pseudo relative humidity (RH_S), and total surface pressure (P_S). Previous studies have discussed the influence of the two different momentum control variables in assimilating radar radial velocity [9,12,13,23].

In order to make full use of the radar data, control variables are extended to include cloud and precipitation information. The control variables used in this study can be designed as follows:

CV5: stream function (ψ), unbalanced velocity potential (Chi_u), unbalanced surface pressure (Ps_u), unbalanced temperature (T_u), pseudo relative humidity (RH_s).

CV7: zonal wind (U), meridional wind (V), surface pressure (P_s), temperature (T), pseudo relative humidity (RH_s).

CV8: zonal wind (U), meridional wind (V), surface pressure (P_s), temperature (T), pseudo relative humidity (RH_s), cloud water (q_c), rain water (q_r), ice water (q_i), snow water (q_s), graupel (q_g).

2.2. Radar Observation Operator

According to Tong and Xue (2005) [24], the observation operator of radar radial wind is calculated based on the wind field as:

$$V_r=u\frac{x-x_i}{r_i}+v\frac{y-y_i}{r_i}+\left(w-v_T\right)\frac{z-z_i}{r_i}$$

(9)

where (x, y, z) denotes the radar location elevation, (x_i, y_i, z_i) is the location for the radar observation, and (u, v, w) is the three-dimensional wind field. r_i is the distance between the observations and the radar location. v_T (m/s) is the terminal speeds. The effects of atmospheric refraction and earth curvature on radar-beam height and slope angle is neglected [25].

For reflectivity factor (RF) data, it should be noted that the z-q_r (reflectivity-rain) relationship [26] is used as the observation operator in WRFDA for direct assimilation. Usually, the humidity control variable is expanded to the total hydrometeor variable with the warm rain scheme without any ice phase process considered. Thus, there are obvious defects in terms of describing the microphysical process of the deep convection system. In addition, WRFDA adopts the incremental method in the minimization based on the linearization of the forward observation operator. The linearization of the RF operator is rather sensitive to the humidity field in the model background field. When the model background field is dry, a large analysis error is introduced. Therefore, indirect assimilation of RF data is popularly used based on the assumption that the water vapor in the cloud is saturated (Wang et al., 2013) [27]. To be specific, when the reflectivity factor is greater than 30 dBZ, the relative humidity in the cloud is considered as 100%. In this way, the pseudo observation ${\mathrm{q}}_{\mathrm{v}}^{\mathrm{o}}$ can be obtained based on the pressure and temperature at that time. For this pseudo observation ${\mathrm{q}}_{\mathrm{v}}^{\mathrm{o}}$, its nonlinear observation operator is:

$$q_v=rh\times q_{vs},$$

(10)

where q_v stands for the water vapor mixing ratio (unit, kg/kg), rh is the relative humidity, and q_vs is the saturated water vapor mixing ratio, respectively. The forward observation operator of reflectivity factor is based on the interaction of rain mixing ratio, snow mixing ratio, and graupel mixing ratio. A more advanced water vapor assimilation technique to alleviate the potential overprediction of precipitation is beyond the scope of the current study (refer to Xu et al. (2010) [28]).

3. Case Introduction and Experimental Setup

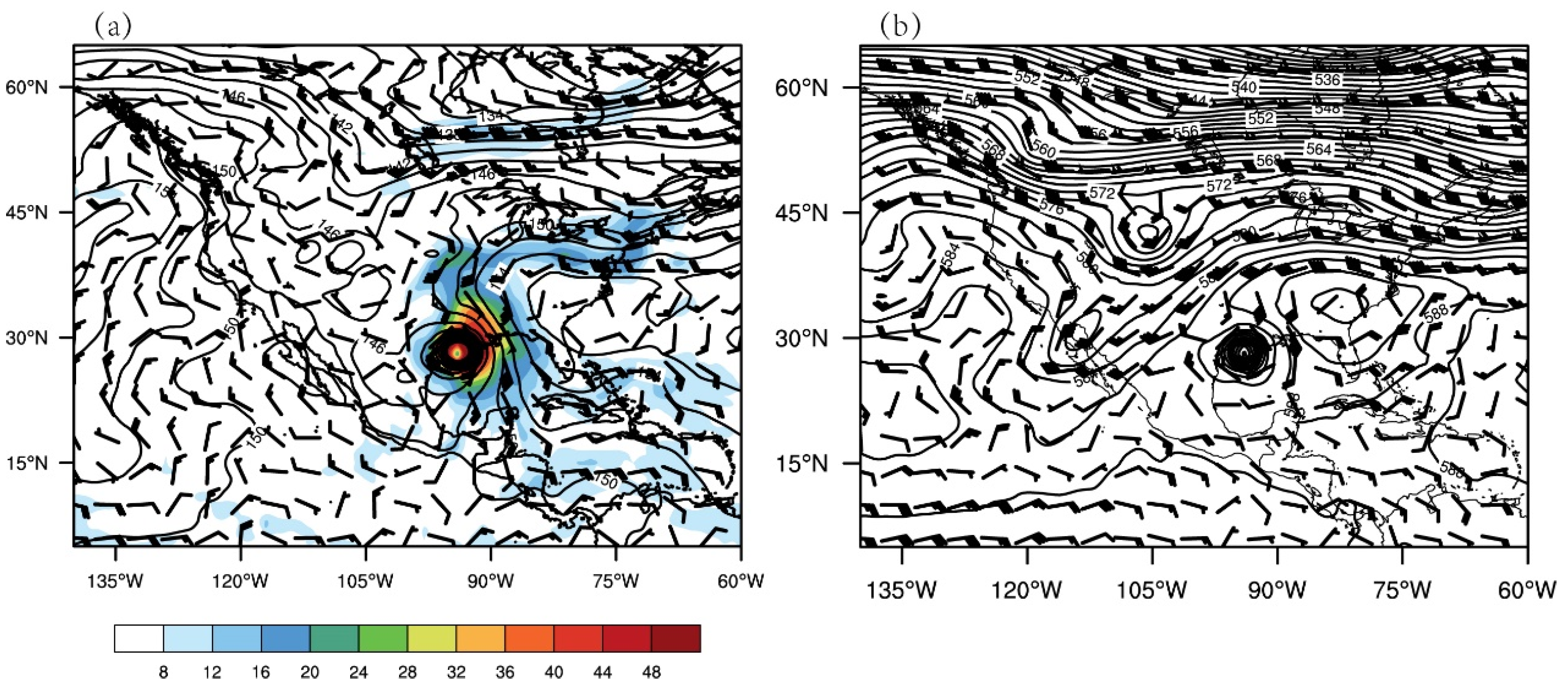
3.1. Hurricane IKE

On 1 September 2008, Hurricane IKE developed from a tropical disturbance in the west of Cape Verde. Later, its intensity gradually increased to Category 4 hurricane in the central Atlantic on September 4 by moving westward. On September 9, IKE made landfall in eastern Cuba and was weakened prior to entering the Gulf of Mexico. On 13 September, it increased by the time of the final landfall in Galveston, Texas, as an extratropical storm, causing considerable damage inland.

The environment had a great influence on the evolution of TC. Figure 1 is the circulation from FNL analysis data. As can be seen from Figure 1a at 850 hPa, the TC center was affected by the southerly wind flow, which is able to supply sufficient moisture. It is noted that the water vapor flux near the TC center reached 40 g/(cm·hPa·s). At 500 hPa in Figure 1b, it can be seen that IKE was embedded in the southwest periphery of the subtropical. The easterly jet on the south side of the subtropical made the high-level TC outflow stronger, leading the TC to move westward (Wang (2011) [29]).

3.2. Model and Experimental Design

The WRF model is a commonly used NWP model in weather research and forecast, which mainly serves the meteorological application of space scale from tens of meters to thousands of kilometers. In this study, the ARW (the advanced research WRF) version for research users is used. In this study, the 4.2 version of the WRF model is used to simulate Hurricane IKE, and the center of simulation domain is set at 30° N, −95° W. The resolution of the domain is 4 km (Figure 2) following Dong and Xue [1] (2013), and Li et al., [30] (2015). The number of grid points of the domain are 501 × 501, respectively, and the number of vertical layers is 53 with 10 hPa as the model top. To provide initial and boundary conditions for all experiments, 0.5° GFS (Global Forecast System) data with a 6-hour interval are used. The parameterization of the numerical experiment includes: (1) RRTM (rapid radiative transfer model) long wave radiation scheme, (2) WDM6 (WRF Double-Moment 6-class) Microphysics scheme, (3) Dudhia short wave radiation scheme, (4) Noah land surface model land surface scheme, (5) MM5 similarity near ground surface scheme, and (6) YSU (Yonsei University) boundary layer scheme.

The radar data used in this study are from the radars of Weather Surveillance Radar 88 Doppler (WSR-88D) Houston, Texas (KHGX), and Lake Charles, Louisiana (KLCH). Before the data assimilation, the 88D2ARPS module is used to perform the quality control of the radar observations. Finally, the processed data are interpolated to the grid of WRF model for assimilation. In this study, the observation error of radial wind is set as 2.5 m/s, and the observation error of reflectivity is 5 dBZ. The details of the radar observations can be found in Shen et al. (2017) [7] for reference.

In this study, three experiments are performed. The first experiment is the control experiment named as Conv, which only assimilates conventional observations from Global Telecommunications System by using the UV control variable scheme; the second experiment conducted the radar data assimilation with the same control variable scheme as in the first experiment; the third experiment further includes the control variables of hydrometeors in the radar data assimilation named as DA_Radar_CVH.

In the control experiment, a 6 h forecast is first carried out from 1800 UTC on 12 September 2008, before GTS conventional observations are assimilated from 0000 UTC on 13 September 2008 to 0600 UTC on 13 September 2008 every 30 min. At the end of DA, an 18 h deterministic forecast is launched at 0600 UTC on 13 September 2008. Figure 3 shows the distribution of conventional observation data of GTS in two different analysis times.

Similarly, two sets of radar data assimilation experiments are conducted with the same background used in the DA_Conv experiment at 0000 UTC 13 September. Then, the radar radial velocity and reflectivity were assimilated from 0000 UTC 13 September to 0600 UTC 13 September every 30 min. With the final analysis, a deterministic 18 h forecast is carried out from 0600 UTC 13 September to 0000 UTC 14 September (Figure 4).

4. Results

4.1. Wind Analysis

Figure 5 shows the wind increment at 700 hPa of the radar DA experiment at the first assimilation time (i.e., 0000 UTC 13 September). The corresponding radar radial velocity from the observation can be referred to in Shen et al. [8] (2018). It can be seen that the inner-core area of TC is totally covered by radar observations, and the wind increment is generated in both the TC core area and the outer environment field. It should be noted that the pattern of wind increment is cyclonic circulation, and the wind increment at the center of TC is most obvious. The results suggested that the intensity of TC simulated by DA_Conv experiment is still weak after assimilating the GTS observation data, which is commonly found in the simulation of the IKE case without any radar data assimilation [1,8]. On the other hand, the direct assimilation of radar radial wind observations is able to enhance the intensity of TC by adjusting the dynamic field of Hurricane IKE.

In order to objectively check whether the radar data are properly assimilated, the scatter plots of the radar radial velocity in the background and the analysis versus the observed radar radial velocity are shown (Figure 6). It can be seen that the scatters of the radar radial velocity of the background and the observations are obviously divergent from the diagonal. It means that the wind speed simulated by the model background has significant bias from the observation. It also can be seen that the assimilation of radar radial wind data is able to adjust the background field significantly in Figure 6b to fit the observation with reduced root mean square error (RMSE) and standard deviation.

The influence of radar data assimilation is also evaluated by calculating the RMSE of the simulated radial velocity against the observed radial velocity. The RMSE variations from each background and analysis for the 13 DA cycles are illustrated in Figure 7. It can be found that after radar data assimilation, the error of the analysis field at each assimilation time is significantly reduced. The RMSE error of the first analysis cycle (0000 UTC on 13 September 2008) is reduced from 9.4 m/s to 2.8 m/s, while the RMSE of the second analysis cycle is 2.6 m/s. Generally, the RMSE of each analysis in subsequent cycles is lower than 2.4 m/s. The magnitude of the RMSE is consistent with the radar observation error of 2.5 m/s that is applied in our current study.

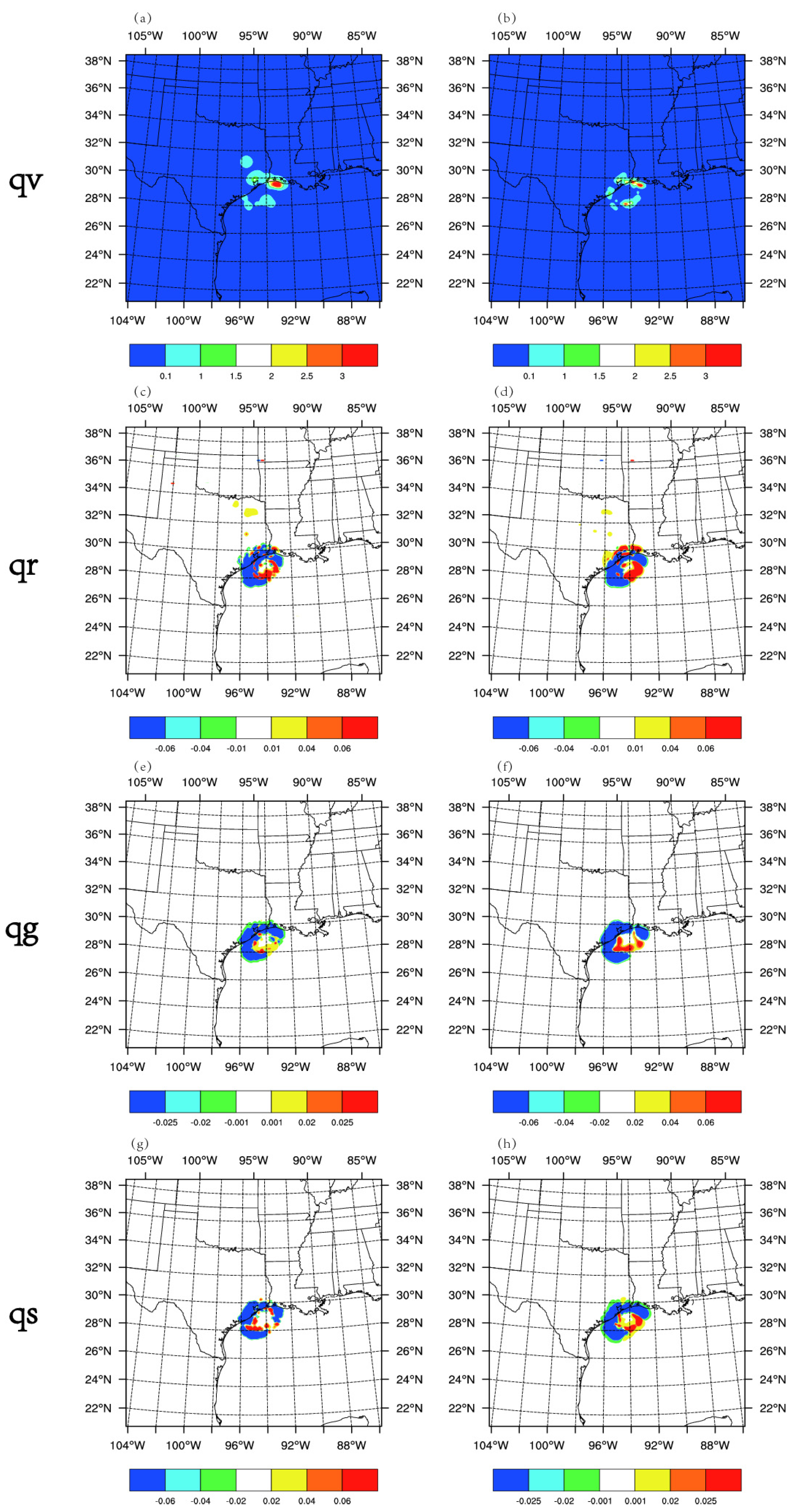
4.2. Increment for the Hydrometeors

Figure 8 shows the increment of the hydrometeors water path of DA_Radar experiment (Figure 8a,c,e,g) and DA_Radar_CVH experiment (Figure 8b,d,f,h) at 0300 UTC on 13 September 2008. In the Radar experiment, increments of these hydrometeors are created in the procedure of radar data assimilation, since the observation operators of the indirect assimilation include the variables of rain, snow water, and hail water. Compared with the Radar experiment, the increment of hydrometeors in the DA_Radar_CVH experiment is more obvious, especially near the core of the TC, due to the use of rain water, snow water, and hail water variables as the inputs in the observation operator as well as the inclusion of all hydrometeors in the control variables.

Figure 9 shows the RMS profile of analysis increment of the model variables and hydrometeors variables at 0000 UTC on 13 September, 0300 UTC on 13 September, 0600 UTC on 13 September. It can be seen that at 0000 UTC on 13 September, the increment of hydrometeors was less than 0.06 g/kg. With the increase in assimilation times, the increment of hydrometeors gradually increased for most hydrometeors. At 0600 UTC on 13 September, the maximum of the hydrometeor increment reached 0.08 g/kg, indicating that the radar data assimilation has made significant modifications in the hydrometeors. In addition, it is worth noting that the maximum increment of q_r existed mainly lower than the 19th level, while the maximum increment of q_s was located higher than the 23th level, and the maximum increment of q_g was at about the 20th level.

4.3. Precipitation Forecasts

The accurate forecast of TC precipitation is of great significance to the flood warning of inland coastal areas. Figure 10 shows the 3 h accumulated precipitation of all the experiments from 0600 UTC, 13 September to 0900 UTC, 13 September. The observed large precipitation center is located southeast of the State of Texas. All the experiments are able to simulate the distribution of the rainfall to some extent, while the precipitation center in the northeast of TC core is largely underestimated. It can be seen that the predicted precipitation intensity in the DA_Conv experiment in the southeast of the TC core is weaker than the observation, while the intensity in two radar data assimilation experiments is stronger than the observation.

Furtherly, the TS (Threat Score) of 3 h accumulated precipitation in each experiment is evaluated for different thresholds (Figure 11). Two radar data assimilation experiments obviously yield higher TS scores than DA_Conv experiment does for all thresholds. For thresholds less than 25mm, the score of DA_Radar_CVH experiment is much higher than those of the Radar experiment. However, the score of the DA_Radar_CVH experiment is similar to that of the Radar experiment for a 25 mm threshold.

4.4. Track Forecasts

In this study, an 18 h deterministic forecast was carried out at the end of the analysis. As shown in Figure 12, the DA_Conv experiment had a significant westward bias for the track, whereas the tracks from the two radar DA experiments match better with the best track. Compared to the Radar experiment, the DA_Radar_CVH experiment yielded track fitting better with the best track, especially after 6 h. The track error of the DA_Conv experiment at the initial time was less than 14 km, while the errors of the two radar data assimilation experiments were reduced to about 4.5 km at the initial time. After 12 h of prediction, it can be found that the tracks from the three experiments all shifted to the northwest to some extent, which is consistent with the best track. At 0000 UTC on 14 September, the track errors of the DA_Conv, DA_Radar, and DA_Radar_CVH experiments were 92.8 km, 70.5 km, and 50.7 km, respectively, which are their maximum errors. Overall, the mean value of track error of DA_Radar_CVH was the smallest of all the three experiments.

5. Summary

In this study, the impact of assimilating radar radial velocity and reflectivity on the analysis and forecast of the Hurricane IKE is evaluated with hydrometeors considered as control variables. The WRF model and its assimilation system WRFDA are applied for the simulation of the strong Hurricane IKE in 2008. The main results and conclusions are as follows:

The TC intensity simulated by the model is weak without radar data assimilation. After assimilating the radar radial velocity data, a more obvious cyclonic circulation is generated in the TC area of the model analysis. Generally, the assimilation of radar radial velocity data can effectively enhance the dynamic field of the TC. The hydrometeors are added to the control variables to improve the analysis of the cloud and precipitation. Outstanding increments for all hydrometeors exist after considering the all-type hydrometeors in the control variables. Compared with the control experiment, the forecast skills of the precipitation and track from the two radar data assimilation experiments are enhanced. The forecasts of the precipitation and track are further improved with the use of the hydrometeor control variables.

Although the results are encouraging, there are areas for further improvements and explorations. Further studies with nested domains with more advanced data assimilation methods (such as 4DVar and ensemble techniques) are needed for better understanding of the impacts of including additional control variables from hydrometers. Our effort in this study represents a step in that direction. It is also worth pointing out that the impact of hydrometeors on the TCs in different regions and different stages of the development of TCs need to be further investigated. For better utilization of all types of observations (such as infrared radiance) that detect hydrometeors, it is necessary to explore the different contributions of various observations in the analytical procedure.