A Graphics Processing Unit (GPU) Approach to Large Eddy Simulation (LES) for Transport and Contaminant Dispersion
Abstract
1. Introduction
1.1. Ensemble-Average and Single-Realization Dispersion Solutions
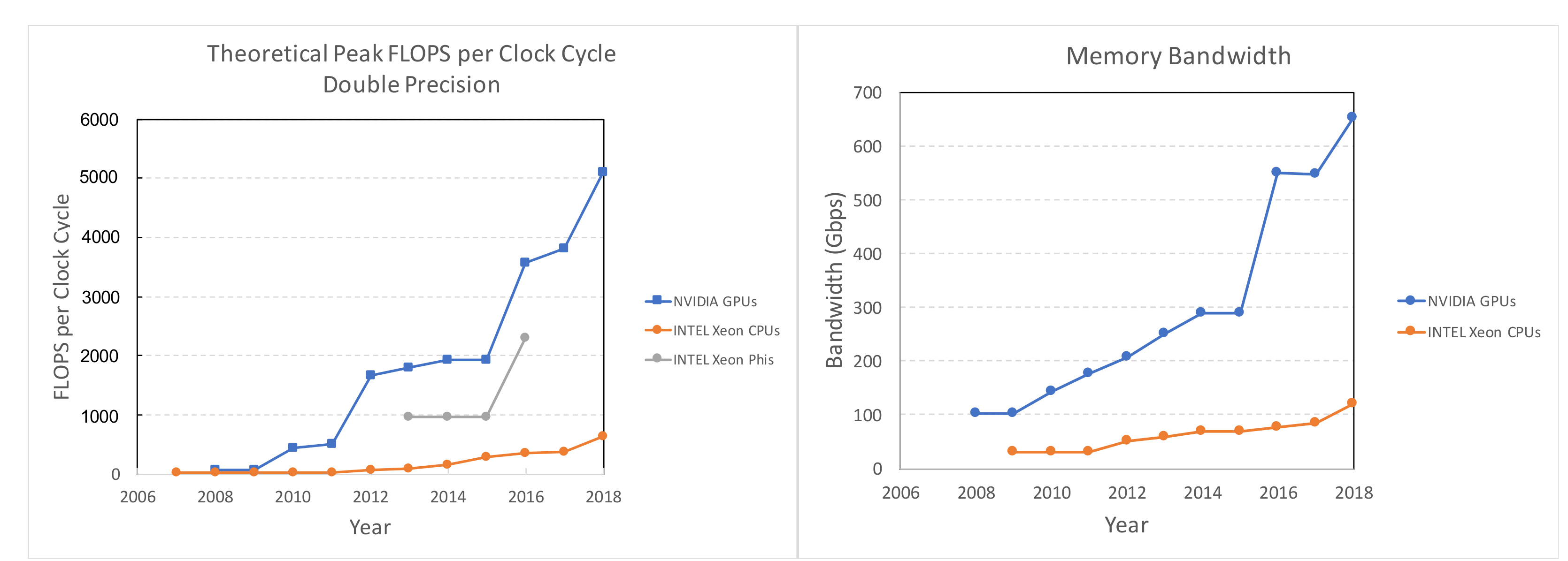
1.2. GPU-Enabled Atmospheric Computing
1.3. Atmospheric Dispersion Modeling on a GPU-LES Model
2. Materials and Methods
2.1. Observational Data
2.1.1. Willis and Deardorff Water Tank Experiments
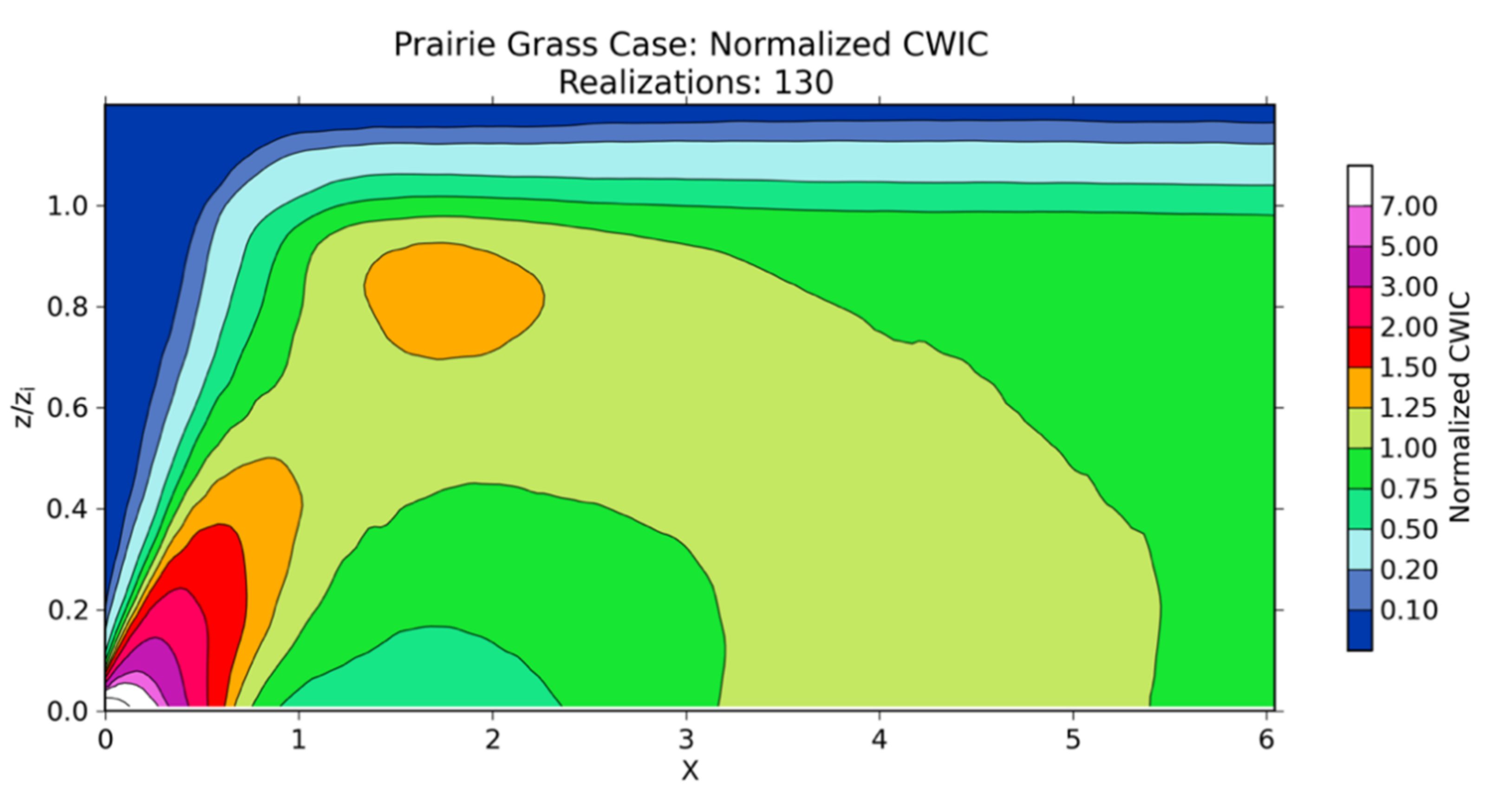
2.1.2. Project Prairie Grass Experiment
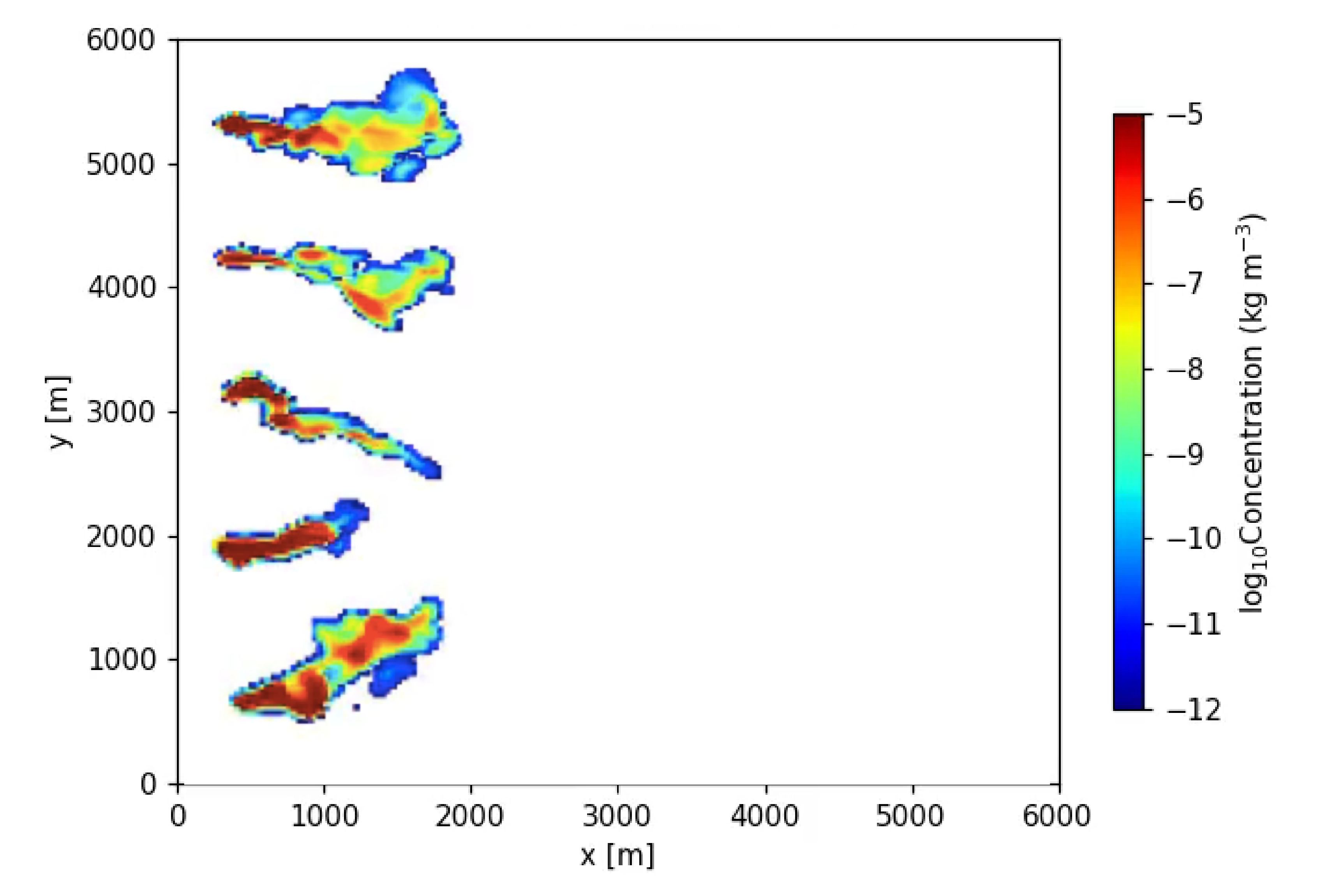
2.1.3. COnvective Diffusion Observed by Remote Sensors (CONDORS) Experiment
2.2. Categorization of the Observations
- The convective water tank experimental data from Case 1 in Willis and Deardorff [26], comprising data from seven experimental trials;
- All the surface-based releases of oil and chaff, for eight releases and five locations, in the CONDORS experiment;
- Seven Project Prairie Grass trials—Trials 7, 8, 10, 16, 25, 44, and 51.
2.3. Scaling Methodology
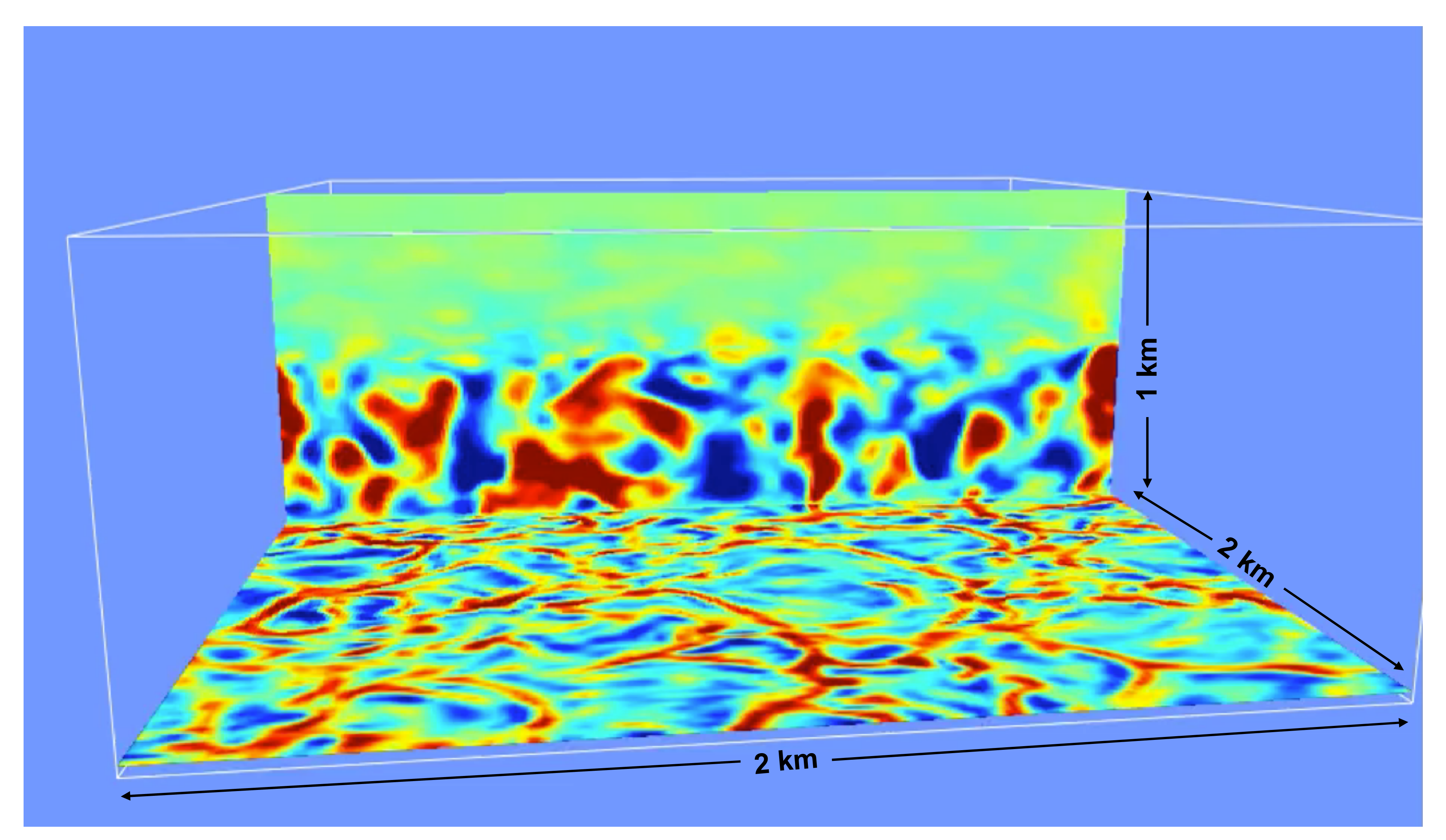
2.4. GPU-LES Model Simulations
3. Results
3.1. Unstable PBL Comparison
3.2. Neutral and Stable PBL Comparison
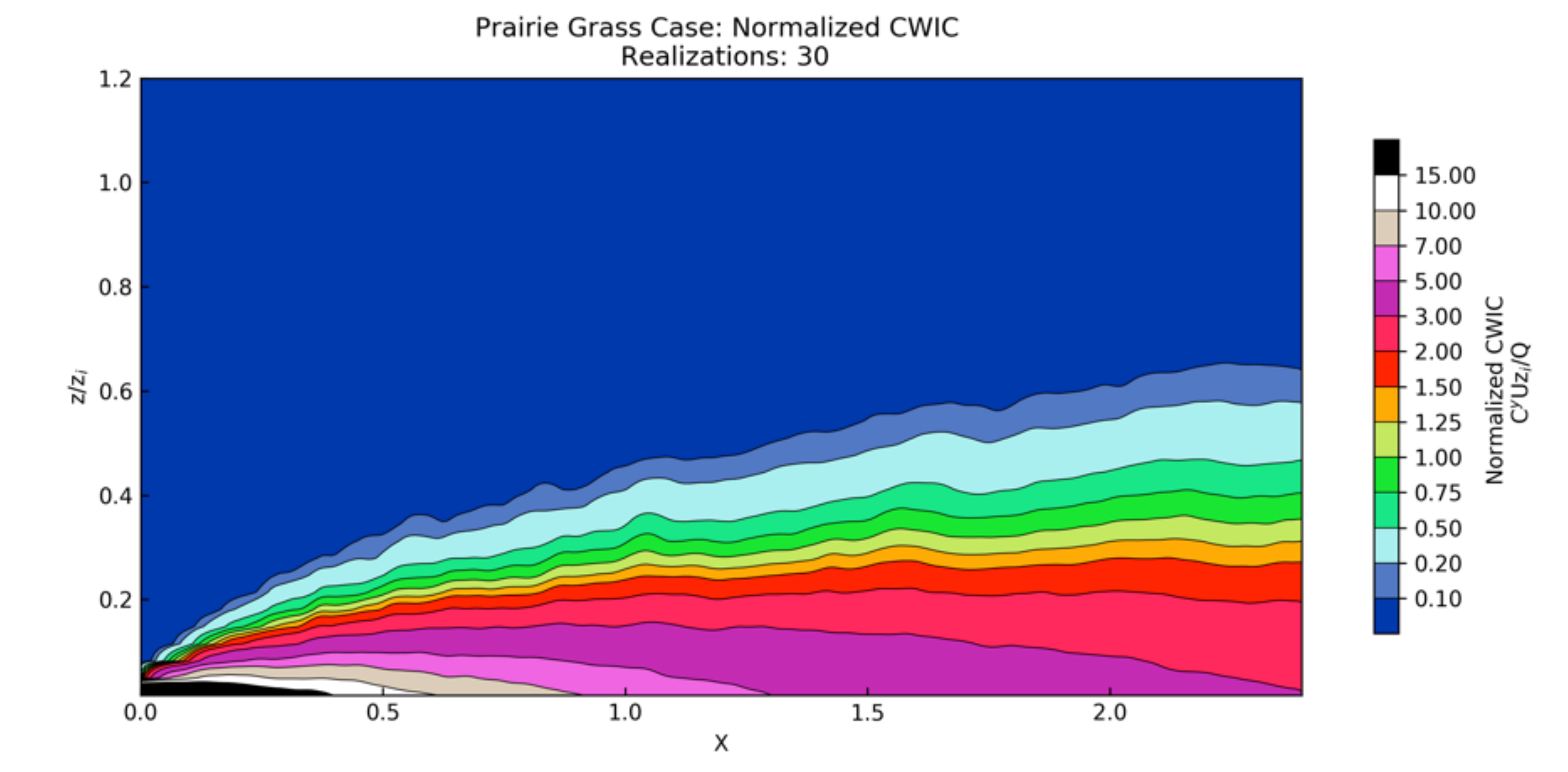
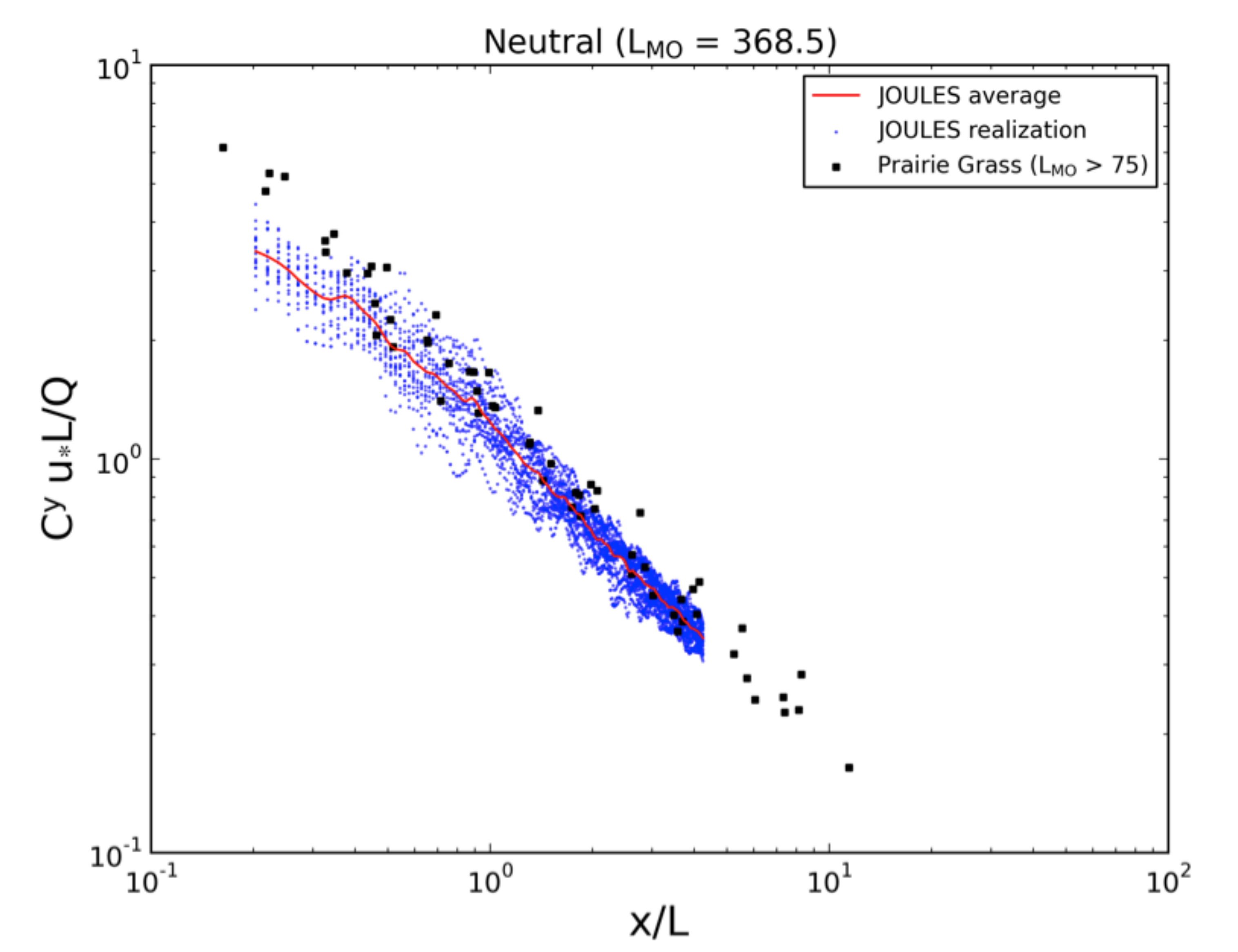
3.2.1. Neutral PBL Comparison
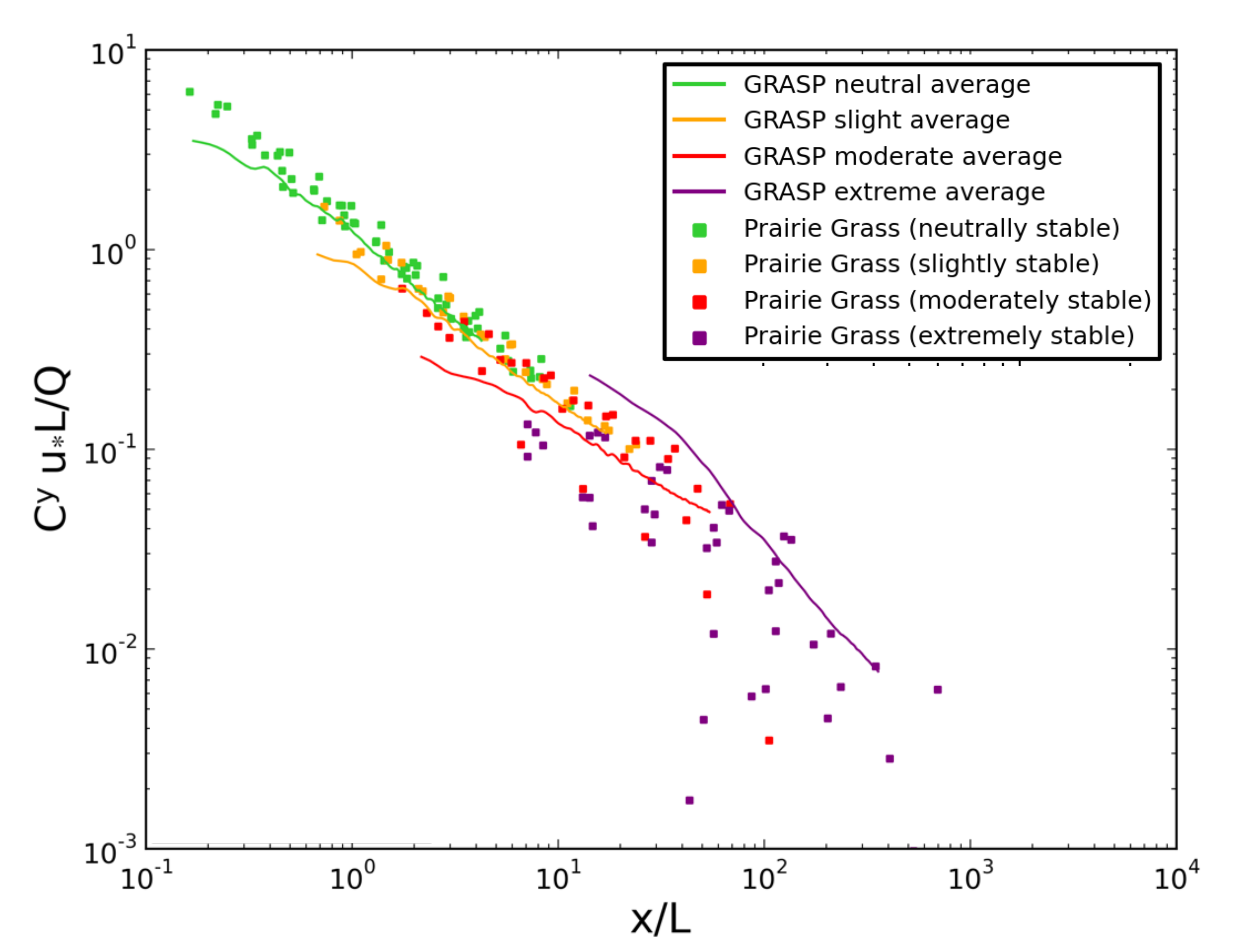
3.2.2. Stable PBL Comparison
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bieringer, P.E.; Annunzio, A.J.; Platt, N.; Bieberbach, G.; Hannan, J. Contrasting the use of single-realization versus ensemble-average atmospheric dispersion solutions for chemical and biological defense analyses. J. Appl. Meteor. Climatol. 2014, 53, 1399–1415. [Google Scholar] [CrossRef]
- Bass, A. Modelling long range transport and diffusion. In Proceedings of the 2nd Joint Conference on Applications of Air Pollution Meteorology, New Orleans, LA, USA, 24–27 March 1980; pp. 193–215. [Google Scholar]
- Sykes, R.I.; Parker, S.; Henn, D.; Chowdhury, B. SCIPUFF Version 3.0 Technical Documentation; Sage Management: Princeton, NJ, USA, 2016; 403p. [Google Scholar]
- Thomson, D.J. Criteria for the selection of stochastic models of particle trajectories in turbulent flows. J. Fluid Mech. 1987, 180, 529–556. [Google Scholar] [CrossRef]
- Wilson, J.D.; Sawford, B.L. Review of Lagrangian stochastic models for trajectories in the turbulent atmosphere. Bound.-Layer Meteor. 1996, 78, 191–220. [Google Scholar] [CrossRef]
- Haupt, S.E.; Annunzio, A.J.; Schmehl, K.J. Evolving turbulence realizations of atmospheric flow. Bound.-Layer Meteorol. 2013, 149, 197–217. [Google Scholar] [CrossRef]
- Gunatilaka, A.; Skvortsov, A.; Gailis, R. A review of toxicity models for realistic atmospheric applications. Atmos. Environ. 2014, 84, 230–243. [Google Scholar] [CrossRef]
- Bieberbach, G.; Bieringer, P.E.; Cabell, R.; Hurst, J.; Weil, J.; Wyszogrodzki, A.; Hannan, J. A Framework for Developing Synthetic Chemical and Biological Agent Release Data Sets. In Proceedings of the 13th International Conference on Harmonisation within Atmospheric Dispersion Modeling for Regulatory Purposes, Paris, France, 1–4 June 2010. [Google Scholar]
- Platt, N.; DeRiggi, D.; Warner, S.; Bieringer, P.E.; Bieberbach, G.; Wyszogrodzki, A.; Weil, J. Method for comparison of large eddy simulation generated wind fluctuations with short-range observations. Int. J. Environ. Pollut. 2012, 48, 22–30. [Google Scholar] [CrossRef]
- Wyngaard, J.C. Turbulence in the Atmosphere; Cambridge University Press: Cambridge, UK, 2010; 393p. [Google Scholar]
- Weil, J.C.; Sullivan, P.P.; Moeng, C.H. The use of large-eddy simulations in Lagrangian particle dispersion models. J. Atmos. Sci. 2004, 61, 2877–2887. [Google Scholar] [CrossRef]
- Weil, J.C.; Sullivan, P.P.; Moeng, C.H. Statistical variability of dispersion in the convective boundary layer: Ensembles of simulations and observations. Bound.-Layer Meteorol. 2012, 145, 185–210. [Google Scholar] [CrossRef]
- Henn, D.S.; Sykes, R.I. Large-eddy simulation of dispersion in the convective boundary layer. Atmos. Environ. 1992, 26a, 3145–3159. [Google Scholar] [CrossRef]
- Caulton, D.R.; Li, Q.; Bou-Zeid, E.; Fitts, J.P.; Golston, L.M.; Pan, D.; Lu, J.; Lane, H.M.; Buchholz, B.; Guo, X.; et al. Quantifying uncertainties from mobile-laboratory-derived emissions of well pads using inverse Gaussian methods. Atmos. Chem. Phys. 2018, 18, 15145–15168. [Google Scholar] [CrossRef]
- Lundquist, K.A.; Chow, F.K.; Lundquist, J.K. An immersed boundary method enabling large-eddy simulations of flow over complex terrain in the WRF model. Mon. Weather. Rev. 2012, 140, 3936–3955. [Google Scholar] [CrossRef]
- Tomas, J.M.; Eisma, H.E.; Pourquie, M.J.B.M.; Eisinga, G.E.; Jonker, H.J.J.; Westerweel, J. Pollutant Dispersion in Boundary Layers Exposed to Rural-to-Urban Transitions: Varying the Spanwise Length Scale of the Roughness. Bound. Layer Meteorol. 2017, 163, 225–251. [Google Scholar] [CrossRef]
- Bieringer, P.E.; Piña, A.J.; Sohn, M.D.; Jonker, H.J.J.; Bieberbach, G., Jr.; Lorenzetti, D.M.; Fry, R.N., Jr. Large Eddy Simulation (LES) Based System for Producing Coupled Urban and Indoor Airborne Contaminant Transport and Dispersion Solutions. In Proceedings of the 18th International Conference on Harmonisation within Atmospheric Dispersion Modeling for Regulatory Purposes, Bologna, Italy, 9–12 October 2017. [Google Scholar]
- Du, P.; Weber, R.; Luszczek, P.; Tomov, S.; Peterson, G.; Dongarra, J. From CUDA to OpenCL: Towards a performance-portable solution for multi-platform GPU programming. Parallel Comput. 2012, 38, 391–407. [Google Scholar] [CrossRef]
- NVIDIA Corporation. Design and Visualization. Available online: https://www.nvidia.com/en-us/data-center/a100/ (accessed on 13 June 2021).
- Skamarock, W.C.; Klemp, J.B. A time-split nonhydrostatic atmospheric model for weather research and forecasting applications. J. Comput. Phys. 2008, 227, 3465–3485. [Google Scholar] [CrossRef]
- Michalakes, J.; Vachharajani, M. GPU acceleration of numerical weather prediction. Parallel Process. Lett. 2008, 18, 531–548. [Google Scholar] [CrossRef]
- Mielikainen, J.; Huang, B.; Huang, H.L.A.; Goldberg, M.D. Improved GPU/CUDA based parallel weather and research forecast (WRF) single moment 5-class (WSM5) cloud microphysics. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2012, 5, 1256–1265. [Google Scholar] [CrossRef]
- Silva, J.P.; Hagopian, J.; Burdiat, M.; Dufrechou, E.; Pedemonte, M.; Gutiérrez, A.; Ezzatti, P. Another step to the full GPU implementation of the weather research and forecasting model. J. Supercomput. 2014, 70, 746–755. [Google Scholar] [CrossRef]
- Wahib, M.; Maruyama, N. Highly optimized full GPU-acceleration of non-hydrostatic weather model SCALE-LES. In Proceedings of the 2013 IEEE International Conference on Cluster Computing (CLUSTER), Indianapolis, IN, USA, 23–24 September 2013; pp. 1–8. [Google Scholar]
- Schalkwijk, J.; Griffith, E.J.; Post, F.H.; Jonker, H.J.J. High-performance simulations of turbulent clouds on a desktop PC: Exploiting the GPU. Bull. Am. Meteorol. 2012, 93, 307–314. [Google Scholar] [CrossRef]
- Schalkwijk, J.; Jonker, H.J.J.; Siebesma, A.P.; Bosveld, F.C. A year-long large-eddy simulation of the weather over Cabauw: An overview. Mon. Weather Rev. 2015, 143, 828–844. [Google Scholar] [CrossRef][Green Version]
- Schalkwijk, J.; Jonker, H.J.J.; Siebesma, A.P. An Investigation of the Eddy-Covariance Flux Imbalance in a Year-Long Large-Eddy Simulation of the Weather at Cabauw. Bound.-Layer Meteorol. 2016, 160, 17–39. [Google Scholar] [CrossRef]
- Maronga, B.; Gryschka, M.; Heinze, R.; Hoffmann, F.; Kanani-Sưhring, F.; Keck, M.; Raasch, S. The Parallelized Large-Eddy Simulation Model (PALM) version 4.0 for atmospheric and oceanic flows: Model formulation, recent developments, and future perspectives. Geosci. Model Dev. Discuss. 2015, 8, 1539–1637. [Google Scholar]
- Van Heerwaarden, C.; Van Stratum, B.J.; Heus, T.; Gibbs, J.A.; Fedorovich, E.; Mellado, J.P. MicroHH 1.0: A computational fluid dynamics code for direct numerical simulation and large-eddy simulation of atmospheric boundary layer flows. Geosci. Model Dev. 2017, 3145–3165. [Google Scholar] [CrossRef]
- Sauer, J.A.; Muñoz-Esparza, D. The FastEddy® resident-GPU accelerated large-eddy simulation framework: Model formulation, dynamical-core validation and performance benchmarks. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002100. [Google Scholar] [CrossRef]
- Moeng, C.H.; Dudhia, J.; Klemp, J.; Sullivan, P. Examining two-way grid nesting for large eddy simulation of PBL using the WRF model. Mon. Weather. Rev. 2007, 135, 2295–2311. [Google Scholar] [CrossRef]
- Rybchuk, A.; Alden, C.B.; Lundquist, J.K.; Rieker, G.B. A Statistical Evaluation of WRF-LES Trace Gas Dispersion Using Project Prairie Grass Measurements. Mon. Weather. Rev. 2021, 149, 1619–1633. [Google Scholar]
- Intel Corporation. Product Specifications. Available online: https://ark.intel.com (accessed on 10 November 2018).
- NVIDIA Corporation. Design and Visualization. Available online: https://www.nvidia.com/en-us/design-visualization/ (accessed on 10 November 2018).
- Willis, G.E.; Deardorff, J.W. A laboratory model of diffusion into the convective planetary boundary layer. Q. J. R. Meteorol. Soc. 1976, 102, 427–445. [Google Scholar] [CrossRef]
- Barad, M.L. Project Prairie Grass. A field program in diffusion. In Geophysical Research Paper No. 59, Vols I and II AFCRF-TR-235; Air Force Cambridge Research Center: Bedford, MA, USA, 1958. [Google Scholar]
- Arhus. The Project Prairie Grass Data. Available online: http://envs.au.dk/en/knowledge/air/models/background/omlprairie/excelprairie/ (accessed on 5 May 2017).
- Eberhard, W.L.; Moninger, W.R.; Briggs, G.A. Plume dispersion in the convective boundary layer. Part I: CONDORS field experiment and example measurements. J. Appl. Meteorol. 1988, 27, 599–616. [Google Scholar] [CrossRef]
- Briggs, G.A. Plume dispersion in the convective boundary layer. Part II: Analyses of CONDORS field experiment data. J. Appl. Meteorol. 1993, 32, 1388–1425. [Google Scholar] [CrossRef]
- Kaimal, J.C.; Eberhard, W.L.; Moninger, W.R.; Gaynor, J.E.; Troxel, S.W.; Uttal, T.; Briggs, G.A.; Start, G.E. PROJECT CONDORS Convective Diffusion Observed by Remote Sensors; NOAA/ERL Wave Propagation Laboratory, U.S. Department of Commerce: Boulder, CO, USA, 1986. [Google Scholar]
- Willis, G.E.; Deardorff, J.W. A laboratory model of the unstable planetary boundary layer. J. Atmos. Sci. 1974, 31, 1297–1307. [Google Scholar] [CrossRef]
- Lamb, R.G. A numerical simulation of dispersion from an elevated point source in the convective planetary boundary layer. Atmos. Environ. 1978, 12, 1297–1304. [Google Scholar] [CrossRef]
- Deardorf, J.W.; Willis, G.E. Ground level concentration fluctuations from a buoyant and a non-buoyant source within a laboratory convectively mixed layer. Atmos. Environ. 1984, 18, 1297. [Google Scholar] [CrossRef]
- Pasquill, F. The Estimation of the Dispersion of Windborne Material. Meteorol. Mag. 1961, 90, 33–49. [Google Scholar]
- Gifford, F.A. Use of Routine Meteorological Observations for Estimating Atmospheric Dispersion. Nucl. Saf. 1961, 2, 47–57. [Google Scholar]
- Pasquill, F.; Smith, F.B. The physical and meteorological basis for the estimation of the dispersion of windborne material. In Proceedings of the Second International Clean Air Congress, Washington, DC, USA, 6–11 December 1970; Englund, H.M., Beery, W.T., Eds.; Academic Press: New York, NY, USA, 1971; pp. 1067–1072. [Google Scholar]
- Woodward, J.L. Appendix A: Atmospheric stability classification schemes. In Estimating the Flammable Mass of a Vapor Cloud: A CCPS Concept Book; Center for Chemical Process Safety of the American Institute of Chemical Engineers: New York, NY, USA, 1998; pp. 209–212. [Google Scholar]
- Briggs, G.A. Analysis of diffusion field experiments. In Lectures on Air Pollution Modeling; Venkatram, A., Wyngaard, J.C., Eds.; American Meteorological Society: Boston, MA, USA, 1988. [Google Scholar]
- Khaled, S.M.E.; Etman, S.M.; Embaby, M. New analytical solution of the dispersion equation. Atmos. Res. 2007, 84, 337–344. [Google Scholar]
- Venkatram, A.; Snyder, M.G.; Heist, D.K.; Perry, S.G.; Petersen, W.B.; Isakov, V. Re-formulation of plume spread for near-surface dispersion. Atmos. Environ. 2013, 77, 846–855. [Google Scholar] [CrossRef]
- Stull, R. An Introduction to Boundary Layer Meteorology; Springer: Amsterdam, The Netherlands, 1988; 670p. [Google Scholar]
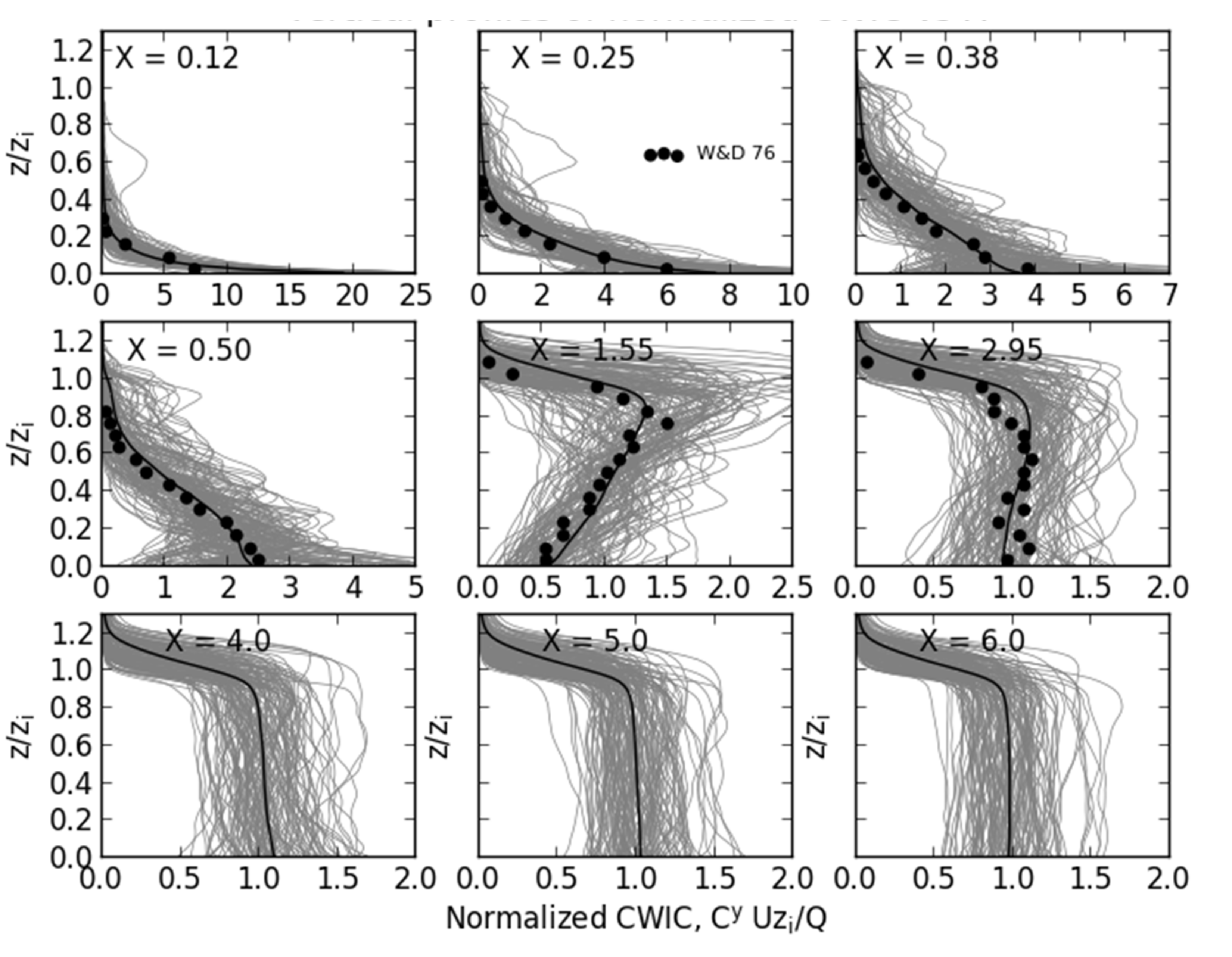
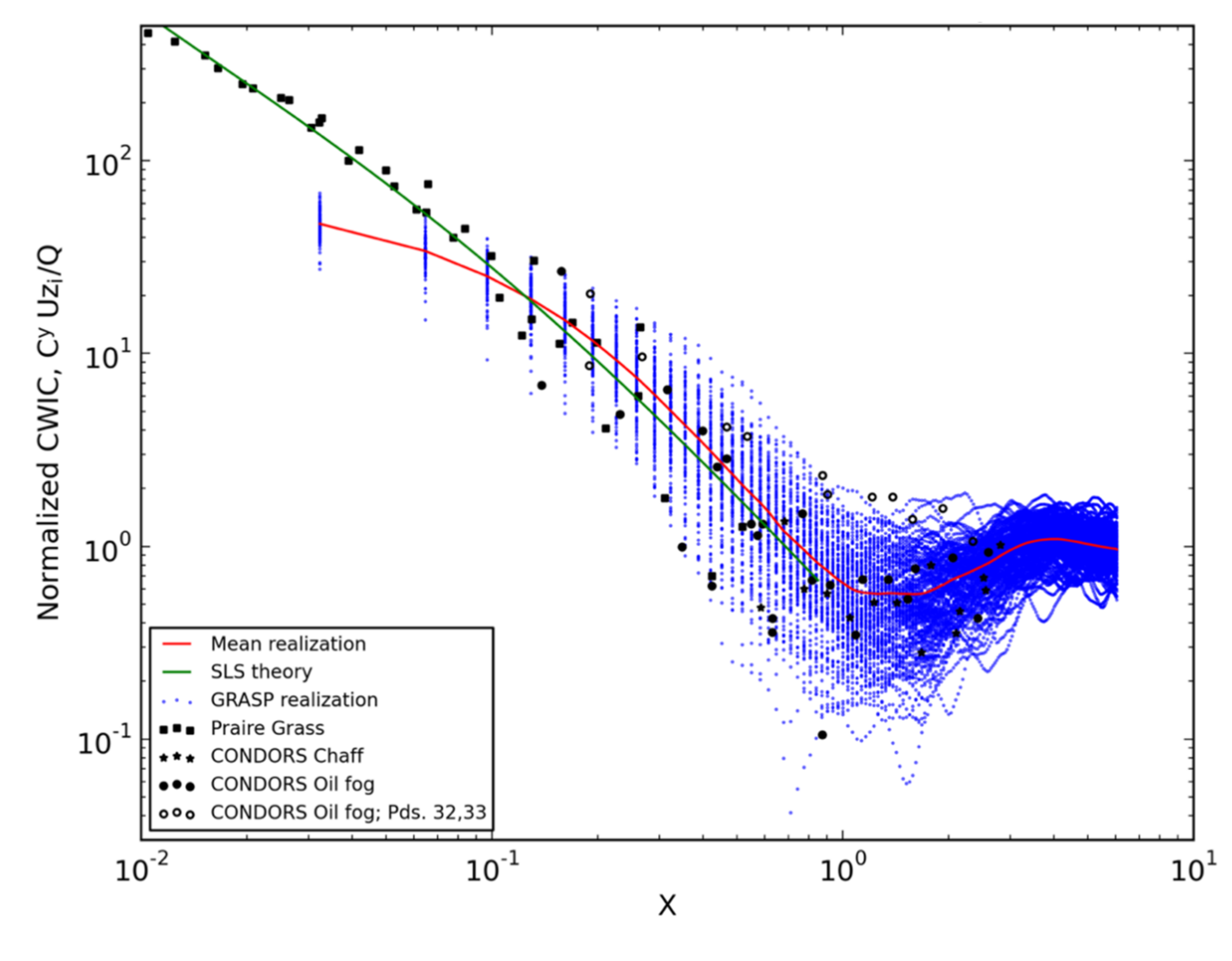

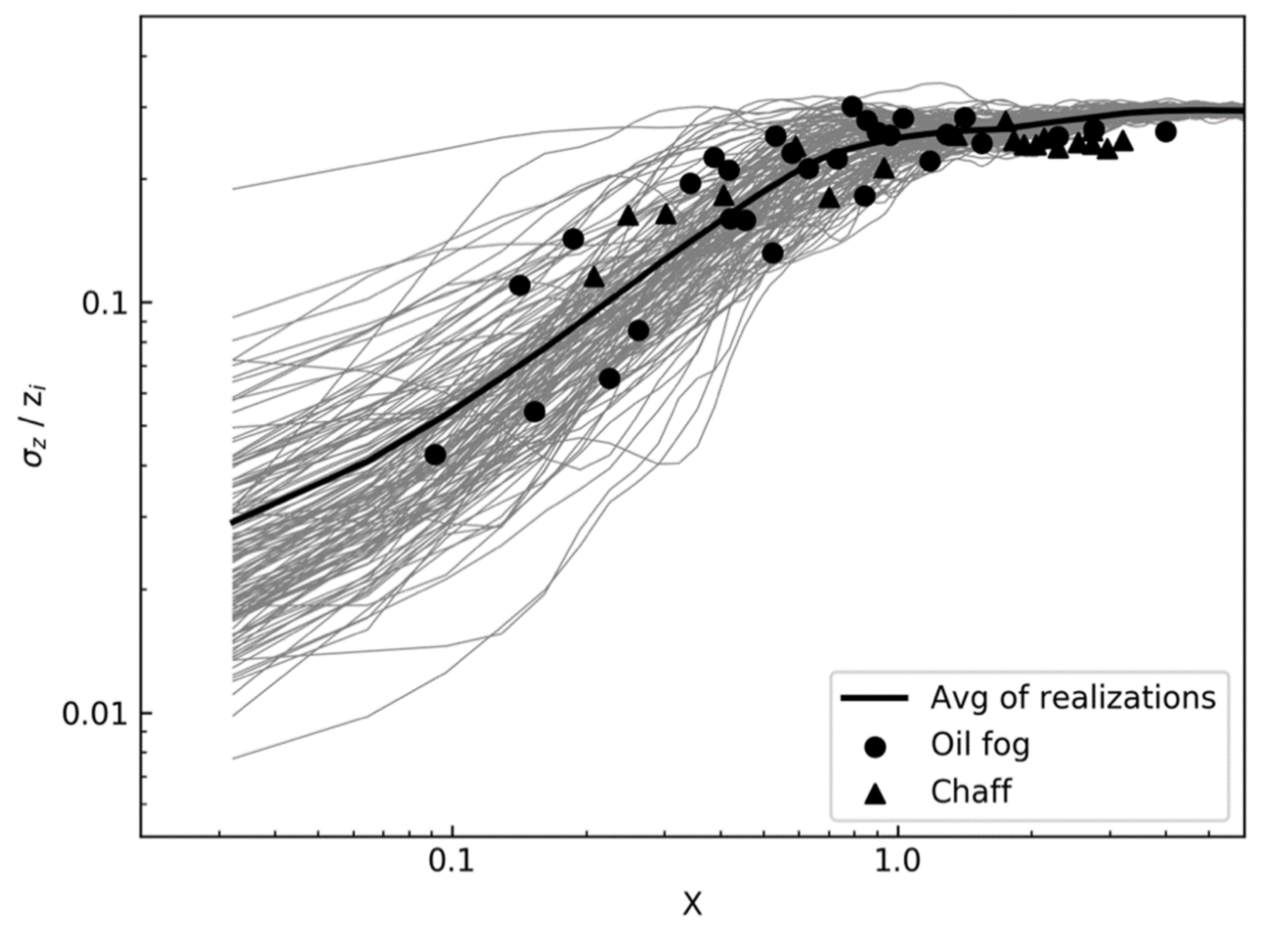
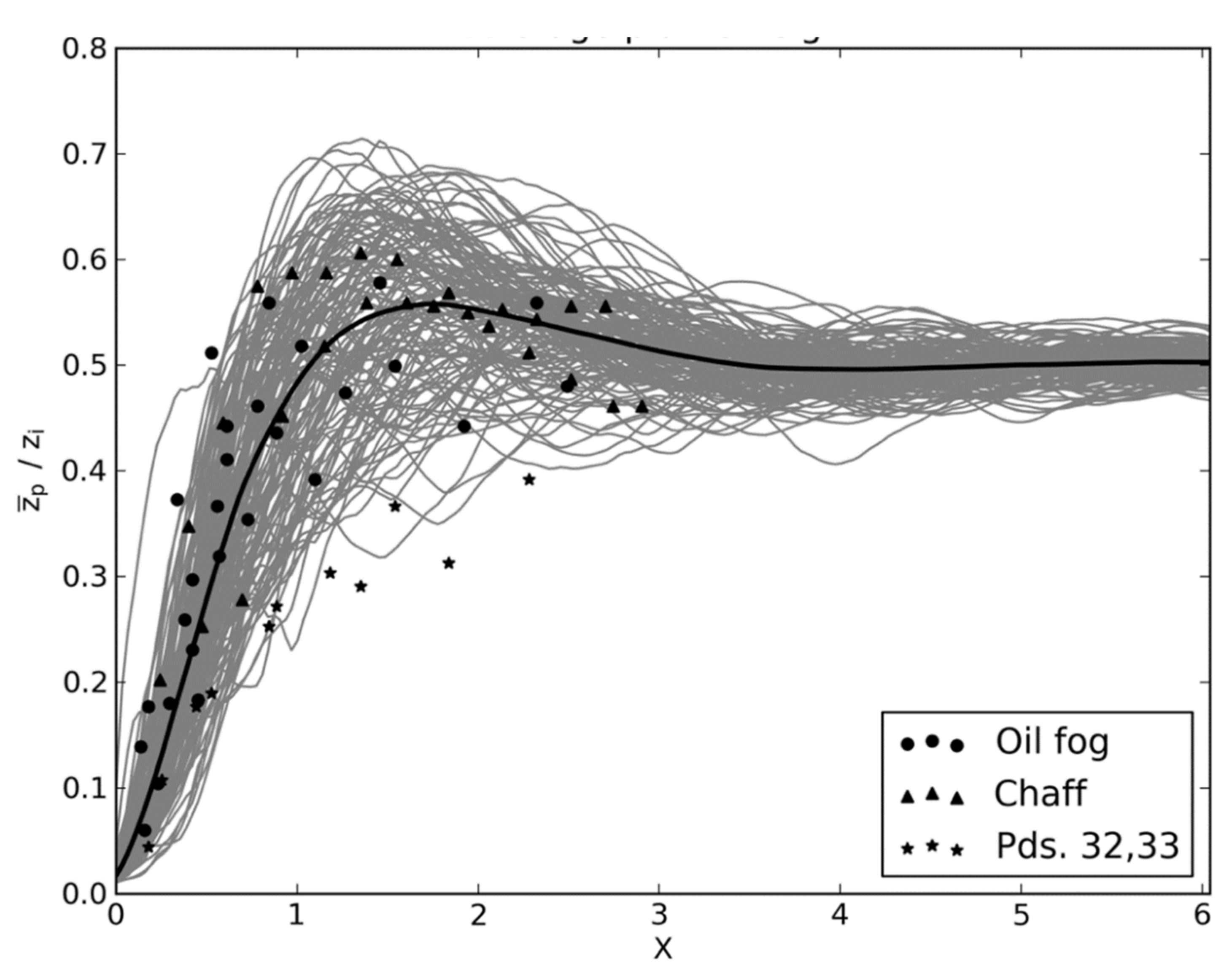




| Stability | L (m) |
|---|---|
| Unstable | <−2 |
| Neutral stability | >75 |
| Slightly Stable | 35 to 75 |
| Moderately Stable | 8 to 35 |
| Extremely Stable | 1 to 8 |
| Stability | Number of Trials | U @ 1m (m s−1) | Heat Flux (W m−2) | T (°C) | θ (K) | L (m) | ||
|---|---|---|---|---|---|---|---|---|
| Unstable | 47 | 4.054 | 0.331 | 200.517 | 28.96 | 307.10 | 1.613 | −18.33 |
| Neutral stability | 12 | 4.84 | 0.38 | −29.39 | 22.33 | 300.36 | −0.54 | 167.25 |
| Slightly Stable | 7 | 2.74 | 0.21 | −25.94 | 22.15 | 300.19 | −0.50 | 54.20 |
| Moderately Stable | 6 | 2.21 | 0.16 | −22.07 | 21.73 | 299.68 | −0.49 | 18.91 |
| Extremely Stable | 9 | 1.24 | 0.07 | −10.74 | 19.03 | 297.13 | −0.36 | 4.29 |
| Simulation Category | Grid Points (nx,ny,nz) | Model Resolution (Hor,Vert) (m) | U (m/s) | Ug (m/s) | Vg (m/s) | Heat Flux (W/m2) | zi (m) | L (m) |
|---|---|---|---|---|---|---|---|---|
| Unstable | (192,192,96) | (52.1,20.8) | 2.8 | 2.8 | −1.5 | 240 | 1000 | −11.5 |
| Neutral stability | (256,256,64) | (6.25,6.25) | 8 | 8 | −5.5 | −10 | 190 | 372.2 |
| Slightly Stable | (256,256,64) | (6.25,6.25) | 4 | 3.5 | −4.5 | −10 | 116 | 47.6 |
| Moderately Stable | (256,256,64) | (6.25,6.25) | 4 | 3.2 | −4.2 | −10 | 103 | 28.9 |
| Extremely Stable | (256,256,64) | (6.25,6.25) | 3 | 2.5 | −2.5 | −10 | 78 | 7.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bieringer, P.E.; Piña, A.J.; Lorenzetti, D.M.; Jonker, H.J.J.; Sohn, M.D.; Annunzio, A.J.; Fry, R.N., Jr. A Graphics Processing Unit (GPU) Approach to Large Eddy Simulation (LES) for Transport and Contaminant Dispersion. Atmosphere 2021, 12, 890. https://doi.org/10.3390/atmos12070890
Bieringer PE, Piña AJ, Lorenzetti DM, Jonker HJJ, Sohn MD, Annunzio AJ, Fry RN Jr. A Graphics Processing Unit (GPU) Approach to Large Eddy Simulation (LES) for Transport and Contaminant Dispersion. Atmosphere. 2021; 12(7):890. https://doi.org/10.3390/atmos12070890
Chicago/Turabian StyleBieringer, Paul E., Aaron J. Piña, David M. Lorenzetti, Harmen J. J. Jonker, Michael D. Sohn, Andrew J. Annunzio, and Richard N. Fry, Jr. 2021. "A Graphics Processing Unit (GPU) Approach to Large Eddy Simulation (LES) for Transport and Contaminant Dispersion" Atmosphere 12, no. 7: 890. https://doi.org/10.3390/atmos12070890
APA StyleBieringer, P. E., Piña, A. J., Lorenzetti, D. M., Jonker, H. J. J., Sohn, M. D., Annunzio, A. J., & Fry, R. N., Jr. (2021). A Graphics Processing Unit (GPU) Approach to Large Eddy Simulation (LES) for Transport and Contaminant Dispersion. Atmosphere, 12(7), 890. https://doi.org/10.3390/atmos12070890





