Comparing the Air Turbulence above Smooth and Rough Surfaces in the Amazon Region
Abstract
:1. Introduction
2. Materials and Methods
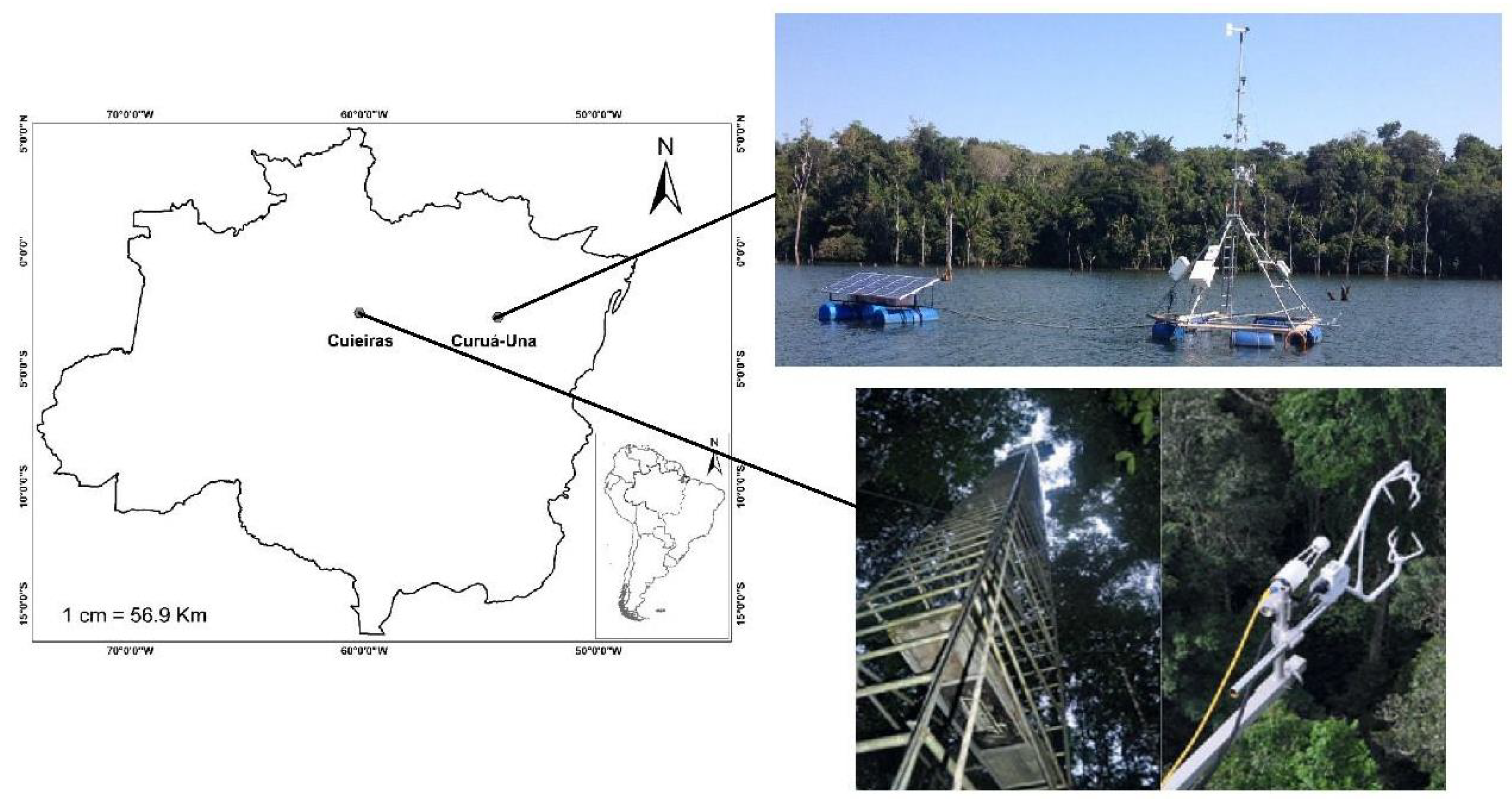
2.1. Study Area
2.2. Data
2.3. Data Quality Control and Methodology
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Garratt, J. The Atmospheric Boundary Layer; Cambridge University Press: Cambridge, UK, 1994; pp. 316–335. [Google Scholar]
- Richey, J.E.; Melack, J.M.; Aufdenkampe, A.K.; Ballester, V.M.; Hess, L.L. Outgassing from Amazonian rivers and wetlands as a large tropical source of atmospheric CO2. Nature 2002, 416, 617. [Google Scholar] [CrossRef]
- Fisch, G.; Tota, J.; Machado, L.A.T.; Silva Dias, M.A.F.; da Lyra, R.F.F.; Nobre, C.A.; Dolman, A.J.; Gash, J.H.C. The convective boundary layer over pasture and forest in Amazonia. Theor. Appl. Climatol. 2004, 78, 47–59. [Google Scholar] [CrossRef] [Green Version]
- Von Randow, C.; Zeri, M.; Restrepo-Coupe, N.; Muza, M.N.; de Gonçalves, L.G.G.; Costa, M.H.; Araujo, A.C.; Manzi, A.O.; da Rocha, H.R.; Saleska, S.R.; et al. Inter-annual variability of carbon and water fluxes in Amazonian forest, Cerrado and pasture sites, as simulated by terrestrial biosphere models. Agric. For. Meteorol. 2013, 182–183, 145–155. [Google Scholar] [CrossRef]
- Arya, P.S. Introduction to Micrometeorology; Elsevier: Amsterdam, The Netherlands, 2001; Volume 79. [Google Scholar]
- Kaimal, J.C.; Wyngaard, J.C. The Kansas and Minesotta experiments. Bound. Layer Meteorol. 1990, 50, 31–47. [Google Scholar] [CrossRef]
- Fitzjarrald, D.R.; Moore, K.E.; Cabral, O.M.R.; Scolar, J.; Manzi, A.O.; de Abreu Sá, L.D. Daytime turbulent exchange between the Amazon forest and the atmosphere. J. Geophys. Res. Atmos. 1990, 95, 16825–16838. [Google Scholar] [CrossRef] [Green Version]
- Kruijt, B.; Malhi, Y.; Lloyd, J.; Norbre, A.D.; Miranda, A.C.; Pereira, M.G.P.; Culf, A.; Grace, J. Turbulence Statistics Above And Within Two Amazon Rain Forest Canopies. Bound. Layer Meteorol. 2000, 94, 297–331. [Google Scholar] [CrossRef]
- Santos, D.M.; Acevedo, O.C.; Chamecki, M.; Fuentes, J.D.; Gerken, T.; Stoy, P.C. Temporal Scales of the Nocturnal Flow Within and Above a Forest Canopy in Amazonia. Bound. Layer Meteorol. 2016, 161, 73–98. [Google Scholar] [CrossRef] [Green Version]
- Dias-Júnior, C.Q.; Sá, L.D.; Filho, E.P.M.; Santana, R.A.; Mauder, M.; Manzi, A.O. Turbulence regimes in the stable boundary layer above and within the Amazon forest. Agric. For. Meteorol. 2017, 233, 122–132. [Google Scholar] [CrossRef]
- Freire, L.S.; Gerken, T.; Ruiz-Plancarte, J.; Wei, D.; Fuentes, J.D.; Katul, G.G.; Dias, N.L.; Acevedo, O.C.; Chamecki, M. Turbulent mixing and removal of ozone within an Amazon rainforest canopy. J. Geophys. Res. Atmos. 2017, 122, 2791–2811. [Google Scholar] [CrossRef]
- Dias-Júnior, C.Q.; Dias, N.L.; dos Santos, R.M.N.; Sörgel, M.; Araújo, A.; Tsokankunku, A.; Ditas, F.; de Santana, R.A.; Von Randow, C.; Sá, M.; et al. Is there a classical inertial sublayer over the Amazon forest? Geophys. Res. Lett. 2019, 46, 5614–5622. [Google Scholar] [CrossRef]
- Chamecki, M.; Freire, L.S.; Dias, N.L.; Chen, B.; Dias-Junior, C.Q.; Toledo Machado, L.A.; Sörgel, M.; Tsokankunku, A.; Araújo, A.C.D. Effects of vegetation and topography on the boundary layer structure above the Amazon forest. J. Atmos. Sci. 2020, 77, 2941–2957. [Google Scholar] [CrossRef]
- Vale, R.S. Medições de Gases de Efeito Estufa e Variáveis Ambientais em Reservatórios Hidrelétricos na Amazônia Central. Ph.D. Thesis, Instituto Nacional de Pesquisas da Amazônia, Manaus, Spain, 2016. [Google Scholar]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Springer: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Kundu, P.K.; Cohen, I.M. Fluid Mechanics; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Kaimal, J.C.; Finnigan, J.J. Atmospheric Boundary Layer Flows: Their Structure and Measurement; Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Anderson, D.E.; Verma, S.B.; Clement, R.J.; Baldocchi, D.D.; Matt, D.R. Turbulence spectra of CO2, water vapor, temperature and velocity over a deciduous forest. Agric. For. Meteorol. 1986, 38, 81–99. [Google Scholar] [CrossRef]
- Lee, X. Turbulence spectra and eddy diffusivity over forests. J. Appl. Meteorol. 1996, 35, 1307–1318. [Google Scholar] [CrossRef] [Green Version]
- Moraes, O.L.; Fitzjarrald, D.R.; Acevedo, O.C.; Sakai, R.K.; Czikowsky, M.J.; Degrazia, G.A. Comparing spectra and cospectra of turbulence over different surface boundary conditions. Phys. A Stat. Mech. Its Appl. 2008, 387, 4927–4939. [Google Scholar] [CrossRef]
- Sahlée, E.; Rutgersson, A.; Podgrajsek, E.; Bergström, H. Influence from surrounding land on the turbulence measurements above a lake. Bound. Layer Meteorol. 2014, 150, 235–258. [Google Scholar] [CrossRef]
- Kaimal, J.C.; Wyngaard, J.C.; Izumi, Y.; Coté, O.R. Spectral characteristics of surface-layer turbulence. Q. J. R. Meteorol. Soc. 1972, 98, 563–589. [Google Scholar] [CrossRef]
- Walter, R.K.; Nidzieko, N.J.; Monismith, S.G. Similarity scaling of turbulence spectra and cospectra in a shallow tidal flow. J. Geophys. Res. Ocean. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Araújo, A.C.; Nobre, A.D.; Kruijt, B.; Elbers, J.A.; Dallarosa, R.; Stefani, P.; von Randow, C.; Manzi, A.O.; Culf, A.D.; Gash, J.H.C.; et al. Comparative measurements of carbon dioxide fluxes from two nearby towers in a central Amazonian rainforest: The Manaus LBA site. J. Geophys. Res. Atmos. 2002, 107. [Google Scholar] [CrossRef] [Green Version]
- Fearnside, P.M. Do hydroelectric dams mitigate global warming? The case of Brazil’s Curuá-Una Dam. Mitig. Adapt. Strateg. Glob. Chang. 2005, 10, 675–691. [Google Scholar] [CrossRef]
- Fuentes, J.D.; Chamecki, M.; dos Santos, R.M.N.; Randow, C.V.; Stoy, P.C.; Katul, G.; Fitzjarrald, D.; Manzi, A.; Gerken, T.; Trowbridge, A.; et al. Linking Meteorology, Turbulence, and Air Chemistry in the Amazon Rain Forest. Bull. Am. Meteorol. Soc. 2016, 97, 2329–2342. [Google Scholar] [CrossRef]
- Wilczak, J.M.; Oncley, S.P.; Stage, S.A. Sonic anemometer tilt correction algorithms. Bound. Layer Meteorol. 2001, 99, 127–150. [Google Scholar] [CrossRef]
- Vickers, D.; Mahrt, L. Quality Control and Flux Sampling Problems for Tower and Aircraft Data. J. Atmos. Ocean. Technol. 1997, 14, 512–526. [Google Scholar] [CrossRef]
- Mahrt, L.; Lee, X.; Black, A.; Neumann, H.; Staebler, R. Nocturnal mixing in a forest subcanopy. Agric. For. Meteorol. 2000, 101, 67–78. [Google Scholar] [CrossRef]
- Fitzjarrald, D.R.; Stormwind, B.L.; Fisch, G.; Cabral, O.M.R. Turbulent transport observed just above the Amazon forest. J. Geophys. Res. Atmos. 1988, 93, 1551–1563. [Google Scholar] [CrossRef]
- Santana, R.A.; Dias-Júnior, C.Q.; Tóta, J.; Fuentes, J.D.; do Vale, R.S.; Alves, E.G.; dos Santos, R.M.N.; Manzi, A.O. Air turbulence characteristics at multiple sites in and above the Amazon rainforest canopy. Agric. For. Meteorol. 2018, 260–261, 41–54. [Google Scholar] [CrossRef]
- Acevedo, O.C.; Fitzjarrald, D.R. In the Core of the Night-Effects of Intermittent Mixing on a Horizontally Heterogeneous Surface. Bound. Layer Meteorol. 2003, 106, 1–33. [Google Scholar] [CrossRef]
- Oliveira, P.E.; Acevedo, O.C.; Moraes, O.L.; Zimermann, H.R.; Teichrieb, C. Nocturnal intermittent coupling between the interior of a pine forest and the air above it. Bound. Layer Meteorol. 2013, 146, 45–64. [Google Scholar] [CrossRef]
- De Oliveira, F.P.; Oyama, M.D. Antecedent Atmospheric Conditions Related to Squall-Line Initiation over the Northern Coast of Brazil in July. Weather Forecast. 2015, 30, 1254–1264. [Google Scholar] [CrossRef]
- Yi, C. Momentum transfer within canopies. J. Appl. Meteorol. Climatol. 2008, 47, 262–275. [Google Scholar] [CrossRef] [Green Version]
- De Souza, C.M.; Dias-Júnior, C.Q.; Tóta, J.; de Abreu Sá, L.D. An empirical-analytical model of the vertical wind speed profile above and within an Amazon forest site. Meteorol. Appl. 2016, 23, 158–164. [Google Scholar] [CrossRef] [Green Version]
- Santana, R.A.S.D.; Dias-Júnior, C.Q.; Vale, R.S.D.; Tóta, J.; Fitzjarrald, D.R. Observing and Modeling the Vertical Wind Profile at Multiple Sites in and above the Amazon Rain Forest Canopy. Adv. Meteorol. 2017, 2017, 5436157. [Google Scholar] [CrossRef] [Green Version]
- Poggi, D.; Porporato, A.; Ridolfi, L.; Albertson, J.D.; Katul, G.G. The Effect of Vegetation Density on Canopy Sub-Layer Turbulence. Bound. Layer Meteorol. 2004, 111, 565–587. [Google Scholar] [CrossRef]
- Malhi, Y.; Pegoraro, E.; Nobre, A.D.; Pereira, M.G.P.; Grace, J.; Culf, A.D.; Clement, R. Energy and water dynamics of a central Amazonian rain forest. J. Geophys. Res. Atmos. 2002, 107, LBA 45-1–LBA 45-17. [Google Scholar] [CrossRef] [Green Version]
- Lumley, J.L.; Panofsky, H.A. The Structure of Atmospheric Turbulence; John Wiley & Sons: New York, NY, USA, 1964. [Google Scholar]
- Shaw, R.; Brunet, Y.; Finnigan, J.; Raupach, M. A wind tunnel study of air flow in waving wheat: Two-point velocity statistics. Bound. Layer Meteorol. 1995, 76, 349–376. [Google Scholar] [CrossRef]
- Vesala, T.; Eugster, W.; Ojala, A. Eddy Covariance—A Practical Guide to Measurement and Data Analysis; Eddy Covariance Measurements over Lake Fluxes; Springer Atmospheric Sciences: Berlin/Heidelberg, Germany, 2012; pp. 335–375. [Google Scholar]
- Raupach, M.R.; Finnigan, J.J.; Brunei, Y. Coherent eddies and turbulence in vegetation canopies: The mixing-layer analogy. Bound. Layer Meteorol. 1996, 78, 351–382. [Google Scholar] [CrossRef]
- Bezerra, V.L.; Dias-Júnior, C.Q.; Vale, R.S.; Santana, R.A.; Botía, S.; Manzi, A.O.; Cohen, J.C.; Martins, H.S.; Chamecki, M.; Fuentes, J.D. Near-surface atmospheric turbulence in the presence of a squall line above a forested and deforested region in the central amazon. Atmosphere 2021, 12, 461. [Google Scholar] [CrossRef]






| K34-Daytime | CU-Daytime | K34-Nighttime | CU-Nighttime | |
|---|---|---|---|---|
| 0.08 ± 0.03 | 0.01 ± 0.005 | 0.02 ± 0.07 | 0.01 ± 0.007 | |
| (s) | 18.3 ± 15.6 | 16.6 ± 20.9 | 4.5 ± 15.0 | 2.9 ± 11.1 |
| (s) | 6.0 ± 2.7 | 3.5 ± 2.4 | 6.1 ± 5.2 | 5.2 ± 3.5 |
| (m) | 35.2 ± 28.2 | 48.0 ± 60.8 | 5.3 ± 17.3 | 2.3 ± 9.3 |
| (m) | 11.1 ± 3.2 | 9.3 ± 5.4 | 5.2 ± 8.6 | 4.6 ± 2.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santana, R.A.S.; Dias-Júnior, C.Q.; do Vale, R.S.; Tóta, J.; da Silva, R.; Tapajós, R.; Manzi, A.O.; Beldini, T.P. Comparing the Air Turbulence above Smooth and Rough Surfaces in the Amazon Region. Atmosphere 2021, 12, 1043. https://doi.org/10.3390/atmos12081043
Santana RAS, Dias-Júnior CQ, do Vale RS, Tóta J, da Silva R, Tapajós R, Manzi AO, Beldini TP. Comparing the Air Turbulence above Smooth and Rough Surfaces in the Amazon Region. Atmosphere. 2021; 12(8):1043. https://doi.org/10.3390/atmos12081043
Chicago/Turabian StyleSantana, Raoni A. S., Cléo Q. Dias-Júnior, Roseilson S. do Vale, Júlio Tóta, Rodrigo da Silva, Raphael Tapajós, Antônio O. Manzi, and Troy P. Beldini. 2021. "Comparing the Air Turbulence above Smooth and Rough Surfaces in the Amazon Region" Atmosphere 12, no. 8: 1043. https://doi.org/10.3390/atmos12081043
APA StyleSantana, R. A. S., Dias-Júnior, C. Q., do Vale, R. S., Tóta, J., da Silva, R., Tapajós, R., Manzi, A. O., & Beldini, T. P. (2021). Comparing the Air Turbulence above Smooth and Rough Surfaces in the Amazon Region. Atmosphere, 12(8), 1043. https://doi.org/10.3390/atmos12081043







