Simulation of the Dynamic and Thermodynamic Structure and Microphysical Evolution of a Squall Line in South China
Abstract
:1. Introduction
2. Observation Data and Methods
2.1. Observational Data Set
2.2. Introduction and Analysis of Complete Q Vectors
3. Meteorological Background and Numerical Simulation of the Squall Line
3.1. Atmospheric Conditions of the Squall Line
3.1.1. Introduction to the Squall Line Process
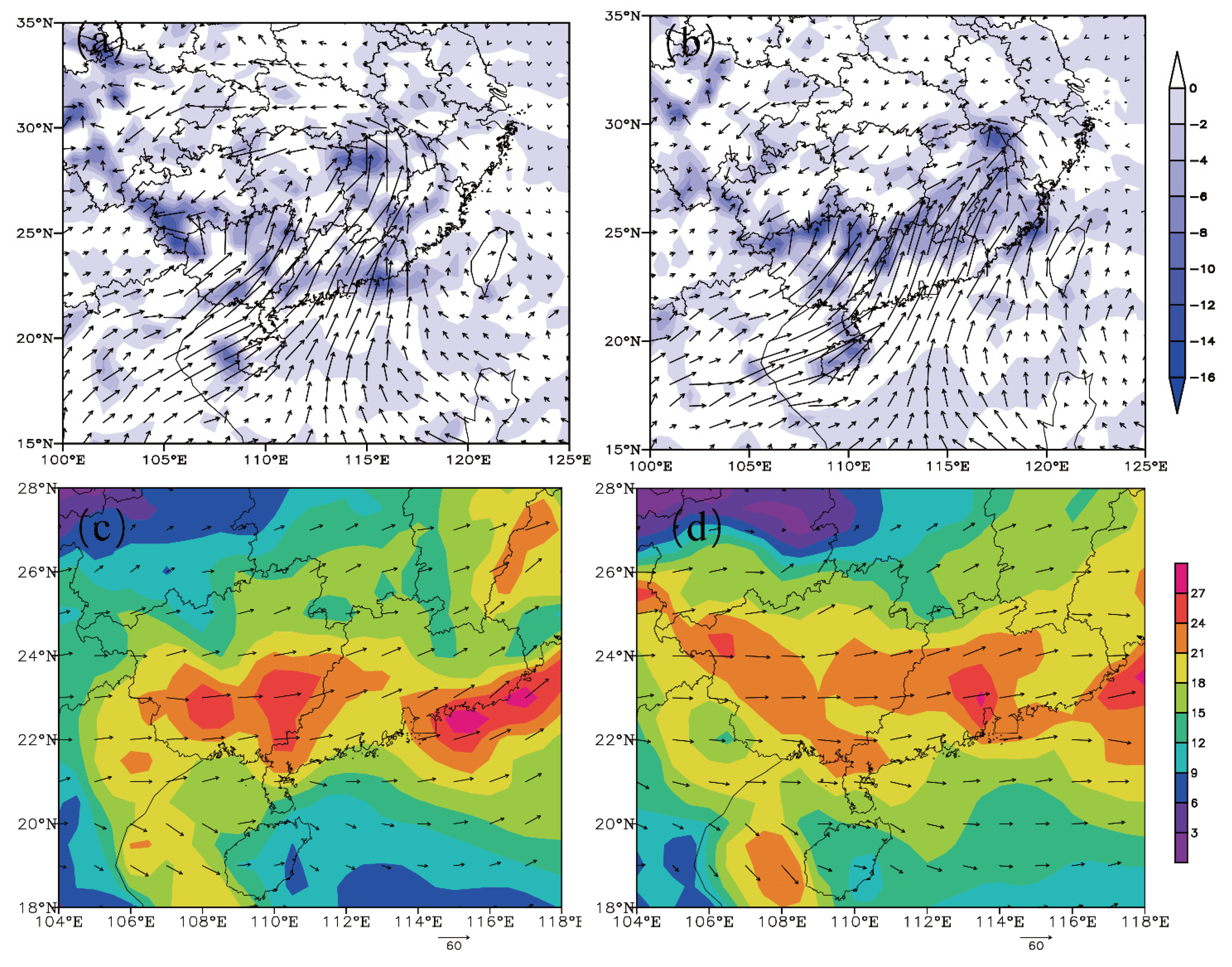
3.1.2. Evolution of Atmospheric Circulation during the Squall Line Process
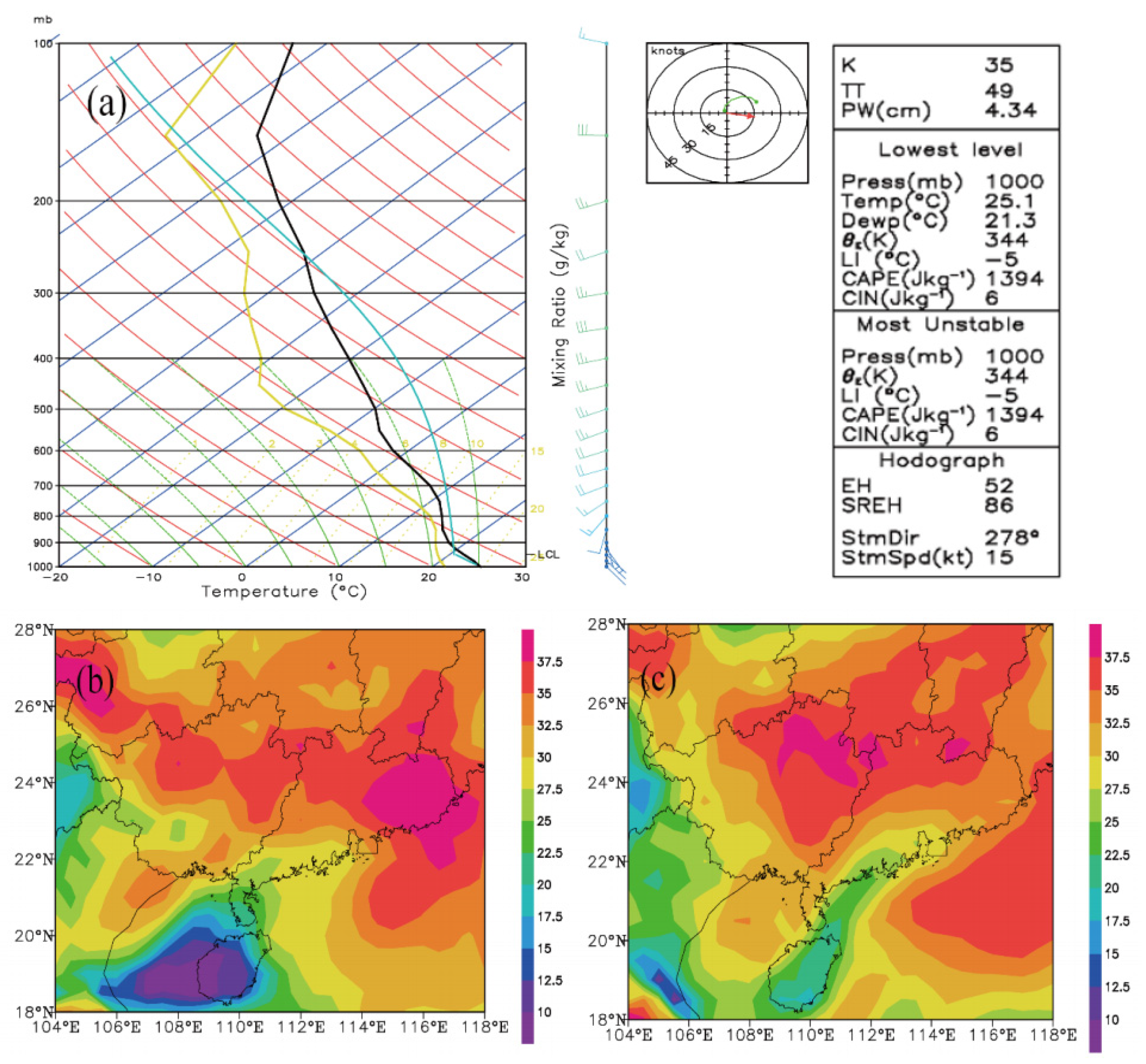
3.1.3. Unstable Stratification
3.1.4. Water Vapor Conditions and Vertical Wind Shear
3.2. Design and Testing of the Numerical Simulation
3.2.1. Data and Model Configuration
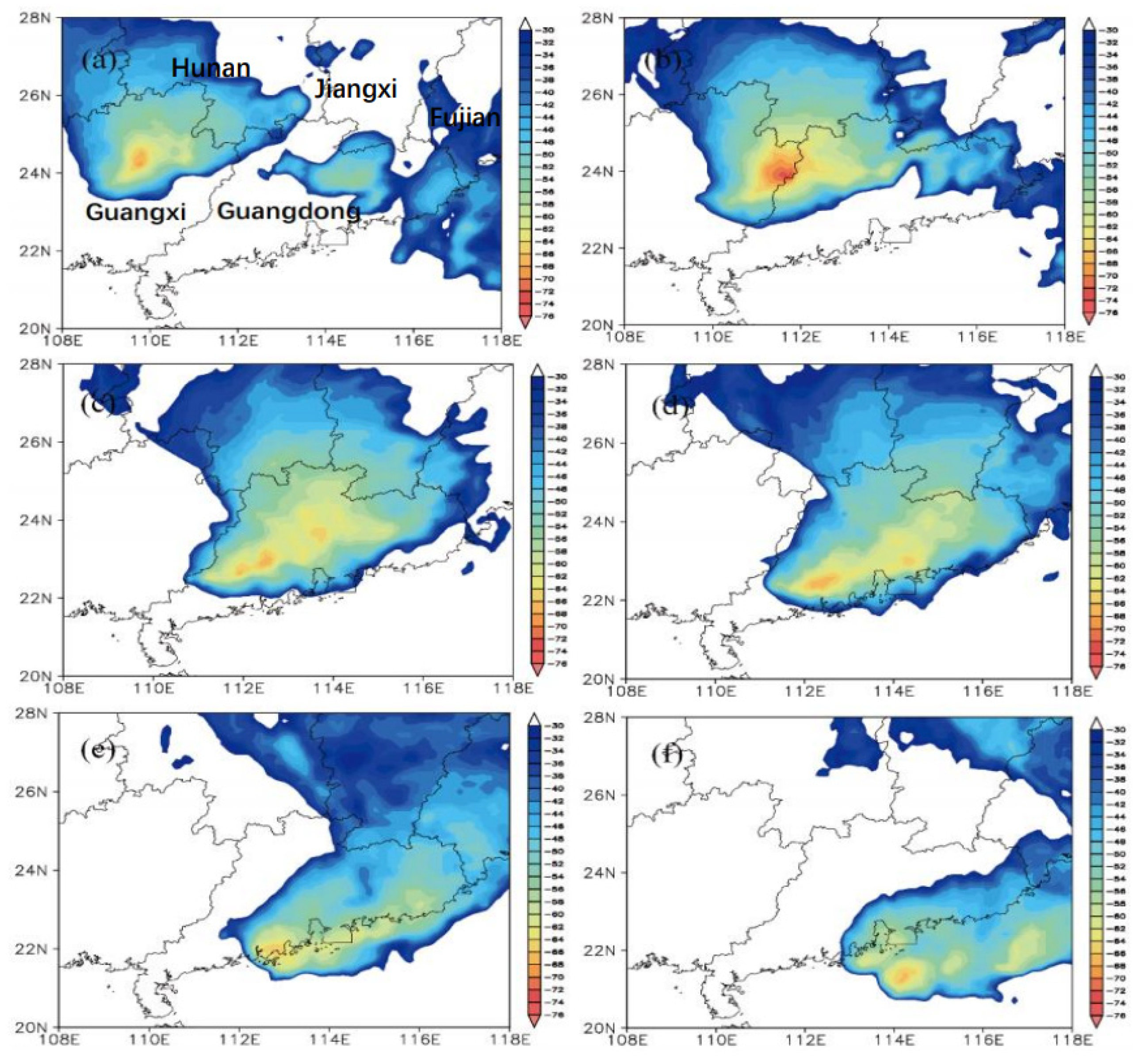
3.2.2. Testing of the Simulation Results
4. Results
4.1. The Dynamic and Thermodynamic Structure and Microphysical Characteristics of the Squall Line
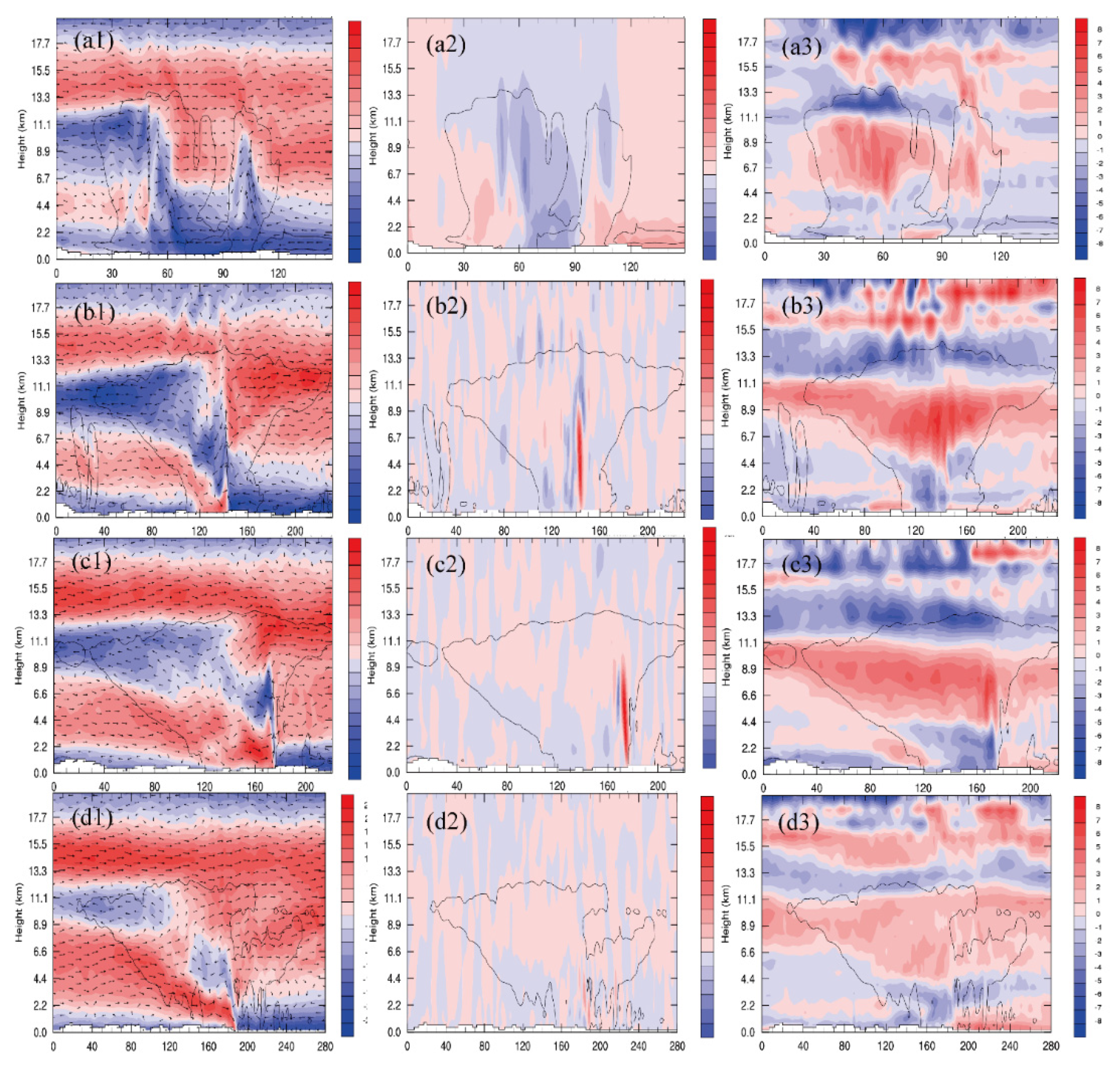
4.1.1. Spatiotemporal Evolution and the Dynamic and Thermodynamic Structure of the Squall Line
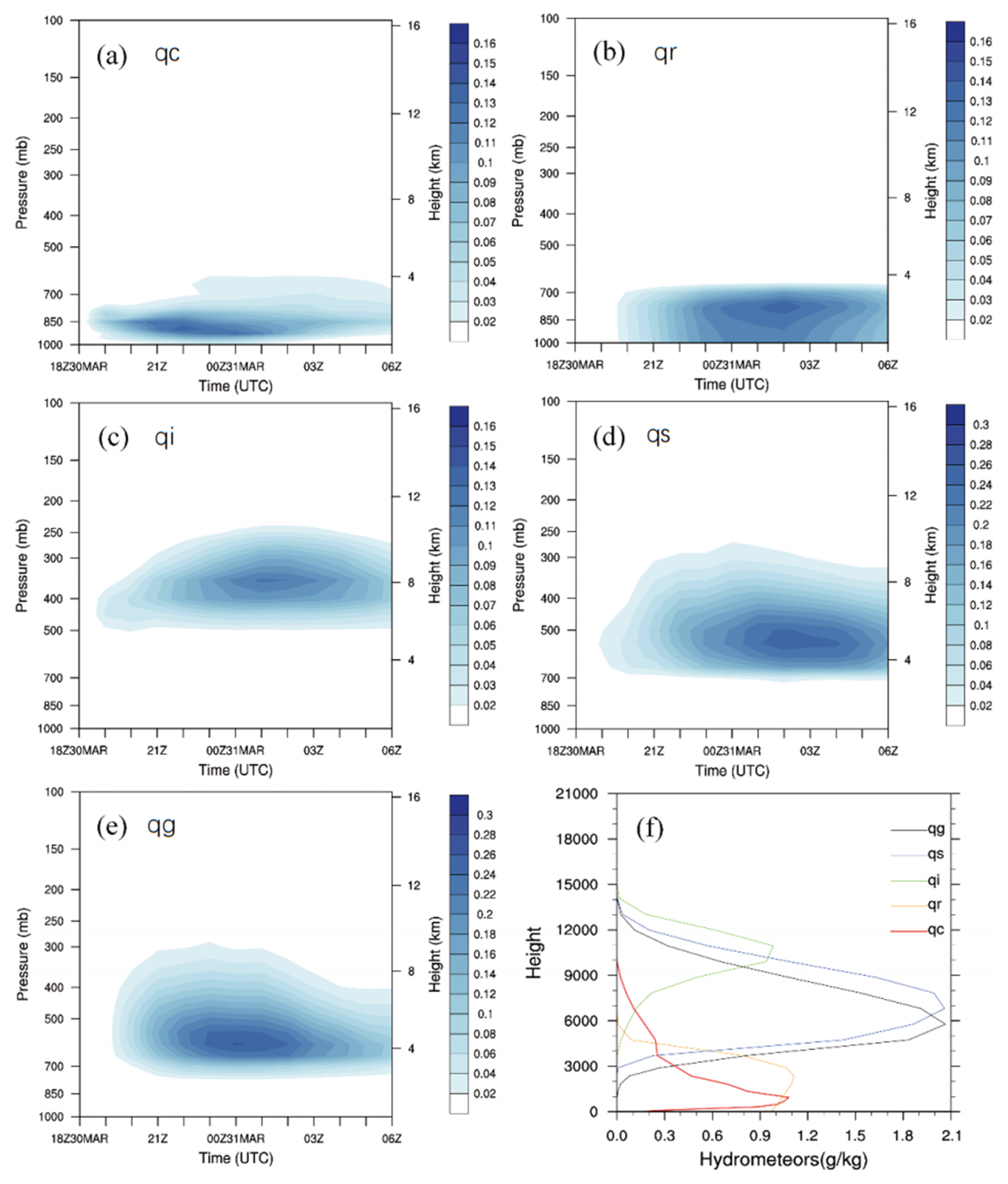
4.1.2. Microphysical Characteristics and Structure of the Squall Line in Different Periods of Development
4.2. Possible Mechanism of Development and Evolution of the Squall Line
4.2.1. Introduction and Analysis of Complete Q Vectors
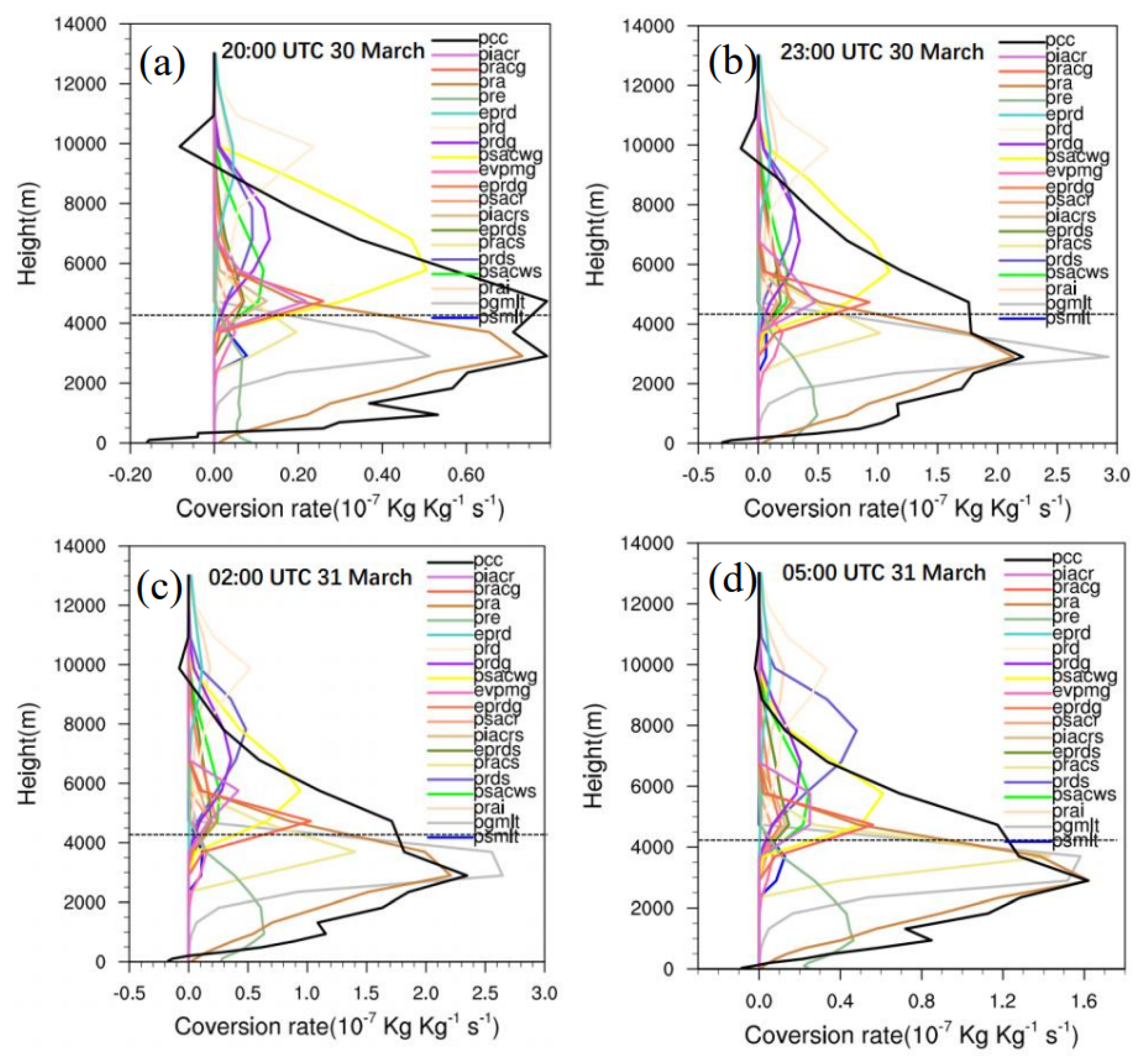
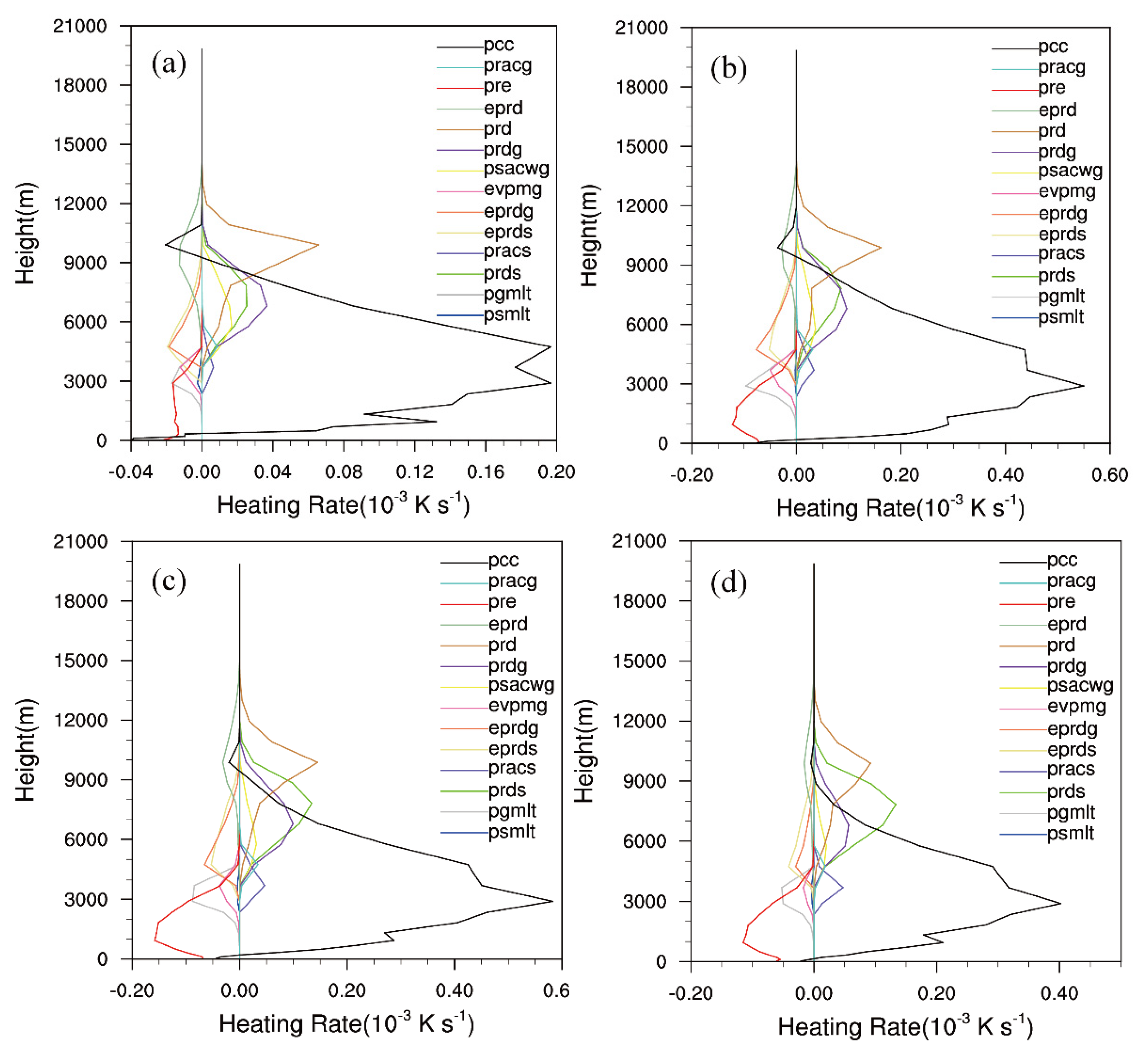
4.2.2. Microphysical Heat Budget during the Development of the Squall Line
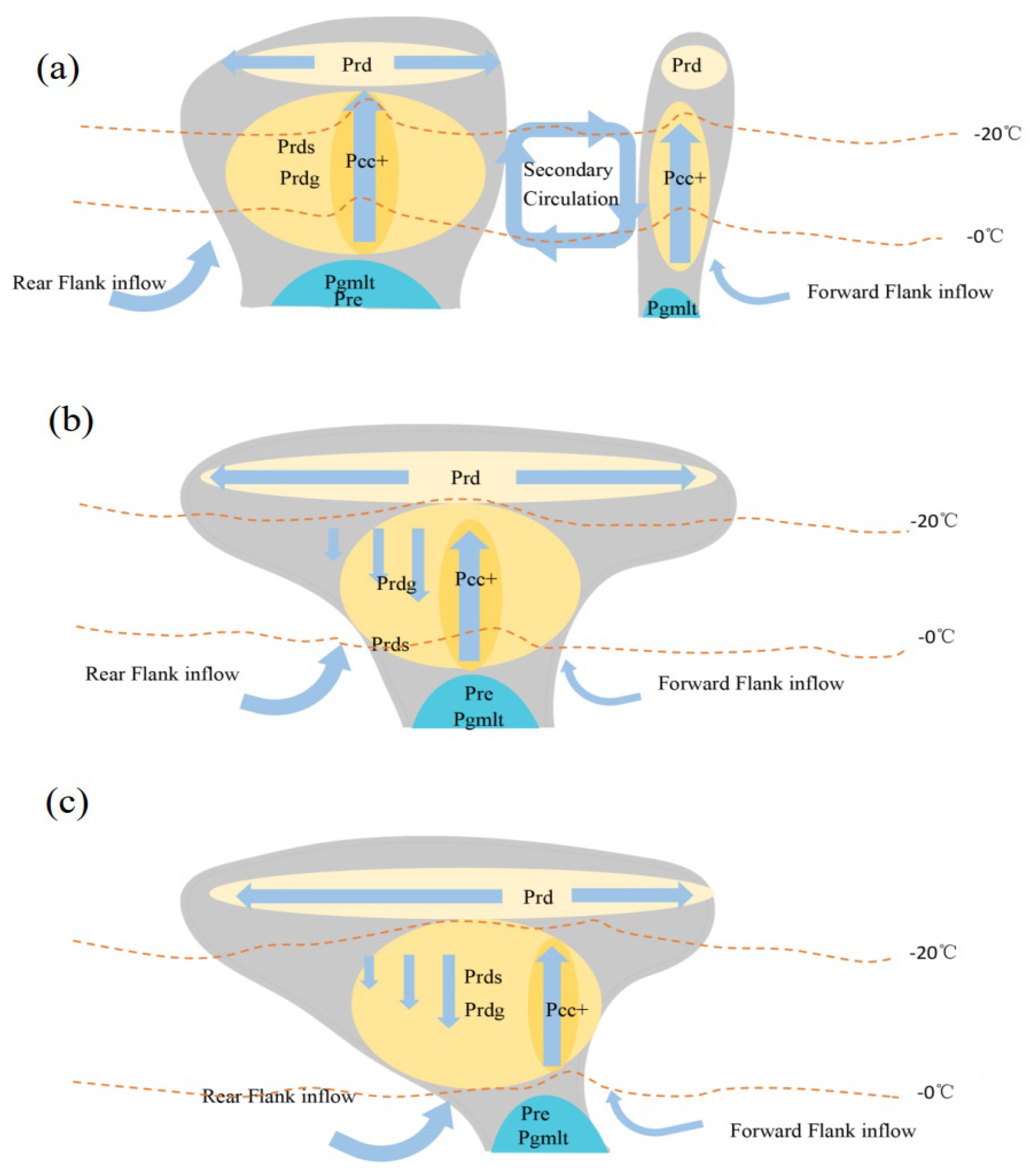
4.2.3. Possible Mechanism of the Squall Line’s Development and Evolution
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Abbreviation | Microphysical Processes of Morrison Scheme | From | To |
|---|---|---|---|
| evpms | Melting and evaporation of QS | qs | qv |
| evpmg | Melting and evaporation of QG | qg | qv |
| eprd | Sublimation of Q | qi | qv |
| eprds | Sublimation of QS | qs | qv |
| eprdg | Sublimation of QG | qg | qv |
| piacr | Collection QR by QI, conversion to QG | qr | qg |
| piacrs | Collision QR by QI, conversion to QS | qr | qs |
| pracs | Collection QS by QR | qr | qs |
| pracg | Collection QR by QG | qr | qg |
| pra | Accretion QC by QR | qc | qr |
| pre | Evaporation of QR | qr | qv |
| prd | Deposition of QI | qv | qi |
| prds | Deposition of QS | qv | qs |
| prdg | Deposition of QG | qv | qg |
| prai | Autoconversion of QI | qi | qs |
| psacws | Accretion QC by QS | qc | qs |
| psacwg | Collection QC by QG | qc | qg |
| psmlt | Melting of QS | qs | qr |
| pgmlt | Melting of QG | qg | qr |
| pcc | Condensation of QV/Evaporation of QC | qv/qc | qc/qv |
Appendix B
References
- Meng, Z.; Yan, D.; Zhang, Y. General Features of Squall Lines in East China. Mon. Weather Rev. 2013, 141, 1629–1647. [Google Scholar] [CrossRef]
- Bluestein, H.B.; Jain, M.H. Formation of mesoscale lines of precipitation: Severe squall lines in Oklahoma during the spring. J. Atmos. Sci. 1985, 42, 1711–1732. [Google Scholar] [CrossRef]
- Paker, M.D.; Johnson, R.H. Organizational modes of midlatitude mesoscale convective systems. Mon. Weather Rev. 2000, 128, 3413–3436. [Google Scholar] [CrossRef]
- Fujita, T.T. Results of detailed synoptic studies of squall lines. Tellus 1955, 4, 405–436. [Google Scholar]
- Johnson, R.H.; Hamilton, P.J. The Relationship of Surface Pressure Features to the Precipitation and Airflow Structure of an Intense Midlatitude Squall Line. Mon. Weather Rev. 1988, 116, 1444–1473. [Google Scholar] [CrossRef] [Green Version]
- Takemi, T. A sensitivity of squall line intensity to environmental static stability under various shear and moisture conditions. Atmos. Res. 2007, 84, 374–389. [Google Scholar] [CrossRef]
- Rotunno, R.; Klemp, J.B.; Weisman, M.L. A theory for strong, long-lived squall lines. J. Atmos. Sci. 1988, 45, 463–485. [Google Scholar] [CrossRef] [Green Version]
- Wakimoto, R. The Life Cycle of Thunderstorm Gust Fronts as Viewed with Doppler Radar and Rawinsonde Data. Mon. Weather Rev. 1982, 110, 1060–1082. [Google Scholar] [CrossRef] [Green Version]
- Engerer, N.A.; Stensrud, D.J.; Coniglio, M.C. Surface Characteristics of Observed Cold Pools. Mon. Weather Rev. 2008, 136, 4839–4849. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, J.; Ying, Z.; Xiao, X. Initiation and Development of a Squall Line Crossing Hangzhou Bay. J. Geophys. Res. Atmos. 2021, 126. [Google Scholar] [CrossRef]
- Fujita, T. Precipitation and cold air production in mesoscale thunderstorm systems. J. Meteorol. 1959, 16, 454–466. [Google Scholar] [CrossRef] [Green Version]
- Biggerstaff, M.I.; Houze, R.A. Kinematic and Precipitation Structure of the 10–11 June 1985 Squall Line. Mon. Weather Rev. 1991, 119, 3034–3065. [Google Scholar] [CrossRef]
- Braun, S.A.; Houze, R.A. The Transition Zone and Secondary Maximum of Radar Reflectivity behind a Midlatitude Squall Line: Results Retrieved from Doppler Radar Data. J. Atmos. Sci. 1994, 51, 2733–2755. [Google Scholar] [CrossRef] [Green Version]
- Braun, S.A.; Houze, R.A. The Evolution of the 10–11 June 1985 PRE-STORM Squall Line: Initiation, Development of Rear Inflow, and Dissipation. Mon. Weather Rev. 1997, 125, 478–504. [Google Scholar] [CrossRef]
- Leary, C.A.; Houze, R.A. The Structure and Evolution of Convection in a Tropical Cloud Cluster. J. Atmos. Sci. 1979, 36, 437–457. [Google Scholar] [CrossRef] [Green Version]
- Lord, S.J.; Willoughby, H.E.; Piotrowicz, J.M. Role of a Parameterized Ice-Phase Microphysics in an Axisymmetric, Nonhydrostatic Tropical Cyclone Model. J. Atmos. Sci. 1984, 41, 2836–2848. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.L.; Fu, D. Formation process and cloud physical characteristics of a typical disastrous hailstorm and gale in Beijing. Atmos. Sci. 2003, 27, 618–627 (In Chinese). (In Chinese) [Google Scholar]
- Adams-Selin, R.D.; Heever, S.C.V.D.; Johnson, R.H. Sensitivity of Bow-Echo Simulation to Microphysical Parameterizations. Weather 2013, 28, 1188–1209. [Google Scholar] [CrossRef]
- Szeto, K.K.; Cho, H.R. A numerical investigation of squall lines. Part II: The mechanics of evolution. J. Atmos. Sci. 1994, 51, 425–433. [Google Scholar]
- Van Weverberg, K.; van Lipzig, N.P.; Delobbe, L. The impact of size distribution assumptions in a bulk one-moment microphysics scheme on simulated surface precipitation and storm dynamics during a low-topped supercell case in Belgium. Mon. Weather Rev. 2011, 139, 1131–1147. [Google Scholar] [CrossRef] [Green Version]
- Morrison, H.; Milbrandt, J. Comparison of Two-Moment Bulk Microphysics Schemes in Idealized Supercell Thunderstorm Simulations. Mon. Weather Rev. 2011, 139, 1103–1130. [Google Scholar] [CrossRef]
- Han, B.; Fan, J.; Varble, A.; Morrison, H.; Williams, C.R.; Chen, B.; Dong, X.; Giangrande, S.E.; Khain, A.; Mansell, E.; et al. Cloud-resolving model intercomparison of an mc3e squall line case: Part II: Stratiform precipitation properties. J. Geophys. Res. Atmos. 2018, 124, 1090–1117. [Google Scholar] [CrossRef] [Green Version]
- Qian, Q.; Lin, Y.; Luo, Y.; Zhao, X.; Zhao, Z.; Luo, Y.; Liu, X. Sensitivity of a Simulated Squall Line during Southern China Monsoon Rainfall Experiment to Parameterization of Microphysics. J. Geophys. Res. Atmos. 2018, 123, 4197–4220. [Google Scholar] [CrossRef]
- Hoskins, B.J.; Draghici, I.; Davies, H.C. A new look at the ω-equation. Quart. J. Roy. Meteor. Soc. 1978, 104, 31−38. [Google Scholar] [CrossRef]
- Huang, W.G.; Deng, B.S.; Xiong, T.N. The primary analysis on a typhoon torrential rain. Quart. J. Appl. Meteor. 1997, 8, 247−251. [Google Scholar]
- Lawrence, B.D. Evaluation of vertical motion: Past, present, and future. Weather Forecast. 1991, 6, 65−73. [Google Scholar] [CrossRef]
- Yang, S.; Wang, D. The Curl of Q Vector: A New Diagnostic Parameter Associated with Heavy Rainfall. Atmos. Ocean. Sci. Lett. 2008, 1, 36–39. [Google Scholar] [CrossRef]
- Yao, X.; Yu, Y.; Shou, S. Diagnostic analyses and application of the moist ageostrophic vector. Adv. Atmos. Sci. 2004, 21, 96–102. [Google Scholar] [CrossRef]
- Yang, S.; Gao, S.T.; Wang, D.H. Diagnostic analyses of the ageostrophic Q vector in the non-uniformly saturated, frictionless, and moist adiabatic flow. J. Geophys. Res. 2007, 112, D09114. [Google Scholar] [CrossRef] [Green Version]
- Hjelmfelt, M.R.; Roberts, R.D.; Orville, H.D.; Chen, J.P.; Kopp, F.J. Observational and Numerical Study of a Microburst Line-Producing Storm. J. Atmos. Sci. 1989, 46, 2731–2744. [Google Scholar] [CrossRef] [Green Version]



| Model | WRF3.6 |
|---|---|
| Background field | NCAR/NCEP GFS 0.5° |
| Horizontal resolution | 13.5 km (D01); 4.5 km (D02); 1.5 km (D03) |
| Vertical top height | 50 hPa |
| Vertical layers | 61 |
| Microphysical parameterization schemes | Morrison double-moment scheme; |
| Longwave radiation scheme | Dudhia |
| Shortwave radiation scheme | Dudhia |
| Land surface parameterization scheme | Noah Land Surface Model |
| Planetary boundary layer scheme | Yonsei University scheme |
| Cumulus parameterization | Krain-Fritsch (D01, D02); None (D03) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Su, Y.; Ping, F.; Tang, J. Simulation of the Dynamic and Thermodynamic Structure and Microphysical Evolution of a Squall Line in South China. Atmosphere 2021, 12, 1187. https://doi.org/10.3390/atmos12091187
Li J, Su Y, Ping F, Tang J. Simulation of the Dynamic and Thermodynamic Structure and Microphysical Evolution of a Squall Line in South China. Atmosphere. 2021; 12(9):1187. https://doi.org/10.3390/atmos12091187
Chicago/Turabian StyleLi, Jingyuan, Yang Su, Fan Ping, and Jiahui Tang. 2021. "Simulation of the Dynamic and Thermodynamic Structure and Microphysical Evolution of a Squall Line in South China" Atmosphere 12, no. 9: 1187. https://doi.org/10.3390/atmos12091187
APA StyleLi, J., Su, Y., Ping, F., & Tang, J. (2021). Simulation of the Dynamic and Thermodynamic Structure and Microphysical Evolution of a Squall Line in South China. Atmosphere, 12(9), 1187. https://doi.org/10.3390/atmos12091187






