Particle Shape Impact on the Radiative Forcing Efficiency Estimated from Single Levitated (NH₄)₂SO₄ Particles

Abstract

Levitation of single trapped particles enables the exploration of fundamental physicochemical aerosol properties never previously achieved. Experimental measurements showed that (NH₄)₂SO₄’s particle shape deviated from sphericity during the crystallization process. Despite that, salt aerosols are assumed to be spheres even in low relative humidity (RH) in most climate models. In the analysis performed here, Mie and T-Matrix codes were operated to simulate crucial parameters needed to estimate the radiative forcing efficiency: extinction efficiency, asymmetry parameter and backscattering fraction. The incorporation of non-spherical effects in (NH₄)₂SO₄ particles can cause a difference of up to 46% radiative forcing efficiency compared to the assumption of sphericity in the 0.3–0.6 µm particle radius range.

1. Introduction

It is known that black carbon (BC) and sulfate aerosols are significant contributors to the radiation absorption and scattering effects of anthropogenic aerosols on a global scale. Bond et al. [1] have estimated that the industrial-era (1750–2005) direct radiative forcing (DRF) of BC was 0.71 Wm⁻². Sulfate particles are the largest anthropogenic contributors to atmospheric fine-mode aerosol [2]. Despite the extensive research effort from different viewpoints (laboratory analysis, light scattering, remote sensing platforms, and radiative transfer codes) devoted to studying the physicochemical properties of inorganic salts, they have commonly been treated as aqueous particles spherical even at low relative humidity (RH) in most climate models [3,4,5,6,7,8].

Nevertheless, according to the analysis reported by [9] the solids mass fraction on a sulfate basis can reach up to 0.34, which is not negligible. One of the great challenges of atmospheric aerosol physics properties is to understand how shape and morphology influence light extinction by the particles. The parameter that governs how light interacts with an aerosol particle is the extinction cross section (σ_ext) which depends on the complex refractive index (m), the radius of the particle (r), and the wavelength of the radiation (λ) [10]. σ_ext has been evaluated by [11] for different particle morphologies. They have established from experimental measurements a significant deviation (26.1%) in σ_ext values against Mie theory predictions when particle shape is accounted for. Moreover, Bi et al. [12] have modelled dry sea salt shapes based on superellipsoidal geometries to validate the linear depolarization ratios. Consequently, they have found that particle shape parameters are critical to interpreting data. Specifically, the inhomogeneity of sea salts has a significant impact on the asymmetry parameter (g), which is known to be a critical optical parameter in climate models. An reasonable approximation about the error caused by the assumption of aqueous and spherical particle shapes has been given by Wang et al. [13], who evaluated the effects of solid–aqueous phase transitions on sulfate direct climate forcing (SDCF) using both a column model and a global chemical transport model. They found that hysteresis of the phase transition can cause an uncertainty in the SDCF of 20%. In marine environments, the influence of the RH is crucial to calculate the morphology and the refractive index of sea salts. Wang et al. [14] reported that the inhomogeneity effect can cause up to 10% radiative forcing of sea salts. Therefore, an accurate assessment of the impact of inorganic salt shapes on optical properties and hence on the radiation field is still demanded.

Laboratory analyses are crucial to understanding the effect of the irregularity of particle shape on microphysical and optical properties. Conventional methods have focused on determining either indirect σ_ext values through the independent contribution of σ_scat and σ_abs measurements, which makes less precise the reported values of σ_ext or the evaluation of the impact of aspect ratio and the shape factor on the aerosol optical properties [15,16,17,18]. Moreover, only a few works have used tools able to collect direct measurements of σ_ext in the laboratory [19,20,21,22,23,24,25]. An additional inconvenience of these last techniques is that they provide information on σ_ext for particles from bulk samples. The study of macroscopic solutions is challenging because these systems are highly dynamic and polydisperse, exhibiting non-ideal properties. Approaches are still being developed to identify and quantify their unique chemical and physical attributes. To overcome this inconvenience, one strategy is to use methods of manipulation of single aerosol particles [26,27,28,29,30,31,32]. These approaches are based on optical levitation methods [33] which facilitate the confinement, levitation and monitoring of single particles over time and generally have focused on trapping transparent particles. However, levitating absorbing and irregular particles with optical traps is challenging, as unstable confinement appears from the force imbalance arising from the different faces of a non-spherical particle having different associated radiative scattering forces. Recently, a new electrodynamic linear quadrupole (ELQ) trap has been coupled to a cavity ring-down spectrometer (CRDS) to directly measure σ_ext from any single levitated material (aqueous, dry, spherical or non-spherical) [34]. In their analysis, the experimental σ_ext values measured were used to gain information about particle shapes through modelling with the T-Matrix/extended boundary-condition method (EBCM) implementations for random orientation with spheroid parameterization. The shape of a spheroidal particle can be specified by its aspect ratio (the ratio of the largest to the smallest axes), whereas the volume of the particle can be specified by an equivalent-sphere radius, r_eq. The modelled σ_ext values (prolate spheroid with aspect ratio up to 1.1) agreed with those measured from the CRDS, set up for one individual particle of dry (NH₄)₂SO₄. This information is crucial for estimating (NH₄)₂SO₄’s physicochemical properties and establishing potential dry parametrizations.

Therefore, in this paper, following the previous procedure, the analysis has been extended to ten individual (NH₄)₂SO₄ particles to calculate an average aspect ratio value which was assumed to be representative for dry (NH₄)₂SO₄ particles. Subsequently, the optical properties were modelled in two cases: in the first case, for the complete RH ranges, all particles were considered aqueous and spheres; in the second case, below 35% RH, all (NH₄)₂SO₄ particles were dry and non-spherical, between 35 and 80%RH, there was a mixture of aqueous spherical and dry irregular (NH₄)₂SO₄ particles and above 80%RH all particles were aqueous and spherical. The deviation of the radiative forcing efficiency between the two cases was analyzed.

2. Instruments, Data and Results

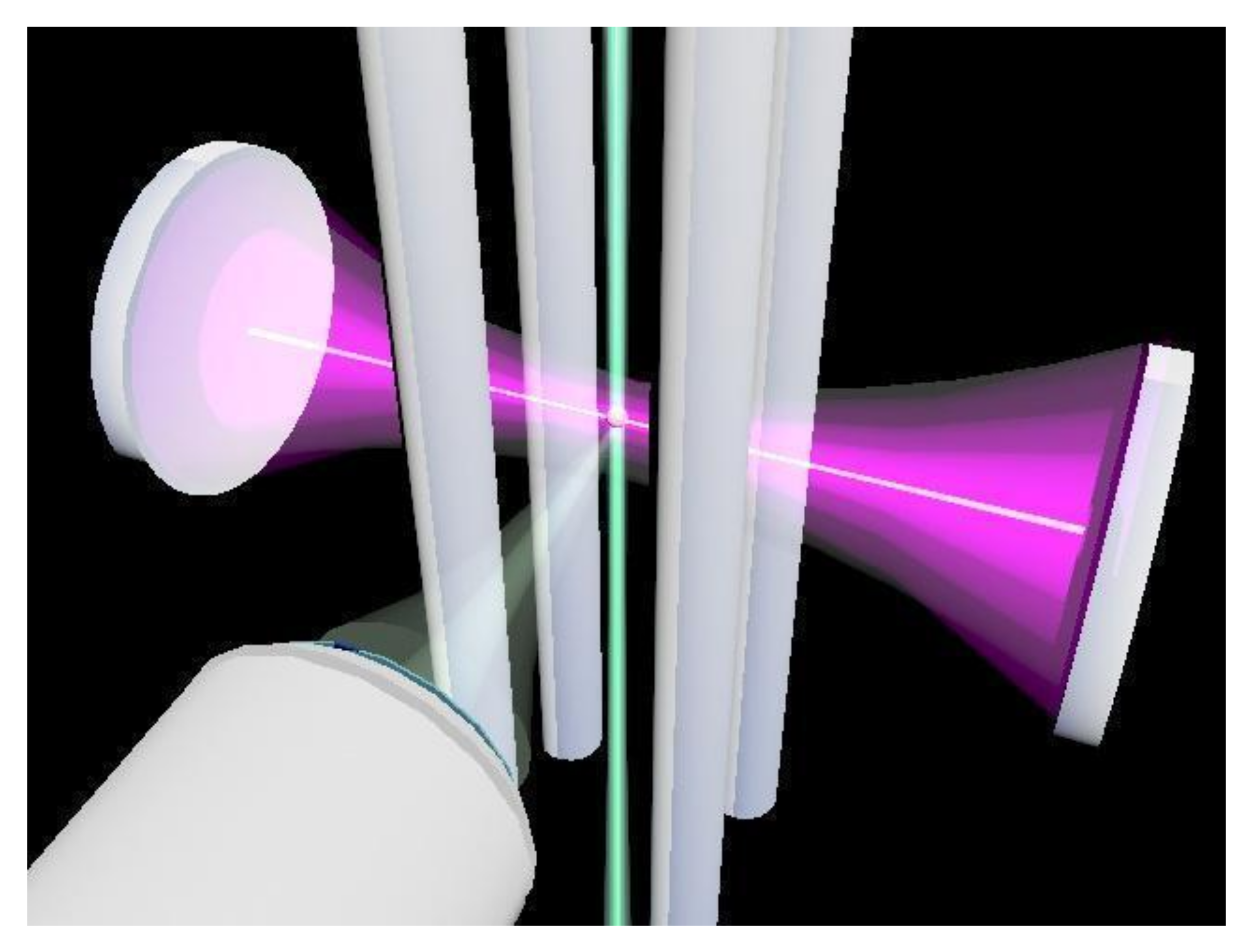
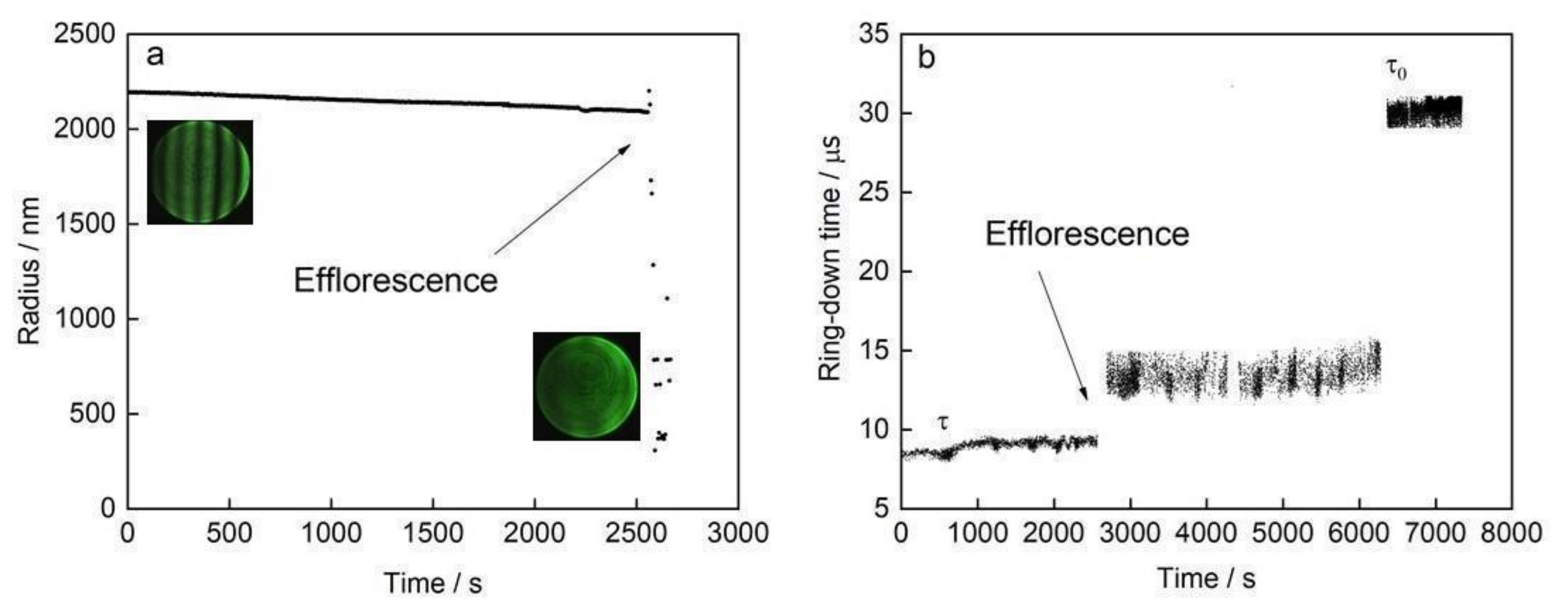
2.1. Cavity Ring-Down Spectrometer and Electrodynamic Linear Quadrupole: Direct Measurements of σ_ext in 405 nm Wavelength

In a first stage, the fitting between experimental σ_ext values from CRDS measurements and those modelled using T-Matrix/extended boundary-condition method (EBCM) implementations for random orientation with spheroid parameterization, as explained in detail by [34], was extended to ten individual (NH₄)₂SO₄ particles. In this section, the procedure to measure direct extinction cross-sections from CRDS measurements is summarized.

CRDS has been described elsewhere [27]. The new setup implementing CRDS in combination with the ELQ trap is shown in Figure 1.

The extinction cross section in a 405 nm wavelength, ${\sigma }_{ext}$, is determined from ring-down times recorded without and with a particle positioned centrally in the TEM₀₀ cavity, mode ${\tau }_0$ and τ, respectively [35]:

$${\sigma }_{ext}=\frac{\pi L{w}_0^2}{2c}\left(\frac{1}{\tau }-\frac{1}{{\tau }_0}\right)$$

(1)

where $w_0$ is the beam waist of the intra-cavity beam at the longitudinal position of the particle, c is the speed of light and L is the distance between the two highly reflective mirrors forming the high finesse optical cavity. An individual particle was captured within the ELQ trap. The vertical position of the particle was controlled by careful variation of the magnitudes of the bottom variable electrostatic potential of the ELQ trap, balancing the aerodynamic drag and gravitational forces acting on the particle. This feature was exploited to optimize the position of the particle at the centre of the optical cavity TEM₀₀ mode excited by a λ = 405 nm laser to retrieve accurate measurements of the extinction cross-section. A detailed explanation of the CRDS technique and analysis as applied to single particle measurements can be found in previous papers [27,28,29,30,31,32].

A second laser beam at a 532 nm wavelength was operated to interact with the levitated particle and collect the elastic scattering on a CCD camera placed at 90° to the direction of the laser beam. An aperture at the side of the trapping cell gave access to a horizontally propagating Gaussian laser beam of λ = 532 nm which illuminated the droplet for angularly resolved elastic scattering measurements of the droplet size. The CMOS camera (Thorlabs, DCC1546M) coupled to a 20× long working distance objective (Mitutoyo) with a numerical aperture (NA) of 0.42 orientated 90° to the laser beam was used to capture the phase function (PF) from a single trapped droplet. Insets in Figure 2a show images when a (NH₄)₂SO₄ particle was spherical (well-defined fringes) and after the crystallization (fringes are incoherent) in RH below 35%. The angular scattering lobe structure predicted by Mie theory is clearly observed. Experimental phase functions were fitted to a library of PFs of Mie theory in order to estimate radius and refractive index. Detailed explanation about this procedure can be found in [24,34,36,37].

Figure 2a shows the fitted radius from experimental measurements of elastic scattering, since the (NH₄)₂SO₄ particle was spherical (2230 nm) up to crystallization (2115 nm). At this point, the fringes became incoherent and Mie fitting was not effective. No information about experimental phase functions could be retrieved from crystallization RH. Simultaneously with the collected elastic scattering, Figure 2b shows ring-down time measurements from CRDS when a particle was spherical with typical node and antinode standing wave structure up to crystallization took place. At this point, ring-down time values jumped up as a consequence of the rapid loss of particle mass. A complete and detailed explanation about this new setup and the crystallization analysis can be found in [30]. Ten individual experiments were performed as crystallization occurred. (NH₄)₂SO₄ particle shape deviated from sphericity (aspect ratios ranging from 1.1 to 1.3) and modelled σ_ext values fitted reasonably well to experimental σ_ext data from CRDS measurements. It was calculated an average aspect ratio of 1.2 and it was assumed to be representative of dry (NH₄)₂SO₄ particles.

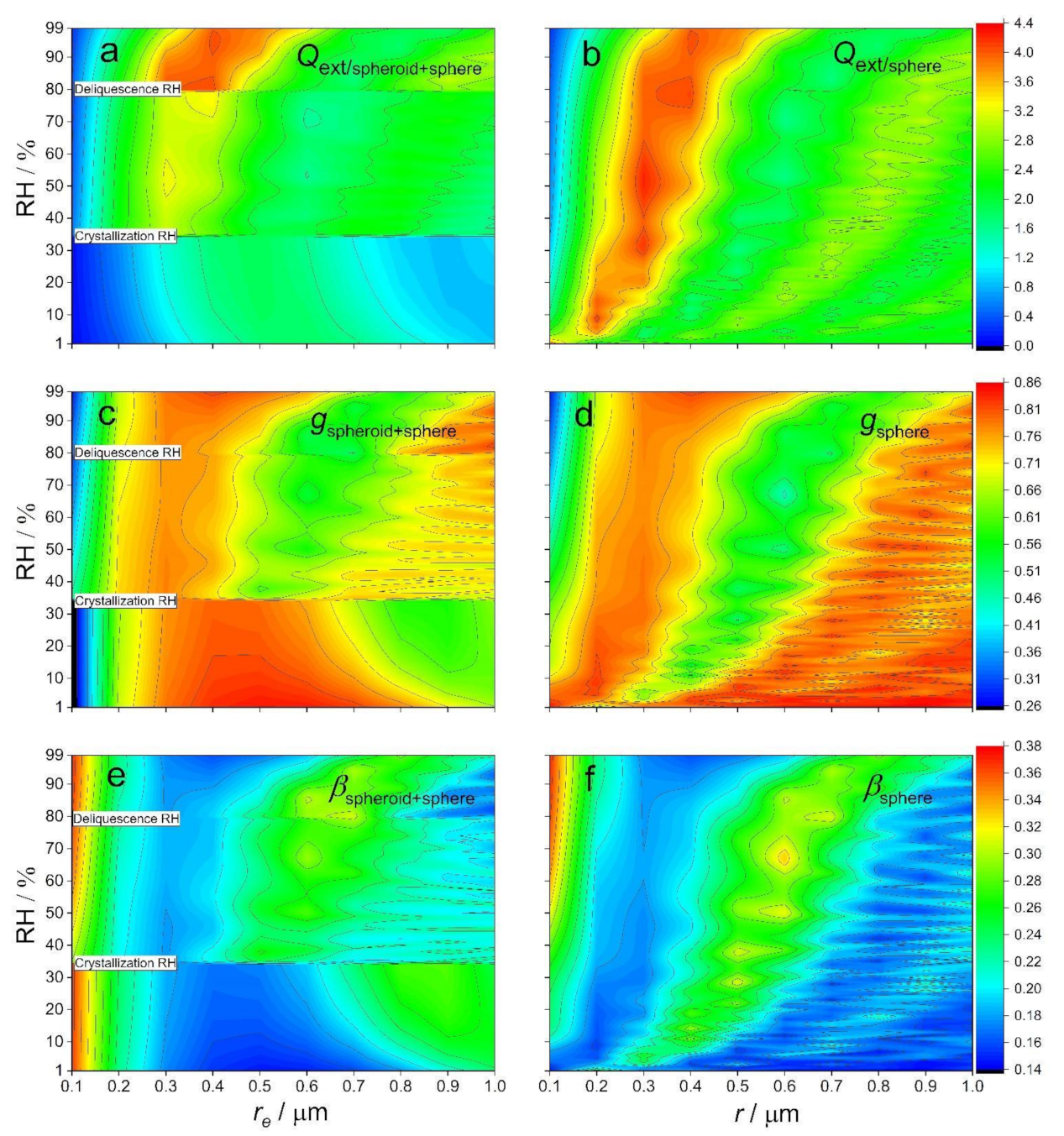
2.2. Parameterizations of r and n with RH and 532 nm Wavelength: Optical Properties and Radiative Effects of Dry (NH₄)₂SO₄ Particles

In a second stage, optical properties for aqueous and dry (NH₄)₂SO₄ particles have been modelled using Mie theory/T-Matrix spheroid codes. Different assumptions were made for ease of analysis. This was a quantitative and qualitative analysis to estimate the effect of particle shape on optical properties and hence the radiative forcing efficiency. Although the sulfate–ammonium ratio presents different extents of neutralization defined as X (X = 1, (ammonium sulfate) (NH₄)₂SO₄; X = 1.5, (levocite) (NH₄)₃H(SO₄)₂; X = 2, (ammonium bisulfate) NH₄HSO₄), the percentage found in the atmosphere can be divided into 93% (NH₄)₂SO₄, 6% (NH₄)₂SO₄ and 1% NH₄HSO₄ [9]. Therefore, the most general case, (NH₄)₂SO₄, was considered. No core or shell was incorporated into the modelling process. To simulate optical properties, binary particles were taken (water and pure (NH₄)₂SO₄ solute) and although crystallization RH is a stochastic process, it was established that (NH₄)₂SO₄ particles crystallize at 35% RH. The weight of the solid fraction against aqueous particles, between 35 and 80% of the RH region, was 0.34 based on the analysis of the RH history given by [9]. Below 35% RH it was assumed all (NH₄)₂SO₄ particles were a mixture of solid and liquid and above 80% RH all (NH₄)₂SO₄ particles were aqueous and spherical.

The approximate κ-Köhler model proposed by [38] was used to provide the relation between the particle radius, r, measured at different water activities (a_w) with the radius in dry conditions, r₀. For 100 nm particles and typical growth factors, this approximation generally leads to a 1–2% error in the water activity [39]:

$$r=r_0{\left(1+\kappa ·\frac{a_w}{1-a_w}\right)}^{\frac{1}{3}}$$

(2)

where a_w is equivalent to RH (%)/100 when neglecting the Kelvin effect based on droplet size. If the influence of surface curvature is ignored, the a_w is equal to the saturation ratio or the ratio of the vapor pressure of water over the drop to the saturation vapor pressure of water at that temperature. This was justified in our case, because the Kelvin effect is small for large particles (diameter > 100 nm), which are the most relevant to light scattering and absorption [40]. κ characterizes the hygroscopicity response of the solute. In this study, the κ value used for (NH₄)₂SO₄ was that reported by [39].

It was reasonable to evaluate optical parameters and radiative effects at the 532 nm wavelength because it is in the centre of the solar visible spectral range. The wavelength dependence of n for many transparent and absorbing materials in the visible range can be described by the well-known Sellmeier equation with expansion to the first order term [41]:

$$n^2=1+\frac{B{\lambda }^2}{{\lambda }^2-C}$$

(3)

where n is the refractive index at the wavelength λ and B and C are fitting coefficients. The B and C Sellmeier coefficients were calculated from the fits to the experimental data and were smooth functions of the RH, parameterized as quadratic polynomials in terms of the a_w.

It was assumed in this analysis that particles were homogeneous in the refractive index. Considering the parameterizations for particle radius (r) and real refractive index, (n) as a function of RH and wavelength, the interaction of the light with a single particle can be calculated using Mie theory for spherical particles [42,43]. Nevertheless, in the case of irregular shapes, Mie theory is not an efficient method and alternative approaches are needed such as the T-Matrix/EBCM spheroid method [44,45]. The T-Matrix/EBCM spheroid approach was used in this analysis according to the parameters reported by [34] for dry (NH₄)₂SO₄ particles. The input parameters used to supply the Mie theory or T-Matrix/EBCM spheroid method were n, the size parameter (x) and size equivalent parameter (x_eq = kr_eq) for spherical and irregular particles, respectively. r_eq is the equivalent radius and was calculated as $r_{eq}=\sqrt[3]{a^{2}c}$, where a is the semi-axis length along the x- and y-axes, and c is the semi-axis length along the z-axis, which is the axis of revolution. In this study, three aerosol radiative parameters were determined: the extinction efficiency (Q_ext), calculated as ratio of the ${\sigma }_{ext}$ to the geometric section (${\sigma }_{geo}$), the asymmetry parameter (g) and the backscattering fraction (β) including dependence on particle size, composition, RH, and wavelength. These optical parameters were needed to estimate the RFE at a 532 nm wavelength at the top of the atmosphere caused by a thin aerosol layer in the lower troposphere from Equation (4), proposed by [46]. Some previous publications have reported the usefulness of this treatment for studying the RFE [19,47,48,49,50,51].

$$RFE=\frac{∆F}{AOD}=SD \left(1-A_{cld}\right)T_{atm}^2{\left(1-R_{sfc}\right)}^2\left[2R_{sfc}\frac{1-\omega }{{\left(1-R_{sfc}\right)}^2}-\beta \omega \right]$$

(4)

where AOD is the aerosol optical depth and S is the solar constant (set to 1370 W/m²). For the rest of the parameters, we assumed standard conditions of a continental area. D is the fractional day length (set to 0.5), A_cld is the fractional cloud cover (set to 0.61), T_atm is the solar atmospheric transmittance (set to 0.76), and R_sfc is the surface albedo (set to 0.15). The β is the average upscatter fraction (the fraction of scattered sunlight that is scattered into the upward hemisphere), which is a function of hemispheric backscatter fraction b, defined as the ratio of backscattering efficiency to total scattering efficiency and ω is the single scattering albedo caused by a uniform and optically thin aerosol layer. As the (NH₄)₂SO₄ particles are transparent to the light, ω is equal to the unity. The parameter β was calculated from the Henyey–Greenstein phase function:

$$\beta =0.082+1.85·b-2.97· b^2$$

(5)

where b was derived from g through the equation [52]:

$$b=\frac{1-g^2}{2g}\left(\frac{1}{\sqrt{1+g^2}}-\frac{1}{1+g}\right)$$

(6)

To distinguish the effects of non-spherical (NH₄)₂SO₄ on radiative forcing efficiency regarding that caused by the spherical approach, it was defined the parameter ΔRFE, which was presented as a percentage and calculated from the equation:

$$∆RFE=\frac{RF{E}_{spheroid+sphere}-RF{E}_{sphere}}{RF{E}_{sphere}}\times 100$$

(7)

For the convenience of the analysis, particles of 1 μm and smaller in radius were considered because they have the largest climate impact [13,53]. Modelled values of Q_ext, g and β for combined T-Matrix/Mie theory codes (Figure 3a,c,e) and those evaluated only with Mie theory method (Figure 3b,d,f) are shown as function of RH and particle radius. According to only Mie theory predictions for a specific radius, three parameters showed almost no dependency on RH making the extinction more efficient when particle size is of the order of the wavelength, and the forward scattering increased with the increase in particle size. As non-spherical approximation was included, all optical parameters evaluated presented a drastic change in their values in the phase transition RHs (crystallization and deliquescence points). Overall, Q_ext for non-spherical (NH₄)₂SO₄ particles was always smaller than a sphere. The strong impact of particle shape in optical properties was evident, as RHs below 80% were sharper than RHs below 35% compared to Mie theory calculations. Non-sphericity enhanced g (0.86) toward a lower particle radius interval from 0.2 to 0.7 µm for RHs below 35% (Figure 3c). The opposite occured for β where the non-sphericity introduced less backscattering. Therefore, the non-inclusion of the irregularity in the shape, especially at low RHs, could underestimate the solar irradiation that reaches the surface, enhancing the cooling of the atmosphere.

The RFE_{spheroid+sphere} (spheroid approach and Mie theory) and RFE_sphere (Mie theory) are shown in Figure 4a,b, respectively. Radiative effects were strongly dominated by g in both cases. Nevertheless, RFE_{spheroid+sphere} exhibited properties different to those evaluated only for sphere approximation. As illustrated in Figure 3a,c,e optical properties at various RHs differed too much. Further, differences in the RFE_{spheroid+sphere} between deliquescence and crystallization RHs indicated the relevance of relative humidity plays on (NH₄)₂SO₄ particles. In most typical environmental RHs (35–80%), the incorporation of particle shape in the RFE_{spheroid+sphere} caused stronger cooling (around −22 Wm⁻²AOD⁻¹) for particles larger than 0.7 µm in radius. Although less common in the atmosphere, for RHs below 35%, RFE_{spheroid+sphere} presented strong dependency on the particle size with a different redistribution of radiative effects. A lower cooling (−14 Wm⁻²AOD⁻¹) was shown in the interval of radius from 0.3 to 0.7 µm.

Figure 5 shows the ΔRFE calculated using Equation (7). Spherical particles were taken as reference to assess the RFE deviation. Positive values of ΔRFE indicated that the addition of non-spherical (NH₄)₂SO₄ particles had a stronger radiative cooling effect (higher than 90% difference for RHs below 35% with a radius smaller than 0.2 µm and larger than 0.8 µm). This was in accordance with lower values of g. However, in the RH range (35–80%) the assumption of sphericity only caused an overestimation of the cooling radiative effects of up to 18% with regard to particles of a radius of 0.3 and 0.6 µm.

3. Conclusions

Although the hysteresis of the phase transition for (NH₄)₂SO₄ has been extensively treated, the incorporation of non-sphericity into climate models has not yet been assessed. The analysis performed here illustrates that non-sphericity had a stronger effect on optical properties in deliquescence and crystallization RHs. Non-sphericity enhanced g toward a lower particle radius interval from 0.2 to 0.7 µm for RHs below 35%. The incorporation of the non-spherical effects of (NH₄)₂SO₄ particles led to a difference of up to 46% in radiative forcing efficiency compared to the assumption of sphericity for a 0.3 to 0.6 µm particle radius range. I would like to emphasize that for a precise evaluation of radiative effects it is needs to incorporate the particle shape impact on the physicochemical properties. A complete assessment of the effects of the aerosol phase transition in the real atmosphere would be recommendable. However, it would also require a detailed RH history analysis to extend the calculations to larger particle sizes, which implies more computing time consumed. In future work this study will be performed on a global scale.