Abstract
The aim of this paper is to statistically examine whether there are different patterns in daily numbers of deaths during the quiet periods of solar activity, in contrast to the periods of the strong solar storms. We considered three periods of solar storms (storm of 14 July 2000 Bastille Day Event, storm of 28 October 2003 Halloween Solar Storms, and storm of 17 March 2015 St. Patrick’s Day event) and three periods of continuous very low solar activity (13 September–24 October 1996, 21 July–20 August 2008, and 31 July–31 August 2009) during the Solar Cycles No. 23 and No. 24. In particular, we focus on diseases of the nervous system (group VI from ICD-10) and diseases of the circulatory system (group IX from ICD-10) separately for both sexes and two age groups (under 39 and 40+). We demonstrate that in the resulting graphical models there was a connection between the daily number of deaths and all indices of solar and geomagnetic activity in periods of low solar activity in contrast to periods of strong solar storms in some monitored groups according to age, sex, and group of diagnosis.
1. Introduction
Changes in the Earth’s magnetic field, which permeates the entire biosphere, induce an electric field in the conductors that every living tissue is. The direct effects of high-energy solar radiation, especially during solar storms, have a measurable impact on living organisms, including human organisms [1]. Biomedical experiments confirmed changes in the cardiograms of higher animals under the influence of fluctuations in the electromagnetic field to which they were exposed [2]. Naturally, it can be expected that even changes in the Earth’s magnetic and electric field will affect human heart and nerve activities. Electromagnetic field mainly affects the condition of the patients with brain, nerve, or heart diseases, non-specifically also the nervous system and hormonal activity. On days of magnetic storms, changes in blood clotting, sedimentation rates, and pulse are detected [2,3,4,5,6].
The geosphere is exposed to severe episodic changes associated with heliospheric disturbances. Environmental changes are monitored in both quiescent and disturbed states, magnetohydrodynamic models are built, which describe physical processes taking place under disturbed conditions (e.g., acceleration of electrons in radiation belts during magnetic storms, which often occur spontaneously and without precursors) and on this basis predict the extent of these changes. The magnetosphere is a large three-dimensional structure, the spatially distant parts of which can be quickly and directly connected by plasma phenomena. As in the ionosphere–thermosphere system, there are a number of very complex bonds in the magnetosphere–ionosphere system, on which heliosphere disorders have a major impact. The high-energy solar radiation, especially during solar flares, has an underlying impact on all living (including human) organisms [1]. The paper [7] assumes that neuropsychological diseases and psychiatric disorders exhibit during the periods of increase and decrease solar activity.
The delay of the geomagnetic storm after the solar flare is 25–60 h. Geomagnetic storms usually have four phases in medium latitudes (including the Czech Republic). Typical is the rapid onset of a storm with a sharply increasing intensity of the horizontal component of the geomagnetic field lasting 2.5–5 min. This occurs by the densification of the magnetic field lines of the Earth’s magnetic field due to their compression by the interplanetary shock wave of the solar wind. During the next initial phase (Initial phase), which lasts a maximum of several hours, the intensity of the horizontal component of the magnetic field further increases due to the passed interplanetary shock wave. During the main phase, the geomagnetic lines are connected to the lines of the magnetic field carried by the plasmoid from the Sun, which accelerates the equatorial annular current and weakens the intensity of the horizontal component of the magnetic field. This decline can take several hours to a day. In the final phase (Recovery phase), the equatorial annular current decays due to plasma instability and diffusion. The intensity of the horizontal component of the Earth’s magnetic field returns to its original values within a few hours to days [8,9].
Changes in the Earth’s magnetic field caused by solar storms are also reflected in the change in the electric field between the ionosphere and the Earth’s surface. This field is also affected by induced currents from the Earth’s liquid core in the Earth’s mantle. Its intensity at the Earth’s surface is approximately 60,000 nT at the pole and 30,000 nT at the equator [10] (pp. 4–7). It is possible to quantify the impact of magnetic field changes at a specific location on Earth by measuring ground magnetometers. These measurements are performed using the worldwide SuperMAG network using 3D vector measurements. In the Czech Republic, these measurements are performed by the geomagnetic station of the Geophysical Institute of the ASCR Budkov in South Bohemia (BDV, 49.08° N, 14.02° E) days [8,9].
Correlations of changes in state of human health with solar activity were identified in papers [11,12,13,14,15]. These effects were also noted [16,17,18] as the onset of nervous diseases and genetic disorders. A similar study was conducted [19] and reached similar results. According to these studies, geomagnetic activity plays only a minor role in the cardiovascular mortality, a finding that has been confirmed in a study [20]. Strong solar storms affect the human circulatory system indirectly through the concentration of electric charges and also changes in the magnetic field in the terrestrial environment in which the monitored population lives [21]. Moreover, the impact of geomagnetic disturbances may depend on solar magnetic field polarity [22], the course and phase of the solar cycle, and on the strength of the exceptional solar events during the given period of observation [23,24,25,26,27,28]. The recent studies investigate also the simultaneous effects of space weather and meteorological situations on cardiovascular diseases [29,30,31,32], which can be important in the context of climate change.
To compare the characteristic patterns in daily numbers of death, a period with lower solar activity was chosen in our analysis. These periods were then confronted with periods of strong solar storms and their temporal impact.
The mortality level in the Czech Republic (population of about 10 million) during the investigated period from years 1994 to 2015 has evenly decreased. Registration of deaths by cause of death and coding praxis is longitudinally very well established and organized in the Czech Republic. The data series were provided by Czech Statistical Office [33]. The whole observed period belongs to term of validity of ICD-10 (International Statistical Classification of Diseases and Related Health Problems 10th Revision), and the unified version of the electronic coding system IRIS (Language independent coding system) was operated throughout this period in the Czech Republic [34].
The time series of daily aggregated numbers of deaths by cause, men and women separately at the age groups under 39 and 40+ were used for this analysis. For detailed analysis, causes of death classified in chapter VI, diseases of the nervous system, and classified in chapter IX of ICD-10, diseases of the circulatory system, were chosen. Time series of daily numbers of deaths per group of diagnoses of ICD-10 VI, diseases of the nervous system (codes G00–G99), and IX, circulatory system diseases (codes I00–I99), per group of diagnoses together were used for the analysis, due to the length of the observed period. We chose the analysis of daily numbers of deaths for the whole group of diagnoses due to low daily numbers of deaths for detailed diagnoses [35,36].
According to the description of detailed diagnoses and already performed studies [1,11,14], there is no presumption that an acute severe reaction of the human organism to changes in geophysical parameters could have a delay longer than 30 days [35,36,37,38], the same long period after the solar storm was analyzed. The period of 30 days was chosen to monitor specific changes in the number of deaths after a solar storm because there is no assumption that the acute deterioration after the solar/geomagnetic storm could be causally reflected in mortality over a longer period than 30 days in the conditions of medical care in the Czech Republic. We focused to the situations when solar-flare or shock waves associated with coronal mass ejections produce strong solar energetic particles (SEP) events with geomagnetic impact.
The investigated period (1994–2015) was chosen for the analysis also because the mortality level in the Czech Republic did not fluctuate sharply. For example, it would not be possible to perform the analysis in the current situation where the mortality level is affected by COVID-19 disease and can be problematic in the future as well [39,40].
As a result, we focused on three exceptionally strong solar events in this period:
- -
- class X5 storm on 14 July 2000 Bastille Day Event;
- -
- class X17 storm on 28 October 2003 Halloween Solar Storms;
- -
- class G4 storm on 17 March 2015 St. Patrick’s Day Event.
Daily numbers of deaths in the studied groups of diagnoses were also observed in approximately 30 day long quiet periods. To compare the mortality patterns, a period with lower solar activity was chosen, namely just 30 days of quiet period of very low solar activity during Solar Cycles No. 23 and No. 24 when the relative number of sunspots R was completely zero (R = 0):
- -
- 13 September–24 October 1996;
- -
- 21 July–20 August 2008;
- -
- 31 July–31 August 2009.
These storms and continuous quiet periods were selected according to the NWRA/CoRA catalog, NorthWest Research Associates in Boulder, CA, USA, and the Deutsches GeoForschungsZentrum so that they occurred evenly throughout the study period. The radiation solar activity indices F10.7 (Intensity of the Solar Radio Flux) [36], the geomagnetic solar activity indices Kp planetary index [41,42], and Dst (Disturbance Storm Time), and Proton density and Proton Flux > 30 MeV (FP30) represent the solar activity in our study.
2. Data and Methods
2.1. Data Sets
For detailed analysis, causes of death of the chapters VI. diseases of the nervous system and IX. diseases of the circulatory system of ICD-10 were chosen. Time series of daily numbers of deaths per group of diagnoses of ICD-10 VI. diseases of the nervous system (codes G00–G99) and IX. circulatory system diseases (codes I00–I99) per group of diagnoses together were used for the analysis, due to the length of the observed period. The time series of daily aggregated numbers of deaths by cause, men and women separately at the age groups under 39 and 40+ were used in this study. The data were provided by Czech Statistical Office (http://www.czso.cz, accessed on 2 November 2019). The time series of daily numbers of deaths from studied causes of death, which met the criteria of observation frequency for time series analysis using graphical models of conditional independence, and the series of geophysical and solar parameters expressing the level of solar activity were included in the complete graphical model of conditional independences CIG (solar radio flux F10.7, geomagnetic index Kp, and solar proton flux > 30MeV PF30) which we will describe in the method section. As already mentioned, Dst index was used to determine the onset time of a geomagnetic storm. Moreover, the Dst time series did not pass the test for normality and independence of logarithmic data (at significance level of 0.05) and therefore it was not possible to compute the minimalized graphical model of conditional independence for it.
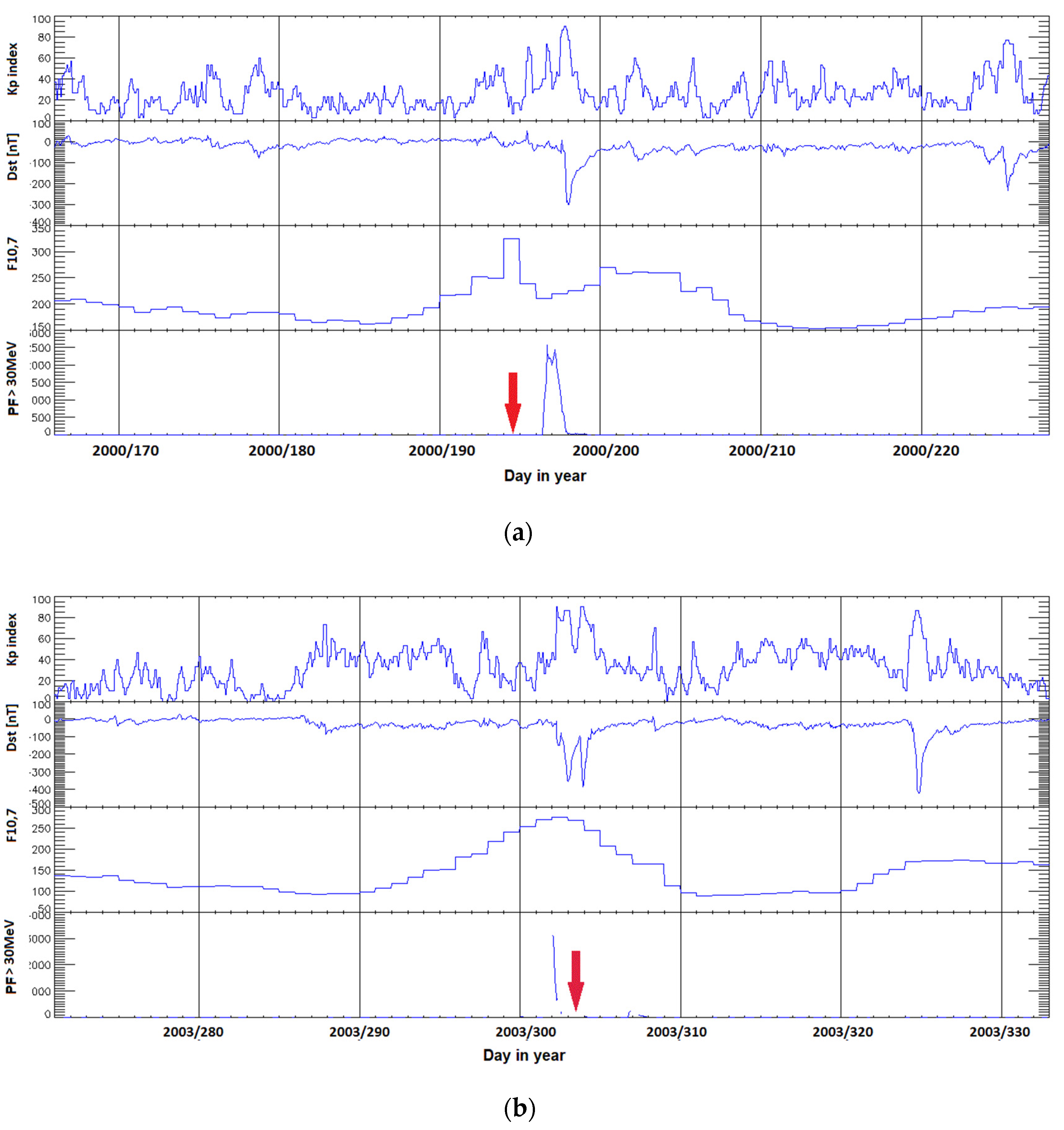
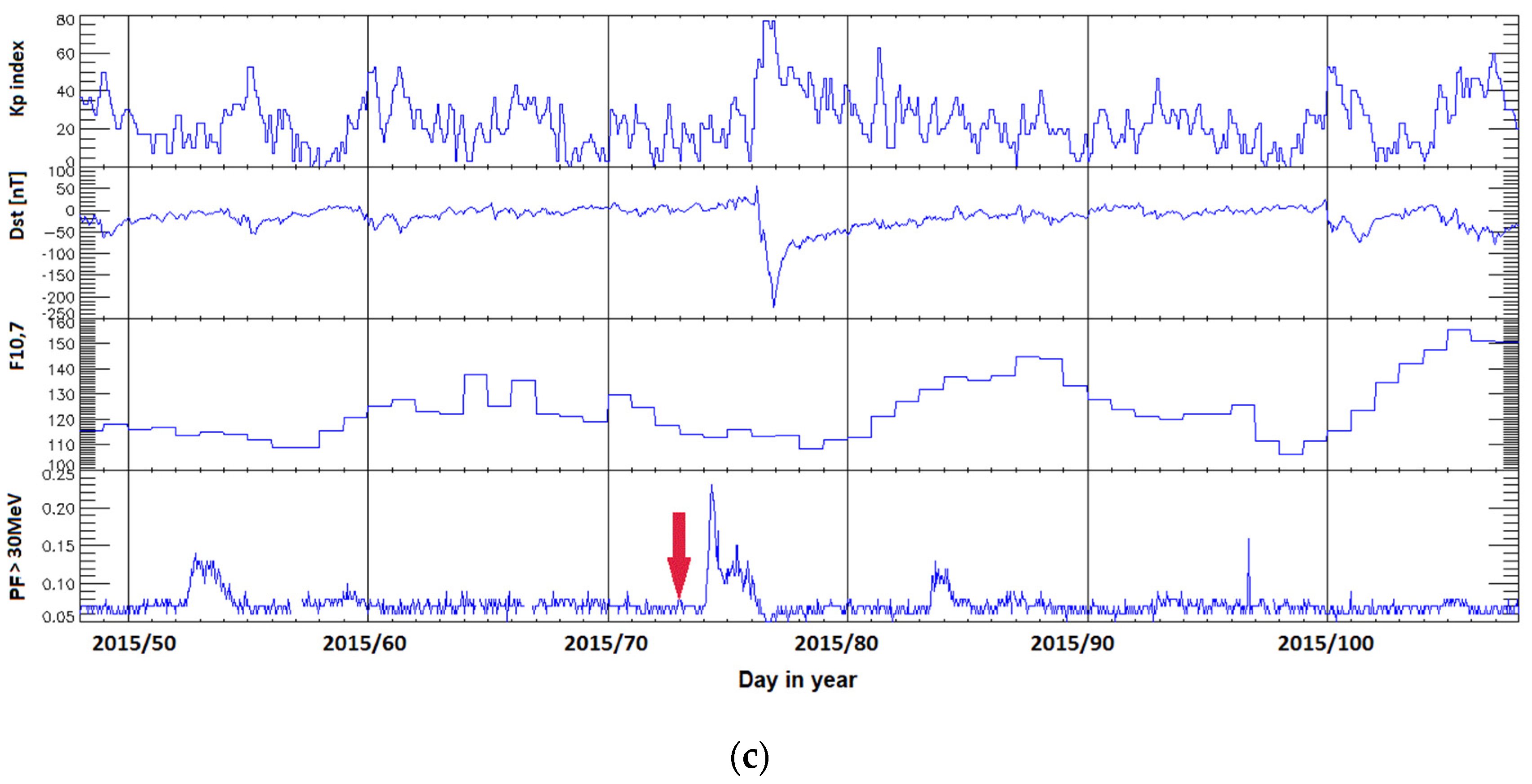
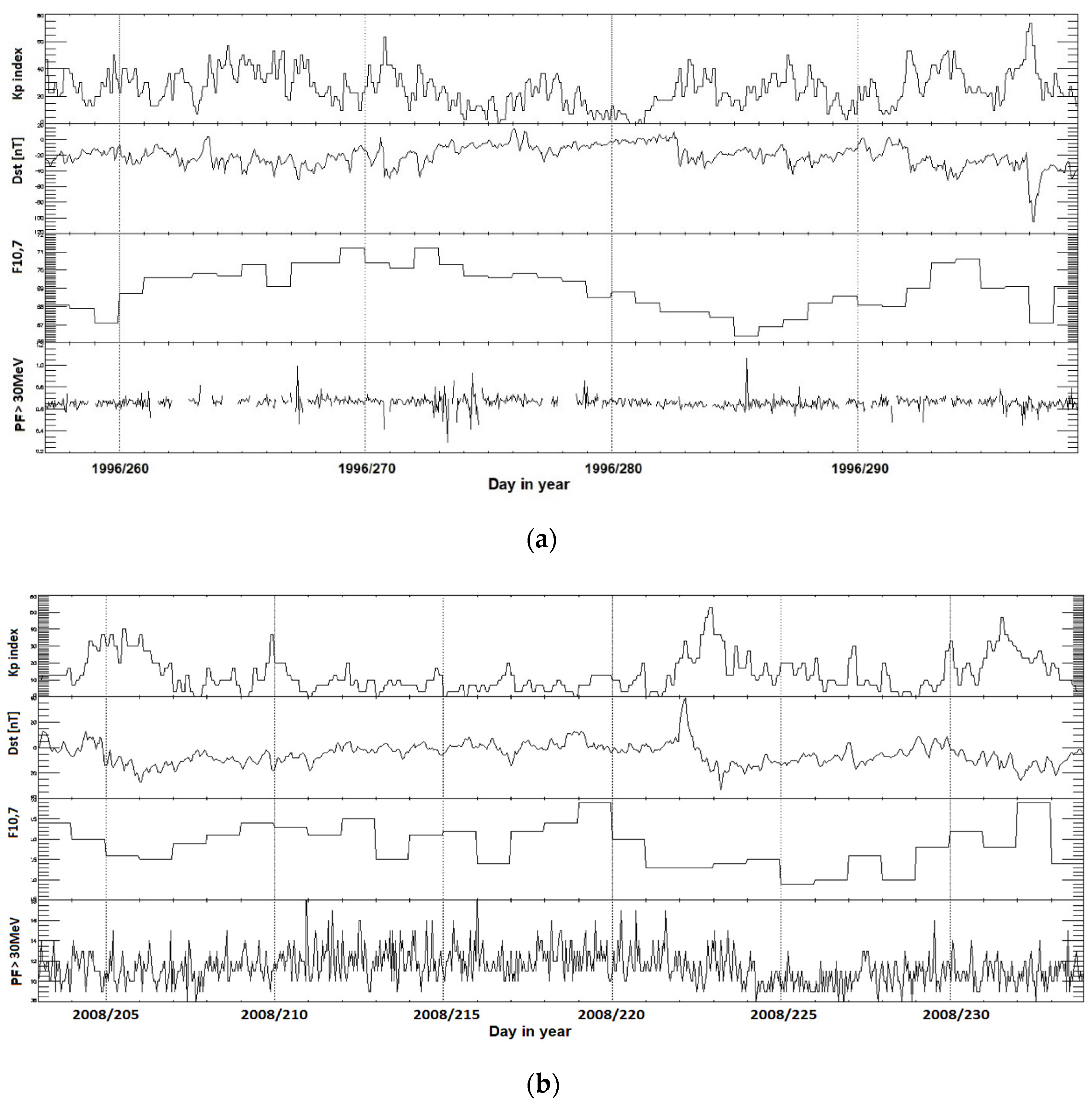
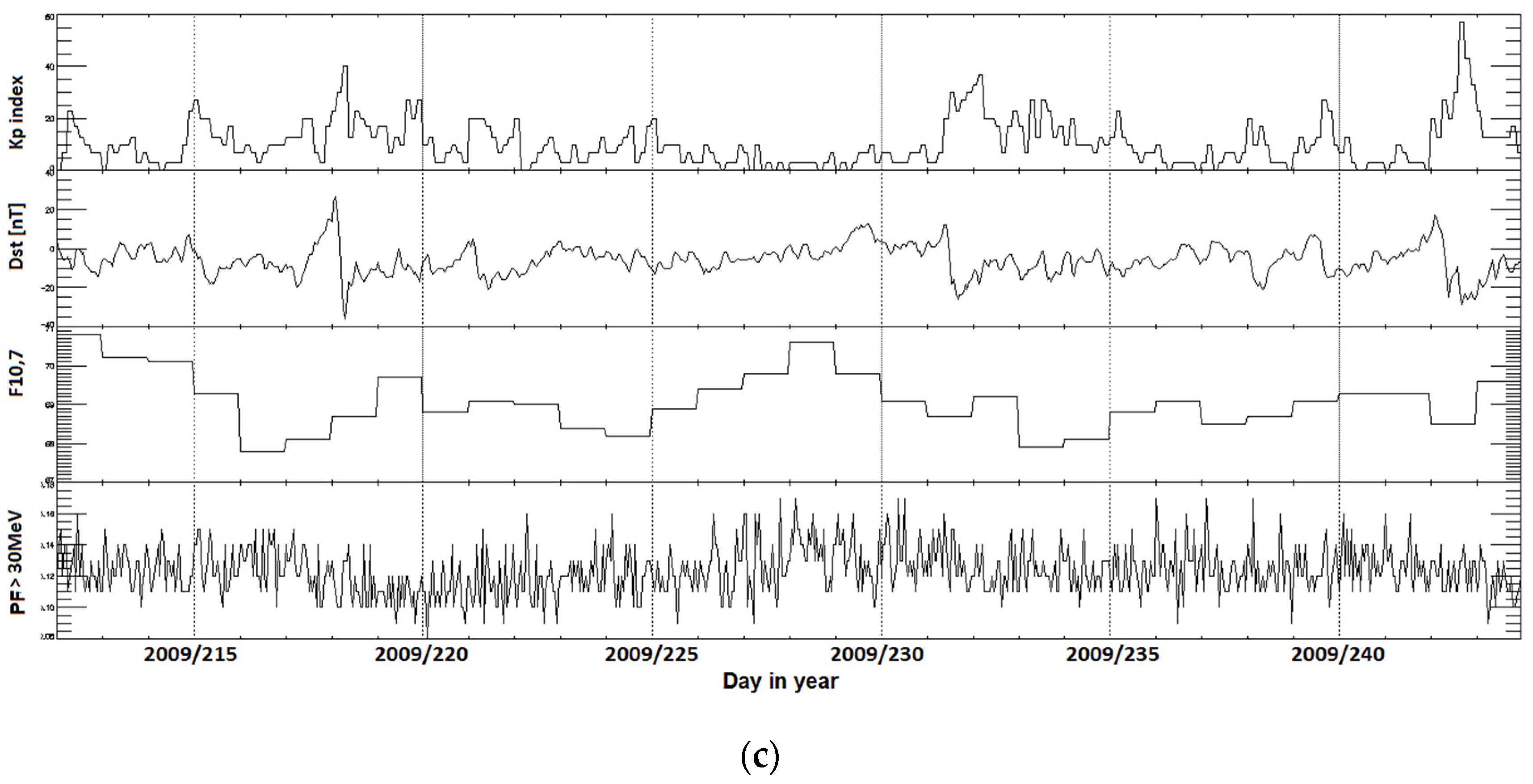
Figure 1 shows the changes (from top to bottom) of the values of the three-hour Kp index, the hourly values of the Dst index, the daily values of the solar radio flux F10.7, and the hourly PF30 values of the solar proton flux with energy greater than 30 MeV in the observed period. The analyzed solar storms are marked by red arrow in the graphs of the course of solar and geophysical parameters in Figure 1a–c. The Kp index was chosen in the model to represent the geomagnetic activity in geographical latitudes where the territory of the Czech Republic lies [43]. Dst was used to determine the onset time of a geomagnetic storm. In Figure 2 same time series of solar and geomagnetic indices during investigated quiet periods of solar activity are shown. For the terrestrial impact scenario, it is important if the observed geographic location, territory of the Czech Republic in this case, is affected on day or night side of the Earth.
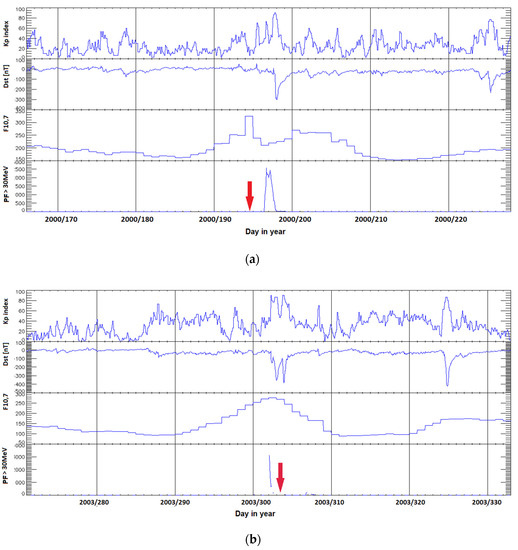
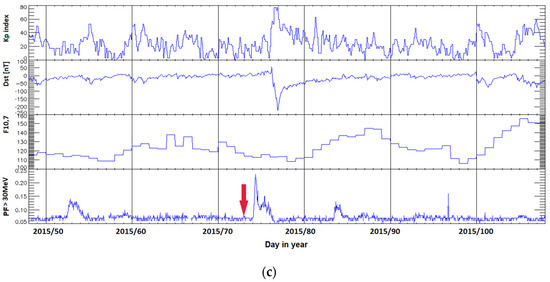
Figure 1.
Solar activity variability during the investigated solar and geomagnetic storms belonging to the Solar Cycles No. 23 and No. 24. Class X5 storm on 14 July 2000 Bastille Day Event in panel (a), class X17 storm on 28 October 2003 Halloween Solar Storms in panel (b), class G4 storm on 17 March 2015 St. Patrick’s Day Event in panel (c). Time of solar storms are marked by red arrow in the graphs. Note that y−axis scales are not equal on all events.
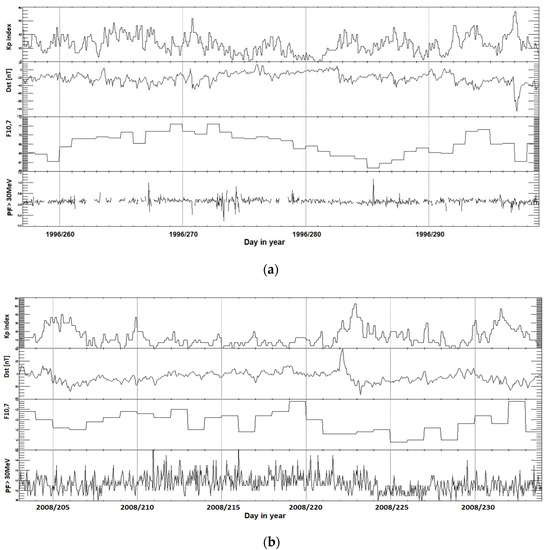
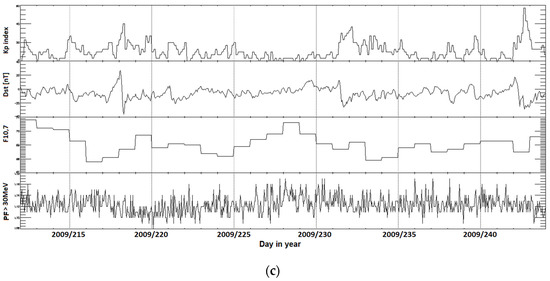
Figure 2.
Solar activity variability during the investigated quiet periods from years 1994 to 2015 belonging to the Solar Cycles No. 23 and No. 24. Period 13 September 1996–24 October 1996 in panel (a), 21 July 2008–20 August 2008 in panel (b), and 31 July 2009–31 August 2009 in panel (c). Note that y-axis scales are not equal on all events.
2.2. Method
The graphical models are important modern instruments of multivariate statistics. They are used for description and transparent representation of structure of the dependence relationships in a given set of random vectors.
Today, probabilistic graphical models for climate data analysis have been developed, to determine which variables interact, and how strongly, and to decide if the data can be condensed without loss of information [44,45,46]. The theoretical basis to this technique is the concept of conditional independence, and the prime theoretical and practical tool is the conditional independence graph [47,48].
We used the graphical models method of conditional dependencies (CIG) [47], a stochastic approach to find out dependencies between solar, geomagnetic, and other time series. Due to the character of the solved problem, this method appears useful for studying the conditional dependence between physical parameters in evolving solar cycle and daily numbers of deaths.
The computational procedure by this method is described in detail in [49], as a means to investigate the relationship between the Earth’s ionosphere and magnetosphere. This method has been implemented in the field of the impact of space on human health, in [50] which also describes in detail the calculation procedures.
In this work, we consider a structure dependence relationship of the random vector component part. We take all full graphs of conditional independence relationships for selecting tests of fit graphs. In this method, the best likelihood estimation of variance matrix in conditions given by graphical model is found [51,52,53].
Model solutions were performed for the above-mentioned solar storms and quiet periods. We used the procedure Backward2 [47] (pp. 182–185) realized in Mathematica 8.0 software. On account of computational complexity, the geomagnetic index Dst was not finally used in the resulting graphical models of conditional independence. The random vector employed in our models is marked:
where I is the daily number of deaths in the group of diagnoses by age and sex, Kp is geomagnetic index, F10.7 solar radio flux, and PF30 is solar radio flux > 30 MeV. The number of realizations of this random vector is 31 (lengths of observed periods after solar storm or during continuous quiet period in days). All graphs in the calculations have 4 vertices, so the maximum number of possible graphs is 63 in each calculation. These time series were tested for independence and normality of logarithmic data series. The test of the normality of logarithmical series (and not of the series themselves) is the mathematical assumption for computing the maximum likelihood estimator of the constrained covariance matrix [50]. The data are transformed by differences of logarithms to fulfill the assumption of normality and independence of observed realizations within this step. In the absence of the assumption of local normality, calculation is stopped and the model cannot be created. The likelihood function requirements follow from the graphical model selection, using the goodness of Ht test to select the graphical model with data [54]. The test statistics have the deviance with χ2 asymptotic probability distribution. In our selection of minimized model, all edges with computed deviance less than 3.84 (the critical value 3.84 is the standard 5% point of χ2 (1) distribution with 1 degree of freedom), were excluded from the entire graph. The stopping threshold for this calculation, thus, was the value 0.05 [55].
X = (I; Kp; F10.7; PF30),
3. Results
In the results of the analyses described in this section, it can be observed for all monitored solar storms that the daily numbers of deaths in groups of diagnoses VI. diseases of the nervous system (codes G00-G99) and IX. circulatory system diseases (codes I00-I99) by age and sex have different statistical characteristics in the period of 30 days after the solar storms compared to the three periods of low solar activity. For age groups in which the daily death rates are low due to the nature of the disease, the results of the model calculation are not statistically significant. There are usually age groups 0–39 years for men and women with diseases of the circulatory system and nervous system with very low daily numbers of deaths.
The results of the calculation of graphical models of conditional independence for both groups of diagnoses at the time of the analyzed solar storms are presented in Table 1 and Table 2. For each investigated solar storm, the table contains the parameters of the minimized graphical models after the solar storm, for the analyzed groups by sex and age. In Table 3 and Table 4 results of the calculation of graphical models of conditional independence during spotless day periods are presented. For each model, the table also shows the total deviance of the minimized model.
The time series of number of deaths of men and women in the age group over 40 completed years inclusive, for all the mentioned solar storms and quiet periods, passed the tests for independence and normality of logarithmic data series. For the residual components of the random vector in the model, it is indicated whether the given edge remained in the resulting minimized model by X mark (the edge is in the model) or by a dash (the edge was excluded from the model). Furthermore, in the tables, we present the number of edges in the final model, the total sum of the degrees of freedom f in the model calculation, and p-value of the test model is shown. The stopping threshold for calculation was 0.05 in all calculation cases. Thus, if the p-value of the test of the minimized model is greater than 0.05, the model is statistically significant. If the time series did not pass the test for independence and normality of logarithmic data series (due to the uncertainty of the variance matrix it was not possible to calculate the model), this information is given in the relevant row in the tables.
The results for groups of women up to and including 39 completed years are indicated by the title of the Females 0–39 panel, and the results for women aged 40 and over completed years inclusive are indicated by the title of the Females 40+ panel. The results for men up to and including 39 completed years are indicated by the title of the panel Males 0–39, and the results for men aged 40 and more completed years inclusive are indicated by the title of the panel Males 40+.

Table 1.
Summary of conditional independence graphs (CIG) model computation. Diseases of the nervous system (codes G00-G99).
Table 1.
Summary of conditional independence graphs (CIG) model computation. Diseases of the nervous system (codes G00-G99).
| Solar storm X5 14 July 2000 Bastille Day Event | ||||||||
| Model | Deviance of minimized graphical model | F10.7 | Kp | PF30 | Edge number of minimized graphical model | f | p-value | |
| Males 0–39 | does not pass the test for normality and independence of logarithmic data | |||||||
| Males 40+ | 1.12680 | - | X | - | 1 | 46 | 0.26918 | |
| Females 0–39 | 0.37453 | - | X | - | 1 | 6 | 0.43892 | |
| Females 40+ | 1.23286 | - | - | - | 0 | 55 | 0.01914 | |
| Solar storm X17 28 October 2003 Halloween Solar Storms | ||||||||
| Model | Deviance of minimized graphical model | F10.7 | Kp | PF30 | Edge number of minimized graphical model | f | p-value | |
| Males 0–39 | 0.71428 | X | - | X | 2 | 12 | 0.37100 | |
| Males 40+ | 1.10720 | X | - | X | 2 | 65 | 0.21850 | |
| Females 0–39 | does not pass the test for normality and independence of logarithmic data | |||||||
| Females 40+ | 2.12049 | X | - | X | 2 | 77 | 0.21858 | |
| Solar storm G4 17 March 2015 St. Patrick’s Day Event | ||||||||
| Model | Deviance of minimized graphical model | F10.7 | Kp | PF30 | Edge number of minimized graphical model | f | p-value | |
| Males 0–39 | does not pass the test for normality and independence of logarithmic data | |||||||
| Males 40+ | 1.55689 | X | - | X | 2 | 110 | 0.11307 | |
| Females 0–39 | does not pass the test for normality and independence of logarithmic data | |||||||
| Females 40+ | 1.99264 | X | - | - | 1 | 138 | 0.14996 | |

Table 2.
Summary of conditional independence graphs (CIG) model computation, diseases of the circulatory system (codes I00-I99).
Table 2.
Summary of conditional independence graphs (CIG) model computation, diseases of the circulatory system (codes I00-I99).
| Solar storm X5 14 July 2000 Bastille Day Event | ||||||||
| Model | Deviance of minimized graphical model | F10.7 | Kp | PF30 | Edge number of minimized graphical model | f | p-value | |
| Males 0–39 | does not pass the test for normality and independence of logarithmic data | |||||||
| Males 40+ | 6.29273 | X | X | X | 3 | 2060 | 0.17833 | |
| Females 0–39 | 0.32790 | - | X | - | 1 | 5 | 0.73121 | |
| Females 40+ | 9.00699 | X | - | - | 1 | 2506 | 0.06246 | |
| Solar storm X17 28 October 2003 Halloween Solar Storms | ||||||||
| Model | Deviance of minimized graphical model | F10.7 | Kp | PF30 | Edge number of minimized graphical model | f | p-value | |
| Males 0–39 | 0.46596 | X | - | X | 2 | 18 | 0.28350 | |
| Males 40+ | 8.08860 | - | - | X | 1 | 2022 | 0.06981 | |
| Females 0–39 | 0.10372 | X | - | X | 2 | 5 | 0.96414 | |
| Females 40+ | 8.71907 | X | X | X | 3 | 2486 | 0.09763 | |
| Solar storm G4 17 March 2015 St. Patrick’s Day Event | ||||||||
| Model | Deviance of minimized graphical model | F10.7 | Kp | PF30 | Edge number of minimized graphical model | f | p-value | |
| Males 0–39 | 0.81789 | - | - | - | 0 | 13 | 0.06826 | |
| Males 40+ | 8.40326 | X | - | X | 2 | 2105 | 0.03101 | |
| Females 0–39 | does not pass the test for normality and independence of logarithmic data | |||||||
| Females 40+ | 10.39334 | X | - | - | 1 | 2626 | 0.09645 | |
In the group of nervous system diseases in the period 30 days after the Halloween Solar Storms, an increase in the conditional dependence was found for the daily number of deaths in men and women over 40 years for the solar radio flux F10.7 and solar proton flux FP30. The same applies to men in this age group after the St. Patrick’s Day Event.
The results of our analysis, performed by the method of graphical models of conditional independence for the group of nervous system diseases, showed the conditional dependence of the daily number of deaths during the solar storm on 28 October 2003 (Halloween Solar Storms), for all monitored age groups on solar radio flux F10.7 and solar proton flux PF30, with the exception of the group of women 0–39. At the time of the solar storm on 14 July 2000 (Bastille Day Event), no connection between the daily number of deaths and all indices of solar and geomagnetic activity was found in the group of diseases of the nervous system, during any period of the observed solar storms.
The connection of the daily number of deaths with all indices of the solar and geomagnetic activity was found in the group of diseases of the circulatory system during the solar storm on 28 October 2003 (Halloween Solar Storms) for women over the age of 40, and during the solar storm on 14 July 2000 (Bastille Day Event), in men over the age of 40.
In contrast, in a severe solar storm on 17 March 2015 (St. Patrick’s Day Event), which hit the Earth in the early morning hours of local time, the conditional dependence of the number of deaths on the solar proton flux PF30 manifested itself in men over the age of 40 for both monitored diagnoses groups cardiovascular and nervous diseases, but conditional dependence on solar radio flux F10.7 manifested itself for both sexes over the age of 40.

Table 3.
Summary of conditional independence graphs (CIG) model computation, diseases of the circulatory system (codes I00-I99) during spotless day periods.
Table 3.
Summary of conditional independence graphs (CIG) model computation, diseases of the circulatory system (codes I00-I99) during spotless day periods.
| 13 September 1996–24 October 1996 | ||||||||
| Model | Deviance of minimized graphical model | F10.7 | Kp | PF30 | Edge number of minimized graphical model | f | p-value | |
| Males 0–39 | does not pass the test for normality and independence of logarithmic data | |||||||
| Males 40+ | 0.34000 | X | - | - | 1 | 27 | 0.73121 | |
| Females 0–39 | does not pass the test for normality and independence of logarithmic data | |||||||
| Females 40+ | 0.40022 | X | - | - | 1 | 78 | 0.24884 | |
| 21 July 2008–20 August 2008 | ||||||||
| Model | Deviance of minimized graphical model | F10.7 | Kp | PF30 | Edge number of minimized graphical model | f | p-value | |
| Males 0–39 | does not pass the test for normality and independence of logarithmic data | |||||||
| Males 40+ | 0.33080 | X | - | - | 1 | 43 | 0.35009 | |
| Females 0–39 | does not pass the test for normality and independence of logarithmic data | |||||||
| Females 40+ | 11.03420 | - | - | - | 0 | 47 | 0.034611 | |
| 31 July 2009–31 August 2009 | ||||||||
| Model | Deviance of minimized graphical model | F10.7 | Kp | PF30 | Edge number of minimized graphical model | f | p-value | |
| Males 0–39 | does not pass the test for normality and independence of logarithmic data | |||||||
| Males 40+ | 8.19562 | - | - | - | 0 | 11 | 0.19784 | |
| Females 0–39 | does not pass the test for normality and independence of logarithmic data | |||||||
| Females 40+ | 11.09207 | - | - | - | 0 | 32 | 0.24884 | |

Table 4.
Summary of conditional independence graphs (CIG) model computation. Diseases of the nervous system (codes G00-G99) during spotless day periods.
Table 4.
Summary of conditional independence graphs (CIG) model computation. Diseases of the nervous system (codes G00-G99) during spotless day periods.
| 13 September 1996–24 October 1996 | ||||||||
| Model | Deviance of minimized graphical model | F10.7 | Kp | PF30 | Edge number of minimized graphical model | f | p-value | |
| Males 0–39 | does not pass the test for normality and independence of logarithmic data | |||||||
| Males 40+ | 8.47768 | X | X | - | 2 | 18 | 0.19869 | |
| Females 0–39 | does not pass the test for normality and independence of logarithmic data | |||||||
| Females 40+ | 0.91364 | - | - | - | 0 | 29 | 0.75376 | |
| 21 July 2008–20 August 2008 | ||||||||
| Model | Deviance of minimized graphical model | F10.7 | Kp | PF30 | Edge number of minimized graphical model | f | p-value | |
| Males 0–39 | does not pass the test for normality and independence of logarithmic data | |||||||
| Males 40+ | 0.29791 | - | X | X | 2 | 76 | 0.37100 | |
| Females 0–39 | does not pass the test for normality and independence of logarithmic data | |||||||
| Females 40+ | 1.03767 | - | - | - | 0 | 34 | 0.02735 | |
| 31 July 2009–31 August 2009 | ||||||||
| Model | Deviance of minimized graphical model | F10.7 | Kp | PF30 | Edge number of minimized graphical model | f | p-value | |
| Males 0–39 | does not pass the test for normality and independence of logarithmic data | |||||||
| Males 40+ | 0.90116 | - | - | - | 0 | 15 | 0.22743 | |
| Females 0–39 | does not pass the test for normality and independence of logarithmic data | |||||||
| Females 40+ | 0.91364 | - | - | - | 0 | 62 | 0.16517 | |
In the observed spotless periods of low solar activity, there are no model connections with geomagnetic indices in diseases of the circulatory system compared to the period after the solar storm in women in the age group over 40 years of completed age. During these periods of low solar activity, in the minimized graphical models, no connection of the daily number of deaths was found in parallel with all indices of solar and geomagnetic activity (F10.7, Kp, FP30) in any of the monitored groups according to age, sex, and group of diagnoses.
From the minimized graphs of conditional independence, the conditional dependence in pairs of random vectors representing time series of the circulatory system diseases and F10.7 is evident for both sexes in the age group over 40 years, and only for men over 40 years in the quiet period in the year 1996.
The time series of daily numbers of men over the age of 40 who have died of nervous system diseases (codes G00-G99) are conditionally dependent in this period only in men over the age of 40, in the quiet period 13 September–24 October 1996 on solar radio flux (F10.7) and Kp index, and in the quiet period July 21–August 20 2008 on Kp index and solar proton flux PF30. In the quiet period of 31 July–31 August 2009, no conditional dependences with the number of deaths for both monitored groups of diagnoses were found in any of the time series.
In these periods, in contrast to the periods of the analyzed solar storms, in the minimized graphical models in none of the monitored groups according to age, sex and group of diagnoses was a connection found between the daily number of deaths and all indices of solar and geomagnetic activity.
4. Discussion
The results of our analysis are influenced by the geoefficiency of the individual analyzed solar storm and the time course of the monitored indices of solar and geophysical activity. The results of minimization of graphical model for the periods of three major solar storms (storm of 14 July 2000 Bastille Day Event, storm of 28 October 2003 Halloween Solar Storms, and storm of 17 March 2015 St. Patrick’s Day event) show a clearer difference in the connection of time series in comparison to analyzed periods after a solar storm. This result is consistent with other studies that show that the impact of solar activity on human health also depends on the intensity of the solar events occurring during a given observational period [23,24,25].
It is therefore possible to identify specific changes in connection to time series of daily number of deaths of men and women over 40 years of circulatory system diseases and nervous system diseases in the time series of solar radio flux F10.7, geomagnetic index Kp, and solar proton flux PF30 between observed periods after monitored solar storms. However, none of these connections are present in the same form in all three solar storms. Such connection is consistent with the results published in [20,22], where the influence of the geomagnetic field was also identified and a connection with the geomagnetic parameters (Kp).
The analysis took into account the specific conditions of the population in the Czech Republic in the observed period [35,38]. The conditions correspond with local effect of the observed solar storms, the differential characteristics of the population living in the Czech Republic, the level of health care in the monitored period, and other determinants of the health status of the population [36,37]. Thus, it is possible that the same geophysical manifestation may have a different effect in different populations.
In the periods of analyzed solar storms in the minimized graphical models we did not find any connection between the daily number of deaths and all indices of solar and geomagnetic activity for any of the monitored groups according to age, sex, and group of diagnoses. Exceptions here are groups of women in the age group over 40 years during Halloween Solar Storm, and men in the age group over 40 years during Bastille Day Event. In the observed periods of low solar activity, there is no model connection with geomagnetic indices in diseases of the circulatory system compared to the period after the solar storm for women in the age group over 40 years of completed age. During these periods of low solar activity, in the minimized graphical models, no connection of the daily number of deaths was found in parallel with all indices of solar and geomagnetic activity in any of the monitored groups according to age, sex, and group of diagnoses.
5. Conclusions
In quiet periods of solar activity (13 September–24 October 1996, 21 July–20 August 2008, and 31 July–31 August 2009) none of the monitored groups according to age, sex, and group of diagnoses was found to have a connection between the daily number of deaths and all indices of solar and geomagnetic activity in the minimized graphical models, in contrast to the periods of the analyzed solar storms (storm of 14 July 2000 Bastille Day Event, storm of 28 October 2003 Halloween Solar Storms, and storm of 17 March 2015 St. Patrick’s Day event) where Male 40+ and Female 40+ dependence is found for diseases of the circulatory system.
The impact of exceptional solar events is evident in the case of neurological diseases, and less evident for circulatory diseases. For all solar storms described in this paper, it can be observed that daily numbers of deaths in the diagnostic groups VI, diseases of nervous system (codes G00–G99), and IX, diseases of circulatory system (codes I00–I99), according to age and sex, differ in statistical characteristics in the time period 30 days before solar storm and 30 days after solar storm. For age groups with low daily numbers of deaths due to the character of the diseases the results are not significant.
For time periods after strong solar storms, a connection between daily numbers of deaths for diseases of circulatory system and geomagnetic index Kp, Solar proton flux PF30, and solar radio flux F10.7 was identified. For men in age group over 40 years a higher conditional dependence with solar radio flux F10.7 and geomagnetic index Kp was observed after the event. For women over 40 years of age, a higher conditional dependence with geomagnetic index Kp was also identified.
The connection of the daily number of deaths with all indices of the solar and geomagnetic activity was found in the group of diseases of the circulatory system during the solar storm on 28 October 2003 (Halloween Solar Storms), for women in the age group over 40; and solar storm 14 July 2000 (Bastille Day Event), in men over the age of 40. During the periods of low solar activity, in the minimized graphical models, no connection of the daily number of deaths was found in parallel with all indices of solar and geomagnetic activity in any of the monitored groups according to age, sex, and group of diagnoses.
Funding
This research was funded by the Czech Science Foundation, grant number SAV-21-01.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Number of deaths by cause: Czech Statistical Office (CZSO). Available online: https://www.czso.cz/csu/czso/obypz_cr (accessed on 2 November 2019). Kp index: World Data Center for Geomagnetism, Kyoto University, Japan. The data used for time series assembling was provided in case of Kp by World Data Center for Geomagnetism, Kyoto University, Japan, available online: http:/wdc.kugi.kyoto-u.ac.jp/kp/index.html (accessed on 1 April 2020). In case of F10.7 by NWRA/CoRA, NorthWest Research Associates, Boulder, USA, available online: http:/www.nwra.com/spawx/spawx.html (accessed on 1 April 2020).Dst, F10.7: Space Physics Interactive Data Resource, National Geophysical Data Center, Boulder, USA. Proton density, Proton Flux: OMNIWeb Plus, NASA/Goddard Space Flight Center, USA, available online: https://omniweb.gsfc.nasa.gov.Solar (accessed on 1 April 2020). Cycle evolving: NWRA/CoRA, NorthWest Research Associates, Boulder, USA; Deutsches GeoForschungs Zentrum, Germany.
Acknowledgments
The support under the grant SAV-21-01 by the Czech Science Foundation is acknowledged. World Data Center for Geomagnetism, Deutsches GeoForschungsZentrum (GFZ), NWRA/CoRA, NorthWest Research Associates, and UK Solar System Data Centre (UKSSDC) Rutherford Appleton Laboratory is acknowledged for providing geomagnetic measurement.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Katsavrias, C.; Preka-Papadema, P.; Moussas, X.; Apostolou, T.; Theodoropoulou, A.; Papadima, T. Helio-geomagnetic influence in cardiological cases. Adv. Space Res. 2013, 51, 96–106. [Google Scholar] [CrossRef]
- Cornelissen, G.; Halberg, F.; Breus, T.; Syutkina, E.V.; Baevsky, R.; Weydahl, A.; Watanabe, Y.; Otsuka, K.; Siegelova, J.; Fiser, B.; et al. Non-photic solar associations of heart rate variability and myocardial infarction. J. Atmos. Sol. Terr. Phys. 2002, 64, 707–720. [Google Scholar] [CrossRef]
- Otsuka, K.; Cornélissen, G.; Weydahl, A.; Holmeslet, B.; Hansen, T.; Shinagawa, M.; Kubo, Y.; Nishimura, Y.; Omori, K.; Yano, S.; et al. Geomagnetic disturbance associated with decrease in heart rate variability in a subarctic area. Biomed. Pharmacother. 2000, 55, 51–56. [Google Scholar] [CrossRef]
- Azcárate, T.; Mendoza, B.; Levi, J. Influence of geomagnetic activity and atmospheric pressure on human arterial pressure during the solar cycle 24. Adv. Space Res. 2016, 58, 2116–2125. [Google Scholar] [CrossRef]
- Gurfinkel, Y.; Vasin, A.L.; Pishchalnikov, R.Y.; Sarimov, R.M.; Sasonko, M.L.; Matveeva, T.A. Geomagnetic storm under laboratory conditions: Randomized experiment. Int. J. Biometeorol. 2017, 62, 501–512. [Google Scholar] [CrossRef]
- Gurfinkel, Y.I.; At’kov, O.Y.; Vasin, A.L.; Breus, T.K.; Sasonko., M.L.; Pishchalnikov, R.Y. Effect of zero magnetic field on cardiovascular system and microcirculation. Life Sci. Space Res. 2016, 8, 1–7. [Google Scholar] [CrossRef]
- Johnsen, S.; Lohmann, K.J. The physics and neurobiology of magnetoreception. Nat. Rev. Neurosci. 2005, 6, 703–712. [Google Scholar] [CrossRef] [PubMed]
- Gjerloev, J.W. A Global Ground-Based Magnetometer Initiative. EOS 2009, 90, 230–231. [Google Scholar] [CrossRef]
- Gjerloev, J.W. The SuperMAG data processing technique. J. Geophys. Res. 2012, 117, A09213. [Google Scholar] [CrossRef]
- Jursa, A.S. Handbook of Geophysics and the Space Environment; Air force geophysics laboratory; National Technical Information Service: Springfield, MA, USA, 1985. [Google Scholar]
- Stoupel, E.; Kalediene, R.; Petrauskiene, J.; Starkuviene, S.; Abramson, E.; Israelevich, P.; Sulkes, J. Clinical Cosmobiology: Distribution of Deaths during 180 Months and Cosmo Physical Activity. The Lithuanian Study, 1990–2004. In The Role of Cosmic Rays. Study Report; Division of Cardiology Rabin Medical Center Tel Aviv University: Tel Aviv, Israel, 2004. [Google Scholar]
- Watanabe, Y.; Cornellissen, G.; Halberg, F.; Otsuka, K.; Ohkawa, S.I. Associations by signatures and coherences between the human circulation and helio- and geomagnetic activity. Biomed. Pharmacother. 2001, 55 (Suppl. 1), 76–83. [Google Scholar] [CrossRef]
- Stoupel, E.; Kalediene, R.; Petrauskiene, J.; Starkuviene, S.; Abramson, E.; Israelevich, P.; Sulkes, J. Twenty years study of solar, geomagnetic, cosmic ray activity links with monthly deaths number (n-850304). J. Biomed. Sci. Eng. 2011, 4, 426–434. [Google Scholar] [CrossRef] [Green Version]
- Stoupel, E. The effect of geomagnetic activity on cardiovascular parameters. Biomed. Pharmacother. 2002, 56, 247. [Google Scholar] [CrossRef] [Green Version]
- Stoupel, E.; Birk, E.; Kogan, A.; Klinger, G.; Abramson, E.; Israelevich, P.; Sulkes, J.; Linder, N. Congenital heart disease: Correlation with fluctuations in cosmophysical activity, 1995–2005. Int. J. Cardiol. 2009, 135, 207–210. [Google Scholar] [CrossRef] [PubMed]
- Halberg, F.; Cornelissen, G.; Otsuka, K.; Watanabe, Y.; Katinas, G.; Burioka, N.; Delyukov, A.; Gorgo, Y.; Zhao, Z.; Weydahl, A.; et al. 21-year biological and physical cycles, magnetic storms and myocardial infarctions. Neuro Endocrinol. Lett. 2000, 21, 233. [Google Scholar] [PubMed]
- Halberg, F.; Cornélissen, G.; Otsuka, K.; Fiser, B.; Mitsutake, G.; Wendt, H.; Johnson, P.; Gigolashvili, M.; Breus, T.; Sonkowsky, R.; et al. Near 10-Year and Longer Periods Modulate Circadians: Intersecting Anti-aging and Chronoastrobiological Research. J. Gerontol. A Biol. Sci. Med. Sci. 2001, 56, M304–M324. [Google Scholar] [CrossRef] [Green Version]
- Halberg, F.; Cornélissen, G.; Otsuka, K.; Fiser, B.; Mitsutake, G.; Wendt, H.; Johnson, P.; Gigolashvili, M.; Breus, T.; Sonkowsky, R.; et al. Incidence of sudden cardiac death, myocardial infarction and far- and near-transyears. Biomed. Pharmacother. 2005, 59, S239–S261. [Google Scholar] [CrossRef]
- Dorman, L.I.; Iucci, N.; Ptitsyna, N.G.; Villoresi, G. Cosmic rays as indicator of space weather influence on frequency of infract myocardial, brain strokes, car and train accidents. In Proceedings of the 27th International Cosmic Ray Conference, Hamburg, Germany, 7–15 August 2001; p. 3511. [Google Scholar]
- Ebrille, E.; Konecny, T.; Konecny, D.; Spacek, R.; Jones, P.; Ambroz, P.; DeSimone, C.V.; Powell, B.D.; Hayes, D.L.; Friedman, P.A.; et al. Correlation of Geomagnetic Activity With Implantable Cardioverter Defibrillator Shocks and Antitachycardia Pacing. Mayo Clin. Proc. 2015, 90, 202–208. [Google Scholar] [CrossRef] [Green Version]
- Podolská, K. The Impact of Ionospheric and Geomagnetic Changes on Mortality from Diseases of the Circulatory System. J. Stroke Cerebrovasc. Dis. 2018, 27, 404–417. [Google Scholar] [CrossRef]
- Mavromichalaki, H.; Preka-Papadema, P.; Theodoropoulou, A.; Paouris, E.; Apostolou, T. A study of the possible relation of the cardiac arrhythmias occurrence to the polarity reversal of the solar magnetic field. Adv. Space Res. 2017, 59, 366–378. [Google Scholar] [CrossRef]
- Vencloviene, J.; Babarskiene, R.; Milvidaite, I.; Kubilius, R.; Stasionyte, J. The effect of solar–geomagnetic activity during hospital admission on coronary events within 1 year in patients with acute coronary syndromes. Adv. Space Res. 2013, 52, 2192–2198. [Google Scholar] [CrossRef]
- Vencloviene, J.; Antanaitiene, J.; Babarskiene, R. The association between space weather conditions and emergency hospital admissions for myocardial infarction during different stages of Solar activity. J. Atmos. Sol. Terr. Phys. 2016, 149, 52–58. [Google Scholar] [CrossRef]
- Jaruševičius, G.; Rugelis, T.; McCraty, R.; Landauskas, M.; Berškienė, K.; Vainoras, A. Correlation between Changes in Local Earth’s Magnetic Field and Cases of Acute Myocardial Infarction. Int. J. Environ. Res. Public Health 2018, 15, 399. [Google Scholar] [CrossRef] [Green Version]
- Geronikolou, S.; Leontitsis, A.; Petropoulos, V.; Davos, C.; Cokkinos, D.; Chrousos, G. Cyclic stroke mortality variations follow sunspot patterns. F1000Research 2020, 9, 1088. [Google Scholar] [CrossRef] [PubMed]
- Vencloviene, J.; Radisauskas, R.; Vaiciulis, V.; Kiznys, D.; Bernotiene, G.; Kranciukaite-Butylkiniene, D.; Tamosiunas, A. Associations between Quasi-biennial Oscillation phase, solar wind, geomagnetic activity, and the incidence of acute myocardial infarction. Int. J. Biometeorol. 2020, 64, 1207–1220. [Google Scholar] [CrossRef] [PubMed]
- Kiznys, D.; Vencloviene, J.; Milvidaite, I. The associations of geomagnetic storms, fast solar wind, and stream interaction regions with cardiovascular characteristic in patients with acute coronary syndrome. Life Sci. Space Res. 2020, 25, 1–8. [Google Scholar] [CrossRef]
- Vencloviene, J.; Babarskiene, R.; Slapikas, R.; Sakalyte, G. The association between phenomena on the sun, geomagnetic activity, meteorological variables, and cardiovascular characteristic of patients with myocardial infarction. Int. J. Biometeorol. 2013, 57, 797–804. [Google Scholar] [CrossRef] [PubMed]
- Pishchalnikov, R.Y.; Gurfinkel, Y.I.; Sarimov, R.M.; Vasin, A.L.; Sasonko, M.L.; Matveeva, T.A.; Binhi, V.N.; Baranov, M.V. Cardiovascular response as a marker of environmental stress caused by variations in geomagnetic field and local weather. Biomed. Signal Process. Control. 2019, 51, 401–410. [Google Scholar] [CrossRef]
- Vencloviene, J.; Radisauskas, R.; Tamosiunas, A.; Luksiene, D.; Sileikiene, L.; Milinaviciene, E.; Rastenyte, D. Possible Associations between Space Weather and the Incidence of Stroke. Atmosphere 2021, 12, 334. [Google Scholar] [CrossRef]
- Vaičiulis, V.; Venclovienė, J.; Tamošiūnas, A.; Kiznys, D.; Lukšienė, D.; Krančiukaitė-Butylkinienė, D.; Radišauskas, R. Associations between Space Weather Events and the Incidence of Acute Myocardial Infarction and Deaths from Ischemic Heart Disease. Atmosphere 2021, 12, 306. [Google Scholar] [CrossRef]
- ÚZIS ČR: Czech Health Statistics Yearbook 2015; ÚZIS ČR: Prague, Czech Republic, 2016.
- Poppová, M. IRIS: Language-Independent Software for Coding Causes of Death—Implementation in Czech Republic. IRIS: Jazykově nezávislý software pro kódování příčin smrti—implementace v ČR. Demografie 2011, 53, 392–396. [Google Scholar]
- Cífková, R.; Škodová, Z.; Bruthans, J.; Holub, J.; Adámková, V.; Jozífová, M.; Galovcová, M.; Wohlfahrt, P.; Krajčoviechová, A.; Petržílková, Z.; et al. Longitudinal trends in cardiovascular mortality and blood pressure levels, prevalence, awareness, treatment, and control of hypertension in the Czech population from 1985 to 2007/2008. J. Hypertens. 2010, 28, 2196–2203. [Google Scholar] [CrossRef]
- Cífková, R.; Bruthans, J.; Wohlfahrt, P.; Krajčoviechová, A.; Šulc, P.; Jozífová, M.; Eremiášová, L.; Pudil, J.; Linhart, A.; Widimský, J.; et al. 30-year trends in major cardiovascular risk factors in the Czech population, Czech MONICA and Czech post-MONICA, 1985-2016/17. PLoS ONE 2020, 15, e0232845. [Google Scholar] [CrossRef]
- Cífková, R.; Bruthans, J.; Wohlfahrt, P.; Krajčoviechová, A.; Šulc, P.; Eremiášová, L.; Pudil, J.; Linhart, A.; Widimský, J.; Filipovský, J.; et al. The prevalence of major cardiovascular risk factors in the Czech population in 2015–2018. The Czech post-MONICA study. COR ET VASA 2020, 62, 6–15. [Google Scholar] [CrossRef] [Green Version]
- Bruthans, J.; Cífková, R.; Lánská, V.; O’Flaherty, M.; Critchley, J.A.; Holub, J.; Janský, P.; Zvárová, J.; Capewell, S. Explaining the decline in coronary heart disease mortality in the Czech Republic between 1985 and 2007. Eur. J. Prev. Cardiol. 2014, 21, 829–839. [Google Scholar] [CrossRef] [PubMed]
- Riffe, T.; Acosta, E. Data Resource Profile: COVerAGE-DB: A global demographic database of COVID-19 cases and deaths. Int. J. Epidemiol. 2021, 50, 390–390f. [Google Scholar] [CrossRef]
- Hulíková Tesárková, K. Demographic aspects of the COVID-19 pandemic in Italy, Spain, Germany, and South Korea. Geografie 2020, 125, 139–170. [Google Scholar] [CrossRef]
- Jürgen, M.; Oliver, B.; Katrin, T.; Kirsten, E.; Claudia, S. Geomagnetic Kp index. V. 1.0. GFZ Data Serv. 2021. [Google Scholar] [CrossRef]
- Matzka, J.; Stolle, C.; Yamazaki, Y.; Bronkalla, O.; Morschhauser, A. The geomagnetic Kp index and derived indices of geomagnetic activity. Space Weather 2021, 19, e2020SW002641. [Google Scholar] [CrossRef]
- Tapping, K.F. The 10.7 cm solar radio flux (F10.7). Space Weather 2013, 11, 394–406. [Google Scholar] [CrossRef]
- Ebert-Uphoff, I.; Deng, Y. Causal discovery for climate networks. Res. Rep. 2010. Available online: http://smartech.gatech.edu/handle/1853/36564 (accessed on 11 July 2019).
- Ebert-Uphoff, I.; Deng, Y. Causal discovery for climate research using graphical models. J. Clim. 2012, 25, 5648–5665. [Google Scholar] [CrossRef] [Green Version]
- Bannerjee, A. Probabilistic graphical models for climate data analysis, paper presented at Supercomputing Workshop on Climate Knowledge Discovery (CKD-SC11). IEEE Comput. Soc. Seattle Wash 2011, 13. [Google Scholar] [CrossRef]
- Whittaker, J. Graphical Models in Applied Multivariate Statistics; Wiley: New York, NY, USA, 1990; pp. 182–185. [Google Scholar]
- Lauritzen, S.L. Graphical Models; Oxford Science Publications: New York, NY, USA, 1996; ISBN 0-19-852219-3. [Google Scholar]
- Podolská, K.; Koucká Knížová, P.; Chum, J.; Kozubek, M.; Burešová, D. Analysis of relationship between ionospheric and solar parameters using graphical models. J. Geophys. Res. Space Phys. 2021, 126, e2020JA029063. [Google Scholar] [CrossRef]
- Podolská, K. Changes of Circulatory and Nervous Diseases Mortality Patterns during Periods of Exceptional Solar Events. Atmosphere 2021, 12, 203. [Google Scholar] [CrossRef]
- Buhl, S. On the existence of maximum likelihood estimators for graphical Gaussian models. Scand. J. Statist. 1993, 20, 263–270. [Google Scholar]
- Cramer, E. Conditional iterative proportional fitting for Gaussian distributions. J. Multivar. Anal. 1998, 65, 261–276. [Google Scholar] [CrossRef] [Green Version]
- Jordan, M.I. Graphical models. Stat. Sci. 2004, 19, 140–155. [Google Scholar] [CrossRef]
- Koller, D.; Friedman, N. Probabilistic Graphical Models–Principles and Techniques, 1st ed.; MIT Press: Cambridge, MA, USA, 2009; 1280p, ISBN 978-0-262-01319-2. [Google Scholar]
- Edwards, D. Introductions to Graphical Modeling, 2nd ed.; Includes MIM software; Springer: New York, NY, USA, 2000; ISBN 978-1-4612-0493-0. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).