Analytical Study on the Steady-State Thermal Blooming of Incoherent Combining Beam
Abstract
:1. Introduction
2. Theory of the Steady-State Thermal Blooming
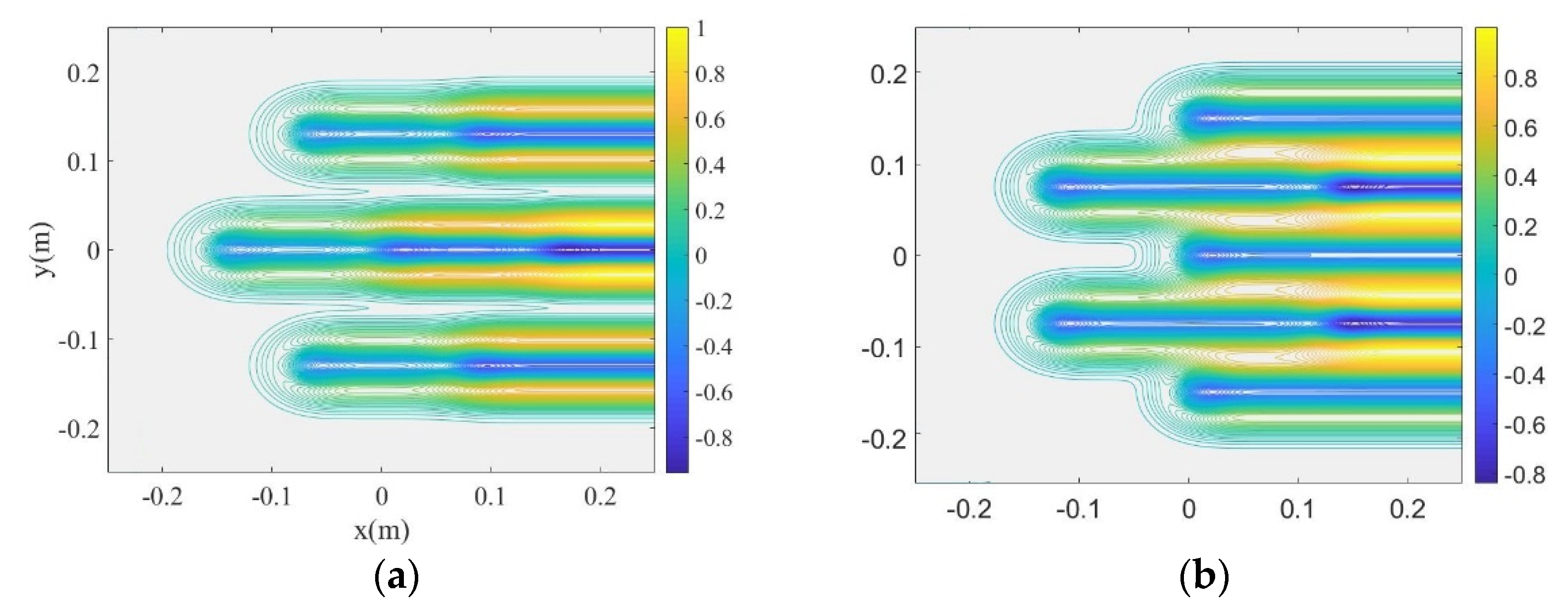
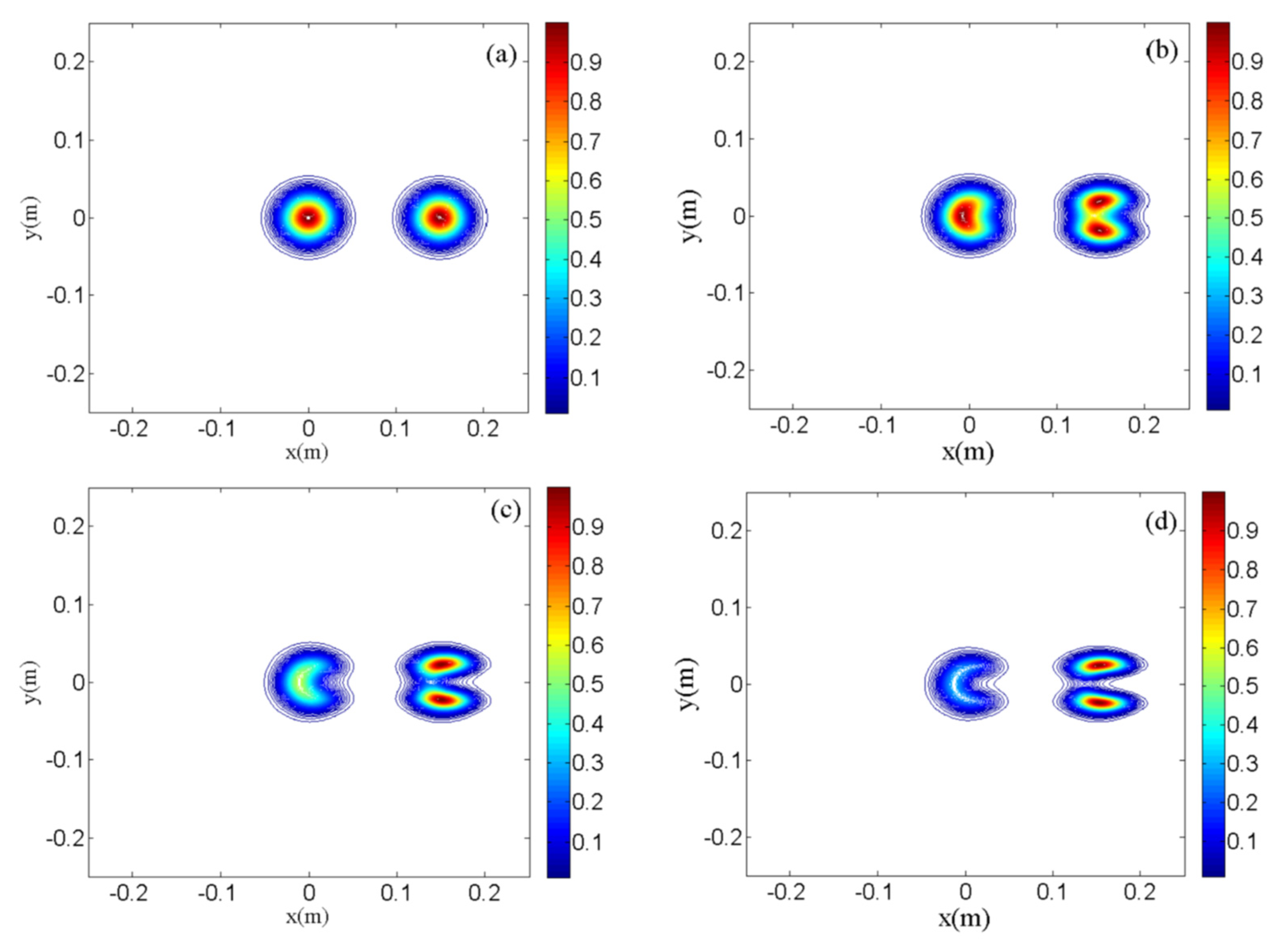
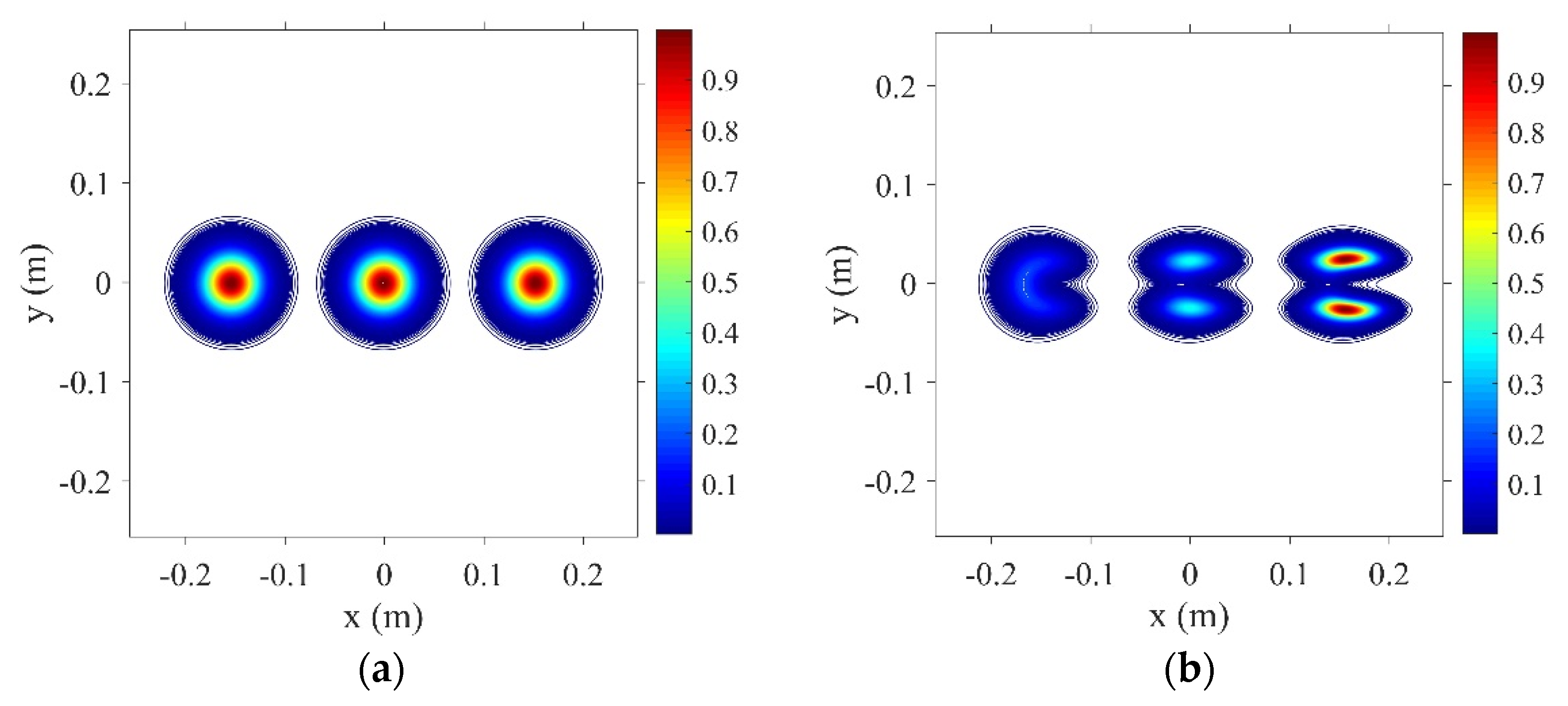
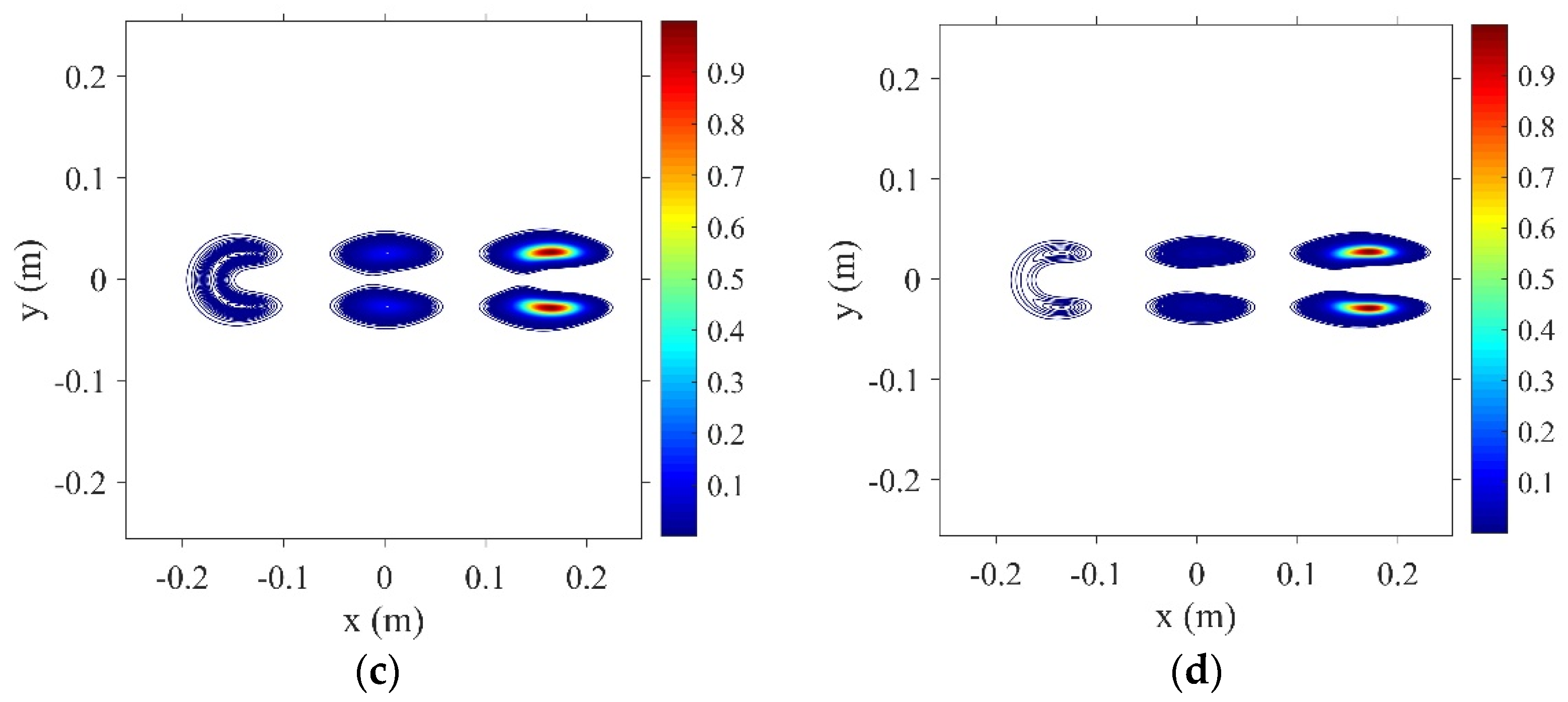
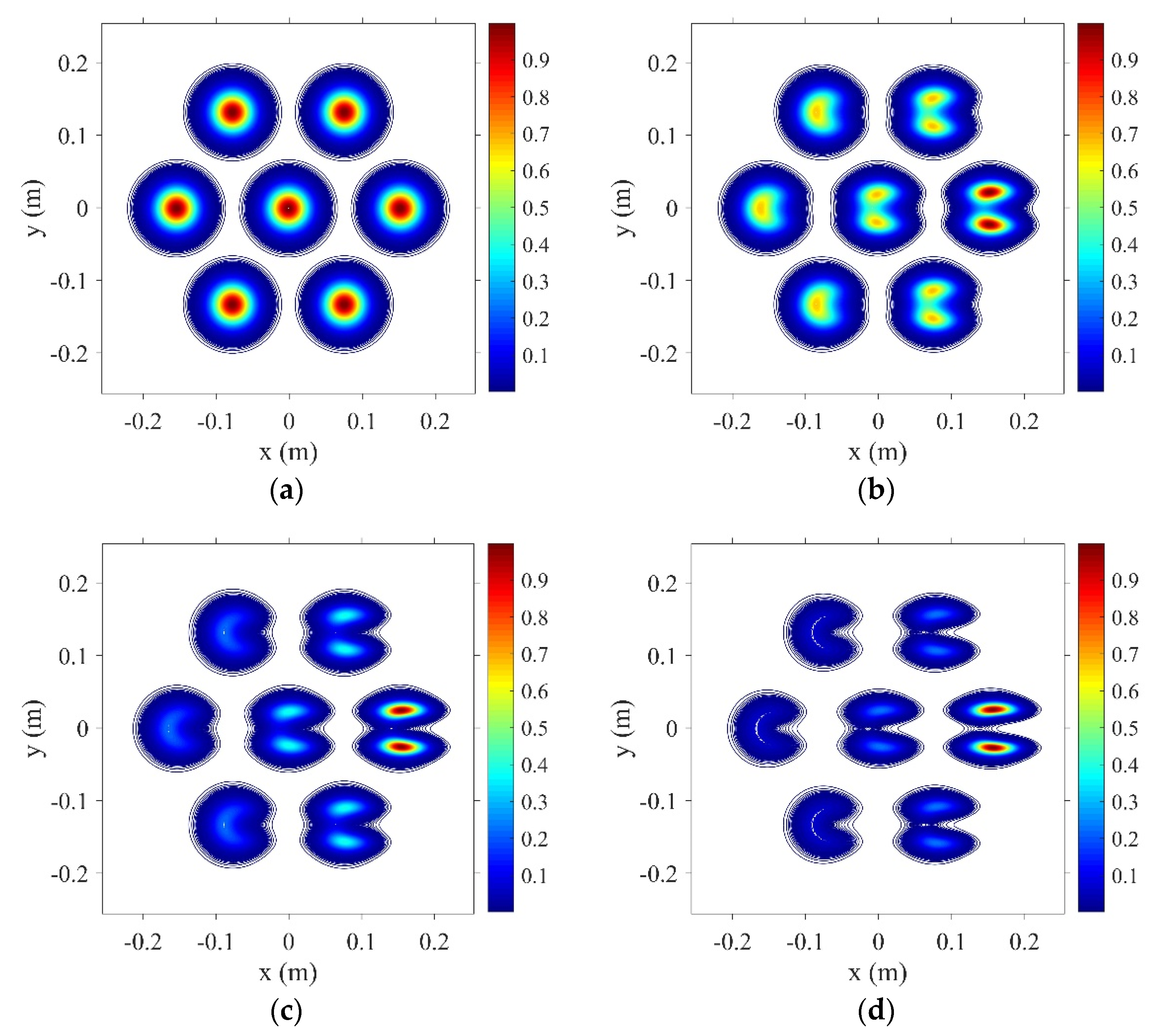
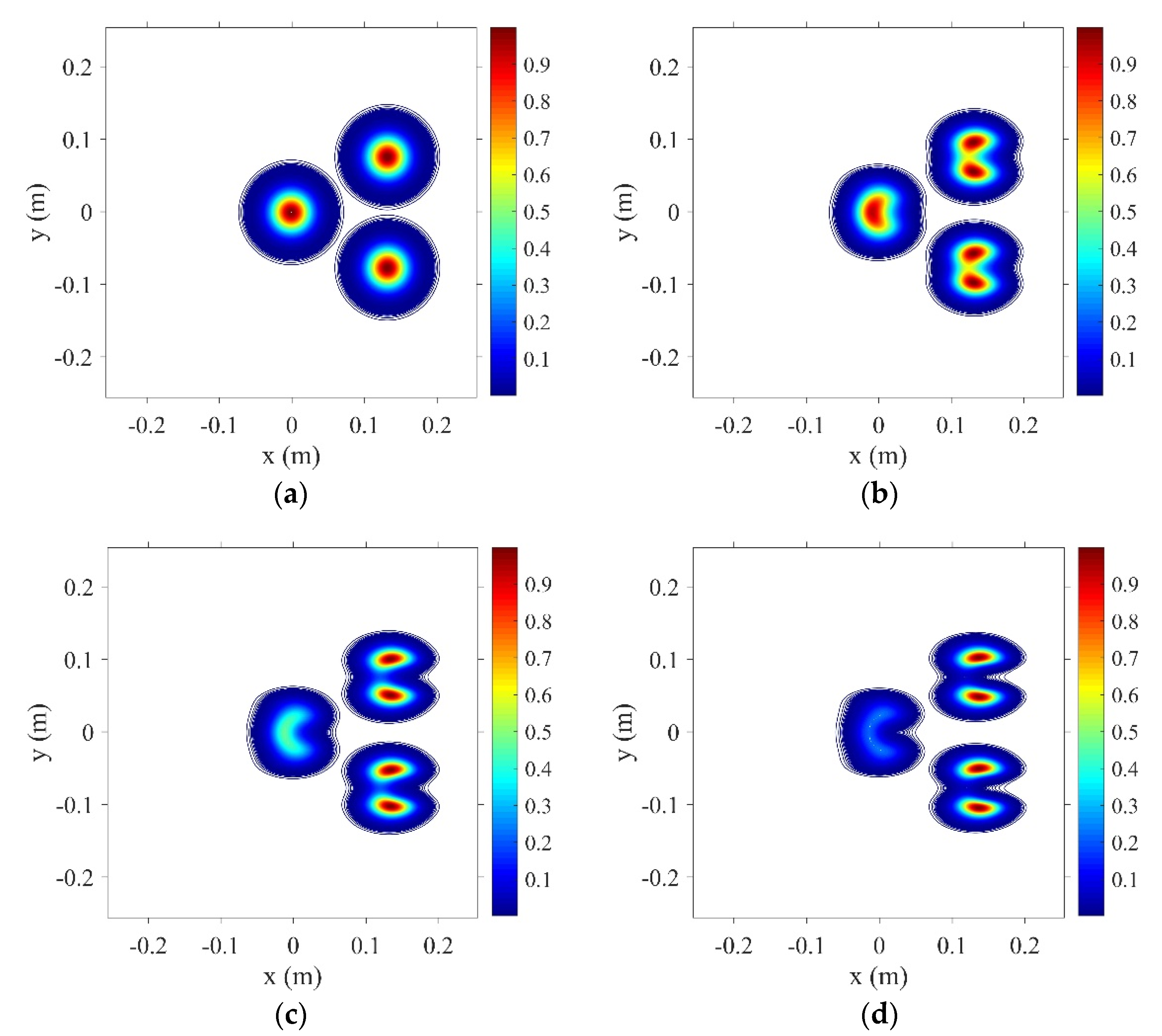
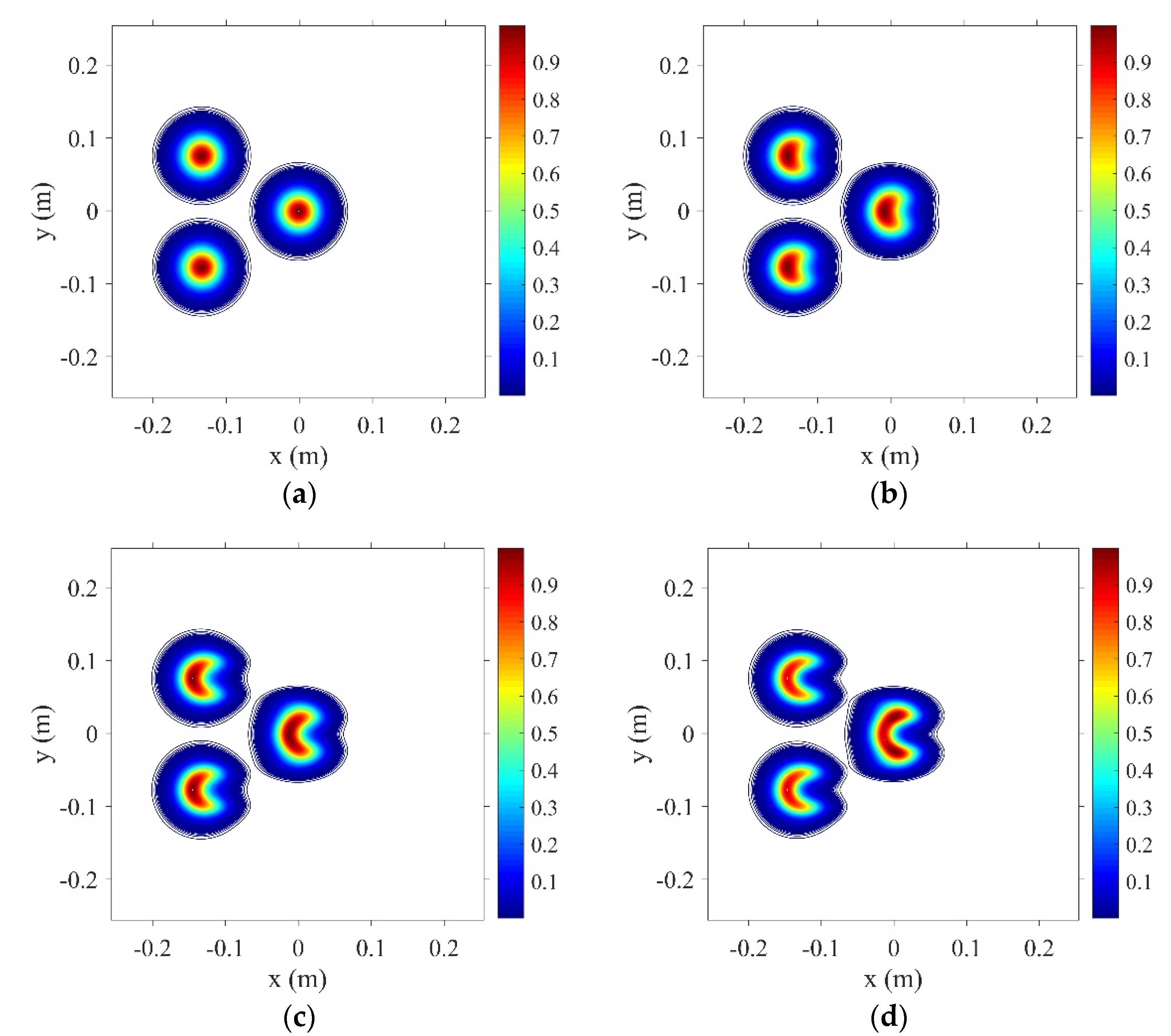
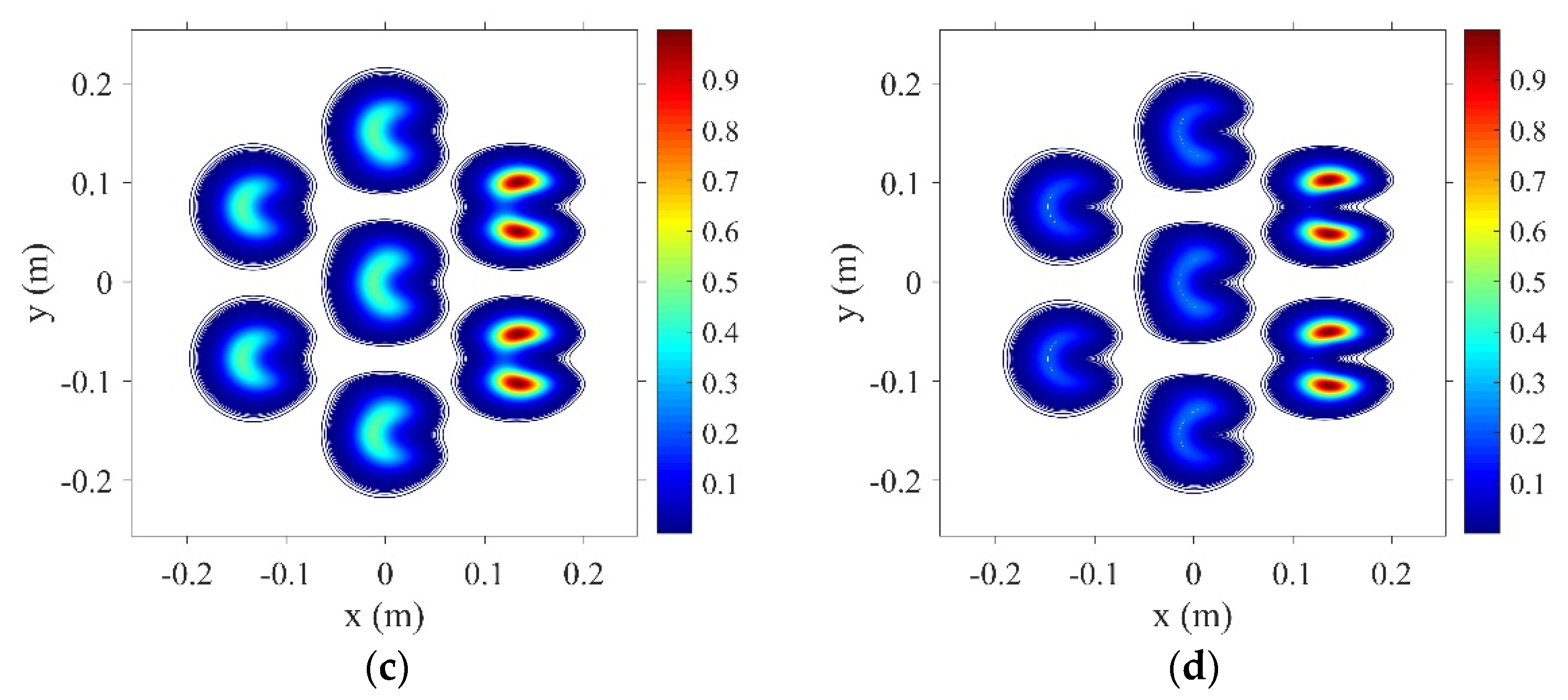
3. Thermal Blooming of the Incoherent Combined Beams
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Han, P.; Guo, J.; Bao, Q.; Qin, T.; Liu, Y. Optical design and stray light control for a space-based laser space debris removal mission. Appl. Opt. 2021, 60, 7721. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Hao, X.; Wang, D.; Wang, Q. Study of application and key technology of the high-energy laser weapon in optoelectronic countermeasure. Appl. Opt. Photonics 2015, 9673, 967307. [Google Scholar]
- Rezunkov, Y.R. High-Power Laser Propulsion; Springer International Publishing: Edinburgh, UK, 2021. [Google Scholar]
- Syed, A.A.; Mohsin, M.; Ali, S. Survey and technological analysis of laser and its defense applications. Def. Technol. 2020, 17, 583–592. [Google Scholar]
- Dawson, J.W.; Messerly, M.J.; Beach, R.J.; Shverdin, M.Y.; Barty, C. Analysis of the Scalability of Diffraction-Limited Fiber Lasers and Amplifiers to High Average Power. Opt. Express 2008, 16, 13240–13266. [Google Scholar] [CrossRef]
- Sevian, A.; Andrusyak, O.; Ciapurin, I.; Smirnov, V.; Glebov, L. Efficient power scaling of laser radiation by spectral beam combining. Opt. Lett. 2008, 33, 384–386. [Google Scholar] [CrossRef]
- Fan, T.Y.; Sanchez, A. Coherent (phased array) and wavelength (spectral) beam combining compared (Invited Paper). In Proceedings of the SPIE—The International Society for Optical Engineering United States, San Diego, CA, USA, 7–9 March 2005. [Google Scholar]
- Pu, Z.; Liu, Z.; Wang, X.; Ma, Y.; Ma, H.; Xu, X. Coherent beam combining of two fiber amplifiers using stochastic parallel gradient descent algorithm. Opt. Laser Technol. 2009, 41, 853–856. [Google Scholar]
- Wirth, C.; Schmidt, O.; Tsybin, I.; Schreiber, T.; Jung, M. 2 kW incoherent beam combining of four narrow-linewidth photonic crystal fiber amplifiers. Opt. Express 2009, 17, 1178–1183. [Google Scholar] [CrossRef]
- Geng, C.; Zhao, B.; Zhang, E.; Luo, W.; Tan, Y.; Zhu, Y.; Yang, H.; Mu, J.; Li, X.; Duan, K.; et al. 1.5 kW Incoherent Beam Combining of Four Fiber Lasers Using Adaptive Fiber-Optics Collimators. IEEE Photonics Technol. Lett. 2013, 25, 1286–1289. [Google Scholar] [CrossRef]
- Laserna, J.J.; Reyes, R.F.; González, R.; Tobaria, L.; Lucena, P. Study on the effect of beam propagation through atmospheric turbulence on standoff nanosecond laser induced breakdown spectroscopy measurements. Opt. Express 2009, 17, 10265–10276. [Google Scholar] [CrossRef]
- Fried, D.L.; Mevers, G.E.; Keister, J. Measurements of Laser-Beam Scintillation in the Atmosphere. J. Opt. Soc. Am. 1967, 57, 787–797. [Google Scholar] [CrossRef]
- Dios, F.; Rubio, J.A.; Rodriguez, A.; Comeron, A. Scintillation and beam-wander analysis in an optical ground station-satellite uplink. Appl. Opt. 2004, 43, 3866–3873. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Al-Habash, A.; Andrews, L.C.; Phillips, R.L. Theory of optical scintillation: Gaussian-beam wave model. In Proceedings of the Eighth International Symposium on Atmospheric and Ocean Optics: Atmospheric Physics, Irkutsk, Russia, 25–29 June 2001. [Google Scholar]
- Gebhardt, F.G.; Ulrich, P.B.; Wilson, L.R.E. Twenty-five years of thermal blooming—An overview. Int. Soc. Opt. Photonics 1990, 1221, 2–25. [Google Scholar]
- Smith, D.C. High-power laser propagation: Thermal blooming. Proc. IEEE 1977, 65, 1679–1714. [Google Scholar] [CrossRef]
- Gebhardt, F.G. High power laser propagation. Appl. Opt. 1976, 15, 1479–1493. [Google Scholar] [CrossRef]
- Kucherov, A.N. Transient thermal blooming of a vertical laser beam. Quantum Electron. 1997, 27, 176. [Google Scholar] [CrossRef]
- Sheldon, S.J.; Knight, L.V.; Thorne, J.M. Laser-induced thermal lens effect: A new theoretical model. Appl. Opt. 1982, 21, 1663–1669. [Google Scholar] [CrossRef] [Green Version]
- Ahn, K.; Lee, S.H.; Park, I.K.; Yang, H.S. Numerical simulation of high-energy laser propagation through the atmosphere and phase correction based on adaptive optics. J. Korean Phys. Soc. 2021, 79, 918–929. [Google Scholar] [CrossRef]
- Wu, S.; Luo, X.; Li, X. Adaptive Optics for Reduction of Thermal Blooming Effects by the Phase Compensation. J. Russ. Laser Res. 2020, 41, 413–423. [Google Scholar] [CrossRef]
- Ding, Z.; Li, X.; Cao, J.; Ji, X. Influence of thermal blooming on the beam quality of an array of Hermite–Gaussian beams propagating in the atmosphere. Appl. Opt. 2020, 59, 10944. [Google Scholar] [CrossRef]
- Li, X.; Cao, J.; Ding, Z.; Ji, X. Influence of fill factors on the thermal blooming of array laser beams in the air. Opt.-Int. J. Light Electron. Opt. 2018, 182, 314–323. [Google Scholar] [CrossRef]
- Zhang, Y.; Hou, T.; Chang, H.; Su, R.; Ma, P.; Zhou, P. Thermal blooming effect and the scaling laws of partial spatially coherent beam array propagating through the atmosphere. Results Phys. 2021, 16, 104444. [Google Scholar] [CrossRef]
- Wallace, J.; Pasciak, J. Thermal blooming of a rapidly moving laser beam. Appl. Opt. 1976, 15, 218–222. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Sun, Q.; Ning, Y.; Xu, X.; Xi, F. Optimization of incoherent beam combining in turbulent atmosphere. Optik 2022, 252, 168482. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Sun, Q.; Chu, X. Analytical Study on the Steady-State Thermal Blooming of Incoherent Combining Beam. Atmosphere 2022, 13, 1678. https://doi.org/10.3390/atmos13101678
Zhang K, Sun Q, Chu X. Analytical Study on the Steady-State Thermal Blooming of Incoherent Combining Beam. Atmosphere. 2022; 13(10):1678. https://doi.org/10.3390/atmos13101678
Chicago/Turabian StyleZhang, Ke, Quan Sun, and Xiuxiang Chu. 2022. "Analytical Study on the Steady-State Thermal Blooming of Incoherent Combining Beam" Atmosphere 13, no. 10: 1678. https://doi.org/10.3390/atmos13101678
APA StyleZhang, K., Sun, Q., & Chu, X. (2022). Analytical Study on the Steady-State Thermal Blooming of Incoherent Combining Beam. Atmosphere, 13(10), 1678. https://doi.org/10.3390/atmos13101678