Numerical Investigation on the Influence of Class Number and Wavelength on the Performance of Curved Vane Demisters
Abstract
:1. Introduction
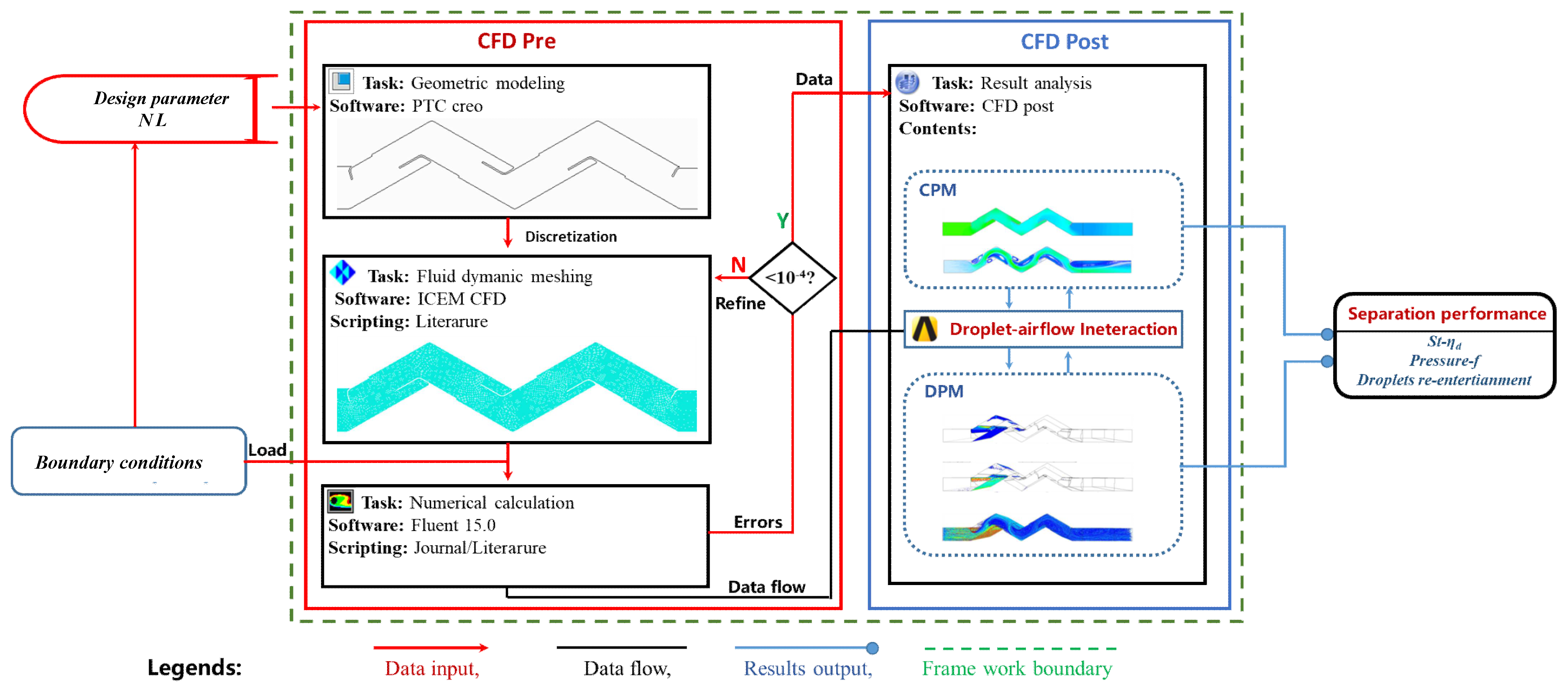
2. Computational Method
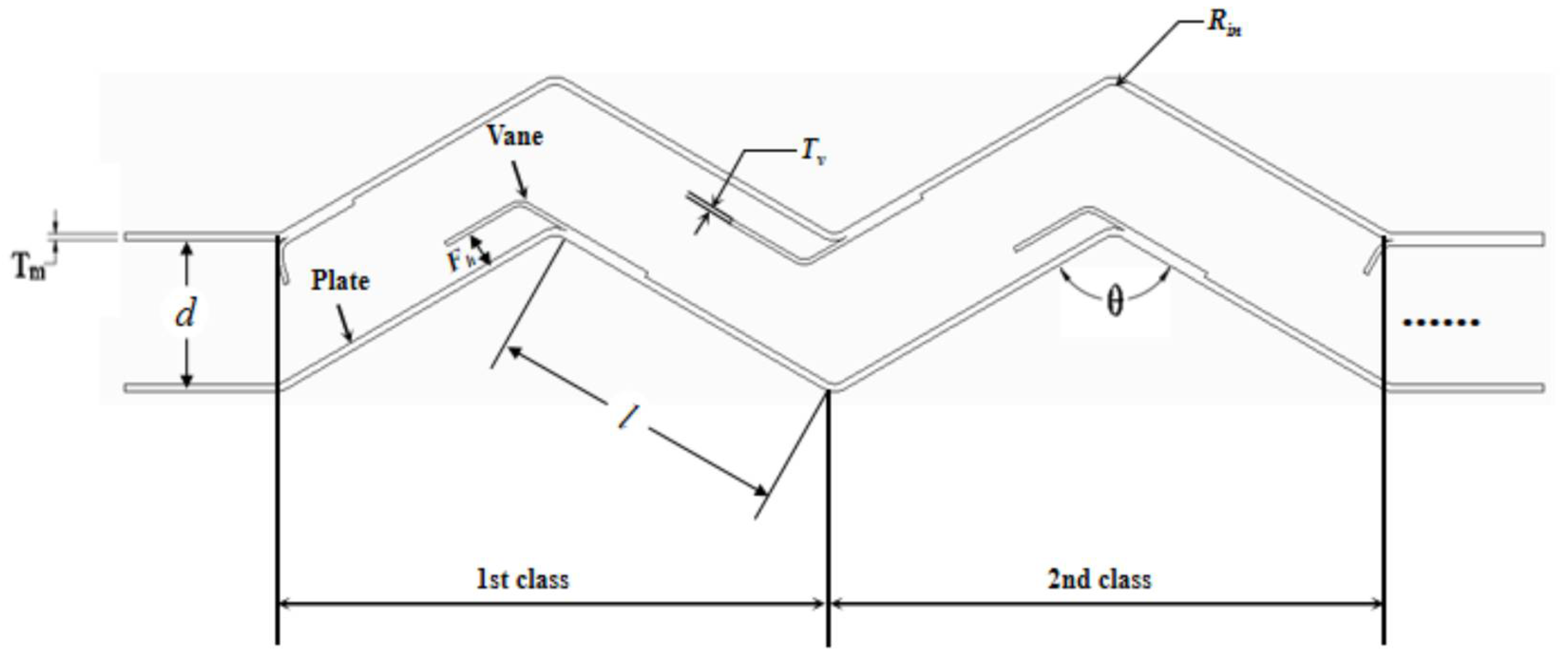
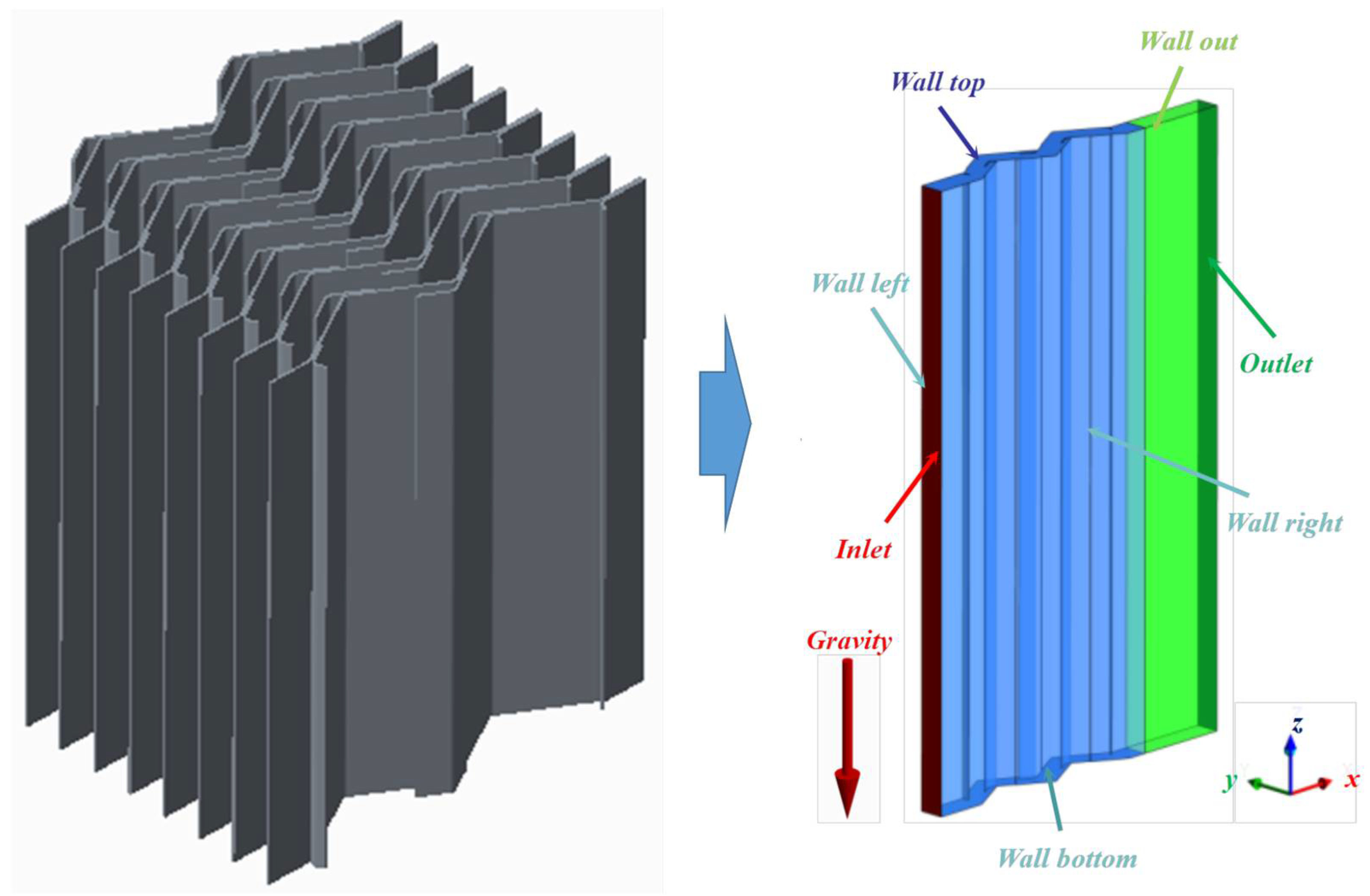
2.1. Geometric Model and Boundary Conditions
- (1)
- Inlet and outlet region:
- (2)
- Top and bottom boundaries:
- (3)
- Plates and vane surface:
- The gas is considered incompressible for the low velocity in the investigation.
- The CFD model with continuous and discrete phase flow is assumed to be steady during the calculation for the constant boundary conditions.
- The phase change is ignored in the simulation. The droplets are considered sufficiently small to be assumed as the sphere given that the volume of droplets inside the vapor is below 10%.
- The wall is considered a hydrophilic material. The droplets are considered sufficiently small; thus, the probability of droplet interaction can be negligible.
- Secondary liquid droplets are mainly stripped from the liquid film for the interaction of vapor with the high flow rate.
2.2. Mathematical Model of Lagrange-Euler Method
2.2.1. Continuous Phase Modeling
2.2.2. Discrete Phase Modeling
2.2.3. Performance Evaluation
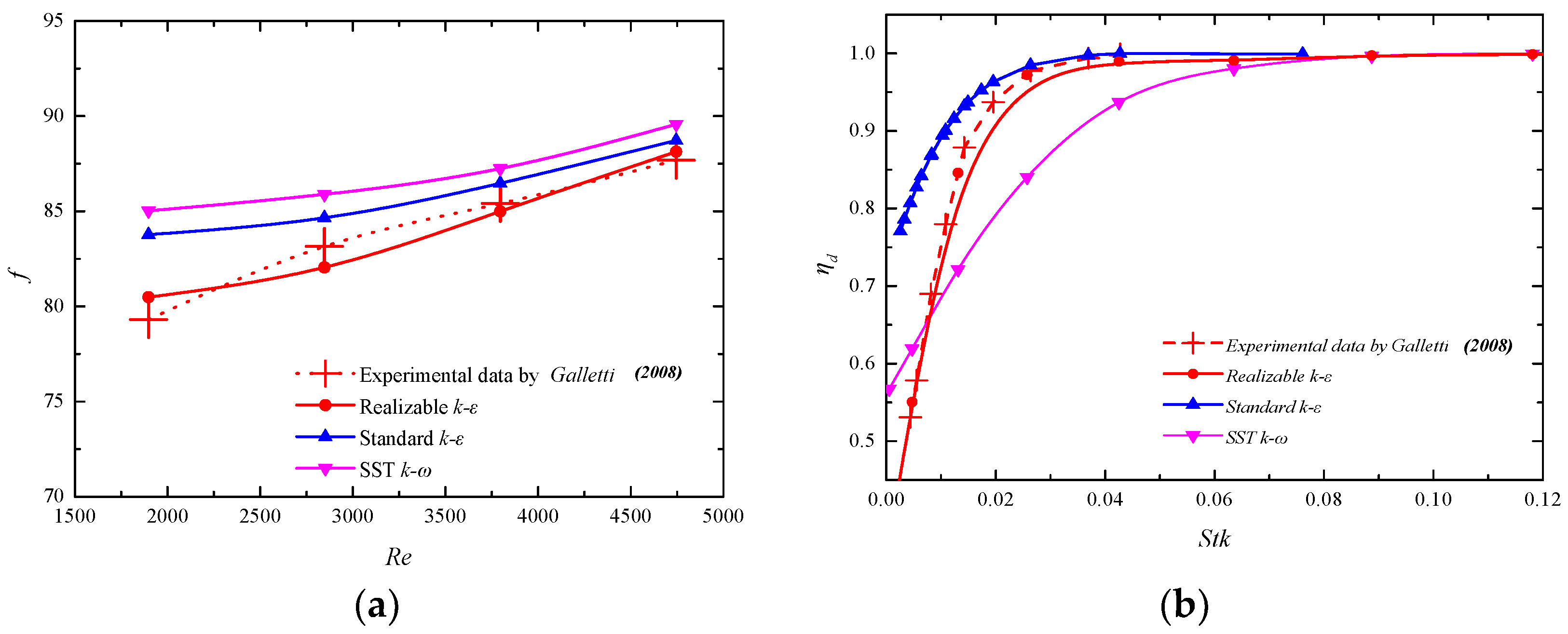
2.3. Mesh Discretization and Model Validation
3. Results and Discussion
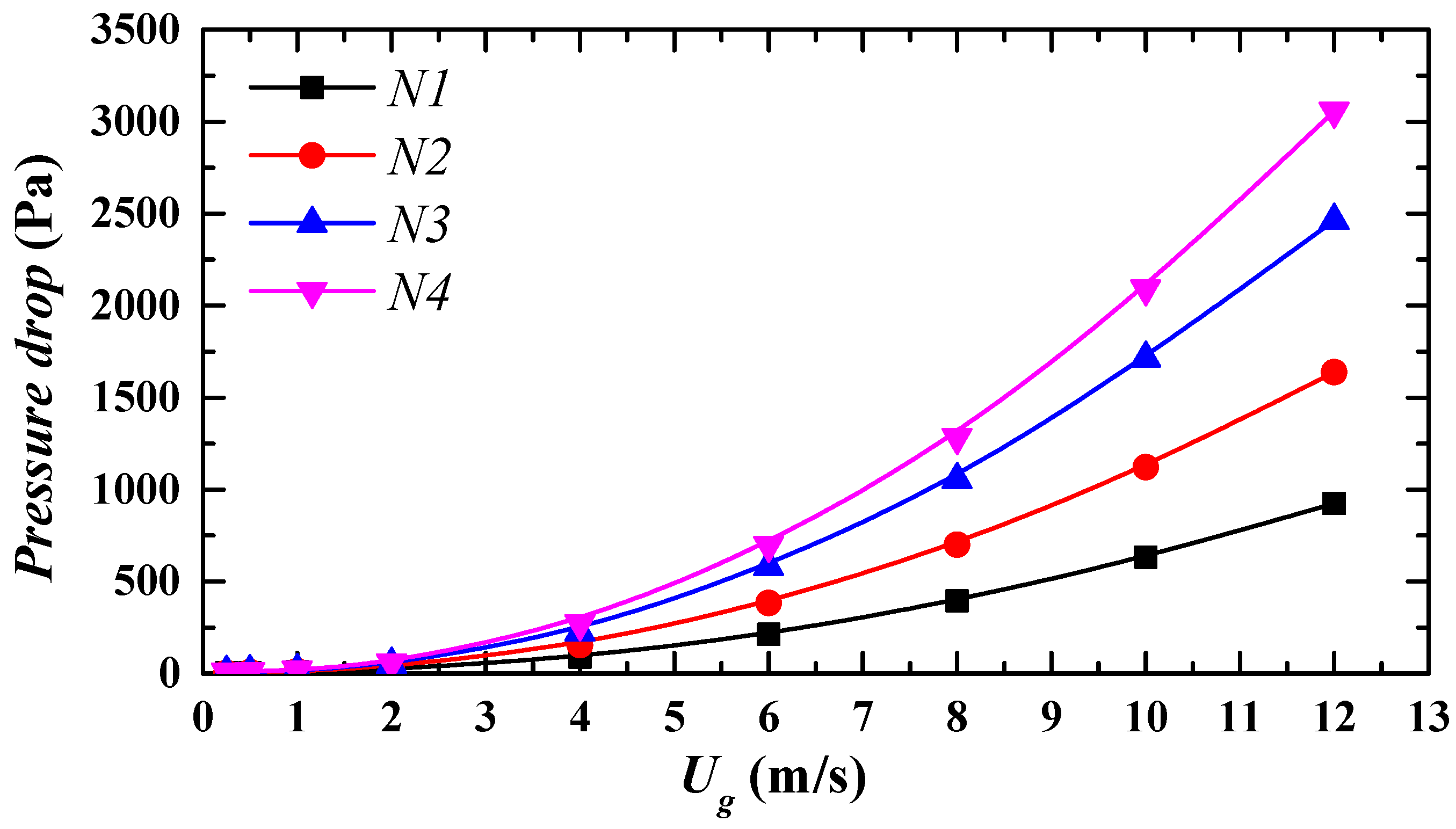
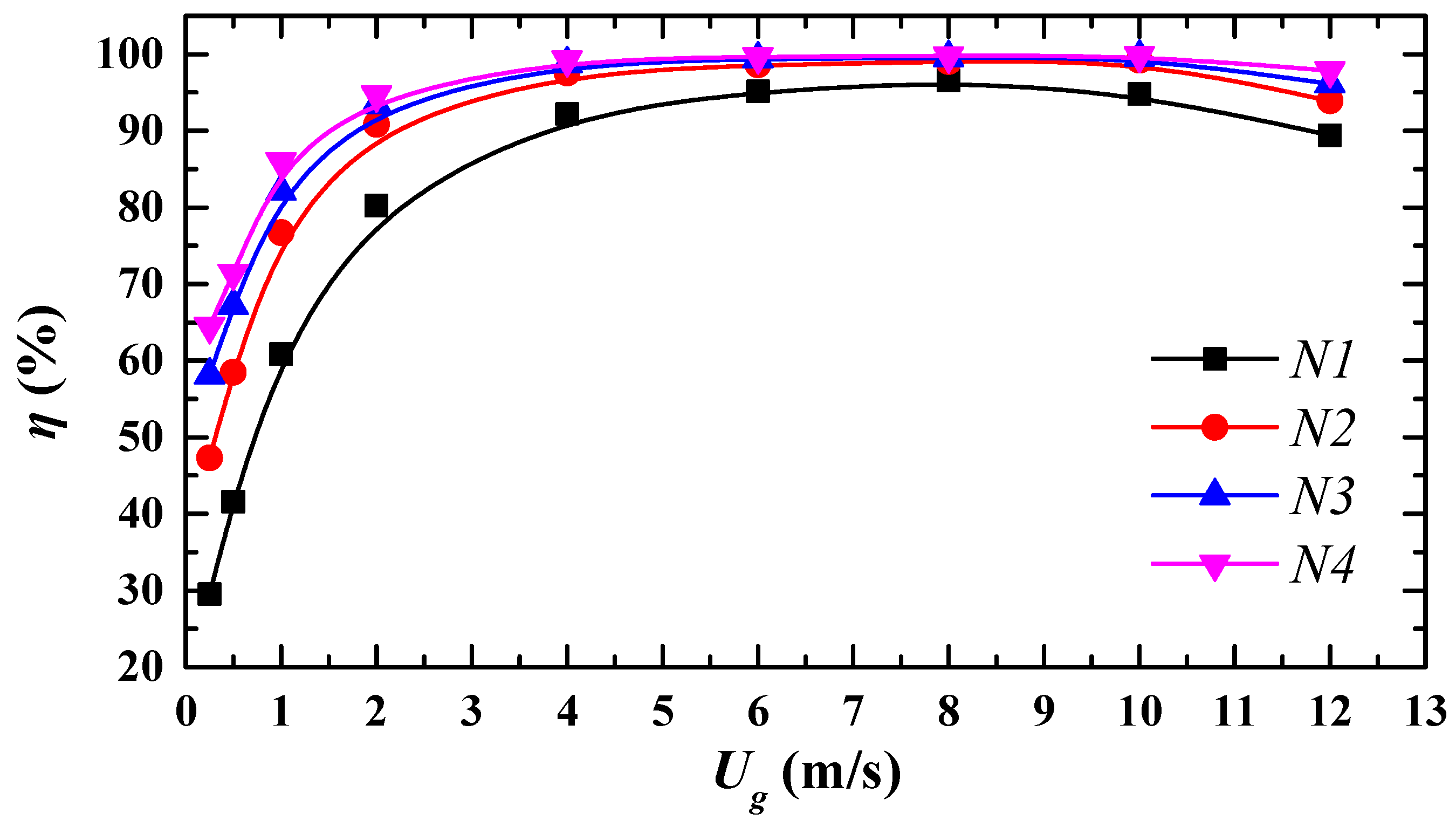
3.1. Investigation of Class Number N on the Separation Performance
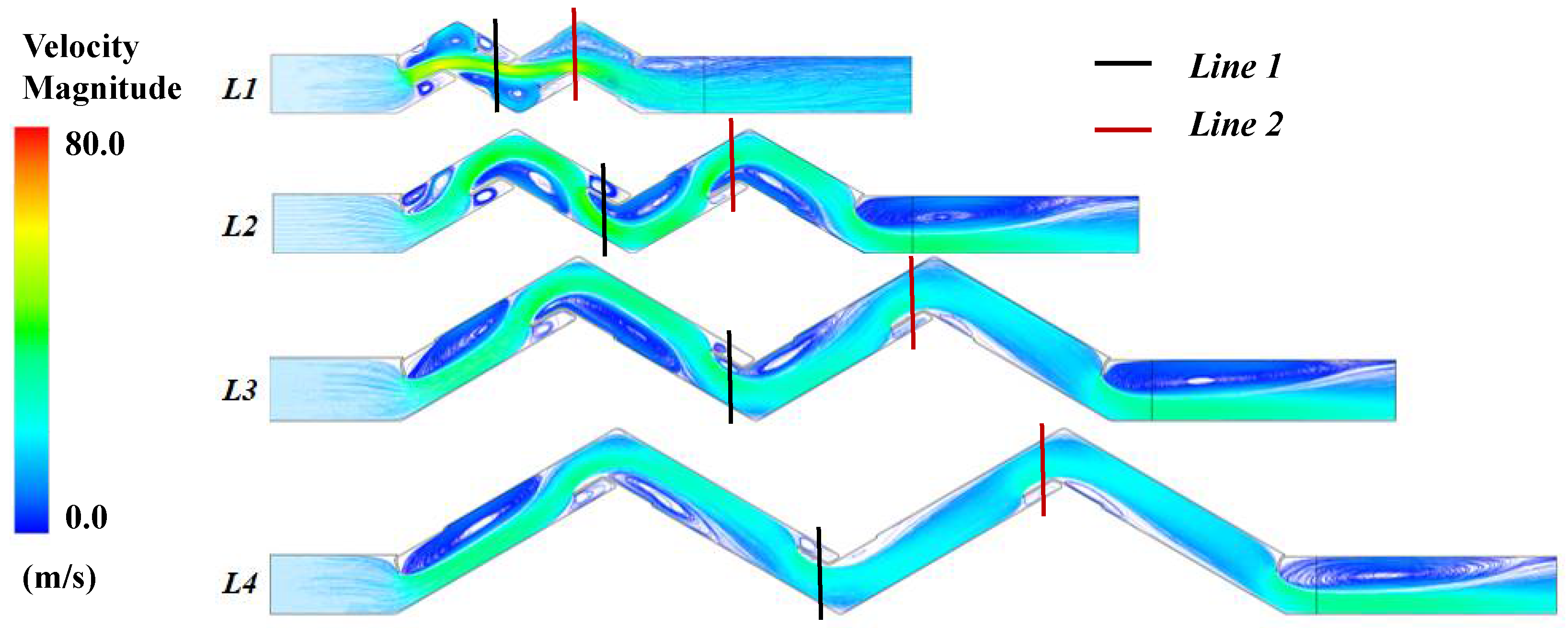
3.2. Investigation of Wavelength L on the Continuous Phase Flow
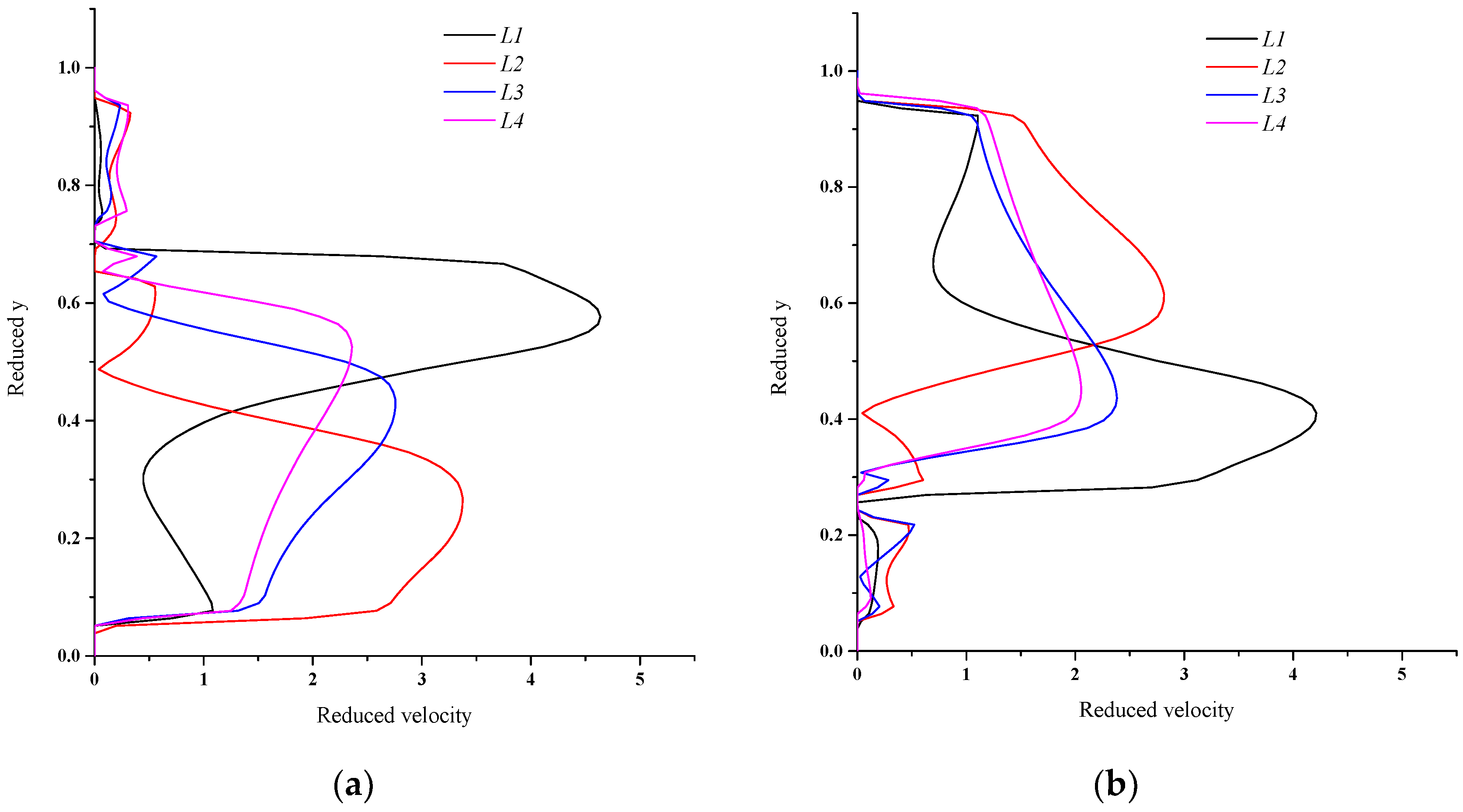
3.2.1. The Analysis of Velocity Distribution
3.2.2. The Analysis of Pressure Drop and Friction Factor
3.3. Investigation of Wavelength L on Disperse Phase Domain
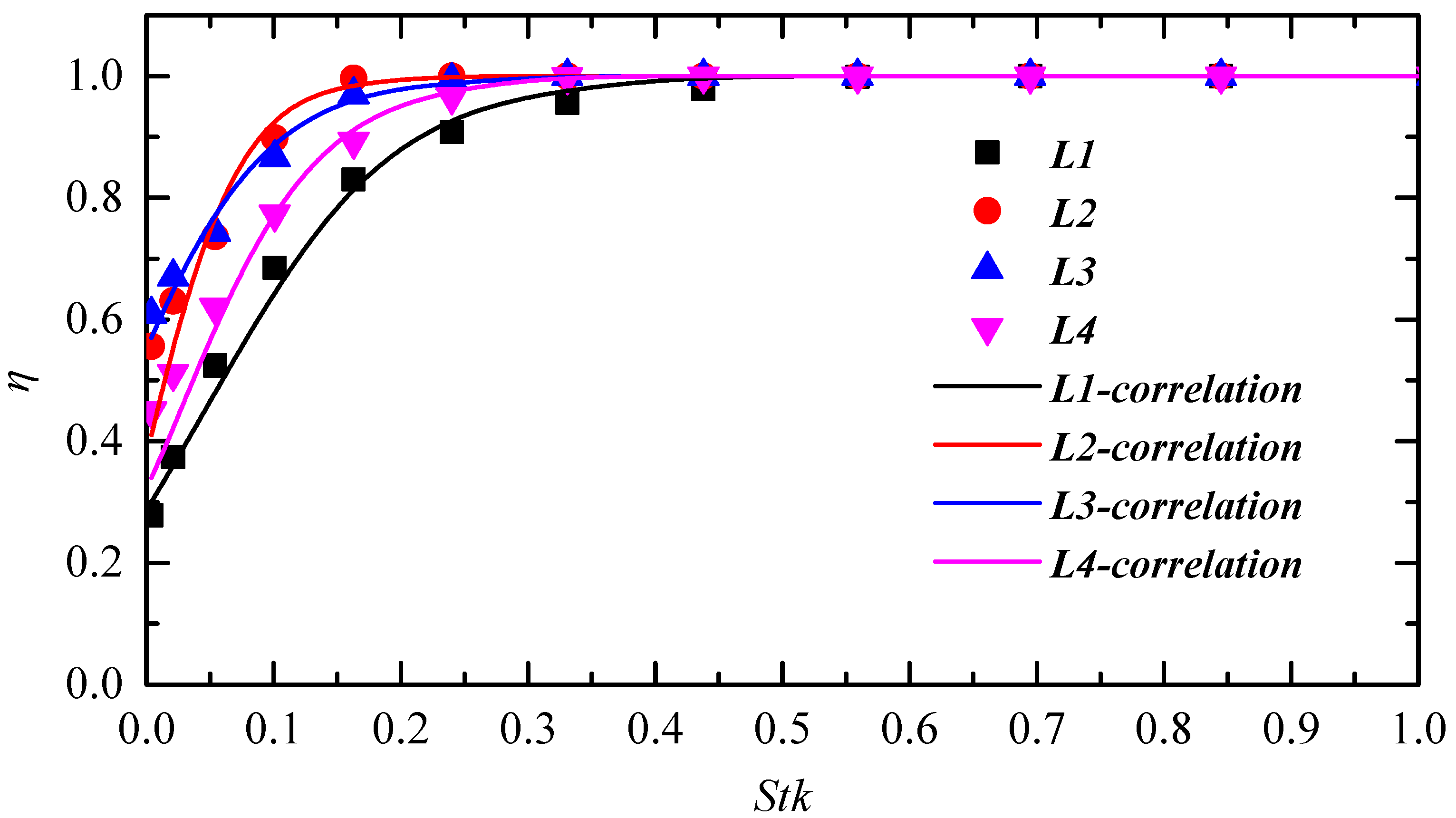
3.3.1. The Analysis of Droplets’ Motion and Separation Efficiency
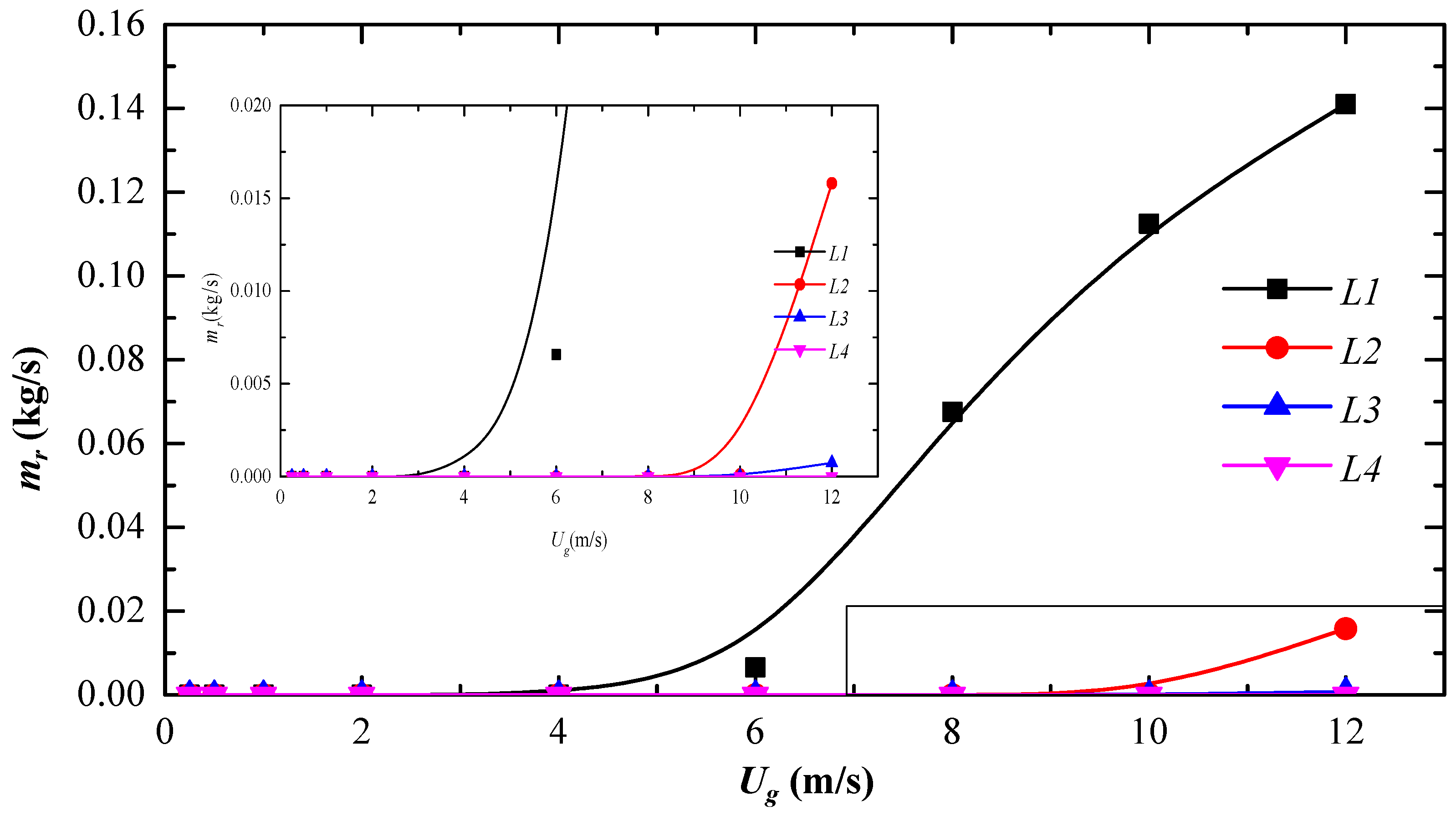
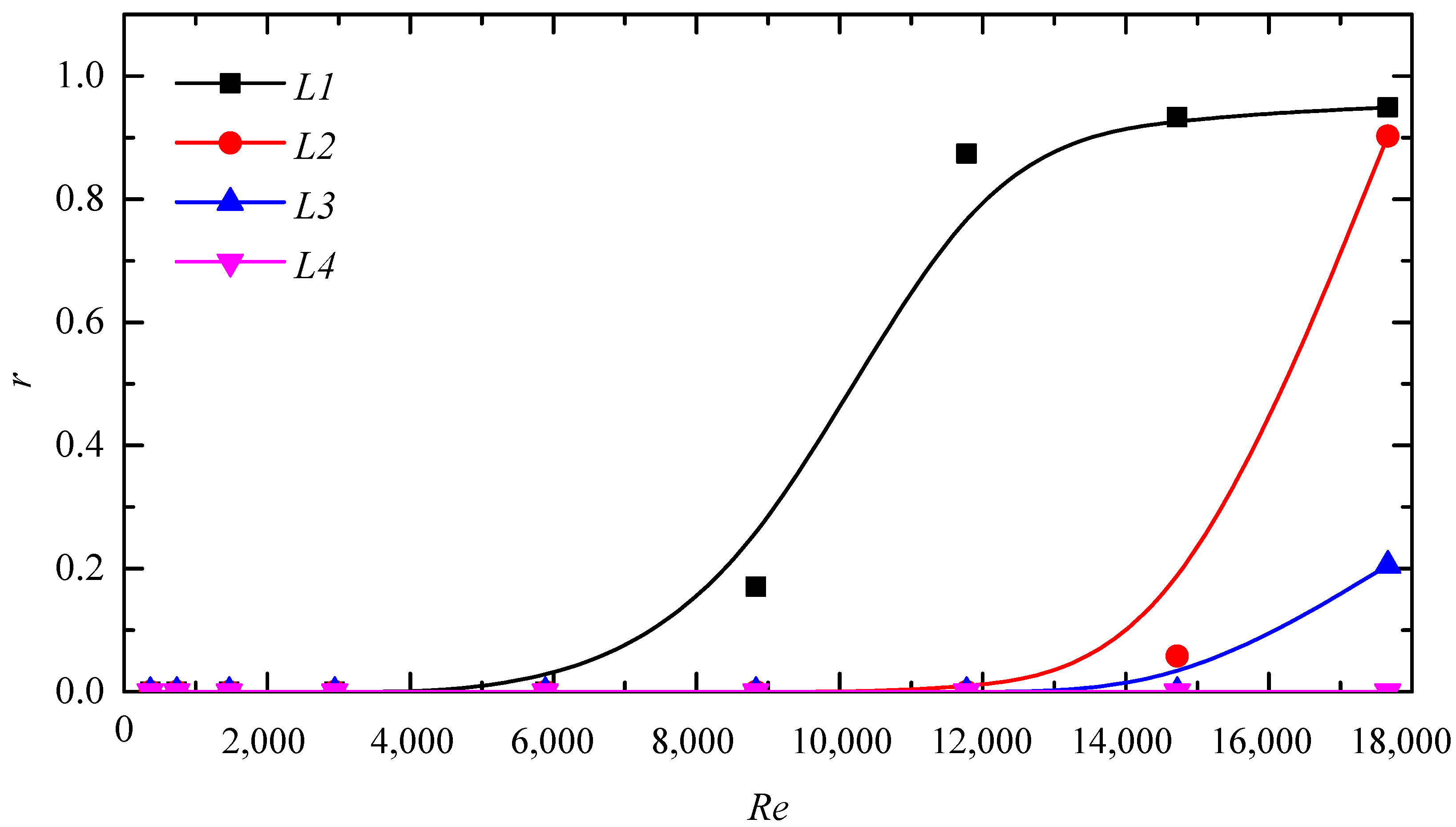
3.3.2. The Analysis of Euler Wall Film (EWF) and Droplets Re-Entrainment
4. Conclusions
- The increase of class number N leads to higher local flow resistance and pressure loss remarkably, but cannot improve the separation efficiency effectively, especially in the high-class number N > 3.
- Prolonging the wavelength L can initially increase and thereafter decrease the separation efficiency. However, when the wavelength increases to a high level, continuously increasing the wavelength decreases the droplet re-entrainment mass source, which is mainly due to the variation of streamline distribution and turbulence dissipation.
- Droplets with large diameters are mainly collected in the first class for the prolonged wavelength and the separation performance, especially for the droplets with large diameters. Additionally, the prolonged wavelength causes the film to spread to the next class mainly due to the flattening of vortex zones due to the prolonged wavelength.
- The prolonged wavelength L can largely reduce the re-entrainment mass flow rate and increase the critical velocity at the high-velocity level, which is mainly because the small secondary droplets become easier to be recollected by the prolonged wavelength L.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbol | Paraphrase | Unit |
| b | demister depth | m |
| CD | drag coefficient | |
| din | inner diameter of the plate | m |
| dp | droplet diameter | m |
| dm | droplet mean diameter | m |
| D | plate spacing | m |
| FD | coefficient of drag force acceleration | |
| additional acceleration | m/s2 | |
| h | film thickness | m |
| H | height of demister | m |
| k | turbulent kinetic energy | m2/s2 |
| L | wavelength | m |
| LA | overall length | m |
| mass source per unit wall | kg/(s·m2) | |
| N | number of classes | |
| Pin | inlet or upstream pressure | Pa |
| Pout | outlet or downstream pressure | Pa |
| r | re-entrainment coefficient | |
| Stk | Stokes number | |
| s | spread diameter | m |
| TM | plate thickness | m |
| Tv | vane thickness | m |
| min | mass flow rate of the entering droplets | kg/s |
| me | mass flow rate of the escape droplets | kg/s |
| mr | mass flow rate of the removed droplets | kg/s |
| Md | mass fraction of droplets | |
| Re | gas Reynolds number | |
| Rij | Reynolds stress tensor | m2/s2 |
| Sφ | source term in the transport equation | |
| t | time | m/s |
| τg | stress tension | Pa |
| ui | velocity of the vapor flow in three directions, | m/s |
| ud | droplet velocity | m/s |
| ug | local gas flow velocity | m/s |
| Ug | inlet gas flow velocity | m/s |
| Vd | droplet velocity | m/s |
| Vl | wall film velocity | m/s |
| Wef | Weber number | |
| Md | mass fraction of droplets | |
| θ | plate angle | deg. |
| ε | dissipation rate | m2/s3 |
| η | overall droplet separation efficiency | % |
| ηi | separation efficiency of droplets with diameter | % |
| μ | turbulent dynamic viscosity | Pa·s |
| μd | dynamic viscosity of the liquid | Pa·s |
| μg | dynamic viscosity of gas | Pa·s |
| ρd | liquid droplet density | kg/m3 |
| ρl | liquid film density | kg/m3 |
| ρg | gas density | kg/m3 |
| σij | molecular viscosity | |
| φ | general variable in the transport equation | |
| ▽s | surface gradient operator | |
| ΔP | pressure difference | Pa |
References
- Graham, I.D. Improved eddy interaction models with random length and timescales. Int. J. Multiph. Flow 1998, 24, 335–345. [Google Scholar] [CrossRef]
- Ruiz, J.; Kaiser, A.S.; Zamora, B.; Cutillas, C.G.; Lucas, M. CFD analysis of drift eliminators using RANS and LES turbulent models. Appl. Therm. Eng. 2016, 105, 979–987. [Google Scholar] [CrossRef]
- Rafee, R.; Rahimzadeh, H.; Ahmadi, G. Numerical simulations of vapor and droplet transport in a wave-plate mist eliminator. Chem. Eng. Res. Des. 2010, 88, 1393–1404. [Google Scholar] [CrossRef]
- Rafee, R.; Rahimzadeh, H. Performance evaluation of a curved type vane separator at different plate spacing in the range of 25 to 35 mm using numerical simulation. Iran J. Chem. Eng. 2010, 29, 95–108. [Google Scholar] [CrossRef]
- Hamedi Estakhrsar, M.H.; Rafee, R. Effects of wavelength and number of bends on the performance of zigzag demisters with drainage channels. Appl. Math. Model. 2016, 40, 685–699. [Google Scholar] [CrossRef]
- James, P.W.; Wang, Y.; Azzopardi, B.J.; Hughes, J.P. The role of drain age channels in the performance of wave-plate mist eliminators. Chem. Eng. Res. Des. 2003, 81, 639–648. [Google Scholar] [CrossRef]
- Wang, Y.; James, P.W. Assessment of an eddy-interaction model and its refinements using predictions of droplet deposition in a wave-plate demister. Chem. Eng. Res. Des. 1999, 77, 692–698. [Google Scholar] [CrossRef]
- Venkatesan, G.; Kulasekharan, N.; Iniyan, S. Numerical analysis of curved vane demisters in estimating water droplet separation efficiency. Desalination 2014, 339, 40–53. [Google Scholar] [CrossRef]
- Venkatesan, G.; Kulasekharan, N.; Iniyan, S. Design and selection of curved vane demisters using Taguchi based CFD analysis. Desalination 2014, 354, 39–52. [Google Scholar] [CrossRef]
- Venkatesan, G.; Kulasekharan, N.; Muthukumar, V. Regression analysis of a curved vane demister with Taguchi based optimization. Desalination 2015, 370, 33–43. [Google Scholar] [CrossRef]
- Zhao, J.; Jin, B.; Zhong, Z. Study of the collecting efficiency of a demister vane with response surface methodology. J. Hazard. Mater. 2007, 147, 363–369. [Google Scholar] [CrossRef] [PubMed]
- Galletti, C.; Brunazzi, E.; Tognotti, L. A numerical model for gas flow and droplet motion in wave-plate mist eliminators with drainage channels. Chem. Eng. Sci. 2008, 63, 5639–5652. [Google Scholar] [CrossRef]
- Zamora, B.; Kaiser, A.S. Comparative efficiency evaluation of four types of cooling tower drift eliminator by numerical investigation. Chem. Eng. Sci. 2011, 66, 1232–1245. [Google Scholar] [CrossRef]
- Wang, Y.; James, P.W. The calculation of wave-plate demister efficiencies using numerical simulation of the flow field and droplet motion. Chem. Eng. Res. Des. 1998, 76, 980–985. [Google Scholar] [CrossRef]
- Tian, L.; Ahmadi, G. Particle deposition in turbulent duct flows comparisons of different model predictions. J. Aerosol Sci. 2007, 38, 377–397. [Google Scholar] [CrossRef]
- Wilkinson, D. Optimizing the design of wave plates for gas-liquid separation, in: Proceedings of Institution Mechanics Engineering. I. Mech. E. Part E 1999, 213, 265–274. [Google Scholar] [CrossRef]
- Azzopardi, B.J.; Sanaullah, K.S. Re-entrainment in wave-plate mist eliminators. Chem. Eng. Sci. 2002, 57, 3557–3563. [Google Scholar] [CrossRef]
- Wang, P.F.; Jiang, J.; Li, S.Y.; Yang, X.L.; Luo, X.Y.; Wang, Y.C.; Thakurd, A.K.; Zhao, W.S. Numerical investigation on the fluid droplet collecting performance of corrugated plate gas-liquid separators. Sep. Purif. Technol. 2020, 248, 117027. [Google Scholar] [CrossRef]
- Li, S.Y.; Wang, P.F.; Luo, X.Y.; Wang, Y.C.; Yang, X.L.; Thakur, A.K.; Zhao, W.S. Numerical analysis of chevron demisters with drainage hooks in optimizing separation performance. Int. J. Heat Mass Transf. 2020, 152, 119522. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Jafaryar, M.; Shafee, A.; Babazadeh, H. Acceleration of discharge process of clean energy storage unit with insertion of porous foam considering nanoparticle enhanced paraffin. J. Clean. Prod. 2020, 261, 121206. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Jafaryar, M.; Abohamzeh, E.; Shafee, A.; Babazadeh, H. Energy and entropy evaluation and two-phase simulation of nanoparticles within a solar unit with impose of new turbulator. Sustain. Energy Techn. 2020, 39, 100727. [Google Scholar] [CrossRef]
- Sun, Q.; Choi, K.S.; Mao, X. An analytical solution of convective heat transfer in microchannel or nanochannel. Int. Commun. Heat Mass Transf. 2020, 117, 104766. [Google Scholar] [CrossRef]
- Wang, J.; Ji, Z.; Liu, Z. Experimental and numerical investigation on the gas–liquid separation performance of a novel vane separator with grooves. Chem. Eng. Res. Des. 2022, 180, 306–317. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Q. Numerical investigation on performance of moisture separator by Lagrangian-Eulerian strategy: Physical mechanisms, theoretical models, and advanced algorithms. Ann. Nucl. Energy 2020, 137, 107081. [Google Scholar] [CrossRef]
- David, S.A.; Valentim, A. Fractional Euler-Lagrange Equations Applied to Oscillatory Systems. Mathematics 2015, 3, 258–272. [Google Scholar] [CrossRef] [Green Version]
- Tarasov, V.E. Poiseuille equation for steady flow of fractal fluid. Inter. J. Mod. Phy. B 2016, 30, 1650128. [Google Scholar] [CrossRef]
- Ostoja-Starzewski, M. Continuum mechanics models of fractal porous media: Integral relations and extremum principles. J. Mech. of Mater. Struct. 2009, 4, 901–912. [Google Scholar] [CrossRef]
- Thakur, A.K.; Kumar, R.; Banerjee, N.; Chaudhari, P.; Kumar Gaurav, G. Hydrodynamic modeling of liquid-solid flow in polyolefin slurry reactors using CFD techniques—A critical analysis. Power. Technol. 2022, 405, 117544. [Google Scholar] [CrossRef]

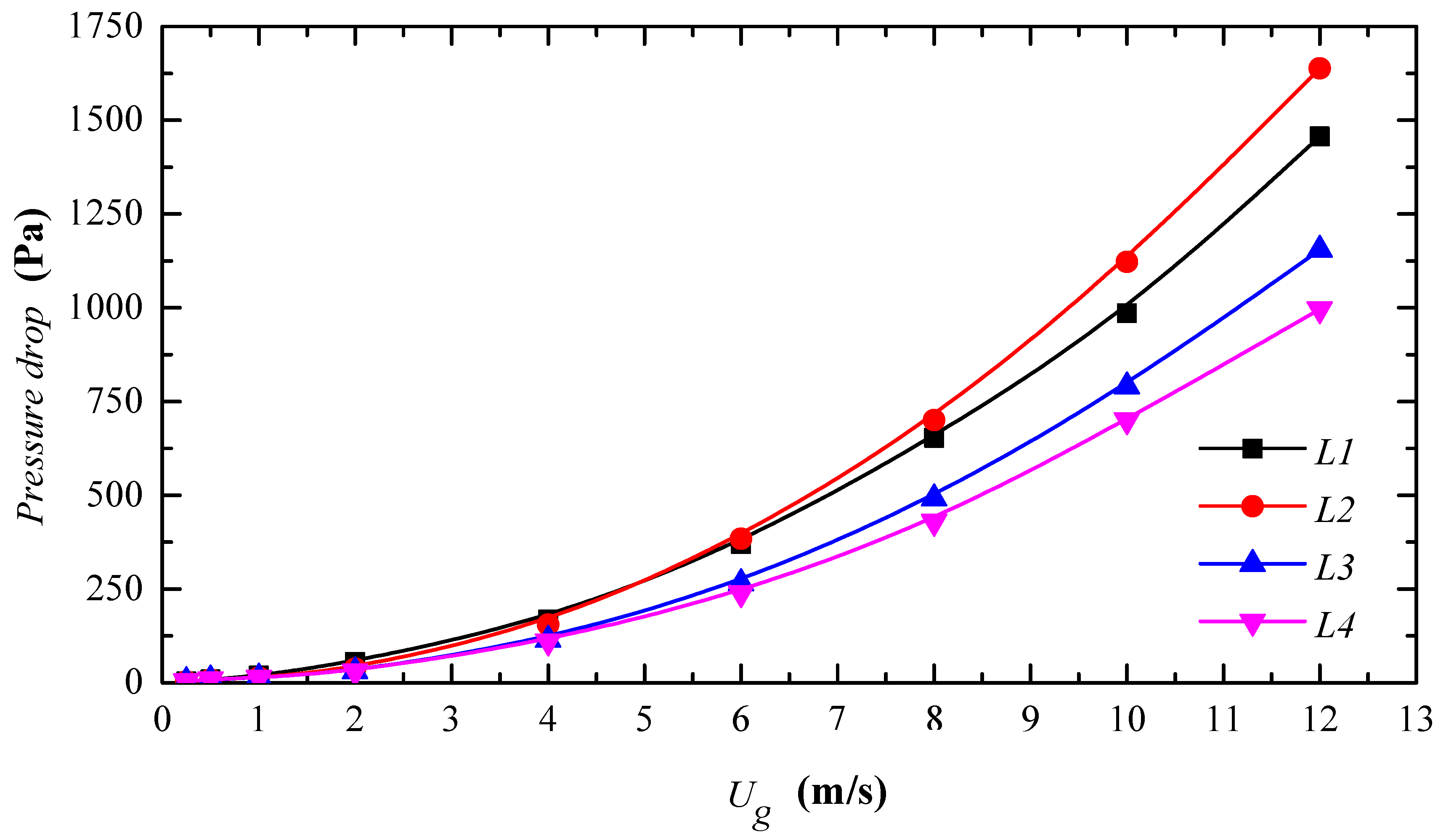
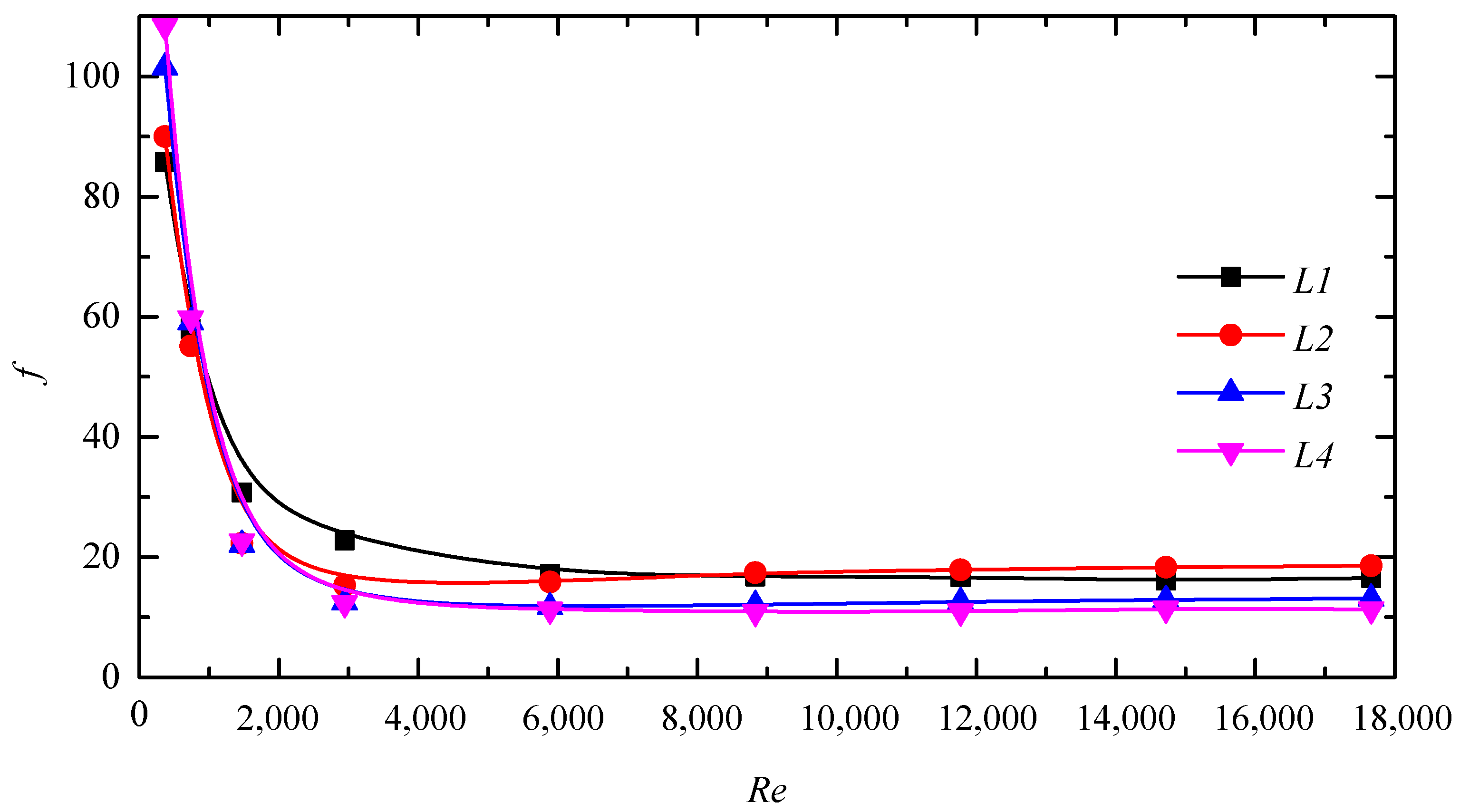


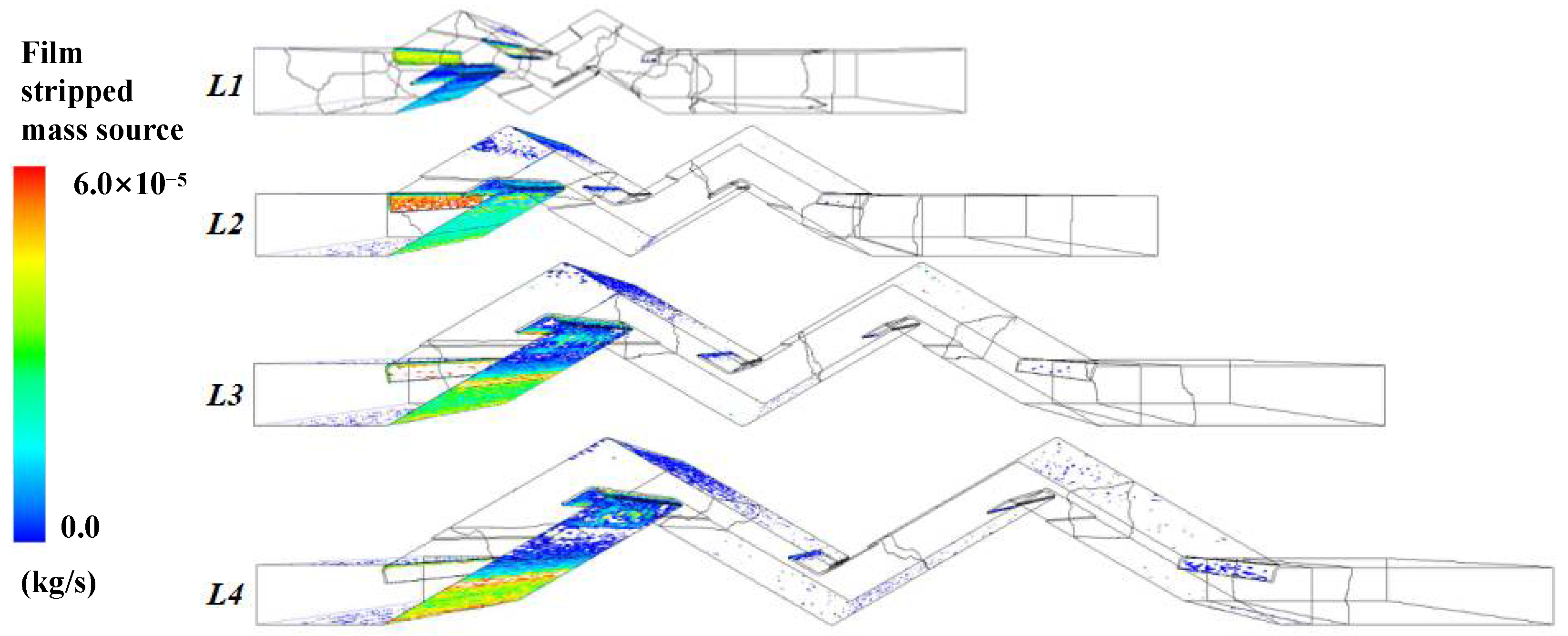
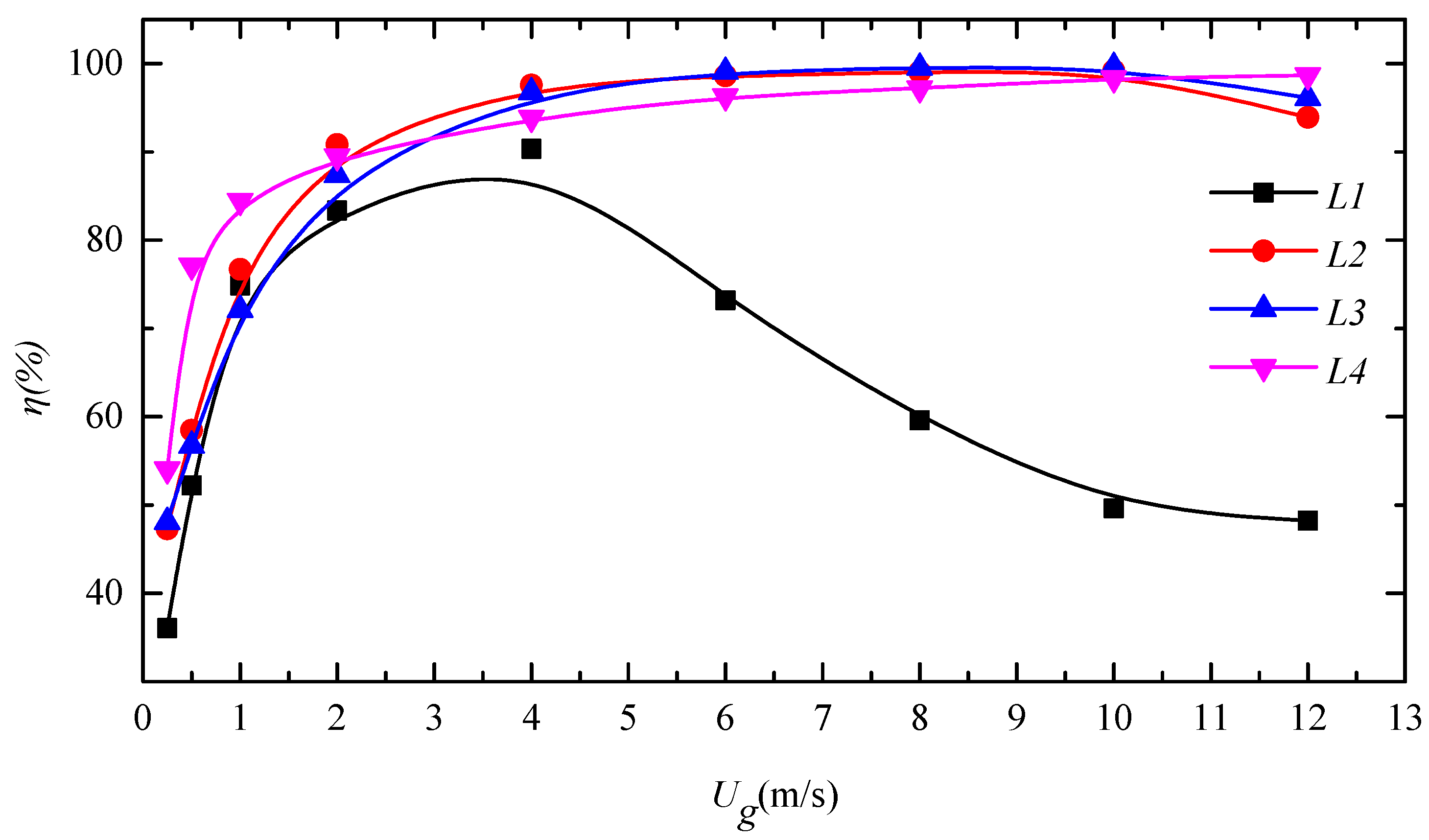
| Case | Class Number N | Wavelength L (mm) | Plate Spacing D (mm) | Overall Length LA (mm) |
|---|---|---|---|---|
| N1 | 1 | 60 | 28.5 | 301 |
| N2 | 2 | 60 | 28.5 | 412 |
| N3 | 3 | 60 | 28.5 | 524 |
| N4 | 4 | 60 | 28.5 | 635 |
| L1 | 2 | 30 | 28.5 | 309 |
| L2 | 2 | 60 | 28.5 | 412 |
| L3 | 2 | 90 | 28.5 | 516 |
| L4 | 2 | 120 | 28.5 | 620 |
| SL. No. | Parameter/Factor | Level |
|---|---|---|
| 1 | Vane thickness TV (mm) | 1.0 |
| 2 | Main plate thickness TM (mm) | 1.5 |
| 3 | Height H (mm) | 685 |
| 4 | Wavelength L (mm) | 30–120 |
| 5 | Plate angle θ (°) | 120° |
| Factor | Level |
|---|---|
| The density of gas flow, ρg (kg/m3) | 1.225 |
| The density of droplets, ρd (kg/m3) | 996 |
| Dynamic viscosity of gas, μg (Pa.s) | 1.7 × 10−5 |
| Dynamic viscosity of droplet, μd (Pa.s) | 9.98 × 10−3 |
| Ug (m/s) | 0~12 |
| Re | 0~2000 |
| Demister | L1 | L2 | L3 | L4 |
|---|---|---|---|---|
| β | −15.163 | −33.892 | −19.961 | −20.171 |
| γ | 0.946 | 0.499 | −0.213 | 0.734 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Z.; Wang, P.; Luo, X.; Huang, J.; Qin, Z.; Mei, J.; Zhao, W. Numerical Investigation on the Influence of Class Number and Wavelength on the Performance of Curved Vane Demisters. Atmosphere 2022, 13, 1711. https://doi.org/10.3390/atmos13101711
Cai Z, Wang P, Luo X, Huang J, Qin Z, Mei J, Zhao W. Numerical Investigation on the Influence of Class Number and Wavelength on the Performance of Curved Vane Demisters. Atmosphere. 2022; 13(10):1711. https://doi.org/10.3390/atmos13101711
Chicago/Turabian StyleCai, Zhen, Pengfei Wang, Xiangyu Luo, Jin Huang, Zhenqi Qin, Jinna Mei, and Wensheng Zhao. 2022. "Numerical Investigation on the Influence of Class Number and Wavelength on the Performance of Curved Vane Demisters" Atmosphere 13, no. 10: 1711. https://doi.org/10.3390/atmos13101711
APA StyleCai, Z., Wang, P., Luo, X., Huang, J., Qin, Z., Mei, J., & Zhao, W. (2022). Numerical Investigation on the Influence of Class Number and Wavelength on the Performance of Curved Vane Demisters. Atmosphere, 13(10), 1711. https://doi.org/10.3390/atmos13101711







