Towards On-Site Implementation of Multi-Step Air Pollutant Index Prediction in Malaysia Industrial Area: Comparing the NARX Neural Network and Support Vector Regression
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Pre-Analysis and Treatment
2.3. Multi-Step Ahead Predictor
2.3.1. The Nonlinear Autoregressive Exogenous (NARX) Neural Network Model
2.3.2. The Support Vector Regression (SVR) Model
2.4. Performance Indicator
3. Results and Discussion
- Is input normalization required?
- Which input parameters are important, and how do they affect the prediction performance?
- How far can reasonable prediction be performed?
- Which model is more robust?
3.1. Input Normalization
3.2. Input Parameters
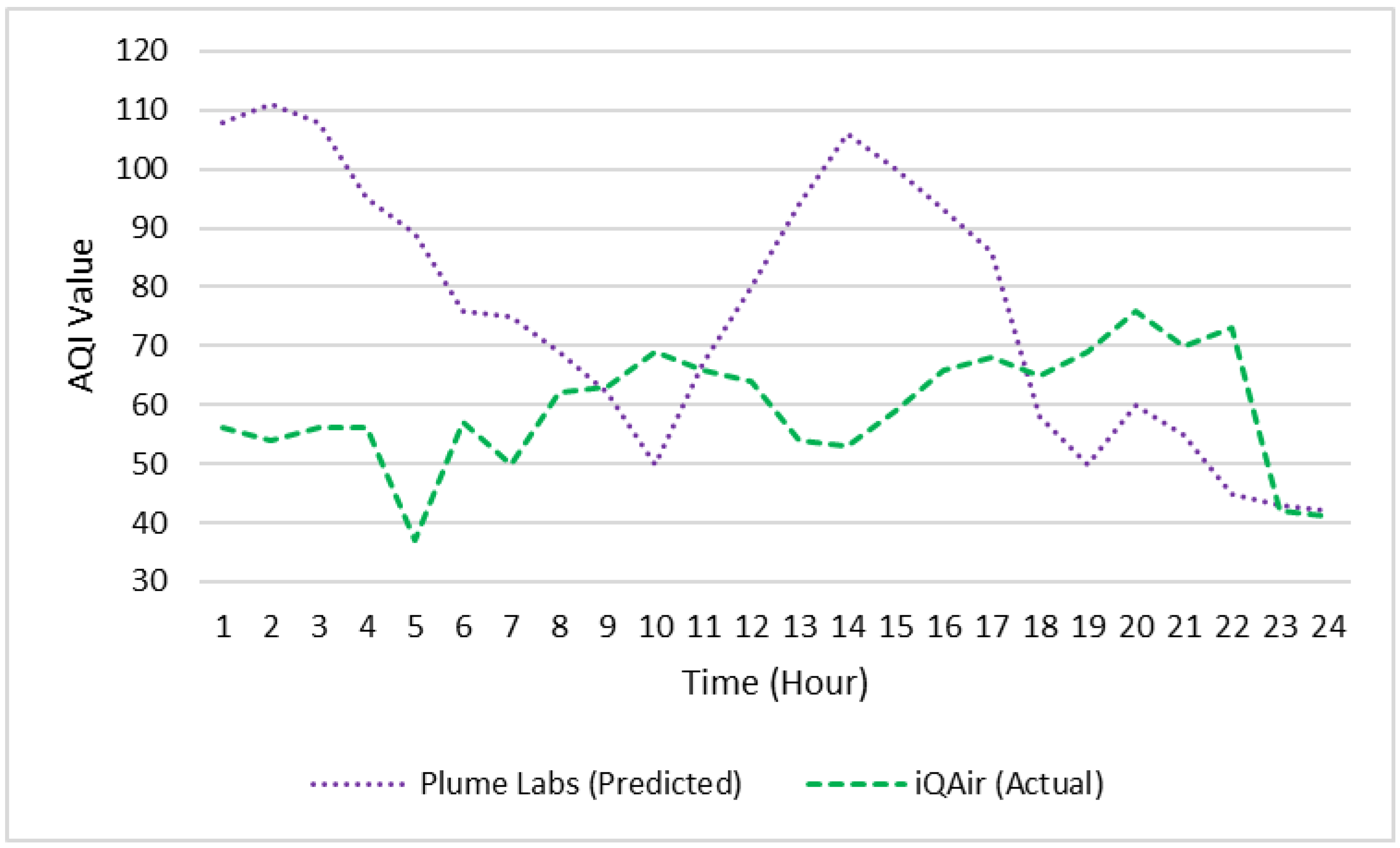
3.3. Practical Predictibality Limit
3.4. Robustness
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Landrigan, P.J. Air Pollution and Health. Lancet Public Health 2017, 2, e4–e5. [Google Scholar] [CrossRef]
- Shaddick, G.; Thomas, M.L.; Mudu, P.; Ruggeri, G.; Gumy, S. Half the World’s Population Are Exposed to Increasing Air Pollution. Npj Clim. Atmos. Sci. 2020, 3, 23. [Google Scholar] [CrossRef]
- Taghizadeh-Hesary, F.; Taghizadeh-Hesary, F. The Impacts of Air Pollution on Health and Economy in Southeast Asia. Energies 2020, 13, 1812. [Google Scholar] [CrossRef]
- Hanafi, N.H.; Hassim, M.H.; Noor, Z.Z.; Ten, J.Y.; Aris, N.M.; Jalil, A.A. Economic Losses Due to Health Hazards Caused by Haze Event in Johor Bahru, Malaysia. In Proceedings of the 7th Conference on Emerging Energy and Process Technology, Johor Bahru, Malaysia, 27–28 November 2018. E3S Web Conf. 2019, 90, 01009. [Google Scholar] [CrossRef]
- Usmani, R.S.A.; Saeed, A.; Abdullahi, A.M.; Pillai, T.R.; Jhanjhi, N.Z.; Hashem, I.A.T. Air Pollution and Its Health Impacts in Malaysia: A Review. Air Qual. Atmos. Health 2020, 13, 1093–1118. [Google Scholar] [CrossRef]
- Tajudin, M.A.B.A.; Khan, M.F.; Mahiyuddin, W.R.W.; Hod, R.; Latif, M.T.; Hamid, A.H.; Rahman, S.A.; Sahani, M. Risk of Concentrations of Major Air Pollutants on the Prevalence of Cardiovascular and Respiratory Diseases in Urbanized Area of Kuala Lumpur, Malaysia. Ecotoxicol. Environ. Saf. 2019, 171, 290–300. [Google Scholar] [CrossRef]
- Ab Manan, N.; Abdul Manaf, M.R.; Hod, R. The Malaysia Haze and Its Health Economic Impact: A Literature Review. Malays. J. Public Health Med. 2018, 18, 38–45. [Google Scholar]
- Shaban, K.B.; Kadri, A.; Rezk, E. Urban Air Pollution Monitoring System with Forecasting Models. IEEE Sens. J. 2016, 16, 2598–2606. [Google Scholar] [CrossRef]
- Lin, K.; Jing, L.; Wang, M.; Qiu, M.; Ji, Z. A Novel Long-Term Air Quality Forecasting Algorithm Based on KNN and NARX. In Proceedings of the ICCSE 2017—12th International Conference on Computer Science and Education, Houston, TX, USA, 22–25 August 2017; pp. 343–348. [Google Scholar] [CrossRef]
- Mohebbi, M.R.; Jashni, A.K.; Jashni, K.; Dehghani, M.; Hadad, K. Short-Term Prediction of Carbon Monoxide Concentration Using Artificial Neural Network (NARX) without Traffic Data: Case Study: Shiraz City. Iran. J. Sci. Technol. Trans. Civ. Eng. 2018, 43, 533–540. [Google Scholar] [CrossRef]
- Kang, G.K.; Gao, J.Z.; Chiao, S.; Lu, S.; Xie, G. Air Quality Prediction: Big Data and Machine Learning Approaches. Int. J. Environ. Sci. Dev. 2018, 9, 8–16. [Google Scholar] [CrossRef]
- Zhou, Y.; Chang, F.J.; Chang, L.C.; Kao, I.F.; Wang, Y.S.; Kang, C.C. Multi-Output Support Vector Machine for Regional Multi-Step-Ahead PM2.5 Forecasting. Sci. Total Environ. 2019, 651, 230–240. [Google Scholar] [CrossRef] [PubMed]
- Gündoğdu, S. Comparison of Static MLP and Dynamic NARX Neural Networks for Forecasting of Atmospheric PM10 and SO2 Concentrations in an Industrial Site of Turkey. Environ. Forensics 2020, 21, 363–374. [Google Scholar] [CrossRef]
- García Nieto, P.J.; Sánchez Lasheras, F.; García-Gonzalo, E.; de Cos Juez, F.J. PM10 Concentration Forecasting in the Metropolitan Area of Oviedo (Northern Spain) Using Models Based on SVM, MLP, VARMA and ARIMA: A Case Study. Sci. Total Environ. 2018, 621, 753–761. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Bai, Y. Research on Prediction of Air Quality Index Based on NARX and SVM. Appl. Mech. Mater. 2014, 602–605, 3580–3584. [Google Scholar] [CrossRef]
- Delavar, M.; Gholami, A.; Shiran, G.; Rashidi, Y.; Nakhaeizadeh, G.; Fedra, K.; Hatefi Afshar, S. A Novel Method for Improving Air Pollution Prediction Based on Machine Learning Approaches: A Case Study Applied to the Capital City of Tehran. ISPRS Int. J. Geo-Inf. 2019, 8, 99. [Google Scholar] [CrossRef]
- Kumar, V.; Pal, Y.; Tripathi, M.M. SVM Tuned NARX Method for Wind Speed Power Prediction in Electricity Generation. In Proceedings of the 8th IEEE Power India International Conference (PIICON 2018), Kurukshetra, India, 10–12 December 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Leong, W.C.; Kelani, R.O.; Ahmad, Z. Prediction of Air Pollution Index (API) Using Support Vector Machine (SVM). J. Environ. Chem. Eng. 2019, 8, 103208. [Google Scholar] [CrossRef]
- Jiang, X.; Wei, P.; Luo, Y.; Li, Y. Air Pollutant Concentration Prediction Based on a CEEMDAN-FE-BiLSTM Model. Atmosphere 2021, 12, 1452. [Google Scholar] [CrossRef]
- Muthukumar, P.; Nagrecha, K.; Comer, D.; Calvert, C.F.; Amini, N.; Holm, J.; Pourhomayoun, M. PM2.5 Air Pollution Prediction through Deep Learning Using Multisource Meteorological, Wildfire, and Heat Data. Atmosphere 2022, 13, 822. [Google Scholar] [CrossRef]
- He, Z.; Guo, Q.; Wang, Z.; Li, X. Prediction of Monthly PM2.5 Concentration in Liaocheng in China Employing Artificial Neural Network. Atmosphere 2022, 13, 1221. [Google Scholar] [CrossRef]
- Wei, F.; Zhu, R.; Jerry Chun, W.L. An air quality prediction model based on improved Vanilla LSTM with multichannel input and multiroute output. Expert Syst. Appl. 2022, 211, 118422. [Google Scholar] [CrossRef]
- Raffee, A.F.; Rahmat, S.N.; Hamid, H.A.; Jaffar, M.I. The Behavior of Particulate Matter (PM10) Concentrations at Industrial Sites in Malaysia. Int. J. Integr. Eng. 2019, 11, 214–222. [Google Scholar] [CrossRef]
- Azid, A.; Juahir, H.; Toriman, M.E.; Endut, A.; Kamarudin, M.K.A.; Rahman, M.N.A.; Hasnam, C.N.C.; Saudi, A.S.M.; Yunus, K. Source Apportionment of Air Pollution: A Case Study in Malaysia. J. Teknol. 2015, 72, 83–88. [Google Scholar] [CrossRef]
- Sentian, J.; Herman, F.; Yih, C.Y.; Hian Wui, J.C. Long-Term Air Pollution Trend Analysis in Malaysia. Int. J. Environ. Impacts Manag. Mitig. Recover. 2019, 2, 309–324. [Google Scholar] [CrossRef]
- Mohamed Noor, N.; Al Bakri Abdullah, M.M.; Yahaya, A.S.; Ramli, N.A. Filling Missing Data Using Interpolation Methods: Study on the Effect of Fitting Distribution. Key Eng. Mater. 2014, 594–595, 889–895. [Google Scholar] [CrossRef]
- Mohamed Noor, N.; Al Bakri Abdullah, M.M.; Yahaya, A.S.; Ramli, N.A. Comparison of Linear Interpolation Method and Mean Method to Replace the Missing Values in Environmental Data Set. Mater. Sci. Forum 2015, 803, 278–281. [Google Scholar] [CrossRef]
- Fitriyah, H.; Budi, A.S. Outlier Detection in Object Counting Based on Hue and Distance Transform Using Median Absolute Deviation (MAD). In Proceedings of the 2019 4th International Conference on Sustainable Information Engineering and Technology (SIET 2019), Lombok, Indonesia, 28–30 September 2019; pp. 217–222. [Google Scholar] [CrossRef]
- Mamat, M.; Samad, S.A. Comparison of Iterative and Direct Approaches for Multi-Steps Ahead Time Series Forecasting Using Adaptive Hybrid-RBF Neural Network. In Proceedings of the IEEE Region 10 Annual International Conference, Fukuoka, Japan, 21–24 November 2010; pp. 2332–2337. [Google Scholar] [CrossRef]
- López Pouso, Ó.; Jumaniyazov, N. Direct versus iterative methods for forward-backward diffusion equations. Numerical comparisons. SeMA 2021, 78, 271–286. [Google Scholar] [CrossRef]
- Boussaada, Z.; Curea, O.; Remaci, A.; Camblong, H.; Bellaaj, N.M. A Nonlinear Autoregressive Exogenous (NARX) Neural Network Model for the Prediction of the Daily Direct Solar Radiation. Energies 2018, 11, 620. [Google Scholar] [CrossRef]
- Mustakim, R.; Mamat, M. The Nonlinear Autoregressive Exogenous Neural Network Performance in Predicting Malaysia Air Pollutant Index. Trans. Sci. Technol. 2021, 8, 305–310. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-Vector Network. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Drucker, H.; Surges, C.J.C.; Kaufman, L.; Smola, A.; Vapnik, V. Support Vector Regression Machines. Adv. Neural Inf. Process. Syst. 1997, 1, 155–161. [Google Scholar]
- Falocchi, M.; Zardi, D.; Giovannini, L. Meteorological Normalization of NO2 Concentrations in the Province of Bolzano (Italian Alps). Atmos. Environ. 2021, 246, 118048. [Google Scholar] [CrossRef]
- Bengio, Y.; Goodfellow, I.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Platt, J.A.; Penny, S.G.; Smith, T.A.; Chen, T.-C.; Abarbanel, H.D.I. A Systematic Exploration of Reservoir Computing for Forecasting Complex Spatiotemporal Dynamics. Neural Netw. 2022, 153, 530–552. [Google Scholar] [CrossRef] [PubMed]
- Passalis, N.; Tefas, A.; Kanniainen, J.; Gabbouj, M.; Iosifidis, A. Deep Adaptive Input Normalization for Time Series Forecasting. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 3760–3765. [Google Scholar] [CrossRef]
- Passalis, N.; Kanniainen, J.; Gabbouj, M.; Iosifidis, A.; Tefas, A. Forecasting Financial Time Series Using Robust Deep Adaptive Input Normalization. Signal Process. Syst. 2021, 93, 1235–1251. [Google Scholar] [CrossRef]
- Gupta, M.; Wadhvani, R.; Rasool, A. Real-Time Change-Point Detection: A Deep Neural Network-Based Adaptive Approach for Detecting Changes in Multivariate Time Series Data. Expert Syst. Appl. 2022, 209, 118260. [Google Scholar] [CrossRef]
- Djerioui, M.; Brik, Y.; Ladjal, M.; Attallah, B. Neighborhood Component Analysis and Support Vector Machines for Heart Disease Prediction. Ing. Yst. d’Inform. 2019, 24, 591–595. [Google Scholar] [CrossRef]
- Wang, Y.; Han, L. Adaptive Time Series Prediction and Recommendation. Inf. Process. Manag. 2021, 58, 102494. [Google Scholar] [CrossRef]








| 2018 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | NO2 | PM10 | PM2.5 | SO2 | CO | O3 | WD. | WS | T | API | |
| TTDI Jaya | Correlation | 0.185 | 0.549 | 0.552 | 0.050 | 0.192 | 0.111 | −0.045 | −0.052 | 0.154 | 1.000 |
| Min | 0.000 | 1.009 | 0.089 | 0.000 | 0.104 | 0.000 | 0.000 | 0.000 | 20.217 | 27.525 | |
| Max | 0.070 | 168.490 | 153.800 | 0.030 | 3.510 | 0.140 | 359.870 | 7.920 | 36.220 | 154.000 | |
| Larkin | Correlation | 0.304 | 0.586 | 0.601 | 0.158 | 0.180 | 0.115 | 0.026 | −0.021 | 0.060 | 1.000 |
| Min | 0.000 | 0.718 | 0.120 | 0.000 | 0.050 | 0.000 | 0.000 | 0.000 | 21.423 | 12.456 | |
| Max | 0.070 | 172.660 | 163.550 | 0.020 | 2.760 | 0.150 | 359.970 | 22.790 | 35.390 | 91.760 | |
| Pasir Gudang | Correlation | 0.323 | 0.579 | 0.576 | 0.319 | 0.189 | 0.093 | 0.084 | −0.075 | 0.224 | 1.000 |
| Min | 0.000 | 1.340 | 0.112 | 0.000 | 0.283 | 0.000 | 0.000 | 0.000 | 22.505 | 16.000 | |
| Max | 0.077 | 199.950 | 181.450 | 0.020 | 4.230 | 0.120 | 359.890 | 5.580 | 35.920 | 101.000 | |
| 2019 | |||||||||||
| Parameter | NO2 | PM10 | PM2.5 | SO2 | CO | O3 | WD. | WS | T | API | |
| TTDI Jaya | Correlation | 0.084 | 0.511 | 0.533 | −0.010 | 0.249 | 0.036 | −0.018 | 0.026 | 0.068 | 1.000 |
| Min | 0.000 | 2.315 | 0.046 | 0.000 | 0.044 | 0.000 | 0.000 | 0.000 | 21.282 | 33.000 | |
| Max | 0.060 | 264.640 | 252.310 | 0.020 | 3.200 | 0.160 | 359.930 | 5.950 | 36.270 | 221.000 | |
| Larkin | Correlation | 0.354 | 0.674 | 0.686 | 0.167 | 0.280 | 0.148 | −0.080 | −0.187 | 0.136 | 1.000 |
| Min | 0.000 | 3.728 | 0.090 | 0.000 | 0.052 | 0.000 | 0.000 | 0.000 | 21.843 | 26.000 | |
| Max | 0.070 | 294.900 | 264.720 | 0.020 | 3.250 | 0.120 | 359.950 | 4.750 | 35.280 | 171.000 | |
| Pasir Gudang | Correlation | 0.399 | 0.679 | 0.695 | 0.458 | 0.261 | 0.137 | −0.037 | −0.017 | 0.186 | 1.000 |
| Min | 0.000 | 1.1940 | 0.0850 | 0.000 | 0.077 | 0.000 | 0.000 | 0.000 | 23.897 | 18.000 | |
| Max | 0.070 | 173.90 | 161.630 | 0.010 | 2.900 | 0.110 | 359.940 | 6.250 | 37.550 | 143.00 | |
| Monitoring Station | NARX | SVR | ||||||
|---|---|---|---|---|---|---|---|---|
| Non-Normalized | Normalized | Non-Normalized | Normalized | |||||
| RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | |
| Pasir Gudang | 1.1800 | 0.9922 | 0.1282 | 0.9923 | 0.7106 | 0.9960 | 0.0787 | 0.9959 |
| Larkin | 1.2322 | 0.9883 | 0.1565 | 0.9886 | 0.7135 | 0.9948 | 0.0913 | 0.9948 |
| TTDI Jaya | 1.5797 | 0.9877 | 0.1842 | 0.9888 | 0.8914 | 0.9938 | 0.1025 | 0.9938 |
| Predictor | Monitoring Station | All Parameters | Relevant Parameters | ||
|---|---|---|---|---|---|
| RMSE | R2 | RMSE | R2 | ||
| NARX | Pasir Gudang | 1.1800 | 0.9922 | 1.1926 | 0.9922 |
| TTDI Jaya | 1.5797 | 0.9877 | 1.3186 | 0.9898 | |
| SVR | Pasir Gudang | 0.7106 | 0.9960 | 0.7237 | 0.9959 |
| TTDI Jaya | 0.8914 | 0.9938 | 0.8864 | 0.9939 | |
| Step Ahead Prediction | Pasir Gudang | Larkin | TTDI Jaya | |||
|---|---|---|---|---|---|---|
| NARX | SVR | NARX | SVR | NARX | SVR | |
| 1 | 0.9923 | 0.9959 | 0.9886 | 0.9948 | 0.9888 | 0.9938 |
| 2 | 0.9878 | 0.9909 | 0.9815 | 0.9883 | 0.9829 | 0.9866 |
| 3 | 0.9808 | 0.9841 | 0.9737 | 0.9794 | 0.9645 | 0.9771 |
| 4 | 0.9738 | 0.9758 | 0.9664 | 0.9689 | 0.9661 | 0.9676 |
| 5 | 0.9656 | 0.9671 | 0.9556 | 0.9570 | 0.9560 | 0.9564 |
| 6 | 0.9578 | 0.9573 | 0.9469 | 0.9443 | 0.9433 | 0.9446 |
| 7 | 0.9508 | 0.9474 | 0.9383 | 0.9308 | 0.9376 | 0.9323 |
| 8 | 0.9444 | 0.9366 | 0.9248 | 0.9171 | 0.9301 | 0.9196 |
| 9 | 0.9341 | 0.9260 | 0.9184 | 0.9024 | 0.9214 | 0.9067 |
| 10 | 0.9236 | 0.9151 | 0.9085 | 0.8877 | 0.9125 | 0.8934 |
| 11 | 0.9132 | 0.9042 | 0.8945 | 0.8731 | 0.9016 | 0.8789 |
| 12 | 0.9052 | 0.8924 | 0.8878 | 0.8577 | 0.8922 | 0.8664 |
| 13 | 0.8919 | 0.8812 | 0.8595 | 0.8439 | 0.8811 | 0.8526 |
| 14 | 0.8899 | 0.8699 | 0.8689 | 0.8278 | 0.8690 | 0.8407 |
| 15 | 0.8848 | 0.8586 | 0.8556 | 0.8141 | 0.8658 | 0.8269 |
| 16 | 0.8707 | 0.8474 | 0.8407 | 0.7994 | 0.8646 | 0.8142 |
| 17 | 0.8630 | 0.8371 | 0.8106 | 0.7831 | 0.8549 | 0.8002 |
| 18 | 0.8471 | 0.8262 | 0.8215 | 0.7707 | 0.8356 | 0.7887 |
| 19 | 0.8097 | 0.8159 | 0.8090 | 0.7562 | 0.7989 | 0.7757 |
| 20 | 0.8266 | 0.8050 | 0.7969 | 0.7429 | 0.8068 | 0.7630 |
| 21 | 0.8194 | 0.7938 | 0.7585 | 0.7306 | 0.7908 | 0.7529 |
| 22 | 0.7968 | 0.7835 | 0.7276 | 0.7164 | 0.7766 | 0.7393 |
| 23 | 0.7940 | 0.7721 | 0.6857 | 0.7030 | 0.7537 | 0.7258 |
| 24 | 0.7745 | 0.7600 | 0.7332 | 0.6881 | 0.7381 | 0.7120 |
| Step Ahead Prediction | Pasir GUDANG | Larkin | TTDI Jaya | |||
|---|---|---|---|---|---|---|
| NARX | SVR | NARX | SVR | NARX | SVR | |
| 1 | 1.1800 | 0.7106 | 1.2322 | 0.7135 | 1.5797 | 0.8914 |
| 2 | 1.5155 | 1.0731 | 1.5780 | 1.0718 | 2.2651 | 1.3052 |
| 3 | 2.0879 | 1.4193 | 1.8970 | 1.4207 | 2.3282 | 1.6941 |
| 4 | 2.2622 | 1.7528 | 2.2183 | 1.7512 | 2.6239 | 2.0248 |
| 5 | 2.6014 | 2.0468 | 2.5332 | 2.0363 | 2.8704 | 2.3275 |
| 6 | 2.8877 | 2.3319 | 2.7644 | 2.3160 | 2.9995 | 2.6360 |
| 7 | 3.3092 | 2.5902 | 2.9673 | 2.5807 | 3.5465 | 2.9113 |
| 8 | 3.4751 | 2.8384 | 3.1963 | 2.8220 | 3.4047 | 3.1732 |
| 9 | 3.9305 | 3.0722 | 3.3331 | 3.0566 | 3.7174 | 3.4352 |
| 10 | 4.4989 | 3.2913 | 3.6986 | 3.2731 | 3.7511 | 3.6636 |
| 11 | 4.7080 | 3.5036 | 3.8684 | 3.4839 | 4.0356 | 3.9097 |
| 12 | 4.8628 | 3.7186 | 4.0434 | 3.6825 | 4.2135 | 4.1243 |
| 13 | 5.0391 | 3.9023 | 4.3225 | 3.8701 | 4.5509 | 4.3245 |
| 14 | 5.3038 | 4.0881 | 4.6690 | 4.0409 | 4.4811 | 4.5119 |
| 15 | 5.6529 | 4.2832 | 4.9659 | 4.2230 | 4.7691 | 4.7013 |
| 16 | 5.9413 | 4.4577 | 5.1250 | 4.3928 | 4.7334 | 4.8971 |
| 17 | 5.7786 | 4.6249 | 5.5615 | 4.5542 | 5.3125 | 5.0703 |
| 18 | 6.2582 | 4.8255 | 5.5849 | 4.7254 | 5.1081 | 5.2186 |
| 19 | 6.5032 | 4.9927 | 5.5537 | 4.8777 | 5.4991 | 5.4078 |
| 20 | 7.1241 | 5.1766 | 6.2972 | 5.0167 | 5.6499 | 5.5586 |
| 21 | 7.0589 | 5.3722 | 6.0056 | 5.2104 | 5.8457 | 5.7227 |
| 22 | 7.0047 | 5.5242 | 6.6550 | 5.3780 | 6.4397 | 5.9267 |
| 23 | 7.5341 | 5.7317 | 7.5295 | 5.5276 | 6.2488 | 6.1325 |
| 24 | 8.0917 | 5.9580 | 7.2495 | 5.7433 | 6.5816 | 6.4285 |
| Month | Predictor | Step Ahead | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| JAN | NARX | 1.5012 | 2.0192 | 2.5765 | 3.0516 | 3.6440 | 3.9949 | 4.3751 | 4.863 |
| SVR | 1.0083 | 1.5452 | 2.0231 | 2.4793 | 2.9155 | 3.3522 | 3.7866 | 4.1557 | |
| FEB | NARX | 1.6690 | 2.1319 | 2.5442 | 2.9640 | 3.3068 | 3.5686 | 3.9424 | 4.1698 |
| SVR | 1.0428 | 1.6669 | 2.1590 | 2.5811 | 2.9831 | 3.3427 | 3.6541 | 3.9496 | |
| MAR | NARX | 1.0146 | 1.2100 | 1.4121 | 1.5875 | 1.7096 | 1.8502 | 2.1070 | 2.1575 |
| SVR | 0.5847 | 0.8097 | 1.0146 | 1.2127 | 1.4194 | 1.5663 | 1.6991 | 1.8356 | |
| APR | NARX | 1.6789 | 1.9057 | 2.0765 | 2.2994 | 2.4587 | 2.6509 | 2.8165 | 2.9065 |
| SVR | 0.6792 | 1.0120 | 1.3578 | 1.6724 | 2.0073 | 2.2806 | 2.5263 | 2.7356 | |
| MAY | NARX | 1.1885 | 1.4758 | 1.8475 | 2.1461 | 2.4324 | 2.5533 | 2.9494 | 3.1601 |
| SVR | 0.7183 | 1.0866 | 1.4484 | 1.7961 | 2.1204 | 2.4282 | 2.7230 | 2.9844 | |
| JUNE | NARX | 1.2823 | 1.6012 | 1.8989 | 2.1201 | 2.3598 | 2.6435 | 2.7535 | 2.9114 |
| SVR | 0.7864 | 1.1608 | 1.5175 | 1.8294 | 2.0734 | 2.3118 | 2.5293 | 2.7184 | |
| JULY | NARX | 0.8256 | 0.9408 | 1.0235 | 1.1289 | 1.1987 | 1.3069 | 1.4257 | 1.5252 |
| SVR | 0.4587 | 0.5814 | 0.7260 | 0.8476 | 0.9831 | 1.0990 | 1.2257 | 1.3482 | |
| AUG | NARX | 0.9711 | 1.0320 | 1.1474 | 1.2873 | 1.4461 | 1.5430 | 1.6986 | 1.8528 |
| SVR | 0.4687 | 0.6090 | 0.7696 | 0.9259 | 1.0837 | 1.2512 | 1.4106 | 1.5599 | |
| SEPT | NARX | 5.7433 | 9.0577 | 7.8669 | 10.487 | 11.1451 | 13.6487 | 14.762 | 15.1999 |
| SVR | 1.0099 | 1.9108 | 2.8232 | 3.7294 | 4.6175 | 5.4374 | 6.2017 | 6.9276 | |
| OCT | NARX | 2.2683 | 2.8434 | 3.3073 | 3.3148 | 3.5509 | 3.6516 | 3.7713 | 3.9953 |
| SVR | 1.3716 | 2.3373 | 3.0473 | 3.4808 | 3.7054 | 3.8332 | 3.9658 | 4.1094 | |
| NOV | NARX | 2.0890 | 2.2234 | 3.280 | 3.4581 | 3.8042 | 3.6561 | 4.9604 | 4.9131 |
| SVR | 0.7519 | 1.2351 | 1.7034 | 2.1482 | 2.5528 | 2.9345 | 3.2891 | 3.6206 | |
| DEC | NARX | 1.8162 | 4.4456 | 4.2650 | 3.7252 | 4.7170 | 5.2585 | 6.6709 | 6.5395 |
| SVR | 1.1349 | 1.8912 | 2.5899 | 3.2491 | 3.8709 | 4.4628 | 5.0284 | 5.6076 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mustakim, R.; Mamat, M.; Yew, H.T. Towards On-Site Implementation of Multi-Step Air Pollutant Index Prediction in Malaysia Industrial Area: Comparing the NARX Neural Network and Support Vector Regression. Atmosphere 2022, 13, 1787. https://doi.org/10.3390/atmos13111787
Mustakim R, Mamat M, Yew HT. Towards On-Site Implementation of Multi-Step Air Pollutant Index Prediction in Malaysia Industrial Area: Comparing the NARX Neural Network and Support Vector Regression. Atmosphere. 2022; 13(11):1787. https://doi.org/10.3390/atmos13111787
Chicago/Turabian StyleMustakim, Rosminah, Mazlina Mamat, and Hoe Tung Yew. 2022. "Towards On-Site Implementation of Multi-Step Air Pollutant Index Prediction in Malaysia Industrial Area: Comparing the NARX Neural Network and Support Vector Regression" Atmosphere 13, no. 11: 1787. https://doi.org/10.3390/atmos13111787
APA StyleMustakim, R., Mamat, M., & Yew, H. T. (2022). Towards On-Site Implementation of Multi-Step Air Pollutant Index Prediction in Malaysia Industrial Area: Comparing the NARX Neural Network and Support Vector Regression. Atmosphere, 13(11), 1787. https://doi.org/10.3390/atmos13111787







