Solar Signature in Climate Indices
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. Methods
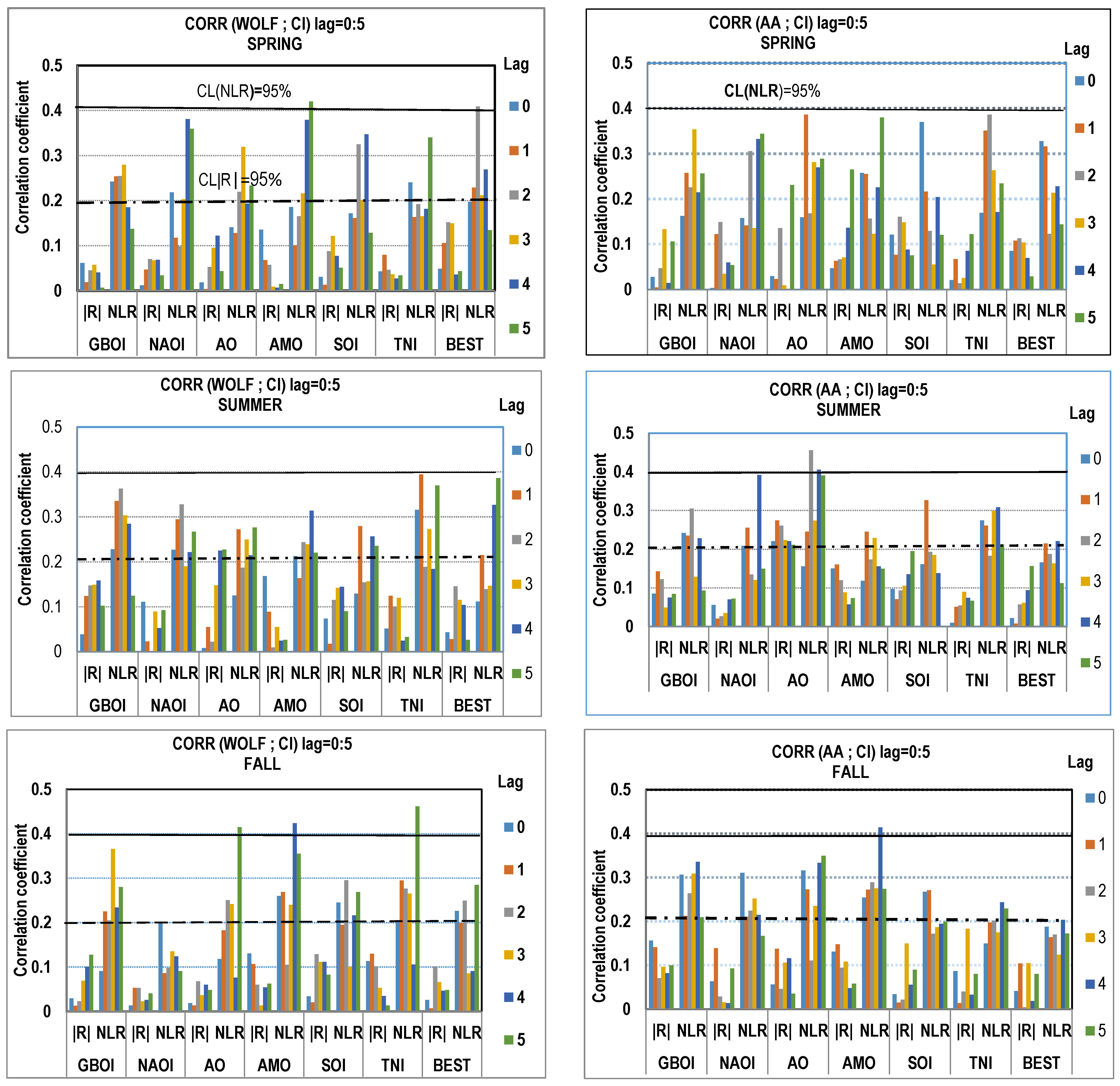
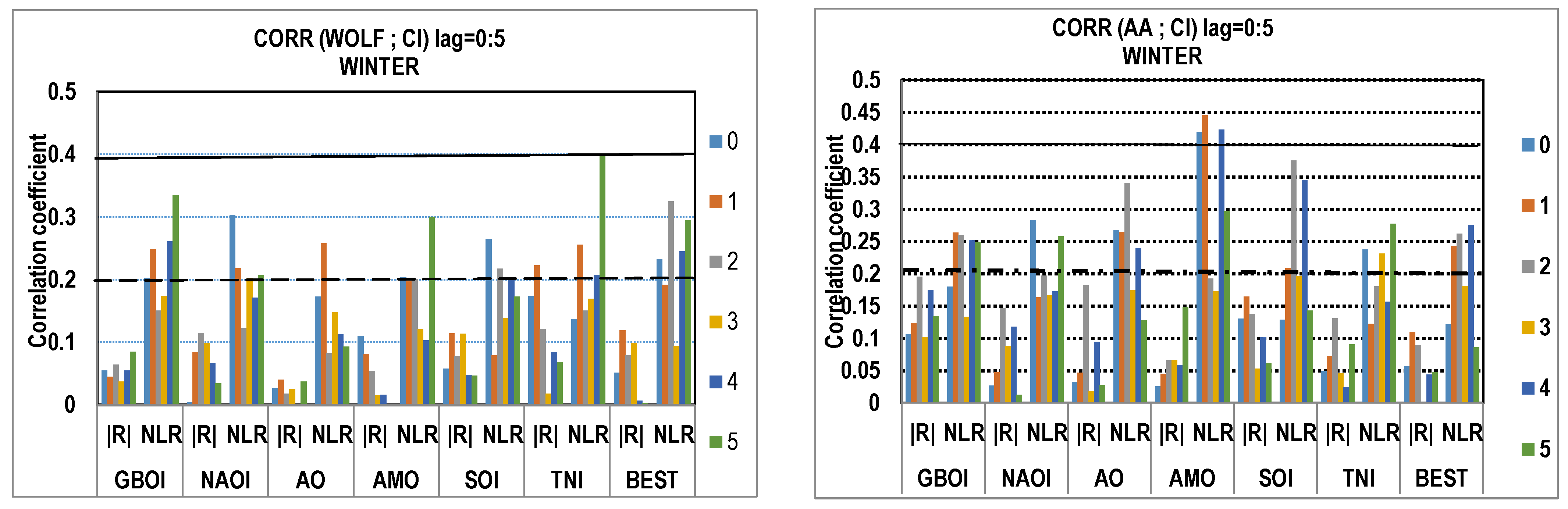
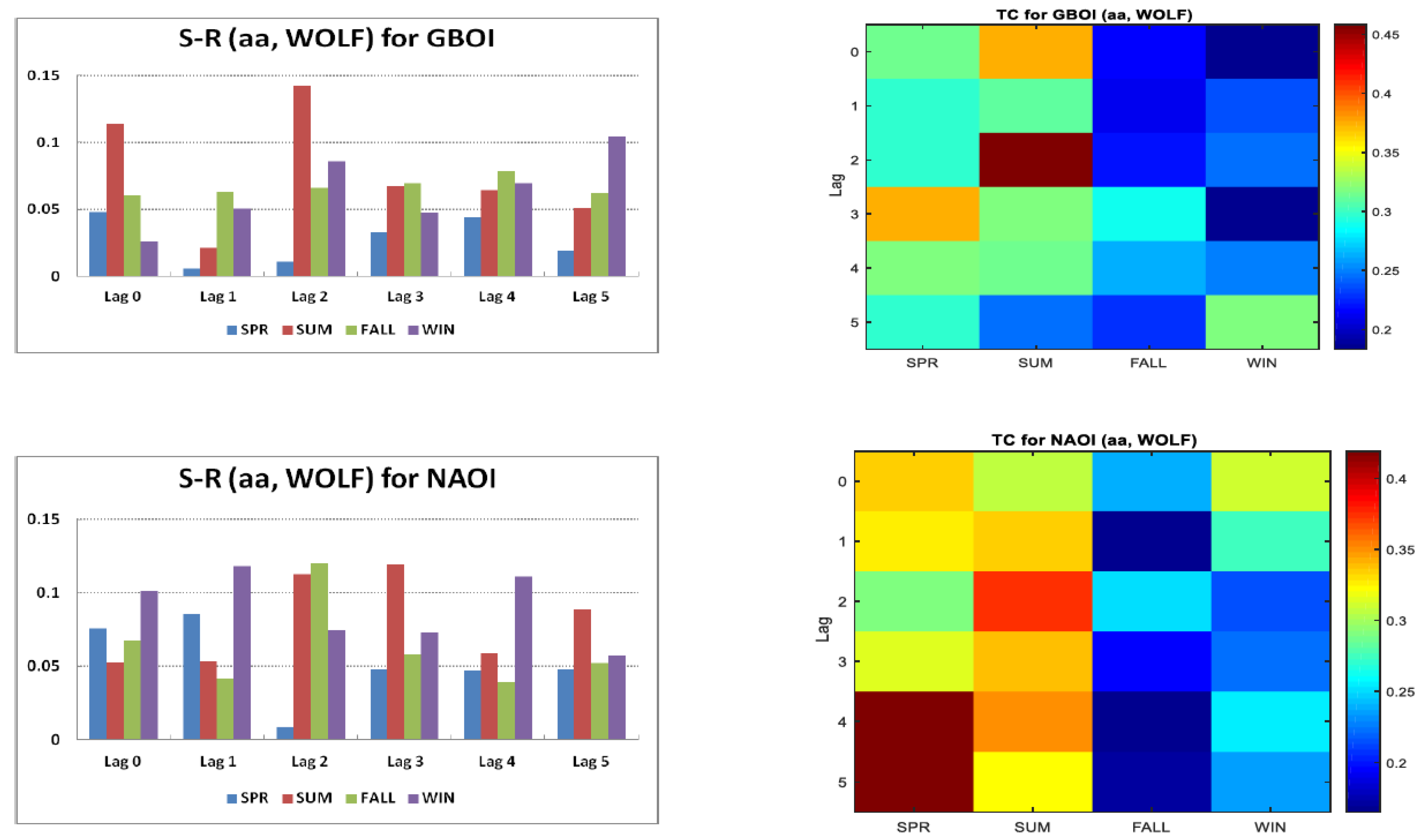
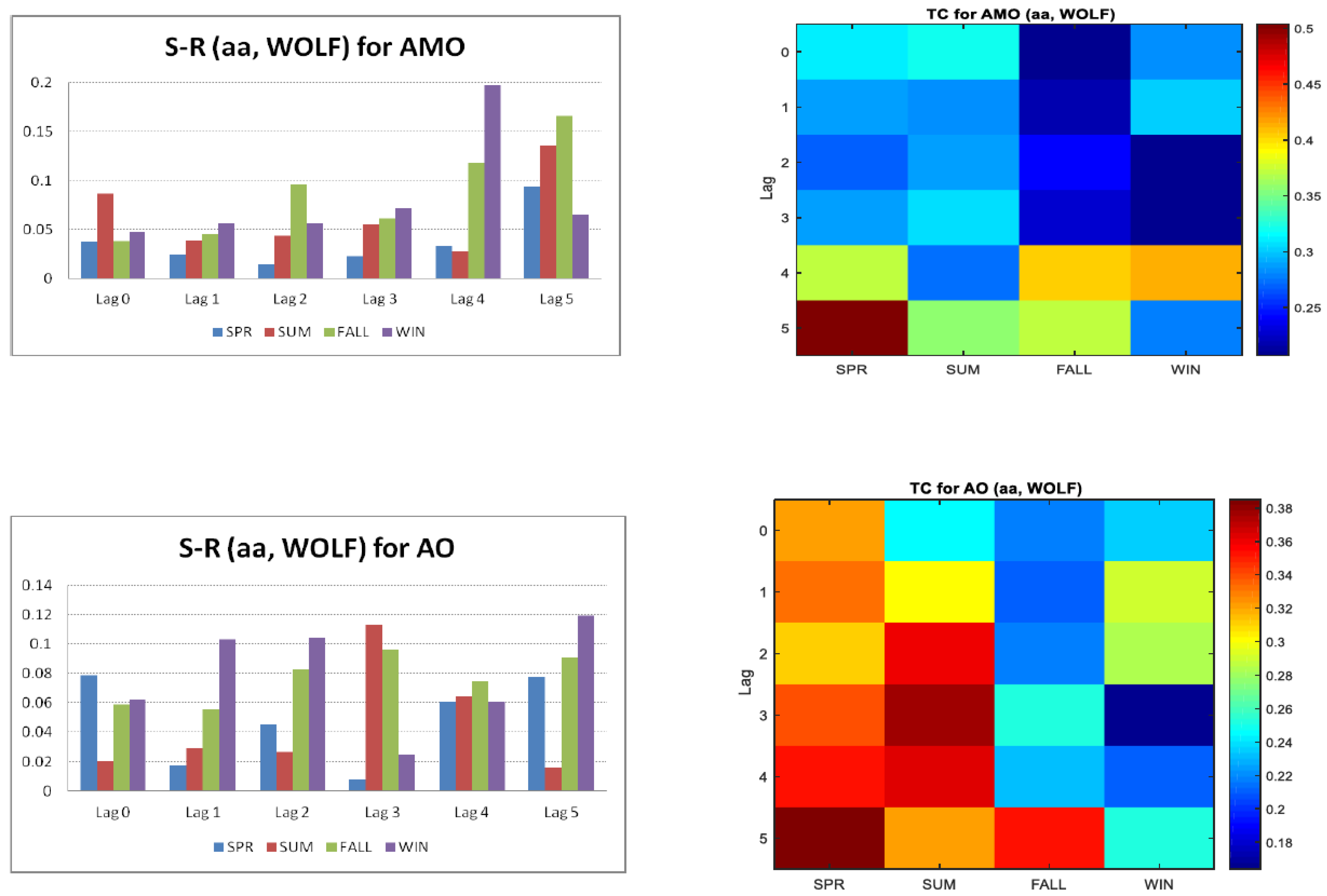
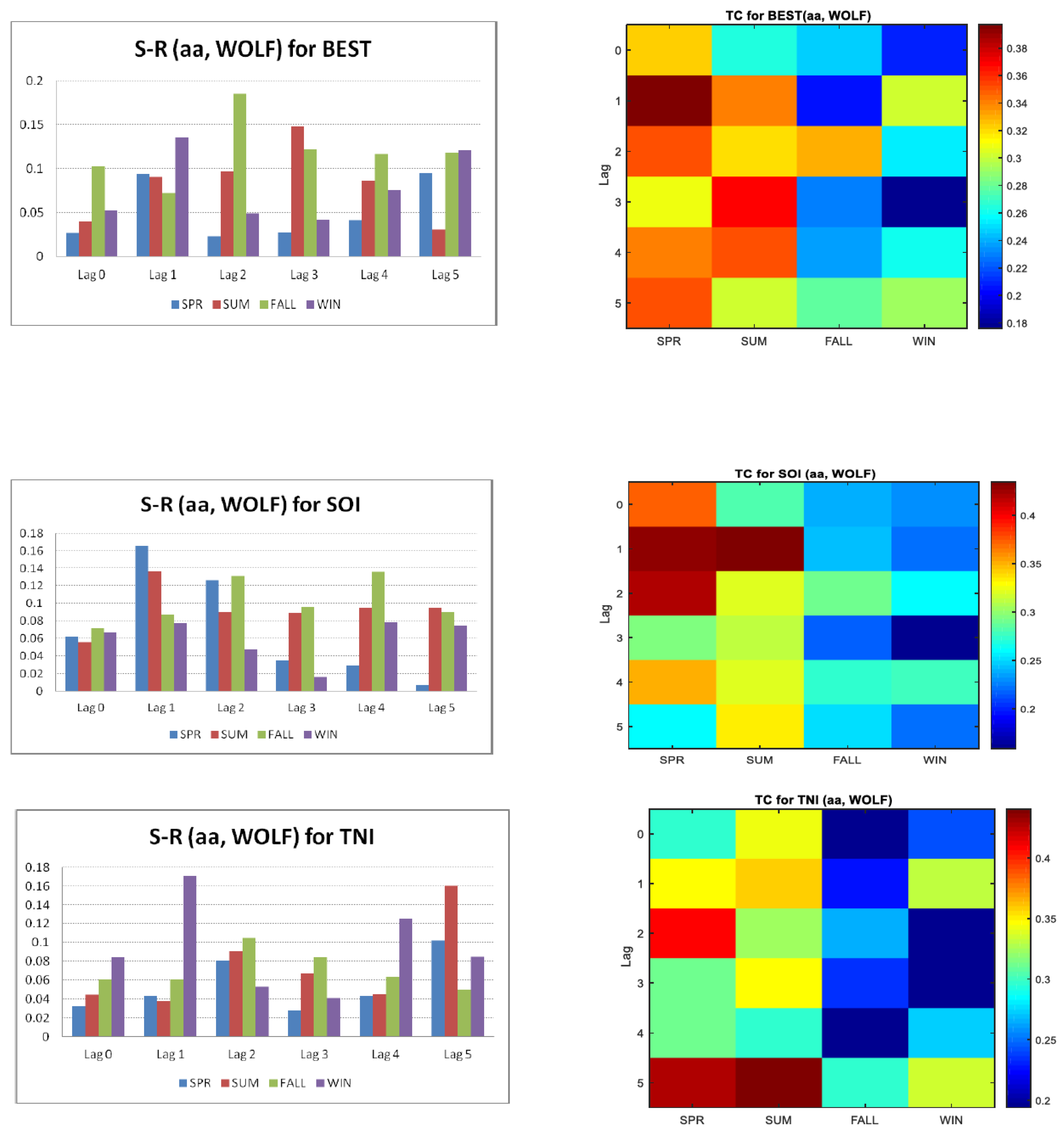
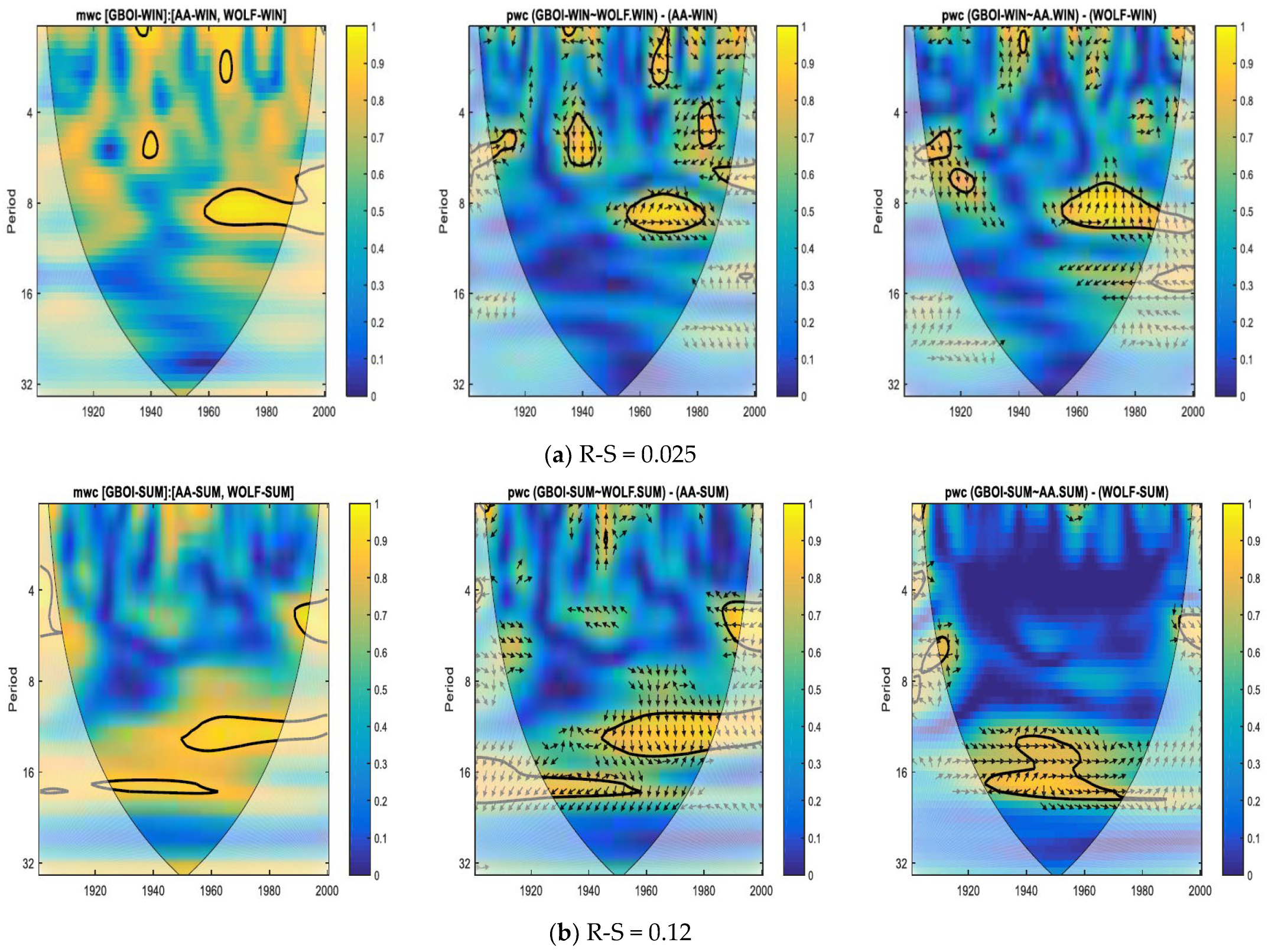
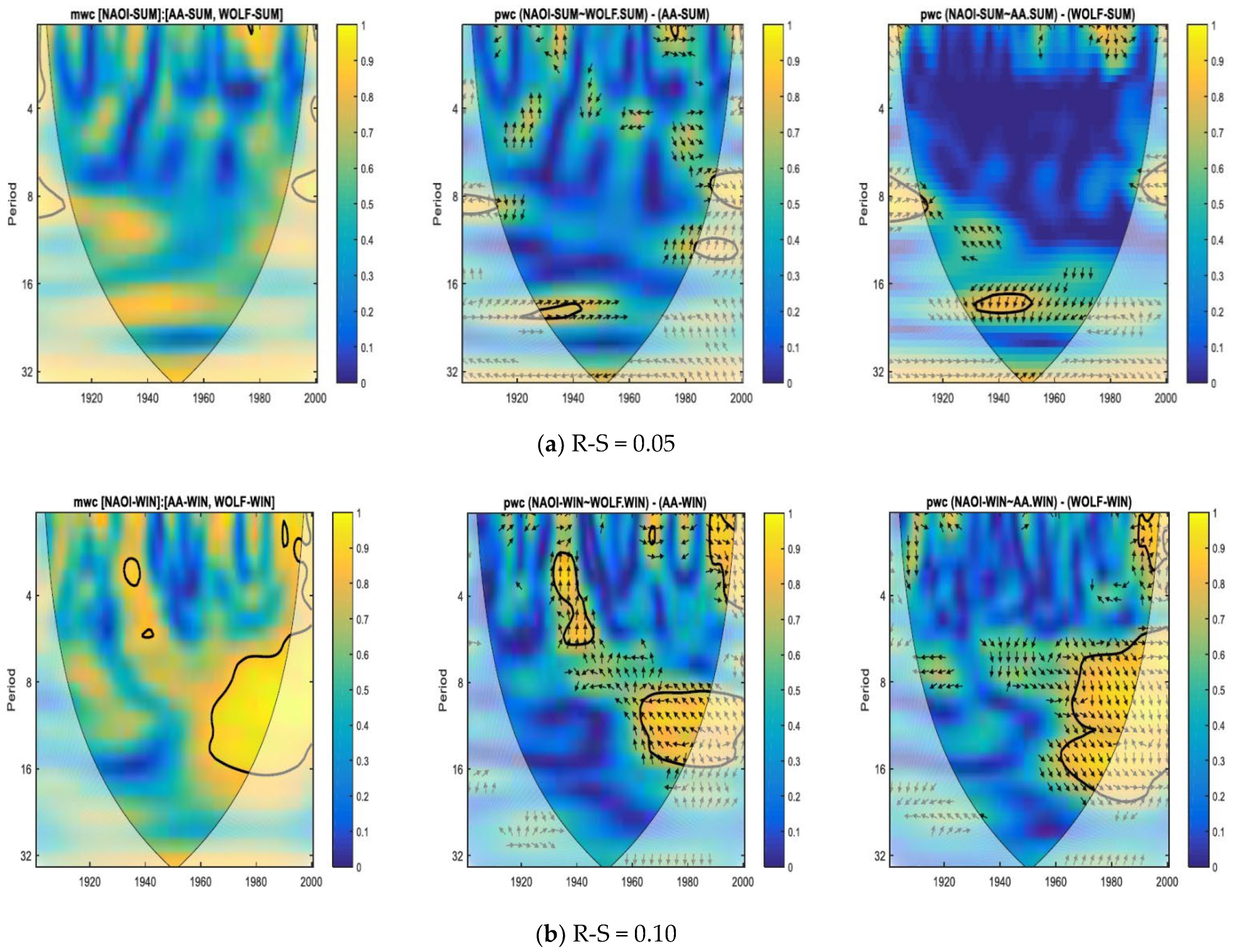
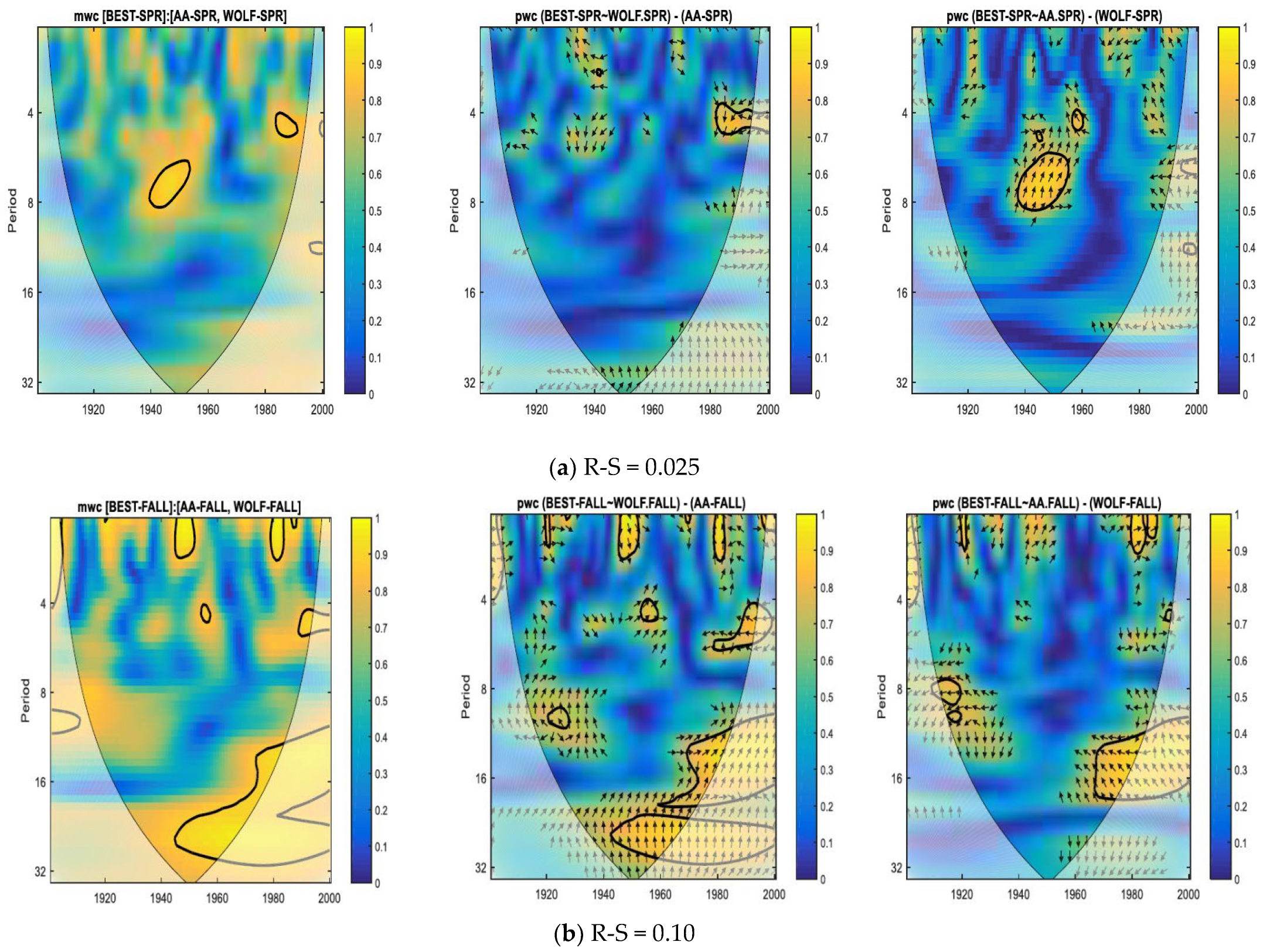
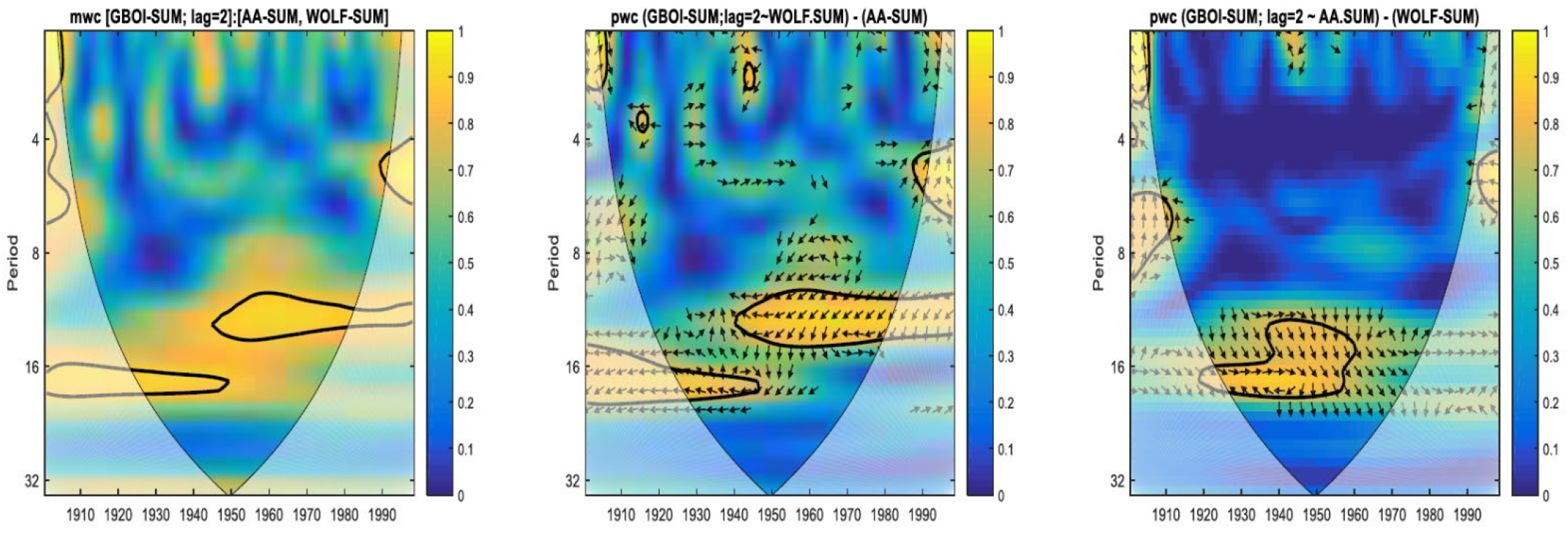
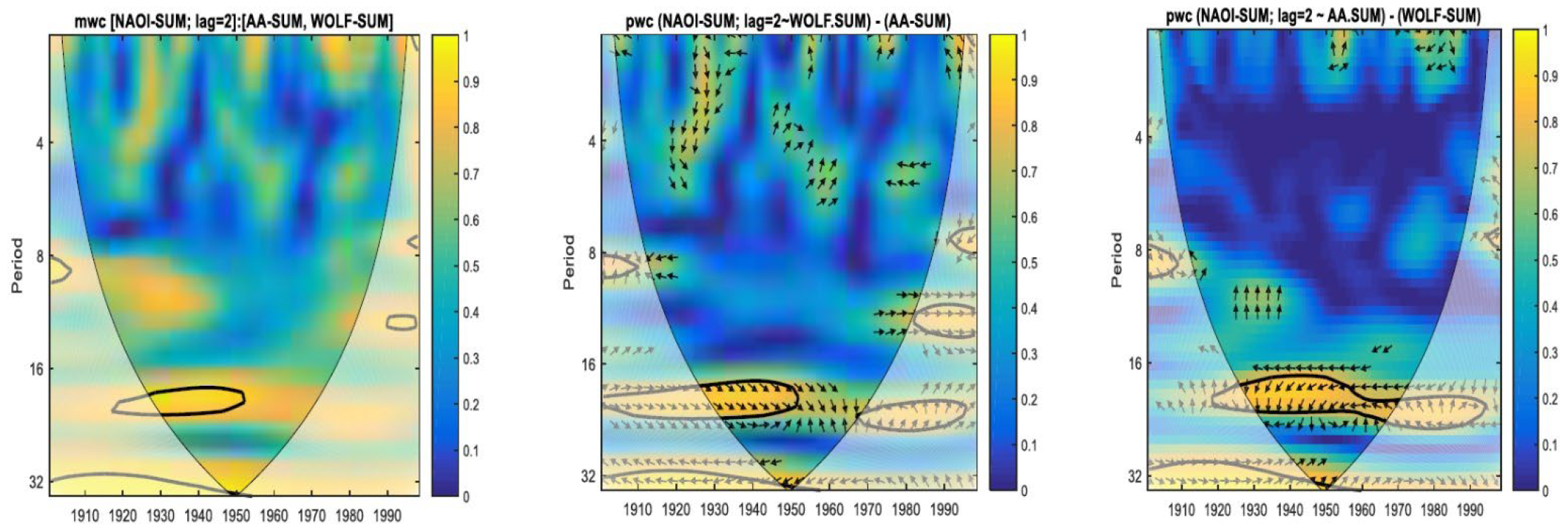
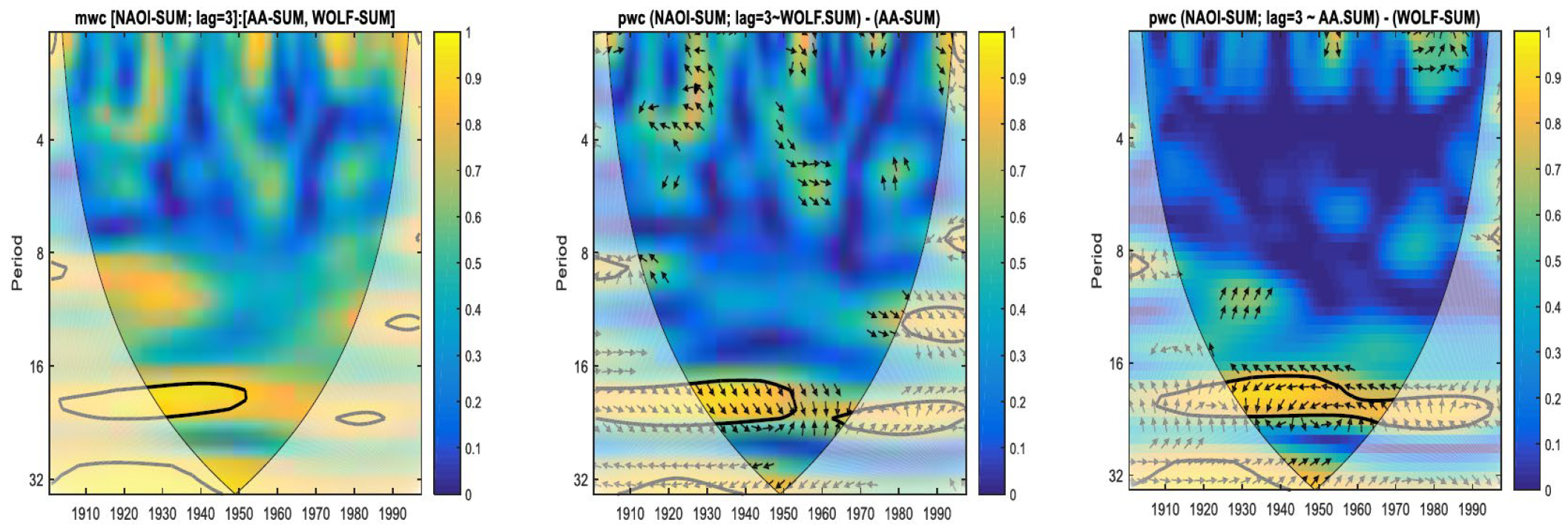
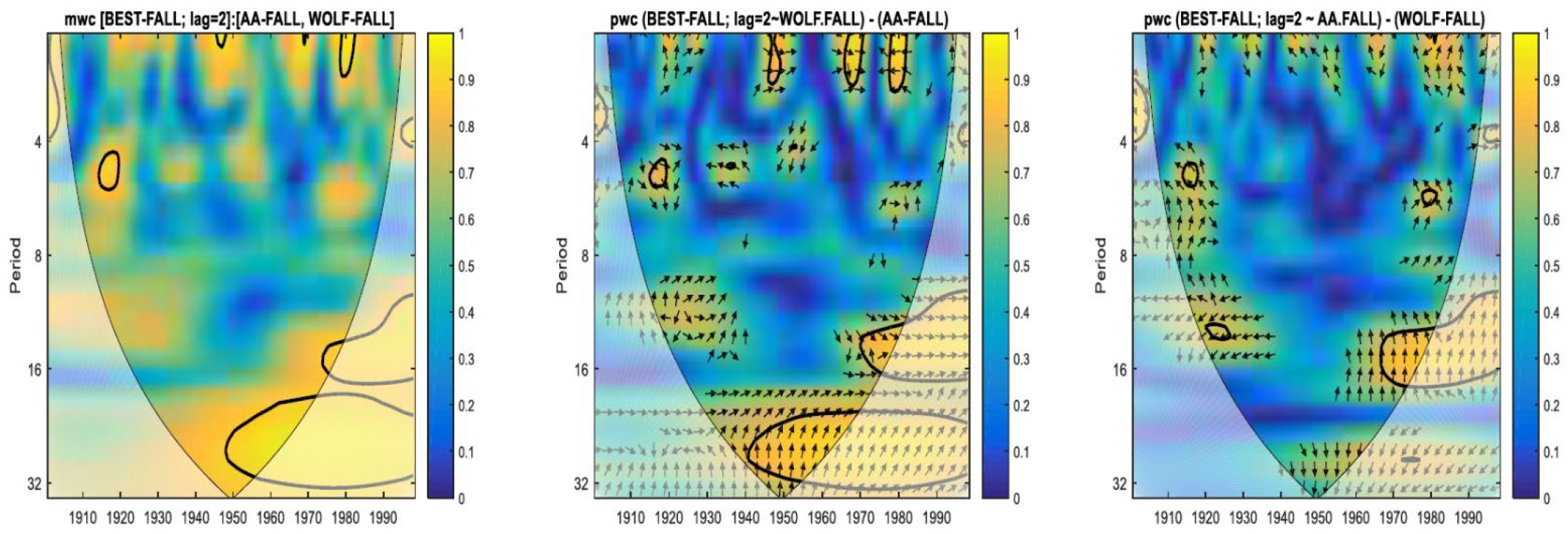
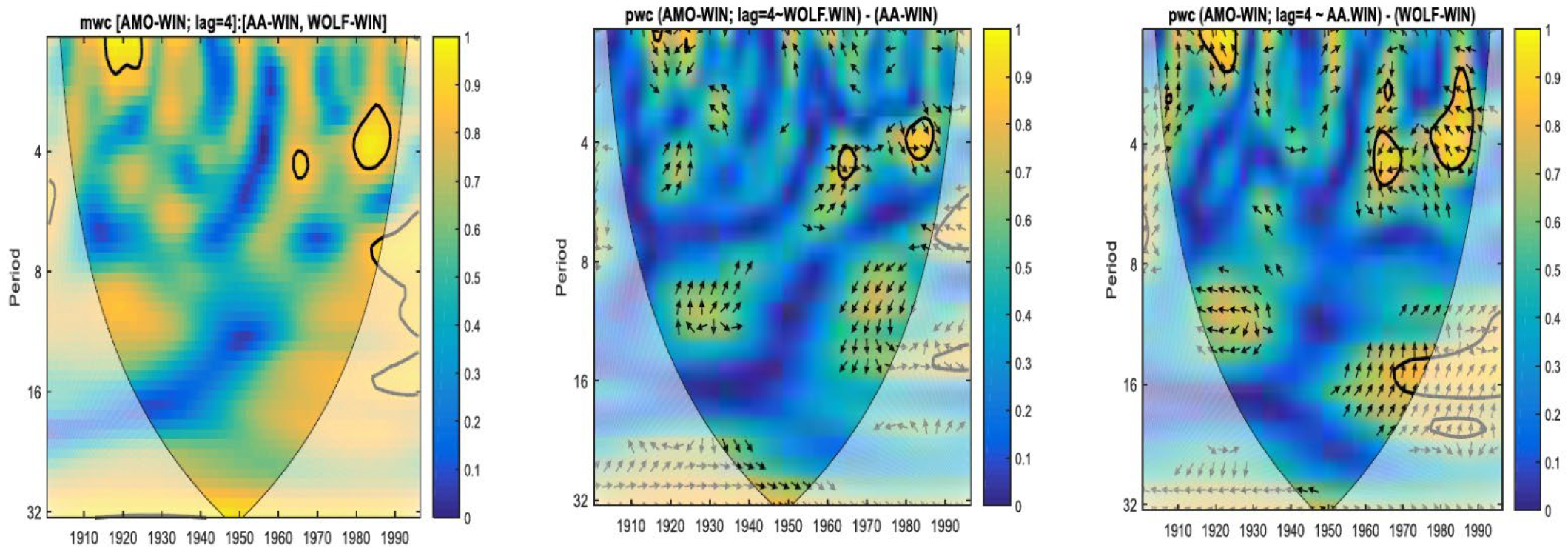
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| aa(AA) | Geomagnetic index |
| AMO | Atlantic Multidecadal Oscillation |
| AO | Arctic Oscillation |
| BEST | Bivariate ENSO Timeseries |
| Cis | Climate Indices |
| CL | Confidence levels |
| ENSO | El Niño–Southern Oscillation |
| GBOI | Greenland-Balkan Oscillation Index |
| IPCCAR6 | Intergovernmental Panel on Climate Change’s Sixth Assessment Report |
| MEI | Multivariates ENSO Index |
| Mwc | Multiple wavelet coherence |
| NAOI | North Atlantic Oscillation Index |
| NLR | Non-linear correlation coefficient |
| Pwc | Partial wavelet coherence |
| QBO | Quasi-Biennial Oscillation |
| R | Pearson correlation coefficient |
| SOI | Southern Oscillation Index |
| SLP | Sea Level Pressure |
| S-R | Synergy and minus Redundancy |
| SST | Sea Surface Temperature |
| TC | Total Correlation |
| TNI | Trans-Niño Index |
| WTC | Wavelet Coherence |
| WOLF | Wolf Number |
| XWT | Cross Wavelet Spectrum |
References
- Haigh, J.D.; Blackburn, M.; Day, R. The response of tropospheric circulation to perturbations in lower-stratospheric temperature. J. Clim. 2005, 18, 3672–3685. [Google Scholar] [CrossRef]
- Haigh, J.D. Mechanisms for solar influence on the Earth’s climate. In Climate and Weather of the Sun-Earth System (CAWSES): Selected Papers from the 2007 Kyoto Symposium; Tsuda, T., Fujii, R., Shibata, K., Geller, M.A., Eds.; TERRAPUB: Tokyo, Japan, 2009; pp. 231–256. [Google Scholar]
- Herschel, W. Observations tending to investigate the nature of the Sun, in order to find the causes or symptoms of its variable emission of light and heat: With remarks on the use that may possibly be drawn from solar observations. Philos. Trans. R. Soc. Lond. 1801, 91, 265–318. [Google Scholar] [CrossRef] [Green Version]
- Mitchell, J.M. An Overview of Climatic Variability and its Causal Mechanisms. Quat. Res. 1976, 6, 481–493. [Google Scholar] [CrossRef]
- Prestes, A.; Rigozo, N.R.; Echer, E.; Vieira, L.E.A. Spectral analysis of sunspot number and geomagnetic indices (1868–2001). J. Atmos. Sol.-Terr. Phys. 2006, 68, 182–190. [Google Scholar] [CrossRef]
- Woollings, T.; Lockwood, M.; Masato, G.; Bell, C.; Gray, L. Enhanced signature of solar variability in Eurasianwinter climate. Geophys. Res. Lett. 2010, 37, L20805. [Google Scholar] [CrossRef]
- Scafetta, N.; Bianchini, A. The planetary theory of solar activity variability: A review. Front. Astron. Space Sci. 2022, 9, 937930. [Google Scholar] [CrossRef]
- Hassan, D.; Iqbal, A.; Hassan, S.A.; Abbas, S.; Ansari, M.R.K. Sunspots and ENSO relationship using Markov method. J. Atmos. Sol.-Terr. Phys. 2016, 137, 53–57. [Google Scholar] [CrossRef]
- von der Heydt, A.; Ashwin, S.P.; Camp, C.D.; Crucifix, M.; Dijkstra, H.A.; Ditlevsen, P.; Lenton, T.M. Quantification and interpretation of the climate variability record. Glob. Planet. Chang. 2021, 197, 103399. [Google Scholar] [CrossRef]
- Song, Y.; Li, Z.; Zhou, Y.; Bi, X.; Sun, B.; Xiao, T.; Suo, L.; Zhang, W.; Xiao, Z.; Wang, C. The Influence of Solar Activity on Snow Cover over the Qinghai–Tibet Plateau and ItsMechanism Analysis. Atmosphere 2022, 13, 1499. [Google Scholar] [CrossRef]
- Gil-Alana, L.A.; Yaya, O.S.; Shittu, O.I. Global temperatures and sunspot numbers. Are they related? Phys. A Stat. Mech. Its Appl. 2014, 413, 329–342. [Google Scholar] [CrossRef]
- Ajayi, O.G.; Ibik, A.L.; Odumosu, J.O.; Babalola, K.H.; Adesina, E.A. Investigation of the Impact of Sunspots on Earth’s Climate Sustainable Built Environment and Climate change. In The Challenges of Post 2015 Development Agenda; School of Environmental Technology International Conference (SETIC); Federal University of Technology (FUT): Minna, Nigeria, 2016; Available online: https://www.researchgate.net/publication/343878002 (accessed on 5 July 2022).
- Chiodo, G.; Oehrlein, J.; Polvani, L.M.; Fyfe, J.C.; Smith, A.K. Insignificant influence of the 11-year solar cycle on the North Atlantic Oscillation. Nat. Geosci. 2019, 12, 94–99. [Google Scholar] [CrossRef]
- Courtillot, V.; Gallet, Y.; Le Mouël, J.L.; Fluteau, F.; Genevey, A. Are there connections between the Earth’s magnetic field and climate? Earth Planet. Sc. Lett. 2007, 253, 328–339. [Google Scholar] [CrossRef]
- Gray, L.J.; Beer, J.; Geller, M.; Haigh, J.D.; Lockwood, M.; Matthes, K.; Cubasch, U.; Fleitmann, D.; Harrison, G.; Hood, L.; et al. Solar influences on climate. Rev. Geophys. 2010, 48, RG4001. [Google Scholar] [CrossRef] [Green Version]
- Gray, L.J.; Scaife, A.A.; Mitchell, D.M.; Osprey, S.; Ineson, S.; Hardiman, S.; Butchart, N.; Knight, J.; Sutton, R.; Kodera, K. A lagged response to the 11 year solar cycle in observed winter Atlantic/European weather patterns. J. Geophys. Res. Atmos. 2013, 118, 13405–13420. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, E.N. Energy and Numerical Weather Prediction. Tellus 1960, 12, 364–373. [Google Scholar] [CrossRef] [Green Version]
- Holton, J.R. An Introduction to Dynamic Meteorology; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Willis, D.M. The Energetics of Sun-Weather Relationships-Magnetospheric Processes. J. Atmos. Terr. Phys. 1976, 38, 685–698. [Google Scholar] [CrossRef]
- Larsen, M.F.; Kelley, M.C. Available Potential Energy in the Middle Atmosphere as it Relates to the Sun-Weather Effect. In Solar-Terrestrial Influences on Weather and Climate; McCormac, B.M., Seliga, T.A., Eds.; Springer: Dordrecht, The Netherlands, 1979; pp. 145–147. [Google Scholar] [CrossRef]
- Peixoto, J.P.; Oort, A.H. Physics of Climate; American Institute of Physics: College Park, MD, USA, 1992; p. 520. [Google Scholar]
- Labitzke, K.; van Loon, H. Associations between the 11‐year solar cycle, the QBO and the atmosphere. Part I: The troposphere and stratosphere in the northern hemisphere in winter. J. Atmos. Terr. Phys. 1988, 50, 197–206. [Google Scholar] [CrossRef]
- Foukal, P. A comparison of variable solar total and ultraviolet irradiance outputs in the 20th century. Geophys. Res. Lett. 2002, 29, 4-1–4-4. [Google Scholar] [CrossRef]
- Kodera, K.; Coughlin, K.; Arakawa, O. Possible modulation of the connection between the Pacific and Indian Ocean variability by the solar cycle. Geophys. Res. Lett. 2007, 34, L03710. [Google Scholar] [CrossRef]
- Meehl, G.A.; Arblaster, J.M.; Matthes, K.; Sassi, F.; van Loon, H. Amplifying the Pacific Climate System Response to a Small 11-Year Solar Cycle Forcing. Science 2009, 325, 1114–1118. [Google Scholar] [CrossRef] [Green Version]
- Benestad, R.E. Low solar activity is blamed for winter chill over Europe. Environ. Res. Lett. 2010, 5, 021001. [Google Scholar] [CrossRef]
- Friis-Christensen, E.; Lassen, K. Length of the solar cycle: An indicator of solar activity closely associated with climate. Science 1991, 254, 698–700. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lean, J.; Beer, J.; Bradley, R.S. Reconstruction of solar irradiance since 1610: Implications for climate change. Geophys. Res. Lett. 1995, 22, 3195–3198. [Google Scholar] [CrossRef] [Green Version]
- Haigh, J.D. The effects of solar variability on the Earth’s climate. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2003, 361, 95–111. [Google Scholar] [CrossRef]
- Lockwood, M. Solar Influence on Global and Regional Climates. Surv. Geophys. 2012, 33, 503–534. [Google Scholar] [CrossRef] [Green Version]
- Saltzman, B. A Survey of Sttisticl-Dynamical Models of the Terrestrial Climate. In Advance in Geophysics; Saltzman, B., Ed.; Academic Press: New York, NY, USA; San Francisco, CA, USA; London, UK, 1978; pp. 278–282. [Google Scholar]
- Hunt, B.G. Nonlinear Influences-A Key to Short-Term Climatic Perturbations. J. Atmos. Sci. 1988, 45, 387–395. [Google Scholar] [CrossRef]
- Chapanov, Y. ENSO Variations Driven by Solar Cycles, Expressed by N-S Solar Asymmetry.Topic: Solar Influences on the Lower Atmosphere and Climate. In Proceedings of the Eleventh Workshop Solar Influences on the Magnetosphere, Ionosphere and Atmosphere, Primorsko, Bulgaria, 3–7 June 2019; p. 152. Available online: http://ws-sozopol.stil.bas.bg (accessed on 5 May 2022).
- Yndestad, H.; Solheim, J.E. The influence of solar system oscillation on the variability of the total solar irradiance. New Astron. 2017, 51, 135–152. [Google Scholar] [CrossRef] [Green Version]
- Clette, F.; Svalgaard, L.; Vaquero, J.M.; Cliver, E.W. Revisiting the Sunspot Number. Space Sci. Rev. 2014, 186, 35–103. [Google Scholar] [CrossRef] [Green Version]
- Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.L.; Péan, C.; Berger, S.; Caud, N.; Chen, Y.; Goldfarb, L.; Gomis, M.I.; et al. IPCC, Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; University Press: Cambridge, UK; New York, NY, USA, 2021; p. 2391. [Google Scholar] [CrossRef]
- Chapman, S.C.; McIntosh, S.W.; Leamon, R.J.; Watkins, N.W. Quantifying the solar cycle modulation of extreme space weather. Geophys. Res. Lett. 2020, 47, e2020GL087795. [Google Scholar] [CrossRef]
- Katsavrias, C.; Papadimitriou, C.; Hillaris, A.; Balasis, G. Application of Wavelet Methods in the Investigation of Geospace Disturbances: A Review and an Evaluation of the Approach for Quantifying Wavelet Power. Atmosphere 2022, 13, 499. [Google Scholar] [CrossRef]
- Mawad, R.; Fathy, M.; Ghamry, E. The Simultaneous Influence of the Solar Wind and Earth’s Magnetic Field on the Weather. Universe 2022, 8, 424. [Google Scholar] [CrossRef]
- Addison, P. The little wave with the big future. Phys. World 2004, 17, 35. [Google Scholar] [CrossRef]
- Stenseth, N.C.; Ottersen, G.; Hurrell, J.W.; Mysterud, A.; Lima, M.; Chan, K.-S.; Yoccoz, N.G.; Adlandsvik, B. Studying climate effects on ecology through the use of climate indices: The North Atlantic Oscillation, El Nino Southern Oscillation and beyond. Proc. R. Soc. Lon. Ser. B Biol. Sci. 2003, 270, 2087–2096. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beniston, M.; Jungo, P. Shifts in the distributions of pressure, temperature and moisture and changes in the typical weather patterns in the Alpine region in response to the behavior of the North Atlantic Oscillation. Theor. Appl. Climatol. 2002, 71, 29–42. [Google Scholar] [CrossRef] [Green Version]
- Zanchettin, D.; Rubino, A.; Traverso, P.; Tomasino, M. Impact of variations in solar activity on hydrological decadal patterns in northern Italy. J. Geophys. Res. Atmos. 2008, 113, D12. [Google Scholar] [CrossRef] [Green Version]
- Fang, G.; Li, X.; Xu, M.; Wen, X.; Huang, X. Spatiotemporal Variability of Drought and Its Multi-Scale Linkages with Climate Indices in the Huaihe River Basin, Central China and East China. Atmosphere 2021, 12, 1446. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Vicente-Serrano, S.M.; Morán-Tejeda, E.; Lorenzo-Lacruz, J.; Kenawy, A.; Beniston, M. Effects of the North Atlantic Oscillation (NAO) on combined temperature and precipitation winter modes in the Mediterranean mountains: Observed relationships and projections for the 21st century. Glob. Planet. Chang. 2011, 77, 62–76. [Google Scholar] [CrossRef]
- Vyshkvarkova, E.; Sukhonos, O. Compound Extremes of Air Temperature and Precipitation in Eastern Europe. Climate 2022, 10, 133. [Google Scholar] [CrossRef]
- Dobrica, V.; Demetrescu, C.; Mares, I.; Mares, C. Long-term evolution of the Lower 608 Danube discharge and corresponding climate variations: Solar signature imprint. Theor. Appl. Climatol. 2018, 133, 985–996. [Google Scholar] [CrossRef]
- Le Mouël, J.L.; Lopes, F.; Courtillot, V. A solar signature in many climate indices. J. Geophys. Res. Atmos. 2019, 124, 2600–2619. [Google Scholar] [CrossRef]
- Drews, A.; Huo, W.; Matthes, K.; Kodera, K.; Kruschke, T. The Sun’s role in decadal climate predictability in the North Atlantic. Atmos. Chem. Phys. 2022, 22, 7893–7904. [Google Scholar] [CrossRef]
- Nuzhdina, M.A. Connection between ENSO phenomena and solar and geomagnetic activity. Nat. Hazards Earth Syst. Sci. 2002, 2, 83–89. [Google Scholar] [CrossRef] [Green Version]
- Fu, C.; James, A.L.; Wachowiak, M.P. Analyzing the combined influence of solar activity and El Niño on streamflow across southern Canada. Water Resour. Res. 2012, 48, W05507. [Google Scholar] [CrossRef]
- Wolter, K.; Timlin, M.S. El Niño/Southern Oscillation behaviour since 1871 as diagnosed in an extended multivariate ENSO index (MEI.ext). Int. J. Climatol. 2011, 31, 1074–1087. [Google Scholar] [CrossRef]
- Smith, C.A.; Sardeshmukh, P.D. The Effect of ENSO on the Intraseasonal Variance of Surface Temperature in Winter. Int. J. Climatol. A J. R. Meteorol. Soc. 2000, 20, 1543–1557. [Google Scholar] [CrossRef]
- Campuzano, S.A.; De Santis, A.; Pavo´n-Carrasco, F.J.; Osete, M.L.; Qamili, E. New perspectives in the study of the Earth’s magnetic field and climate connection: The use of transfer entropy. PLoS ONE. 2018, 13, e0207270. [Google Scholar] [CrossRef] [Green Version]
- Vu, T.M.; Mishra, A.K.; Konapala, G. Information Entropy Suggests Stronger Nonlinear Associations between Hydro-Meteorological Variables and ENSO. Entropy 2018, 20, 38. [Google Scholar] [CrossRef] [Green Version]
- Paluš, M.; Novotná, D. Common oscillatory modes in geomagnetic activity, NAO index and surface air temperature records. J. Atmos. Sol.-Terr. Phys. 2007, 69, 2405–2415. [Google Scholar] [CrossRef]
- Wing, S.; Johnson, J.; Vourlidas, A. Information theoretic approach to discovering causalities in the solar cycle. Astrophys. J. 2018, 854, 85. [Google Scholar] [CrossRef]
- Wing, S.; Johnson, J.R. Applications of information theory in solar and space physics. Entropy 2019, 21, 140. [Google Scholar] [CrossRef] [Green Version]
- Goodwell, A.E.; Jiang, P.; Ruddell, B.L.; Kumar, P. Debates—Does information theory provide a new paradigm for Earth science? Causality, interaction, and feedback. Water Resour. Res. 2020, 56, e2019WR024940. [Google Scholar] [CrossRef] [Green Version]
- Lorenzo-Lacruz, J.; Morán-Tejeda, E.; Vicente-Serrano, S.M.; Hannaford, J.; García, C.; Peña-Angulo, D.; Murphy, C. Streamflow frequency changes across western Europe and interactions with North Atlantic atmospheric circulation patterns. Glob. Planet. Chang. 2022, 212, 103797. [Google Scholar] [CrossRef]
- Sonechkin, D.M.; Vakulenko, N.V. Polyphony of Short-Term Climatic Variations. Atmosphere 2021, 12, 1145. [Google Scholar] [CrossRef]
- Rathinasamy, M.; Agarwal, A.; Parmar, V.; Khosa, R.; Bairwa, A. Partial wavelet coherence analysis for understanding the standalone relationship between Indian Precipitation and Teleconnection patterns. arXiv 2017, arXiv:1702.06568. [Google Scholar]
- Labat, D. Recent advances in wavelet analyses: Part 1. A review of concepts. J. Hydrol. 2005, 314, 275–288. [Google Scholar] [CrossRef]
- Moore, J.; Grinsted, A.; Jevrejeva, S. Is there evidence for sunspot forcing of climate at multi-year and decadal periods? Geophys. Res. Lett. 2006, 33, L17705. [Google Scholar] [CrossRef] [Green Version]
- Mares, C.; Mares, I.; Dobrica, V.; Demetrescu, C. Quantification of the direct solar impact on some components of the hydroclimatic system. Entropy 2021, 23, 691. [Google Scholar] [CrossRef] [PubMed]
- Mares, I.; Dobrica, V.; Mares, C.; Demetrescu, C. Assessing the solar variability signature in climate variables by information theory and wavelet coherence. Sci. Rep. 2021, 11, 11337. [Google Scholar] [CrossRef]
- Mares, I.; Mares, C.; Dobrica, V.; Demetrescu, C. Selection of Optimal Palmer Predictors for Increasing the Predictability of the Danube Discharge: New Findings Based on Information Theory and Partial Wavelet Coherence Analysis. Entropy 2022, 24, 1375. [Google Scholar] [CrossRef]
- Mallat, S.A. Wavelet Tour of Signal Processing; Academic-Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Tary, J.B.; Herrera, R.H.; Han, J.; van der Baan, M. Spectral estimation—What is new? What is next? Rev. Geophys. 2014, 52, 723–749. [Google Scholar] [CrossRef]
- Ghil, M.; Allen, M.R.; Dettinger, M.D.; Ide, K.; Kondrashov, D.; Mann, M.E.; Robertson, A.W.; Saunders, A.; Tian, Y.; Varadi, F.; et al. Advanced spectral methods for climatic time series. Rev. Geophys. 2002, 40, 3-1–3-41. [Google Scholar] [CrossRef] [Green Version]
- Si, B.C. Spatial scaling analyses of soil physical properties: A review of spectral and wavelet methods. Vadose Zone J. 2008, 7, 547–562. [Google Scholar] [CrossRef] [Green Version]
- Sleziak, P.; Hlavčová, K.; Szolgay, J. Advantages of a time series analysis using wavelet transform as compared with a Fourier analysis. Slovak J. Civ. Eng. 2015, 23, 30. [Google Scholar] [CrossRef] [Green Version]
- Hood, L.; Schimanke, S.; Spangehl, T.; Bal, S.; Cubasch, U. The surface climate response to 11-yr solar forcing during northern winter: Observational analyses and comparisons with GCM simulations. J. Clim. 2013, 26, 7489–7506. [Google Scholar] [CrossRef] [Green Version]
- Mares, I.; Mares, C.; Mihailescu, M. Stochastic modeling of the connection between sea level pressure and discharge in the Danube lower basin by means of Hidden Markov Model. EGU Gen. Assem. Conf. Abstr. 2013, 15, EGU2013-7606. [Google Scholar]
- Hurrell, J.W. Decadal trends in the North Atlantic Oscillation and relationships to regional temperature and precipitation. Science 1995, 269, 676–679. [Google Scholar] [CrossRef] [Green Version]
- Thompson, D.W.J.; Wallace, J.M. The Arctic Oscillation signature in the wintertime geopotential height and temperature fields. Geophys. Res. Lett. 1998, 25, 1297–1300. [Google Scholar] [CrossRef] [Green Version]
- Enfield, D.B.; Mestas-Nunez, A.M.; Trimble, P.J. The Atlantic Multidecadal Oscillation and its relationship to rainfall and river flows in the continental U.S. Geophys. Res. Lett. 2001, 28, 2077–2080. [Google Scholar] [CrossRef] [Green Version]
- Ropelewski, C.F.; Jones, P.D. An extension of the Tahiti-Darwin Southern Oscillation Index. Mon. Weather Rev. 1987, 115, 2161–2165. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Stepaniak, D.P. Indices of El Niño Evolution. J. Clim. 2001, 14, 1697–1701. Available online: https://www.jstor.org/stable/26247387 (accessed on 27 October 2022). [CrossRef]
- Mares, C.; Mares, I.; Mihailescu, M. Identification of extreme events using drought indices and their impact on the Danube lower basin discharge. Hydrol. Proc. 2016, 30, 3839–3854. [Google Scholar] [CrossRef]
- Mares, I.; Dobrica, V.; Demetrescu, C.; Mares, C. Hydrological response in the Danube lower basin to some internal and external climate forcing factors. Hydrol. Earth Syst. Sci. Discuss. 2016. preprint. [Google Scholar] [CrossRef] [Green Version]
- Mares, I.; Mares, C.; Dobrica, V.; Demetrescu, C. Comparative study of statistical methods to identify a predictor for discharge at Orsova in the Lower Danube Basin. Hydrol. Sci. J. 2020, 65, 371–386. [Google Scholar] [CrossRef]
- Lüdecke, H.; Müller-Plath, G.; Wallace, M.G.; Lüning, S. Decadal and multidecadal natural variability of African rainfall. J. Hydrol. Reg. Stud. 2021, 34, 100795. [Google Scholar] [CrossRef]
- Laurenz, L.; Lüdecke, H.-J.; Lüning, S. Influence of solar activity changes on European rainfall. J. Atmos. Sol.-Terr. Phys. 2019, 185, 29–42. [Google Scholar] [CrossRef]
- Khan, S.; Ganguly, A.R.; Bandyopadhyay, S.; Saigal, S.; Erickson, D.J.; Protopopescu, V.; Ostrouchov, G. Nonlinear statistics reveals stronger ties between ENSO and the tropical hydrological cycle. Geophys. Res. Lett. 2006, 33, L24402. [Google Scholar] [CrossRef] [Green Version]
- Steuer, R.; Kurths, J.; Daub, C.O.; Weise, J.; Selbig, J. The mutual information: Detecting and evaluating dependencies between variables. Bioinformatics 2002, 18, S231–S240. [Google Scholar] [CrossRef] [Green Version]
- Theiler, J.; Eubank, S.; Longtin, A.; Galdrikian, B.; Farmer, J.D. Testing for nonlinearity in time series: The method of surrogate data. Phys. D Nonlinear Phenom. 1992, 58, 77–94. [Google Scholar] [CrossRef] [Green Version]
- Timme, N.; Alford, W.; Flecker, B.; Beggs, J.M. Synergy, redundancy, and multivariate information measures: An experimentalist’s perspective. J. Comput. Neurosci. 2014, 36, 119–140. [Google Scholar] [CrossRef]
- Mihanovic, H.; Orlie, M.; Pasaria, Z. Diurnal thermocline oscillations driven by tidal flow around an island in the Middle Adriatic. J. Mar. Syst. 2009, 78, S157–S168. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Sreedevi, V.; Adarsh, S.; Nourani, V. Multiscale coherence analysis of reference evapotranspiration of north-western Iran using wavelet transform. J. Water Clim. Chang. 2022, 13, 505–521. [Google Scholar] [CrossRef]
- Gu, X.; Sun, H.; Zhang, Y.; Zhang, S.; Lu, C. Partial Wavelet Coherence to Evaluate Scale-dependent Relationships Between Precipitation/Surface Water and Groundwater Levels in a Groundwater System. Water Resour. Manag. 2022, 36, 2509–2522. [Google Scholar] [CrossRef]
- Hu, W.; Si, B.C. Technical Note: Improved partial wavelet coherency for understanding scale- specific and localized bivariate relationships in geosciences. Hydrol. Earth Syst. Sci. 2021, 25, 321–331. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, S.; Ding, Y.; Fu, Q.; Wang, Y.; Cai, H.; Shi, H. Assessing the responses of vegetation to meteorological drought and its influencing factors with partial wavelet coherence analysis. J. Environ. Manag. 2022, 311, 114879. [Google Scholar] [CrossRef] [PubMed]
- Firouzi, S.; Wang, X. The interrelationship between order flow, exchange rate, and the role of American economic news. N. Am. J. Econ. Financ. 2021, 58, 101492. [Google Scholar] [CrossRef]
- Hu, W.; Si, B.C. Multiple wavelet coherence for untangling scale-specific and localized multivariate relationships in geosciences. Hydrol. Earth Syst. Sci. 2016, 20, 3183–3191. [Google Scholar] [CrossRef] [Green Version]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Maraun, D.; Kurths, J.; Holschneider, M. Nonstationary Gaussian processes in wavelet domain: Synthesis, estimation, and significance testing. Phys. Rev. E 2007, 75, 016707. [Google Scholar] [CrossRef] [Green Version]
- Jevrejeva, S.; Moore, J.C.; Grinsted, A. Influence of the Arctic Oscillation and ElNiño-Southern Oscillation (ENSO) on ice conditions in the Baltic Sea: The wavelet approach. J. Geophys. Res. 2003, 108, 4677. [Google Scholar] [CrossRef]
- Torrence, C.; Webster, P. Interdecadal changes in the ESNO-Monsoon System. J. Clim. 1999, 12, 2679–2690. [Google Scholar] [CrossRef]
- Zaidan, M.A.; Haapasilta, V.; Relan, R.; Paasonen, P.; Kerminen, V.-M.; Junninen, H.; Kulmala, M.; Foster, A.S. Exploring non-linear associations between atmospheric new-particle formation and ambient variables: A mutual information approach. Atmos. Chem. Phys. 2018, 18, 12699–12714. [Google Scholar] [CrossRef] [Green Version]
- Scaife, A.A.; Ineson, S.; Knight, J.R.; Gray, L.; Kodera, K.; Smith, D.M. A mechanism for lagged North Atlantic climate response to solar variability. Geophys. Res. Lett. 2013, 40, 434–439. [Google Scholar] [CrossRef]
- Thiéblemont, R.; Matthes, K.; Omrani, N.-E.; Kodera, K.; Hansen, F. Solar forcing synchronizes decadal North Atlantic climate variability. Nat. Commun. 2015, 6, 8268. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Ma, H.; Li, X.; Sun, S. Solar influences on spatial patterns of Eurasian winter temperature and atmospheric general circulation anomalies. J. Geophys. Res. Atmos. 2015, 120, 8642–8657. [Google Scholar] [CrossRef] [Green Version]
- Demetrescu, C.; Dobrica, V. Signature of Hale and Gleissberg solar cycles in the geomagnetic activity. J. Geophys. Res. 2008, 113, A02103. [Google Scholar] [CrossRef] [Green Version]
- Du, Z.L. The correlation between solar and geomagnetic activity–Part 3: An integral response model. Ann. Geophys. 2011, 29, 1005–1018. [Google Scholar] [CrossRef] [Green Version]
- Gray, L.J.; Woollings, T.J.; Andrews, M.; Knight, J. Eleven-year solar cycle signal in the NAO and Atlantic/European blocking. Quart. J. Roy. Meteorol. Soc. 2016, 142, 1890–1903. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.-F.; Yu, J.-Y.; Wu, C.-R.; Zheng, F. The footprint of the 11-year solar cycle in Northeastern Pacific SSTs and its influence on the Central Pacific El Niño. Geophys. Res. Let. 2021, 48, e2020GL091369. [Google Scholar] [CrossRef]
- Kuroda, Y.; Kodera, K.; Yoshida, K.; Yukimoto, S.; Gray, L. Influence of the solar cycle on the North Atlantic Oscillation. J. Geophys. Res.-Atmos. 2022, 127, e2021JD035519. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mares, C.; Dobrica, V.; Mares, I.; Demetrescu, C. Solar Signature in Climate Indices. Atmosphere 2022, 13, 1898. https://doi.org/10.3390/atmos13111898
Mares C, Dobrica V, Mares I, Demetrescu C. Solar Signature in Climate Indices. Atmosphere. 2022; 13(11):1898. https://doi.org/10.3390/atmos13111898
Chicago/Turabian StyleMares, Constantin, Venera Dobrica, Ileana Mares, and Crisan Demetrescu. 2022. "Solar Signature in Climate Indices" Atmosphere 13, no. 11: 1898. https://doi.org/10.3390/atmos13111898
APA StyleMares, C., Dobrica, V., Mares, I., & Demetrescu, C. (2022). Solar Signature in Climate Indices. Atmosphere, 13(11), 1898. https://doi.org/10.3390/atmos13111898





