A Novel Hybrid Model Combining the Support Vector Machine (SVM) and Boosted Regression Trees (BRT) Technique in Predicting PM10 Concentration
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Acquisition
2.2. Feature Description
2.3. Data Pre-Processing
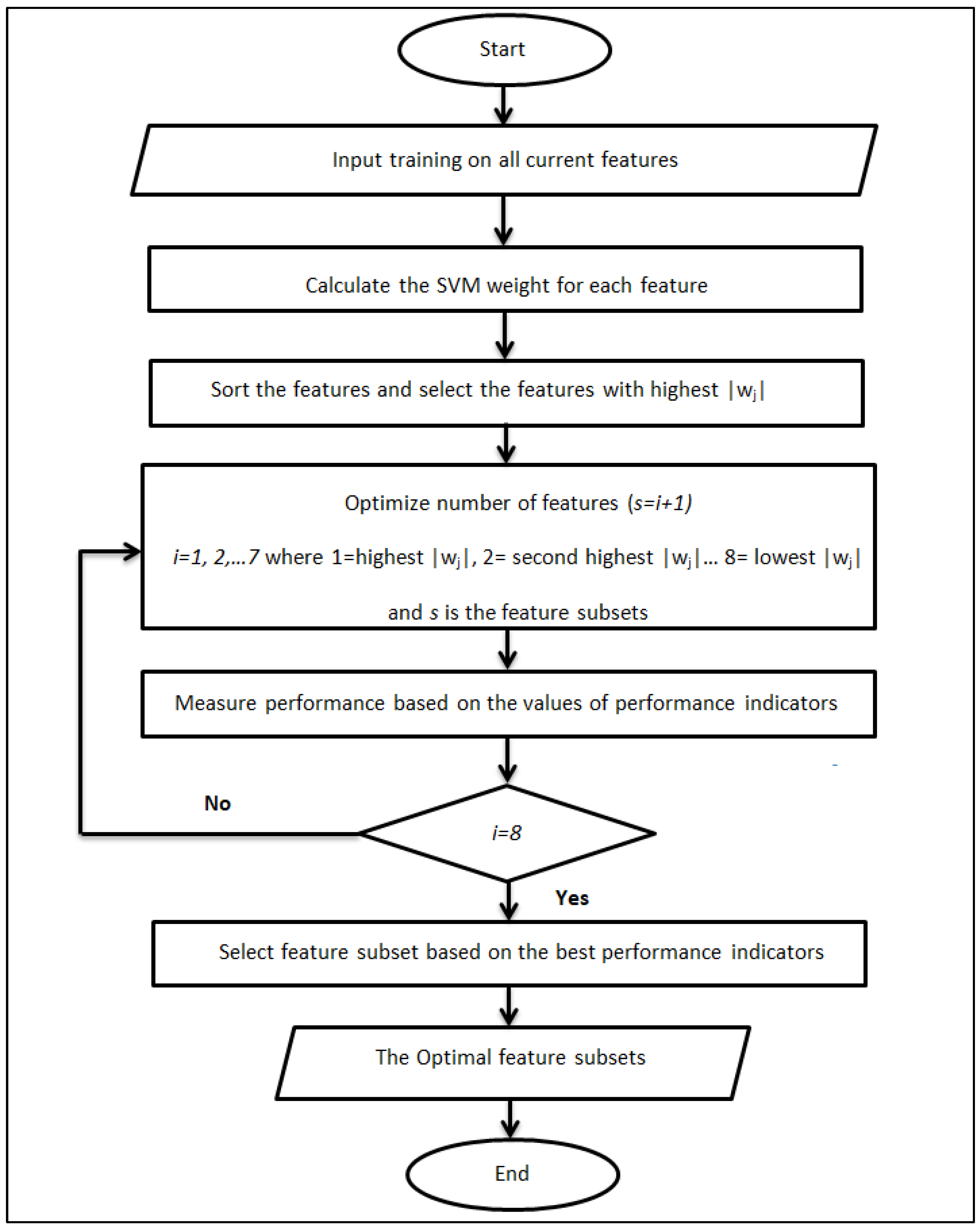
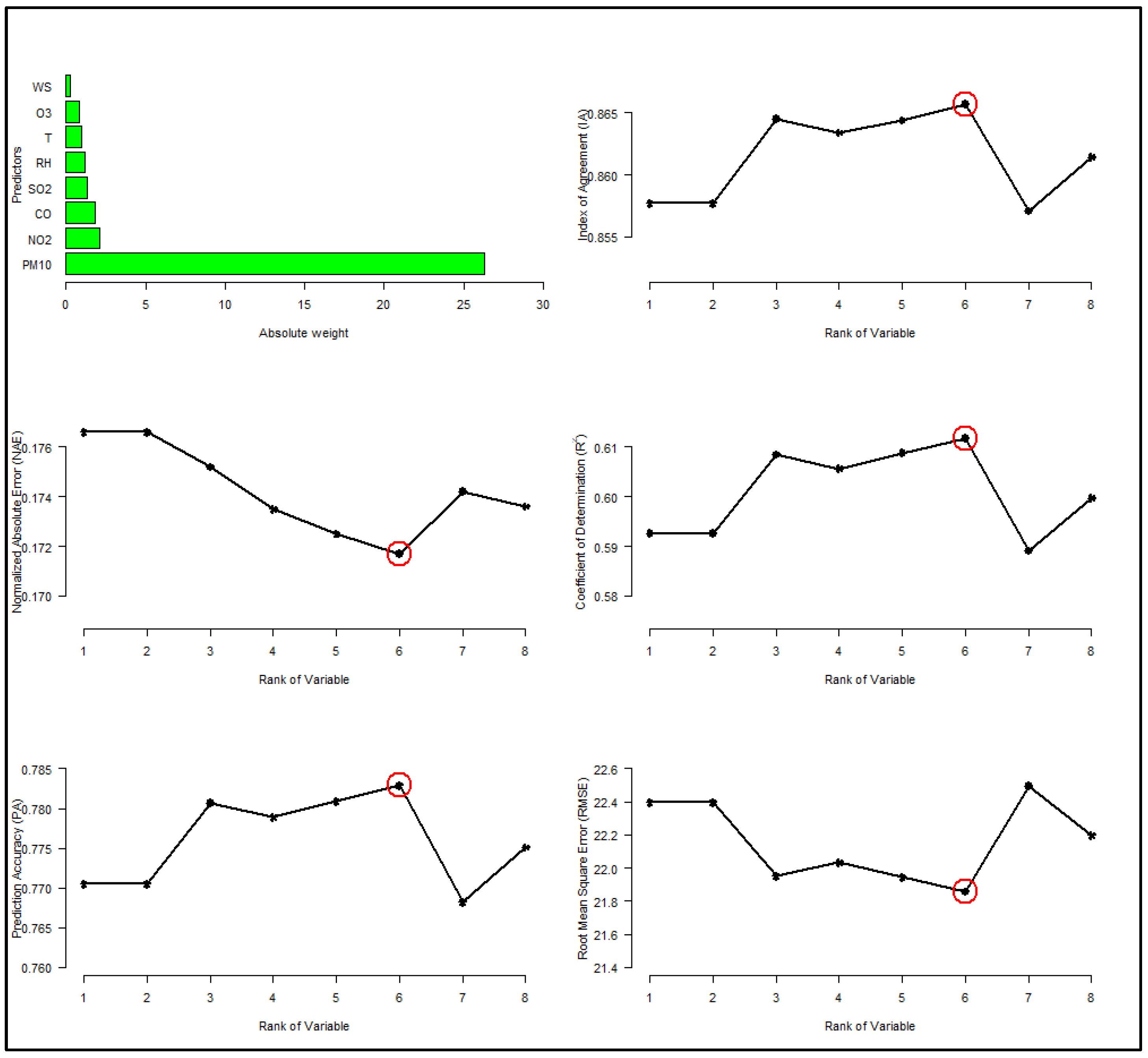
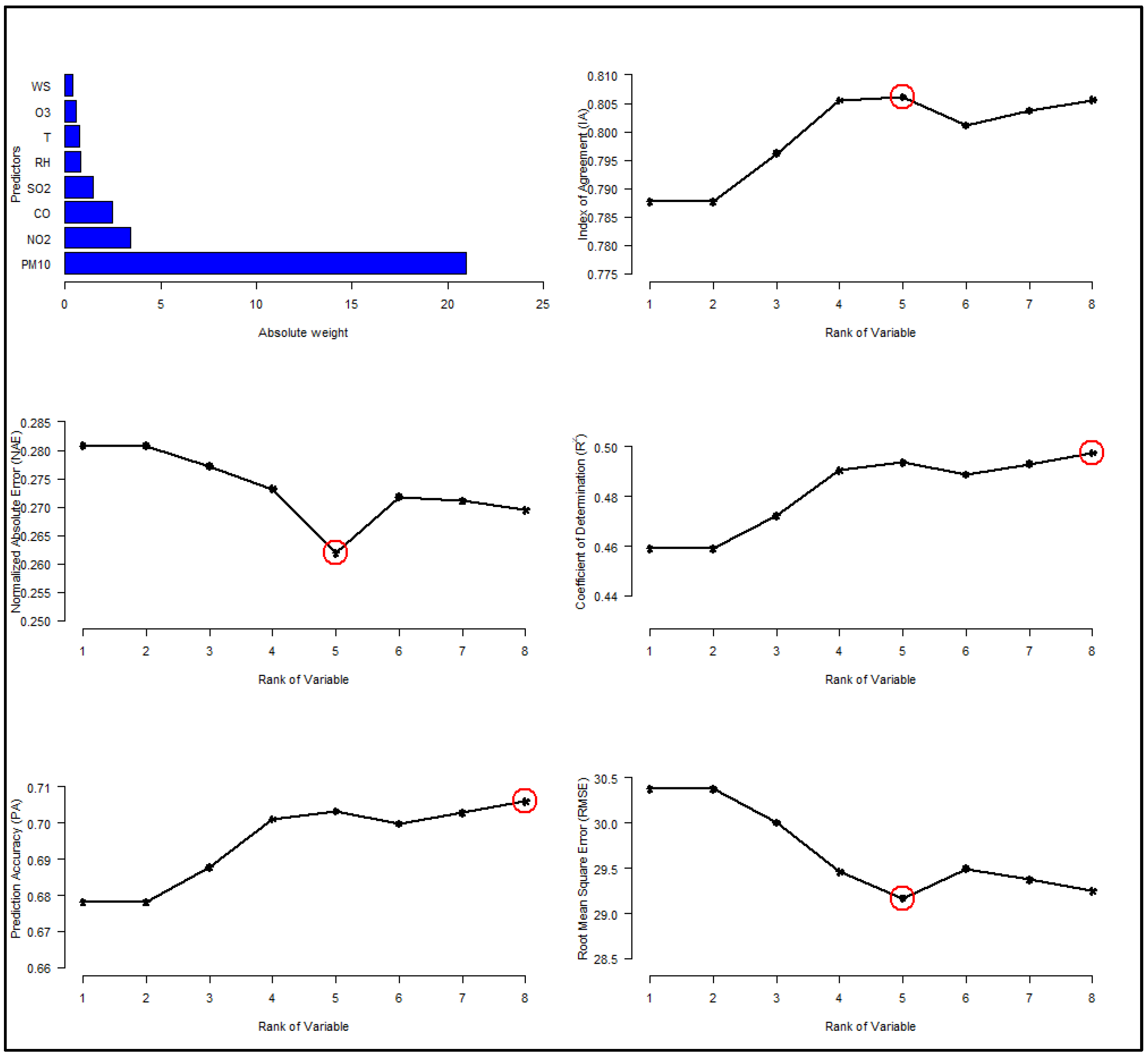
2.4. Feature Selection Using SVM Weight
2.5. BRT Model
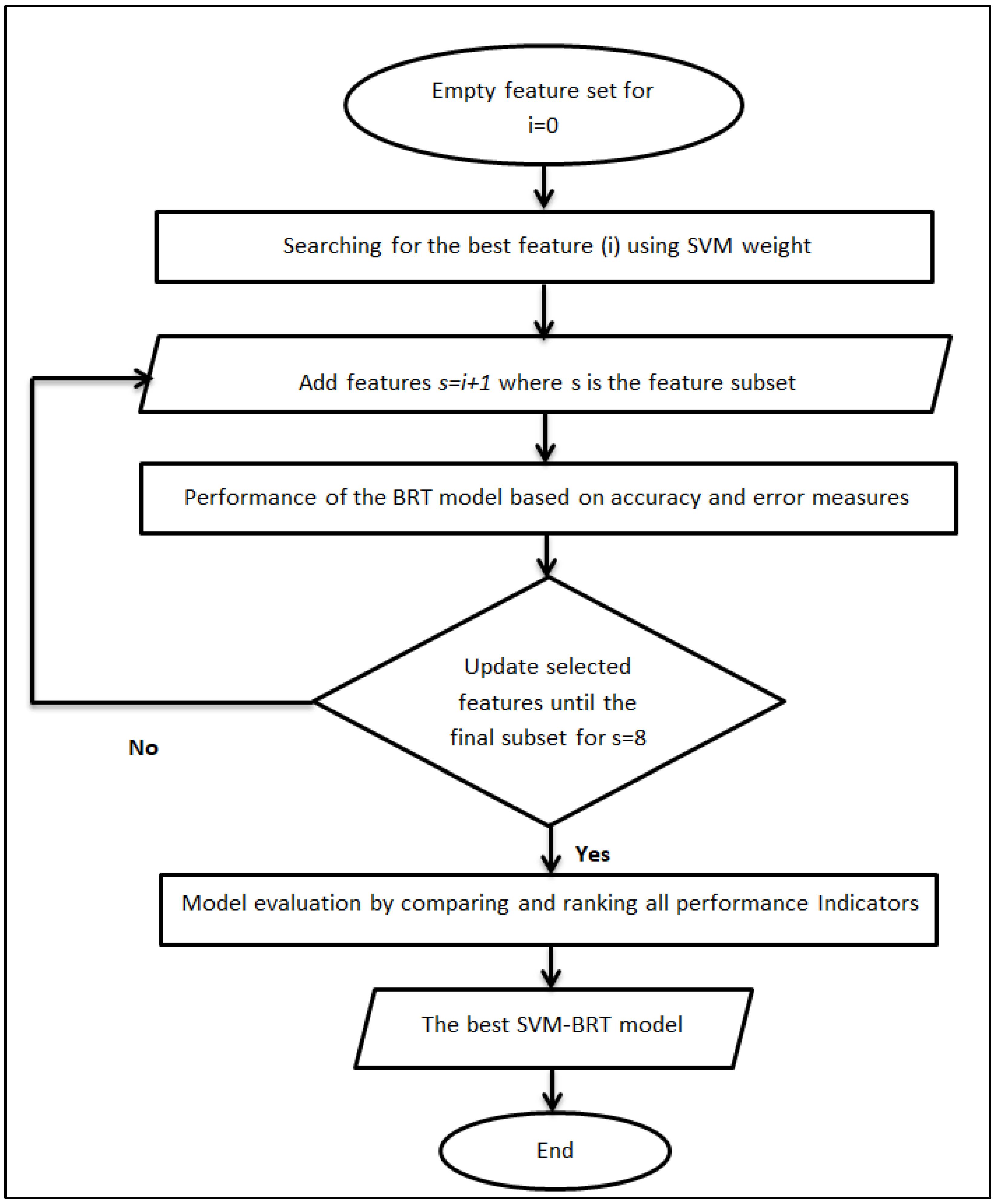
2.6. Hybrid Model
2.7. Performance Indictor
3. Results and Discussion
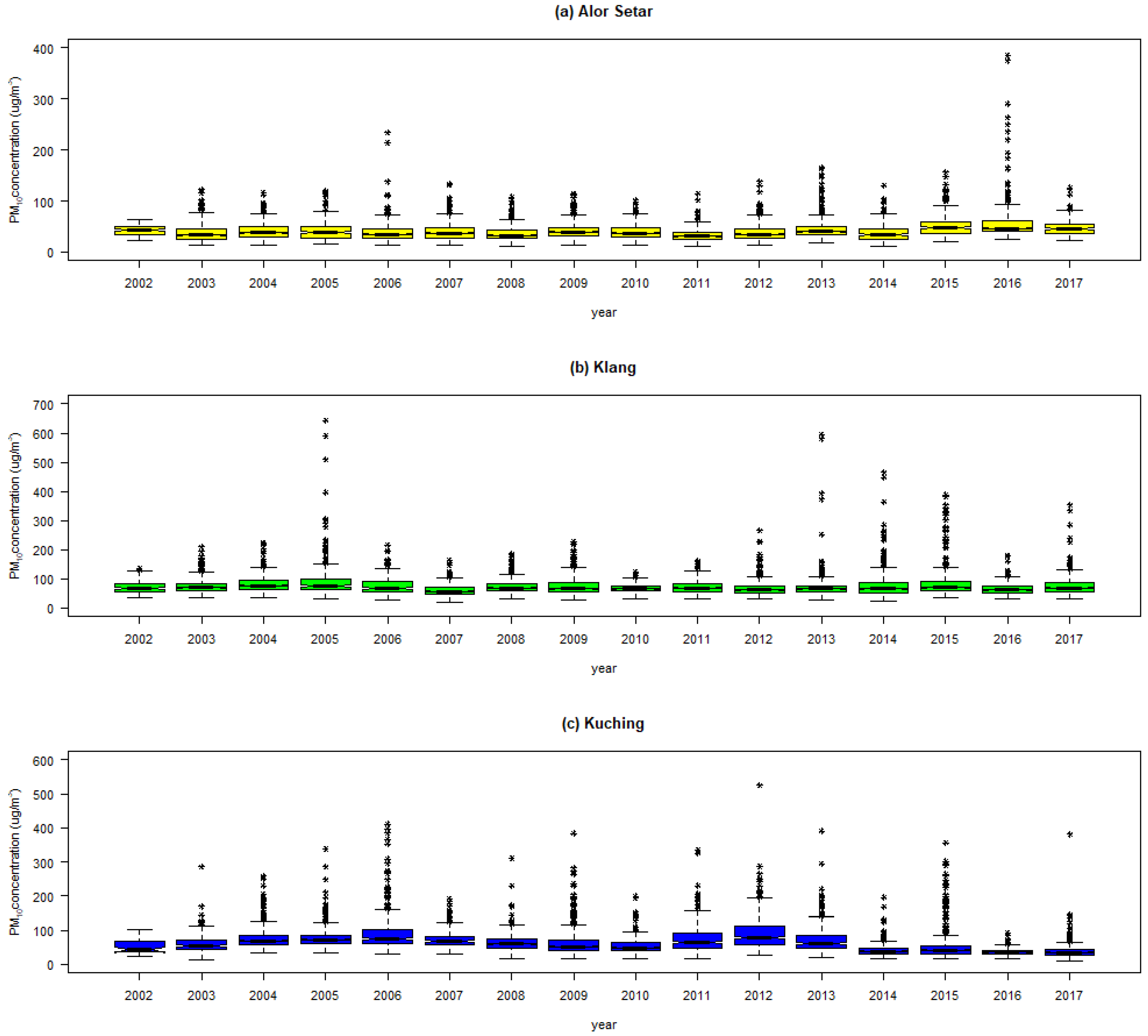
3.1. Descriptive Statistics
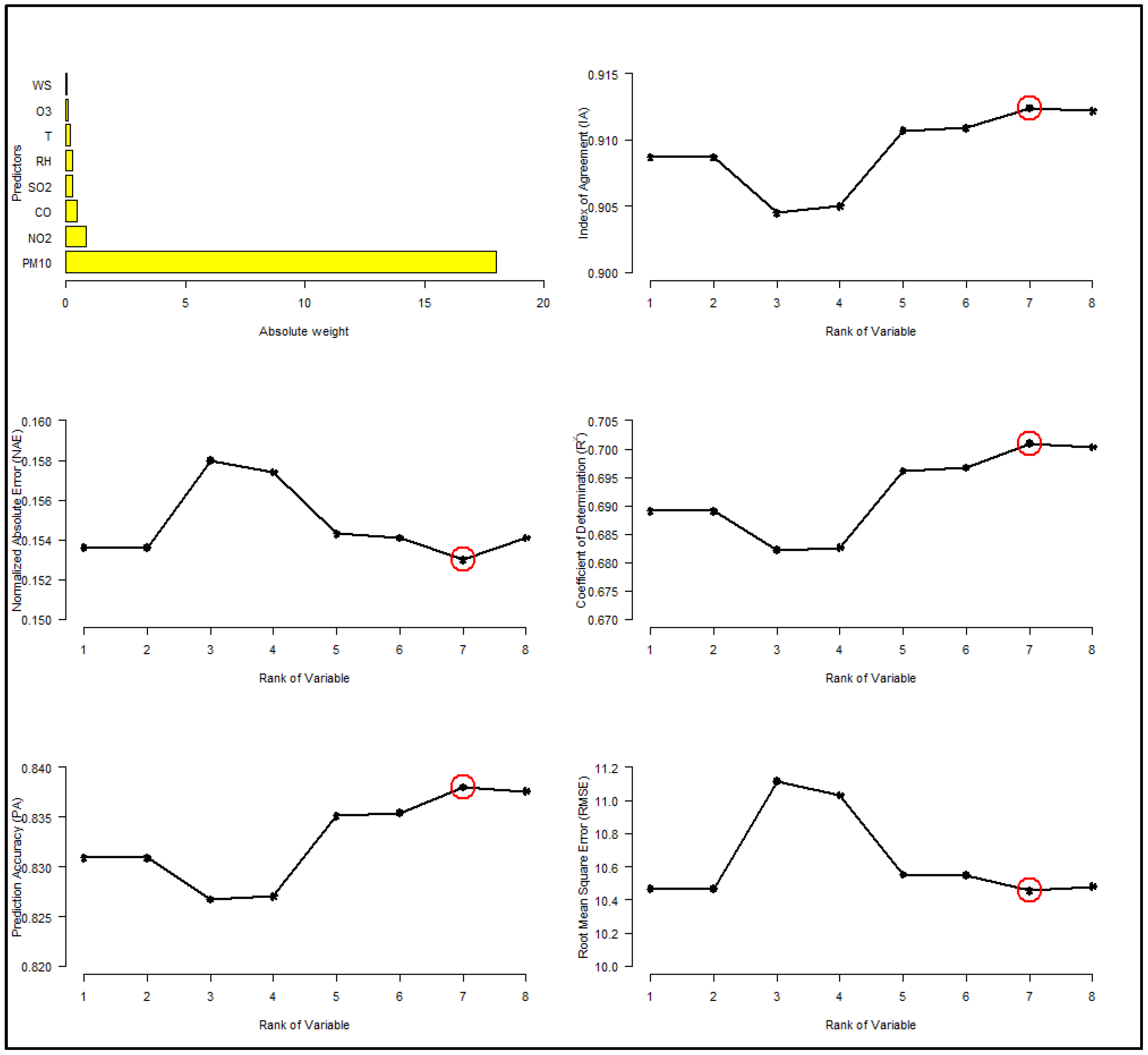
3.2. Optimizing the Number of Predictors (SVM Weight)
3.3. Hybrid Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Department of Environment, Malaysia. Malaysia Environmental Quality Report 2018. Available online: https://enviro2.doe.gov.my/ekmc/wp-content/uploads/2019/09/FULL-FINAL-EQR-30092019.pdf.pdf (accessed on 5 June 2022).
- Elbayoumi, M.; Ramli, N.A.; Md Yusof, N.F.F.; Yahaya, A.S.; Al Madhoun, W.; Ul-Saufie, A.Z. Multivariate methods for indoor PM10 and PM2.5 modelling in naturally ventilated schools buildings. Atmos. Environ. 2014, 94, 11–21. [Google Scholar] [CrossRef]
- Perez, P.; Reyes, J. An integrated neural network model for PM10 forecasting. Atmos. Environ. 2006, 40, 2845–2851. [Google Scholar] [CrossRef]
- Kukkonen, J.; Partanen, L.; Karppinen, A.; Ruuskanen, J.; Junninen, H.; Kolehmainen, M.; Niska, H.; Dorling, S.; Chatterton, T.; Foxall, R.; et al. Extensive Evaluation of Neural Network Models for The Prediction of NO2 and PM10 Concentrations, Compared with a Deterministic Modeling System and Measurements in Central Helsinski. Atmos. Environ. 2003, 37, 4539–4550. [Google Scholar] [CrossRef]
- Biancofiore, F.; Busilacchio, M.; Verdecchia, M.; Tomassetti, B.; Aruffo, E.; Bianco, S.; Tomasso, S.D.; Colangeli, C.; Rosatelli, G.; Carlo, P.D. Recursive Neural Network Model for Analysis and Forecast of PM10 and PM2.5. Atmos. Pollut. Res. 2017, 8, 652–659. [Google Scholar] [CrossRef]
- Cabaneros, S.M.; Calautit, J.K.; Hughes, B.R. A review of artificial neural network models for ambient air pollution prediction. Environ. Model. Softw. 2019, 119, 285–304. [Google Scholar] [CrossRef]
- Stafoggia, M.; Bellander, T.; Bucci, S.; Davoli, M.; de Hoogh, K.; de’ Donato, F.; Gariazzo, C.; Lyapustin, A.; Michelozzi, P.; Renzi, M.; et al. Estimation of daily PM10 and PM2.5 concentrations in Italy, 2013–2015, using a spatiotemporal land-use random-forest model. Environ. Int. 2019, 124, 170–179. [Google Scholar] [CrossRef] [PubMed]
- Sayegh, A.; Tate, J.E.; Ropkins, K. Understanding how roadside concentrations of NOx are influenced by the background levels, traffic density, and meteorological conditions using Boosted Regression Trees. Atmos. Environ. 2016, 127, 163–175. [Google Scholar] [CrossRef]
- Yahaya, Z.; Phang, S.M.; Samah, A.A.; Azman, I.N.; Ibrahim, Z.F. The international journal by the Thai Society of Higher Education Institutes on Environment Analysis of Fine and Coarse Particle Number Count Concentrations Using Boosted Regression Tree Technique in Coastal Environment. EnvironmentAsia 2018, 11, 221–234. [Google Scholar]
- Asri, M.A.M.; Ahmad, S.; Afthanorhan, A. Algorithmic Modelling of Boosted Regression Trees’ on Environment’s Big Data Algorithmic Modelling of Boosted Regression Trees’ on Environment’s Big Data. Elixir Stat. Int. J. 2015, 82, 32419–32424. [Google Scholar]
- Zhang, T.; He, W.; Zheng, H.; Cui, Y.; Song, H.; Fu, S. Satellite-based ground PM2.5 estimation using a gradient boosting decision tree. Chemosphere 2021, 26, 128801. [Google Scholar] [CrossRef]
- Ivanov, A.; Gocheva-Ilieva, S.; Stoimenova, M. Hybrid boosted trees and regularized regression for studying ground ozone and PM10 concentrations. AIP Conf. Proc. 2020, 2302, 060005. [Google Scholar]
- Guyon, I.; Elisseeff, A. An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Geng, X.; Liu, T.; Qin, T.; Li, H. Feature Selection for Ranking. In Proceedings of the 30th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR’07), Amsterdam, The Netherlands, 23–27 July 2007; pp. 407–414. [Google Scholar]
- Mladenic, D.; Brank, J.; Grobelnik, M.; Milic-Frayling, N. Feature selection using linear classifier weights. In Proceedings of the 27th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Sheffield, UK, 25–29 July 2004; pp. 234–241. [Google Scholar]
- Bron, E.E.; Smits, M.; Niessen, W.J.; Klein, S. Feature Selection Based on the SVM Weight Vector for Classification of Dementia. IEEE J. Biomed. Health Inform. 2015, 19, 1617–1626. [Google Scholar] [CrossRef]
- Sanchez-Marono, N.; Alonso-Betanzos, A.; Tombilla-Sanromán, M. Filter Methods for Feature Selection—A Comparative Study. Intell. Data Eng. Autom. Learn. IDEAL 2007, 4881, 178–187. [Google Scholar]
- Maldonado, S.; Flores, A.; Verbraken, T.; Baesens, B.; Weber, R. Profit-based feature selection using support vector machines—General framework and an application for customer retention. Appl. Soft Comput. J. 2015, 35, 740–748. [Google Scholar] [CrossRef]
- Ul-Saufie, A.Z.; Yahaya, A.S.; Ramli, N.A.; Rosaida, N.; Hamid, H.A. Future daily PM10 concentrations prediction by combining regression models and feedforward backpropagation models with principle component analysis (PCA). Atmos. Environ. 2013, 77, 621–630. [Google Scholar] [CrossRef]
- Suleiman, A.; Tight, M.R.; Quinn, A.D. Hybrid Neural Networks and Boosted Regression Tree Models for Predicting Roadside Particulate Matter. Environ. Model. Assess. 2016, 21, 731–750. [Google Scholar] [CrossRef] [Green Version]
- Perimula, Y. HAZE: Steps taken to reduce hot spots. New Strait Times 2012. Available online: http://www.nst.com.my/opinion/letters-to-the-editor/haze-steps-taken-to-reduce-hot-spots-1.98115 (accessed on 8 May 2022).
- Sukatis, F.F.; Mohamed, N.; Zakaria, N.F.; Ul-Saufie, A.Z. Estimation of Missing Values in Air Pollution Dataset by Using Various Imputation Methods. Int. J. Conserv. Sci. 2019, 10, 791–804. [Google Scholar]
- Noor, N.M.; Yahaya, A.S.; Ramli, N.A.; Abdullah, M.M.A.B. Mean imputation techniques for filling the missing observations in air pollution dataset. Key Eng. Mater. 2014, 594–595, 902–908. [Google Scholar] [CrossRef]
- Noor, N.M.; Yahaya, A.S.; Ramli, N.A.; Abdullah, M.M.A.B. Filling the Missing Data of Air Pollutant Concentration Using Single Imputation Methods. Appl. Mech. Mater. 2015, 754–755, 923–932. [Google Scholar] [CrossRef]
- Libasin, Z.; Suhailah, W.; Fauzi, W.M.; ul-Saufie, A.Z.; Idris, N.A.; Mazeni, N.A. Evaluation of Single Missing Value Imputation Techniques for Incomplete Air Particulates Matter (PM10) Data in Malaysia. Pertanika J. Sci. Technol. 2021, 29, 3099–3112. [Google Scholar] [CrossRef]
- Huang, M.; Hung, Y.; Lee, W.M.; Li, R.K.; Jiang, B. SVM-RFE Based Feature Selection and Taguchi Parameters Optimization for Multiclass SVM Classifier. Sci. World J. 2014, 2014, 795624. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef] [PubMed]
- Shaziayani, W.N.; Ul-Saufie, A.Z.; Ahmat, H.; Al-Jumeily, D. Coupling of Quantile Regression into Boosted Regression Trees (BRT) Technique in Forecasting Emission Model of PM10 Concentration. Air Qual. Atmos. Health 2021, 14, 1647–1663. [Google Scholar] [CrossRef]
- Ridgeway, G. Generalized Boosted Models: A guide to the gbm package. Compute 2020, 1, 1–12. [Google Scholar]
- Yahaya, N.Z.; Ibrahim, Z.F.; Yahaya, J. The used of the Boosted Regression Tree Optimization Technique to Analyse an Air Pollution data. Int. J. Recent Technol. Eng. 2019, 8, 1565–1575. [Google Scholar] [CrossRef]
- Shaziayani, W.N.; Ul-Saufie, A.Z.; Yusoff, S.A.M.; Ahmat, H.; Libasin, Z. Evaluation of boosted regression tree for the prediction of the maximum 24-h concentration of particulate matter. Int. J. Environ. Sci. Dev. 2021, 12, 126–130. [Google Scholar] [CrossRef]
- Abdullah, S.; Napi, N.N.L.M.; Ahmed, A.N.; Mansor, W.N.W.; Mansor, A.B.; Ismail, M.; Abdullah, A.M.; Ramly, Z.T.A. Development of multiple linear regression for particulate matter (PM10) forecasting during episodic transboundary haze event in Malaysia. Atmosphere 2020, 11, 289. [Google Scholar] [CrossRef] [Green Version]
- Rahman, S.R.A.; Ismail, S.N.S.; Ramli, M.F.; Latif, M.T.; Abidin, E.Z.; Praveena, S.M. The Assessment of Ambient Air Pollution Trend in Klang Valley. World Environ. 2015, 5, 1–11. [Google Scholar]
- Zakri, N.L.; Saudi, A.S.M.; Juahir, H.; Toriman, M.E.; Abu, I.F.; Mahmud, M.M.; Khan, M.F. Identification Source of Variation on Regional Impact of Air Quality Pattern using Chemometric Techniques in Kuching, Sarawak. Int. J. Eng. Technol. 2018, 7, 49. [Google Scholar] [CrossRef]
- Jamil, M.S.; Ul-Saufie, A.Z.; Abu Bakar, A.A.; Ali, K.A.M.; Ahmat, H. Identification of source contributions to air pollution in Penang using factor analysis. Int. J. Integr. Eng. 2019, 11, 221–228. [Google Scholar]
- Sayegh, A.; Munir, S.; Habeebullah, T. Comparing the performance of statistical models for predicting PM10 concentrations. Aerosol Air Qual. Res. 2014, 14, 653–665. [Google Scholar] [CrossRef]
| Location | Latitude | Longitude | Station ID |
|---|---|---|---|
| Islamic Religious Secondary School, Mergong, Alor Setar, Kedah | 06°08.218′ N | 100°20.880′ E | CA0040 |
| Raja Zarina Secondary School, Klang, Selangor | 03°00.620′ N | 101°24.484′ E | CA0011 |
| Medical Store, Kuching, Sarawak | 01°33.734′ N | 110°23.329′ E | CA0004 |
| Feature | Role | Unit | Measurements Level |
|---|---|---|---|
| NO2,D | independent variable | ppb | Continuous |
| COD | independent variable | ppb | Continuous |
| SO2,D | independent variable | ppb | Continuous |
| PM10,D | independent variable | µg/m3 | Continuous |
| O3,D | independent variable | ppb | Continuous |
| TD | independent variable | °C | Continuous |
| RHD | independent variable | % | Continuous |
| WSD | independent variable | km/hour | Continuous |
| PM10,D+1 | dependent variable | µg/m3 | Continuous |
| PM10,D+2 | dependent variable | µg/m3 | Continuous |
| PM10,D+3 | dependent variable | µg/m3 | Continuous |
| Stations | RH Available Date | Total Data Sets | Stations |
|---|---|---|---|
| Alor Setar | 22 October 2002–28 December 2017 | 5548 | Alor Setar |
| Klang | 1 October 2002–28 December 2017 | 5569 | Klang |
| Kuching | 3 December 2002–28 December 2017 | 5505 | Kuching |
| Stations | Parameters (Unit) | Statistical Parameter | |||||
|---|---|---|---|---|---|---|---|
| Mean | Median | Standard Deviation | Skewness | Kurtosis | Maximum | ||
| Alor Setar | PM10 (μg/m3) | 41.99 | 38 | 20.84 | 4.03 | 40.05 | 385 |
| O3 (ppb) | 34.27 | 32 | 14.86 | 0.82 | 1.05 | 118 | |
| CO (ppb) | 560.3 | 540 | 246.71 | 1.71 | 7.36 | 3060 | |
| NO2 (ppb) | 15.2 | 14 | 5.85 | 1.1 | 2.97 | 58 | |
| SO2 (ppb) | 1.05 | 1 | 0.93 | 0.99 | 2.32 | 8 | |
| RH (%) | 89.35 | 91 | 8.07 | −1.77 | 3.81 | 100 | |
| T (°C) | 32.42 | 32.7 | 2.77 | −1.23 | 3.21 | 39.5 | |
| WS (Km/h) | 10.53 | 10.7 | 3.74 | 0.3 | 1.78 | 33.5 | |
| Klang | PM10 (μg/m3) | 75.05 | 68 | 37.78 | 4.89 | 44.82 | 643 |
| O3 (ppb) | 44.74 | 42 | 19.33 | 0.66 | 0.48 | 127 | |
| CO (ppb) | 1611.43 | 1440 | 774.87 | 2.65 | 16.04 | 10500 | |
| NO2 (ppb) | 38.34 | 37 | 12.67 | 0.36 | 0.89 | 128 | |
| SO2 (ppb) | 6.6 | 5 | 6.52 | 8.67 | 119.11 | 150 | |
| RH (%) | 83.71 | 84 | 6.93 | −0.71 | 1.37 | 100 | |
| T (°C) | 33.34 | 33.6 | 2.22 | −0.74 | 0.74 | 38.5 | |
| WS (Km/h) | 9.15 | 9.6 | 5.02 | 25.33 | 1326.95 | 271 | |
| Kuching | PM10 (μg/m3) | 65.38 | 57 | 39.51 | 2.99 | 15.72 | 526 |
| O3 (ppb) | 23.66 | 22 | 9.74 | 0.78 | 1.54 | 82 | |
| CO (ppb) | 892.21 | 780 | 486.34 | 1.66 | 5.28 | 5080 | |
| NO2 (ppb) | 12.64 | 12 | 5.85 | 2.94 | 40.09 | 123 | |
| SO2 (ppb) | 3.66 | 3 | 4.13 | 7.42 | 121.54 | 100 | |
| RH (%) | 94.6 | 95 | 3.29 | −1.03 | 6.37 | 100 | |
| T (°C) | 33.24 | 33.21 | 2.47 | −0.38 | 2.83 | 53 | |
| WS (Km/h) | 11.29 | 11.3 | 3.56 | 5 | 110.71 | 99 | |
| Stations | Selected Predictors |
|---|---|
| Alor Setar | PM10,D+1 ~ gbm(PM10, NO2, CO, SO2, RH, T, O3) PM10,D+2 ~ gbm(PM10, NO2, CO, SO2, RH, T, O3) PM10,D+3 ~ gbm(PM10, NO2, CO, SO2, RH, T, O3) |
| Klang | PM10,D+1 ~ gbm(PM10, CO, RH, O3, NO2, T) PM10,D+2 ~ gbm(PM10, CO, RH, O3, NO2, T) PM10,D+3 ~ gbm(PM10, CO, RH, O3, NO2, T) |
| Kuching | PM10,D+1 ~ gbm(PM10, CO, RH, O3, NO2) PM10,D+2 ~ gbm(PM10, CO, RH, O3, NO2) PM10,D+3 ~ gbm(PM10, CO, RH, O3, NO2) |
| Days | Station | Method | Best Iteration | RMSE | NAE | PA | R2 | IA |
|---|---|---|---|---|---|---|---|---|
| Alor Setar | CV | 663 | 10.4559 | 0.1539 | 0.8380 | 0.701 | 0.9124 | |
| OOB | 256 | 10.0815 | 0.1527 | 0.8366 | 0.6986 | 0.9113 | ||
| TEST | 243 | 10.0011 | 0.1528 | 0.8371 | 0.6994 | 0.9111 | ||
| D | Klang | CV | 1049 | 21.9435 | 0.1725 | 0.7809 | 0.6088 | 0.8644 |
| + | OOB | 252 | 22.3999 | 0.1754 | 0.8450 | 0.5979 | 0.8450 | |
| 1 | TEST | 1094 | 21.9316 | 0.1725 | 0.7812 | 0.6092 | 0.8642 | |
| Kuching | CV | 931 | 29.3651 | 0.2719 | 0.7032 | 0.4936 | 0.8061 | |
| OOB | 251 | 29.8344 | 0.2800 | 0.6973 | 0.4854 | 0.7725 | ||
| TEST | 335 | 29.5637 | 0.2757 | 0.7004 | 0.4897 | 0.7866 | ||
| Alor Setar | CV | 347 | 13.2992 | 0.222 | 0.6521 | 0.4245 | 0.7909 | |
| OOB | 236 | 13.17 | 0.2228 | 0.6491 | 0.4206 | 0.7813 | ||
| TEST | 238 | 13.169 | 0.2228 | 0.6494 | 0.421 | 0.7817 | ||
| D | Klang | CV | 245 | 27.2112 | 0.2318 | 0.6176 | 0.3807 | 0.7062 |
| + | OOB | 227 | 27.246 | 0.2321 | 0.6176 | 0.3808 | 0.7 | |
| 2 | TEST | 478 | 27.2512 | 0.2313 | 0.6144 | 0.3768 | 0.7244 | |
| Kuching | CV | 357 | 34.5616 | 0.3199 | 0.6083 | 0.3694 | 0.6903 | |
| OOB | 244 | 34.6437 | 0.3219 | 0.6111 | 0.3728 | 0.675 | ||
| TEST | 307 | 34.5745 | 0.3203 | 0.6094 | 0.3706 | 0.6858 | ||
| Alor Setar | CV | 475 | 14.7962 | 0.2554 | 0.5357 | 0.2864 | 0.6837 | |
| OOB | 228 | 14.76 | 0.2563 | 0.5293 | 0.2796 | 0.6583 | ||
| TEST | 345 | 14.83 | 0.2562 | 0.53 | 0.2805 | 0.6743 | ||
| D | Klang | CV | 245 | 31.0173 | 0.2555 | 0.5018 | 0.2514 | 0.5918 |
| + | OOB | 222 | 31.033 | 0.2555 | 0.5017 | 0.2513 | 0.5824 | |
| 3 | TEST | 859 | 31.2269 | 0.2567 | 0.4967 | 0.2463 | 0.619 | |
| Kuching | CV | 429 | 32.6196 | 0.3259 | 0.5742 | 0.3291 | 0.6844 | |
| OOB | 238 | 32.6295 | 0.3281 | 0.5764 | 0.3316 | 0.6633 | ||
| TEST | 250 | 32.6036 | 0.3276 | 0.5768 | 0.3321 | 0.6664 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shaziayani, W.N.; Ahmat, H.; Razak, T.R.; Zainan Abidin, A.W.; Warris, S.N.; Asmat, A.; Noor, N.M.; Ul-Saufie, A.Z. A Novel Hybrid Model Combining the Support Vector Machine (SVM) and Boosted Regression Trees (BRT) Technique in Predicting PM10 Concentration. Atmosphere 2022, 13, 2046. https://doi.org/10.3390/atmos13122046
Shaziayani WN, Ahmat H, Razak TR, Zainan Abidin AW, Warris SN, Asmat A, Noor NM, Ul-Saufie AZ. A Novel Hybrid Model Combining the Support Vector Machine (SVM) and Boosted Regression Trees (BRT) Technique in Predicting PM10 Concentration. Atmosphere. 2022; 13(12):2046. https://doi.org/10.3390/atmos13122046
Chicago/Turabian StyleShaziayani, Wan Nur, Hasfazilah Ahmat, Tajul Rosli Razak, Aida Wati Zainan Abidin, Saiful Nizam Warris, Arnis Asmat, Norazian Mohamed Noor, and Ahmad Zia Ul-Saufie. 2022. "A Novel Hybrid Model Combining the Support Vector Machine (SVM) and Boosted Regression Trees (BRT) Technique in Predicting PM10 Concentration" Atmosphere 13, no. 12: 2046. https://doi.org/10.3390/atmos13122046
APA StyleShaziayani, W. N., Ahmat, H., Razak, T. R., Zainan Abidin, A. W., Warris, S. N., Asmat, A., Noor, N. M., & Ul-Saufie, A. Z. (2022). A Novel Hybrid Model Combining the Support Vector Machine (SVM) and Boosted Regression Trees (BRT) Technique in Predicting PM10 Concentration. Atmosphere, 13(12), 2046. https://doi.org/10.3390/atmos13122046








