Multi-Scale Interaction between a Squall Line and a Supercell and Its Impact on the Genesis of the “0612” Gaoyou Tornado
Abstract
:1. Introduction
2. Data and Methodology
2.1. Event Overview
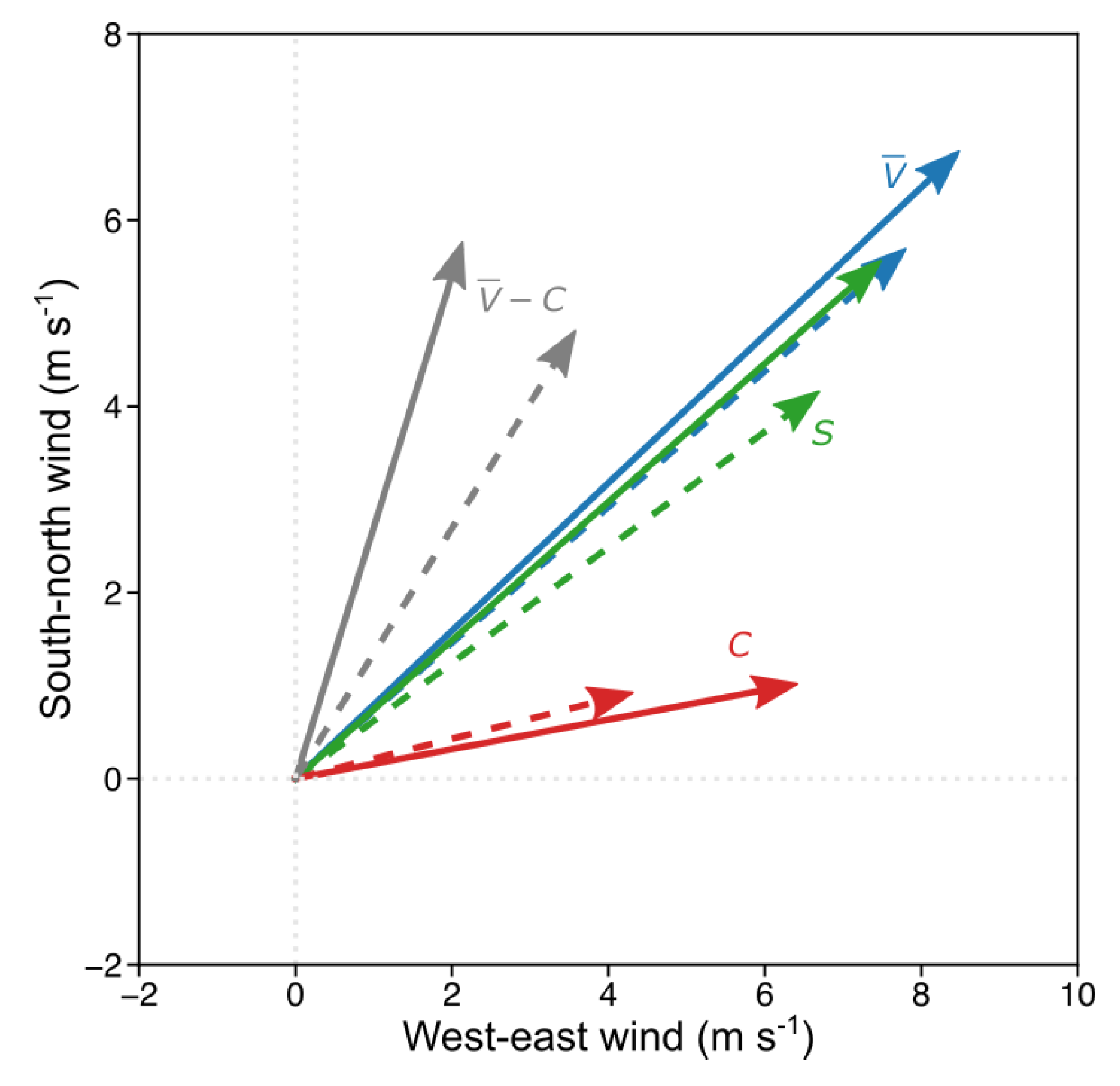
2.2. Wind Retrieval
3. Observation Analysis
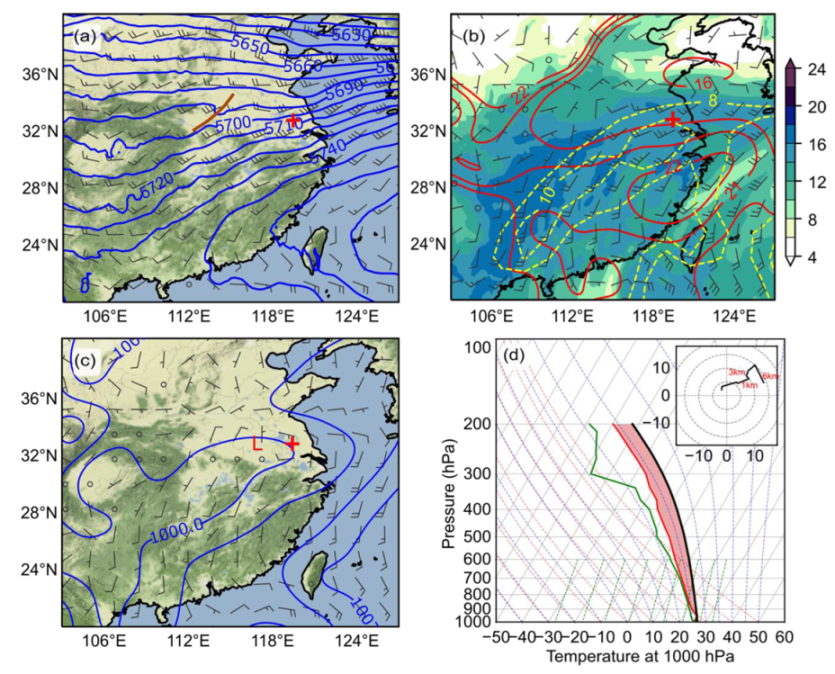
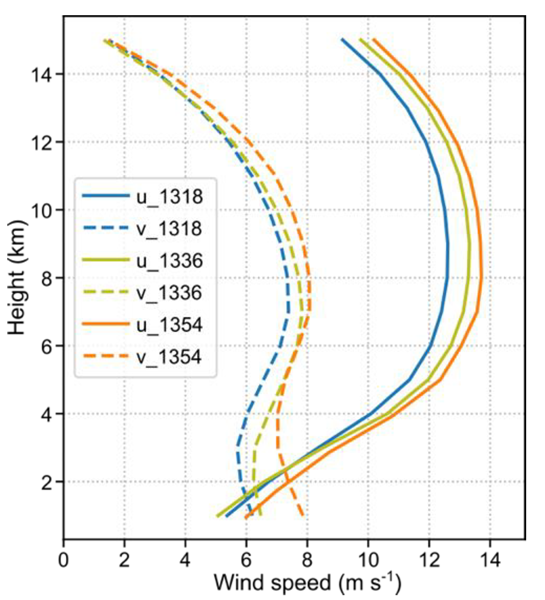
3.1. Synoptic Background
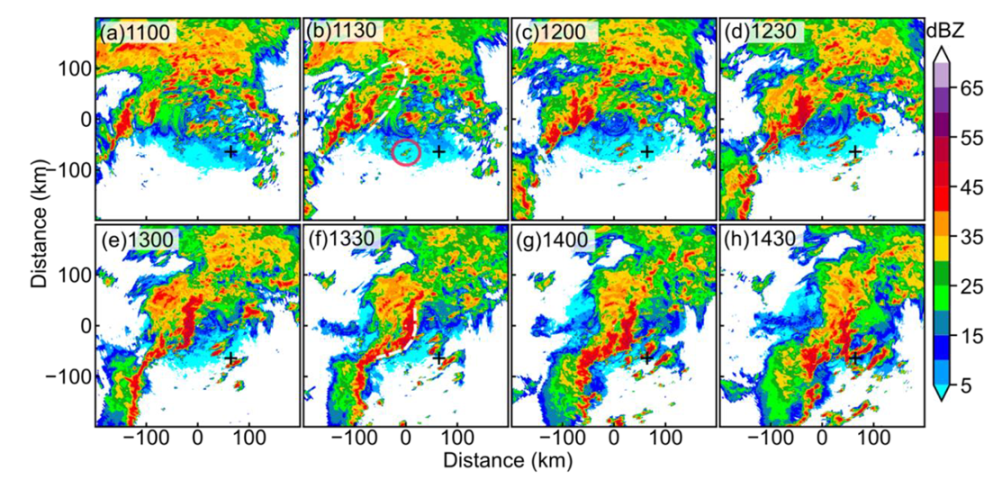
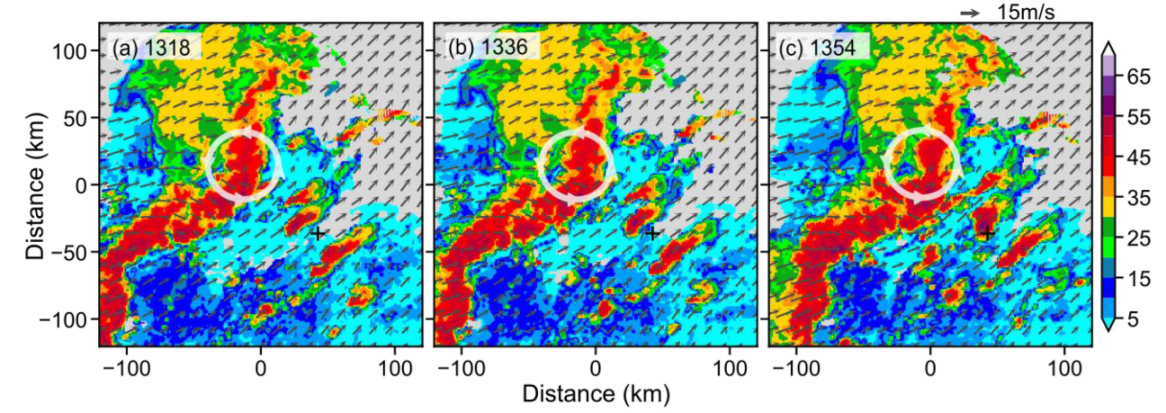
3.2. Evolution of the Squall Line and the Supercell
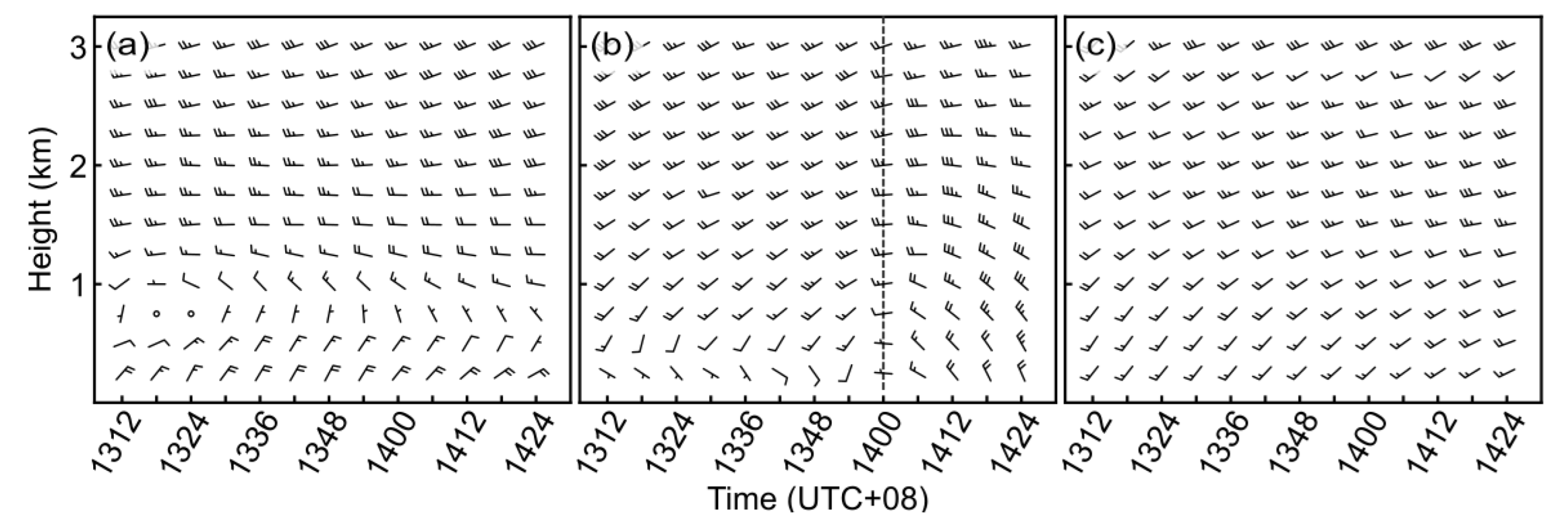
3.3. Intensity Evolution of the Supercell
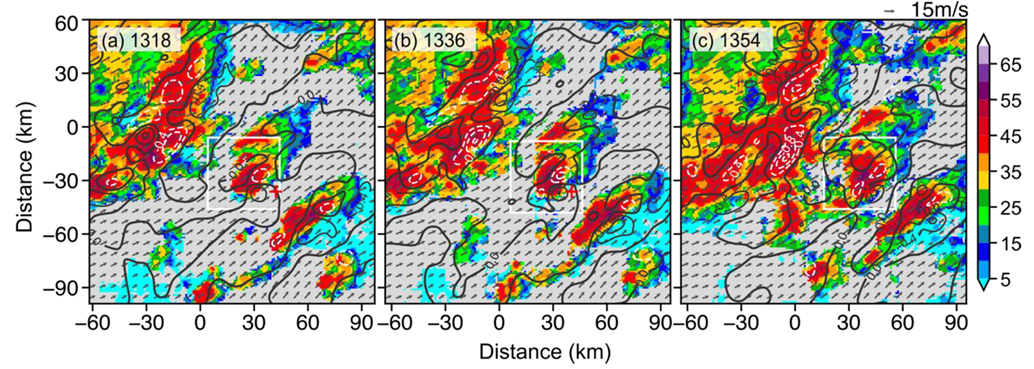
4. Interaction between the Squall Line and the Supercell
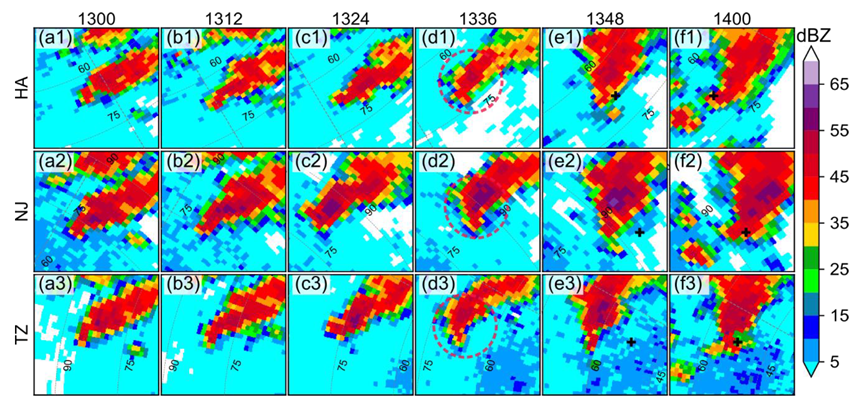
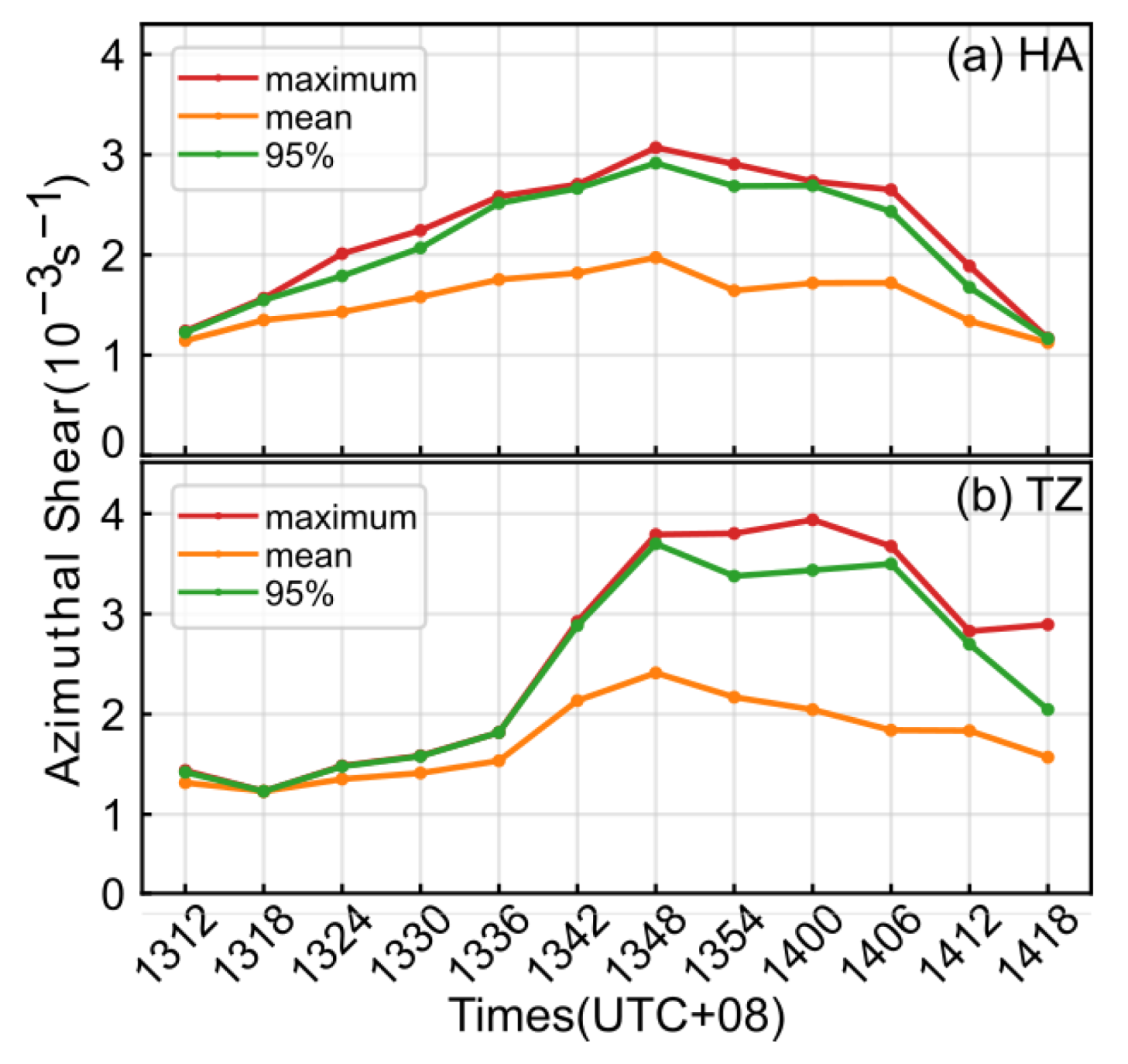
4.1. The Squall Line
4.2. The Bow Echo
5. Discussion and Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brooks, H.E.; James, W.L.; Jeffrey, P.C. The Spatial Distribution of Severe Thunderstorm and Tornado Environments from Global Reanalysis Data. Atmos. Res. 2003, 67, 73–94. [Google Scholar] [CrossRef]
- Fan, W.J.; Yu, X.D. Characteristics of Spatial-Temporal Distribution of Tornadoes in China. Meteorol. Mon. 2015, 41, 793–805. [Google Scholar]
- Bai, L.Q.; Meng, Z.Y.; Huang, L.; Yan, L.J.; Li, Z.H.; Mai, X.H.; Huang, Y.P.; Yao, D.; Wang, X. An Integrated Damage, Visual, and Radar Analysis of the 2015 Foshan, Guangdong, EF3 Tornado in China Produced by the Landfalling Typhoon Mujigae (2015). Bull. Am. Meteorol. Soc. 2017, 98, 2619–2640. [Google Scholar] [CrossRef]
- Meng, Z.Y.; Bai, L.Q.; Zhang, M.R.; Wu, Z.F.; Li, Z.H.; Pu, M.J.; Zheng, Y.G.; Wang, X.H.; Yao, D.; Xue, M.; et al. The Deadliest Tornado (EF4) in the Past 40 Years in China. Weather Forecast. 2018, 33, 693–713. [Google Scholar] [CrossRef]
- Hirth, B.D.; Schroeder, J.L.; Weiss, C.C. Surface Analysis of the Rear-Flank Downdraft Outflow in Two Tornadic Supercells. Mon. Weather Rev. 2008, 136, 2344–2363. [Google Scholar] [CrossRef]
- Karstens, C.D.; Samaras, T.M.; Lee, B.D.; Gallus, W.A.; Finley, C.A. Near-Ground Pressure and Wind Measurements in Tornadoes*. Mon. Weather Rev. 2010, 138, 2570–2588. [Google Scholar] [CrossRef] [Green Version]
- Edwards, R.; LaDue, J.G.; Ferree, J.T.; Scharfenberg, K.; Maier, C.; Coulbourne, W.L. Tornado Intensity Estimation: Past, Present, and Future. Bull. Am. Meteorol. Soc. 2013, 94, 641–653. [Google Scholar] [CrossRef]
- Stout, G.E.; Huff, F.A. Radar Records Illinois Tornadogenesis. Bull. Am. Meteorol. Soc. 1953, 34, 281–284. [Google Scholar]
- Garrett, R.A.; Rockney, V.D. Mornadoes in northeastern Kansas, May 19, 1960. Mon. Weather Rev. 1962, 90, 231–240. [Google Scholar] [CrossRef]
- Donaldson, R.J. Vortex Signature Recognition by a Doppler Radar. J. Appl. Meteorol. 1970, 9, 661–670. [Google Scholar] [CrossRef] [Green Version]
- Brown, R.A.; Lemon, L.R.; Burgess, D.W. Tornado Detection by Pulsed Doppler Radar. Mon. Weather Rev. 1978, 106, 29–38. [Google Scholar] [CrossRef]
- Stumpf, G.J.; Witt, A.; Mitchell, E.D.; Spencer, P.L.; Johnson, J.T.; Eilts, M.D.; Thomas, K.W.; Burgess, D.W. The National Severe Storms Laboratory Mesocyclone Detection Algorithm for the WSR-88D*. Weather Forecast. 1998, 13, 304–326. [Google Scholar] [CrossRef]
- Mitchell, E.; Vasiloff, S. The national severe storms laboratory tornado detection algorithm. Weather Forecast. 1998, 13, 352–366. [Google Scholar] [CrossRef]
- Trapp, R.J.; Tessendorf, S.A.; Godfrey, E.S.; Brooks, H.E. Tornadoes from Squall Lines and Bow Echoes. Part I: Climatological Distribution. Weather Forecast. 2005, 20, 23–34. [Google Scholar] [CrossRef]
- Markowski, P.; Richardson, Y. Mesoscale Meteorology in Midlatitudes; John Wiley & Scons, Ltd.: Hoboken, NJ, USA, 2010; pp. 32–33. ISBN 978-047-074-213-6. [Google Scholar]
- Forbes, G.S. On the Reliability of Hook Echoes as Tornado Indicators. Mon. Weather Rev. 1981, 109, 1457–1466. [Google Scholar] [CrossRef] [Green Version]
- Trapp, R.J.; Stumpf, G.J.; Manross, K.L. A Reassessment of the Percentage of Tornadic Mesocyclones. Weather Forecast. 2005, 20, 680–687. [Google Scholar] [CrossRef]
- Burgess, D.W.B.; Donaldson, R.J.; Desrochers, P.R. Tornado detection and warning by radar. In Geophysical Monograph Series; Church, C., Burgess, D., Doswell, C., Davies-Jone, R., Eds.; American Geophysical Union: Washington, DC, USA, 1993; Volume 79, pp. 203–221. [Google Scholar]
- Wakimoto, R.M.; Wilson, J.W. Non-supercell Tornadoes. Mon. Weather Rev. 1989, 117, 1113–1140. [Google Scholar] [CrossRef]
- Brady, R.H.; Szoke, E.J. A Case Study of Nonmesocyclone Tornado Development in Northeast Colorado: Similarities to Waterspout Formation. Mon. Weather Rev. 1989, 117, 843–856. [Google Scholar] [CrossRef] [Green Version]
- Funk, T.W.; Darmofal, K.E.; Kirkpatrick, J.D.; DeWald, V.L.; Przybylinski, R.W.; Schmocker, G.K.; Lin, Y.-J. Storm Reflectivity and Mesocyclone Evolution Associated with the 15 April 1994 Squall Line over Kentucky and Southern Indiana. Weather Forecast. 1999, 14, 976–993. [Google Scholar] [CrossRef]
- DeWald, V.L.; Funk, T.W. WSR-88D reflectivity and velocity trends of a damaging squall line event on 20 April 1996 over south-central Indiana and central Kentucky. In Proceedings of the 20th Conference on Severe Local Storms, Orlando, FL, USA, 11–15 September 2000. [Google Scholar]
- Trapp, R.J.; Weisman, M.L. Low-Level Mesovortices within Squall Lines and Bow Echoes. Part II: Their Genesis and Implications. Mon. Weather Rev. 2003, 131, 2804–2823. [Google Scholar] [CrossRef] [Green Version]
- Atkins, N.T.; Laurent, M.S. Bow Echo Mesovortices. Part I: Processes That Influence Their Damaging Potential. Mon. Weather Rev. 2009, 137, 1497–1513. [Google Scholar] [CrossRef]
- Penn, S.; Pierce, C.; McGuire, J.K. The Squall Line and Massachusetts Tornadoes of June 9, 1953. Bull. Am. Meteorol. Soc. 1955, 36, 109–122. [Google Scholar] [CrossRef]
- Goodman, S.J.; Knupp, K.R. Tornadogenesis via Squall Line and Supercell Interaction: The November 15, 1989, Huntsville, Alabama, Tornado, in the Tornado: Its Structure, Dynamics, Prediction, and Hazards; Church, C., Burgess, D., Dosewell, C., Davies-Jone, R., Eds.; American Geophysical Union: Washington, DC, USA, 1993; Volume 79, pp. 183–199. ISBN 978-087-590-038-4. [Google Scholar]
- Wolf, P.L. WSR-88D Radar Depiction of Supercell–Bow Echo Interaction: Unexpected Evolution of a Large, Tornadic, “Comma-Shaped” Supercell over Eastern Oklahoma. Weather Forecast. 1998, 13, 492–504. [Google Scholar] [CrossRef]
- French, A.J.; Parker, M.D. Observations of Mergers between Squall Lines and Isolated Supercell Thunderstorms. Weather Forecast. 2012, 27, 255–278. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Yu, X.; Zhang, Y.; Zhou, Z.; Xie, W.; Lu, Y.; Yu, J.; Wei, L. Climate analysis of tornadoes in China. J. Meteorol. Res. 2015, 29, 359–369. [Google Scholar] [CrossRef]
- Bargen, D.W.; Brown, R.C. Interactive Radar Velocity Unfolding. In Proceedings of the 19th Conference on Radar Meteorology, Miami Beach, FL, USA, 15–18 April 1980; Volume 60, pp. 1485–1519. [Google Scholar]
- Steiner, M.; Smith, J.A. Use of Three-Dimensional Reflectivity Structure for Automated Detection and Removal of Nonprecipitating Echoes in Radar Data. J. Atmos. Ocean. Technol. 2002, 19, 673–686. [Google Scholar] [CrossRef]
- Bell, M.M.; Lee, W.-C.; Wolff, C.A.; Cai, H. A Solo-Based Automated Quality Control Algorithm for Airborne Tail Doppler Radar Data. J. Appl. Meteorol. Climatol. 2013, 52, 2509–2528. [Google Scholar] [CrossRef] [Green Version]
- Lee, W.-C.; Tang, X.; Jou, B.J.-D. Distance Velocity–Azimuth Display (DVAD)—New Interpretation and Analysis of Doppler Velocity. Mon. Weather. Rev. 2014, 142, 573–589. [Google Scholar] [CrossRef] [Green Version]
- Tang, X.; Lee, W.-C.; Wang, Y. Nonlinear Wind Analysis of Single-Doppler Radar Observations within a DVAD Framework. J. Appl. Meteorol. Climatol. 2015, 54, 1538–1555. [Google Scholar] [CrossRef]
- Gamache, J.F. Evaluation of a fully-three dimensional variational Doppler analysis technique. In Proceedings of the 28th Conference on Radar Meteorology, Austin, TX, USA, 7–12 September 1997; pp. 422–423. [Google Scholar]
- Edwards, R.; Thompson, R.L. RUC-2 supercell proximity soundings, Part II: An independent assessment of supercell forecast parameters. In Proceedings of the 20th Conference on Severe Local Storms, Orlando, FL, USA, 11–15 September 2000. [Google Scholar]
- Tompson, R.L.; Edwards, R.; Hart, J.A.; Elmore, K.L.; Markowski, P. Close Proximity Soundings within Supercell Environments Obtained from the Rapid Update Cycle. Weather Forecast. 2003, 18, 1243–1261. [Google Scholar] [CrossRef] [Green Version]
- Resmussen, E.N. Refined supercell and tornado forecast parameters. Weather. Forecast. 2003, 18, 530–535. [Google Scholar] [CrossRef] [Green Version]
- Weisman, M.L. Bow Echoes: A Tribute to T. T. Fujita. Bull. Am. Meteorol. Soc. 2001, 82, 97–116. [Google Scholar] [CrossRef] [Green Version]
- Smith, T.M.; Elmore, K. The use of radial velocity derivative to diagnose rotation and divergence. In Proceedings of the 11th Conference on Aviation, Range and Aerospace, Hyannis, MA, USA, 3–8 October 2004. [Google Scholar]
- Palmer, R.D.; Bodine, D.; Kumjian, M.; Cheong, B.; Zhang, G.; Cao, Q.; Bluestein, H.B.; Ryzhkov, A.; Yu, T.-Y.; Wang, Y. Observations of the 10 May 2010 Tornado Outbreak Using OU-PRIME: Potential for New Science with High-Resolution Polarimetric Radar. Bull. Am. Meteorol. Soc. 2011, 92, 871–891. [Google Scholar] [CrossRef] [Green Version]
- Noda, A.T.; Niino, H. Genesis and Structure of a Major Tornado in a Numerically-Simulated Supercell Storm: Importance of Vertical Vorticity in a Gust Front. SOLA 2005, 1, 5–8. [Google Scholar] [CrossRef]
- Li, N.; Wei, M.; Tang, X.; Pan, Y. An improved velocity volume processing method. Adv. Atmos. Sci. 2007, 24, 893–906. [Google Scholar] [CrossRef]
- Chrisman, J.; Smith, S. Enhanced Velocity Azimuth Display Wind Profile (EVWP) Function for the WSR-88D. In Proceedings of the 34th Conference on Radar Meteorology, Williamsburg, VA, USA, 5–9 October 2009. [Google Scholar]
- Lee, B.D.; Wilhelmson, R.B. The Numerical Simulation of Non-Supercell Tornadogenesis. Part I: Initiation and Evolution of Pretornadic Misocyclone Circulations along a Dry Outflow Boundary. J. Atmos. Sci. 1997, 54, 32–60. [Google Scholar] [CrossRef]
- Schenkman, A.D.; Xue, M. Bow-echo mesovortices: A review. Atmos. Res. 2016, 170, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Weisman, M.L. The Genesis of Severe, Long-Lived Bow Echoes. J. Atmos. Sci. 1993, 50, 645–670. [Google Scholar] [CrossRef]
- Davies-Jones, R. Streamwise Vorticity: The Origin of Updraft Rotation in Supercell Storms. J. Atmos. Sci. 1984, 41, 2991–3006. [Google Scholar] [CrossRef] [Green Version]
- Davies-Jones, R.; Trapp, R.J.; Bluestein, H.B. Tornadoes and Tornadic Storms. In Severe Convective Storms, Boston; Meteorological Society: Boston, MA, USA, 2001; pp. 167–221. [Google Scholar]
- Dahl, J.M.L. Tilting of Horizontal Shear Vorticity and the Development of Updraft Rotation in Supercell Thunderstorms. J. Atmos. Sci. 2017, 74, 2997–3020. [Google Scholar] [CrossRef]
- Rotunno, R.; Klemp, J.B. The Influence of the Shear-Induced Pressure Gradient on Thunderstorm Motion. Mon. Weather Rev. 1982, 110, 136–151. [Google Scholar] [CrossRef] [Green Version]
- Rotunno, R.; Klemp, J.B. On the Rotation and Propagation of Simulated Supercell Thunderstorms. J. Atmos. Sci. 1985, 42, 271–292. [Google Scholar] [CrossRef]
- Thompson, R.L.; Mead, C.M.; Edwards, R. Effective Storm-Relative Helicity and Bulk Shear in Supercell Thunderstorm Environments. Weather Forecast. 2007, 22, 102–115. [Google Scholar] [CrossRef]
- Davenport, C.E. Environmental Evolution of Long-Lived Supercell Thunderstorms in the Great Plains. Weather Forecast. 2021, 36, 2187–2209. [Google Scholar] [CrossRef]


| Radar | Longitude | Latitude | Band | Resolution (m) | Detection Range (km) | ||
|---|---|---|---|---|---|---|---|
| Reflectivity | Velocity | Reflectivity | Velocity | ||||
| NJ | 118.69 | 32.191 | S | 1000 | 250 | 460 | 230 |
| TZ | 119.99 | 32.557 | S | 1000 | 250 | 460 | 230 |
| HA | 119.02 | 33.62 | S | 1000 | 250 | 460 | 230 |
| JH | 119.11 | 32.979 | X | 60 | 60 | 75 | 75 |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| CAPE | SRH0–1 | VWS0–1 | |||
| CIN | SRH0–3 | VWS0–3 | |||
| VWS0–6 |
| Time | VWS0–1 | VWS0–3 | VWS0–6 | SRH0–1 | SRH0–3 |
|---|---|---|---|---|---|
| 1318 | 46 m2 s−2 | ||||
| 1336 | |||||
| 1354 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Tang, X.; Xu, F.; Zhang, F. Multi-Scale Interaction between a Squall Line and a Supercell and Its Impact on the Genesis of the “0612” Gaoyou Tornado. Atmosphere 2022, 13, 272. https://doi.org/10.3390/atmos13020272
Tang J, Tang X, Xu F, Zhang F. Multi-Scale Interaction between a Squall Line and a Supercell and Its Impact on the Genesis of the “0612” Gaoyou Tornado. Atmosphere. 2022; 13(2):272. https://doi.org/10.3390/atmos13020272
Chicago/Turabian StyleTang, Jiajia, Xiaowen Tang, Fen Xu, and Fugui Zhang. 2022. "Multi-Scale Interaction between a Squall Line and a Supercell and Its Impact on the Genesis of the “0612” Gaoyou Tornado" Atmosphere 13, no. 2: 272. https://doi.org/10.3390/atmos13020272
APA StyleTang, J., Tang, X., Xu, F., & Zhang, F. (2022). Multi-Scale Interaction between a Squall Line and a Supercell and Its Impact on the Genesis of the “0612” Gaoyou Tornado. Atmosphere, 13(2), 272. https://doi.org/10.3390/atmos13020272






