Spatio-Temporal Variability in Hydroclimate over the Upper Yangtze River Basin, China
Abstract
:1. Introduction
2. Study Site and Climatic Data
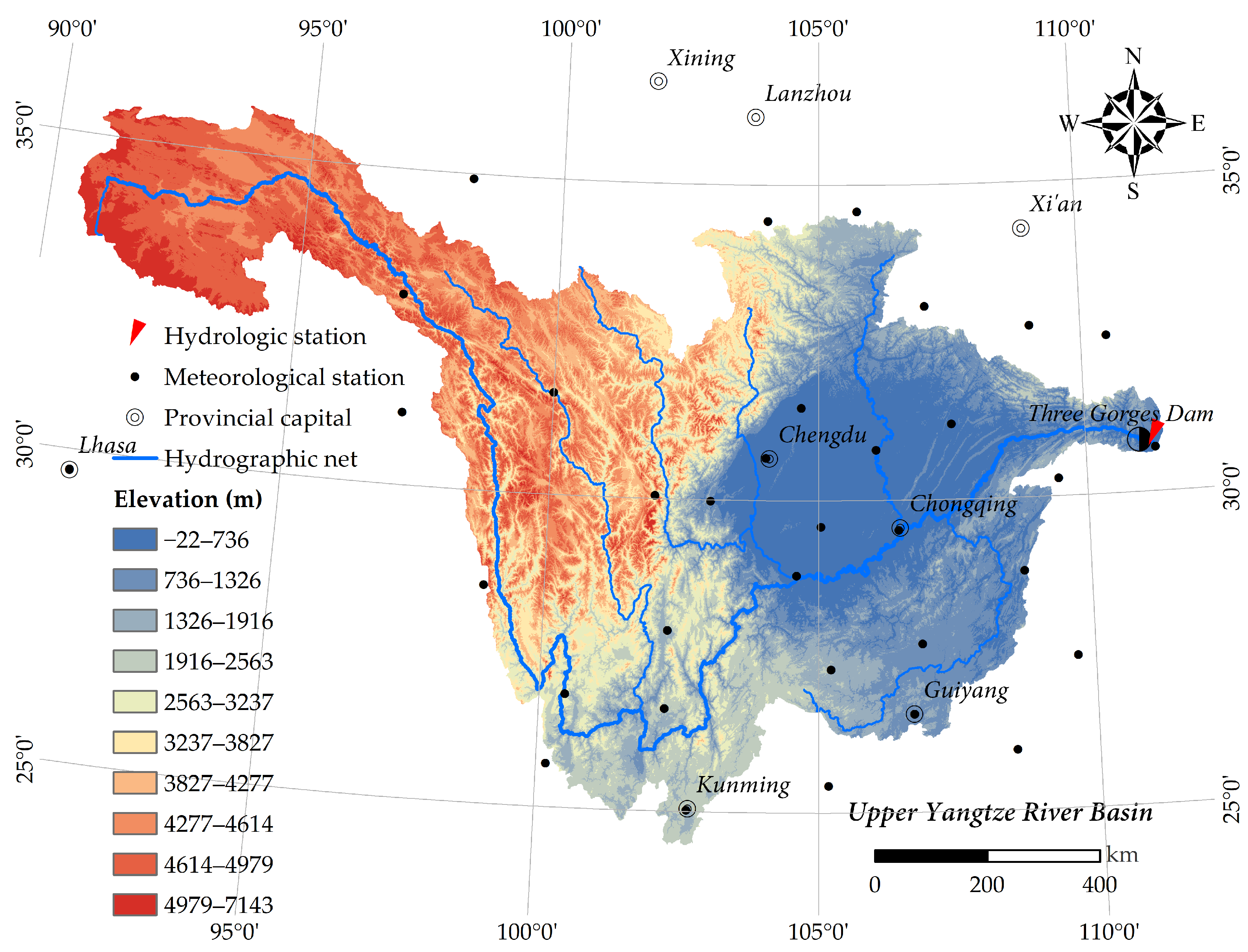
2.1. Study Site
2.2. Climatic Data
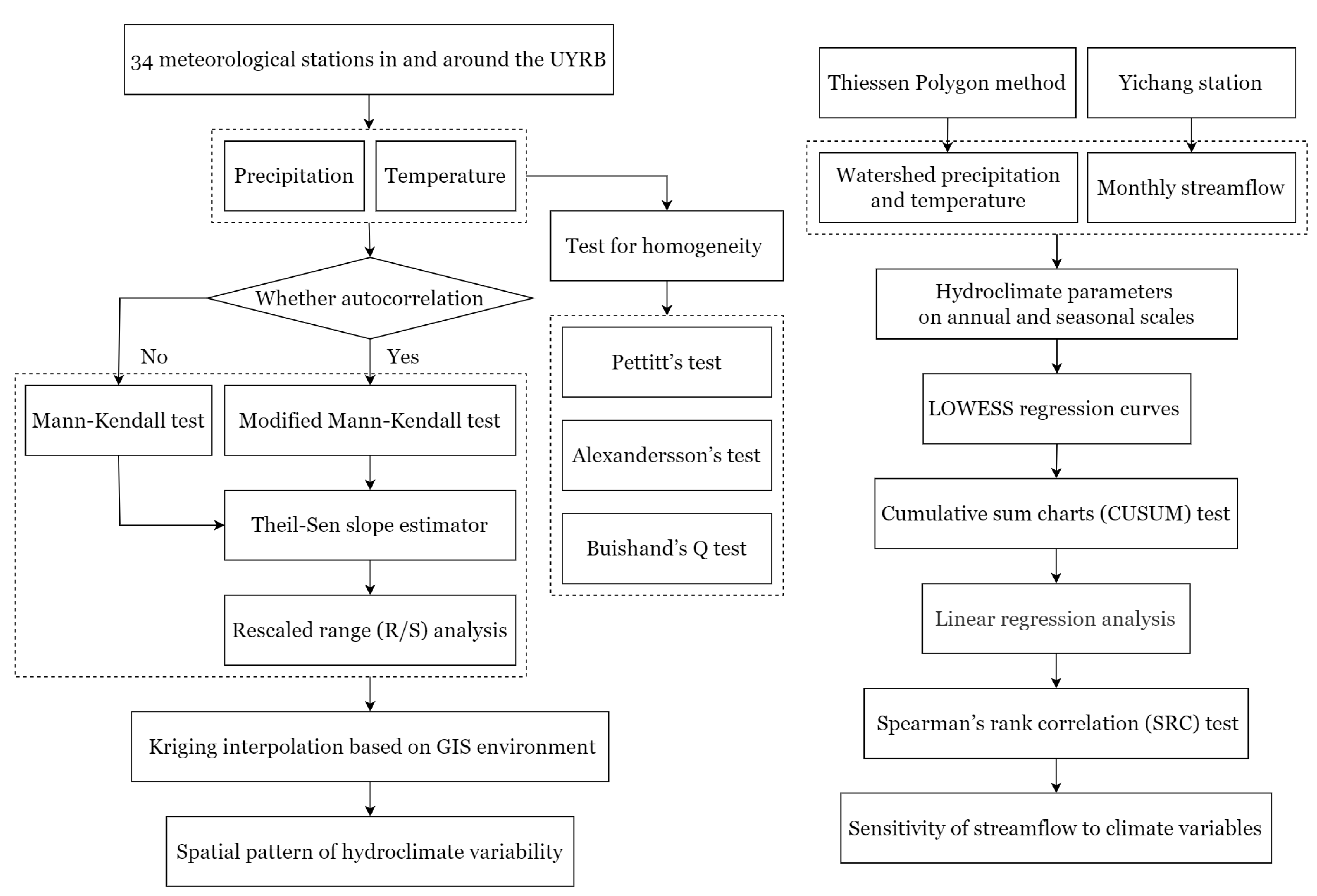
3. Methodology
4. Results and Discussion
4.1. Preliminary Analysis
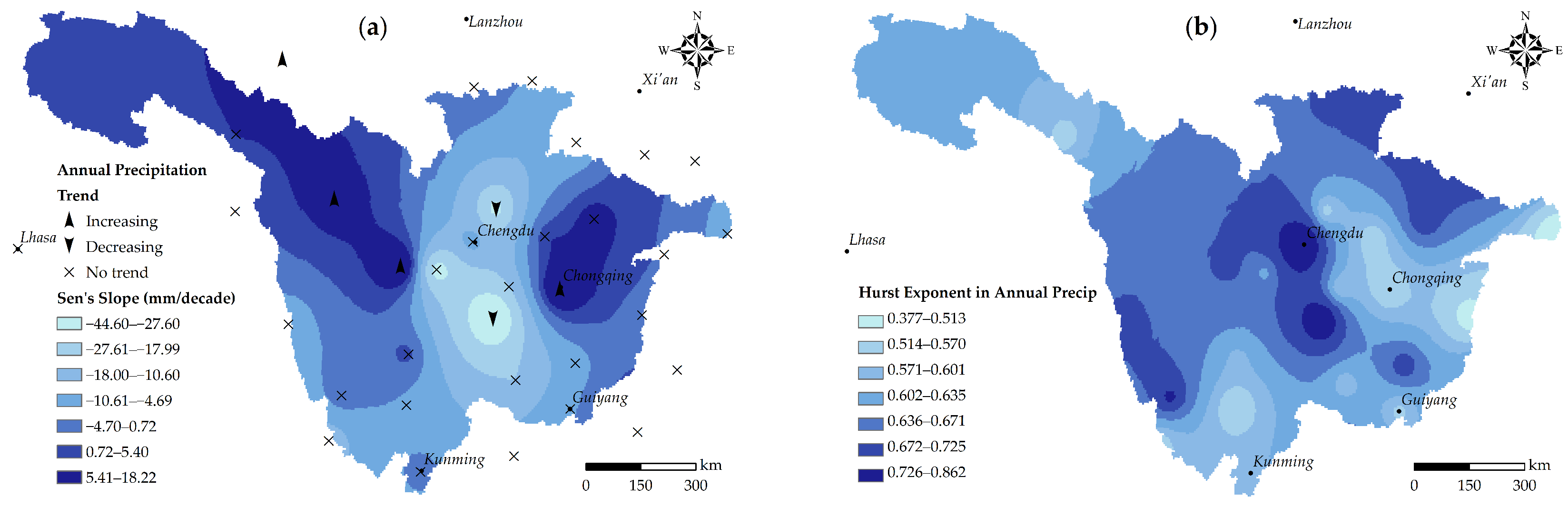
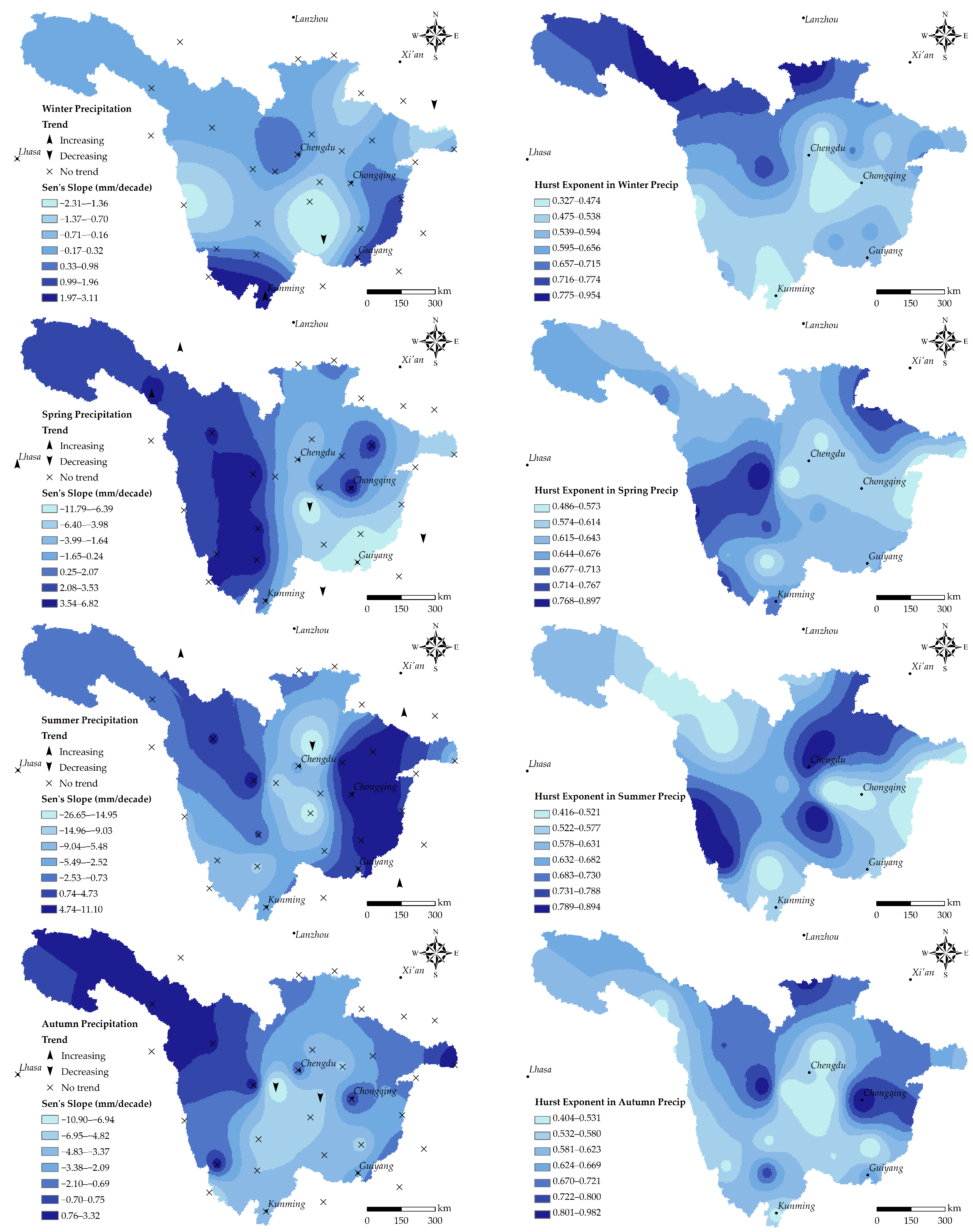
4.2. Temporal and Spatial Patterns of Precipitation Variability
4.2.1. Rainfall Trends on Annual and Seasonal Scales
4.2.2. Homogeneity Test
4.3. Temporal and Spatial Patterns of Temperature Variability
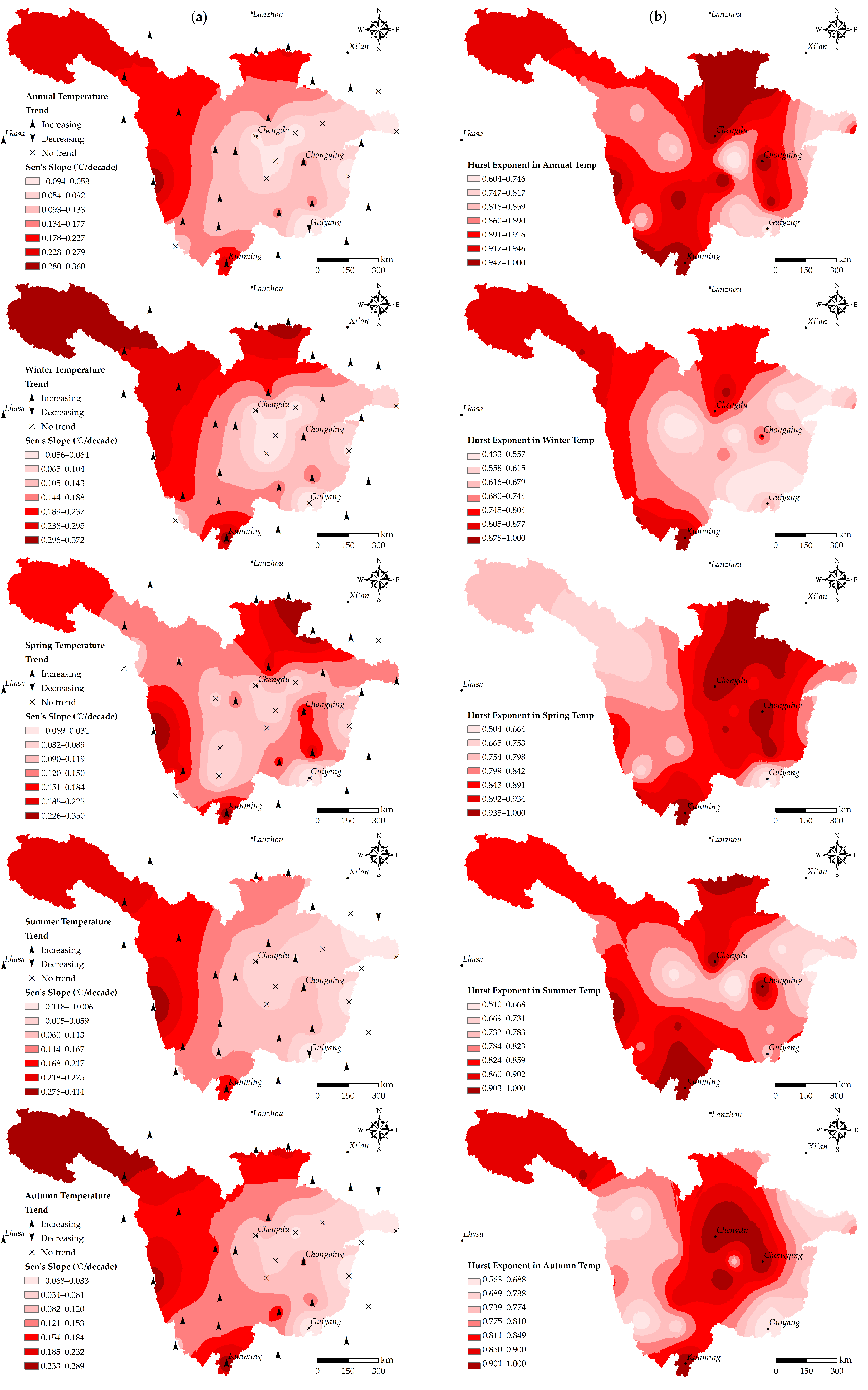
4.3.1. Temperature Trends on Annual and Seasonal Scales
4.3.2. Homogeneity Test
4.4. Temporal Variations in Hydroclimatic Variables
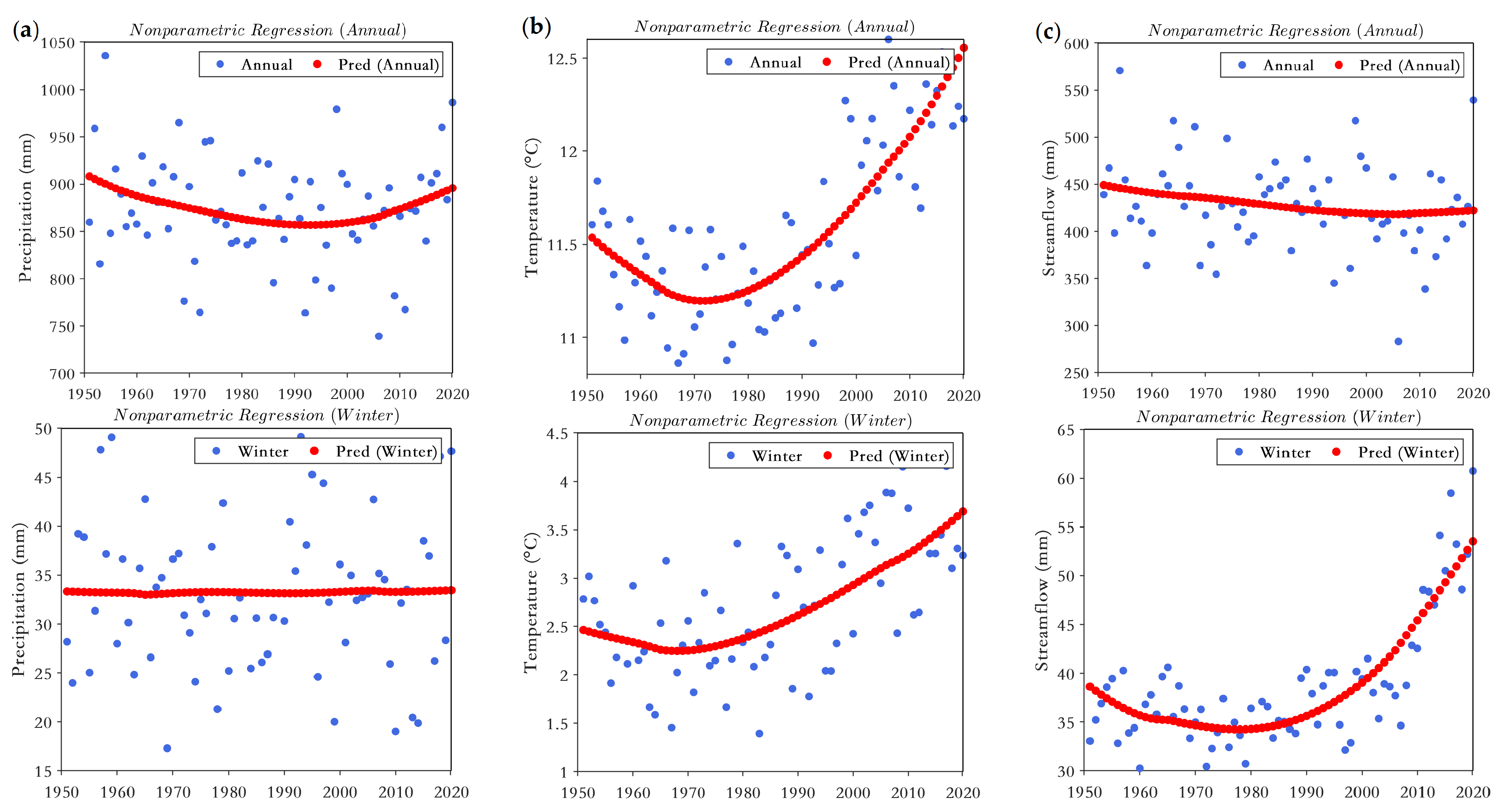
4.4.1. Long-Term Pattern on Annual and Seasonal Scales
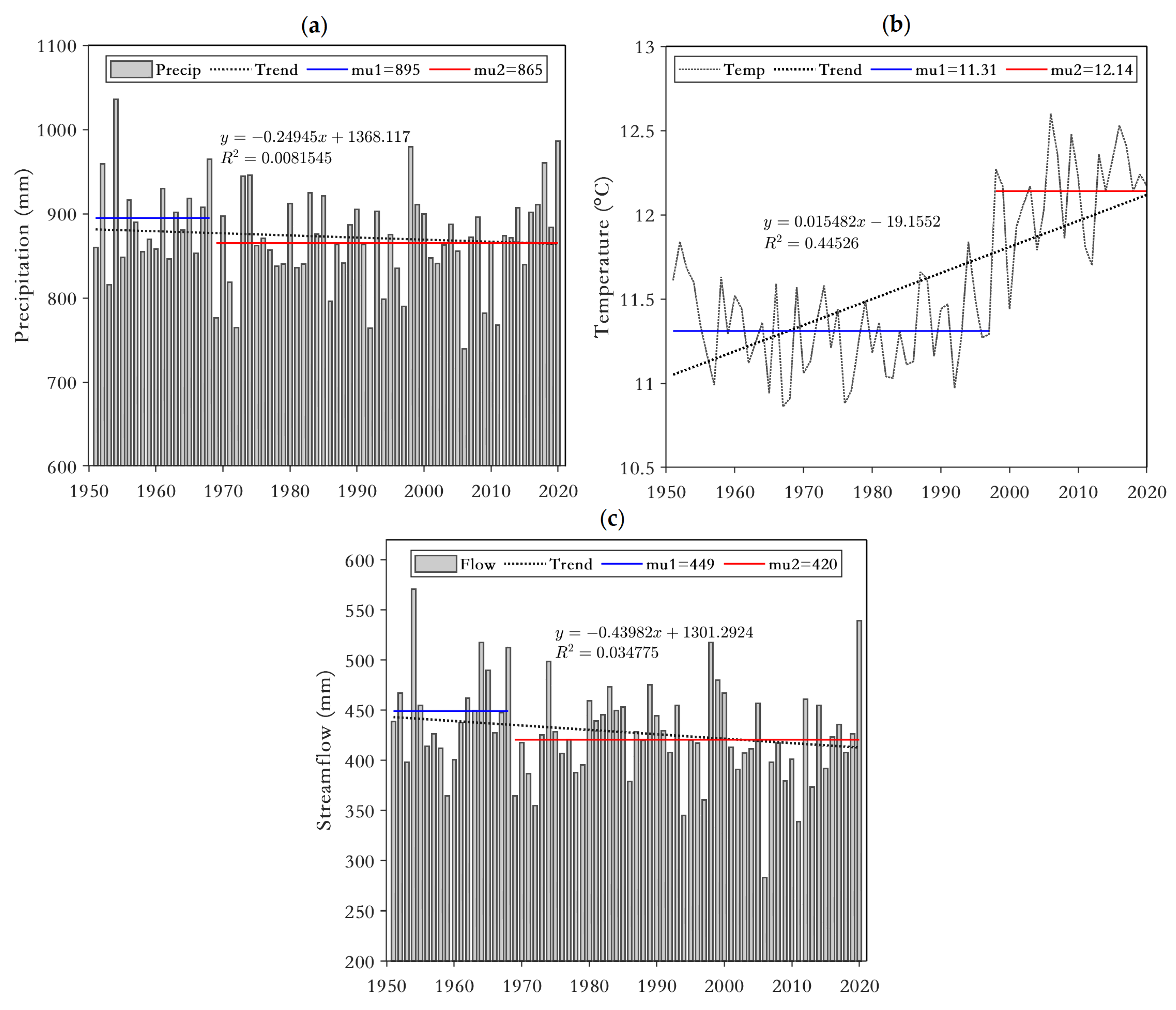
4.4.2. Change Point Detection
4.4.3. Linear Regression Analysis
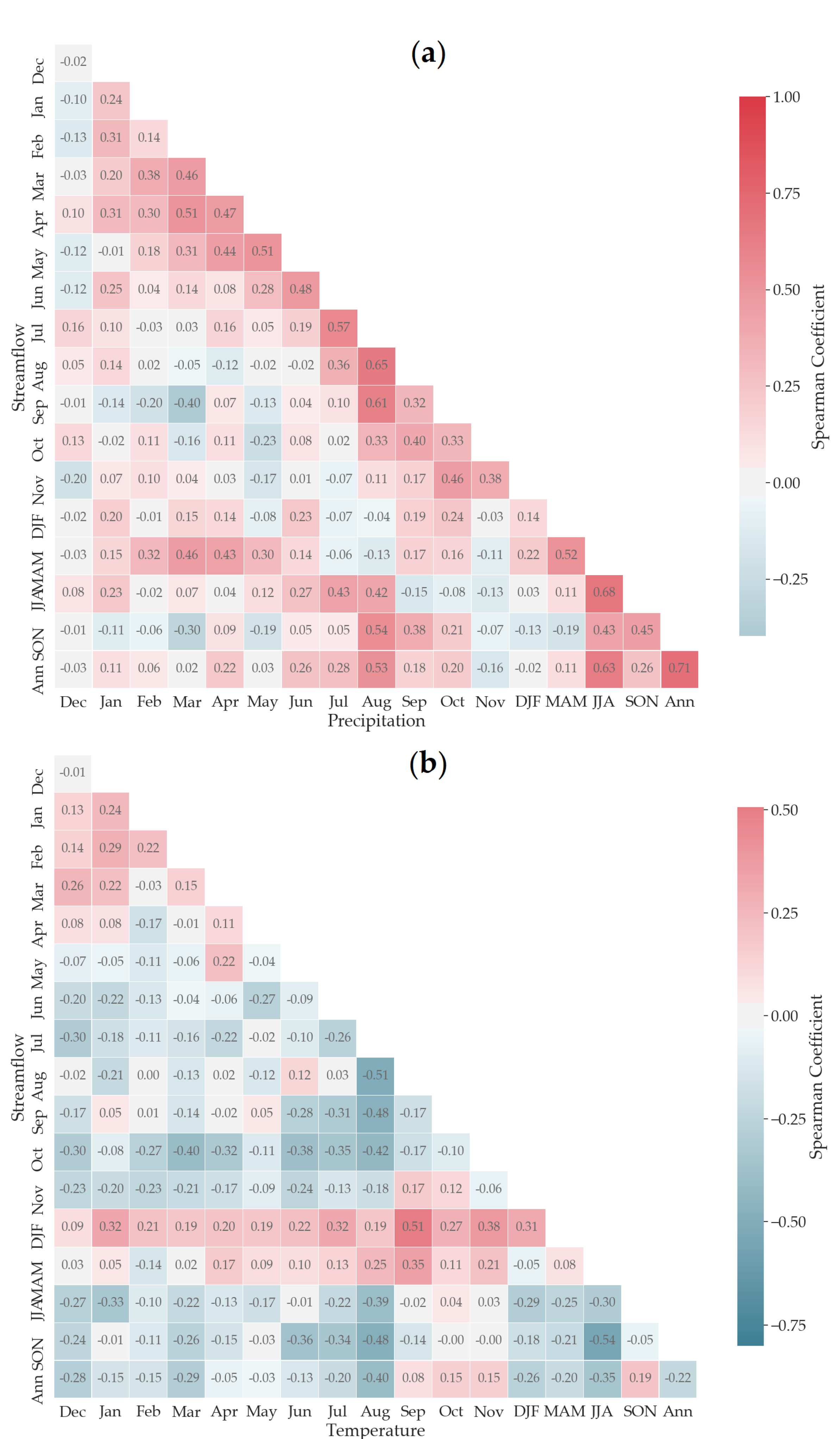
4.5. Sensibility of Streamflow to Climatic Variables
5. Conclusions
- (i).
- The annual rainfall series of 29 out of 34 stations appear homogeneous, while only 3 out of 34 stations are homogeneous in temperature, indicating that 31 series of annual mean temperature have long-term movement during the recorded period, among which the change years (jump points in the mean value) of 20 series occur around the year 1997; that is, the multi-year average value in annual mean temperature has changed thereafter.
- (ii).
- Annual precipitation in the central basin shows a significant decreasing trend, decreasing mainly in summer, while the annual precipitation in the eastern and western parts of the basin show a significant increasing trend. However, for annual and seasonal scales, there are few detectable trends and consistent significant changes in precipitation at most stations. However, mean air temperature shows a significant upward trend on both annual and seasonal scales throughout the basin, except for a minority of sites in the eastern catchment.
- (iii).
- In general, the increasing magnitude in temperature in high altitudes (Tibetan Plateau) is higher than that in low altitudes (Sichuan Plain). The mean air temperature exhibit a Hurst phenomenon on annual and seasonal scales, i.e., the (positive) persistence of temperature. The significant uptrend in high-altitude (such as Tibetan Plateau) temperatures in the future may be comparable with that of the last seven decades in this region.
- (iv).
- The Three Gorges Dam (TGD) provides an effective water-storage and regulation effect on seasonal runoff of Yichang station. Since the TGD was put into operation in 2003, runoff has increased sharply in winter and spring (dry season) and decreased in summer and autumn (rainy season), especially in autumn, while there is no consistent change in precipitation in the basin on the corresponding scale. Hence, the seasonal streamflow variation in the basin can be attributed to high-intensity anthropogenic activities, mainly the intra-annual regulation of the Three Gorges Reservoir (TGR). The TGR releases water during the dry season and stores water during the rainy season to provide water for the dry season.
- (v).
- The watershed precipitation and streamflow from 1951 to 2020 both changed abruptly in 1968, and the mean temperature changed significantly abruptly in 1997 (with a p-value of <0.001 by the Pettitt test). The significant upward trend in annual mean temperature combined with the downward trend in annual precipitation and runoff indicate the amount of available water resources in the basin decreased and the climate tended to be warmer and drier.
- (vi).
- Although the runoff at Yichang station has been strongly impacted by the TGD, the response of annual runoff to dam operation cannot be detected. The annual streamflow is mainly controlled by climatic fluctuation (i.e., variations in precipitation). Changes in post-dam runoff are governed by changing rainfall and dam regulation [39]. The variations in post-dam runoff can be interpreted by considering the probable effects of rainfall variability and dam regulation.
- (vii).
- Runoff in the UYRB is more sensitive to changes in precipitation than changes in temperature. The variation in annual precipitation can explain 71% of annual runoff variability. In contrast, the mean annual temperature has a smaller effect on annual runoff, explaining only −22% of the variability. Overall, runoff is positively correlated with precipitation and negatively correlated with temperature, with increased temperature promoting increased evapotranspiration over the watershed, which leads to a decrease in runoff.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Methodology
Appendix A.1. Autocorrelation Test
Appendix A.2. Trend Detection
Appendix A.2.1. Mann–Kendall Test
Appendix A.2.2. Modified Mann–Kendall Test
Appendix A.3. Trend Slope
Appendix A.4. Test for Homogeneity
Appendix A.4.1. Pettitt’s Test
Appendix A.4.2. Alexandersson’s SNHT Test
Appendix A.4.3. Buishand’s Q Test
Appendix A.5. R/S Analysis
Appendix A.6. Kriging Method
Appendix A.7. Thiessen Polygon Method
Appendix A.8. Cumulative Sum Charts
Appendix A.9. Spearman’s Rank Correlation Coefficient Test
Appendix B
| Number | Station | Code | WMO Number | Latitude (°N) | Longitude (°E) |
|---|---|---|---|---|---|
| 1 | Yushu | YUS | 56029 | 33.02 | 97.02 |
| 2 | Ganzi | GAN | 56146 | 31.62 | 100 |
| 3 | Mianyang | MAY | 56196 | 31.47 | 104.68 |
| 4 | Ya’an | YAN | 56287 | 29.98 | 103 |
| 5 | Chengdu | CHE | 56294 | 30.67 | 104.02 |
| 6 | Kangding | KAN | 56374 | 30.05 | 101.97 |
| 7 | Yibin | YIB | 56492 | 28.8 | 104.6 |
| 8 | Xichang | XIC | 56571 | 27.9 | 102.27 |
| 9 | Lijiang | LIJ | 56651 | 26.83 | 100.47 |
| 10 | Huili | HUI | 56671 | 26.65 | 102.25 |
| 11 | Kunming | KUN | 56778 | 25.02 | 102.68 |
| 12 | Daxian | DAX | 57328 | 31.2 | 107.5 |
| 13 | Nanchong | NAN | 57411 | 30.8 | 106.08 |
| 14 | Enshi | ENS | 57447 | 30.28 | 109.47 |
| 15 | Yichang | YIC | 57461 | 30.7 | 111.3 |
| 16 | Neijiang | NEI | 57504 | 29.58 | 105.05 |
| 17 | Chongqing | CHO | 57516 | 29.52 | 106.48 |
| 18 | Youyang | YOU | 57633 | 28.83 | 108.77 |
| 19 | Bijie | BIJ | 57707 | 27.3 | 105.23 |
| 20 | Zunyi | ZUN | 57713 | 27.7 | 106.88 |
| 21 | Guiyang | GUI | 57816 | 26.58 | 106.72 |
| 22 | Maduo | MAD | 56033 | 34.92 | 98.22 |
| 23 | Minxian | MIN | 56093 | 34.43 | 104.01 |
| 24 | Changdu | CHA | 56137 | 31.15 | 97.17 |
| 25 | Deqin | DEQ | 56444 | 28.5 | 98.9 |
| 26 | Dali | DAL | 56751 | 25.7 | 100.18 |
| 27 | Tianshui | TAS | 57006 | 34.58 | 105.75 |
| 28 | Hanzhong | HAN | 57127 | 33.07 | 107.03 |
| 29 | Ankang | ANK | 57245 | 32.72 | 109.03 |
| 30 | Zhijiang | ZHI | 57745 | 27.45 | 109.68 |
| 31 | Xingren | XIN | 57902 | 25.43 | 105.18 |
| 32 | Lahsa | LAS | 55591 | 29.67 | 91.13 |
| 33 | Rongjiang | RON | 57932 | 25.97 | 108.53 |
| 34 | Yunxian | YUN | 57253 | 32.51 | 110.49 |
| Station | Annual | Winter | Spring | Summer | Autumn | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Z | Slope | Z | Slope | Z | Slope | Z | Slope | Z | Slope | |
| YUS | 1.04 | 5.45 | 0.10 | 0.00 | 3.15 | 4.00 | −0.41 | −2.07 | 1.82 | 2.41 |
| GAN | 2.33 | 11.90 | 0.38 | 0.18 | 1.35 | 3.75 | 1.24 | 5.45 | 0.40 | 1.05 |
| MAY | −2.00 | −29.21 | −0.23 | 0.00 | −1.77 | −3.79 | −2.15 | −26.67 | −0.98 | −4.44 |
| YAN | −1.83 | −30.00 | 0.36 | 0.40 | 0.02 | 0.00 | −0.69 | −12.29 | −5.04 | −10.88 |
| CHE | −0.69 | −8.75 | 0.53 | 0.43 | −1.31 | −3.64 | −0.51 | −4.21 | −0.24 | −0.95 |
| KAN | 5.39 | 16.47 | −0.10 | 0.00 | 1.95 | 6.79 | 1.72 | 7.41 | 0.49 | 1.67 |
| YIB | −2.98 | −44.67 | −1.90 | −1.89 | −4.10 | −11.76 | −1.88 | −20.48 | −1.29 | −6.18 |
| XIC | 0.14 | 1.61 | −0.64 | −0.36 | 1.18 | 4.80 | 0.09 | 1.11 | −1.54 | −6.59 |
| LIJ | −0.25 | −1.88 | 1.23 | 0.33 | 1.17 | 3.53 | −1.03 | −7.02 | 0.27 | 1.67 |
| HUI | −0.43 | −5.67 | 0.93 | 0.54 | 1.86 | 6.49 | −1.17 | −10.00 | −0.85 | −4.80 |
| KUN | −0.45 | −2.80 | 4.64 | 2.67 | 0.14 | 0.71 | −0.55 | −3.72 | nan | −3.53 |
| DAX | 0.66 | 9.60 | −0.01 | 0.00 | 1.00 | 4.55 | 1.19 | 11.03 | −0.23 | −2.13 |
| NAN | 0.34 | 3.70 | −0.48 | −0.39 | 0.11 | 0.50 | 0.82 | 8.48 | −0.96 | −5.22 |
| ENS | −0.01 | −0.17 | −0.61 | −0.48 | −0.72 | −4.50 | 0.13 | 1.76 | −0.15 | −1.67 |
| YIC | −1.10 | −8.37 | 0.05 | 0.00 | −1.79 | −6.44 | −0.64 | −8.44 | 1.02 | 3.33 |
| NEI | −1.19 | −18.15 | −1.45 | −1.00 | 0.48 | 1.61 | nan | −6.47 | −1.97 | −5.64 |
| CHO | 2.55 | 18.00 | 0.05 | 0.00 | 1.05 | 5.56 | 1.24 | 10.48 | 0.07 | 0.50 |
| YOU | −0.15 | −2.59 | 0.83 | 1.18 | −0.79 | −4.74 | 0.44 | 4.40 | −0.58 | −2.94 |
| BIJ | −1.86 | −17.50 | −2.16 | −1.85 | −1.75 | −5.17 | −0.66 | −4.00 | −0.92 | −3.83 |
| ZUN | −0.90 | −8.26 | 0.08 | 0.00 | −1.75 | −8.33 | 1.04 | 7.71 | −1.01 | −5.79 |
| GUI | −0.46 | −6.11 | 0.72 | 1.07 | −1.42 | −8.89 | 0.32 | 3.03 | −0.60 | −2.92 |
| MAD | 2.75 | 11.67 | 0.80 | 0.36 | 3.52 | 3.85 | 2.04 | 5.33 | 1.79 | 2.38 |
| MIN | 0.17 | 1.25 | −0.53 | 0.00 | −0.38 | −0.74 | 0.46 | 1.77 | −0.22 | −0.43 |
| CHA | −0.05 | −0.47 | −0.27 | 0.00 | 1.28 | 2.08 | −0.93 | −3.44 | 1.65 | 3.49 |
| DEQ | −1.44 | −10.81 | −1.85 | −1.61 | 0.69 | 2.33 | −1.67 | −6.50 | −0.47 | −1.52 |
| DAL | −1.14 | −15.08 | 1.35 | 2.63 | 1.02 | 4.69 | −1.33 | −8.51 | −1.18 | −7.65 |
| TAS | −0.95 | −5.24 | −0.26 | 0.00 | 0.74 | 1.86 | −0.75 | −4.07 | −1.35 | −4.00 |
| HAN | −1.31 | −13.25 | −1.72 | −1.16 | −0.25 | −0.86 | −0.76 | −7.00 | −0.11 | −0.94 |
| ANK | 0.85 | 7.42 | −0.37 | −0.25 | −1.32 | −4.17 | 2.17 | 8.97 | −0.25 | −1.82 |
| ZHI | −0.10 | −0.86 | 0.70 | 2.25 | −2.50 | −16.73 | 1.69 | 17.12 | −0.23 | −1.43 |
| XIN | −0.88 | −8.57 | −0.09 | 0.00 | −2.43 | −13.75 | 0.94 | 7.21 | −1.10 | −4.55 |
| LAS | 0.98 | 5.29 | 0.84 | 0.00 | 3.00 | 2.55 | −0.10 | −0.89 | 0.35 | 0.70 |
| RON | 1.54 | 16.67 | 1.43 | 2.26 | 0.30 | 0.98 | 2.59 | 13.67 | 1.03 | 5.38 |
| YUN | −0.41 | −4.00 | −3.32 | −2.34 | −1.19 | −4.92 | 0.28 | 1.90 | −0.20 | −1.11 |
| Station | Pettitt’s Test | SNHT | Buishand’s Q Test | ||||||
|---|---|---|---|---|---|---|---|---|---|
| K Value | Year | Trend | To Value | Year | Trend | Q Value | Year | Trend | |
| YUS | 256 | 2007 | Ho | 5.13 | 2016 | Ho | 0.82 | 2007 | Ho |
| GAN | 336 | 2010 | Ho | 9.65 | 2011 | Ha | 1.09 | 2010 | Ho |
| MAY | 479 | 1984 | Ha | 10.09 | 1961 | Ha | 1.40 | 1984 | Ha |
| YAN | 325 | 1992 | Ho | 4.88 | 1961 | Ho | 0.95 | 1992 | Ho |
| CHE | 368 | 1967 | Ho | 7.64 | 2012 | Ho | 1.10 | 1967 | Ho |
| KAN | 559 | 1983 | Ha | 11.00 | 1983 | Ha | 1.67 | 1983 | Ha |
| YIB | 547 | 1991 | Ha | 8.98 | 1991 | Ha | 1.49 | 1991 | Ha |
| XIC | 249 | 1959 | Ho | 4.07 | 1957 | Ho | 0.66 | 1959 | Ho |
| LIJ | 292 | 2004 | Ho | 4.21 | 2004 | Ho | 0.87 | 2004 | Ho |
| HUI | 225 | 2005 | Ho | 1.98 | 2005 | Ho | 0.58 | 2005 | Ho |
| KUN | 193 | 1976 | Ho | 1.41 | 2001 | Ho | 0.53 | 1986 | Ho |
| DAX | 217 | 1962 | Ho | 2.78 | 1962 | Ho | 0.67 | 1972 | Ho |
| NAN | 220 | 2006 | Ho | 4.60 | 1952 | Ho | 0.71 | 1975 | Ho |
| ENS | 223 | 1961 | Ho | 2.75 | 2019 | Ho | 0.57 | 1961 | Ho |
| YIC | 148 | 1970 | Ho | 6.58 | 2019 | Ho | 0.39 | 1965 | Ho |
| NEI | 313 | 1991 | Ho | 4.39 | 1991 | Ho | 1.04 | 1991 | Ho |
| CHO | 304 | 2013 | Ho | 7.86 | 2013 | Ho | 0.90 | 1995 | Ho |
| YOU | 171 | 1977 | Ho | 5.10 | 2019 | Ho | 0.54 | 1983 | Ho |
| BIJ | 482 | 1984 | Ha | 10.63 | 1957 | Ha | 1.39 | 1983 | Ha |
| ZUN | 327 | 2002 | Ho | 3.31 | 2004 | Ho | 0.80 | 2002 | Ho |
| GUI | 230 | 2013 | Ho | 4.62 | 1954 | Ho | 0.78 | 1977 | Ho |
| MAD | 585 | 1988 | Ha | 10.71 | 2004 | Ha | 1.55 | 1988 | Ha |
| MIN | 276 | 2011 | Ho | 9.24 | 2017 | Ha | 0.89 | 2011 | Ho |
| CHA | 316 | 1986 | Ho | 3.41 | 1986 | Ho | 0.93 | 1986 | Ho |
| DEQ | 268 | 1966 | Ho | 3.94 | 2010 | Ho | 0.71 | 1966 | Ho |
| DAL | 297 | 2002 | Ho | 5.12 | 2009 | Ho | 0.87 | 2002 | Ho |
| TAS | 317 | 1990 | Ho | 3.19 | 1968 | Ho | 0.79 | 1990 | Ho |
| HAN | 364 | 1990 | Ho | 4.78 | 1984 | Ho | 1.10 | 1984 | Ho |
| ANK | 277 | 2002 | Ho | 3.63 | 2002 | Ho | 0.84 | 2002 | Ho |
| ZHI | 234 | 1972 | Ho | 4.61 | 2019 | Ho | 0.77 | 1972 | Ho |
| XIN | 314 | 1997 | Ho | 4.64 | 2008 | Ho | 0.92 | 1997 | Ho |
| LAS | 380 | 1997 | Ho | 3.55 | 1997 | Ho | 0.89 | 1997 | Ho |
| RON | 310 | 2014 | Ho | 11.80 | 2014 | Ha | 0.97 | 2014 | Ho |
| YUN | 210 | 1990 | Ho | 1.25 | 1964 | Ho | 0.55 | 1990 | Ho |
| Station | Annual | Winter | Spring | Summer | Autumn | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Z | Slope | Z | Slope | Z | Slope | Z | Slope | Z | Slope | |
| YUS | 5.22 | 0.22 | 3.75 | 0.29 | 3.06 | 0.13 | 5.52 | 0.25 | 4.41 | 0.25 |
| GAN | 3.60 | 0.21 | 4.39 | 0.28 | 2.56 | 0.12 | 4.26 | 0.21 | 2.59 | 0.16 |
| MAY | 2.49 | 0.15 | 3.24 | 0.20 | 2.51 | 0.20 | 2.19 | 0.11 | 3.30 | 0.13 |
| YAN | 3.44 | 0.10 | 2.19 | 0.12 | 2.65 | 0.14 | 2.09 | 0.07 | 3.84 | 0.11 |
| CHE | 0.96 | 0.04 | 0.98 | 0.05 | 0.95 | 0.07 | 0.38 | 0.01 | 1.73 | 0.08 |
| KAN | 3.96 | 0.12 | 2.98 | 0.17 | 1.18 | 0.07 | 3.32 | 0.12 | 4.25 | 0.16 |
| YIB | 1.07 | 0.05 | 0.10 | 0.00 | 1.16 | 0.10 | 1.30 | 0.05 | 1.87 | 0.08 |
| XIC | 3.08 | 0.10 | 2.15 | 0.14 | 0.88 | 0.04 | 3.32 | 0.11 | 3.12 | 0.14 |
| LIJ | 5.02 | 0.17 | 4.78 | 0.22 | 3.73 | 0.19 | 5.06 | 0.17 | 3.23 | 0.13 |
| HUI | 1.98 | 0.10 | 3.89 | 0.15 | 0.16 | 0.02 | 2.32 | 0.09 | 2.31 | 0.12 |
| KUN | 3.96 | 0.27 | 3.69 | 0.33 | 3.14 | 0.25 | 4.83 | 0.23 | 4.07 | 0.27 |
| DAX | 1.90 | 0.07 | 2.48 | 0.11 | 2.28 | 0.11 | 0.52 | 0.03 | 1.59 | 0.06 |
| NAN | 0.20 | 0.01 | 0.57 | 0.02 | 0.97 | 0.05 | −0.43 | −0.02 | 0.24 | 0.01 |
| ENS | 1.99 | 0.08 | 2.42 | 0.12 | 2.57 | 0.11 | 0.37 | 0.02 | 1.29 | 0.05 |
| YIC | 1.24 | 0.04 | 1.65 | 0.07 | 3.08 | 0.14 | −1.36 | −0.07 | −0.28 | −0.01 |
| NEI | 0.83 | 0.02 | 0.40 | 0.02 | 0.73 | 0.04 | −0.08 | 0.00 | 1.95 | 0.05 |
| CHO | 2.85 | 0.14 | 2.88 | 0.15 | 2.68 | 0.18 | 2.24 | 0.11 | 2.76 | 0.12 |
| YOU | 0.09 | 0.00 | 0.84 | 0.04 | 0.67 | 0.03 | −1.26 | −0.06 | −0.51 | −0.03 |
| BIJ | 4.45 | 0.14 | 2.78 | 0.17 | 2.40 | 0.16 | 2.97 | 0.11 | 3.77 | 0.17 |
| ZUN | 5.44 | 0.15 | 3.46 | 0.18 | 3.85 | 0.21 | 2.94 | 0.11 | 4.74 | 0.14 |
| GUI | −2.26 | −0.09 | −0.99 | −0.06 | −1.66 | −0.09 | −2.87 | −0.12 | −1.79 | −0.07 |
| MAD | 5.62 | 0.29 | 4.63 | 0.39 | 3.98 | 0.15 | 4.81 | 0.24 | 4.50 | 0.31 |
| MIN | 3.86 | 0.22 | 5.06 | 0.30 | 2.66 | 0.17 | 3.10 | 0.18 | 3.37 | 0.19 |
| CHA | 3.41 | 0.14 | 4.31 | 0.22 | 1.10 | 0.05 | 3.13 | 0.14 | 2.21 | 0.11 |
| DEQ | 7.13 | 0.37 | 5.33 | 0.31 | 5.63 | 0.36 | 5.21 | 0.42 | 5.36 | 0.29 |
| DAL | 1.74 | 0.08 | 0.70 | 0.05 | 1.69 | 0.11 | 2.18 | 0.09 | 2.87 | 0.10 |
| TAS | 4.65 | 0.26 | 5.61 | 0.40 | 3.99 | 0.29 | 3.16 | 0.18 | 4.76 | 0.21 |
| HAN | 4.01 | 0.22 | 5.63 | 0.26 | 3.92 | 0.32 | 2.12 | 0.11 | 4.38 | 0.18 |
| ANK | 2.59 | 0.10 | 3.95 | 0.18 | 2.82 | 0.18 | −1.08 | −0.05 | 3.04 | 0.09 |
| ZHI | 4.66 | 0.12 | 4.35 | 0.19 | 4.13 | 0.18 | 0.48 | 0.02 | 1.96 | 0.09 |
| XIN | 3.20 | 0.15 | 2.59 | 0.18 | 2.03 | 0.14 | 4.55 | 0.13 | 3.83 | 0.18 |
| LAS | 5.54 | 0.38 | 6.52 | 0.47 | 3.95 | 0.25 | 6.81 | 0.33 | 6.47 | 0.41 |
| RON | 3.99 | 0.14 | 2.73 | 0.18 | 3.52 | 0.16 | 3.38 | 0.12 | 5.12 | 0.15 |
| YUN | −0.57 | −0.03 | 2.76 | 0.06 | 1.75 | 0.12 | −3.37 | −0.20 | −2.10 | −0.10 |
| Station | Pettitt’s Test | SNHT | Buishand’s Q Test | ||||||
|---|---|---|---|---|---|---|---|---|---|
| K Value | Year | Trend | To Value | Year | Trend | Q Value | Year | Trend | |
| YUS | 900 | 1986 | Ha | 31.33 | 1997 | Ha | 2.65 | 1997 | Ha |
| GAN | 832 | 1997 | Ha | 30.43 | 2002 | Ha | 2.46 | 1997 | Ha |
| MAY | 988 | 1993 | Ha | 36.70 | 1996 | Ha | 2.93 | 1993 | Ha |
| YAN | 832 | 1996 | Ha | 27.59 | 1996 | Ha | 2.51 | 1996 | Ha |
| CHE | 710 | 1993 | Ha | 19.77 | 1993 | Ha | 2.18 | 1993 | Ha |
| KAN | 819 | 1997 | Ha | 29.01 | 1997 | Ha | 2.55 | 1997 | Ha |
| YIB | 651 | 1997 | Ha | 18.90 | 1997 | Ha | 2.06 | 1997 | Ha |
| XIC | 714 | 1997 | Ha | 22.13 | 2001 | Ha | 2.13 | 2000 | Ha |
| LIJ | 885 | 1993 | Ha | 35.74 | 2004 | Ha | 2.80 | 1997 | Ha |
| HUI | 730 | 2004 | Ha | 29.16 | 2008 | Ha | 2.27 | 2004 | Ha |
| KUN | 1134 | 1992 | Ha | 48.12 | 1993 | Ha | 3.40 | 1993 | Ha |
| DAX | 748 | 1997 | Ha | 27.40 | 2012 | Ha | 2.28 | 1997 | Ha |
| NAN | 441 | 1996 | Ha | 9.61 | 2005 | Ha | 1.48 | 1996 | Ha |
| ENS | 648 | 1997 | Ha | 26.39 | 2012 | Ha | 2.07 | 1997 | Ha |
| YIC | 503 | 1996 | Ha | 12.69 | 1996 | Ha | 1.70 | 1996 | Ha |
| NEI | 434 | 1997 | Ho | 8.45 | 1997 | Ho | 1.37 | 1997 | Ha |
| CHO | 905 | 1996 | Ha | 31.49 | 1997 | Ha | 2.67 | 1996 | Ha |
| YOU | 383 | 2011 | Ho | 12.79 | 2011 | Ha | 1.21 | 2011 | Ho |
| BIJ | 889 | 1997 | Ha | 32.80 | 1997 | Ha | 2.71 | 1997 | Ha |
| ZUN | 942 | 1997 | Ha | 37.30 | 1997 | Ha | 2.89 | 1997 | Ha |
| GUI | 629 | 1999 | Ha | 15.70 | 1999 | Ha | 1.83 | 1999 | Ha |
| MAD | 1023 | 1997 | Ha | 38.34 | 1997 | Ha | 2.93 | 1997 | Ha |
| MIN | 1018 | 1996 | Ha | 40.52 | 1997 | Ha | 3.03 | 1996 | Ha |
| CHA | 816 | 1997 | Ha | 30.07 | 2004 | Ha | 2.40 | 1997 | Ha |
| DEQ | 1059 | 1993 | Ha | 41.94 | 1993 | Ha | 3.18 | 1993 | Ha |
| DAL | 662 | 1997 | Ha | 23.08 | 2004 | Ha | 2.05 | 2002 | Ha |
| TAS | 1123 | 1993 | Ha | 47.95 | 1993 | Ha | 3.40 | 1993 | Ha |
| HAN | 1074 | 1996 | Ha | 48.19 | 1996 | Ha | 3.32 | 1996 | Ha |
| ANK | 800 | 1996 | Ha | 23.98 | 1996 | Ha | 2.34 | 1996 | Ha |
| ZHI | 881 | 1997 | Ha | 30.86 | 1997 | Ha | 2.63 | 1997 | Ha |
| XIN | 805 | 1997 | Ha | 27.41 | 1997 | Ha | 2.48 | 1997 | Ha |
| LAS | 1105 | 1992 | Ha | 48.07 | 1997 | Ha | 3.32 | 1992 | Ha |
| RON | 986 | 1997 | Ha | 41.62 | 1997 | Ha | 3.05 | 1997 | Ha |
| YUN | 407 | 1979 | Ho | 8.11 | 2012 | Ho | 1.37 | 1979 | Ha |
References
- Caloiero, T. Analysis of rainfall trend in New Zealand. Environ. Earth Sci. 2015, 73, 6297–6310. [Google Scholar] [CrossRef]
- IPCC Working Group I Contribution to the IPCC Fifth Assessment Report, Climate Change 2013: The Physical Science Basis: Summary for Policymakers. Available online: http://www.cmcc.it/wp-content/uploads/2012/12/lista-autori-wgi-ar5.pdf (accessed on 27 January 2021).
- Chen, J.; Gao, C.; Zeng, X.; Xiong, M.; Wang, Y.; Jing, C.; Krysanova, V.; Huang, J.; Zhao, N.; Su, B. Assessing changes of river discharge under global warming of 1.5 °C and 2 °C in the upper reaches of the Yangtze River Basin: Approach by using multiple-GCMs and hydrological models. Quat. Int. 2017, 453, 63–73. [Google Scholar] [CrossRef]
- Chen, Y.; Takeuchi, K.; Xu, C.; Chen, Y.; Xu, Z. Regional climate change and its effects on river runoff in the Tarim Basin, China. Hydrol. Process. 2006, 20, 2207–2216. [Google Scholar] [CrossRef]
- Yue, S.; Hashino, M. Long term trends of annual and monthly precipitation in japan. J. Am. Water Resour. Assoc. 2003, 39, 587–596. [Google Scholar] [CrossRef]
- Arnell, N. Climate change and global water resources. Glob. Environ. Change 1999, 9, S31–S49. [Google Scholar] [CrossRef]
- Shen, Z.; Zhang, Q.; Singh, V.; Sun, P.; Song, C.; Yu, H. Agricultural drought monitoring across Inner Mongolia, China: Model development, spatiotemporal patterns and impacts. J. Hydrol. 2019, 571, 793–804. [Google Scholar] [CrossRef]
- Yang, Y.; Weng, B.; Man, Z.; Yu, Z.; Zhao, J. Analyzing the contributions of climate change and human activities on runoff in the Northeast Tibet Plateau. J. Hydrol. Reg. Stud. 2020, 27, 100639. [Google Scholar] [CrossRef]
- Zhao, Y.; Dong, N.; Wang, H. Quantifying the climate and human impacts on the hydrology of the Yalong River Basin using two approaches. River Res. Appl. 2021, 37, 591–604. [Google Scholar] [CrossRef]
- Miller, W.; Piechota, T.; Gangopadhyay, S.; Pruitt, T. Development of streamflow projections under changing climate conditions over Colorado River basin headwaters. Hydrol. Earth Syst. Sci. 2011, 15, 2145–2164. [Google Scholar] [CrossRef] [Green Version]
- Rottler, E.; Francke, T.; Bürger, G.; Bronstert, A. Long-term changes in central European river discharge for 1869–2016: Impact of changing snow covers, reservoir constructions and an intensified hydrological cycle. Hydrol. Earth Syst. Sci. 2020, 24, 1721–1740. [Google Scholar] [CrossRef] [Green Version]
- Okafor, G.; Jimoh, O.; Larbi, I. Detecting Changes in Hydro-Climatic Variables during the Last Four Decades (1975-2014) on Downstream Kaduna River Catchment, Nigeria. Atmos. Clim. Sci. 2017, 7, 161–175. [Google Scholar] [CrossRef] [Green Version]
- Zhao, G.; Hörmann, G.; Fohrer, N.; Zhang, Z.; Zhai, J. Streamflow Trends and Climate Variability Impacts in Poyang Lake Basin, China. Water Resour. Manag. 2010, 24, 689–706. [Google Scholar] [CrossRef]
- Dogan, M.; Ulke, A.; Cigizoglu, H. Trend direction changes of Turkish temperature series in the first half of 1990s. Theor. Appl. Climatol. 2015, 121, 23–39. [Google Scholar] [CrossRef]
- Novotny, E.; Stefan, H. Stream flow in Minnesota: Indicator of climate change. J. Hydrol. 2007, 334, 319–333. [Google Scholar] [CrossRef]
- Adeyeri, O.; Lamptey, B.; Lawin, A.; Sanda, I. Spatio-Temporal Precipitation Trend and Homogeneity Analysis in Komadugu-Yobe Basin, Lake Chad Region. J. Climatol. Weather. Forecast. 2017, 5, 1000214. [Google Scholar] [CrossRef]
- Xu, J.; Chen, Y.; Ji, M.; Lu, F. Climate change and its effects on runoff of Kaidu River, Xinjiang, China: A multiple time-scale analysis. Chin. Geogr. Sci. 2008, 18, 331–339. [Google Scholar] [CrossRef]
- Salehi, S.; Dehghani, M.; Mortazavi, S.; Singh, V. Trend analysis and change point detection of seasonal and annual precipitation in Iran. Int. J. Climatol. 2020, 40, 308–323. [Google Scholar] [CrossRef]
- Taxak, A.; Murumkar, A.; Arya, D. Long term spatial and temporal rainfall trends and homogeneity analysis in Wainganga basin, Central India. Weather. Clim. Extrem. 2014, 4, 50–61. [Google Scholar] [CrossRef] [Green Version]
- Akinsanola, A.; Ogunjobi, K. Recent homogeneity analysis and long-term spatio-temporal rainfall trends in Nigeria. Theor. Appl. Climatol. 2017, 128, 275–289. [Google Scholar] [CrossRef]
- Ologunorisa, T.; Durowoju, O.; Akinbobola, A. Hydroclimatology of the Kaduna River Basin. Am. J. Clim. Change 2021, 10, 353–369. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Climate Change, the Hurst Phenomenon, and Hydrological Statistics. Hydrolog. Sci. J. 2003, 48, 3–24. [Google Scholar] [CrossRef]
- Ray, L.; Goel, N. Spatio-temporal change in rainfall over five different climatic regions of India. J. Water Clim. Chang. 2021, 12, 3124–3142. [Google Scholar] [CrossRef]
- Dabanlı, İ.; Şen, Z.; Yeleğen, M.; Şişman, E.; Selek, B.; Güçlü, Y. Trend Assessment by the Innovative-Şen Method. Water Resour. Manag. 2016, 30, 5193–5203. [Google Scholar] [CrossRef]
- Zhang, X.; Harvey, K.; Hogg, W.; Yuzyk, T. Trends in Canadian streamflow. Water Resour. Res. 2001, 37, 987–998. [Google Scholar] [CrossRef]
- Milly, P.; Betancourt, J.; Falkenmark, M.; Hirsch, R.; Kundzewicz, Z.; Lettenmaier, D.; Stouffer, R. Stationarity Is Dead: Whither Water Management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Guo, S.; Xu, C.; Singh, V. Historical temporal trends of hydro-climatic variables and runoff response to climate variability and their relevance in water resource management in the Hanjiang basin. J. Hydrol. 2007, 344, 171–184. [Google Scholar] [CrossRef]
- Şen, Z. Innovative Trend Analysis Methodology. J. Hydrol. Eng. 2012, 17, 1042–1046. [Google Scholar] [CrossRef]
- Kukul Kurttaş, Y.; Anaç, S.; Yeşilırmak, E.; de Moraes, J. Trends of precipitation and stream-flow in Gediz river basin, Western Turkey. Fresenius Environ. Bull. 2007, 16, 477–488. [Google Scholar]
- Wu, Z.; Huang, N.; Long, S.; Peng, C. On the trend, detrending, and variability of nonlinear and nonstationary time series. Proc. Natl. Acad. Sci. USA 2007, 104, 14889–14894. [Google Scholar] [CrossRef] [Green Version]
- Kahya, E.; Kalayc, S. Trend analysis of streamflow in Turkey. J. Hydrol. 2004, 289, 128–144. [Google Scholar] [CrossRef]
- Tuomenvirta, Heikki Homogeneity testing and adjustment of climatic time series in Finland. Geophysicsa 2002, 38, 15–41.
- Su, B.; Jiang, T.; Jin, W. Recent trends in observed temperature and precipitation extremes in the Yangtze River basin, China. Theor. Appl. Climatol. 2006, 83, 139–151. [Google Scholar] [CrossRef]
- Falarz, M.; Wibig, J.; Matuszko, D.; Filipiak, J.; Hajto, M.; Taszarek, M.; Bielec-Bąkowska, Z.; Wypych, A.; Ustrnul, Z. Homogeneity of Climate Series. In Climate Change in Poland, Springer Climate; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- Zhang, X.; Vincent, L.; Hogg, W.; Niitsoo, A. Temperature and Precipitation Trends in Canada During the 20th Century. Atmosphere-ocean 2000, 38, 395–429. [Google Scholar] [CrossRef]
- Hall, M. The interpretation of non-homogeneous hydrometeorological time series: A case study. Meteorol. Appl. 2003, 10, 61–67. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, C.; Xu, C.; Xu, Y.; Jiang, T. Observed trends of annual maximum water level and streamflow during past 130 years in the Yangtze River basin, China. J. Hydrol. 2006, 324, 255–265. [Google Scholar] [CrossRef]
- Tu, M. Assessment of the effects of climate variability and land use change on the hydrology of the Meuse River Basin. In Hydrology and Geo-Environmental Sciences; A.A. Balkema Publishers: Avereest, The Netherlands, 2006. [Google Scholar]
- Su, Z.; Ho, M.; Hao, Z.; Lall, U.; Sun, X.; Chen, X.; Yan, L. The impact of the Three Gorges Dam on summer streamflow in the Yangtze River Basin. Hydrol. Process. 2020, 34, 705–717. [Google Scholar] [CrossRef]
- Shi, G.; Ye, P. Assessment on Temporal and Spatial Variation Analysis of Extreme Temperature Indices: A Case Study of the Yangtze River Basin. Int. J. Environ. Res. Public Health 2021, 18, 10936. [Google Scholar] [CrossRef]
- Yuan, Z.; Yin, J.; Wei, M.; Yuan, Y. Spatio-Temporal Variations in the Temperature and Precipitation Extremes in Yangtze River Basin, China during 1961–2020. Atmosphere 2021, 12, 1423. [Google Scholar] [CrossRef]
- Niu, Z.; Feng, L.; Chen, X.; Yi, X. Evaluation and Future Projection of Extreme Climate Events in the Yellow River Basin and Yangtze River Basin in China Using Ensembled CMIP5 Models Data. Int. J. Environ. Res. Public Health 2021, 18, 6029. [Google Scholar] [CrossRef]
- IPCC. Climate change 2013: The physical science basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Cannarozzo, M.; Noto, L.; Viola, F. Spatial distribution of rainfall trends in Sicily (1921–2000). Phys. Chem. Earth 2006, 31, 1201–1211. [Google Scholar] [CrossRef]
- He, B.; Miao, C.; Shi, W. Trend, abrupt change, and periodicity of streamflow in the mainstream of Yellow River. Environ. Monit. Assess. 2013, 185, 6187–6199. [Google Scholar] [CrossRef]
- Tongal, H. Spatiotemporal analysis of precipitation and extreme indices in the Antalya Basin, Turkey. Theor. Appl. Climatol. 2019, 138, 1735–1754. [Google Scholar] [CrossRef]
- Wang, J.; Wang, K.; Qin, T.; Nie, H.; Lv, Z.; Liu, F.; Shi, X.; Hu, Y. Analysis and prediction of LUCC change in Huang-Huai-Hai river basin. Open Geosci. 2020, 12, 1406–1420. [Google Scholar] [CrossRef]
- Khalili, K.; Tahoudi, M.; Mirabbasi, R.; Ahmadi, F. Investigation of spatial and temporal variability of precipitation in Iran over the last half century. Stoch. Environ. Res. Risk Assess. 2016, 30, 1205–1221. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, C.; Tao, H.; Jiang, T.; Chen, Y. Climate changes and their impacts on water resources in the arid regions: A case study of the Tarim River basin, China. Stoch. Environ. Res. Risk Assess. 2010, 24, 349–358. [Google Scholar] [CrossRef]
- Proutsos, N.; Tigkas, D. Growth Response of Endemic Black Pine Trees to Meteorological Variations and Drought Episodes in a Mediterranean Region. Atmosphere 2020, 11, 554. [Google Scholar] [CrossRef]
- Fang, L.; Wang, L.; Chen, W.; Sun, J.; Cao, Q.; Wang, S.; Wang, L. Identifying the impacts of natural and human factors on ecosystem service in the Yangtze and Yellow River Basins. J. Clean. Prod. 2021, 314, 127995. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C. A study of variability of annual river flow of the southern African region. Hydrol. Sci. J. 2002, 47, 983–987. [Google Scholar] [CrossRef]
- Fu, G.; Charles, S.; Viney, N.; Chen, S.; Wu, J. Impacts of climate variability on stream-flow in the Yellow River. Hydrol. Process. 2007, 21, 3431–3439. [Google Scholar] [CrossRef]
- Kundzewicz, Z.; Robson, A. Change detection in hydrological records—A review of the methodology. Hydrolog. Sci. J. 2004, 49, 7–19. [Google Scholar] [CrossRef]
- von Storch, H. Misuses of statistical analysis in climate research. In Analysis of Climate Variability; Springer: Berlin/Heidelberg, Germany, 1999; pp. 11–26. [Google Scholar]
- Fang, Y.; Zhang, X.; Niu, G.; Zeng, W.; Zhu, J.; Zhang, T. Study of the Spatiotemporal Characteristics of Meltwater Contribution to the Total Runoff in the Upper Changjiang River Basin. Water 2017, 9, 165. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Liu, P.; Cheng, L.; Xie, K.; Han, D.; Zhou, L. The temporal variations in runoff-generation parameters of the Xinanjiang model due to human activities: A case study in the upper Yangtze River Basin, China. J. Hydrol. Reg. Stud. 2021, 37, 100910. [Google Scholar] [CrossRef]
- Chen, J.; Finlayson, B.; Wei, T.; Sun, Q.; Webber, M.; Li, M.; Chen, Z. Changes in monthly flows in the Yangtze River, China—With special reference to the Three Gorges Dam. J. Hydrol. 2016, 536, 293–301. [Google Scholar] [CrossRef]
- Sun, J.; Tian, Y.; Liao, W.; Wang, Y. Hydrological impacts of climate change in the upper reaches of the Yangtze River Basin. Quat. Int. 2013, 304, 62–74. [Google Scholar] [CrossRef]
- Yang, X.; Yu, X.; Wang, Y.; Liu, Y.; Zhang, M.; Ren, L.; Yuan, F.; Jiang, S. Estimating the response of hydrological regimes to future projections of precipitation and temperature over the upper Yangtze River. Atmos. Res. 2019, 230, 104627. [Google Scholar] [CrossRef]
- Xu, J.; Yang, D.; Yi, Y.; Lei, Z.; Chen, J.; Yang, W. Spatial and temporal variation of runoff in the Yangtze River Basin during the past 40 years. Quat. Int. 2008, 186, 32–42. [Google Scholar] [CrossRef]
- Zhang, Q.; Tong, J.; Gemmer, M.; Becker, S. Precipitation, temperature and runoff analysis from 1950 to 2002 in the Yangtze basin, China. Hydrolog. Sci. J. 2005, 50, 65–80. [Google Scholar] [CrossRef] [Green Version]
- Hu, M.; Dong, M.; Tian, X.; Wang, L.; Jiang, Y. Trends in Different Grades of Precipitation over the Yangtze River Basin from 1960 to 2017. Atmosphere 2021, 12, 413. [Google Scholar] [CrossRef]
- Wei, X.; Cai, S.; Ni, P.; Zhan, W. Impacts of climate change and human activities on the water discharge and sediment load of the Pearl River, southern China. Sci. Rep. 2020, 10, 16743. [Google Scholar] [CrossRef]
- Solaimani, K.; Habaibnejad, M.; Pirnia, A. Temporal trends of hydro-climatic variables and their relevance in water resource management. Int. J. Sediment Res. 2021, 36, 63–75. [Google Scholar] [CrossRef]
- Peterson, T.; Easterling, D.; Karl, T.; Groisman, P.; Nicholls, N.; Plummer, N.; Torok, S.; Auer, I.; Boehm, R.; Gullett, D.; et al. Homogeneity adjustments of in situ atmospheric climate data: A review. Int. J. Climatol. 1998, 18, 1493–1517. [Google Scholar] [CrossRef]
- Huang, Y.; Xiao, W.; Hou, B.; Zhou, Y.; Hou, G.; Yi, L.; Cui, H. Hydrological projections in the upper reaches of the Yangtze River Basin from 2020 to 2050. Sci. Rep. 2021, 11, 9720. [Google Scholar] [CrossRef] [PubMed]
- Thilessen, A. Precipitation Averages for Large Areas. Mon. Weather. Rev. 1911, 39, 1082–1089. [Google Scholar] [CrossRef]
- Birsan, M.; Molnar, P.; Burlando, P.; Pfaundler, M. Streamflow trends in Switzerland. J. Hydrol. 2005, 314, 312–329. [Google Scholar] [CrossRef]
- Wang, Y.; Lei, X.; Wen, X.; Fang, G.; Tan, Q.; Tian, Y.; Wang, C.; Wang, H. Effects of damming and climatic change on the eco-hydrological system: A case study in the Yalong River, southwest China. Ecol. Indic. 2019, 105, 663–674. [Google Scholar] [CrossRef]
- Chen, J.; Wu, X.; Finlayson, B.; Webber, M.; Wei, T.; Mao, T.; Chen, Z. Variability and trend in the hydrology of the Yangtze River, China: Annual precipitation and runoff. J. Hydrol. 2014, 513, 403–412. [Google Scholar] [CrossRef]
- Xiao, Z.; Shi, P.; Jiang, P.; Hu, J.; Qu, S.; Chen, X.; Chen, Y.; Dai, Y.; Wang, J. The Spatiotemporal Variations of Runoff in the Yangtze River Basin under Climate Change. Adv. Meteorol. 2018, 2018, 5903451. [Google Scholar] [CrossRef] [Green Version]
- Asarian, J.; Walker, J. Long-Term Trends in Streamflow and Precipitation in Northwest California and Southwest Oregon, 1953–2012. J. Am. Water Resour. Assoc. 2016, 52, 241–261. [Google Scholar] [CrossRef]
- Tsiros, I.; Nastos, P.; Proutsos, N.; Tsaousidis, A. Variability of the aridity index and related drought parameters in Greece using climatological data over the last century (1900–1997). Atmos. Res. 2020, 240, 104914. [Google Scholar] [CrossRef]
- World Meteorological Organization. Statement on the Status of the Global Climate in 1997; WMO-No.877; WMO: Geneva, Switzerland, 1997. [Google Scholar]
- Hurrell, J.; van Loon, H. Decadal variations in climate associated with the North Atlantic Oscillation. Clim. Change 1997, 36, 301–326. [Google Scholar] [CrossRef]
- Burn, D. Climatic influences on streamflow timing in the headwaters of the Mackenzie River Basin. J. Hydrol. 2008, 352, 225–238. [Google Scholar] [CrossRef]
- Hamed, K.; Rao, A. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Patakamuri, S.; Muthiah, K.; Sridhar, V. Long-Term Homogeneity, Trend, and Change-Point Analysis of Rainfall in the Arid District of Ananthapuramu, Andhra Pradesh State, India. Water 2020, 12, 211. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Xu, Z.; Li, J.; li, Z. Shift trend and step changes for runoff time series in the Shiyang River basin, northwest China. Hydrol. Process. 2008, 22, 4639–4646. [Google Scholar] [CrossRef]
- Fathian, F.; Morid, S.; Kahya, E. Identification of trends in hydrological and climatic variables in Urmia Lake basin, Iran. Theor. Appl. Climatol. 2015, 119, 443–464. [Google Scholar] [CrossRef]
- Mann, H. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M. Rank Correlation Methods; Griffin; American Psychological Association: Washington, DC, USA, 1948. [Google Scholar]
- Sönmez, A.; Kale, S. Climate change effects on annual streamflow of Filyos River (Turkey). J. Water Clim. Chang. 2020, 11, 420–433. [Google Scholar] [CrossRef]
- Kisi, O.; Santos, C.; da Silva, R.; Zounemat-Kermani, M. Trend analysis of monthly streamflows using Sen’s innovative trend method. Geofizika 2018, 35, 53–68. [Google Scholar] [CrossRef]
- Fu, G.; Chen, S.; Liu, C.; Shepard, D. Hydro-Climatic Trends of the Yellow River Basin for the Last 50 Years. Hydrolog. Sci. J. 2004, 65, 149–178. [Google Scholar] [CrossRef] [Green Version]
- Gebremicael, T.; Mohamed, Y.; Zaag, P.; Hagos, E. Temporal and spatial changes of rainfall and streamflow in the Upper Tekeze–Atbara River Basin, Ethiopia. Hydrol. Earth Syst. Sci. 2017, 21, 2127–2142. [Google Scholar] [CrossRef] [Green Version]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Alexandersson, H. A homogeneity test applied to precipitation data. J. Climatol. 1986, 6, 661–675. [Google Scholar] [CrossRef]
- Alexandersson, H.; Moberg, A. Homogenization of Swedish Temperature Data. Part i: Homogeneity Test for Linear Trends. Int. J. Climatol. 1997, 17, 25–34. [Google Scholar] [CrossRef]
- Buishand, T. Some methods for testing the homogeneity of rainfall records. J. Hydrol. 1982, 58, 11–27. [Google Scholar] [CrossRef]
- Wu, S.; Hu, Z.; Wang, Z.; Cao, S.; Yang, Y.; Qu, X.; Zhao, W. Spatiotemporal variations in extreme precipitation on the middle and lower reaches of the Yangtze River Basin (1970–2018). Quat. Int. 2021, 592, 80–96. [Google Scholar] [CrossRef]
- Sánchez-Granero, M.; Trinidad Segovia, J.; García Pérez, J. Some comments on Hurst exponent and the long memory processes on capital markets. Phys. A Stat. Mech. Appl. 2008, 387, 5543–5551. [Google Scholar] [CrossRef]
- Gumus, V. Spatio-temporal precipitation and temperature trend analysis of the Seyhan–Ceyhan River Basins, Turkey. Meteorol Appl. 2019, 26, 369–384. [Google Scholar] [CrossRef] [Green Version]
- Spearman, C. The proof and measurement of association between two things. Int. J. Epidemiol. 2010, 39, 1137–1150. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Xing, B. Spatio-Temporal Variability in Hydroclimate over the Upper Yangtze River Basin, China. Atmosphere 2022, 13, 317. https://doi.org/10.3390/atmos13020317
Yang R, Xing B. Spatio-Temporal Variability in Hydroclimate over the Upper Yangtze River Basin, China. Atmosphere. 2022; 13(2):317. https://doi.org/10.3390/atmos13020317
Chicago/Turabian StyleYang, Ruting, and Bing Xing. 2022. "Spatio-Temporal Variability in Hydroclimate over the Upper Yangtze River Basin, China" Atmosphere 13, no. 2: 317. https://doi.org/10.3390/atmos13020317
APA StyleYang, R., & Xing, B. (2022). Spatio-Temporal Variability in Hydroclimate over the Upper Yangtze River Basin, China. Atmosphere, 13(2), 317. https://doi.org/10.3390/atmos13020317






