Intra-Seasonal and Intra-Annual Variation of the Latent Heat Flux Transfer Coefficient for a Freshwater Lake
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. The Eddy Covariance Measurements and the Monin-Obukhov Similarity Theory
2.3. Energy Balance Calculations
2.4. Water Balance Method
2.5. Penman-Monteith and Priestly-Taylor Methods
3. Results
3.1. Energy Balance Characteristics of Lake Balaton
3.2. Comparison of Latent Heat Flux Estimations
3.3. Seasonal Variability of the Water Vapor Transfer Coefficient
3.4. Seasonal Variability of Roughness Lengths for Water Vapor and Heat
3.5. Drivers of Latent Heat Flux and Its Transfer Coefficient
3.6. Intra-Annual Variation of the Water Vapor Transfer Coefficient
4. Discussion
4.1. Latent Heat Flux Estimation Using Time-Varying Transfer Coefficients
4.2. Hysteresis Behavior of Evaporation and Its Transfer Coefficient to Radiative Heat Flux
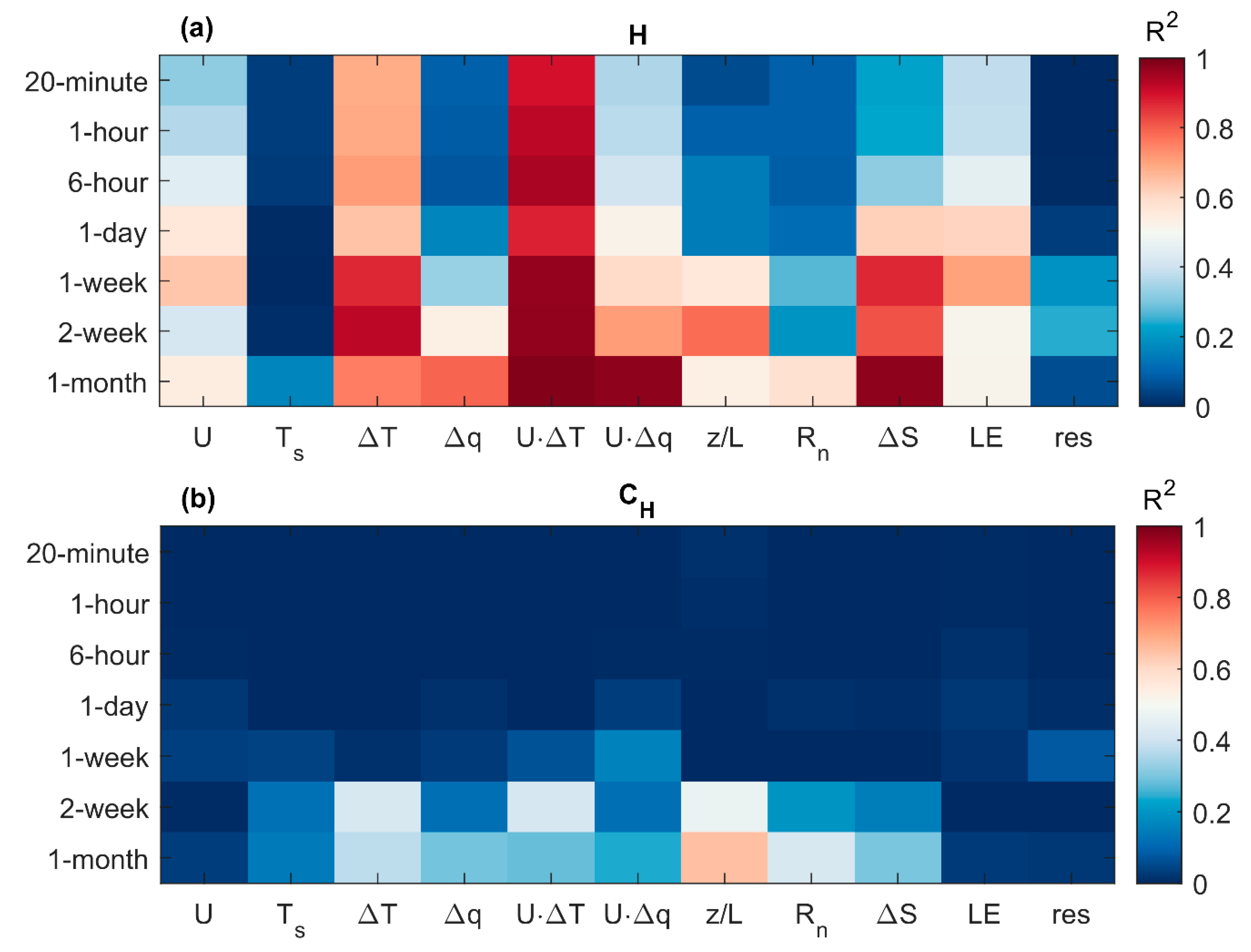
4.3. Drivers of Sensible Heat Flux and Its Transfer Coefficient
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lenters, J.D.; Cutrell, G.J.; Istanbulluoglu, E.; Scott, D.T.; Herrman, K.S.; Irmak, A.; Eisenhauer, D.E. Seasonal energy and water balance of a Phragmites australis-dominated wetland in the Republican River basin of south-central Nebraska (USA). J. Hydrol. 2011, 408, 19–34. [Google Scholar] [CrossRef] [Green Version]
- Xing, Z.; Fong, D.A.; Tan, K.M.; Lo, E.Y.M.; Monismith, S.G. Water and heat budgets of a shallow tropical reservoir. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]
- Lenters, J.D.; Kratz, T.K.; Bowser, C.J. Effects of climate variability on lake evaporation: Results from a long-term energy budget study of Sparkling Lake, northern Wisconsin (USA). J. Hydrol. 2005, 308, 168–195. [Google Scholar] [CrossRef]
- Nordbo, A.; Launiainen, S.; Mammarella, I.; Leppäranta, M.; Huotari, J.; Ojala, A.; Vesala, T. Long-term energy flux measurements and energy balance over a small boreal lake using eddy covariance technique. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Li, Z.; Lyu, S.; Zhao, L.; Wen, L.; Ao, Y.; Wang, S. Turbulent transfer coefficient and roughness length in a high-altitude lake, Tibetan Plateau. Theor. Appl. Climatol. 2016, 124, 723–735. [Google Scholar] [CrossRef]
- Riveros-Iregui, D.A.; Lenters, J.D.; Peake, C.S.; Ong, J.B.; Healey, N.C.; Zlotnik, V.A. Evaporation from a shallow, saline lake in the Nebraska Sandhills: Energy balance drivers of seasonal and interannual variability. J. Hydrol. 2017, 553, 172–187. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Ma, Y.; Ma, W.; Su, Z. Physical controls on half-hourly, daily, and monthly turbulent flux and energy budget over a high-altitude small lake on the Tibetan Plateau. J. Geophys. Res. 2017, 122, 2289–2303. [Google Scholar] [CrossRef]
- Yusup, Y.; Liu, H. Effects of atmospheric surface layer stability on turbulent fluxes of heat and water vapor across the water-atmosphere interface. J. Hydrometeorol. 2016, 17, 2835–2851. [Google Scholar] [CrossRef]
- Wang, B.; Ma, Y.; Chen, X.; Ma, W.; Su, Z.; Menenti, M. Observation and simulation of lake-air heat and water transfer processes in a high-altitude shallow lake on the Tibetan plateau. J. Geophys. Res. 2015, 120, 12327–12344. [Google Scholar] [CrossRef] [Green Version]
- Xiao, W.; Liu, S.; Wang, W.; Yang, D.; Xu, J.; Cao, C.; Li, H.; Lee, X. Transfer Coefficients of Momentum, Heat and Water Vapour in the Atmospheric Surface Layer of a Large Freshwater Lake. Boundary-Layer Meteorol. 2013, 148, 479–494. [Google Scholar] [CrossRef]
- Assouline, S.; Tyler, S.W.; Tanny, J.; Cohen, S.; Bou-Zeid, E.; Parlange, M.B.; Katul, G.G. Evaporation from three water bodies of different sizes and climates: Measurements and scaling analysis. Adv. Water Resour. 2008, 31, 160–172. [Google Scholar] [CrossRef]
- Choi, T.; Hong, J.; Kim, J.; Lee, H.; Asanuma, J.; Ishikawa, H.; Tsukamoto, O.; Zhiqui, G.; Ma, Y.; Ueno, K.; et al. Turbulent exchange of heat, water vapor, and momentum over a Tibetan prairie by eddy covariance and flux variance measurements. J. Geophys. Res. D Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Metzger, J.; Nied, M.; Corsmeier, U.; Kleffmann, J.; Kottmeier, C. Dead Sea evaporation by eddy covariance measurements vs. aerodynamic, energy budget, Priestley-Taylor, and Penman estimates. Hydrol. Earth Syst. Sci. 2018, 22, 1135–1155. [Google Scholar] [CrossRef] [Green Version]
- Xiao, W.; Zhang, Z.; Wang, W.; Zhang, M.; Liu, Q.; Hu, Y.; Huang, W.; Liu, S.; Lee, X. Radiation Controls the Interannual Variability of Evaporation of a Subtropical Lake. J. Geophys. Res. Atmos. 2020, 125. [Google Scholar] [CrossRef]
- Zhao, D.; Li, M. Dependence of wind stress across an air–sea interface on wave states. J. Oceanogr. 2019, 75, 207–223. [Google Scholar] [CrossRef]
- Blanken, P.D.; Spence, C.; Hedstrom, N.; Lenters, J.D. Evaporation from Lake Superior: 1. Physical controls and processes. J. Great Lakes Res. 2011, 37, 707–716. [Google Scholar] [CrossRef]
- Subin, Z.M.; Riley, W.J.; Mironov, D. An improved lake model for climate simulations: Model structure, evaluation, and sensitivity analyses in CESM1. J. Adv. Model. Earth Syst. 2012, 4. [Google Scholar] [CrossRef]
- Heikinheimo, M.; Kangas, M.; Tourula, T.; Venäläinen, A.; Tattari, S. Momentum and heat fluxes over lakes Tamnaren and Raksjo determined by the bulk-aerodynamic and eddy-correlation methods. Agric. For. Meteorol. 1999, 98–99, 521–534. [Google Scholar] [CrossRef]
- Zou, Z.; Zhao, D.; Liu, B.; Zhang, J.A.; Huang, J. Observation-based parameterization of air-sea fluxes in terms of wind speed and atmospheric stability under low-to-moderate wind conditions. J. Geophys. Res. Ocean. 2017, 122, 4123–4142. [Google Scholar] [CrossRef]
- McGloin, R.; McGowan, H.; McJannet, D.; Burn, S. Modelling sub-daily latent heat fluxes from a small reservoir. J. Hydrol. 2014, 519, 2301–2311. [Google Scholar] [CrossRef] [Green Version]
- Honti, M.; Somlyódy, L. Stochastic water balance simulation for Lake Balaton (Hungary) under climatic pressure. Water Sci. Technol. 2009, 59, 453–459. [Google Scholar] [CrossRef] [PubMed]
- Torma, P.; Krámer, T. Modeling the effect of waves on the diurnal temperature stratification of a shallow lake. Period. Polytech. Civ. Eng. 2017, 61, 165–175. [Google Scholar] [CrossRef] [Green Version]
- Mauder, M.; Foken, T. Documentation and Instruction Manual of the Eddy-Covariance Software Package TK3. Arbeitsergebnisse 2011, 3, 60. [Google Scholar] [CrossRef]
- Moore, C.J. Frequency response corrections for eddy correlation systems. Boundary-Layer Meteorol. 1986, 37, 17–35. [Google Scholar] [CrossRef]
- Webb, E.K.; Pearman, G.I.; Leuning, R. Correction of flux measurements for density effects due to heat and water vapour transfer. Q. J. R. Meteorol. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Schotanus, P.; Nieuwstadt, F.T.M.; De Bruin, H.A.R. Temperature measurement with a sonic anemometer and its application to heat and moisture fluxes. Bound.-Layer Meteorol. 1983, 26, 81–93. [Google Scholar] [CrossRef]
- Foken, T.; Gockede, M.; Mauder, M.; Mahrt, L.; Amiro, B.; Munger, W. Handbook of Micrometeorology: A Guide for Surface Flux Measurement and Analysis: Chapter 9: Post-Field Data Quality Control; Springer: Dordrecht, The Netherlands, 2004; ISBN 978-1-4020-2264-7. [Google Scholar]
- Lükő, G.; Torma, P.; Krámer, T.; Weidinger, T.; Vecenaj, Z.; Grisogono, B. Observation of wave-driven air–water turbulent momentum exchange in a large but fetch-limited shallow lake. Adv. Sci. Res. 2020, 17, 175–182. [Google Scholar] [CrossRef]
- Dyer, A.J. A review of flux-profile relationships. Bound.-Layer Meteorol. 1974, 7, 363–372. [Google Scholar] [CrossRef]
- Shabani, B.; Nielsen, P.; Baldock, T. Direct measurements of wind stress over the surf zone. J. Geophys. Res. Ocean 2014, 119, 2949–2973. [Google Scholar] [CrossRef] [Green Version]
- Mauder, M.; Oncley, S.P.; Vogt, R.; Weidinger, T.; Ribeiro, L.; Bernhofer, C.; Foken, T.; Kohsiek, W.; Bruin, H.A.R.; Liu, H. The energy balance experiment EBEX-2000. Part II: Intercomparison of eddy-covariance sensors and post-field data processing methods. Bound.-Layer Meteorol. 2007, 123, 29–54. [Google Scholar] [CrossRef]
- Kanda, M.; Inagaki, A.; Letzel, M.O.; Raasch, S.; Watanabe, T. Les study of the energy imbalance problem with eddy covariance fluxes. Bound.-Layer Meteorol. 2004, 110, 381–404. [Google Scholar] [CrossRef]
- Foken, T. Micrometerology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; ISBN 9783540746652. [Google Scholar]
- Wang, W.; Xiao, W.; Cao, C.; Gao, Z.; Hu, Z.; Liu, S.; Shen, S.; Wang, L.; Xiao, Q.; Xu, J.; et al. Temporal and spatial variations in radiation and energy balance across a large freshwater lake in China. J. Hydrol. 2014, 511, 811–824. [Google Scholar] [CrossRef]
- Brutsaert, W. Evaporation into the Atmosphere; Springer Netherlands: Dordrecht, The Netherlands, 1982; ISBN 978-90-481-8365-4. [Google Scholar]
- Winter, T.C. Uncertainties in Estimating the Water Balance of Lakes. JAWRA J. Am. Water Resour. Assoc. 1981, 17, 82–115. [Google Scholar] [CrossRef]
- Central-Transdanubian Water Directorate. Determination of Lake Balaton’s monthly Water Balance Components for 2019; Central-Transdanubian Water Directorate: Székesfehérvár, Hungary, 2019. [Google Scholar]
- Dos Reis, R.J.; Dias, N.L. Multi-season lake evaporation: Energy-budget estimates and CRLE model assessment with limited meteorological observations. J. Hydrol. 1998, 208, 135–147. [Google Scholar] [CrossRef]
- Assouline, S.; Li, D.; Tyler, S.; Tanny, J.; Cohen, S.; Bou-Zeid, E.; Parlange, M.; Katul, G.G. On the variability of the Priestley-Taylor coefficient over water bodies. Water Resour. Res. 2016, 52, 150–163. [Google Scholar] [CrossRef] [Green Version]
- Meng, X.; Liu, H.; Du, Q.; Xu, L.; Liu, Y. Evaluation of the performance of different methods for estimating evaporation over a highland open freshwater lake in mountainous area. Water 2020, 12, 3491. [Google Scholar] [CrossRef]
- De Bruin, H.A.R.; Keijman, J.Q. The Priestley-Taylor evaporation model applied to a large, shallow lake in the Netherlands. J. Appl. Meteorol. 1979, 18, 898–903. [Google Scholar] [CrossRef] [Green Version]
- Gan, G.; Liu, Y.; Pan, X.; Zhao, X.; Li, M.; Wang, S. Seasonal and diurnal variations in the priestley-taylor coefficient for a large ephemeral lake. Water 2020, 12, 839. [Google Scholar] [CrossRef] [Green Version]
- Charuchittipan, D.; Babel, W.; Mauder, M.; Leps, J.P.; Foken, T. Extension of the Averaging Time in Eddy-Covariance Measurements and Its Effect on the Energy Balance Closure. Bound.-Layer Meteorol. 2014, 152, 303–327. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Ma, Y.; Wang, Y.; Su, Z.; Ma, W. Significant differences exist in lake-atmosphere interactions and the evaporation rates of high-elevation small and large lakes. J. Hydrol. 2019, 573, 220–234. [Google Scholar] [CrossRef]
- Du, Q.; Liu, H.Z.; Liu, Y.; Wang, L.; Xu, L.J.; Sun, J.H.; Xu, A.L. Factors controlling evaporation and the CO2 flux over an open water lake in southwest of China on multiple temporal scales. Int. J. Climatol. 2018, 38, 4723–4739. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, Y. Variability of Surface Heat Fluxes and Its Driving Forces at Different Time Scales Over a Large Ephemeral Lake in China. J. Geophys. Res. Atmos. 2018, 123, 4939–4957. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, Y.; Gan, G.; Wang, R. Hysteresis Behavior of Surface Water Fluxes in a Hydrologic Transition of an Ephemeral Lake. J. Geophys. Res. Atmos. 2020, 125. [Google Scholar] [CrossRef]
- Shao, C.; Chen, J.; Chu, H.; Stepien, C.A.; Ouyang, Z. Intra-Annual and Interannual Dynamics of Evaporation Over Western Lake Erie. Earth Sp. Sci. 2020, 7. [Google Scholar] [CrossRef]



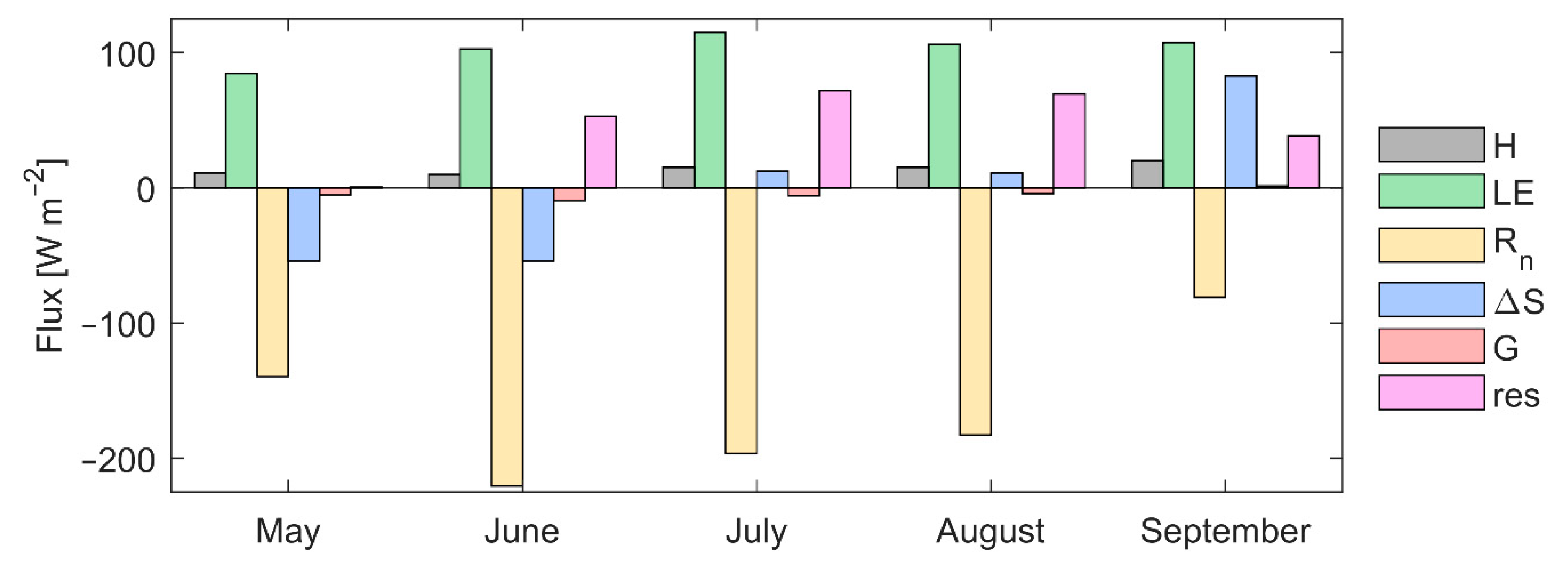
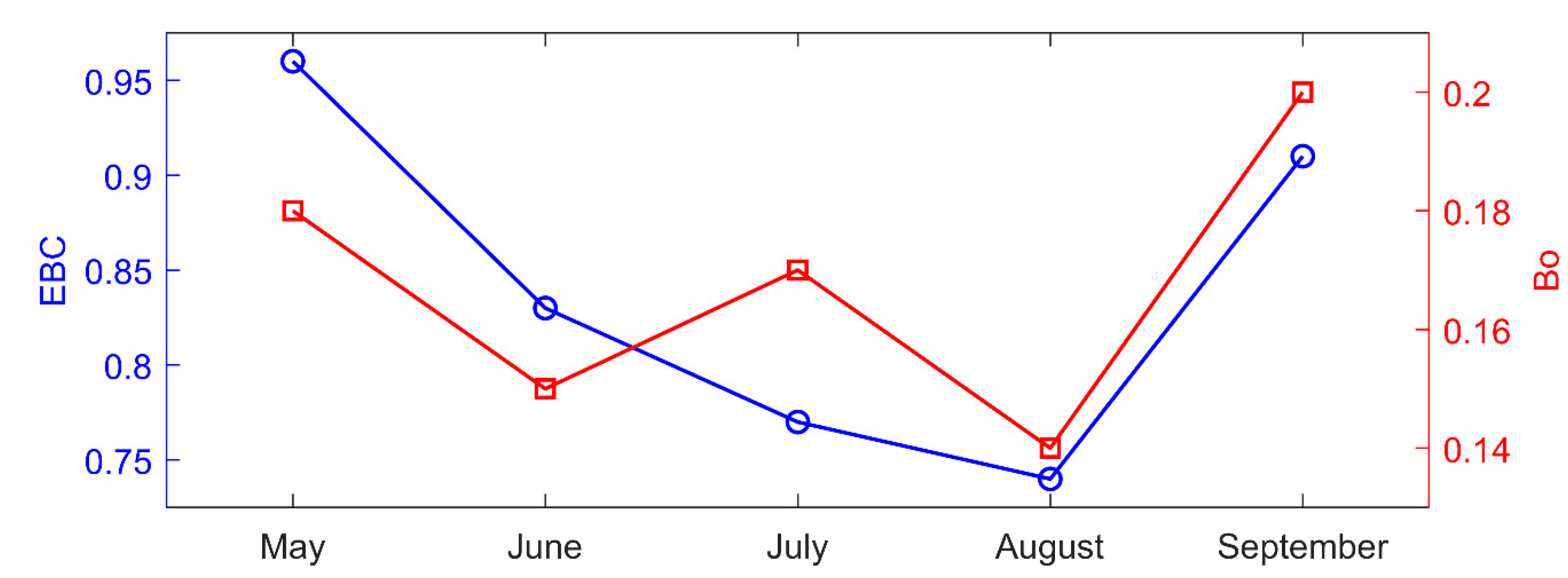
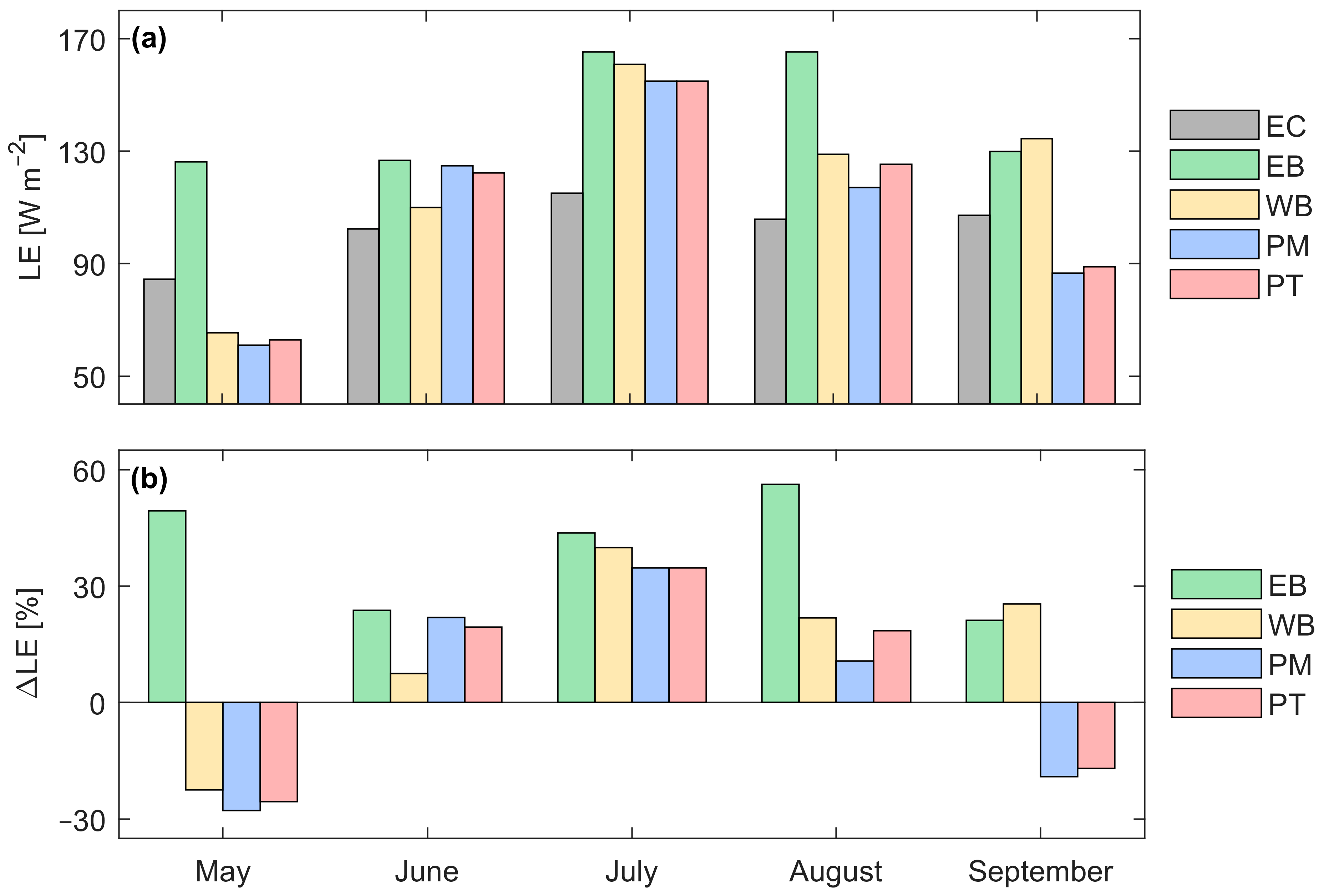
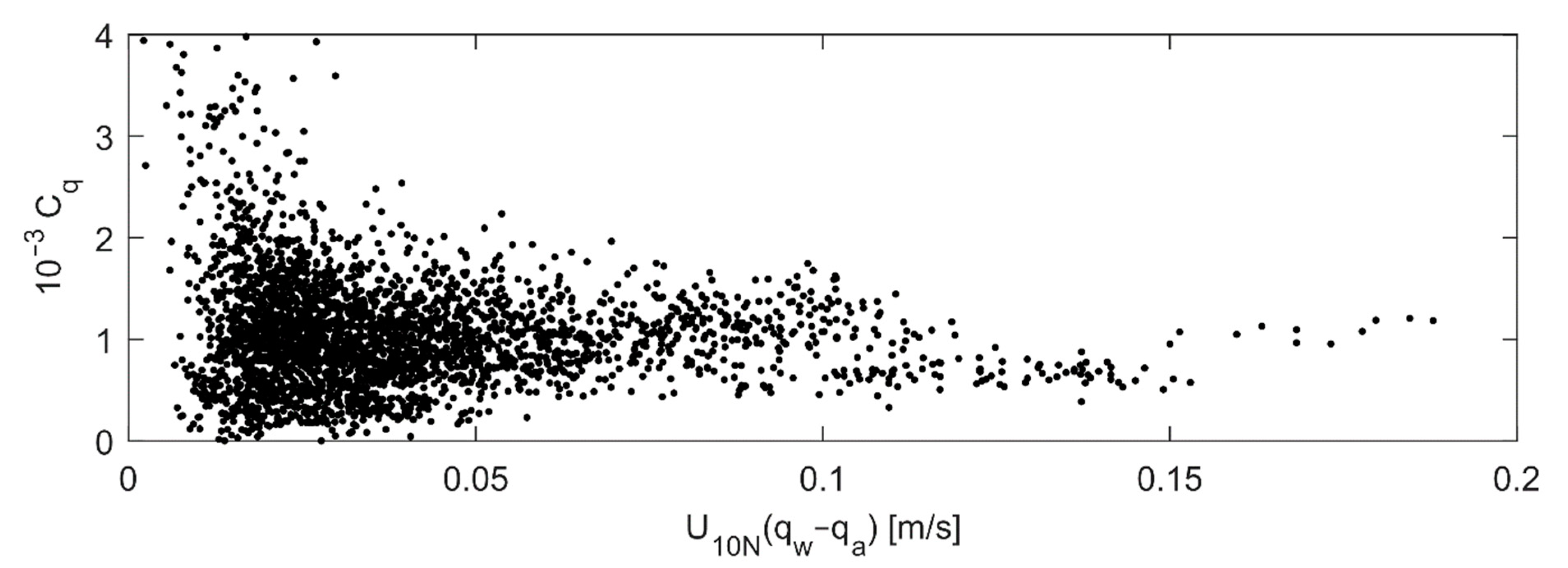
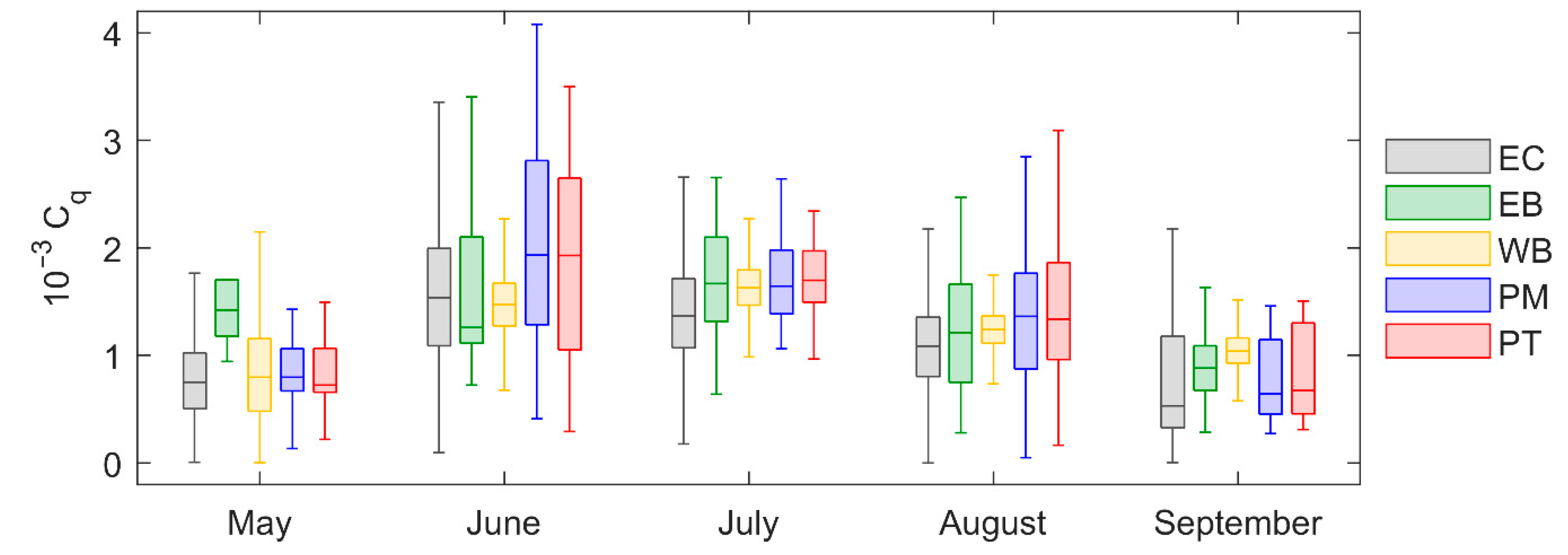
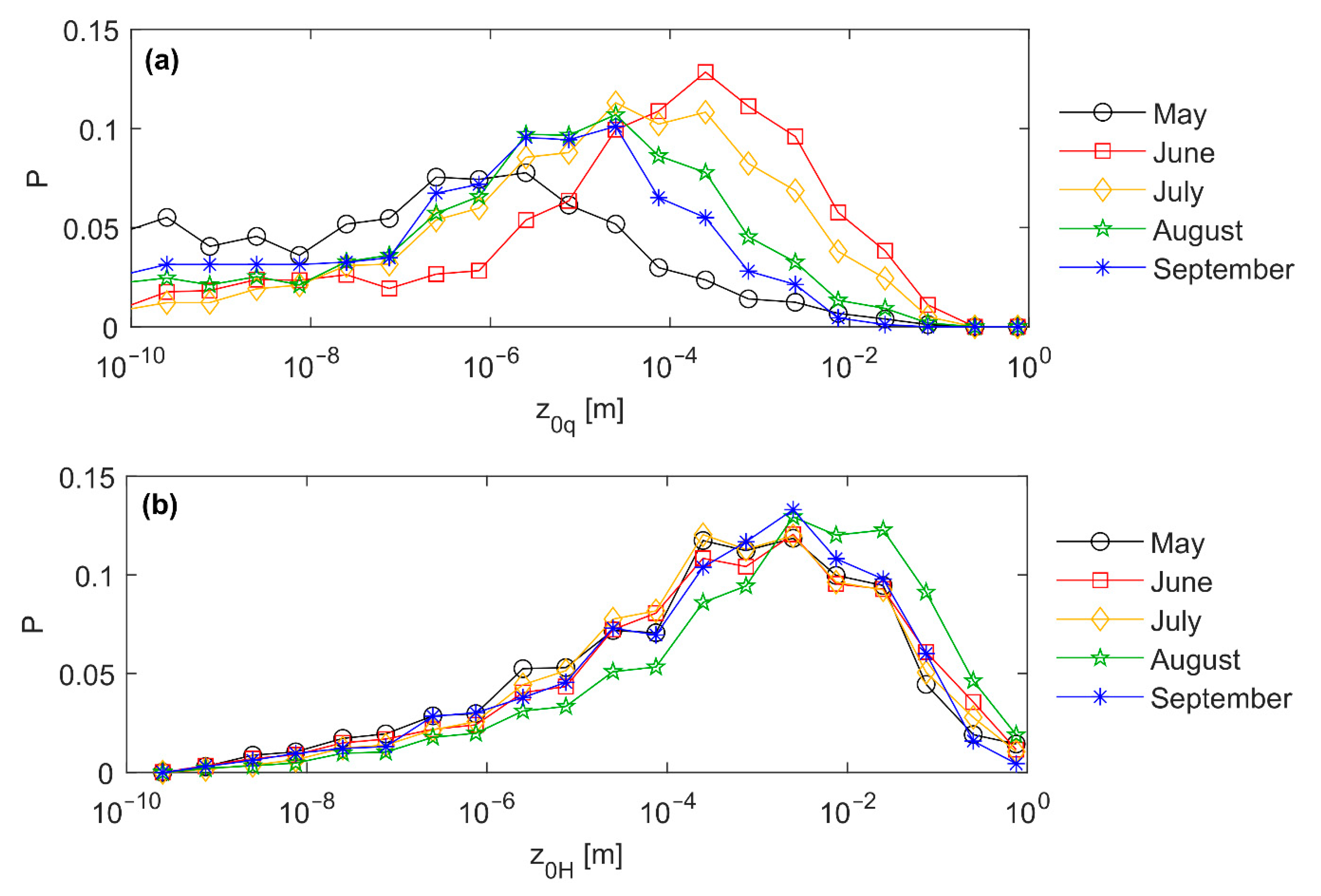

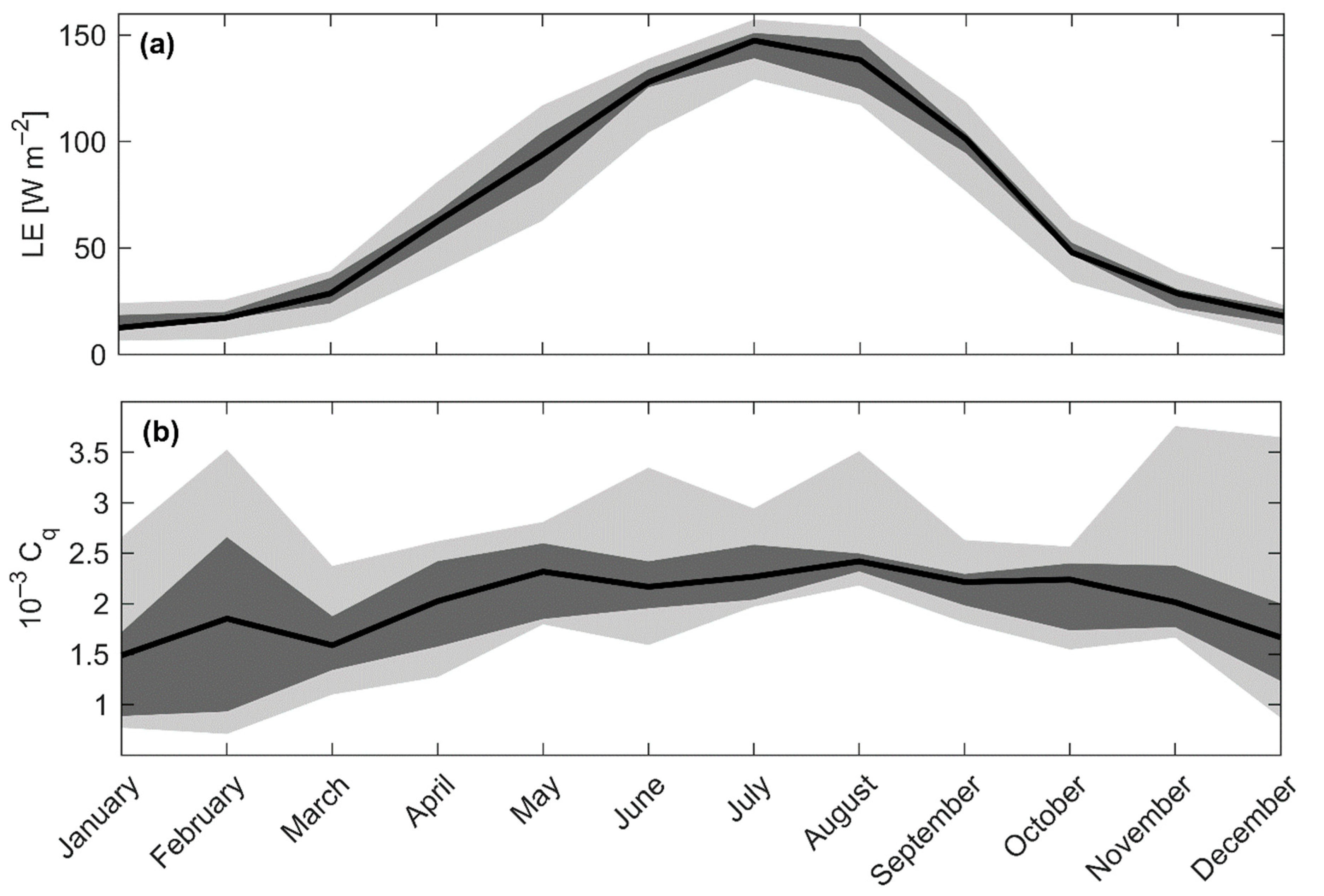

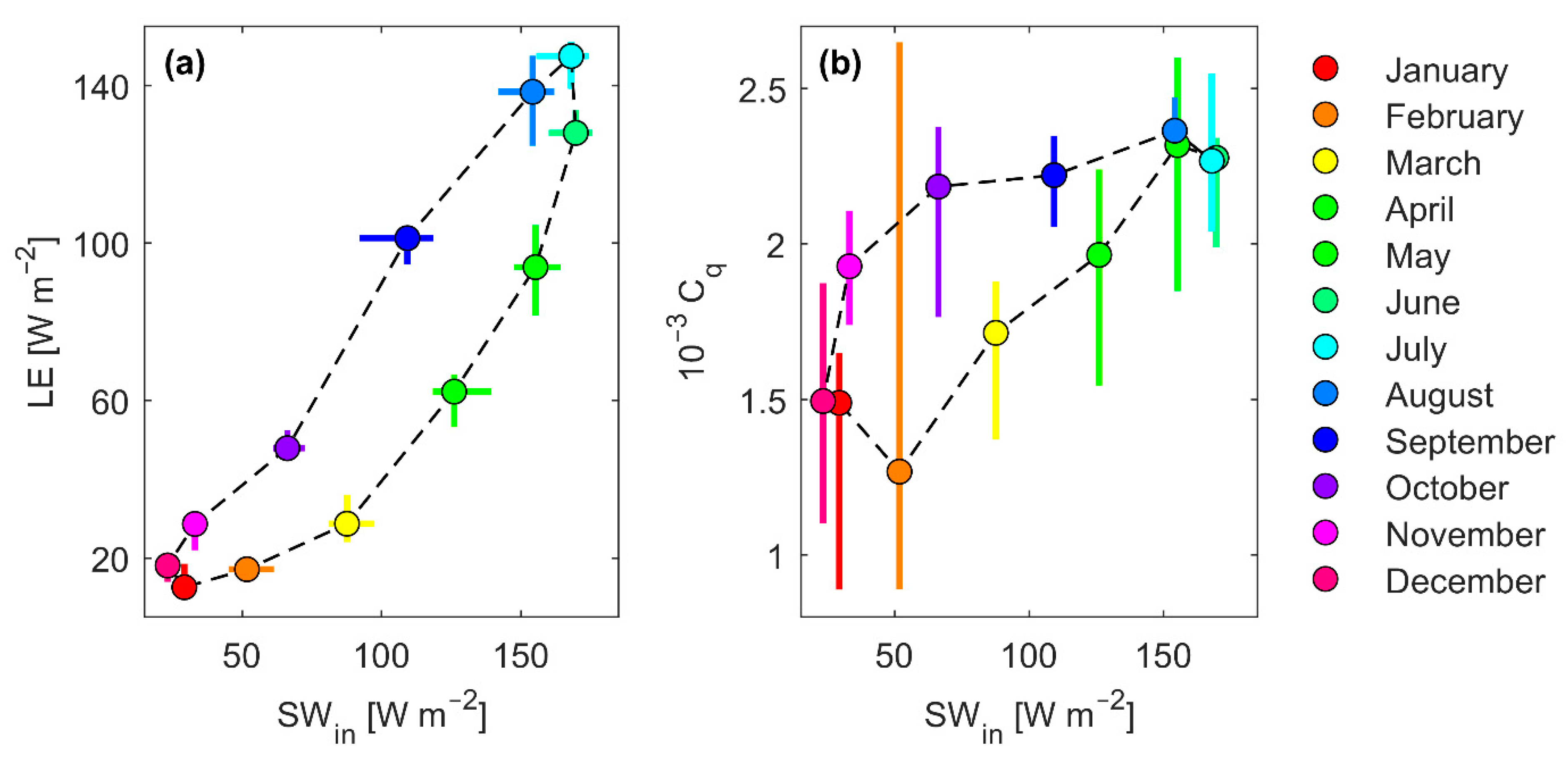
| [mm] | May | June | July | August | September |
|---|---|---|---|---|---|
| P | 123 ± 30 | 65 ± 16 | 67 ± 17 | 56 ± 14 | 28 ± 7 |
| I | 56 ± 13 | 45 ± 13 | 27 ± 7 | 23 ± 6 | 15 ± 2 |
| E | 63 ± 16 | 100 ± 34 | 169 ± 43 | 136 ± 34 | 133 ± 31 |
| O | 7 ± 2 | 23 ± 6 | 0 ± 0 | 0 ± 0 | 0 ± 0 |
| W | 2 ± 0 | 2 ± 0 | 2 ± 0 | 2 ± 0 | 1 ± 0 |
| ΔV | 108 ± 27 | −15 ± 4 | −78 ± 19 | −59 ± 14 | −91 ± 22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lükő, G.; Torma, P.; Weidinger, T. Intra-Seasonal and Intra-Annual Variation of the Latent Heat Flux Transfer Coefficient for a Freshwater Lake. Atmosphere 2022, 13, 352. https://doi.org/10.3390/atmos13020352
Lükő G, Torma P, Weidinger T. Intra-Seasonal and Intra-Annual Variation of the Latent Heat Flux Transfer Coefficient for a Freshwater Lake. Atmosphere. 2022; 13(2):352. https://doi.org/10.3390/atmos13020352
Chicago/Turabian StyleLükő, Gabriella, Péter Torma, and Tamás Weidinger. 2022. "Intra-Seasonal and Intra-Annual Variation of the Latent Heat Flux Transfer Coefficient for a Freshwater Lake" Atmosphere 13, no. 2: 352. https://doi.org/10.3390/atmos13020352
APA StyleLükő, G., Torma, P., & Weidinger, T. (2022). Intra-Seasonal and Intra-Annual Variation of the Latent Heat Flux Transfer Coefficient for a Freshwater Lake. Atmosphere, 13(2), 352. https://doi.org/10.3390/atmos13020352






