Wind-Ramp Predictability
Abstract
:1. Introduction
2. Materials and Methods
2.1. NAM Model
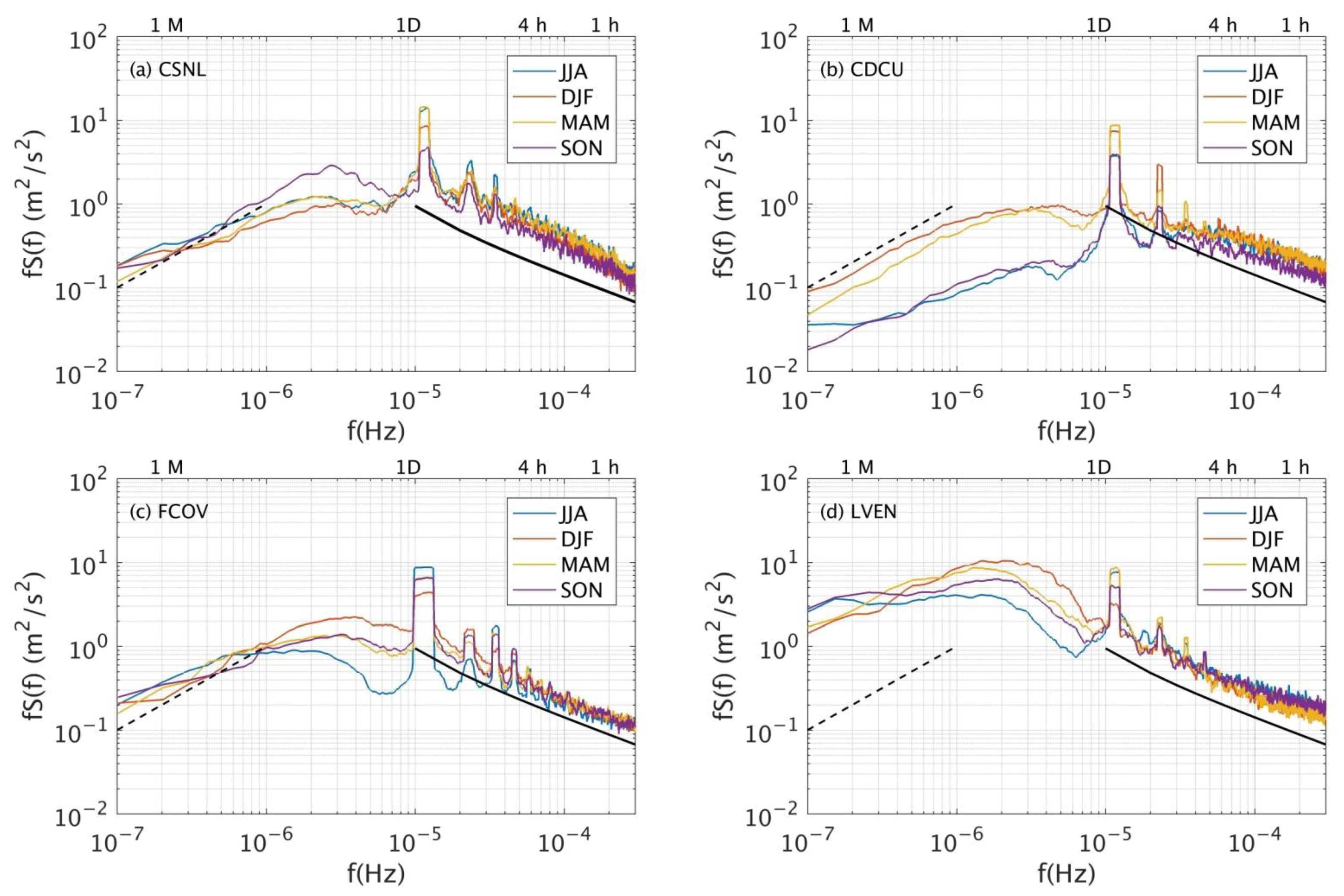
2.2. Wind-Power Spectra
2.3. Wind Ramps
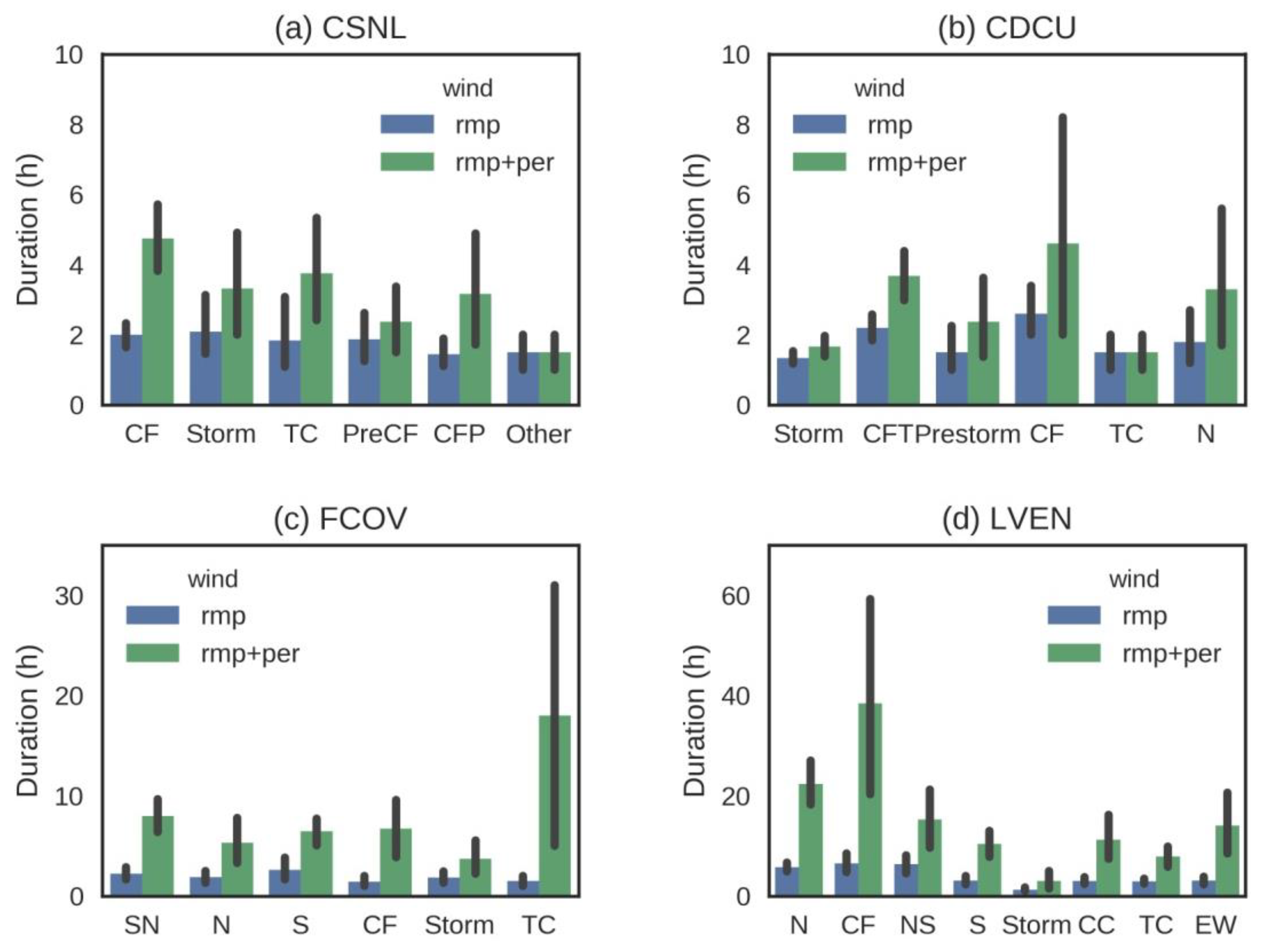
2.4. Ramp Categorization
2.5. Downdrafts
2.6. Bias-Correction Methods
2.7. Contingency Table
3. Results
3.1. Wind-Power Spectra
3.2. Characteristics of the Persistence of Wind Ramps
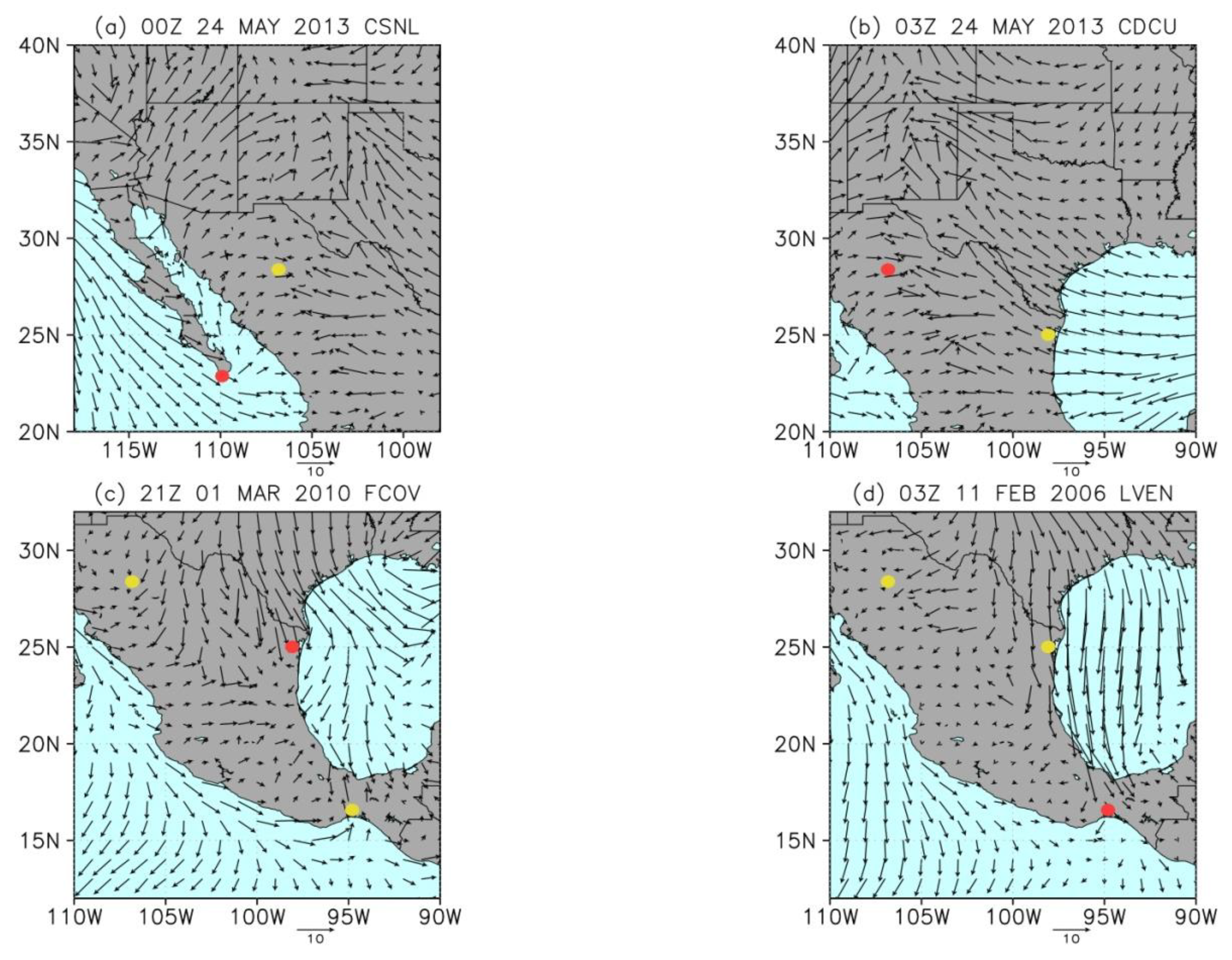
3.3. Weather Conditions Generating Extreme Wind Ramps
3.4. Ramp Distribution Correction
4. Discussion and Conclusions
5. Simple Summary
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bossavy, A.; Girard, R.; Kariniotakis, G. Forecasting Uncertainty Related to Ramps of Wind Power Production. In Proceedings of the European Wind Energy Conference and Exhibition 2010, Warsaw, Poland, 20–23 April 2010; European Wind Energy Association: Warsaw, Poland, 2010; Volume 2, pp. 1–9, ISBN 9781617823107. [Google Scholar]
- Gallego-Castillo, C.; Cuerva-Tejero, A.; Lopez-Garcia, O. A review on the recent history of wind power ramp forecasting. Renew. Sustain. Energy Rev. 2015, 52, 1148–1157. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Cui, M.; Hodge, B.M.; Florita, A.; Freedman, J. Ramp forecasting performance from improved short-term wind power forecasting over multiple spatial and temporal scales. Energy 2017, 122, 528–541. [Google Scholar] [CrossRef] [Green Version]
- Pichault, M.; Vincent, C.; Skidmore, G.; Monty, J. Characterisation of intra-hourly wind power ramps at the wind farm scale and associated processes. Wind Energy Sci. 2021, 6, 131–147. [Google Scholar] [CrossRef]
- Bianco, L.; Djalalova, I.V.; Wilczak, J.M.; Cline, J.; Calvert, S.; Konopleva-Akish, E.; Finley, C.; Freedman, J. A Wind Energy Ramp Tool and Metric for Measuring the Skill of Numerical Weather Prediction Models. Weather Forecast. 2016, 31, 1137–1156. [Google Scholar] [CrossRef]
- Storm, B.; Dudhia, J.; Basu, S.; Swift, A.; Giammanco, I. Evaluation of the weather research and forecasting model on forecasting low-level jets: Implications for wind energy. Wind Energy 2009, 12, 81–90. [Google Scholar] [CrossRef]
- Olson, J.B.; Kenyon, J.S.; Djalalova, I.; Bianco, L.; Turner, D.D.; Pichugina, Y.; Choukulkar, A.; Toy, M.D.; Brown, J.M.; Angevine, W.M.; et al. Improving Wind Energy Forecasting through Numerical Weather Prediction Model Development. Bull. Am. Meteorol. Soc. 2019, 100, 2201–2220. [Google Scholar] [CrossRef]
- Wilczak, J.; Finley, C.; Freedman, J.; Cline, J.; Bianco, L.; Olson, J.; Djalalova, I.; Sheridan, L.; Ahlstrom, M.; Manobianco, J.; et al. The Wind Forecast Improvement Project (WFIP): A Public–Private Partnership Addressing Wind Energy Forecast Needs. Bull. Am. Meteorol. Soc. 2015, 96, 1699–1718. [Google Scholar] [CrossRef]
- Vannitsem, S.; Bremnes, J.B.; Demaeyer, J.; Evans, G.R.; Flowerdew, J.; Hemri, S.; Lerch, S.; Roberts, N.; Theis, S.; Atencia, A.; et al. Statistical Postprocessing for Weather Forecasts: Review, Challenges, and Avenues in a Big Data World. Bull. Am. Meteorol. Soc. 2021, 102, E681–E699. [Google Scholar] [CrossRef]
- Siuta, D.; West, G.; Stull, R. WRF hub-height wind forecast sensitivity to PBL scheme, grid length, and initial condition choice in complex terrain. Weather Forecast. 2017, 32, 493–509. [Google Scholar] [CrossRef]
- Benjamin, S.G.; Weygandt, S.S.; Brown, J.M.; Hu, M.; Alexander, C.R.; Smirnova, T.G.; Olson, J.B.; James, E.P.; Dowell, D.C.; Grell, G.A.; et al. A North American Hourly Assimilation and Model Forecast Cycle: The Rapid Refresh. Mon. Weather Rev. 2016, 144, 1669–1694. [Google Scholar] [CrossRef]
- Pereyra-Castro, K.; Caetano, E.; Martínez-Alvarado, O.; Quintanilla-Montoya, A.L. Wind and Wind Power Ramp Variability over Northern Mexico. Atmosphere 2020, 11, 1281. [Google Scholar] [CrossRef]
- López-Bravo, C.; Caetano, E.; Magaña, V. Forecasting Summertime Surface Temperature and Precipitation in the Mexico City Metropolitan Area: Sensitivity of the WRF Model to Land Cover Changes. Front. Earth Sci. 2018, 6, 6. [Google Scholar] [CrossRef] [Green Version]
- NCEI. North American Mesoscale Forecast System. Available online: https://www.ncei.noaa.gov/products/weather-climate-models/north-american-mesoscale (accessed on 1 October 2021).
- NCEP. North American Mesoscale Forecast System. Available online: https://www.emc.ncep.noaa.gov/emc/pages/numerical_forecast_systems/nam.php (accessed on 1 October 2021).
- Rogers, E.; DiMego, G.; Black, T.; Ek, M.; Ferrier, B.; Gayno, G.; Janjic, Z.; Lin, Y.; Pyle, M.; Wong, V. The NCEP North American mesoscale modeling system: Recent changes and future plans. In Proceedings of the 23rd Conference on Weather Analysis and Forecasting/19th Conference on Numerical Weather Prediction, Omaha, NE, USA, 1 June 2009; pp. 1–21. [Google Scholar]
- Rogers, E.; Lin, Y.; Mitchell, K.; Wu, W.; Ferrier, B.; Gayno, G.; Pondeca, M.; Pyle, M.; Wong, V.; Ek, M. The NCEP North American Mesoscale Modeling System: Final Eta model/analysis changes and preliminary experiments using the WRF-NMM. In Proceedings of the, 21st Conference on Weather Analysis and Forecasting/17th Conference on Numerical Weather, Prediction, Washington, DC, USA, 1 August 2005; pp. 1–21. [Google Scholar]
- Colbert, M.; Stensrud, D.J.; Markowski, P.M.; Richardson, Y.P. Processes Associated with Convection Initiation in the North American Mesoscale Forecast System, Version 3 (NAMv3). Weather Forecast. 2019, 34, 683–700. [Google Scholar] [CrossRef]
- Janjić, Z.; Black, T.L.; Pyle, H.-Y.; Chuang, E.R.; DiMego, G.J. The NCEP WRF-NMM Core. Available online: https://www2.mmm.ucar.edu/wrf/users/workshops/WS2005/presentations/session2/9-Janjic.pdf (accessed on 15 October 2021).
- Ferrier, B.S.; Janjić, Z.; Aligo, E.; Jovic, D.; Roger, E.; Carley, J.R.; Pyle, M.; DiMego, G.J. NMMB Model Changes as Part of the NAMv4 Upgrade. Available online: https://ams.confex.com/ams/97Annual/webprogram/Paper312628.html (accessed on 15 October 2021).
- Stull, R. An Introduction to Boundary Layer, 1st ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Finnigan, J.J.; Einaudi, F.; Fua, D. The Interaction between an Internal Gravity Wave and Turbulence in the Stably-Stratified Nocturnal Boundary Layer. J. Atmos. Sci. 1984, 41, 2409–2436. [Google Scholar] [CrossRef]
- Kang, S.-L.; Won, H. Spectral structure of 5 year time series of horizontal wind speed at the Boulder Atmospheric Observatory. J. Geophys. Res. Atmos. 2016, 121, 11946–11967. [Google Scholar] [CrossRef]
- Demarco, A.; Basu, S. On the tails of the wind ramp distributions. Wind Energy 2018, 21, 892–905. [Google Scholar] [CrossRef]
- MODIS Characterization Support Team MODIS 250m Calibrated Radiances Product. Available online: https://doi.org/10.5067/MODIS/MYD02QKM.061 (accessed on 1 July 2021).
- Vázquez-Aguirre, J.L. Caracterización Objetiva de Los Nortes del Golfo de México y su Variabilidad Interanual. Bachelor’s Thesis, Universidad Veracruzana, Veracruz, México, 1999. [Google Scholar]
- Méndez-Pérez, I.R.; Rodríguez-Damián, J.J.; Tejeda-Martínez, A. Caracterización y Tipología de eventos de “Suradas” del Golfo de Tehuantepec al Centro del estado de Veracruz, México. In Proceedings of the El Clima: Aire, Agua, Tierra y Fuego, Cartagena, Colombia, 17–19 October 2018; Montávez Gómez, J.P., Ed.; Asociación Española de Climatología; Agencia Estatal de Meteorología: Madrid, Spain, 2018; pp. 529–538. [Google Scholar]
- Atlantic Hurricane Season. Available online: https://www.nhc.noaa.gov/data/tcr/index.php?season=2013&basin=atl (accessed on 1 October 2021).
- AIRS Project Aqua/AIRS L2 Near Real Time (NRT) Standard Physical Retrieval (AIRS-only) V7.0. Available online: https://disc.gsfc.nasa.gov/datasets/AIRS2RET_NRT_7.0/summary (accessed on 1 October 2021).
- NASA MODIS Adaptive Processing System MODIS Atmosphere L2 Cloud Product (06_L2). Available online: http://doi.org/10.5067/MODIS/MYD06_L2.061 (accessed on 1 October 2021).
- Valdés Manzanilla, A.; Cortéz Vázquez, M.; Francisco, P.; José, J. Un estudio explorativo de los Sistemas Convectivos de Mesoescala de México. Investig. Geográficas 2005, 56, 26–42. [Google Scholar] [CrossRef]
- Nakamura, K.; Kershaw, R.; Gait, N. Prediction of near-surface gusts generated by deep convection. Meteorol. Appl. 1996, 3, 157–167. [Google Scholar] [CrossRef]
- Sheridan, P. Review of Techniques and Research for Gust Forecasting and Parameterisation. 2011. Available online: https://digital.nmla.metoffice.gov.uk (accessed on 15 October 2021).
- Li, D.; Feng, J.; Xu, Z.; Yin, B.; Shi, H.; Qi, J. Statistical Bias Correction for Simulated Wind Speeds Over CORDEX-East Asia. Earth Space Sci. 2019, 6, 200–211. [Google Scholar] [CrossRef]
- Torralba, V.; Doblas-Reyes, F.J.; MacLeod, D.; Christel, I.; Davis, M. Seasonal Climate Prediction: A New Source of Information for the Management of Wind Energy Resources. J. Appl. Meteorol. Climatol. 2017, 56, 1231–1247. [Google Scholar] [CrossRef]
- Enayati, M.; Bozorg-Haddad, O.; Bazrafshan, J.; Hejabi, S.; Chu, X. Bias correction capabilities of quantile mapping methods for rainfall and temperature variables. J. Water Clim. Chang. 2020, 12, 401–419. [Google Scholar] [CrossRef]
- Jakob Themeßl, M.; Gobiet, A.; Leuprecht, A. Empirical-statistical downscaling and error correction of daily precipitation from regional climate models. Int. J. Climatol. 2011, 31, 1530–1544. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Science, 2nd ed.; Academic Press: San Diego, CA, USA, 2006; ISBN 0-12-064490-8. [Google Scholar]
- Zhao, H.; Raga, G.B. On the distinct interannual variability of tropical cyclone activity over the eastern North Pacific. Atmósfera 2015, 28, 161–178. [Google Scholar] [CrossRef]
- Cannon, D.J.; Brayshaw, D.J.; Methven, J.; Coker, P.J.; Lenaghan, D. Using reanalysis data to quantify extreme wind power generation statistics: A 33 year case study in Great Britain. Renew. Energy 2015, 75, 767–778. [Google Scholar] [CrossRef] [Green Version]
- Thomas, S.R.; Martínez-Alvarado, O.; Drew, D.; Bloomfield, H. Drivers of extreme wind events in Mexico for windpower applications. Int. J. Climatol. 2021, 41, E2321–E2340. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method that Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Larsén, X.G.; Ott, S.; Badger, J.; Hahmann, A.N.; Mann, J. Recipes for Correcting the Impact of Effective Mesoscale Resolution on the Estimation of Extreme Winds. J. Appl. Meteorol. Climatol. 2012, 51, 521–533. [Google Scholar] [CrossRef]
- Pereyra-Castro, K.; Caetano, E.; Altamirano del Razo, D. WRF wind forecast over coastal complex terrain: Baja California Peninsula (Mexico) case study. Arab. J. Geosci. 2021, 14, 1972. [Google Scholar] [CrossRef]
- Chow, F.K.; Schär, C.; Ban, N.; Lundquist, K.A.; Schlemmer, L.; Shi, X. Crossing Multiple Gray Zones in the Transition from Mesoscale to Microscale Simulation over Complex Terrain. Atmosphere 2019, 10, 274. [Google Scholar] [CrossRef] [Green Version]
- Schultz, M.G.; Betancourt, C.; Gong, B.; Kleinert, F.; Langguth, M.; Leufen, L.H.; Mozaffari, A.; Stadtler, S. Can deep learning beat numerical weather prediction? Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2021, 379, 20200097. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Serinaldi, F.; Porcu, E. Advancing Space-Time Simulation of Random Fields: From Storms to Cyclones and Beyond. Water Resour. Res. 2021, 57, e2020WR029466. [Google Scholar] [CrossRef]
- Mora, E.; Cifuentes, J.; Marulanda, G. Short-term forecasting of wind energy: A comparison of deep learning frameworks. Energies 2021, 14, 7943. [Google Scholar] [CrossRef]
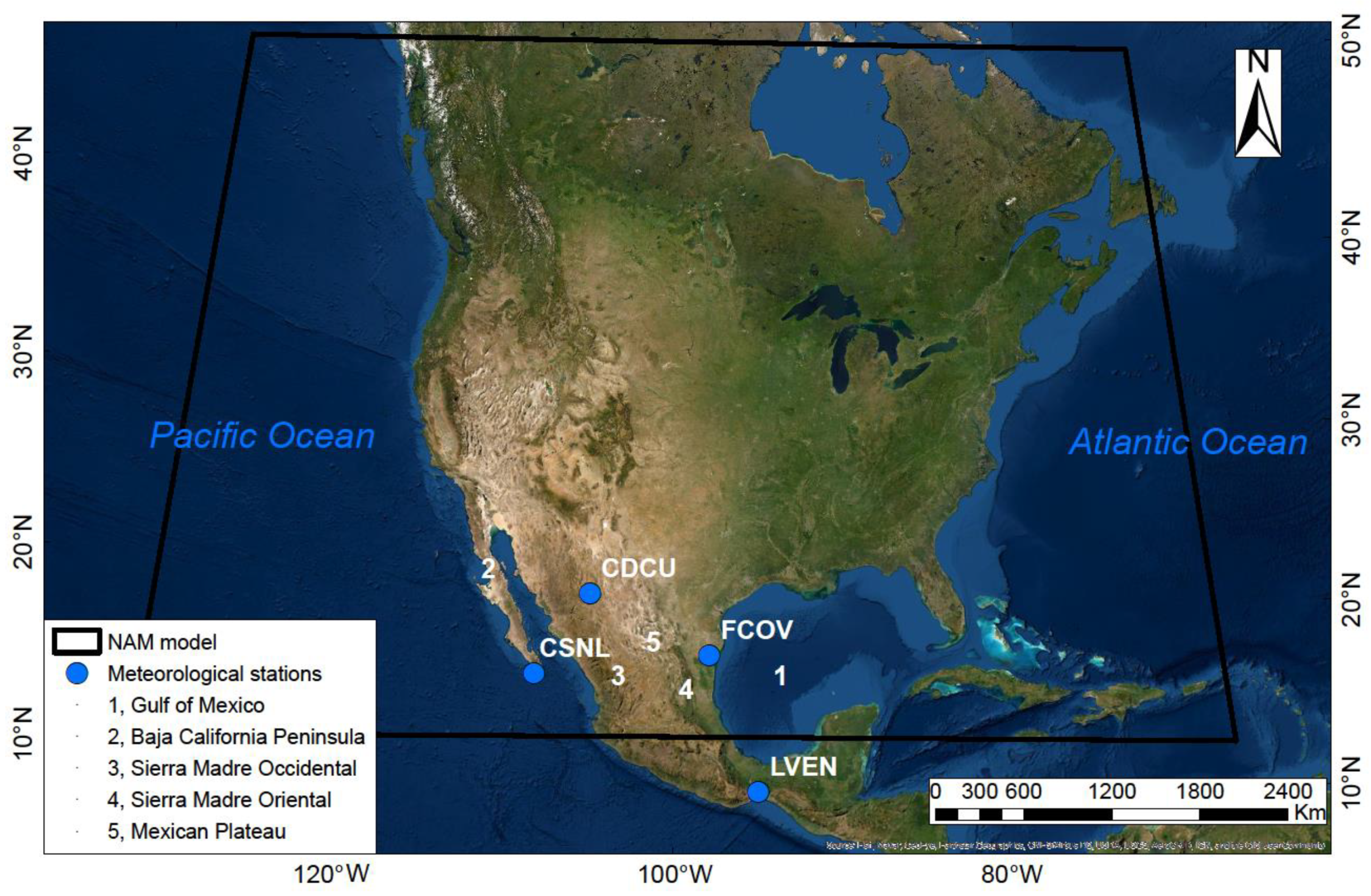
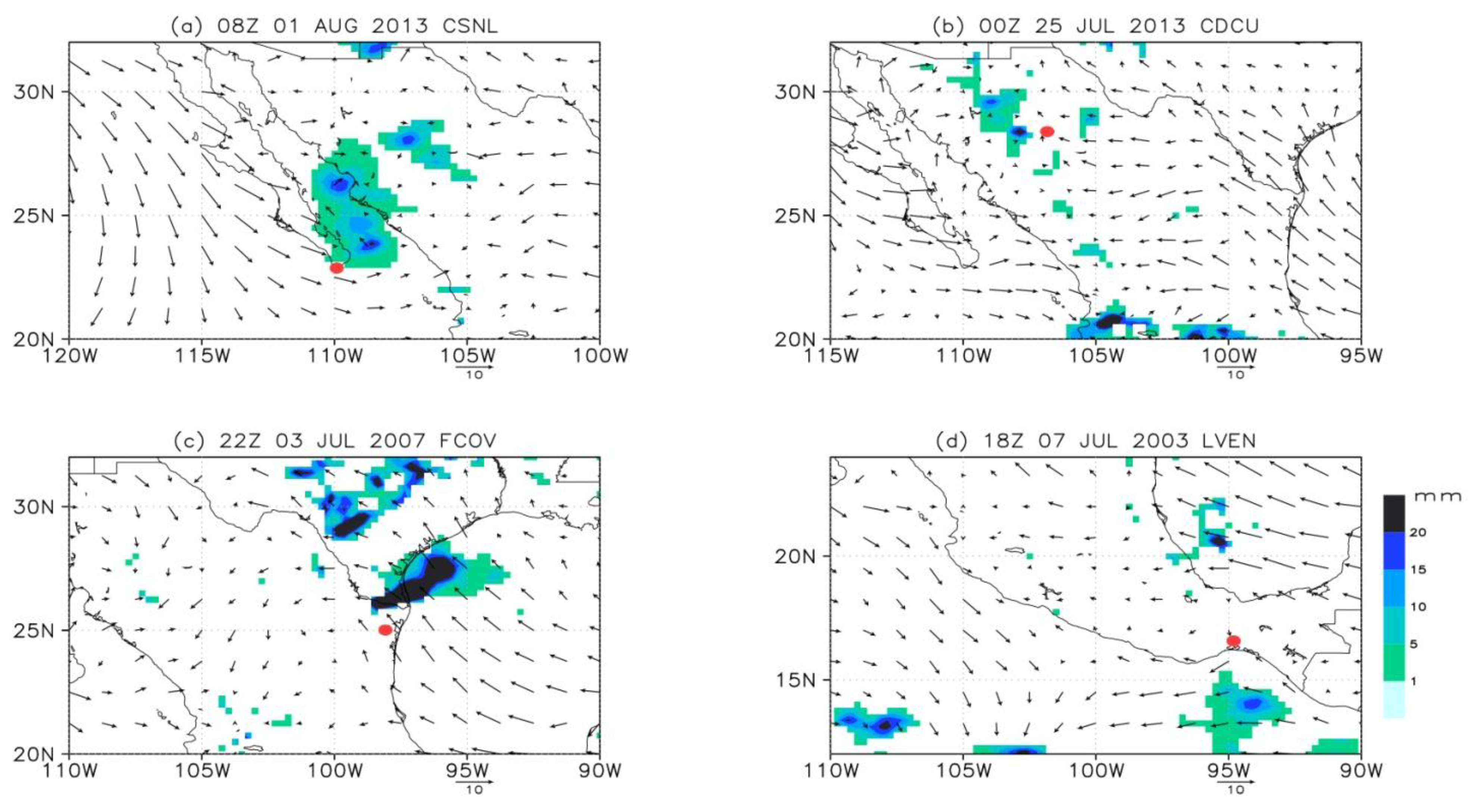
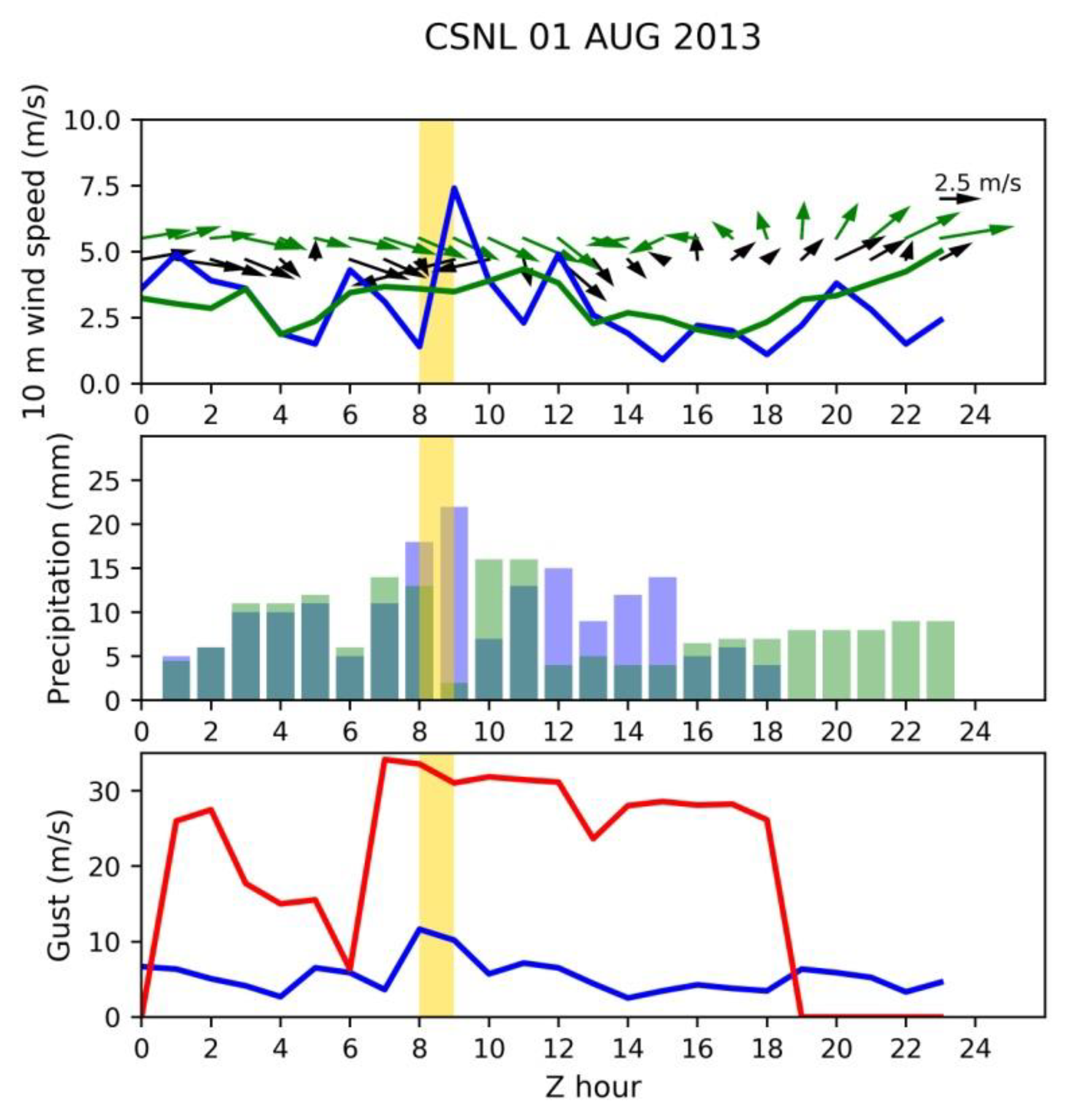

| Station | ID | Latitude | Longitude | Period |
|---|---|---|---|---|
| Cabo San Lucas | CSNL | 22.881 | −109.926 | 2010–2016 |
| Ciudad Cuauhtemoc | CDCU | 28.396 | −106.839 | 2010–2016 |
| Francisco Villa | FCOV | 25.020 | −98.0875 | 2006–2007 and 2010–2012 |
| La Venta | LVEN | 16.579 | −94.816 | 2000–2007 and 2012 |
| |Ramp| ≤ 0.5 m/s | Ramp > 0.5 m/s | Ramp < −0.5 m/s | |
|---|---|---|---|
| POD | |||
| NAM forecast | 0.673 | 0.288 | 0.272 |
| Simple bias-corrected | 0.547 | 0.365 | 0.343 |
| QM-corrected | 0.461 | 0.388 | 0.397 |
| FAR | |||
| NAM forecast | 0.490 | 0.596 | 0.615 |
| Simple bias-corrected | 0.485 | 0.614 | 0.635 |
| QM-corrected | 0.489 | 0.627 | 0.651 |
| FBIAS | |||
| NAM forecast | 1.320 | 0.712 | 0.708 |
| Simple bias-corrected | 1.063 | 0.947 | 0.938 |
| QM-corrected | 0.902 | 1.040 | 1.138 |
| CSI | |||
| NAM forecast | 0.409 | 0.202 | 0.190 |
| Simple bias-corrected | 0.361 | 0.230 | 0.215 |
| QM-corrected | 0.319 | 0.234 | 0.228 |
| |Ramp| ≤ 0.5 m/s | Ramp > 0.5 m/s | Ramp < −0.5 m/s | |
|---|---|---|---|
| POD | |||
| NAM forecast | 0.669 | 0.189 | 0.183 |
| Simple bias-corrected | 0.369 | 0.325 | 0.351 |
| QM-corrected | 0.478 | 0.291 | 0.281 |
| FAR | |||
| NAM forecast | 0.563 | 0.655 | 0.720 |
| Simple bias-corrected | 0.559 | 0.672 | 0.725 |
| QM-corrected | 0.557 | 0.671 | 0.719 |
| FBIAS | |||
| NAM forecast | 1.529 | 0.548 | 0.654 |
| Simple bias-corrected | 0.837 | 0.990 | 1.274 |
| QM-corrected | 1.079 | 0.884 | 1.001 |
| CSI | |||
| NAM forecast | 0.359 | 0.139 | 0.125 |
| Simple bias-corrected | 0.251 | 0.195 | 0.182 |
| QM-corrected | 0.298 | 0.182 | 0.163 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pereyra-Castro, K.; Caetano, E. Wind-Ramp Predictability. Atmosphere 2022, 13, 453. https://doi.org/10.3390/atmos13030453
Pereyra-Castro K, Caetano E. Wind-Ramp Predictability. Atmosphere. 2022; 13(3):453. https://doi.org/10.3390/atmos13030453
Chicago/Turabian StylePereyra-Castro, Karla, and Ernesto Caetano. 2022. "Wind-Ramp Predictability" Atmosphere 13, no. 3: 453. https://doi.org/10.3390/atmos13030453
APA StylePereyra-Castro, K., & Caetano, E. (2022). Wind-Ramp Predictability. Atmosphere, 13(3), 453. https://doi.org/10.3390/atmos13030453






