Study on the Associations between Meteorological Factors and the Incidence of Pulmonary Tuberculosis in Xinjiang, China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Meteorological and PTB Data
2.3. Spearman’s Rank Correlation
2.4. Statistical Method
2.5. Parameter Estimation
2.6. Sensitivity Analysis
3. Results
3.1. Descriptive Statistics of PTB Cases and Meteorological Factors
3.2. Spearman’s Rank Correlation Analysis
3.3. The Influences of Air Temperature on the Incidence of PTB
3.4. The Influences of Relative Humidity on the Incidence of PTB
3.5. The Influences of Wind Speed on the Incidence of PTB
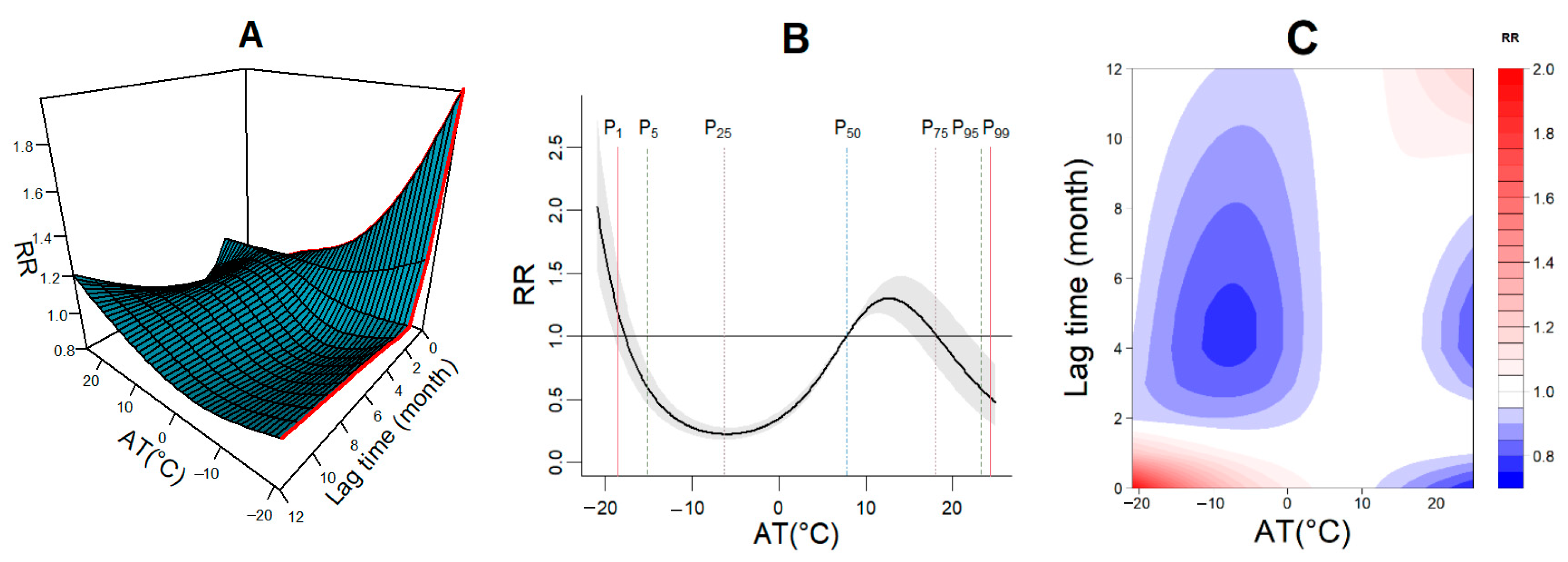
3.6. The Effect of AT on PTB Incidence
3.7. Sensitivity Analysis
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Health Organization. Global Tuberculosis Report; World Health Organization: Switzerland, Geneva, 2020.
- Turner, R.D. Cough in pulmonary tuberculosis: Existing knowledge and general insights. Pulm. Pharmacol. Ther. 2019, 55, 89–94. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.L.; Zhao, S.; Niu, Y.; Peng, Z.; Wang, K.; He, D.H.; Wang, W.M. Modelling the effects of the contaminated en-vironments on tuberculosis in Jiangsu, China. J. Theor. Biol. 2021, 508, 110453. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.Q.; Liu, Q.; Zhan, M.Y.; Tao, B.L.; Wang, J.M.; Lu, W. Meteorological factors contribute to the risk of pulmonary tu-berculosis: A multicenter study in eastern China. Sci. Total Environ. 2021, 793, 148621. [Google Scholar] [CrossRef]
- Rivas-Santiago, C.E.; Sarkar, S.; Cantarella, P., IV; Osornio-Vargas, Á.; Quintana-Belmares, R.; Meng, Q.; Kirn, T.J.; Strickland, P.O.; Chow, J.C.; Watson, J.G.; et al. Air pollution particulate matter alters antimycobacterial respiratory epithelium innate immunity. Infect. Immun. 2015, 83, 2507–2517. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Niu, Z.C.; Qi, Y.J.; Zhao, P.Q.; Li, Y.D.; Tao, Y.; Peng, L.; Qiao, M.L. Short-term effects of ambient air pollution and meteorological factors on tuberculosis in semi-arid area, northwest China: A case study in Lanzhou. Environ. Sci. Pollut. Res. Int. 2021, 28, 69190–69199. [Google Scholar] [CrossRef]
- Petersen, W.F. Tuberculosis: Weather and resistance. In Proceedings of theAnnual Meeting of the American College of Chest Physicians, Atlantic City, NJ, USA, 6 June 1942. [Google Scholar]
- Guo, C.; DU, Y.; Shen, S.Q.; Lao, X.Q.; Qian, J.; Ou, C.Q. Spatiotemporal analysis of tuberculosis incidence and its associated factors in mainland China. Epidemiol. Infect. 2017, 145, 2510–2519. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.Y.; Zhang, A. Climate and air pollution alter incidence of tuberculosis in Beijing, China. Ann. Epidemiol. 2019, 37, 71–76. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, M.; Chen, Y.; Ma, L.; Yadikaer, R.; Lu, Y.; Lou, P.; Pu, Y.; Xiang, R.; Rui, B. A study on the relationship between air pollution and pulmonary tuberculosis based on the general additive model in Wulumuqi, China. Int. J. Infect. Dis. 2020, 96, 42–47. [Google Scholar] [CrossRef]
- An, Q.; He, H.; Gao, J.; Nie, Q.; Cui, Y.; Wei, C.; Xie, X. Analysis of Temporal-Spatial Variation Characteristics of Drought: A Case Study from Xinjiang, China. Water 2020, 12, 741. [Google Scholar] [CrossRef] [Green Version]
- Xu, M.; Li, Y.; Liu, B.; Chen, R.; Sheng, L.; Yan, S.; Chen, H.; Hou, J.; Yuan, L.; Ke, L.; et al. Temperature and humidity associated with increases in tuberculosis notifications: A time-series study in Hong Kong. Epidemiol. Infect. 2021, 149, e8. [Google Scholar] [CrossRef]
- Ghadimi-Moghadam, A.; Salahi, M.; Ghatee, M.A.; Kanannejad, Z.; Mosavi, A.; Ramshk, O.; Khoramrooz, S. Environmental and climatic factors influencing the occurrence and distribution of tuberculosis in southwest Iran: A GIS-based study. Acta Med. Mediterr. 2020, 36, 557–563. [Google Scholar]
- Li, Z.-Q.; Pan, H.-Q.; Liu, Q.; Song, H.; Wang, J.-M. Comparing the performance of time series models with or without meteorological factors in predicting incident pulmonary tuberculosis in eastern China. Infect. Dis. Poverty 2020, 9, 151. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Ma, J.; Liu, F.; Zhang, Y.; Ma, P.; Jin, Y.; Zheng, Z.-J. Associations of apparent temperature with acute cardiac events and subtypes of acute coronary syndromes in Beijing, China. Sci. Rep. 2021, 11, 15229. [Google Scholar] [CrossRef]
- Royé, D.; Zarrabeitia, M.T.; Riancho, J.; Santurtún, A. A time series analysis of the relationship between apparent temperature, air pollutants and ischemic stroke in Madrid, Spain. Environ. Res. 2019, 173, 349–358. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Yang, J.; Liu, M.; Sun, X.; Li, T.; Guo, Y.; Hu, K.; Bell, M.L.; Cheng, Q.; Kan, H.; et al. Nonlinear effect of air pollution on adult pneumonia hospital visits in the coastal city of Qingdao, China: A time-series analysis. Environ. Res. 2022, 209, 112754. [Google Scholar] [CrossRef] [PubMed]
- Chaudhuri, S.; Dutta, D. Mann–Kendall trend of pollutants, temperature and humidity over an urban station of India with forecast verification using different ARIMA models. Environ. Monit. Assess. 2014, 186, 4719–4742. [Google Scholar] [CrossRef] [PubMed]
- Gasparrini, A.; Armstrong, B.; Kenward, M.G. Distributed lag non-linear models. Stat. Med. 2010, 29, 2224–2234. [Google Scholar] [CrossRef] [Green Version]
- Wu, W.; Xiao, Y.Z.; Li, G.C.; Zeng, W.; Lin, H.; Rutherford, S.; Xu, Y.; Luo, Y.; Xu, X.; Chu, C.; et al. Temperature-mortality relationship in four subtropical Chinese cities: A time-series study using a distributed lag non-linear model. Sci. Total Environ. 2013, 449, 355–362. [Google Scholar] [CrossRef]
- Yang, Q.Y.; Yang, Z.C.; Ding, H.Y.; Zhang, X.; Dong, Z.; Hu, W.; Liu, X.; Wang, M.; Hu, G.; Fu, C. The relationship between meteorological factors and mumps incidence in Guangzhou, China, 2005–2012. Hum. Vaccines Immunother. 2014, 10, 2421–2432. [Google Scholar] [CrossRef] [Green Version]
- Gasparrini, A.; Scheipl, F.; Armstrong, B.; Kenward, M.G. A penalized framework for distributed lag non-linear models. Bio-metrics 2017, 73, 938–948. [Google Scholar] [CrossRef]
- Steadman, R.G. A universal scale of apparent temperature. J. Appl. Meteorol. Climatol. 1984, 23, 1674–1687. [Google Scholar] [CrossRef]
- Liu, X.; Wen, Y.; Zhang, K.; Duan, Y.; Li, H.; Yan, S.; Yin, P.; Cheng, J.; Jiang, H. Examining the association between apparent temperature and incidence of acute excessive drinking in Shenzhen, China. Sci. Total Environ. 2020, 741, 140302. [Google Scholar] [CrossRef] [PubMed]
- Statistic Bureau of Xinjiang Uygur Autonomous Region. Available online: http://tjj.xinjiang.gov.cn/tjj/zhhvgh/list_nj1.shtml (accessed on 22 March 2022).
- Hauke, J.; Kossowski, T. Comparison of Values of Pearson’s and Spearman’s Correlation Coefficients on the Same Sets of Data. Quaest. Geogr. 2011, 30, 87–93. [Google Scholar] [CrossRef] [Green Version]
- Ha, Y.S.; Seongjin, P. An Analysis of Correlation between Personality and Visiting Place using Spearman’s Rank Correlation Coefficient. KSII Trans. Internet Inf. Syst. (TIIS) 2020, 14, 1951–1966. [Google Scholar]
- Gasparrini, A.; Armstrong, B. Reducing and meta-analysing estimates from distributed lag non-linear models. BMC Med. Res. Methodol. 2013, 13, 1. [Google Scholar] [CrossRef] [Green Version]
- Gasparrini, A. Modeling exposure-lag-response associations with distributed lag non-linear models. Stat. Med. 2014, 33, 881–899. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kirolos, A.; Thindwa, D.; Khundi, M.; Burke, R.M.; Henrion, M.Y.R.; Nakamura, I.; Divala, T.H.; Nliwasa, M.; Corbett, E.L.; MacPherson, P.; et al. Tuberculosis case notifications in Malawi have strong seasonal and weather-related trends. Sci. Rep. 2021, 11, 4621. [Google Scholar] [CrossRef]
- Xiao, Y.; He, L.; Chen, Y.; Wang, Q.; Meng, Q.; Chang, W.; Xiong, L.; Yu, Z. The influence of meteorological factors on tuberculosis incidence in Southwest China from 2006 to 2015. Sci. Rep. 2018, 8, 10053. [Google Scholar] [CrossRef]
- Jaimni, V.; Shasty, B.A.; Madhyastha, S.P.; Shetty, G.V.; Acharya, R.V.; Bekur, R.; Doddamani, A. Association of Vitamin D Deficiency and Newly Diagnosed Pulmonary Tuberculosis. Pulm. Med. 2021, 2021, 5285841. [Google Scholar] [CrossRef]
- Pinto, C.T.; Nano, F.E. Stable, temperature-sensitive recombinant strain of Mycobacterium smegmatis generated through the substitution of a psychrophilic ligA gene. FEMS Microbiol. Lett. 2015, 362, fnv152. [Google Scholar] [CrossRef] [Green Version]
- Fahy, J.V.; Dickey, B.F. Airway Mucus Function and Dysfunction. N. Engl. J. Med. 2010, 363, 2233–2247. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Q.; Liu, M.; Zhang, Y.; Wu, S.; Yang, Y.; Liu, Y.; Amsalu, E.; Tao, L.; Liu, X.; Zhang, F.; et al. The spatio-temporal analysis of the incidence of tuberculosis and the associated factors in mainland China, 2009–2015. Infect. Genet. Evol. 2019, 75, 103949. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Qin, S.; Zhou, Q.; Jiang, H. Medium-term wind speeds forecasting utilizing hybrid models for three different sites in Xinjiang, China. Renew. Energy 2015, 76, 91–101. [Google Scholar] [CrossRef]
- Halonen, J.I.; Zanobetti, A.; Sparrow, D.; Vokonas, P.S.; Schwartz, J. Relationship between outdoor temperature and blood pressure. Occup. Environ. Med. 2010, 68, 296–301. [Google Scholar] [CrossRef] [Green Version]
- Khadadah, M.; Mustafa, S.; Elgazzar, A. Effect of acute cold exposure on lung perfusion and tracheal smooth muscle contraction in rabbit. Eur. J. Appl. Physiol. 2011, 111, 77–81. [Google Scholar] [CrossRef]
- Hensel, H.; Schafer, K. Thermoreception and Temperature Regulation in Man. Recent Adv. Med. Thermol. 1984, 38, 51–64. [Google Scholar] [CrossRef]
- Smith, G.S.; Schoenbach, V.J.; Richardson, D.B.; Gammon, M.D. Particulate air pollution and susceptibility to the development of pulmonary tuberculosis disease in North Carolina: An ecological study. Int. J. Environ. Health Res. 2013, 24, 103–112. [Google Scholar] [CrossRef] [Green Version]




| Group | Range | Percentiles | |||||||
|---|---|---|---|---|---|---|---|---|---|
| P1 | P5 | P25 | P50 | P75 | P95 | P99 | |||
| Pre | 0.4~34.2 | 10.1 ± 7.0 | 1.7 | 2.5 | 4.5 | 8.0 | 14.4 | 24.4 | 30.0 |
| AP | 869.8~908.8 | 898 ± 6.0 | 888.5 | 889.3 | 893.0 | 898.2 | 903.5 | 906.3 | 908.3 |
| WS | 1.4~3.3 | 2.3 ± 0.5 | 1.4 | 1.6 | 1.9 | 2.3 | 2.6 | 3.0 | 3.2 |
| Temp | −16.1~26.5 | 9.2 ± 12.5 | −14.0 | −10.6 | −1.8 | 11.3 | 21.1 | 24.6 | 25.4 |
| RH | 29.1~74.7 | 48.3 ± 10.8 | 31.4 | 33.4 | 40.2 | 45.6 | 57.9 | 67.4 | 70.1 |
| SD | 124.8~328.6 | 239.6 ± 52.7 | 145.2 | 157.6 | 188.1 | 251.0 | 286.3 | 306.9 | 319.8 |
| PTB cases | 1194~8151 | 3427 ± 1152 | 1346 | 1937 | 2661 | 3271 | 4100 | 5279 | 7555 |
| AT | −20.9~25.0 | 5.7 ± 13.5 | −18.5 | −15.1 | −6.3 | 7.8 | 18.0 | 23.3 | 24.3 |
| Lag | P1 | P5 | P25 | P75 | P95 | P99 |
|---|---|---|---|---|---|---|
| Lag 0 | 1.81 (1.73, 1.90) | 1.60 (1.54, 1.67) | 1.22 (1.19, 1.26) | 0.86 (0.83, 0.88) | 0.77 (0.74, 0.81) | 0.76 (0.72, 0.80) |
| Lag 0–1 | 2.18 (2.06, 2.31) | 1.84 (1.74, 1.94) | 1.28 (1.22, 1.34) | 0.84 (0.80, 0.87) | 0.74 (0.70, 0.80) | 0.73 (0.68, 0.78) |
| Lag 0–2 | 2.01 (1.89, 2.14) | 1.67 (1.58, 1.77) | 1.16 (1.09, 1.22) | 0.86 (0.82, 0.91) | 0.76 (0.70, 0.84) | 0.75 (0.68, 0.82) |
| Lag 0–3 | 1.79 (1.65, 1.94) | 1.42 (1.32, 1.54) | 0.95 (0.88, 1.02) | 0.85 (0.78, 0.91) | 0.69 (0.61, 0.78) | 0.66 (0.58, 0.76) |
| Lag 0–4 | 1.61 (1.45, 1.78) | 1.20 (1.09, 1.32) | 0.74 (0.68, 0.81) | 0.80 (0.73, 0.89) | 0.58 (0.49, 0.69) | 0.54 (0.46, 0.65) |
| Lag 0–5 | 1.46 (1.29, 1.66) | 1.02 (0.90, 1.14) | 0.58 (0.53, 0.65) | 0.77 (0.68, 0.87) | 0.49 (0.40, 0.61) | 0.45 (0.36, 0.56) |
| Lag 0–6 | 1.35 (1.17, 1.57) | 0.88 (0.77, 1.01) | 0.47 (0.42, 0.53) | 0.75 (0.64, 0.87) | 0.44 (0.34, 0.56) | 0.39 (0.30, 0.51) |
| Lag 0–7 | 1.27 (1.07, 1.51) | 0.78 (0.67, 0.91) | 0.39 (0.34, 0.45) | 0.74 (0.63, 0.88) | 0.40 (0.31, 0.54) | 0.36 (0.26, 0.48) |
| Lag 0–8 | 1.21 (1.01, 1.47) | 0.70 (0.59, 0.84) | 0.33 (0.28, 0.38) | 0.76 (0.63, 0.91) | 0.39 (0.29, 0.54) | 0.34 (0.24, 0.48) |
| Lag 0–9 | 1.18 (0.95, 1.45) | 0.65 (0.54, 0.79) | 0.29 (0.24, 0.34) | 0.79 (0.64, 0.97) | 0.40 (0.28, 0.57) | 0.35 (0.24, 0.51) |
| Lag 0–10 | 1.16 (0.92, 1.46) | 0.62 (0.50, 0.76) | 0.25 (0.21, 0.31) | 0.84 (0.67, 1.05) | 0.43 (0.30, 0.63) | 0.38 (0.25, 0.57) |
| Lag 0–11 | 1.16 (0.90, 1.49) | 0.59 (0.47, 0.75) | 0.23 (0.19, 0.28) | 0.91 (0.71, 1.16) | 0.49 (0.32, 0.73) | 0.43 (0.27, 0.66) |
| Lag 0–12 | 1.18 (0.90, 1.55) | 0.59 (0.46, 0.75) | 0.22 (0.18, 0.27) | 1.01 (0.78, 1.31) | 0.58 (0.37, 0.89) | 0.51 (0.32, 0.82) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, C.; Wang, Y.; Hu, Z.; Jiao, H.; Wang, L. Study on the Associations between Meteorological Factors and the Incidence of Pulmonary Tuberculosis in Xinjiang, China. Atmosphere 2022, 13, 533. https://doi.org/10.3390/atmos13040533
Gao C, Wang Y, Hu Z, Jiao H, Wang L. Study on the Associations between Meteorological Factors and the Incidence of Pulmonary Tuberculosis in Xinjiang, China. Atmosphere. 2022; 13(4):533. https://doi.org/10.3390/atmos13040533
Chicago/Turabian StyleGao, Chunjie, Yingdan Wang, Zengyun Hu, Haiyan Jiao, and Lei Wang. 2022. "Study on the Associations between Meteorological Factors and the Incidence of Pulmonary Tuberculosis in Xinjiang, China" Atmosphere 13, no. 4: 533. https://doi.org/10.3390/atmos13040533
APA StyleGao, C., Wang, Y., Hu, Z., Jiao, H., & Wang, L. (2022). Study on the Associations between Meteorological Factors and the Incidence of Pulmonary Tuberculosis in Xinjiang, China. Atmosphere, 13(4), 533. https://doi.org/10.3390/atmos13040533







