Vorticity Budget and Formation Mechanisms of a Mesoscale Convective Vortex in a Heavy-Rainstorm Episode
Abstract
:1. Introduction
2. Data and Model Setup
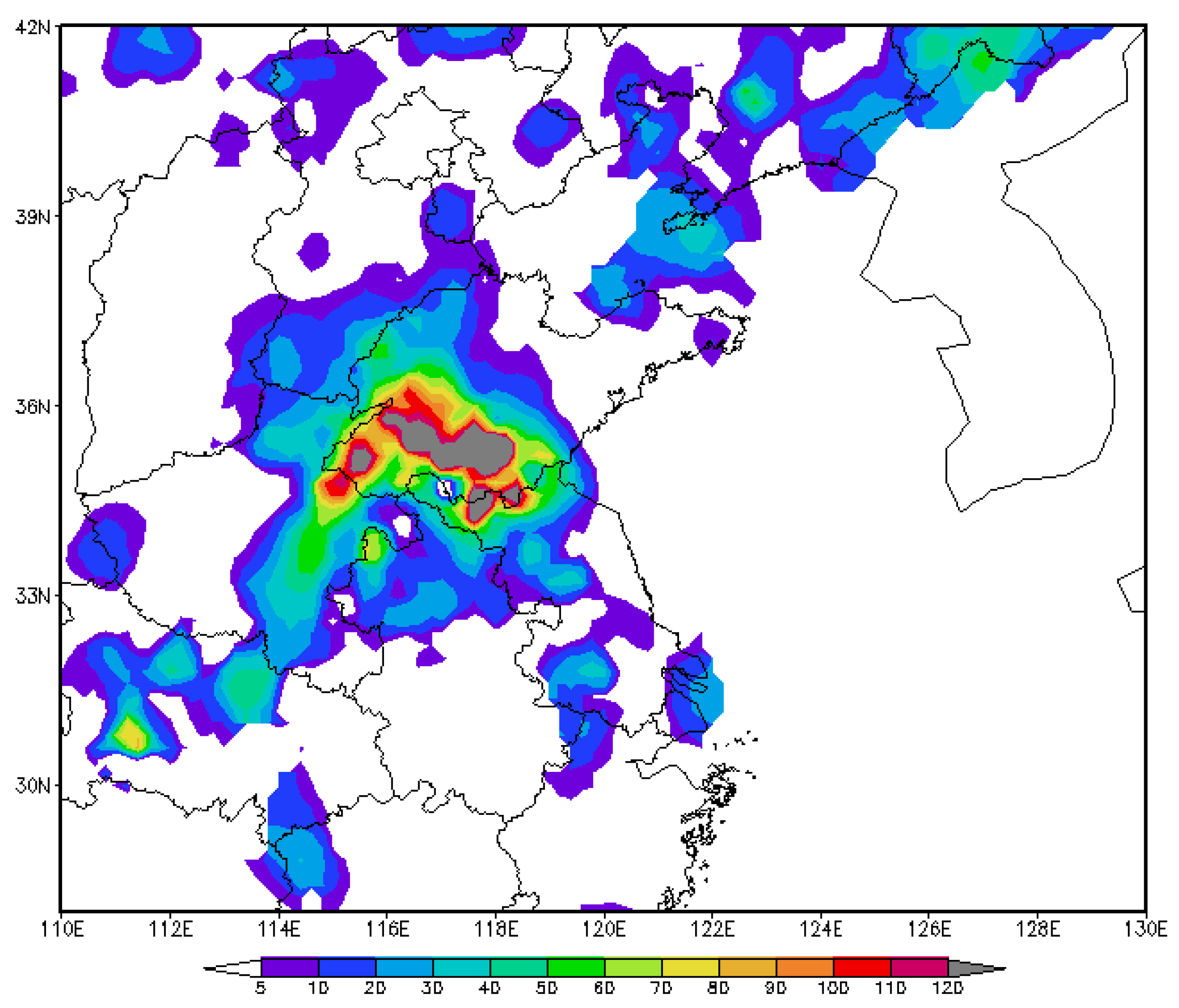
3. The Rainstorm Episode and the Verification of Simulation Results
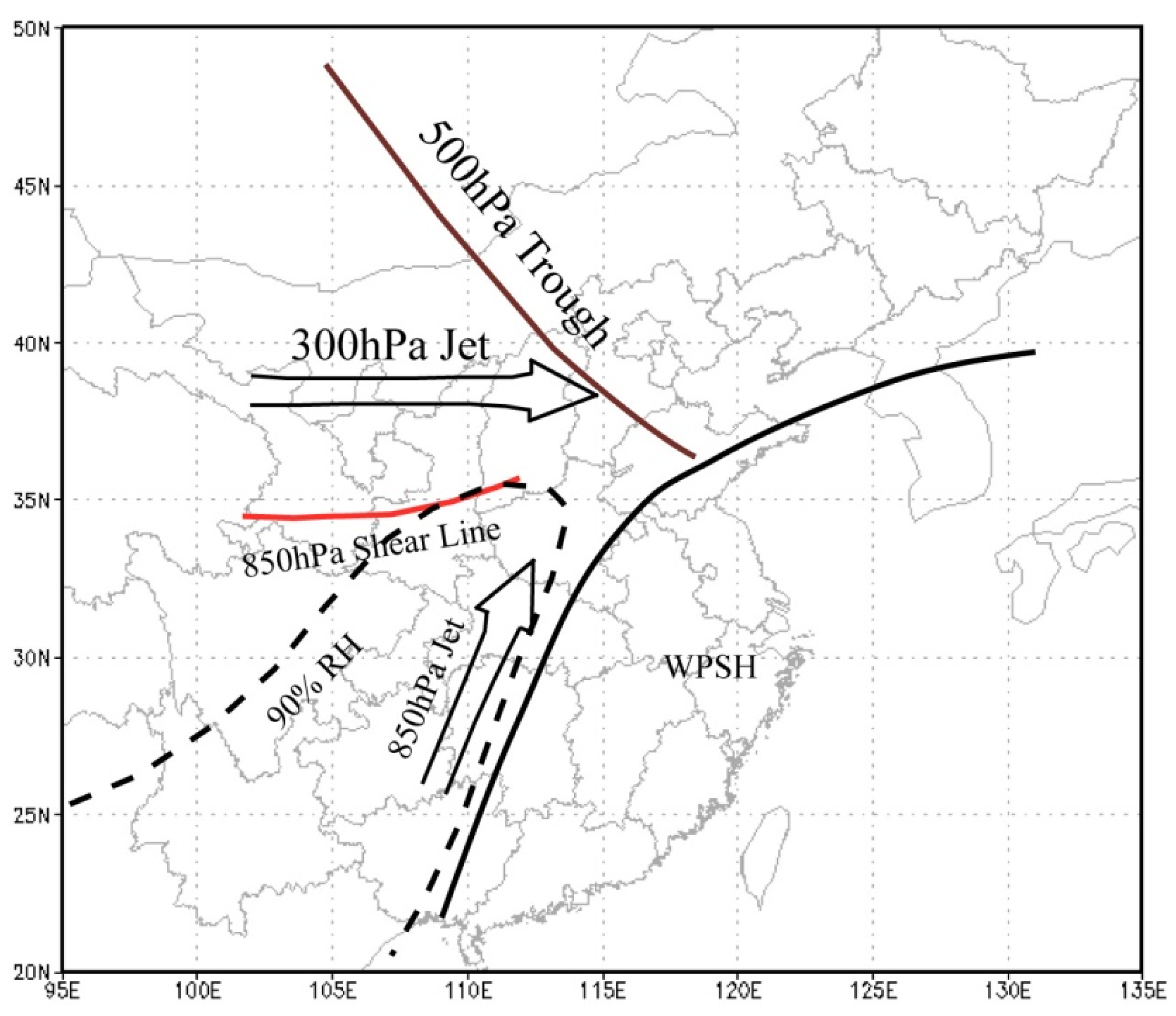
3.1. The Rainstorm Episode and Synoptic Background
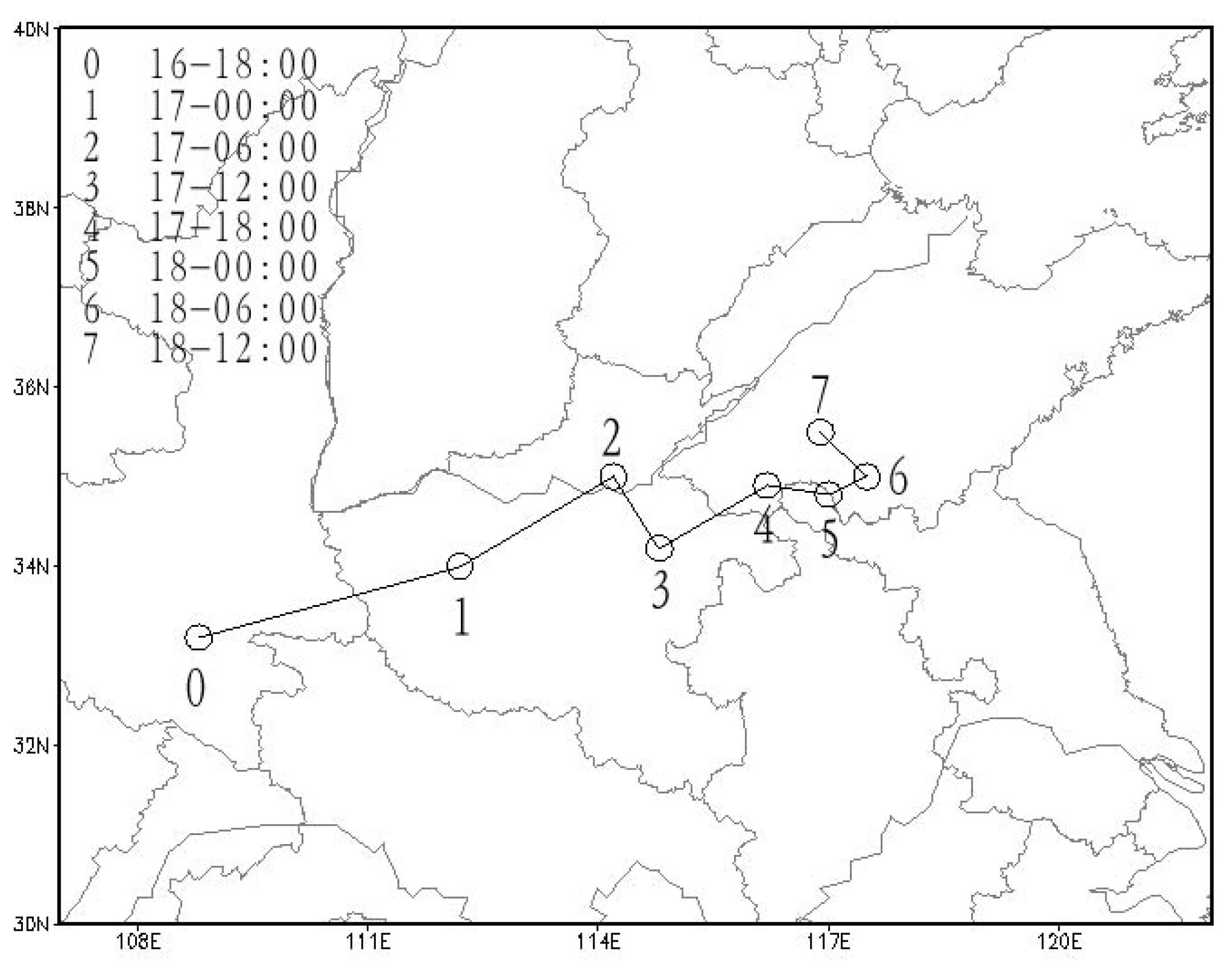
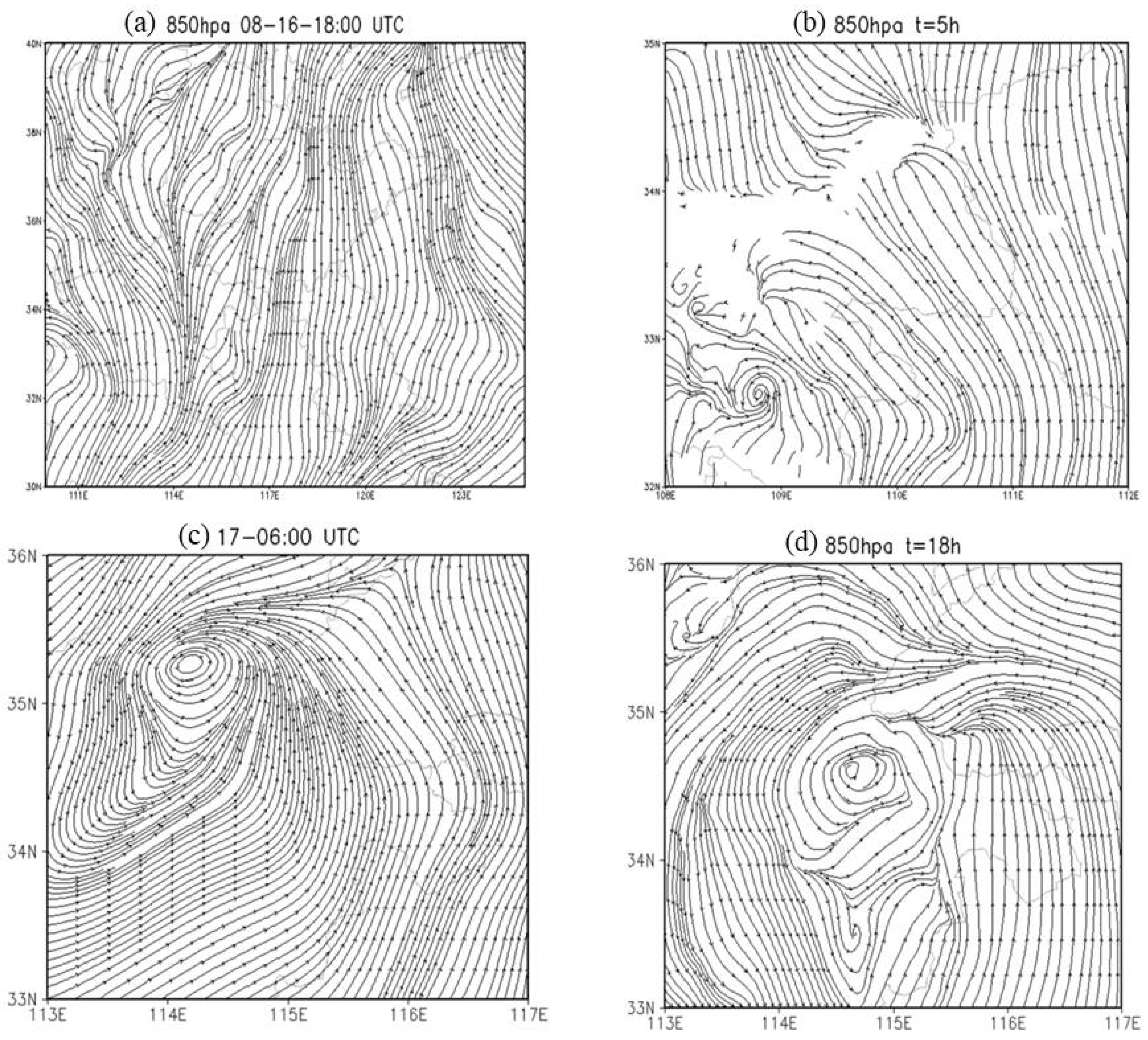
3.2. MCV Activities
3.3. Verification of the Numerical Simulation
3.3.1. Verification of Convective Activities on Infrared Satellite Images
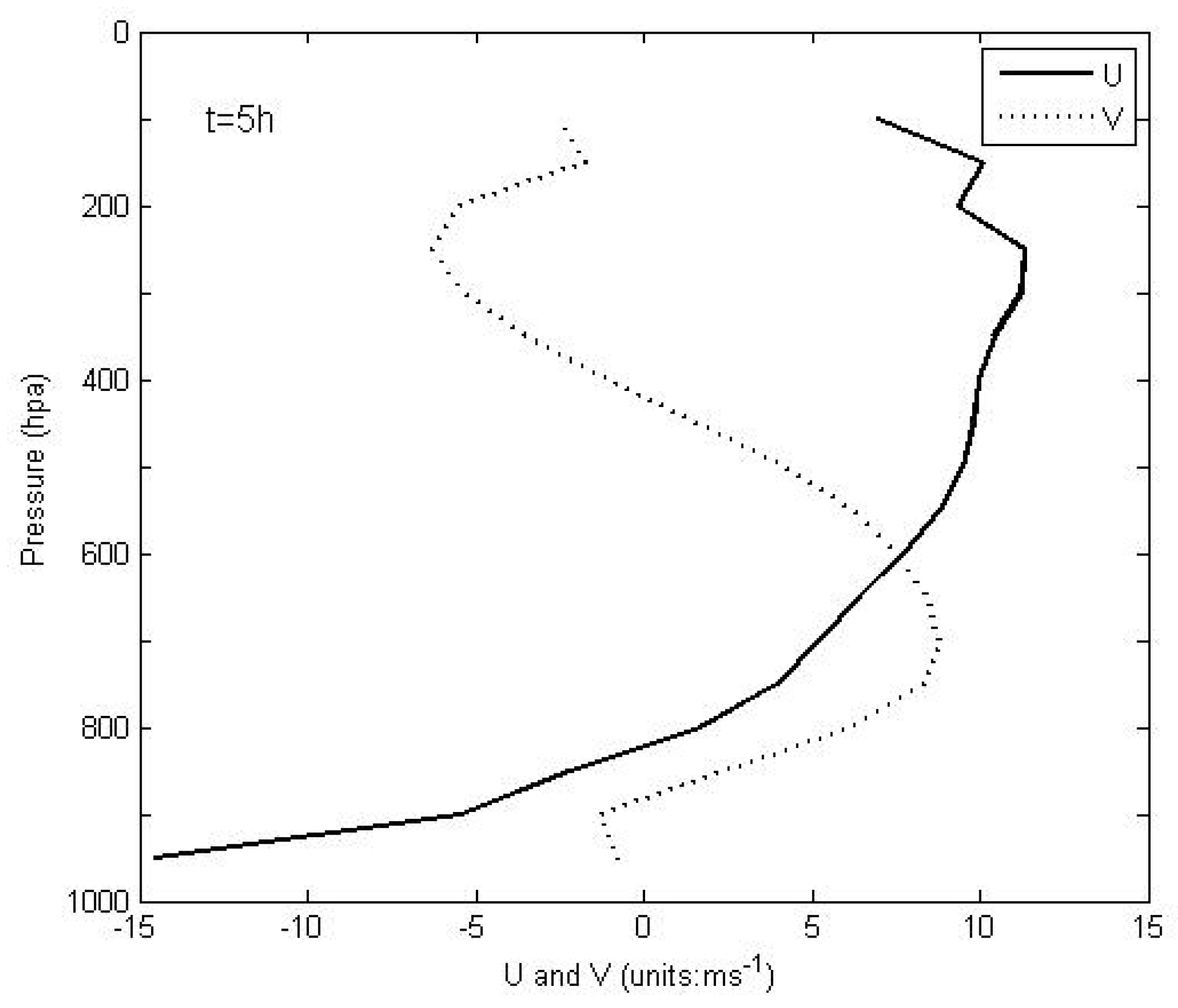
3.3.2. Verification of the Simulated MCV Activities
4. Vorticity-Budget Analysis
4.1. Vorticity Equation
- (1)
- is the advection term of relative vorticity, which is caused by the nonuniform horizontal distribution of relative vorticity;
- (2)
- is the convection term, which indicates the vertical transport of relative vorticity caused by the vertical motion;
- (3)
- is the advection term of planetary vorticity. This term refers to the change of relative vorticity caused by the absolute-vorticity conservation when the air mass moves along the meridional direction;
- (4)
- is the convergence/divergence term. This term indicates the increase or decrease in the preexisted vertical vorticity caused by the horizontal convergence or divergence;
- (5)
- is the tilting term. This term indicates the vertical vorticity change resulting from the nonuniform horizontal distribution of vertical motion.
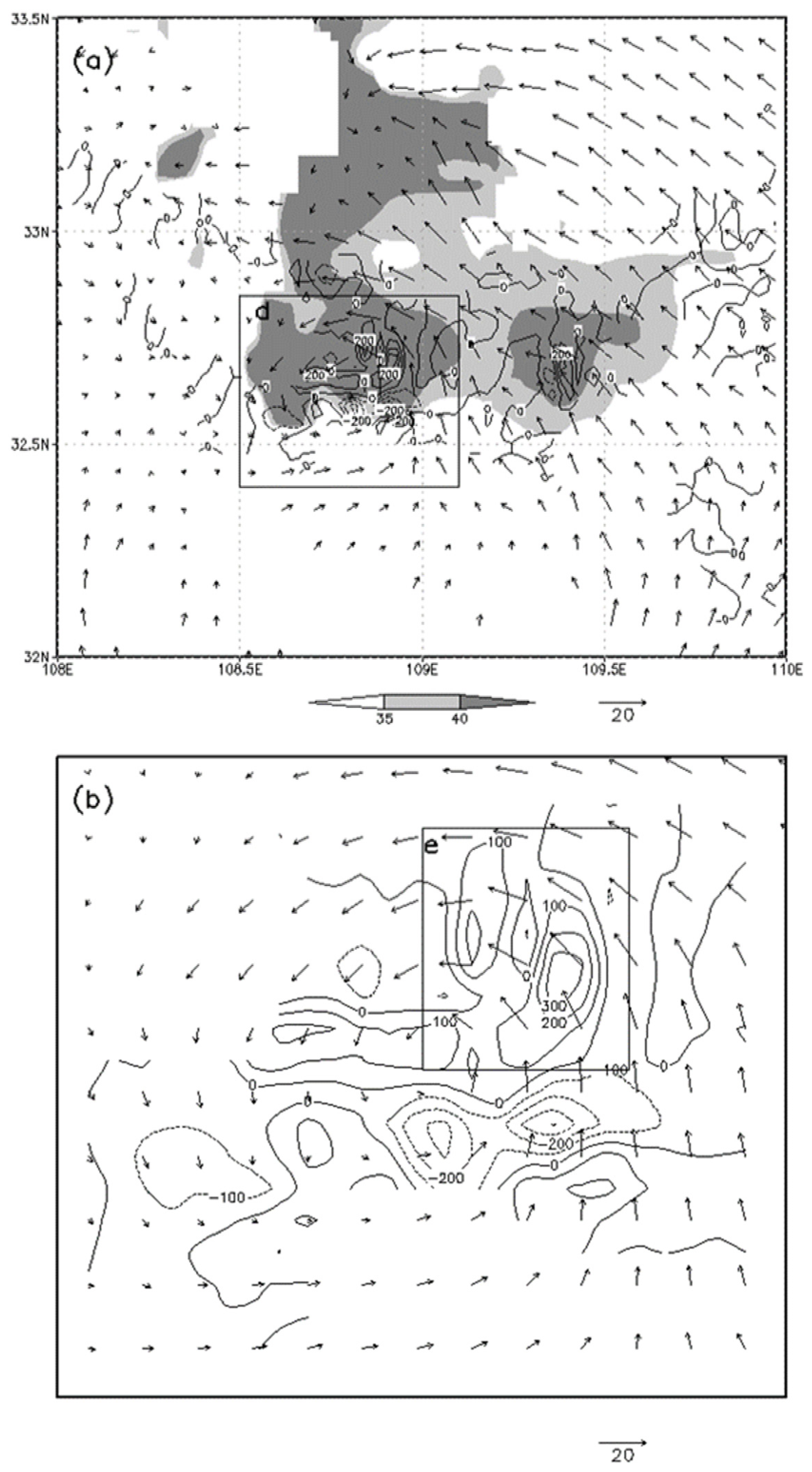
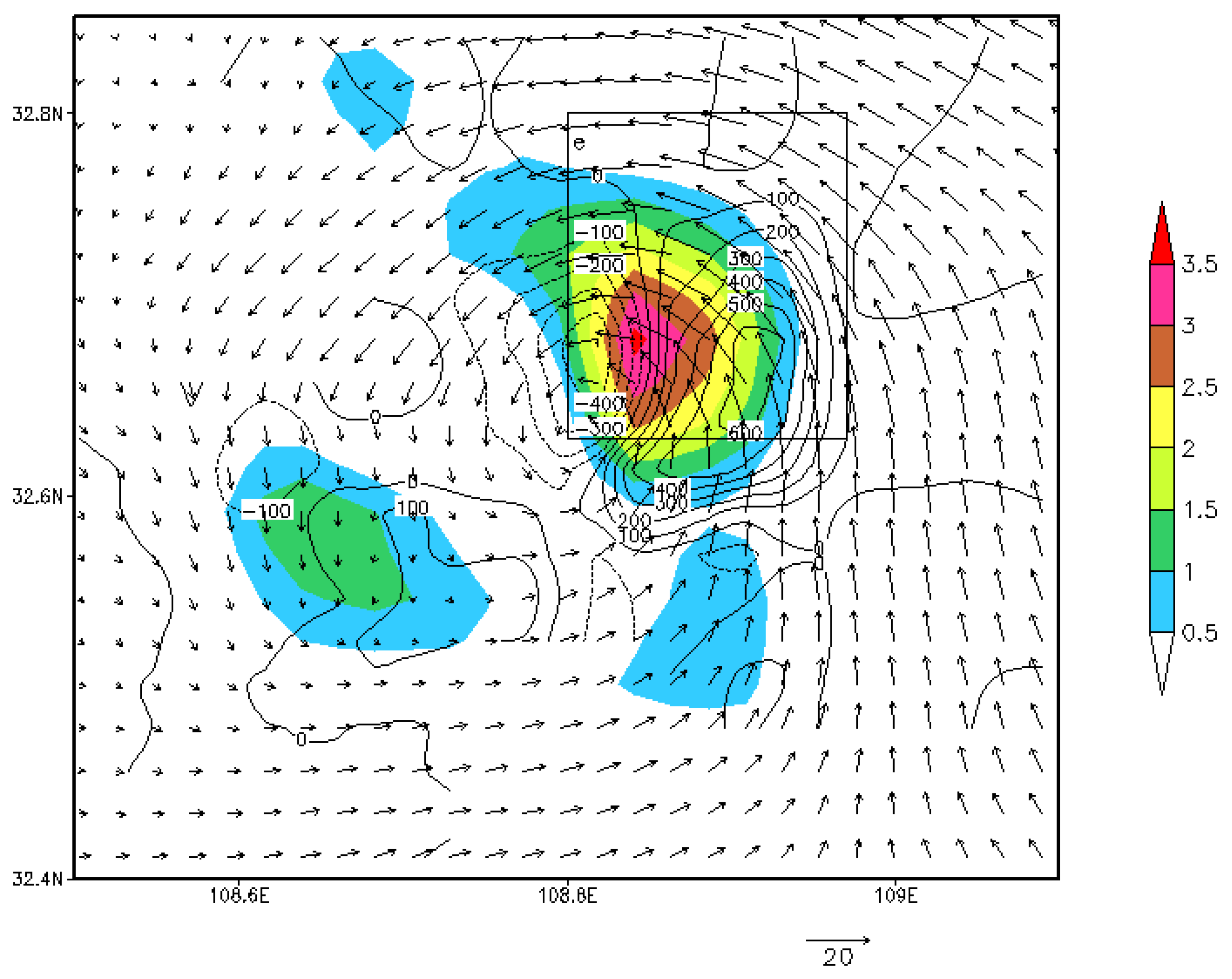
4.2. Vorticity Budget at the MCV Initiation
5. Discussion on the MCV Formation Mechanisms
5.1. Latent-Heat Release and Low-Level Convergence
5.2. Upward Motion and the Titling of Vortex Tube
5.3. Rossby Radius of Deformation
6. Discussions and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ge, J.J.; Zhong, W.; Lu, H.C. A diagnostic analysis of vorticity-divergence effects and the quasi-balanced flow in a mesoscale vortex during the process of flash-flood-producing rainstorm. Acta Meteorol. Sin. 2011, 69, 277–288. (In Chinese) [Google Scholar]
- Green, A.; Gopalakrishnan, S.G.; Alaka, G.J., Jr.; Chiao, S. Understanding the role of mean and eddy momentum transport in the rapid intensification of Hurricane Irma (2017) and Hurricane Michael (2018). Atmosphere 2021, 12, 492. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, T. Numerical simulation of a heavy rainstorm in Northeast China caused by the residual vortex of Typhoon 1909 (Lekima). Atmosphere 2021, 12, 120. [Google Scholar] [CrossRef]
- Fu, S.M.; Yu, F.; Wang, D.H.; Xia, R.T. A comparison of two kinds of eastward-moving mesoscale vortices during the mei-yu period of 2010. Sci. China Earth Sci. 2012, 42, 1282–1300. [Google Scholar] [CrossRef]
- Liu, J.Y.; Tan, Z.M.; Zhang, Y. Study of the three types of torrential rains of different formation mechanism during the meiyu period. Acta Meteorol. Sin. 2012, 70, 452–466. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, F.; Davis, C.; Sun, J. Diurnal evolution and structure of long-lived mesoscale convective vortices along the Mei-yu front over the East China Plains. J. Atmos. Sci. 2018, 75, 1005–1025. [Google Scholar] [CrossRef]
- Fu, S.M.; Mai, Z.; Sun, J.H.; Li, W.L.; Ding, Y.; Wang, Y.Q. Impacts of convective activity over the Tibetan Plateau on plateau vortex, southwest vortex, and downstream precipitation. J. Atmos. Sci. 2019, 76, 3803–3830. [Google Scholar] [CrossRef]
- Bartels, D.L.; Maddox, R.A. Midlevel cyclonic vortices generated by mesoscale convective systems. Mon. Weather Rev. 1991, 119, 104–118. [Google Scholar] [CrossRef] [Green Version]
- Davis, C.A.; Galarneau, T.J. The vertical structure of mesoscale convective vortices. J. Atmos. Sci 2009, 66, 686–704. [Google Scholar] [CrossRef]
- Fritsch, J.M.; Murphy, J.D.; Kain, J.S. Warm core vortex amplification over land. J. Atmos. Sci. 1994, 51, 1780–1807. [Google Scholar] [CrossRef]
- Davis, C.A.; Trier, S.B. Mesoscale convective vortices observed during BAMEX. Part I: Kinematic and thermodynamic structure. Mon. Weather Rev. 2007, 135, 2029–2049. [Google Scholar] [CrossRef] [Green Version]
- Davis, C.A.; Ahijevych, D.A.; Trier, S.B. Detection and prediction of warm season midtropospheric vortices by the Rapid Update Cycle. Mon. Weather Rev. 2002, 130, 24–42. [Google Scholar] [CrossRef]
- Rogers, R.F.; Fritsch, J.M. Surface cyclogenesis from convectively driven amplification of midlevel mesoscale convective vortices. Mon. Weather Rev. 2001, 129, 605–637. [Google Scholar] [CrossRef]
- Shu, Y.; Sun, J.S.; Pan, Y.N. Characteristics of mesoscale vortices over China in 2015. J. Meteorol. Res. 2017, 31, 1149–1160. [Google Scholar] [CrossRef]
- Trier, S.B.; Davis, C.A. Influence of balanced motions on heavy precipitation within a long-lived convectively generated vortex. Mon. Weather Rev. 2002, 130, 877–899. [Google Scholar] [CrossRef]
- Raymond, D.J.; Jiang, H. A theory for long-lived mesoscale convective systems. J. Atmos. Sci. 1990, 47, 3067–3077. [Google Scholar] [CrossRef] [Green Version]
- Trier, S.B.; Davis, C.A. Mesoscale convective vortices observed during BAMEX. Part II: Influences on secondary deep convection. Mon. Weather Rev. 2007, 135, 2051–2075. [Google Scholar] [CrossRef] [Green Version]
- Lai, H.W.; Davis, C.A.; Jou, B.J.D. A subtropical Oceanic mesoscale convective vortex observed during SoWMEX/TiMREX. Mon. Weather Rev. 2011, 139, 2367–2385. [Google Scholar] [CrossRef] [Green Version]
- Rogers, R.F.; Reasor, P.D.; Zawislak, J.A.; Nguyen, L.T. Precipitation Processes and Vortex Alignment during the Intensification of a Weak Tropical Cyclone in Moderate Vertical Shear. Mon. Weather Rev. 2020, 148, 1899–1929. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.S.; Frank, W.M. A numerical study of the genesis of extratropical convective mesovortices. Part I: Evolution and Dynamics. J. Atmos. Sci. 1993, 50, 2401–2406. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.H.; Zhao, S.X.; Xu, G.K.; Meng, Q.T. Study on a mesoscale convective vortex causing heavy rainfall during the Mei-yu season in 2003. Adv. Atmos. Sci. 2010, 27, 1193–1209. [Google Scholar] [CrossRef]
- Yu, F.; Fu, S.M.; Zhao, S.X.; Sun, J.H. Study on the dynamic chararistics of an eastward-offshore mesoscale vortex along the Meiyu-Baiu front. Atmos. Ocean. Sci. Lett. 2012, 5, 360–366. [Google Scholar] [CrossRef] [Green Version]
- Xu, W.H.; Ni, Y.Q.; Wang, X.K.; Qiu, X.X.; Bao, X.H.; Jin, W.Y. A study of structure and mechanism of a meso-beta-scale convective vortex and associated heavy rainfall in the Dabie Mountain area Part I: Diagnostic analysis of the structure. Adv. Atmos. Sci. 2011, 28, 1159–1176. [Google Scholar] [CrossRef]
- Trier, S.B.; Davis, C.A.; Tuttle, J.D. Long-lived meso-convective vortices and their environment. Part I: Observations from the central United States during the 1998 warm season. Mon. Weather Rev. 2000, 128, 3376–3395. [Google Scholar] [CrossRef]
- Fu, S.M.; Tang, H.; Li, Y.; Ma, H.; Sun, J.H. On the Relationship of a Low-Level Jet and the Formation of a Heavy-Rainfall-Producing Mesoscale Vortex over the Yangtze River Basin. Atmosphere 2021, 12, 156. [Google Scholar] [CrossRef]
- Gao, L.X.; Wang, Y.; Wang, M.B.; Liu, C. A study on radar echo and the impact of terrain on the heavy torrential rainfall event in Shandong Province on 17 August 2009. Trans. Atmos. Sci. 2011, 34, 239–245. (In Chinese) [Google Scholar] [CrossRef]
- Hong, S.Y.; Juang, H.M.; Zhao, Q. Implementation of prognostic cloud scheme for a regional spectral model. Mon. Weather Rev. 1998, 126, 2621–2639. [Google Scholar] [CrossRef]
- Hong, S.Y.; Pan, H.L. Nonlocal boundary layer vertical diffusion in a medium-range forecast model. Mon. Weather Rev. 1996, 124, 2322–2339. [Google Scholar] [CrossRef] [Green Version]
- Kain, J.S.; Fritsch, J.M. A one-dimensional entraining/detraining plume model and its application in convective parameterization. J. Atmos. Sci. 1990, 47, 2784–2802. [Google Scholar] [CrossRef] [Green Version]
- Pielke, R.A. Mesoscale Meteorological Modeling, 2nd ed.; Academic Press: San Diego, CA, USA, 2002; p. 676. [Google Scholar]
- Paulson, C.A. The mathematical representation of wind speed and temperature profiles in the unstable atmospheric surface layer. J. Appl. Meteorol. Climatol. 1970, 9, 857–861. [Google Scholar] [CrossRef]
- Dyer, A.J.; Hicks, B.B. Flux-gradient relationships in the constant flux layer. Q. J. R. Meteorol. Soc. 1970, 96, 715–721. [Google Scholar] [CrossRef]
- Webb, E.K. Profile relationships: The log-linear range, and extension to strong stability. Q. J. R. Meteorol. Soc. 1970, 96, 67–90. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmosphere: RRTM, a validated correlated-k model for the long-wave. J. Geophys. Res. 1997, 102, 16663–16682. [Google Scholar] [CrossRef] [Green Version]
- Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Wicker, L.J.; Skamarock, W.C. Time splitting methods for elastic models using forward time schemes. Mon. Weather Rev. 2002, 130, 2088–2097. [Google Scholar] [CrossRef]
- Hertenstein, R.F.A.; Schubert, W.H. Potential vorticity anomalies associated with squall lines. Mon. Weather Rev. 1991, 119, 1663–1672. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.L.; Fritsch, J.M. A numerical investigation of a convectively generated, inertially stable, extratropical warm-core mesovortex over land. Part I: Structure and evolution. Mon. Weather Rev. 1988, 116, 2660–2687. [Google Scholar] [CrossRef] [Green Version]
- Menard, R.D.; Fritsch, J.M. A mesoscale convective complex-generated inertially stable warm core vortex. Mon. Weather Rev. 1989, 117, 1237–1260. [Google Scholar] [CrossRef] [Green Version]
- Bartels, D.L.; Brown, J.M.; Tollerud, E.I. Structure of a midtropospheric vortex induced by a mesoscale convective system. Mon. Weather Rev. 1997, 125, 193–211. [Google Scholar] [CrossRef]
- Houze, R.A. Mesoscale convective systems. Rev. Geophys. 2004, 42, 125–133. [Google Scholar] [CrossRef] [Green Version]
- Verlinde, J.; Cotton, W.R. A mesoscale vortex couplet observed in the trailing anvil of a multicellular convective complex. Mon. Weather Rev. 1990, 118, 993–1010. [Google Scholar] [CrossRef] [Green Version]
- Frank, W.M. The cumulus parameterization problem. Mon. Weather Rev. 1983, 111, 1859–1871. [Google Scholar] [CrossRef]
- Cotton, W.R.; Anthes, R.A. Storm and Cloud Dynamics; Academic Press: San Diego, CA, USA, 1989; p. 883. [Google Scholar]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 2; NCAR Tech Note NCAR/TN-468 + STR; University Corporation for Atmospheric Research: Boulder, CO, USA, 2005; p. 88. [Google Scholar]
- Yang, D.S.; Liu, Y.B.; Liu, S.S. Meteorological Dynamics; China Meteorological Press: Beijing, China, 1980; pp. 34–37. (In Chinese) [Google Scholar]
- Wang, W.; Pan, Y.N.; Shu, Y. The characteristics of mesoscale convective system and mesoscale convective vortex in summers over eastern China. J. Nanjing Univ. Nat. Sci. 2011, 47, 692–702. (In Chinese) [Google Scholar]
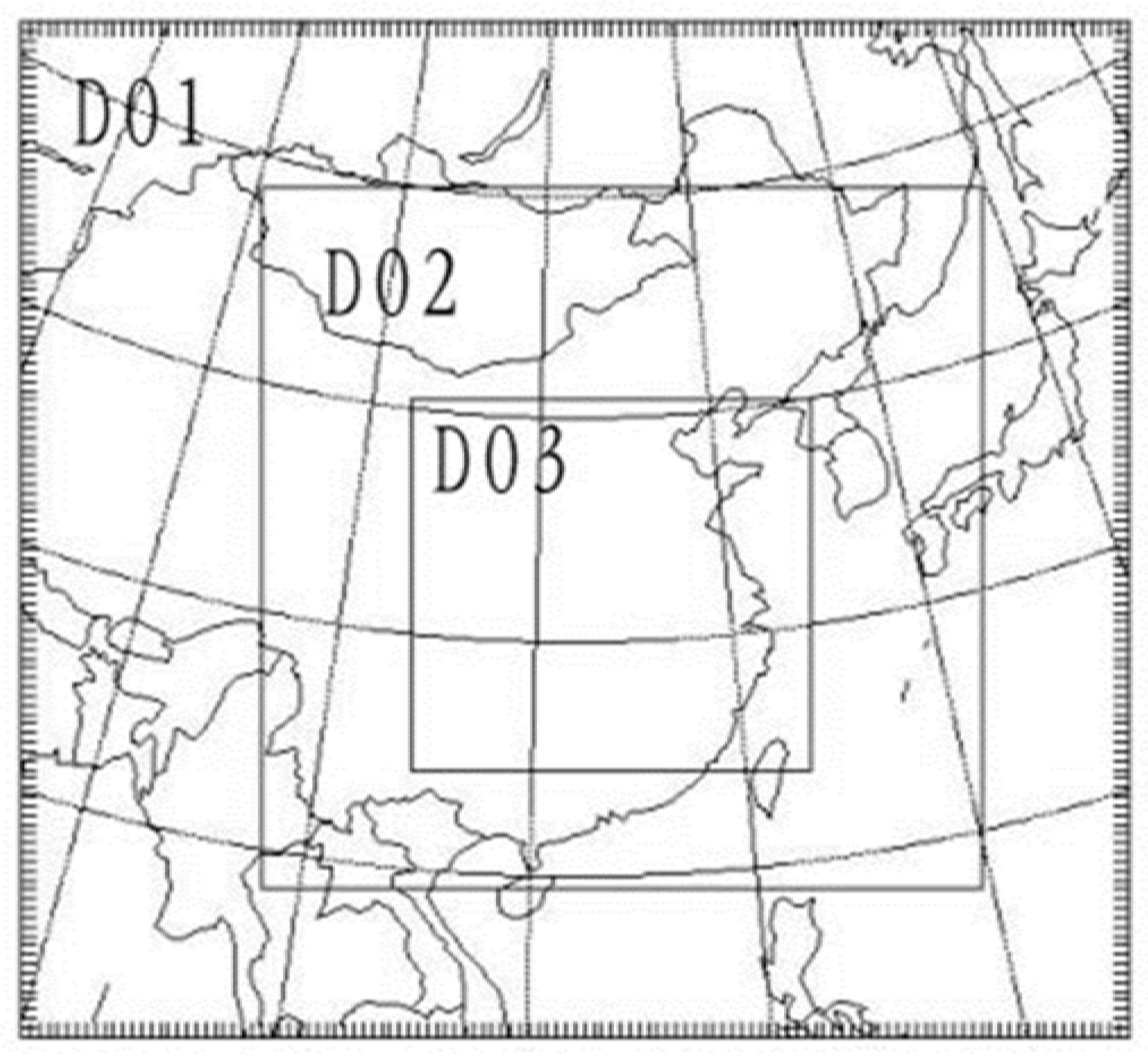



| Domain 1 | Domain 2 | Domain 3 | |
|---|---|---|---|
| Grid spacing | 45 km | 15 km | 5 km |
| Grid points | 121 × 111 | 235 × 229 | 391 × 361 |
| Cumulus parameterization | Kain–Fritsch scheme | none | |
| Integration time | 12:00 UTC on 16 August to 06:00 UTC on 17 August 2009 | ||
| Cloud microphysics | WRF Single Moment 5-class scheme | ||
| Boundary layer | Yonsei University (YSU) scheme | ||
| Parameterization of near-surface layer | Monin–Obukhov scheme | ||
| Parameterization of long-wave radiation | The Rapid Radiative Transfer Model (RRTM) scheme | ||
| Parameterization of short-wave radiation | Dudhia scheme | ||
| Land surface | Thermal diffusion scheme | ||
| Time integration | Third-order Runge–Kutta scheme | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shu, Y.; Sun, J.; Jin, C.; Zhuang, B. Vorticity Budget and Formation Mechanisms of a Mesoscale Convective Vortex in a Heavy-Rainstorm Episode. Atmosphere 2022, 13, 556. https://doi.org/10.3390/atmos13040556
Shu Y, Sun J, Jin C, Zhuang B. Vorticity Budget and Formation Mechanisms of a Mesoscale Convective Vortex in a Heavy-Rainstorm Episode. Atmosphere. 2022; 13(4):556. https://doi.org/10.3390/atmos13040556
Chicago/Turabian StyleShu, Yu, Jisong Sun, Chenlu Jin, and Bingliang Zhuang. 2022. "Vorticity Budget and Formation Mechanisms of a Mesoscale Convective Vortex in a Heavy-Rainstorm Episode" Atmosphere 13, no. 4: 556. https://doi.org/10.3390/atmos13040556
APA StyleShu, Y., Sun, J., Jin, C., & Zhuang, B. (2022). Vorticity Budget and Formation Mechanisms of a Mesoscale Convective Vortex in a Heavy-Rainstorm Episode. Atmosphere, 13(4), 556. https://doi.org/10.3390/atmos13040556






