Knowledge-Enhanced Deep Learning for Simulation of Extratropical Cyclone Wind Risk
Abstract
:1. Introduction
2. ETC Background
2.1. Conceptual Model
2.2. Composite Analysis
2.3. ETC Wind Risk Assessment
3. Methodology
3.1. Knowledge-Enhanced Deep Learning for ETC Boundary-Layer Wind
3.1.1. Rationalism-Based Knowledge
3.1.2. Parametric Pressure Field
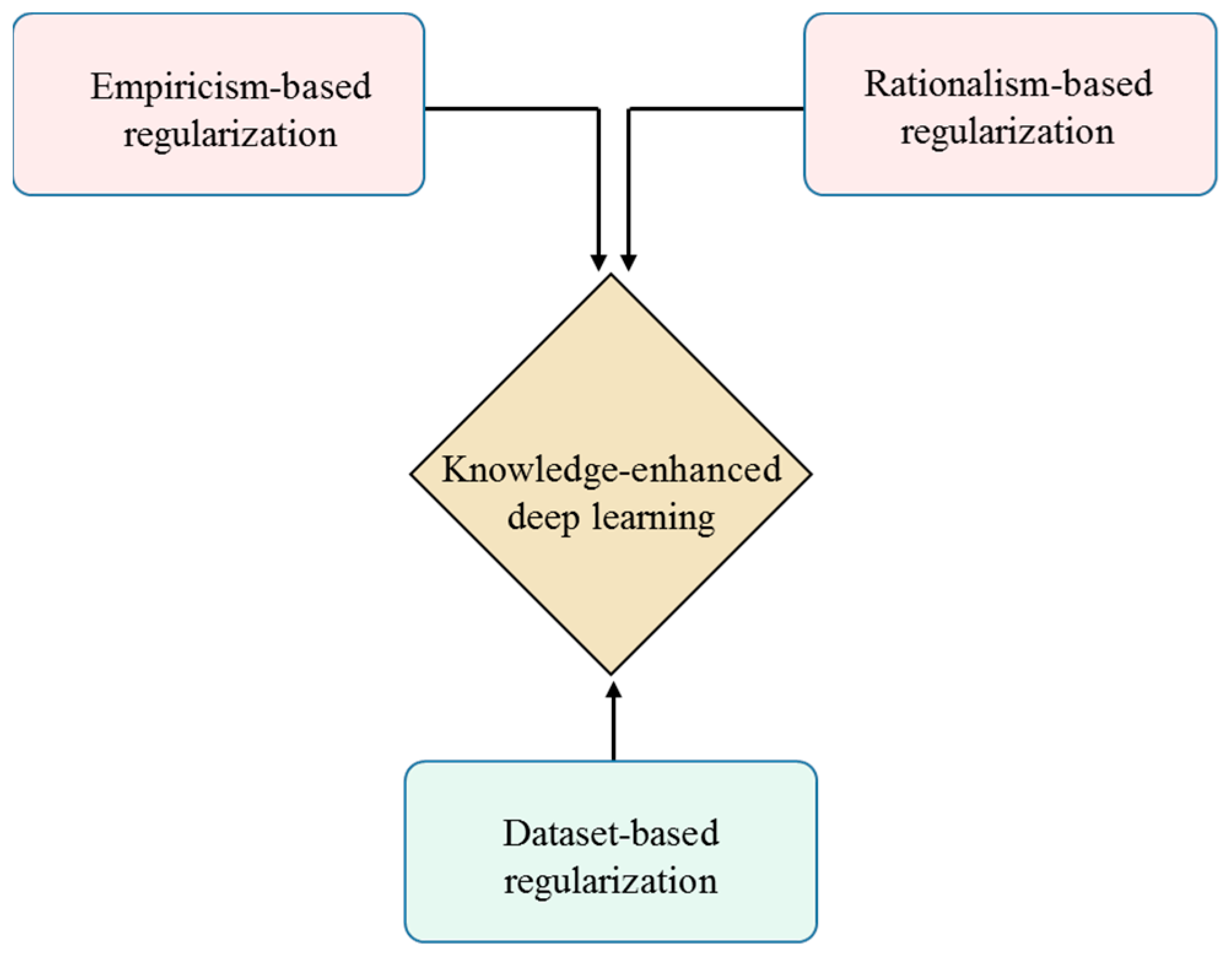
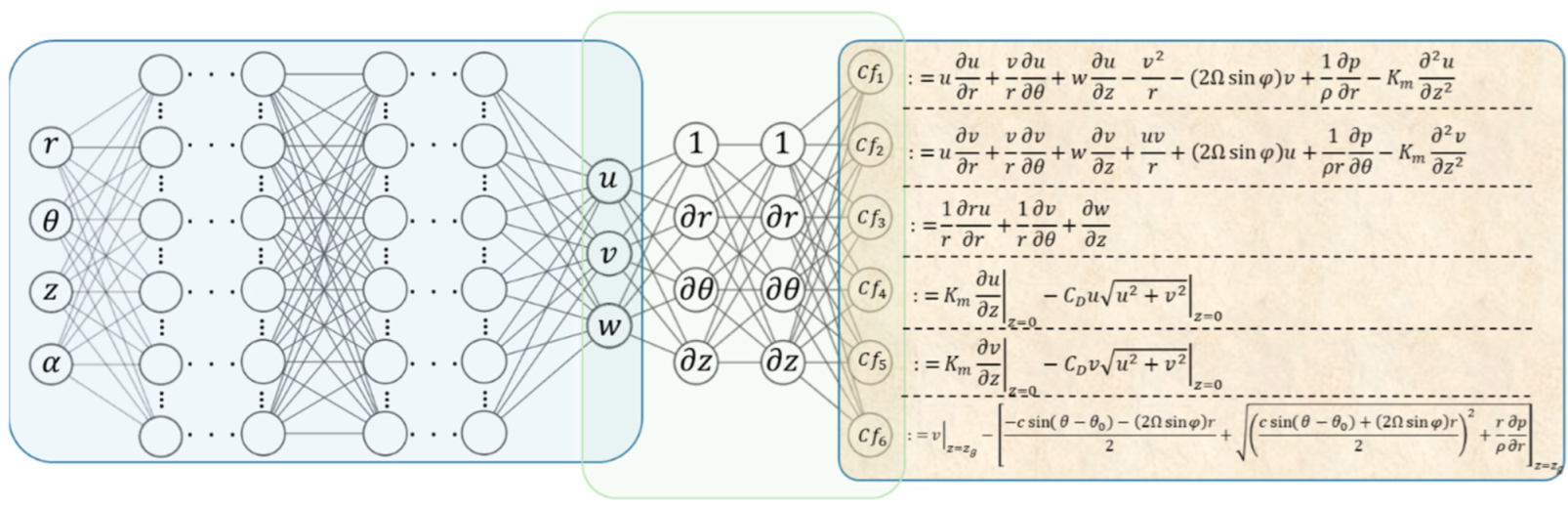
3.1.3. Knowledge-Enhanced Deep Learning Formalization
3.2. Risk Assessment
3.2.1. Synthetic ETC Track
3.2.2. ETC Wind Hazard
4. Results and Discussion
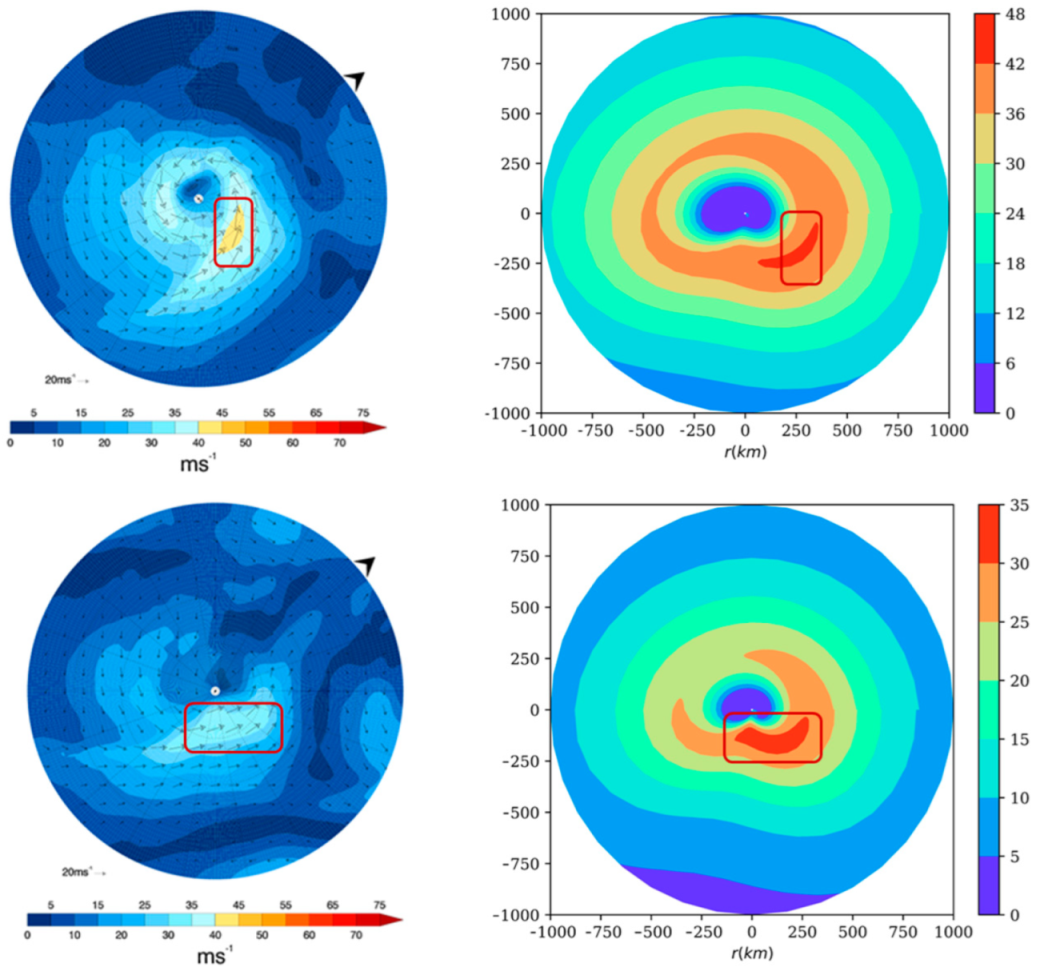
4.1. Model Validation
4.2. Model Application
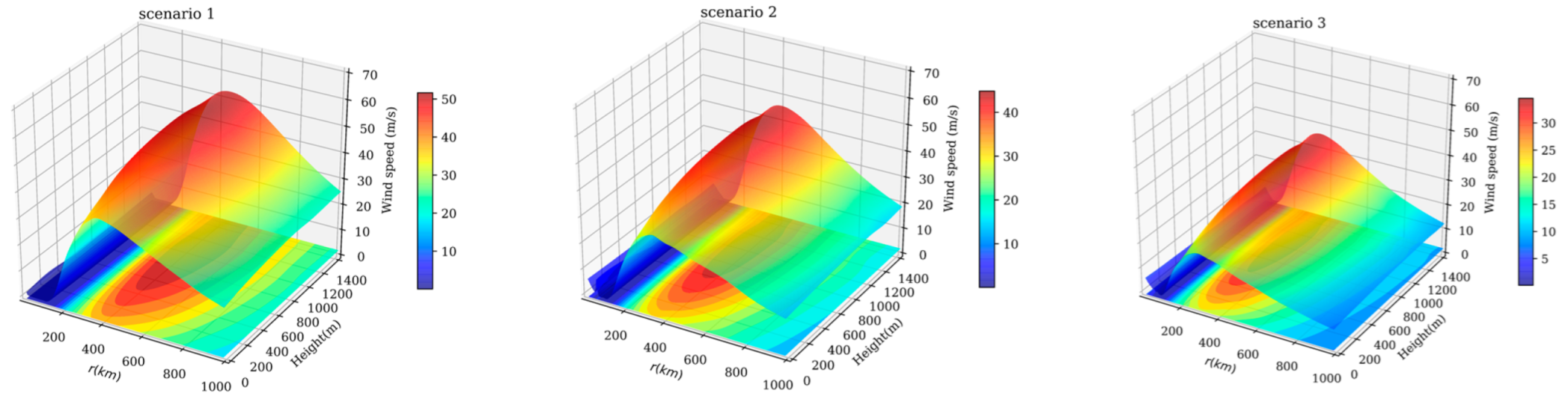
4.3. Risk Analysis
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Von Ahn, J.U.; Sienkiewicz, J.M.; Copridge, J.; Min, J.; Crutch, T. Hurricane force extratropical cyclones as observed by the QuikSCAT scatterometer. In Preprint 8th Symposium on Integrated Observing and Assimilation Systems for Atmosphere, Oceans and Land Surface. AMS Annu. Meet. 2004, 12, 2004. [Google Scholar]
- Hall, T.; Booth, J.F. SynthETC: A statistical model for severe winter storm hazard on eastern North America. J. Clim. 2017, 30, 5329–5343. [Google Scholar] [CrossRef]
- Shimkus, C.E.; Ting, M.; Booth, J.F.; Adamo, S.B.; Madajewicz, M.; Kushnir, Y.; Rieder, H.E. Winter storm intensity, hazards, and property losses in the New York tristate area. Ann. N. Y. Acad. Sci. 2017, 1400, 65–80. [Google Scholar] [CrossRef] [Green Version]
- Kunkel, K.E.; Easterling, D.R.; Kristovich, D.A.; Gleason, B.; Stoecker, L.; Smith, R. Meteorological causes of the secular variations in observed extreme precipitation events for the conterminous United States. J. Hydrometeorol. 2012, 13, 1131–1141. [Google Scholar] [CrossRef]
- Booth, J.F.; Rieder, H.E.; Kushnir, Y. Comparing hurricane and extratropical storm surge for the Mid-Atlantic and Northeast Coast of the United States for 1979–2013. Environ. Res. Lett. 2016, 11, 094004. [Google Scholar] [CrossRef]
- Wu, T.; Kareem, A.; Li, S. On the excitation mechanisms of rain–wind induced vibration of cables: Unsteady and hysteretic nonlinear features. J. Wind Eng. Ind. Aerodyn. 2013, 122, 83–95. [Google Scholar] [CrossRef]
- Snaiki, R.; Wu, T.; Whittaker, A.S.; Atkinson, J.F. Hurricane wind and storm surge effects on coastal bridges under a changing climate. Trans. Res. Rec. 2020, 2674, 23–32. [Google Scholar] [CrossRef]
- Vickery, P.J.; Wadhera, D.; Powell, M.D.; Chen, Y. A hurricane boundary layer and wind field model for use in engineering applications. J. Appl. Meteorol. Climatol. 2009, 48, 381–405. [Google Scholar] [CrossRef]
- Snaiki, R.; Wu, T. A semi-empirical model for mean wind velocity profile of landfalling hurricane boundary layers. J. Wind Eng. Ind. Aerodyn. 2018, 180, 249–261. [Google Scholar] [CrossRef]
- Shapiro, L.J. The asymmetric boundary layer flow under a translating hurricane. J. Atmos. Sci. 1983, 40, 1984–1998. [Google Scholar] [CrossRef] [Green Version]
- Vickery, P.J.; Twisdale, L.A. Wind-field and filling models for hurricane wind-speed predictions. J. Struct. Eng. 1995, 121, 1700–1709. [Google Scholar] [CrossRef]
- Kepert, J. The dynamics of boundary layer jets within the tropical cyclone core. Part I: Linear theory. J. Atmos. Sci. 2001, 58, 2469–2484. [Google Scholar] [CrossRef] [Green Version]
- Snaiki, R.; Wu, T. A linear height-resolving wind field model for tropical cyclone boundary layer. J. Wind Eng. Ind. Aerodyn. 2017, 171, 248–260. [Google Scholar] [CrossRef]
- Snaiki, R.; Wu, T. Modeling tropical cyclone boundary layer: Height-resolving pressure and wind fields. J. Wind Eng. Ind. Aerodyn. 2017, 170, 18–27. [Google Scholar] [CrossRef]
- Adamson, D.S.; Belcher, S.E.; Hoskins, B.J.; Plant, R.S. Boundary-layer friction in midlatitude cyclones. Q. J. R. Meteorol. Soc. A J. Atmos. Sci. Appl. Meteorol. Phys. Oceanogr. 2006, 132, 101–124. [Google Scholar] [CrossRef] [Green Version]
- Beare, R.J. Boundary layer mechanisms in extratropical cyclones. Q. J. R. Meteorol. Soc. A J. Atmos. Sci. Appl. Meteorol. Phys. Oceanogr. 2007, 133, 503–515. [Google Scholar] [CrossRef]
- Huang, W.F.; Xu, Y.L. Prediction of typhoon design wind speed and profile over complex terrain. Struct. Eng. Mech. 2013, 45, 1–18. [Google Scholar] [CrossRef]
- Wei, C.C.; Peng, P.C.; Tsai, C.H.; Huang, C.L. Regional Forecasting of Wind Speeds during Typhoon Landfall in Taiwan: A Case Study of Westward-Moving Typhoons. Atmosphere 2018, 9, 141. [Google Scholar] [CrossRef] [Green Version]
- Shamshirband, S.; Rabczuk, T.; Chau, K.W. A survey of deep learning techniques: Application in wind and solar energy resources. IEEE Access 2019, 7, 164650–164666. [Google Scholar] [CrossRef]
- Banan, A.; Nasiri, A.; Taheri-Garavand, A. Deep learning-based appearance features extraction for automated carp species identification. Aquac. Eng. 2020, 89, 102053. [Google Scholar] [CrossRef]
- Fan, Y.; Xu, K.; Wu, H.; Zheng, Y.; Tao, B. Spatiotemporal modeling for nonlinear distributed thermal processes based on KL decomposition, MLP and LSTM network. IEEE Access 2020, 8, 25111–25121. [Google Scholar] [CrossRef]
- Wu, T.; Snaiki, R. Applications of Machine Learning to Wind Engineering. Front. Built Environ. 2022, 8, 811460. [Google Scholar] [CrossRef]
- Swischuk, R.; Mainini, L.; Peherstorfer, B.; Willcox, K. Projection-Based Model Reduction: Formulations for Physics-Based Machine Learning. Comput. Fluids 2019, 179, 704–717. [Google Scholar] [CrossRef]
- Dissanayake, M.W.M.G.; Phan-Thien, N. Neural-network-based approximations for solving partial differential equations. Commun. Numer. Methods Eng. 1994, 10, 195–201. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics Informed Deep Learning (Part I): Data-driven solutions of nonlinear partial differential equations. arXiv 2017, arXiv:1711.10561. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics informed deep learning (Part II): Data-driven discovery of nonlinear partial differential equations. arXiv 2017, arXiv:1711.10566. [Google Scholar]
- Snaiki, R.; Wu, T. Knowledge-enhanced deep learning for simulation of tropical cyclone boundary-layer winds. J. Wind Eng. Ind. Aerodyn. 2019, 194, 103983. [Google Scholar] [CrossRef]
- Dacre, H.F.; Hawcroft, M.K.; Stringer, M.A.; Hodges, K.I. An extratropical cyclone atlas: A tool for illustrating cyclone structure and evolution characteristics. Bull. Am. Meteorol. Soc. 2012, 93, 1497–1502. [Google Scholar] [CrossRef]
- Dolan, R.; Davis, R.E. An intensity scale for Atlantic coast northeast storms. J. Coast. Res. 1992, 8, 840–853. [Google Scholar]
- Butman, B.; Sherwood, C.R.; Dalyander, P.S. Northeast storms ranked by wind stress and wave-generated bottom stress observed in Massachusetts Bay, 1990–2006. Cont. Shelf Res. 2008, 28, 1231–1245. [Google Scholar] [CrossRef]
- Birchler, J.J.; Dalyander, P.S.; Stockdon, H.F.; Doran, K.S. National Assessment of Nor’easter-Induced Coastal Erosion Hazards: Mid-and Northeast Atlantic Coast; US Geological Survey: Reston, VA, USA, 2015; Open-File Report No. 2015-1154.
- Zhang, K.; Douglas, B.C.; Leatherman, S.P. Beach erosion potential for severe nor’easters. J. Coast. Res. 2001, 17, 309–321. [Google Scholar]
- Ulbrich, U.; Leckebusch, G.C.; Pinto, J.G. Extra-tropical cyclones in the present and future climate: A review. Theor. Appl. Climatol. 2009, 96, 117–131. [Google Scholar] [CrossRef] [Green Version]
- Bjerknes, J.; Solberg, H. Life cycle of cyclones and the polar front theory of atmospheric circulation. Geophys. Publ. 1922, 3, 3–17. [Google Scholar]
- Shapiro, M.A.; Keyser, D. Fronts, jet streams and the tropopause. In Extratropical Cyclones; American Meteorological Society: Boston, MA, USA, 1990; pp. 167–191. [Google Scholar]
- Bauer, M.; Del Genio, A.D. Composite analysis of winter cyclones in a GCM: Influence on climatological humidity. J. Clim. 2006, 19, 1652–1672. [Google Scholar] [CrossRef]
- Chang, E.K.; Song, S. The seasonal cycles in the distribution of precipitation around cyclones in the western North Pacific and Atlantic. J. Atmos. Sci. 2006, 63, 815–839. [Google Scholar] [CrossRef]
- Rudeva, I.; Gulev, S.K. Composite analysis of North Atlantic extratropical cyclones in NCEP–NCAR reanalysis data. Mon. Weather Rev. 2011, 139, 1419–1446. [Google Scholar] [CrossRef] [Green Version]
- Sinclair, M.R.; Revell, M.J. Classification and composite diagnosis of extratropical cyclogenesis events in the southwest Pacific. Mon. Weather Rev. 2000, 128, 1089–1105. [Google Scholar] [CrossRef]
- McLay, J.G.; Martin, J.E. Surface cyclolysis in the North Pacific Ocean. Part III: Composite local energetics of tropospheric-deep cyclone decay associated with rapid surface cyclolysis. Mon. Weather Rev. 2002, 130, 2507–2529. [Google Scholar] [CrossRef] [Green Version]
- Hoskins, B.J.; Hodges, K.I. New perspectives on the Northern Hemisphere winter storm tracks. J. Atmos. Sci. 2002, 59, 1041–1061. [Google Scholar] [CrossRef]
- Hoskins, B.J.; Hodges, K.I. A new perspective on Southern Hemisphere storm tracks. J. Clim. 2005, 18, 4108–4129. [Google Scholar] [CrossRef]
- Simmons, A. ERA-Interim: New ECMWF reanalysis products from 1989 onwards. ECMWF Newsl. 2006, 110, 25–36. [Google Scholar]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, D.P.; et al. The ERA-Interim Reanalysis: Configuration and Performance of the Data Assimilation System. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Wang, C.C.; Rogers, J.C. A composite study of explosive cyclogenesis in different sectors of the North Atlantic. Part I: Cyclone structure and evolution. Mon. Weather Rev. 2001, 129, 1481–1499. [Google Scholar] [CrossRef]
- Catto, J.L.; Shaffrey, L.C.; Hodges, K.I. Can climate models capture the structure of extratropical cyclones? J. Clim. 2010, 23, 1621–1635. [Google Scholar] [CrossRef]
- Russell, L.R. Probability distributions for hurricane effects. J. Waterways Harbors. Coast. Eng. Div. 1971, 97, 139–154. [Google Scholar] [CrossRef]
- FEMA. Region II Storm Surge Project—Joint Probability Analysis of Hurricane and Extratropical Flood Hazards September 2014; Report prepared for Federal Emergency Management Agency; HSFE02-09-J-001; FEMA: Washington, DC, USA, 2014.
- Catalano, A.J.; Broccoli, A.J.; Kapnick, S.B.; Janoski, T.P. High-impact extratropical cyclones along the northeast coast of the United States in a long-coupled climate model simulation. J. Clim. 2019, 32, 2131–2143. [Google Scholar] [CrossRef]
- Kumler-Bonfanti, C.; Stewart, J.; Hall, D.; Govett, M. Tropical and extratropical cyclone detection using deep learning. J. Appl. Meteorol. Climatol. 2020, 59, 1971–1985. [Google Scholar] [CrossRef]
- Lu, C.; Kong, Y.; Guan, Z. A mask R-CNN model for reidentifying extratropical cyclones based on quasi-supervised thought. Sci. Rep. 2020, 10, 15011. [Google Scholar] [CrossRef]
- Shi, M.; He, P.; Shi, Y. Detecting extratropical cyclones of the northern hemisphere with single shot detector. Remote Sens. 2022, 14, 254. [Google Scholar] [CrossRef]
- Xu, G.; Han, G.; Dong, C.; Yang, J.; DeYoung, B. Observing and Modeling the Response of Placentia Bay to an Extratropical Cyclone. Atmosphere 2019, 10, 724. [Google Scholar] [CrossRef] [Green Version]
- Economou, T.; Stephenson, D.B.; Ferro, C.A. Spatio-temporal modelling of extreme storms. Ann. Appl. Stat. 2014, 8, 2223–2246. [Google Scholar] [CrossRef]
- Meng, Y.; Matsui, M.; Hibi, K. An analytical model for simulation of the wind field in a typhoon boundary layer. J. Wind Eng. Ind. Aerodyn. 1995, 56, 291–310. [Google Scholar] [CrossRef]
- Holland, G.J. An analytic model of the wind and pressure profiles in hurricanes. Mon. Weather Rev. 1980, 108, 1212–1218. [Google Scholar] [CrossRef]
- Snaiki, R.; Wu, T. Revisiting hurricane track model for wind risk assessment. Struct. Saf. 2020, 87, 102003. [Google Scholar] [CrossRef]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef] [Green Version]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Wu, T.; Kareem, A. Modeling hysteretic nonlinear behavior of bridge aerodynamics via cellular automata nested neural network. J. Wind Eng. Ind. Aerodyn. 2011, 99, 378–388. [Google Scholar] [CrossRef]
- Bardenet, R.; Brendel, M.; Kégl, B.; Sebag, M. February. Collaborative hyperparameter tuning. In Proceedings of the International Conference on Machine Learning, PMLR, Atlanta, GA, USA, 16–21 June 2013; pp. 199–207. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, PMLR, Chia Laguna Resort, Sardinia, Italy, 13–15 March 2010; pp. 249–256. [Google Scholar]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef] [Green Version]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Vickery, P.J.; Skerlj, P.F.; Twisdale, L.A. Simulation of hurricane risk in the US using empirical track model. J. Struct. Eng. 2000, 126, 1222–1237. [Google Scholar] [CrossRef]
- Hall, T.M.; Jewson, S. Statistical modelling of North Atlantic tropical cyclone tracks. Tellus A Dyn. Meteorol. Oceanogr. 2007, 59, 486–498. [Google Scholar] [CrossRef] [Green Version]
- Pei, B.; Pang, W.; Testik, F.Y.; Ravichandran, N.; Liu, F. Mapping joint hurricane wind and surge hazards for Charleston, South Carolina. Nat. Hazards 2014, 74, 375–403. [Google Scholar] [CrossRef]



| Parameter | |||||
|---|---|---|---|---|---|
| scenario 1 | 80 | 10 | 50 | 45 | 0.001 |
| scenario 2 | 60 | 8 | 70 | 45 | 0.01 |
| scenario 3 | 40 | 6 | 90 | 45 | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Snaiki, R.; Wu, T. Knowledge-Enhanced Deep Learning for Simulation of Extratropical Cyclone Wind Risk. Atmosphere 2022, 13, 757. https://doi.org/10.3390/atmos13050757
Snaiki R, Wu T. Knowledge-Enhanced Deep Learning for Simulation of Extratropical Cyclone Wind Risk. Atmosphere. 2022; 13(5):757. https://doi.org/10.3390/atmos13050757
Chicago/Turabian StyleSnaiki, Reda, and Teng Wu. 2022. "Knowledge-Enhanced Deep Learning for Simulation of Extratropical Cyclone Wind Risk" Atmosphere 13, no. 5: 757. https://doi.org/10.3390/atmos13050757
APA StyleSnaiki, R., & Wu, T. (2022). Knowledge-Enhanced Deep Learning for Simulation of Extratropical Cyclone Wind Risk. Atmosphere, 13(5), 757. https://doi.org/10.3390/atmos13050757







