Evapotranspiration under Drought Conditions: The Case Study of a Seasonally Dry Atlantic Forest
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site Description
2.2. Data Monitoring and Study Period
2.3. Daily Evapotranspiration
2.4. Aerodynamic Conductance
2.5. Bulk Surface Conductance
2.6. Soil Water Storage
2.7. Statistical Analysis
2.8. Priestley–Taylor and Decoupling Coefficients
3. Results
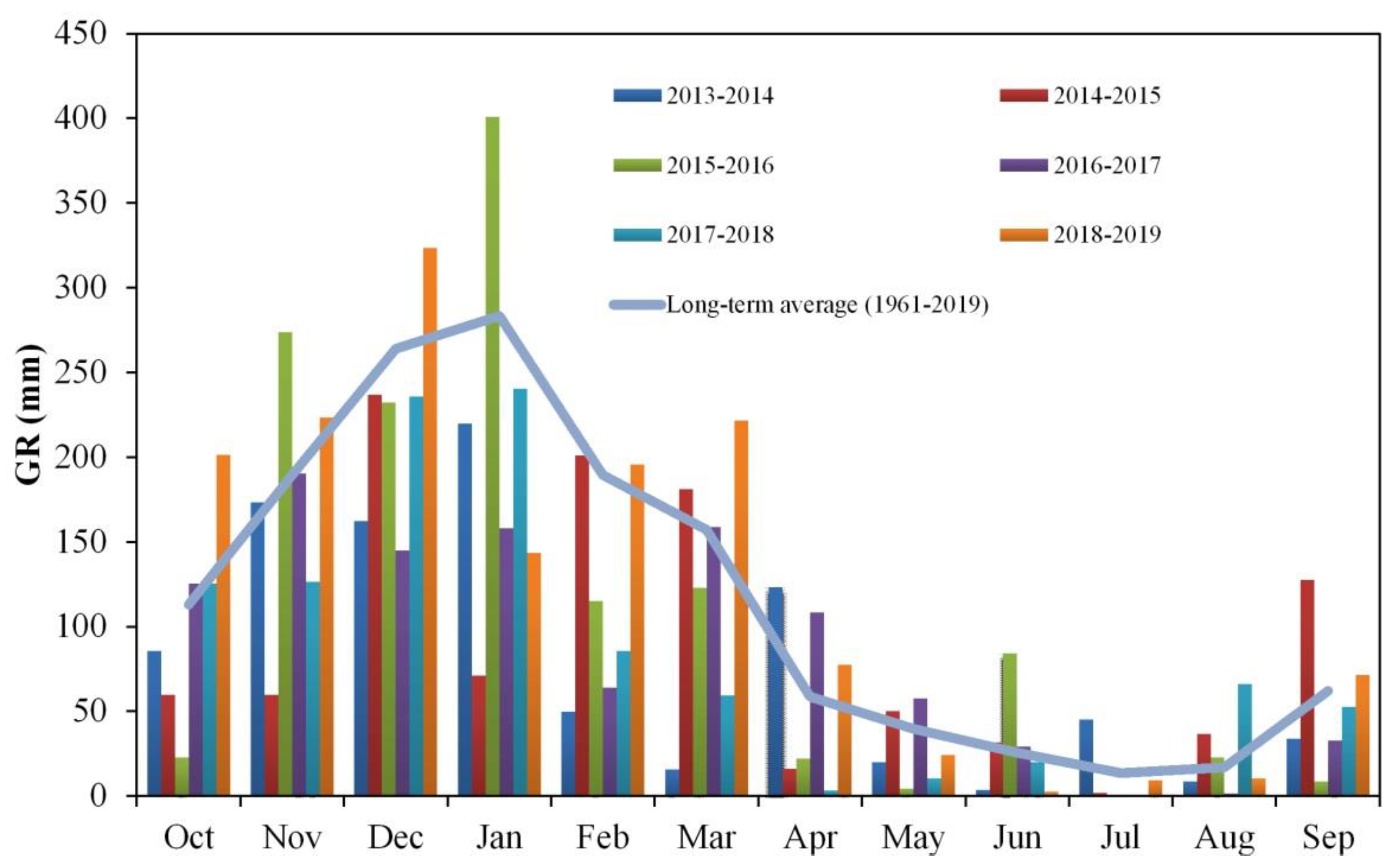
3.1. Gross Rainfall Patterns
3.2. Energy Balance
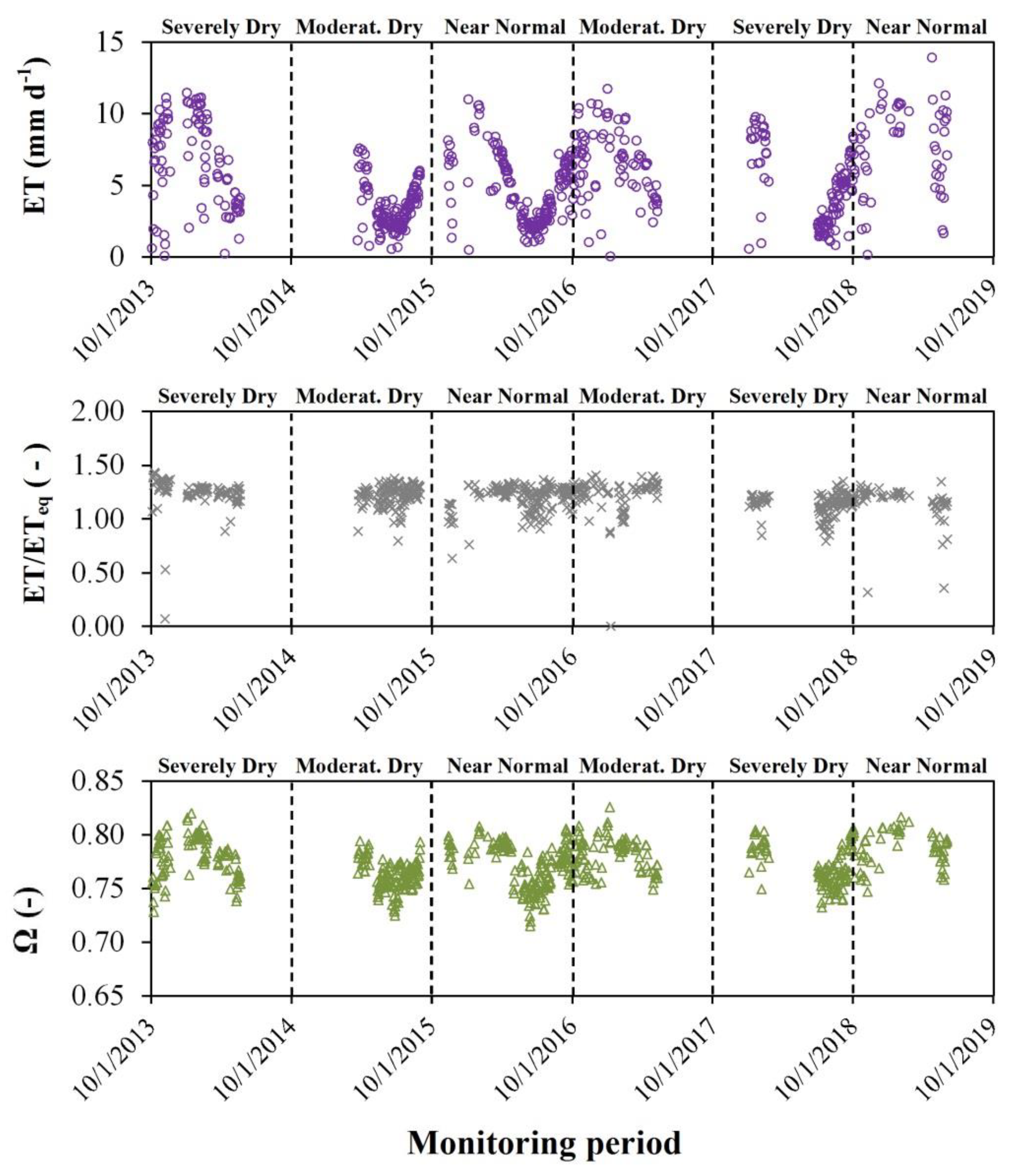
3.3. Daily Evapotranspiration (ET)
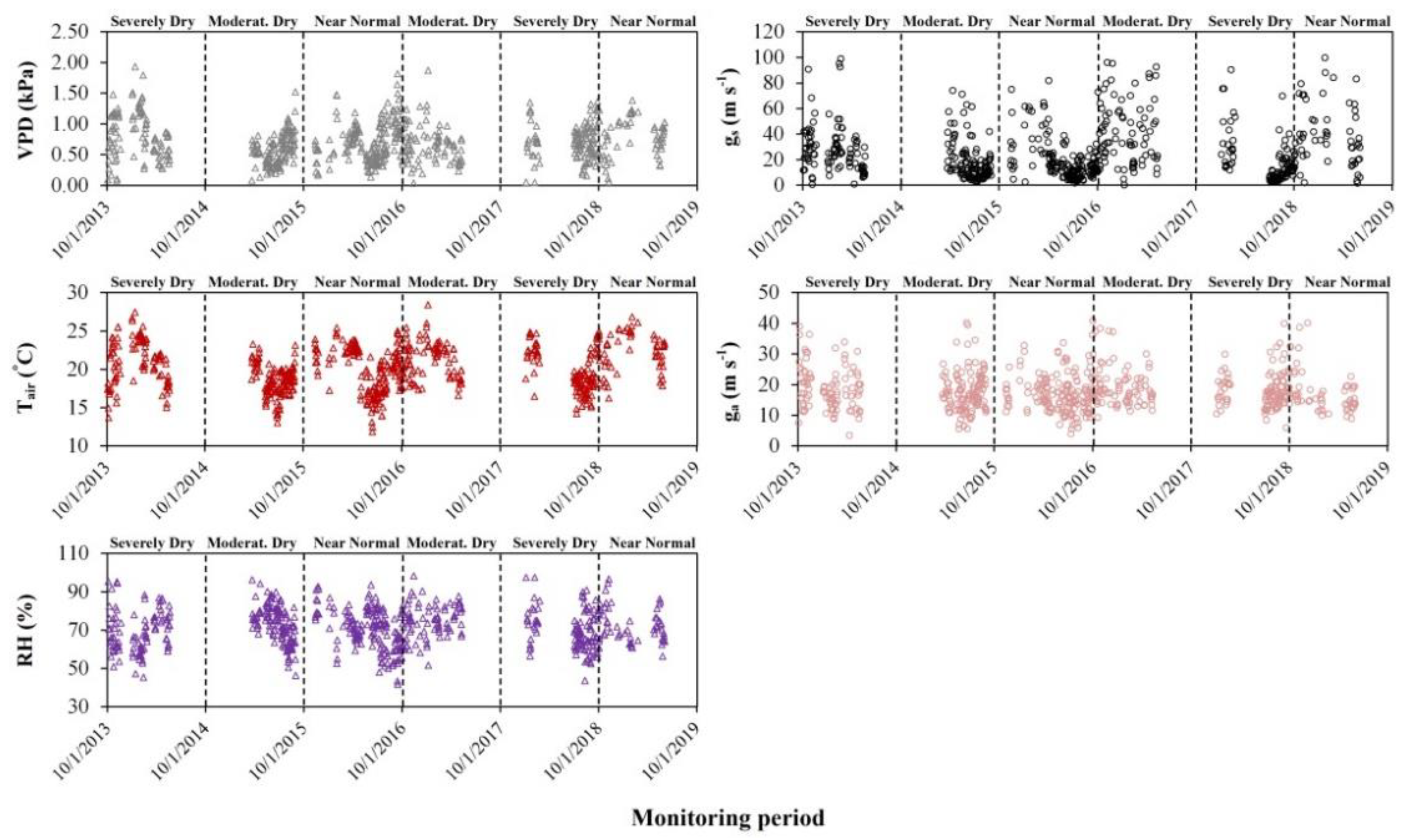
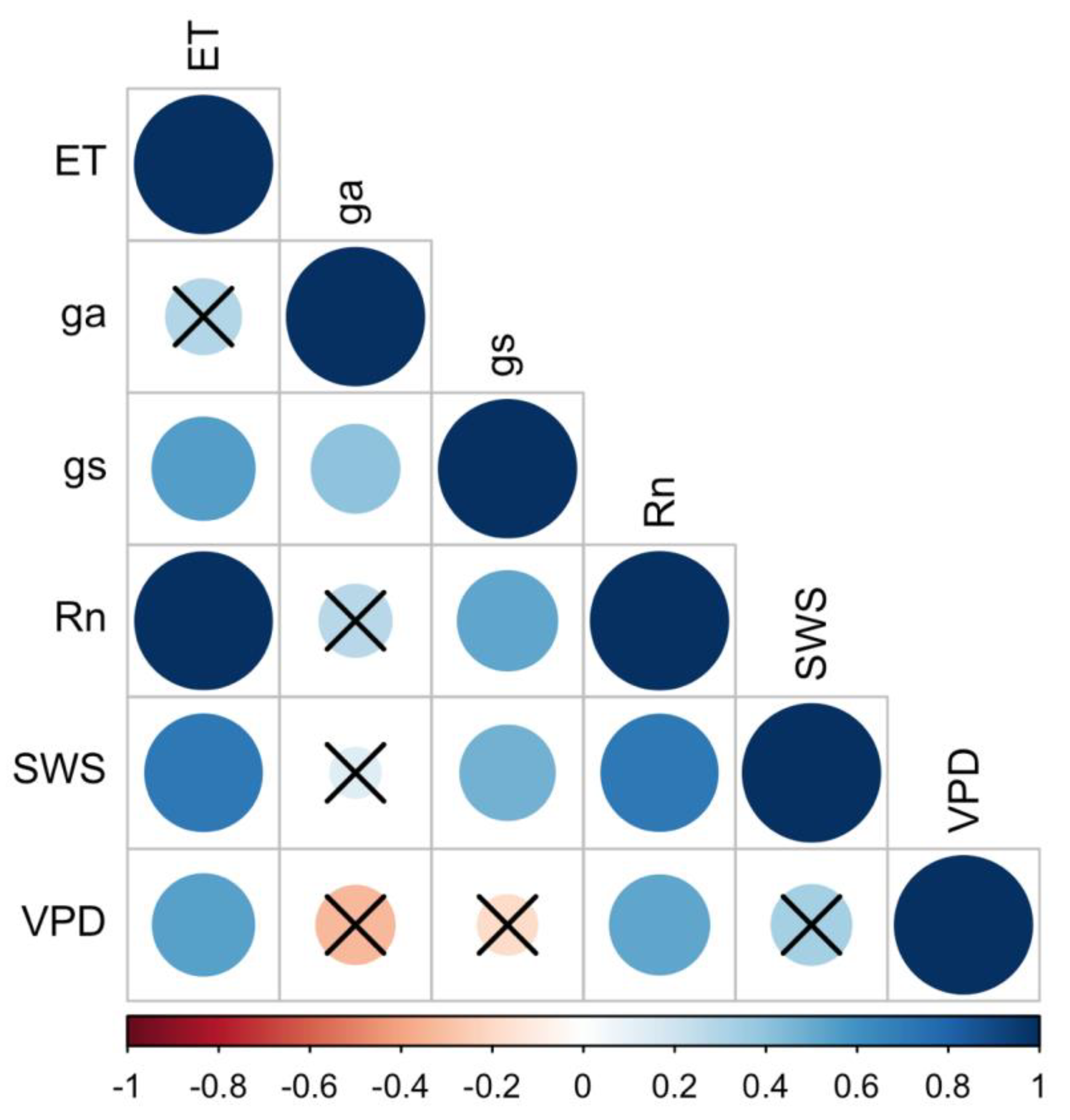
3.4. Environmental and Biophysical Controls of ET
3.5. Priestley–Taylor and Decoupling Coefficients
4. Discussion
4.1. Energy Balance and Daily Evapotranspiration
4.2. Environmental and Biophysical Controls
4.3. Shortcomings and Implications
5. Conclusions
- Soil: the holding water and the infiltration capacities of the dystrophic red latosol were crucial to sustaining ET even in severe drought conditions.
- Weather: Rn was the limiting factor of ET in the near-normal, moderately dry, and severely dry hydrological years.
- Physiological mechanisms: deciduousness and small leaves were crucial for regulating water loss in dry conditions (favoring drought-coping).
- Rainfall distribution: the inter- and intra-annual variability of gross rainfall favored soil recharge and ET.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Term | Abbreviation |
|---|---|
| Evapotranspiration | ET |
| Generalized linear models | GLMs |
| Net radiation | Rn |
| Bulk surface conductance | gs |
| Aerodynamic conductance | ga |
| Atlantic Forest | AF |
| Soil water storage | SWS |
| Vapor pressure deficit | VPD |
| Seasonally dry Atlantic Forest remnant | SDAF |
| Standard Precipitation Index | SPI |
| Near normal | NN |
| Moderately dry | MD |
| Severely dry | SD |
| Latent heat flux | λE |
| Sensible heat flux | H |
| Soil heat flux | G |
| Dry air density | ρ |
| Specific heat capacity of air | Cp |
| Temperature above the forest canopy | Tair |
| Temperature within the forest | Tf |
| von Kárman’s constant | k |
| Wind velocity | u |
| Height of wind velocity monitoring | z |
| Roughness length for momentum transfer | Z0M |
| Roughness length for heat transfer | Z0H |
| Zero-plane displacement height | d |
| Slope of saturation vapor pressure curve | Δ |
| Psychrometric constant | γ |
| Soil moisture | θ |
| Soil layer thickness | h |
| Akaike information criterion | AIC |
| Priestley–Taylor coefficient | ET/ETeq |
| Equilibrium evapotranspiration | ETeq |
| Decoupling coefficient | Ω |
| Gross rainfall | GR |
References
- Allen, R.G.; Jensen, M.E.; Wright, J.L.; Burman, R.D. Operational Estimates of Reference Evapotranspiration. Agron. J. 1989, 81, 650–662. [Google Scholar] [CrossRef]
- Zhang, L.; Traore, S.; Cui, Y.; Luo, Y.; Zhu, G.; Liu, B.; Fipps, G.; Karthikeyan, R.; Singh, V. Assessment of Spatiotemporal Variability of Reference Evapotranspiration and Controlling Climate Factors over Decades in China Using Geospatial Techniques. Agric. Water Manag. 2019, 213, 499–511. [Google Scholar] [CrossRef]
- Valipour, M.; Bateni, S.M.; Sefidkouhi, M.A.G.; Raeini-Sarjaz, M.; Singh, V.P. Complexity of Forces Driving Trend of Reference Evapotranspiration and Signals of Climate Change. Atmosphere 2020, 11, 1081. [Google Scholar] [CrossRef]
- Christoffersen, B.O.; Restrepo-Coupe, N.; Arain, M.A.; Baker, I.T.; Cestaro, B.P.; Ciais, P.; Fisher, J.B.; Galbraith, D.; Guan, X.; Gulden, L.; et al. Mechanisms of Water Supply and Vegetation Demand Govern the Seasonality and Magnitude of Evapotranspiration in Amazonia and Cerrado. Agric. For. Meteorol. 2014, 191, 33–50. [Google Scholar] [CrossRef]
- Marques, T.V.; Mendes, K.; Mutti, P.; Medeiros, S.; Silva, L.; Perez-Marin, A.M.; Campos, S.; Lúcio, P.S.; Lima, K.; dos Reis, J.; et al. Environmental and Biophysical Controls of Evapotranspiration from Seasonally Dry Tropical Forests (Caatinga) in the Brazilian Semiarid. Agric. For. Meteorol. 2020, 287, 107957. [Google Scholar] [CrossRef]
- Rodrigues, A.F.; de Mello, C.R.; Nehren, U.; Pedro de Coimbra Ribeiro, J.; Alves Mantovani, V.; Marcio de Mello, J. Modeling Canopy Interception under Drought Conditions: The Relevance of Evaporation and Extra Sources of Energy. J. Environ. Manag. 2021, 292, 112710. [Google Scholar] [CrossRef] [PubMed]
- Finlayson-Pitts, J.B.; Pitts, J., Jr. Chemistry of the Upper and Lower Atmosphere: Theory, Experiments, and Applications; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Díaz-Torres, J.J.; Hernández-Mena, L.; Murillo-Tovar, M.A.; León-Becerril, E.; López-López, A.; Suárez-Plascencia, C.; Aviña-Rodriguez, E.; Barradas-Gimate, A.; Ojeda-Castillo, V. Assessment of the Modulation Effect of Rainfall on Solar Radiation Availability at the Earth’s Surface. Meteorol. Appl. 2017, 24, 180–190. [Google Scholar] [CrossRef] [Green Version]
- Monteith, J. Evaporation and Environment. Symposia of the Society for Experimental Biology. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar]
- Kramer, P.J.; Boyer, J.S. Water Relations of Plants and Soils; Academic Press: San Diego, CA, USA, 1995. [Google Scholar]
- Yue, P.; Zhang, Q.; Ren, X.; Yang, Z.; Li, H.; Yang, Y. Environmental and Biophysical Effects of Evapotranspiration in Semiarid Grassland and Maize Cropland Ecosystems over the Summer Monsoon Transition Zone of China. Agric. Water Manag. 2022, 264, 107462. [Google Scholar] [CrossRef]
- Hu, Y.; Xiang, W.; Schäfer, K.V.R.; Lei, P.; Deng, X.; Forrester, D.I.; Fang, X.; Zeng, Y.; Ouyang, S.; Chen, L.; et al. Photosynthetic and Hydraulic Traits Influence Forest Resistance and Resilience to Drought Stress across Different Biomes. Sci. Total Environ. 2022, 828, 154517. [Google Scholar] [CrossRef]
- Williams, L.J.; Bunyavejchewin, S.; Baker, P.J. Deciduousness in a Seasonal Tropical Forest in Western Thailand: Interannual and Intraspecific Variation in Timing, Duration and Environmental Cues. Oecologia 2008, 155, 571–582. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Broedel, E.; Tomasella, J.; Cândido, L.A.; von Randow, C. Deep Soil Water Dynamics in an Undisturbed Primary Forest in Central Amazonia: Differences between Normal Years and the 2005 Drought. Hydrol. Process. 2017, 31, 1749–1759. [Google Scholar] [CrossRef]
- Markewitz, D.; Devine, S.; Davidson, E.A.; Brando, P.; Nepstad, D.C. Soil Moisture Depletion under Simulated Drought in the Amazon: Impacts on Deep Root Uptake. New Phytol. 2010, 187, 592–607. [Google Scholar] [CrossRef] [PubMed]
- De Terra, M.C.N.S.; Dos Santos, R.M.; Do Prado Júnior, J.A.; de Mello, J.M.; Scolforo, J.R.S.; Fontes, M.A.L.; Schiavini, I.; dos Reis, A.A.; Bueno, I.T.; Magnago, L.F.S.; et al. Water Availability Drives Gradients of Tree Diversity, Structure and Functional Traits in the Atlantic–Cerrado–Caatinga Transition, Brazil. J. Plant Ecol. 2018, 11, 803–814. [Google Scholar] [CrossRef] [Green Version]
- Ma, N.; Zhang, Y.; Guo, Y.; Gao, H.; Zhang, H.; Wang, Y. Environmental and Biophysical Controls on the Evapotranspiration over the Highest Alpine Steppe. J. Hydrol. 2015, 529, 980–992. [Google Scholar] [CrossRef]
- Rubert, G.C.D.; de Souza, V.A.; Zimmer, T.; Veeck, G.P.; Mergen, A.; Bremm, T.; Ruhoff, A.; de Gonçalves, L.G.G.; Roberti, D.R. Patterns and Controls of the Latent and Sensible Heat Fluxes in the Brazilian Pampa Biome. Atmosphere 2022, 13, 23. [Google Scholar] [CrossRef]
- Igarashi, Y.; Katul, G.G.; Kumagai, T.; Yoshifuji, N.; Sato, T.; Tanaka, N.; Tanaka, K.; Fujinami, H.; Suzuki, M.; Tantasirin, C. Separating Physical and Biological Controls on Long-Term Evapotranspiration Fluctuations in a Tropical Deciduous Forest Subjected to Monsoonal Rainfall. J. Geophys. Res. Biogeosci. 2015, 120, 1262–1278. [Google Scholar] [CrossRef] [Green Version]
- Loescher, H.W.; Gholz, H.L.; Jacobs, J.M.; Oberbauer, S.F. Energy Dynamics and Modeled Evapotranspiration from a Wet Tropical Forest in Costa Rica. J. Hydrol. 2005, 315, 274–294. [Google Scholar] [CrossRef]
- Aguilos, M.; Stahl, C.; Burban, B.; Hérault, B.; Courtois, E.; Coste, S.; Wagner, F.; Ziegler, C.; Takagi, K.; Bonal, D. Interannual and Seasonal Variations in Ecosystem Transpiration and Water Use Efficiency in a Tropical Rainforest. Forests 2019, 10, 14. [Google Scholar] [CrossRef] [Green Version]
- Morellato, P.C.; Haddad, C.F.B. Introduction: The Brazilian Atlantic Forest. Biotropica 2000, 32, 786–792. [Google Scholar] [CrossRef]
- Pires, A.P.F.; Shimamoto, C.Y.; Padgurschi, M.C.G.; Scarano, F.R.; Marques, M.C.M. Atlantic Forest: Ecosystem Services Linking People and Biodiversity. In The Atlantic Forest; Springer International Publishing: Cham, Switzerland, 2021; pp. 347–367. [Google Scholar]
- Mantovani, V.A.; de Terra, M.C.N.S.; de Mello, C.R.; Rodrigues, A.F.; de Oliveira, V.A.; Pinto, L.O.R. Spatial and Temporal Patterns in Carbon and Nitrogen Inputs by Net Precipitation in Atlantic Forest, Brazil. For. Sci. 2022, 68, 113–124. [Google Scholar] [CrossRef]
- Lira, P.K.; Tambosi, L.R.; Ewers, R.M.; Metzger, J.P. Land-Use and Land-Cover Change in Atlantic Forest Landscapes. For. Ecol. Manag. 2012, 278, 80–89. [Google Scholar] [CrossRef]
- de Lima, R.A.F.; Oliveira, A.A.; Pitta, G.R.; de Gasper, A.L.; Vibrans, A.C.; Chave, J.; ter Steege, H.; Prado, P.I. The Erosion of Biodiversity and Biomass in the Atlantic Forest Biodiversity Hotspot. Nat. Commun. 2020, 11, 6347. [Google Scholar] [CrossRef] [PubMed]
- Rezende, C.L.; Scarano, F.R.; Assad, E.D.; Joly, C.A.; Metzger, J.P.; Strassburg, B.B.N.; Tabarelli, M.; Fonseca, G.A.; Mittermeier, R.A. From Hotspot to Hopespot: An Opportunity for the Brazilian Atlantic Forest. Perspect. Ecol. Conserv. 2018, 16, 208–214. [Google Scholar] [CrossRef]
- Coelho, C.A.S.; de Oliveira, C.P.; Ambrizzi, T.; Reboita, M.S.; Carpenedo, C.B.; Campos, J.L.P.S.; Tomaziello, A.C.N.; Pampuch, L.A.; de Custódio, M.S.; Dutra, L.M.M.; et al. The 2014 Southeast Brazil Austral Summer Drought: Regional Scale Mechanisms and Teleconnections. Clim. Dyn. 2016, 46, 3737–3752. [Google Scholar] [CrossRef]
- Macedo, T.M.; da Costa, W.S.; das Brandes, A.F.N.; Valladares, F.; Barros, C.F. Diversity of Growth Responses to Recent Droughts Reveals the Capacity of Atlantic Forest Trees to Cope Well with Current Climatic Variability. For. Ecol. Manag. 2021, 480, 118656. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, T.; Han, Q.; Sun, S.; Liu, C.; Chen, X. Diagnosing Environmental Controls on Actual Evapotranspiration and Evaporative Fraction in a Water-Limited Region from Northwest China. J. Hydrol. 2019, 578, 124045. [Google Scholar] [CrossRef]
- Souza, C.R.; Maia, V.A.; de Aguiar-Campos, N.; Santos, A.B.M.; Rodrigues, A.F.; Farrapo, C.L.; Gianasi, F.M.; de Paula, G.G.P.; Fagundes, N.C.A.; Silva, W.B.; et al. Long-Term Ecological Trends of Small Secondary Forests of the Atlantic Forest Hotspot: A 30-Year Study Case. For. Ecol. Manag. 2021, 489, 119043. [Google Scholar] [CrossRef]
- IBGE. Manual Técnico da Vegetação Brasileira, 2nd ed.; IBGE: Rio de Janeiro, Brazil, 2012; ISBN 9788524042720.
- Vitória, A.P.; Alves, L.F.; Santiago, L.S. Atlantic Forest and Leaf Traits: An Overview. Trees-Struct. Funct. 2019, 33, 1535–1547. [Google Scholar] [CrossRef]
- Junqueira Junior, J.A.; Mello, C.R.; Owens, P.R.; Mello, J.M.; Curi, N.; Alves, G.J. Time-Stability of Soil Water Content (SWC) in an Atlantic Forest-Latosol Site. Geoderma 2017, 288, 64–78. [Google Scholar] [CrossRef]
- Junqueira Junior, J.A.; de Mello, C.R.; de Mello, J.M.; Scolforo, H.F.; Beskow, S.; McCarter, J. Rainfall Partitioning Measurement and Rainfall Interception Modelling in a Tropical Semi-Deciduous Atlantic Forest Remnant. Agric. For. Meteorol. 2019, 275, 170–183. [Google Scholar] [CrossRef]
- INMET Instituto Nacional de Meteorologia. Normais Climatológicas-1991–2020. Available online: https://portal.inmet.gov.br/normais (accessed on 1 April 2022).
- Rodrigues, A.F.; Terra, M.C.N.S.; Mantovani, V.A.; Cordeiro, N.G.; Ribeiro, J.P.C.; Guo, L.; Nehren, U.; Mello, J.M.; Mello, C.R. Throughfall Spatial Variability in a Neotropical Forest: Have We Correctly Accounted for Time Stability? J. Hydrol. 2022, 608, 127632. [Google Scholar] [CrossRef]
- Rodrigues, A.F.; de Mello, C.R.; Terra, M.C.N.S.; Beskow, S. Water Balance of an Atlantic Forest Remnant under a Prolonged Drought Period. Cienc. Agrotecnol. 2021, 45, 1–13. [Google Scholar] [CrossRef]
- WMO. World Meteorological Organization: Standardized Precipitation Index User Guide. Available online: http://www.wamis.org/agm/pubs/SPI/WMO_1090_EN.pdf (accessed on 1 April 2022).
- Van Dijk, A.I.J.M.; Gash, J.H.; Van Gorsel, E.; Blanken, P.D.; Cescatti, A.; Emmel, C.; Gielen, B.; Harman, I.N.; Kiely, G.; Merbold, L.; et al. Rainfall Interception and the Coupled Surface Water and Energy Balance. Agric. For. Meteorol. 2015, 214–215, 402–415. [Google Scholar] [CrossRef] [Green Version]
- Tan, Z.; Zhao, J.; Wang, G.; Chen, M.; Yang, L.; He, C.; Restrepo-Coupe, N.; Peng, S.; Liu, X.; Rocha, H. Surface conductance for evapotranspiration of tropical forests: Calculations, variations, and controls. Agric. For. Meteorol. 2019, 275, 317–328. [Google Scholar] [CrossRef]
- Brutsaert, W. Evaporation into the Atmosphere: Theory, History and Applications; Springer: Dordrecht, The Netherlands, 1982; 302p. [Google Scholar]
- Stewart, J.B. Modelling Surface Conductance of Pine Forest. Agric. For. Meteorol. 1988, 43, 19–35. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Inference: A Practical Information-Theoretic Approach, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Vierling, L.A.; Vierling, K.T.; Adam, P.; Hudak, A.T. Using satellite and airborne LiDAR to model woodpecker habitat occupancy at the landscape scale. PLoS ONE 2013, 8, e80988. [Google Scholar] [CrossRef] [Green Version]
- Barton, K. MuMIn: Multi-model inference. In R Package Version 1.46.0; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://CRAN.R-project.org/package=MuMIn (accessed on 1 April 2022).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 1 April 2022).
- Wilson, K.B.; Baldocchi, D.D. Seasonal and Interannual Variability of Energy Fluxes over a Broadleaved Temperate Deciduous Forest in North America. Agric. For. Meteorol. 2000, 100, 1–18. [Google Scholar] [CrossRef]
- Jarvis, P.G.; Mcnaughton, K.G. Stomatal Control of Transpiration: Scaling up from Leaf to Region. Adv. Ecol. Res. 1986, 15, 1–49. [Google Scholar] [CrossRef]
- Kuricheva, O.A.; Avilov, V.K.; Dinh, D.B.; Sandlersky, R.B.; Kuznetsov, A.N.; Kurbatova, J.A. Seasonality of Energy and Water Fluxes in a Tropical Moist Forest in Vietnam. Agric. For. Meteorol. 2021, 299, 108268. [Google Scholar] [CrossRef]
- Silva, J.B.; Valle Junior, L.C.G.; Faria, T.O.; Marques, J.B.; Dalmagro, H.J.; Nogueira, J.S.; Vourlitis, G.L.; Rodrigues, T.R. Temporal Variability in Evapotranspiration and Energy Partitioning over a Seasonally Flooded Scrub Forest of the Brazilian Pantanal. Agric. For. Meteorol. 2021, 308–309, 108559. [Google Scholar] [CrossRef]
- Mello, C.R.; Ávila, L.F.; Lin, H.; Terra, M.C.N.S.; Chappell, N.A. Water Balance in a Neotropical Forest Catchment of Southeastern Brazil. Catena 2019, 173, 9–21. [Google Scholar] [CrossRef] [Green Version]
- Da Paca, V.H.M.; Espinoza-Dávalos, G.E.; Hessels, T.M.; Moreira, D.M.; Comair, G.F.; Bastiaanssen, W.G.M. The Spatial Variability of Actual Evapotranspiration across the Amazon River Basin Based on Remote Sensing Products Validated with Flux Towers. Ecol. Process. 2019, 8, 6. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Yang, M.; Liu, W.; Mohammadi, K.; Wang, G. Eco-Hydrological Responses to Recent Droughts in Tropical South America. Environ. Res. Lett. 2022, 17, 024037. [Google Scholar] [CrossRef]
- Agurla, S.; Gahir, S.; Munemasa, S.; Murata, Y.; Raghavendra, A.S. Mechanism of Stomatal Closure in Plants Exposed to Drought and Cold Stress. In Advances in Experimental Medicine and Biology; Springer: Berlin/Heidelberg, Germany, 2018; Volume 1081, pp. 215–232. ISBN 9789811312441. [Google Scholar]
- Choat, B.; Brodribb, T.J.; Brodersen, C.R.; Duursma, R.A.; López, R.; Medlyn, B.E. Triggers of Tree Mortality under Drought. Nature 2018, 558, 531–539. [Google Scholar] [CrossRef] [PubMed]
- Feldpausch, T.R.; Phillips, O.L.; Brienen, R.J.W.; Gloor, E.; Lloyd, J.; Malhi, Y.; Alarcón, A.; Dávila, E.Á.; Andrade, A.; Aragao, L.E.O.C.; et al. Amazon Forest Response to Repeated Droughts. Glob. Biochem. Cycles 2016, 30, 964–982. [Google Scholar] [CrossRef]
- Matos, I.S.; Eller, C.B.; Oliveiras, I.; Mantuano, D.; Rosado, B.H.P. Three eco-physiological strategies of response to drought maintain the form and function of a tropical montane grassland. J. Ecol. 2020, 109, 327–341. [Google Scholar] [CrossRef]
- Vico, G.; Dralle, D.; Feng, X.; Thompson, S.; Manzoni, S. How Competitive Is Drought Deciduousness in Tropical Forests? A Combined Eco-Hydrological and Eco-Evolutionary Approach. Environ. Res. Lett. 2017, 12, 065006. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, V.A.; Rodrigues, A.F.; Morais, M.A.V.; de Terra, M.C.N.S.; Guo, L.; de Mello, C.R. Spatiotemporal Modelling of Soil Moisture in an Atlantic Forest through Machine Learning Algorithms. Eur. J. Soil Sci. 2021, 72, 1969–1987. [Google Scholar] [CrossRef]
- Khokhlova, O.S.; Myakshina, T.N.; Kuznetsov, A.N.; Gubin, S.V. Morphogenetic Features of Soils in the Cat Tien National Park, Southern Vietnam. Eurasian Soil Sci. 2017, 50, 158–175. [Google Scholar] [CrossRef]
- Terra, M.C.N.S.; Mello, C.R.; Mello, J.M.; Oliveira, V.A.; Nunes, M.H.; Silva, V.O.; Rodrigues, A.F.; Alves, G.J. Stemflow in a Neotropical Forest Remnant: Vegetative Determinants, Spatial Distribution and Correlation with Soil Moisture. Trees-Struct. Funct. 2018, 32, 323–335. [Google Scholar] [CrossRef]




| Mean | Standard Deviation | Coefficient of Variation | |
|---|---|---|---|
| ET | 6.06 | 2.43 | 40.05 |
| gs | 29.23 | 14.33 | 49.03 |
| ga | 18.02 | 3.03 | 16.81 |
| Rn | 196.05 | 75.37 | 38.44 |
| VPD | 0.74 | 0.25 | 33.99 |
| SWS | 251.43 | 41.44 | 16.48 |
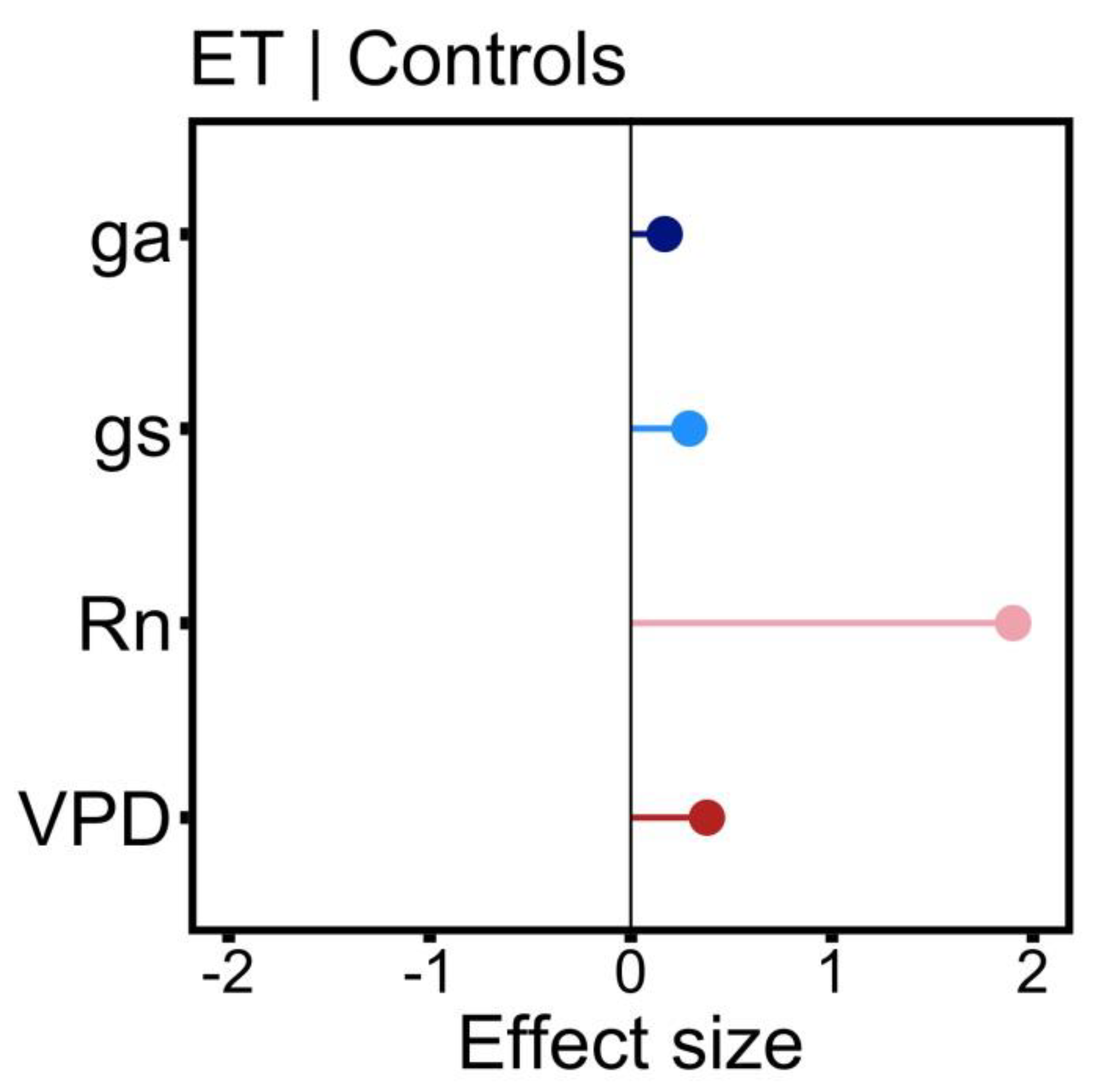
| Estimate | Std. Error | t Value | Pr(>|t|) | Significance | |
|---|---|---|---|---|---|
| Intercept | 5.553619 | 0.169922 | 32.683 | 4.45 × 10−16 | *** |
| MD | −0.007154 | 0.189232 | −0.038 | 0.970311 | |
| SD | 0.10224 | 0.185252 | 0.552 | 0.588643 | |
| gs | 0.312287 | 0.073284 | 4.261 | 0.000597 | *** |
| ga | 0.164458 | 0.059497 | 2.764 | 0.013826 | * |
| Rn | 1.871796 | 0.097384 | 19.221 | 1.76 × 10−12 | *** |
| VPD | 0.384168 | 0.077147 | 4.98 | 0.000136 | *** |
| SWS | 0.011348 | 0.072357 | 0.157 | 0.877338 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guauque-Mellado, D.; Rodrigues, A.; Terra, M.; Mantovani, V.; Yanagi, S.; Diotto, A.; Mello, C.d. Evapotranspiration under Drought Conditions: The Case Study of a Seasonally Dry Atlantic Forest. Atmosphere 2022, 13, 871. https://doi.org/10.3390/atmos13060871
Guauque-Mellado D, Rodrigues A, Terra M, Mantovani V, Yanagi S, Diotto A, Mello Cd. Evapotranspiration under Drought Conditions: The Case Study of a Seasonally Dry Atlantic Forest. Atmosphere. 2022; 13(6):871. https://doi.org/10.3390/atmos13060871
Chicago/Turabian StyleGuauque-Mellado, Daniel, André Rodrigues, Marcela Terra, Vanessa Mantovani, Silvia Yanagi, Adriano Diotto, and Carlos de Mello. 2022. "Evapotranspiration under Drought Conditions: The Case Study of a Seasonally Dry Atlantic Forest" Atmosphere 13, no. 6: 871. https://doi.org/10.3390/atmos13060871
APA StyleGuauque-Mellado, D., Rodrigues, A., Terra, M., Mantovani, V., Yanagi, S., Diotto, A., & Mello, C. d. (2022). Evapotranspiration under Drought Conditions: The Case Study of a Seasonally Dry Atlantic Forest. Atmosphere, 13(6), 871. https://doi.org/10.3390/atmos13060871







