Comparison of the Forecast Performance of WRF Using Noah and Noah-MP Land Surface Schemes in Central Asia Arid Region
Abstract
:1. Introduction
2. Model and Experimental Design
2.1. WRF Model
2.2. Noah and Noah-MP Land Surface Schemes
2.3. Numerical Simulation Setups
2.4. Observational Data and Metrics of the Evaluation
3. Comparison Simulation Results
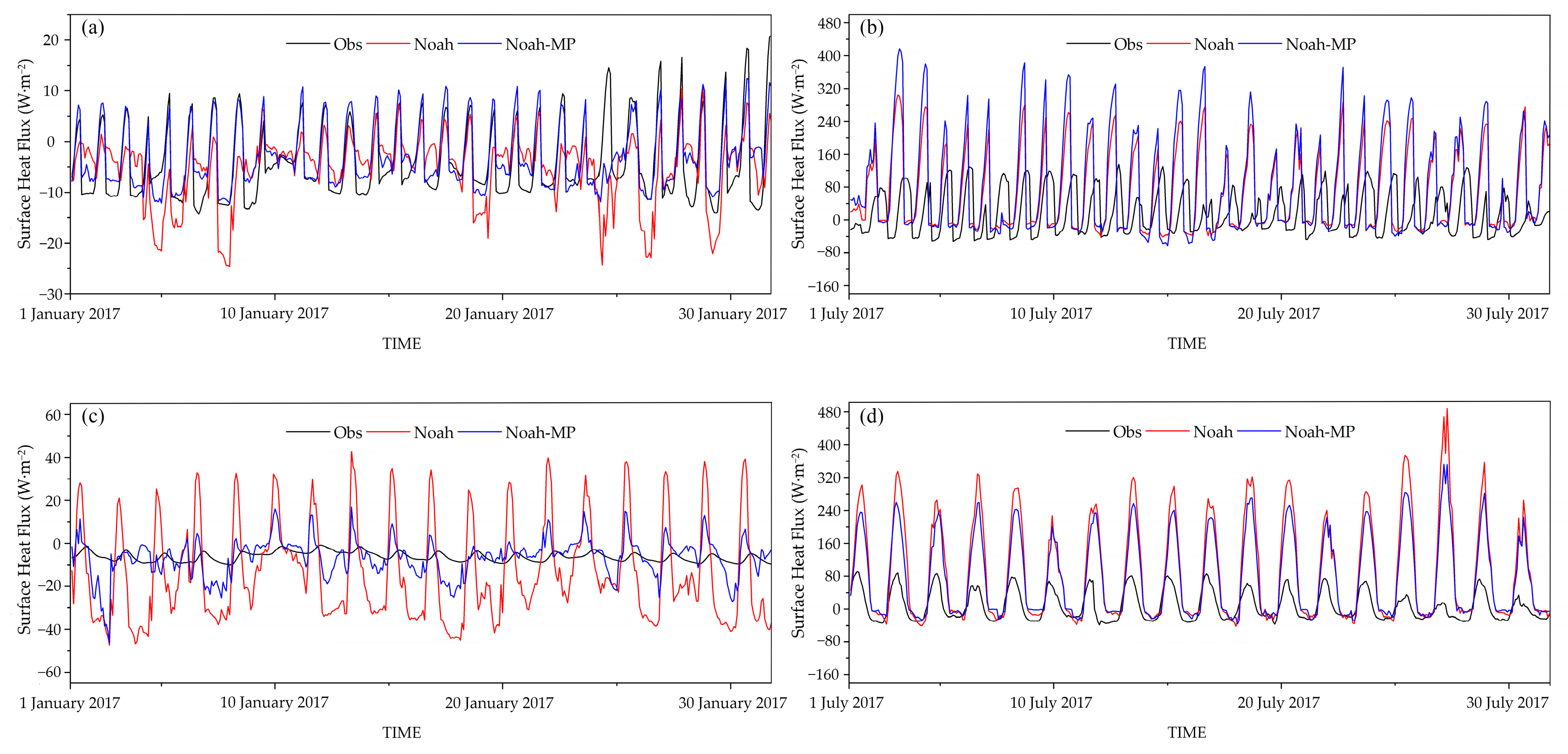
3.1. Surface Flux
3.2. Surface Soil Heat Flux Simulation at Observation Stations
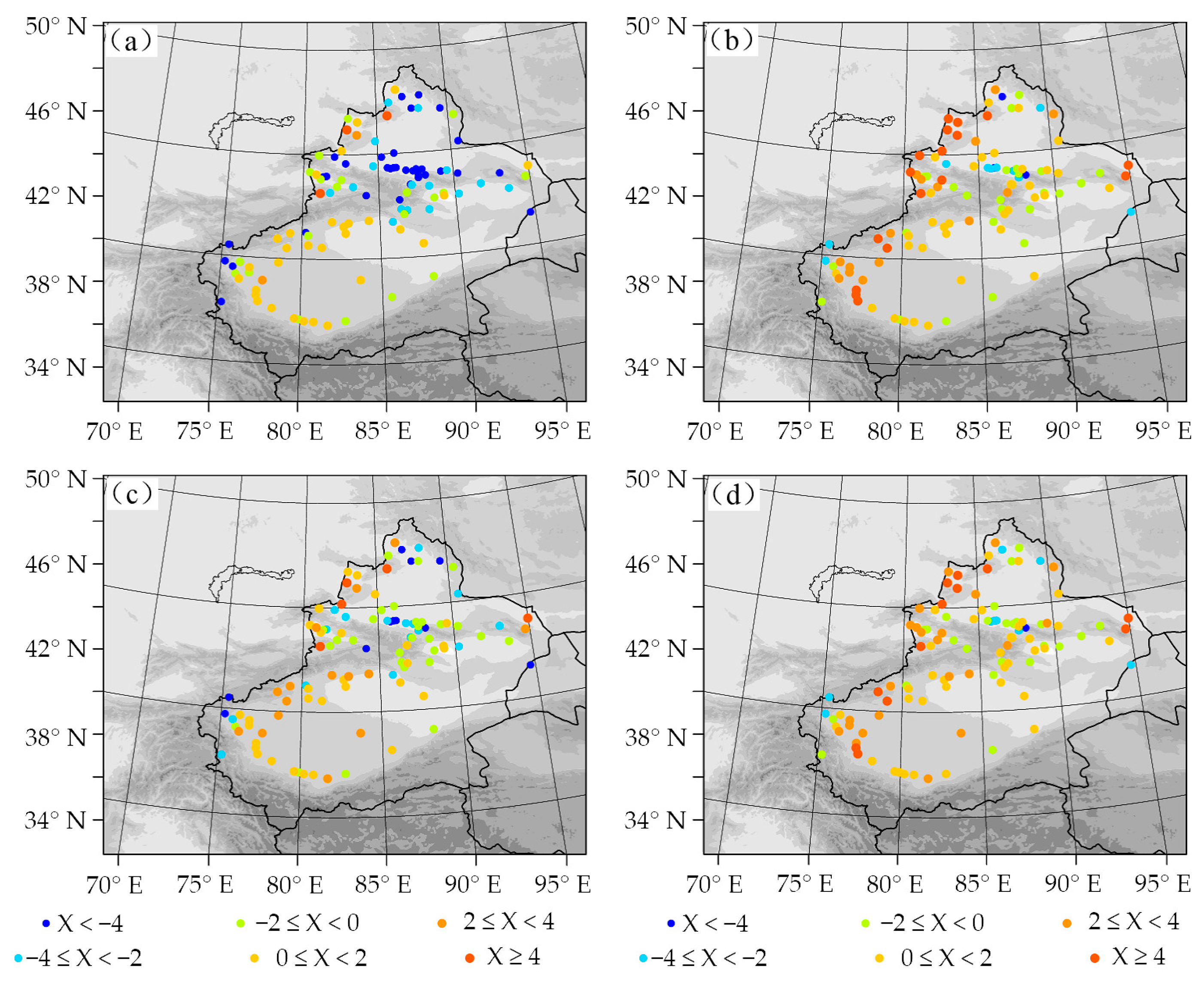
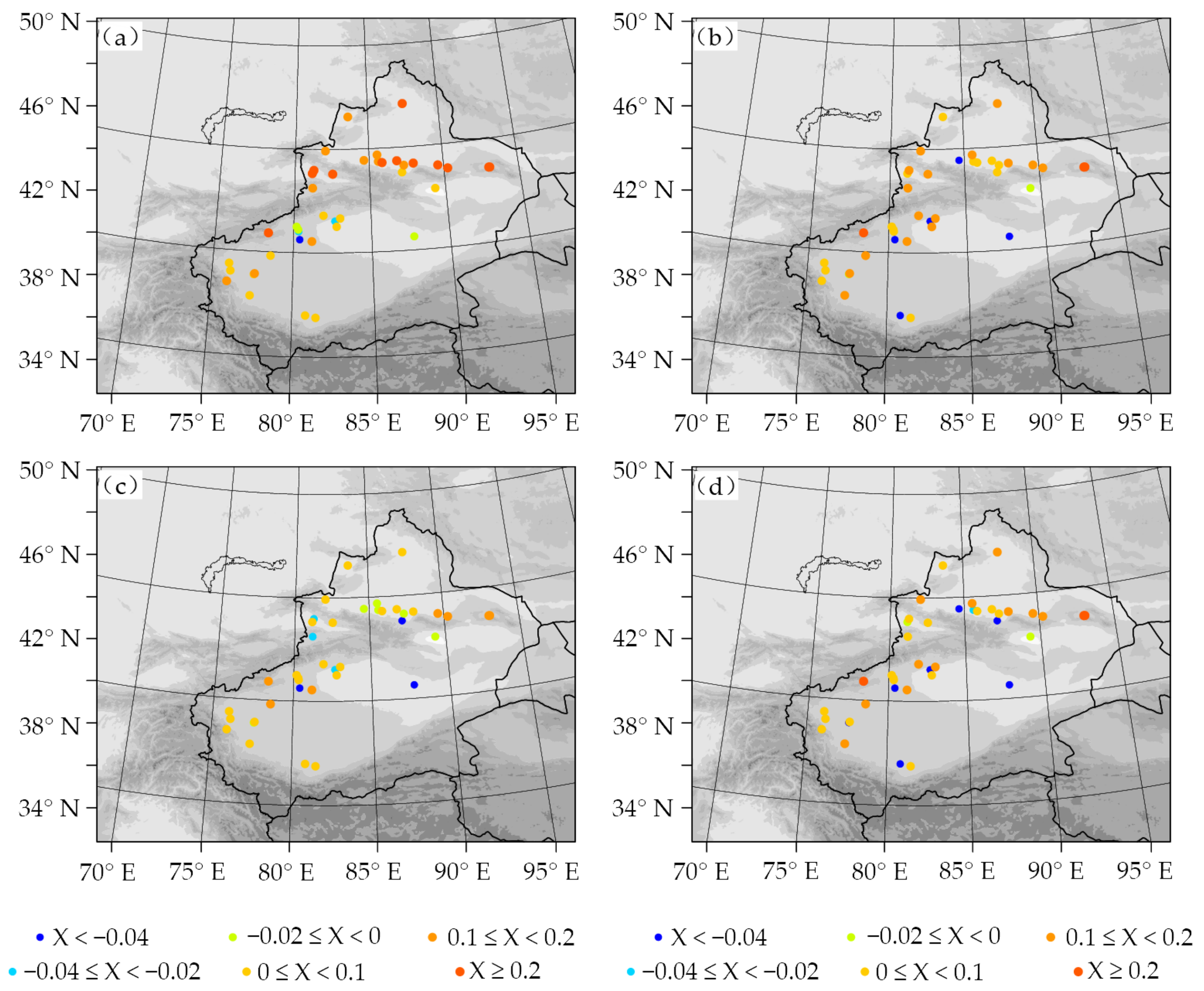
3.3. Simulation of Soil Temperature and Moisture
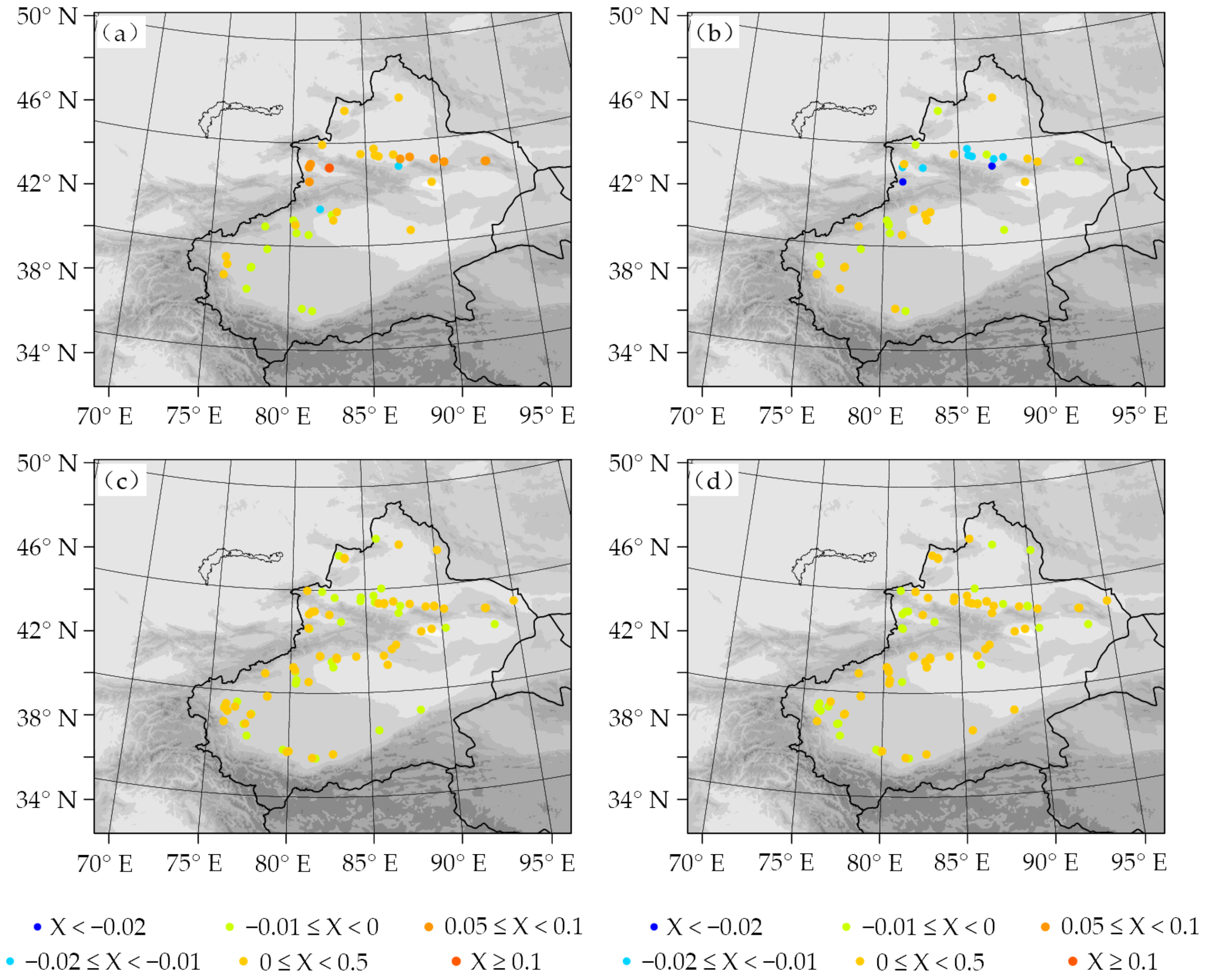
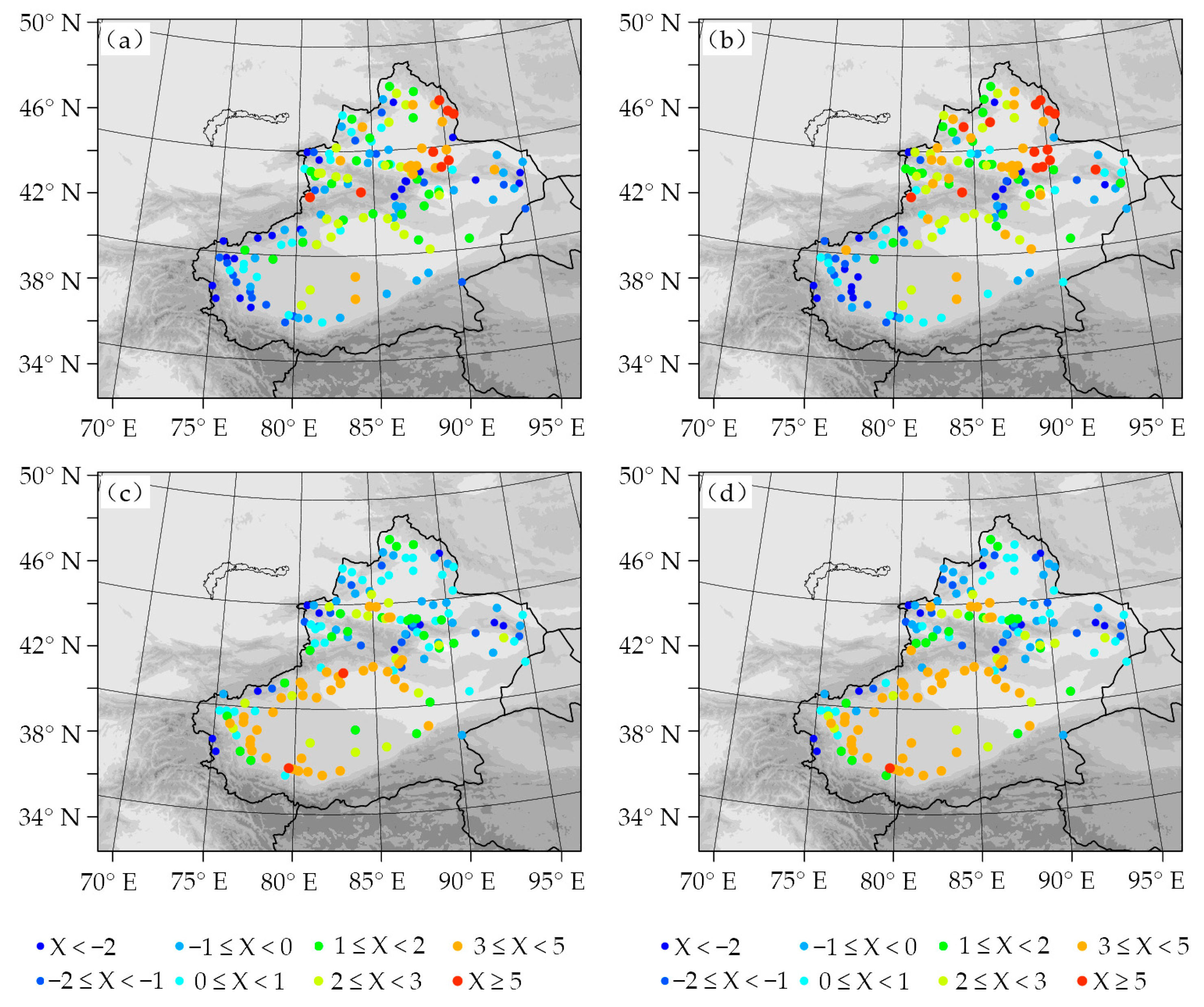
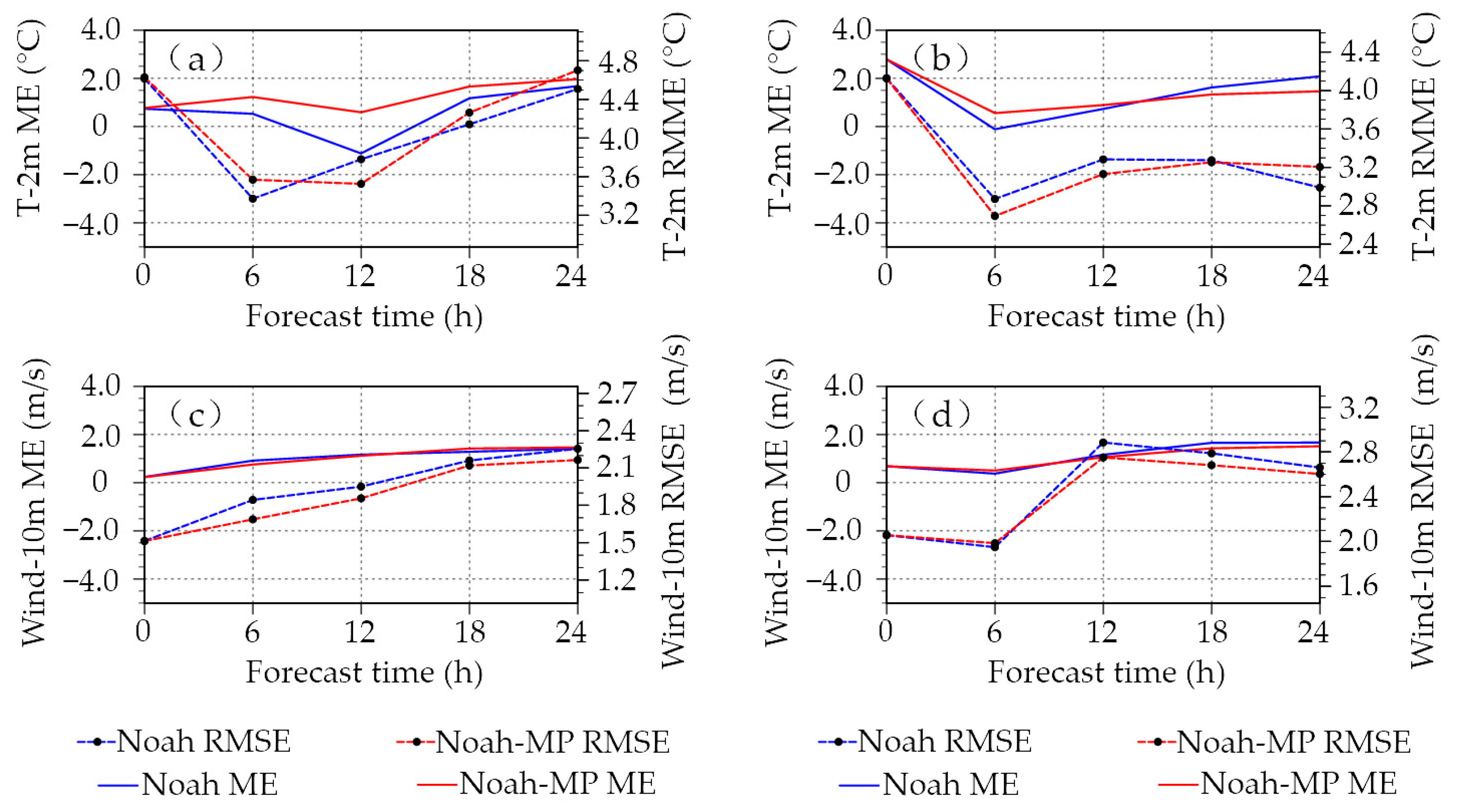
3.4. Near-Surface Variables
4. Summary and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Duan, Z.; Zhang, Y.; Zhang, W.; Wang, Y. Application research of four cold regions land surface and hydrological model to Qinghai-Tibet plateau frozen soil region. J. Water Res. Water Eng. 2012, 23, 43–50. (In Chinese) [Google Scholar]
- Wang, Y.; Zeng, X.; Ge, H.; Zhang, C. Sensitivity simulation of heavy rainfall to land surface characteristics and ensemble forecast test. Meteorol. Mon. 2014, 40, 146–157. [Google Scholar]
- Wei, J.; Dirmeyer, P.; Guo, Z. How much do different land models matter for climate simulation? Part I: Climatology and variability. J. Clin. 2010, 23, 3135–3145. [Google Scholar] [CrossRef]
- Henderson-Sellers, A.; Pitman, A.; Love, J. The project for intercomparison of land surface parameterization schemes (pilps): Phases 2 and 3. Bull. Amer. Meteor. Soc. 1995, 76, 489–503. [Google Scholar] [CrossRef] [Green Version]
- Cao, F.; Dan, L.; Ma, Z. A regional climate coupled model and its influences on climate simulation over East Asia. Chin. J. Atmos. Sci. 2014, 38, 322–336. (In Chinese) [Google Scholar] [CrossRef]
- Zhou, S.; Luo, Y.; Wang, H. Analysis of occurrence frequency of precipitation feature over Tibetan Plateau, East China and Subtropical North America in Boreal Summer using TRMM data. Meteorol. Mon. 2015, 41, 1–16. (In Chinese) [Google Scholar]
- Wang, Q.; Yang, M.; Bao, Y.; Yuan, C. Numerical simulation of a high temperature weather process based on different land surface schemes. Meteor. Sci. Tech. 2011, 39, 537–544. (In Chinese) [Google Scholar]
- Chen, J.; Wang, J. Diurnal cycles of the boundary layer structure simulated by WRF in Beijing. J. Appl. Meteor. Sci. 2006, 17, 403–411. (In Chinese) [Google Scholar]
- Zhang, Y.; Xiao, A.; Ma, L.; Wang, H.; Ma, Z.; Yuan, Z. Simulation of the “19 June 2010” heavy rainfall event by using WRF coupled with four land surface processes. Meteorol. Mon. 2011, 37, 1060–1069. [Google Scholar]
- Zhang, G.; Chen, Y.; Li, J. Effects of organic soil in the noah-mp land-surface model on simulated skin and soil temperature profiles and surface energy exchanges for china. Atmos. Res. 2020, 249, 105284. [Google Scholar] [CrossRef]
- Zhang, G.; Xue, H.; Xu, J.; Chen, J.; He, H. The WRF performance comparison based on noah and noah-mp land surface processes on East Asia. Meteorol. Mon. 2016, 42, 1058–1068. (In Chinese) [Google Scholar]
- Ju, C.; Li, S.; Yu, X.; Li, M. Simulation of a Heavy Rainfall Case in Xinjiang Using the GRAPES Model with Different Land Surface Schemes. Des. OAS Meteor. 2014, 8, 16–22. (In Chinese) [Google Scholar]
- Li, H.; Mamtimin, A.; Ju, C. Simulation and Analysis of Land-Surface Processes in the Taklimakan Desert Based on Noah LSM. Adv. Meteor. 2019, 2019, 1750102. [Google Scholar] [CrossRef]
- Li, M.; Ju, C.; Xin, Y.; Du, J. Evaluation of 24 h precipitation level forecasting of DOGRAFS system during the summer of 2016. Des. OAS Meteor. 2018, 12, 15–21. (In Chinese) [Google Scholar]
- Ju, C.; Li, M.; Du, J.; Li, H.; Li, H.; Liu, J. The effect of DOGRAFS_3 km on the forecast effect of meteorological elements in Xinjiang during summer. Des. OAS Meteor. 2017, 11, 9–16. (In Chinese) [Google Scholar]
- Ju, C.; Liu, J.; Du, J.; Li, H.; Li, M. Forecast effect comparison test and evaluation of RMAPS-CA in Xinjiang. Des. OAS Meteor. 2020, 14, 68–77. (In Chinese) [Google Scholar]
- Ju, C.; Liu, J.; Li, M.; Li, H.; Zhang, H.; Ma, Y.; Mamtimin, A. Objective Verification on RMAPS-CA V2.0 System during 2021. OAS Meteor. 2022, 16, 38–46. (In Chinese) [Google Scholar]
- Zoltan, T. Ensemble Forecasting in WRF. Bull. Am. Meteor. Soc. 2011, 82, 695–698. [Google Scholar]
- Skamarock, W.C.; Klemp, J.B. A time-split nonhydrostatic atmospheric model for weather research and forecasting applications. J. Comput. Phys. 2008, 227, 3465–3485. [Google Scholar] [CrossRef]
- Li, H.; Zhang, H.; Mamtimin, A.; Liu, J. A new land-use dataset for the weather research and forecasting (WRF) model. Atmosphere 2020, 11, 350. [Google Scholar] [CrossRef] [Green Version]
- Shen, X.S.; Chen, Q.Y.; Sun, J.; Han, W.; Gong, J.D.; Li, Z.C.; Wang, J.J. Development of Operational Global Medium-Range Forecast System in National Meteorological Centre. Meteorol. Mon. 2021, 47, 645–654. [Google Scholar]
- Pan, H.; Mahrt, L. Interaction between soil hydrology and boundary-Layerdevelopment. Bound-Layer Meteor. 1987, 38, 185–202. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an advanced land surface-hydrology model with the Penn State-NCAR MM5 modeling system. Part II: Preliminary model validation. Mon. Weather Rev. 2001, 129, 587–604. [Google Scholar] [CrossRef]
- Ek, M.; Mitchell, K.; Lin, Y.; Rogers, E.; Grunmann, P.; Koren, V.; Gayno, G.; Tarpley, J. Implementation of Noah land surface model advances in the National Centers for Environmental Prediction operational mesoscale Eta model. J. Geophys. Res. 2003, 108, 8851. [Google Scholar] [CrossRef]
- Mahrt, L.; Ek, M. The influence of atmospheric stability on potential evaporation. J. Climate Appl. Meteor. 1984, 43, 170–181. [Google Scholar] [CrossRef] [Green Version]
- Schaake, J.; Koren, V.; Duan, Q. A simple water balance model (SWB) for estimating runoff at different spatial and temporal scales. J. Geophys. Res. 1996, 101, 7461–7475. [Google Scholar] [CrossRef]
- Zilitinkevich, S. Non-local turbulent transport: Pollution dispersion aspects of coherent structure of convective flows. In Air Pollution Theory and Simulation; Air Pollution III; Power, H., Moussiopoulos, N., Brebbia, C.A., Eds.; Computational Mechanics Publications: Berlin, Germany, 1995; Volume I, pp. 53–60. [Google Scholar]
- Chen, F.; Janjic, Z.; Mitchell, K. Impact of atmospheric surface layer parameterization in the new land-surface scheme of the NCEP mesoscale Eta numerical model. Bound Layer Meteor. 1997, 85, 391–421. [Google Scholar] [CrossRef]
- Chen, F.; Mitchell, K.; Schaake, J.; Xue, Y.; Hua-Lu, P.; Koren, V.; Duan, Q.; Ek, M.; Betts, A. Modeling of land surface evaporation by four schemes and comparison with FIFE observations. J. Geophys. Res. Atmos. 1996, 101, 7251–7268. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Chen, F.; Barlage, M.; Niyogi, D. Implementing dynamic rooting depth for improved simulation of soil moisture and land surface feedbacks in Noah-MP-Crop. J. Adv. Mod. Earth Sys. 2020, 12, e2019MS001786. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Chen, F.; Barlage, M.; Zhou, G.; Niyogi, D. Noah-MP-Crop: Introducing dynamic crop growth in the Noah-MP land surface model. J. Geo. Res. Atmos. 2016, 121, 13953–13972. [Google Scholar] [CrossRef] [Green Version]
- Niu, G.; Yang, Z.; Mitchell, K.; Chen, F.; EK, M.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Roseroe, E. The Community Noah Land Surface Model with Multi-Parameterization Options (Noah-MP): 1. Model Description and Evaluation with Local-scale Measurements. J. Geophys. Res. 2011, 116, D12109. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.; Yu, X.; Park, S.; Choi, Y.; Myoung, B. Assessing optimal set of implemented physical parameterization schemes in a multi-physics land surface model using genetic algorithm. Geosci. Model Dev. 2014, 7, 2517–2529. [Google Scholar] [CrossRef] [Green Version]
- Jiang, X.; Niu, G.; Yang, Z. Impacts of vegetation and groundwater dynamics on warm season precipitation over the Central United States. J. Geophys. Res. 2009, 114, D06109. [Google Scholar] [CrossRef]
- Yang, Z.; Niu, G.; Mithell, K.; Chen, F.; Ek, M.; Barlage, M.; Longuevergne, L.; Manning, K.; Niyogi, D.; Tewari, M.; et al. The Community Noah Land Surface Model with Multi-Parameterization Options (Noah-MP): 2. Evaluation over global river basins. J. Geophys. Res. Atmos. 2011, 116, D12110. [Google Scholar] [CrossRef]
- Chen, F.; Barlage, M.; Tewari, M. Modeling seasonal snowpack evolution in the complexterrain and forested Colorado Headwaters region: A model inter-comparison study. J. Geophys. Res. 2014, 119, 13795–13819. [Google Scholar] [CrossRef]
- Ball, J.; Woodrow, I.; Berry, J. A model predicting stomatal conductance and its contribution to the control of photosynthesis under different environmental conditions. In Proceedings of the Progress in Photosynthesis Research: VIIth International Congress on Photosynthesis, Providence, RI, USA, 10–15 August 1986; Volume 4, pp. 221–224. [Google Scholar]
- Brutsaert, W.A. Evaporation into the Atomsphere; D. Reidel: Dordrecht, The Netherlands, 1982; 229p. [Google Scholar]
- Niu, G.; Yang, Z.; Dickinson, R. Development of a simple groundwater model for use in climate models and evaluation with Gravity Recovery and Climate Experiment data. J. Geophys. Res. 2007, 112, D07103. [Google Scholar] [CrossRef]
- Niu, G.; Yang, Z. A simple TOPMODEL-based runoff parameterization (SIMTOP) for use in global climate models. J. Geophys. Res. 2006, 110, D21106. [Google Scholar] [CrossRef] [Green Version]
- Verseghy, D. GLASS a Canadian land surface scheme for GCMs. I. soil model. Int. J. Climatol. 1991, 11, 111–133. [Google Scholar] [CrossRef]
- Hong, Y.; Lim, J. The WRF Single-Moment 6-Class Microphysics Scheme (WSM6). J. Korean Meteor. Soc. 2006, 42, 129–151. [Google Scholar]
- Kain, J. The Kain-Fritsch convective parameterization: An update. J. Appl. Meteor. 2004, 43, 170–181. [Google Scholar] [CrossRef] [Green Version]
- Clough, S.; Shephard, M.; Mlawer, E. Atmospheric radiative transfer modeling: A summary of the AER codes. J. Quant. Spectrosc. Radiat. Transf. 2005, 91, 233–244. [Google Scholar] [CrossRef]
- Iacono, M.; Delamere, J.; Mlawer, E.; Shephard, M.; Clough, S.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Kramer, M.; Heinzeller, D.; Hartmann, H.; Wim, V.; Stetneveld, G. Assessment of MPAS variable resolution simulations in the grey-zone of convection against WRF model results and observations. Clim. Dyn. 2020, 55, 253–276. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef] [Green Version]
- Chen, F.; Zhang, Y. On the coupling strength between the land surface and the atmosphere: From viewpoint of surface exchange coefficients. Geophys. Res. Lett. 2009, 36, L10404. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Zhou, G.; Chen, F.; Barlage, M.; Xue, L. A trial to improve surface heat exchange simulation through sensitivity experiments over a desert steppe site. J. Hydrometeor 2014, 15, 664–684. [Google Scholar] [CrossRef]
- Barlage, M.; Tewari, M.; Chen, F. The effect of groundwater interaction in North American regional climate simulations with WRF/Noah-MP. Clim. Change 2015, 129, 485–498. [Google Scholar] [CrossRef]
- Achugbu, I.C.; Dudhia, J.; Olufayo, A.A.; Balogun, I.A.; Gbode, I.E. Assessment of WRF Land Surface Model Performance over West Africa. Adv. Meteor. 2020, 51, 6205308. [Google Scholar] [CrossRef]
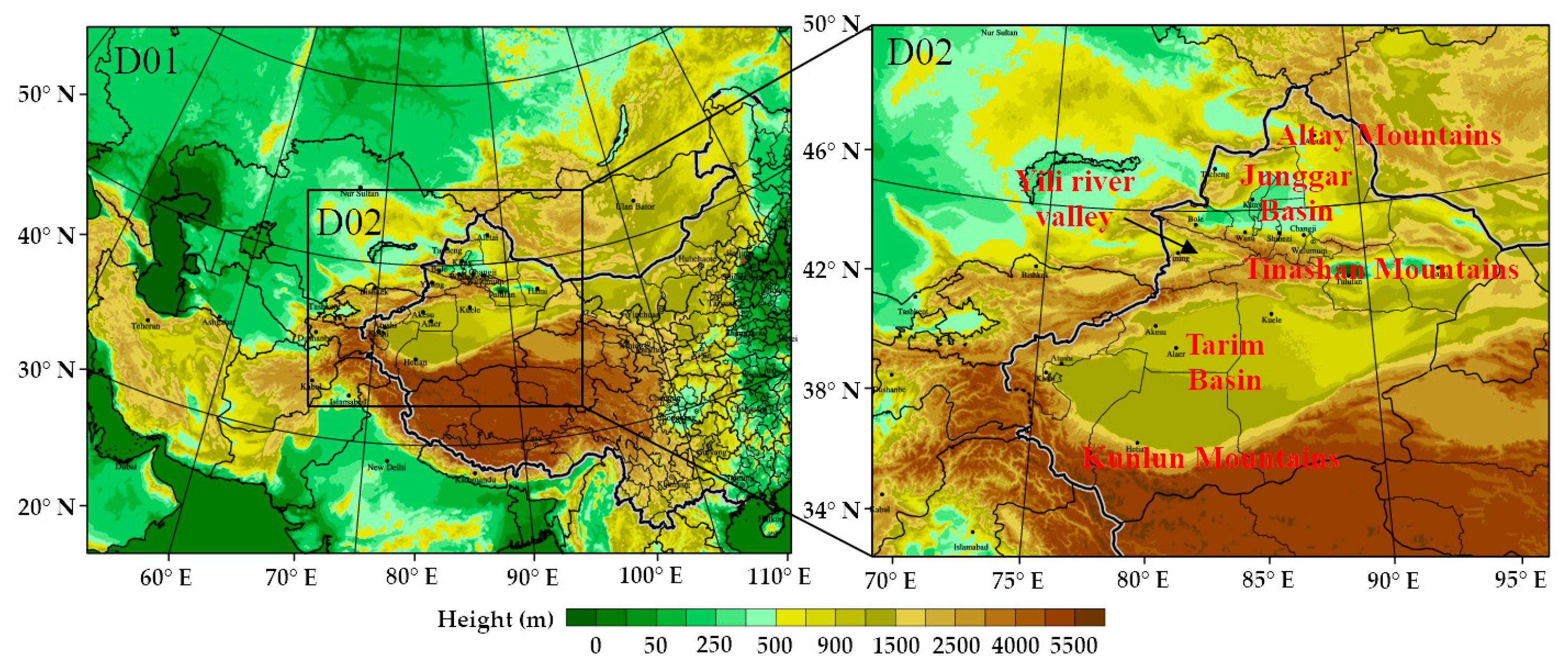



| D01 | D02 | |
|---|---|---|
| Horizontal resolution | 9 km | 3 km |
| Horizontal grid setting | 712 × 532 | 832 × 652 |
| Microphysics | WSM6 | WSM6 |
| Cumulus | K-F | -- |
| Planetary boundary layer | YSU | YSU |
| Long-wave | RRTMG | RRTMG |
| Short-wave | RRTMG | RRTMG |
| Metrics/Station/Scheme | January | July | ||||||
|---|---|---|---|---|---|---|---|---|
| Hongliuhe | Kelameili | Hongliuhe | Xiaotang | |||||
| ME | RMSE | ME | RMSE | ME | RMSE | ME | RMSE | |
| Noah | −0.97 | 7.34 | −7.47 | 25.61 | 45.81 | 77.34 | 87.75 | 131.47 |
| Noah-MP | 1.14 | 4.08 | −1.44 | 9.80 | 62.62 | 104.50 | 71.01 | 104.49 |
| Δ | −17.5% | 44.4% | 80.7% | 61.7% | −36.7% | −35.1% | 19.1% | 20.5% |
| Metrics/Scheme | January | July | ||||||
|---|---|---|---|---|---|---|---|---|
| ME | RMSE | ME | RMSE | |||||
| 10 cm | 30 cm | 10 cm | 30 cm | 10 cm | 30 cm | 10 cm | 30 cm | |
| Noah | −1.87 | 1.19 | 5.06 | 3.08 | −0.28 | −0.93 | 9.71 | 5.03 |
| Noah-MP | −0.28 | 1.24 | 4.38 | 2.90 | 0.06 | −0.39 | 10.31 | 4.91 |
| Δ | 85.0% | −4.2% | 13.4% | 5.8% | 78.6% | 58.1% | −6.2% | 2.4% |
| Metrics/Scheme | January | July | ||||||
|---|---|---|---|---|---|---|---|---|
| ME | RMSE | ME | RMSE | |||||
| 10 cm | 30 cm | 10 cm | 30 cm | 10 cm | 30 cm | 10 cm | 30 cm | |
| Noah | 0.125 | 0.089 | 0.161 | 0128 | 0.003 | 0.007 | 0.109 | 0.109 |
| Noah-MP | 0.041 | 0.069 | 0.137 | 0.131 | 0.002 | 0.007 | 0.106 | 0.109 |
| Δ | 67.2% | 22.4% | 14.9% | −2.3% | 33.3% | -- | 2.8% | -- |
| Metrics/Scheme | January | July | ||||||
|---|---|---|---|---|---|---|---|---|
| ME | RMSE | ME | RMSE | |||||
| T2m | Wind10m | T2m | Wind10m | T2m | Wind10m | T2m | Wind10m | |
| Noah | 0.57 | 1.20 | 3.95 | 2.05 | 1.09 | 1.21 | 3.10 | 2.57 |
| Noah-MP | 1.37 | 1.19 | 4.02 | 1.95 | 1.06 | 1.13 | 3.07 | 2.50 |
| Δ | −140% | 0.8% | −0.18% | 4.9% | 2.8% | 6.7% | 1.0% | 2.8% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ju, C.; Li, H.; Li, M.; Liu, Z.; Ma, Y.; Mamtimin, A.; Sun, M.; Song, Y. Comparison of the Forecast Performance of WRF Using Noah and Noah-MP Land Surface Schemes in Central Asia Arid Region. Atmosphere 2022, 13, 927. https://doi.org/10.3390/atmos13060927
Ju C, Li H, Li M, Liu Z, Ma Y, Mamtimin A, Sun M, Song Y. Comparison of the Forecast Performance of WRF Using Noah and Noah-MP Land Surface Schemes in Central Asia Arid Region. Atmosphere. 2022; 13(6):927. https://doi.org/10.3390/atmos13060927
Chicago/Turabian StyleJu, Chenxiang, Huoqing Li, Man Li, Zonghui Liu, Yufen Ma, Ali Mamtimin, Mingjing Sun, and Yating Song. 2022. "Comparison of the Forecast Performance of WRF Using Noah and Noah-MP Land Surface Schemes in Central Asia Arid Region" Atmosphere 13, no. 6: 927. https://doi.org/10.3390/atmos13060927
APA StyleJu, C., Li, H., Li, M., Liu, Z., Ma, Y., Mamtimin, A., Sun, M., & Song, Y. (2022). Comparison of the Forecast Performance of WRF Using Noah and Noah-MP Land Surface Schemes in Central Asia Arid Region. Atmosphere, 13(6), 927. https://doi.org/10.3390/atmos13060927






