Abstract
Mass balance measurements for Golubin glacier in Northern Tien Shan, Kyrgyzstan, have been discontinuous over the last century, with significant data gaps. We provide a unique over 100-year-long mass balance series on daily resolution. We applied a temperature index model calibrated with glaciological measurements and validated with secular mass balances derived from independent length change observations. A comparison with other recent geodetic studies reveals good agreement. Golubin lost −0.16 ± 0.45 m w.e. a−1 from 1900/1901 to 2020/2021. From the long-term mass balance time series, we identify a shift to a more negative/less positive regime with time, with a steepening of the ablation and accumulation gradients, especially for the past two decades. We observe a parallel shift of the mass balance gradient accompanied by a rotation of the ablation gradient due to increased ablation at the glacier tongue and accumulation above the equilibrium line altitude. This tendency is believed to intensify in the future, affecting glaciers’ mass balance sensitivity to changes in atmospheric conditions and year-to-year variability and resulting in irregular melt water release feeding the rivers that provide water to Bishkek. These kinds of datasets are sparse for Tien Shan and, yet, indispensable to enhancing our understanding of glacier changes in High Mountain Asia.
1. Introduction
Glacier mass balance evolution in Central Asia is a key variable to determining the impact of climate change on water availability [1,2,3,4,5]. Glaciers store water and act as water towers; this water can be used for irrigation and hydropower [6,7,8]. Tien Shan glaciers, as with most mountain glaciers globally, currently present a negative mass balance [9,10,11]. Recent studies on glacier mass balance reconstruction in Tien Shan and Pamir suggest an overall continuous mass loss for the past two decades [10,11,12,13,14,15,16,17]. The Central Asian population is especially vulnerable to changing glaciers as these provide water during the dry summer months, when this is needed for irrigation [18].
A comprehensive glacier-monitoring program was in place during the Soviet era for Central Asia; this included several glaciers in Kyrgyzstan [13,19,20]. By the end of the 1990s, following the collapse of the USSR, all glacier-monitoring activities were stopped in Kyrgyzstan.
Glacier mass balance observations on Golubin span from 1969 to 1994 (Figure 1). In 2010 and 2011, a collaborative effort of the German Research Centre for Geosciences (GFZ), the University of Fribourg, the Central Asian Institute for Applied Geosciences (CAIAG), and the Kyrgyz Hydrometeorologial Service (Kyrgyzhydromet) led to the restoring of a comprehensive glacier monitoring at four selected glaciers in Kyrzgystan: Golubin, Batysh Sook, Abramov, and No. 354 [13,20,21].
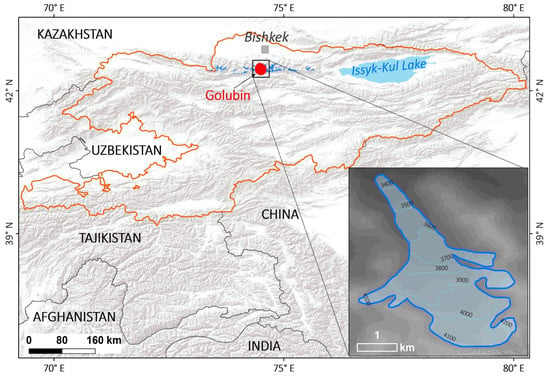
Figure 1.
Location of the study area. Inset shows a topographic map of Golubin glacier.
The aim of the present work is to determine the annual mass balance of Golubin from 1900/1901 to 2020/2021 using multisource data and methods. We applied a distributed mass balance model [22] calibrated with glaciological mass balance point data from 2010 to 2018 and with seasonal glacier-wide mass balances from 1968/1969 to 1993/1994. Average mass balance derived from glacier length change observations was used to independently compare the results for the earlier period, for which no other method or observation was available. We present for the first time a centennial mass balance time series for Golubin by combining different modern and historical remote and direct observations for a glacier located in a data-sparse region in Tien Shan.
2. Study Area and Data
Golubin glacier (N E ) is located in the northern slope of the Kyrgyz Alay Range in the catchment of the Ala Archa River. This is a well-accessible valley glacier with a surface area of 5.42 km2 in 2018 (Figure 1 and Figure 2) and extends over an altitudinal range between 3300 and 4400 m a.s.l. Length change observations started in 1861 [23] (Figure 3). Numerous continuous glaciological, hydrological, and atmospheric observations at Golubin were performed between 1958 and 1994 [24].
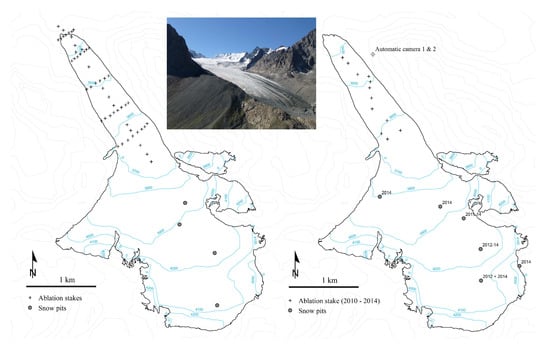
Figure 2.
Left: historical (1969–1994) and right: reestablished (2010–present) monitoring network. The inset shows an image of Golubin taking in 2018.
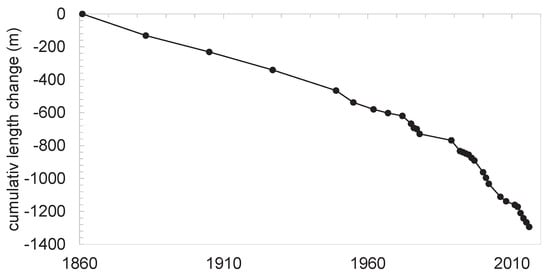
Figure 3.
Cumulative glacier length change of Golubin since the 1860s. Data downloaded from the World Glacier Monitoring Service (WGMS) [25].
Historical seasonal mass balance measurements (Figure 2) are available from the World Glacier Monitoring Service (WGMS) from 1968/1969 to 1993/1994 ([25], Figure 2). This data collection contains winter, summer and annual glacier-wide mass balances as well as the mass balance for each elevation bin for Golubin. For more details please refer to WGMS [25]. In 2010, glacier monitoring was reestablished [20]. The modern monitoring network consists of 15 ablation stakes and three snow pit sites in the accumulation zone [4,21]. All point measurements as well as annual glacier-wide mass balances and the mass balance for each elevation bin are accessible through the WGMS [25]. In 2013, an automatic meteorological station and two automatic cameras for snowline monitoring were installed near the glacier [20,26]. These data are accessible on an open-data platform (http://sdss.caiag.kg/sdss (accessed on 12 April 2022)). Camera images are taken six times a day and meteorological data have 5 min intervals. We used the Shuttle Radar Topography Mission (SRTM, Jarvis et al. [27]) digital elevation model (DEM) for the model runs. Glacier outlines used for modeling were manually delineated from 1962 to 2018 from aerial photographs and WorldView-2 that were available to the authors and from freely accessible Landsat and Sentinel-2 satellite images. Prior to 1962, outlines were obtained from Venukov [23], Aizen [24], and Aizen et al. [1]. Uncertainties are expected to be similar for the different data sources and to range within 5% to 10% of the total glacier area [28]. Glacier outlines were available or generated for 1861, 1883, 1905, 1927, 1949, 1955, 1962, 1967, 1972, 1975, 1976, 1977, 1978, and 1989 and annually after 1990. For years with no observations, we used the outline of the year dating closest to the modeled year. Glacier length change data were obtained from the WGMS [25]. The observed Golubin glacier length change is available since 1861, with a 20-year step between subsequent measurements until the mid 20th century and more frequent after that. We did not adjust the glacier thickness. In the Ala-Archa Valley, the Alplager weather station—located at an altitude of 2145 m a.s.l.—provides daily temperature and precipitation measurements from 1980 to present. These data were provided by the KyrgyzHydromet. Meteorological reanalysis data were used to complete the meteorological time series needed as input data to drive the mass balance model. We used the daily ERA20C reanalysis data [29] at the 0.125° resolution extracted at the Golubin location. For consistency we only used direct meteorological observations from the Alplager station for bias correction and model forcing.
3. Methods
3.1. Secular Mass Balances from Glacier Length Changes
Secular mass balance calculation is based on the approach presented by Hoelzle et al. [30], considering step changes after the full dynamic response and new equilibrium of the glacier have been achieved, when mass balance disturbance leads to a corresponding glacier length change that depends on the original length L and the average annual mass balance (ablation) at the glacier terminus b:
The dynamic response time t is calculated following Jóhannesson et al. [31], where h is a characteristic ice thickness usually taken at the equilibrium line, where ice depths are near maximum. We used a maximum ice thickness of 154 ± 11 m [32] and of −3.5 m, based on the glaciological surveys of the recent monitoring [25].
Therefore, a response time of about 43 years was calculated for Golubin. Based on this response time, we chose periods of minimum 50 years (1905 to 1955, 1927 to 1977, 1949 to 2000, 1955 to 2006, and 1962 to 2012) to estimate average mass balance <b>. To calculate mass balance from b to zero during the dynamic response, <b> can be obtained with the following equation:
Factor n denotes the count of possible response times for each glacier within the considered time period. <b> values are annual mass changes (mw.e. yr−1) averaged over the entire glacier surface, which can be directly compared with the modeled and measured glacier mass balances.
3.2. ERA20C Reanalysis Data Time Series from 1900 to Present
Reanalysis data were corrected for bias separately for each month using the above-mentioned station data for the common period 1974–2010. We obtained an extended temperature and precipitation series for the period 1900–2015 by integrating in situ observations with bias-corrected reanalysis data (Figure 4).
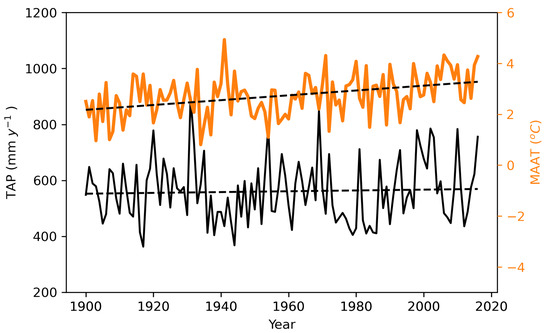
Figure 4.
Bias corrected ERA20C Mean annual air temperature (MAAT) and total annual precipitation (TAP) for the study area. The time series is used to run the mass balance model.
3.3. Glaciological Measurements from 2011 to Present
Glaciological field surveys are usually conducted once a year, preferably at the end of the summer. However, due to logistical reasons, this was not always possible for the present work, and some surveys were conducted in late July or early August. In May 2014, field snow depth surveys improved the spatial snow depth measurement coverage in the accumulation zone. Due to the changing measurement dates, measured surface mass balances (SMBs) might not be representative for the hydrological year. To ensure comparability to the long-term modeled SMB time series, we extrapolated the SMB calculated for the measurement period to match the hydrological year. For this homogenization, we applied the approach used in Huss et al. [22]. Thereby, a mass balance model is used as an interpolation tool to obtain SMB values for each grid cell at daily temporal resolution from in situ field data. With the model spatially distributed accumulation and ablation processes can be better captured when extrapolating direct observations using physical relations. With the mass balance model we furthermore provide mass balances at the end of the mass balance year. Thus, modelled distributed mass balances represent the direct observations as closely as possible. This method has been widely-used in the literature (Huss et al. [12,17,22,33]) and details can be found in Kenzhebaev et al. [16].
3.4. Surface Mass Balance Model
We used a distributed mass balance model by Huss et al. [33], combining a distributed accumulation model with a temperature index melt model [34]. The same model setting was applied in Kronenberg et al. [17] and Kenzhebaev et al. [16]. We use a spatial resolution of 20 m and daily temporal time steps. Degree-day factors are varied as a function of potential direct solar radiation to account for the effects of slope, aspect, and shading. Air temperature is extrapolated from mean glacier elevation to every grid cell with a constant lapse rate of −4.1 °C km−1 based on Aizen et al. [35]. The cumulative snow and ice melt for each grid cell over the glacier surface and for each time step ( = 1 day) is obtained with:
where denotes a melt factor, and are radiation factors for snow and ice surfaces, respectively, and is the potential solar radiation under clear-sky conditions (calculated after Hock [34]).
Snow accumulation C at any location and time t is calculated based on the sum of solid precipitation:
3.5. Model Calibration and Validation
We used a two-step calibration scheme to calibrate the model, using: (1) glaciological point data available from 2010/2011 to 2018/2019; and (2) seasonal glacier SMB records from 1980/1981 to 2018/2019.
(1) We followed the model setup and calibration procedure described in Kronenberg et al. [17] and Kenzhebaev et al. [16]. For the period 2010/2011–2020/2021, we used direct point measurements to obtain the best possible representation of glacier-wide SMB. C(f) was semi-automatically adjusted to minimize the standard deviation—root-mean-square error (RMSE)—between the model and the observed accumulation (ablation) measurements. The RMSE for the years 2010/2011 to 2017/2018 ranges between 0.30 and 0.49 m w.e. yr−1. The ratio between f and r was held constant (Table 1).

Table 1.
Constant and calibrated model parameters after the different calibration steps (first- and second-order calibration steps). The parameters resulting from the second-order calibration were used to model the mass balance years from 1900/1901 to 2009/2010.
(2) From this optimized time series, we defined the arithmetic mean of the annually encountered best fit for C and f as “ideal parameter set” to reconstruct seasonal SMB from 1968/1969 to 1993/1994 (Table 1). This follows the calibration procedure previously used for nearby Central Asian glaciers in Barandun et al. [12], Kronenberg et al. [17] and Kenzhebaev et al. [16]. Unlike previous research, seasonal glacier-wide SMBs were available in the present work, allowing for an additional model optimization strategy. To reconstruct SMB for the time periods 1900/1901–1967/1968 and 1994/1995–2009/2010—where no glaciological data were available—we evaluated and recalibrated the “ideal parameter set” of step (1) with seasonal surveys. In doing so, we reduced the average RMSE of the winter SMB (summer SMB), calculated for each year by manually readjusting C(f) and minimizing the difference in the mean SMB over the entire period (1968/1969–1993/1994). Both parameters were held constant over time (Table 1). This exercise was performed several times, providing us with a range of possible parameter combinations. The best performing parameter combination resulted in an absolute difference in the average annual SMB of 0.05 m w.e. yr−1 from 1968/1969 to 1993/1994 and an average RMSE of the seasonal components of 0.29 m w.e. yr.
The model was applied with the readjusted parameters from 1900/1901 to 2018/2019. The centennial mass balance—obtained from the reconstructed mass balance from 1900/1901 to 2009/2010 and the measured glaciological mass balance from 2010/2011 to 2020/2021—was validated using secular mass balance changes derived from glacier length changes.
3.6. Model Mass Balance Uncertainty
The uncertainty calculated for the years with direct point observations (2010/2011– 2017/2018) is based on the RMSE between the observed and the modeled point mass balance, averaged for the entire period ().
For the period from 1968/1969 to 1993/1994—for which seasonal mass balance observations are available—the uncertainty of the time series provided herein includes an estimated uncertainty resulting from the lack of point data (). We calculated the difference in the mass balance between using direct observation for calibration and running the model without direct observations from 2010/2011 to 2018/2019. We also include an uncertainty introduced by the use of reanalysis meteorological data (). We calculated the RMSE between the modeled mass balance from 1981 to 2010 driven by the meteorological observation from Alplager station and the modeled mass balance for the same period driven by the reanalysis data. We determined the uncertainty related to the first- and second-order model calibration by calculating the RMSE between the modeled mass balance obtained using only the first-order calibration and the one obtained using also the second-order calibration (). We used the average RMSE of winter and summer mass balance.
For the years without any observations—from 1900/1901 to 1967/1968 and from 1994/1995 to 2009/2010—we added an uncertainty introduced by the use of an “ideal parameter set” after the calibration procedure was completed (). We calculated the standard deviation of the mass balances obtained by varying the degree day factors from 0.5 to 2.0 and the precipitation correction from 80% to 180%. All uncertainties are summarized in Table 2.

Table 2.
Different uncertainties of the seasonal components considered to deduce the global uncertainty () in m w.e. yr for the annual mean mass balance (ba), the winter balance (bw), and the summer balance (bs).
4. Results
4.1. Length Change
Length change observations show a predominant glacier retreat of almost 1.3 km from 1861 to 2016 (Figure 3). For the first half of the 20th century, only few observations indicate a continuous retreat of the glacier tongue. The front position became more stagnant shortly after 1960 and until the mid 1970s. This period was followed by a first rapid retreat lasting from 1975 to 1978. The glacier front position barely changed between 1978 and 1989. In the 1990s, glacier retreat accelerated. The slow down during the 1960s corresponds roughly to the glacier advance observed in Pamir-Alai until the mid to late 1970s documented in Hoelzle et al. [30]. An almost uninterrupted acceleration of the glacier retreat persisted until the 1990s. For Golubin, however, this accelerated retreat was interrupted, but the glacier tongue was never observed to advance.
4.2. Observed and Modeled Mass Balance Time Series
Golubin lost −0.17 ± 0.45 m w.e. yr−1 for the entire period 1900/1901–2020/2021 (Figure 5 and Figure 6). Mass loss increased during the second half of the 20th century, with an average mass balance of −0.20 ± 0.42 m w.e. yr−1 from 1949/1950 to 2020/2021. The 2007/2008 is the most negative year simulated. Direct measurements over the last decades confirm a negative trend, with a mass loss of −0.18 ± 0.17 m w.e. yr−1 from 2010/2011 to 2020/2021. Most positive mass balances were observed in the early 1920s to mid 1930s and from the mid 1950s to the mid 1970s (Figure 5). Negative annual mass balances became dominant thereafter. A strongly negative period was also modeled from the mid 1930s to the mid 1950s. We used a nonparametric Mann–Kendall test [36,37] to evaluate the confidence level of the trends (significant at the 99%, 95%, and 80% level or not significant). We found a significant negative annual mass balance trend at the 80% level over the entire period. The summer mass balance decreased significantly (95% level) from 1900/1901 to 2020/2021. No significant trend was encountered for the winter mass balance.
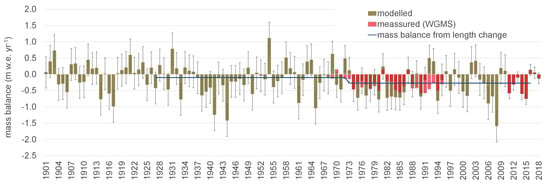
Figure 5.
Modeled (green bars) and measured (red bars) mass balance time series with error bars describing the mass balance uncertainty. Blue line showing mass balance change derived from length change observations for two periods (1927 to 1972; 1972 to 2016).
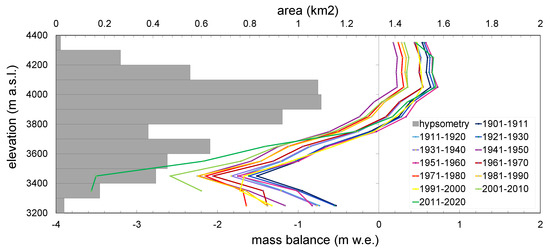
Figure 6.
Mass balance gradient with elevation averaged for 10-year periods from 1900 to present. Gray bars showing hypsometry of glacier.
4.3. Mass Balance Time Series Based on Length Change Observations
Secular glacier mass balance derived from cumulative length changes was estimated to −0.17 m w.e. yr for the period 1861–2016. We calculated separate average mass balance values for the time periods 1861–1927, 1927–1972, and 1972–2016, with average mass balance values of 0.00 m w.e. yr−1, −0.11 m w.e. yr−1 and −0.27 m w.e. yr−1, respectively. We modeled similar mass balances of −0.14 ± 0.49 m w.e. yr from 1927 to 1972 and of −0.30 ± 0.40 m w.e. yr−1 from 1972 to 2016. Table 3 compares mass balance for the different approaches presented herein.

Table 3.
Comparison of modeled mass balance (m w.e. yr) and reconstructed mass balance based on length changes (m w.e. yr).
5. Discussion
5.1. First Centennial Mass Balance Time Series for Golubin Glacier
Secular mass balance reconstruction based on cumulative glacier length changes has been proved to be a robust and simple method [30,38].
Based on available WGMS cumulative length change data, Hoelzle et al. [30] analyzed global secular mass balance since the end of the Little Ice Age. They suggest the mean specific balance for continental climate glaciers to be around −0.12 m w.e. yr since 1900. This region includes Tien Shan and Pamir-Alai. Our results suggest a similar mean specific mass balance for Golubin since 1900.
5.2. Changes in Mass Balance Gradient
When we considered the elevation-dependent distribution of the mass balance, we identified a shift to a more negative/less positive regime with time (Figure 6). At the beginning of the 20th century, the ablation gradient (10-year average) was in the range of 0.4 to 0.5 m w.e. 100 m, followed by a gradual increase to ≈0.55 m w.e. 100 m until the 1980s (Figure 7). For the rather dry and cold period of the 1990s, the gradient dropped again to 0.44 m w.e. 100 m, with a similar shape of the early 20th century ablation gradients. For the past two decades, steepening intensified to values up to 0.30–0.83 m w.e. 100 m (Figure 7). For Abramov, in South Kyrgyzstan, on the contrary, a slight flattening of the gradient was identified by Kronenberg et al. [39]. They found the ablation gradient to be higher for the years 1968/1969–1997/1998 (0.80 m w.e. 100 m) than for the years 1998/1999–2018/2020 (0.70 m w.e. 100 m). However, the mass balance gradient at Golubin is smaller than that at Abramov by a factor of 2, reflecting the difference in climate conditions for the two locations. This is in line with the mass balance sensitivity calculated by Rasmussen [40], highlighting low sensitivity to air temperature changes for Golubin (−0.17 m w.e. yr−1°C) and high sensitivity for Abramov (−0.47 m w.e. yr−1°C). The low mass balance sensitivity and gradient suggests a more continental regime. We compensated for the parallel shift by adjusting the gradients to a fixed equilibrium line altitude (ELA ) at 3850 m a.s.l. to investigate a rotation of the gradient that is clearly visible for the ablation area (Figure 8) but less pronounced for the accumulation area (Figure 8). This steepening of the mass balance gradient (Figure 8) suggests a regime change from a continental to a more maritime setting characterized by steeper gradients (Figure 7). The overall mass balance gradient—including ablation and accumulation—increased from 0.27 to 0.48 m w.e. 100 m, and the accumulation gradient, from 0.09 to 0.12 m w.e. 100 m (Figure 7). For comparison, Kenzhebaev et al. [16] calculated a mean mass balance gradient of around 0.45 m w.e. 100 m for the period from 2004 to 2014 for glaciers in Central Tien Shan, located under higher continentality than Golubin. Kronenberg et al. [17] reported a mean glacier mass balance gradient of 0.68 m w.e. 100 m for glacier No. 354, in the Akshiirak Range, Central Tien Shan, for the same period. Two other glaciers located in Akshiirak were reported to have flatter gradients: Davydov presented a gradient of 0.3 m w.e. 100 m from 1983 to 1995 [41] and Sary-Tor, a value of 0.4 m w.e. 100 m from 1985 to 1989 [42]. Van Tricht et al. [43] found the average mass balance gradient from the Little Ice Age to present to span from 0.50 and 0.60 m w.e. 100 m for glaciers Karabatkak, Sary-Tor, and Bordu. The observed shift and rotation of the mass balance gradient responds to an increase in accumulation and ablation. This is reflected in a significantly decreasing summer balance and a tendency for a larger winter balance (nonsignificant trend, Figure 7).
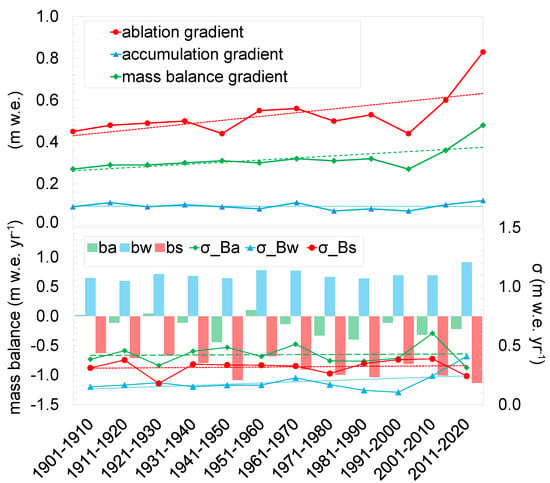
Figure 7.
Top: Ablation, accumulation, and mass balance gradient averaged for 10-year periods. Bottom: 10-year average summer, winter, and annual mass balance (bars) and year-to-year variability of summer, winter, and annual mass balance for 10-year periods (: symbols).
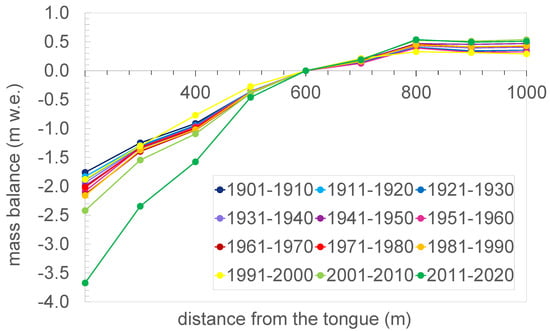
Figure 8.
Reconstructed mass balance gradients of Golubin for 10-year periods from 1901 to 2020 adjusted to a fixed ELA at 3850 m a.s.l.
Aizen [24] reconstructed the mass balance of Golubin based on the assumption that elevation-dependant distribution of the mass balance may migrate from year to year horizontally with a constant mass balance gradient. According to our results, this assumption does not agree with our observations. Dyurgerov and Dwyer [44] analyzed the mass balance gradients of 21 glaciers in the Northern Hemisphere for the period from 1971 to 1995, showing that the shift of mass balance curves from cold to warm periods occur through a rotation rather than parallel shifts, as had been stated in earlier publications [45,46]. Our results suggest both that, on the one hand, parallel shifts of the ablation gradient, mainly for the earlier periods and, on the other, a rotation, pronounced for the past decades. The increased ablation at the tongue is partly compensated by increased accumulation above the equilibrium line (Figure 6 and Figure 8). This might intensify further in the future, affecting glacier mass balance sensitivity and variability. The dryer mountain ranges of Central Asia tend to have higher accumulation and ablation rates during summer seasons. The rotation will therefore be enhanced by further warming, changing both snow accumulation and summer melt and, correspondingly, the annual mass balance. This results in a change of the intensity of the hydrological cycle of a glacier that is strongly dependent on its dynamic activity and on its overall mass turnover [47,48]. Our results show a significant increase of the mass turnover with time (Figure 9). An increase in mass turnover will also affect the glacier flow dynamics so that, in the long term, the observed changes are expected to importantly change the glacier regime and behaviour.
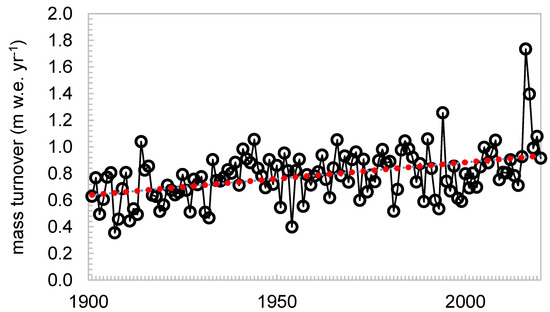
Figure 9.
Annual mass turnover from 1900 to 2020 calculated following Meier et al. [47]. Red dots indicate trend line.
5.3. Mass Balance Variability
The year-to-year variability over 10-year periods increased for all three components of the mass balance, but trends were not significant (Figure 7). Long-term mass balance measurements from glaciers located in Tien Shan and Pamir [25] reveal similar year-to-year variability from the early 1960s to 2018 (Figure 10). Barandun et al. [10]—based on transient snowline and geodetic surveys—modeled similar year-to-year variability ( = 0.39 m w.e.) for Northern/Western Tien Shan. Our results suggest year-to-year variability (decadal average) to be rather high ( = 0.46 m w.e. for 1900/0–2020/2021) and to increase over time (significant for winter balance, Figure 6).
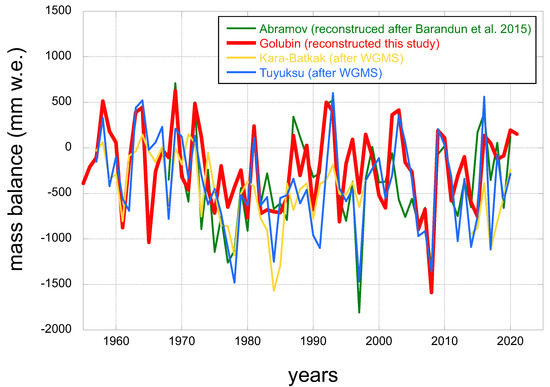
Figure 10.
Comparison of measured and reconstructed mass balance of Golubin with measured mass balance of glaciers located in Tien Shan and Pamir.
Barandun et al. [10] found that higher variability dominates toward the subcontinental western margin of Tien Shan and is generally accompanied by higher mass loss. Glaciers with low mass balance variability generally show low mass balance sensitivity and gentler mass balance gradients. This responds typically to dryer and colder environments [49]. Within more subcontinental regions, a higher year-to-year variability is expected (typically > 0.39 m w.e.) as a result of the elevated sensitivity to changing atmospheric conditions [50]. However, for Golubin, mass balance gradients calculated in the present work are relatively flat and mass balance sensitivity to air temperature changes is low [40]. This highlights ongoing and, so far, not well understood changes, the heterogeneity of glacier response to ongoing climate change [10,11,15,51], and the need for detailed observations and increased process understanding.
5.4. Comparison with Other Mass Balance Estimates for Tien Shan and Pamir
Barandun et al. [10] found a negative mass balance of −0.30 m w.e. yr−1 with a significant negative trend for the time period 1999/2000–2017/2018 for Northern/Western Tien Shan. Kapitsa et al. [52] reported a negative mass balance of −0.35 m w.e. yr−1 for Tuyuksu group from 1958 to 2016. Bolch [14] reported a value of −0.45 m w.e. yr and −0.42 m w.e. yr−1 for the Ala Archa basin from 1964 to 1999 and 1999 to 2012, respectively. Shea et al. [53] reported a mass loss of −0.27 m w.e. yr−1 for Northern/Western Tien Shan from 2000 to 2018. The average annual mass balance of Golubin agrees well with the different regional estimates, underlining its representativeness for Northern/Western Tien Shan proposed in Barandun et al. [10] and highlighting its importance as a glacier monitoring site.
We compared decadal mass balances of Golubin with mass balance estimates found in the literature (Figure 11). Geodetic mass balances published in Barandun et al. [10] (−0.41 m w.e. yr−1 from 2000 to 2006 and −0.30 m w.e. yr−1 from 2006 to 2014) agree well with our results (−0.35 m w.e. yr−1 from 2000/2001 to 2005/2006 and −0.44 m w.e. yr−1 from 2005/2006 to 2013/2014). Bolch [14] calculated geodetic mass balances for Golubin of −0.46 m w.e. yr−1 for the period 1964–1999 and −0.29 m w.e. yr−1 for the period 1999–2012; our results show mass balances of −0.24 m w.e. yr−1 and −0.35 m w.e. yr−1 for the same periods, respectively. The study by Bolch [14] relies on the SRTM DEM for DEM differencing. Unknown penetration depth of the C-band of the SRTM into snow might cause underestimation of the elevation increase in the accumulation area for the first period and overestimation for the second Barandun et al. [12], Kaab et al. [54]. Hugonnet et al. [51] reported geodetic mass balances for Golubin of −0.13 m w.e. yr (2000–2004), −0.28 m w.e. yr (2005–2009), −0.27 m w.e. yr (2010–2014), and −0.35 m w.e. yr (2015–2019). In the present study, we modeled mass balances of −0.11 m w.e. yr (1999/2000–2003/2004) and −0.64 m w.e. yr (2004/2005–2008/2009), and measured mass balances of −0.30 m w.e. yr (2009/2010–2013/2014) and −0.16 m w.e. yr (2014/2015–2018/2019). Our modeled mass balance for the first period agrees well with that in Hugonnet et al. [51]; our modeled mass balance for the second modeled period, however, is more negative, mainly due to above-average mass loss modeled for 2007/2008 (Figure 1). Glaciolocial measurements from nearby Tuyuksu similarly show an exceptional mass loss of −1.357 m w.e. yr for 2007/2008 (Figure 10). Hugonnet et al. [51] calculated a mass loss of −0.56 m w.e. yr for the balance year 2007/2008. Both studies agree for the period from 2010 to 2014; however, direct measurements reveal a reduced mass change in comparison with the most negative mass balance period (2015–2019) in Hugonnet et al. [51]. Hugonnet et al. [51] calculated a geodetic mass balance of −0.26 m w.e. yr from 2000 to 2019. Brun et al. [15] reported close to balanced conditions for Golubin (−0.04 m w.e. yr) from 2000 to 2016. The latter are substantially less negative than our findings (−0.30 m w.e. yr from 2000 to 2019).
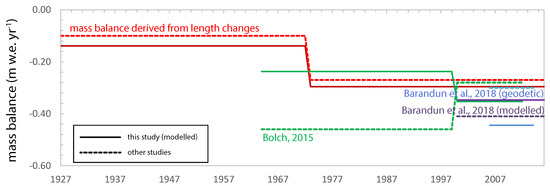
Figure 11.
Comparison of reconstructed mass balance averaged for the corresponding period with previous published results.
Direct glaciological observations for monitored glaciers in Tien Shan and Pamir suggest negative mass balance regimes since the onset of measurements (Figure 10, [25]); For example, observed mean mass balance on Tuyuksu (Central Tuyuksu) is −0.4 m w.e. yr for the period 1999/2000–2011/12 and −0.43 m w.e. yr for the period 1999/2000–2017/2018 [25]. Glaciological measurements for Golubin similarly indicate negative annual mass balances (−0.18 m w.e. yr) from 2010/2011 to 2020/2021. In comparison with Tuyusku (−0.50 m w.e. yr from 2010/2011 to 2019/2020) [25], Golubin lost less mass during the past decade. This is also true for periods further back in time—despite a similar year-to-year variability (Figure 10)—suggesting similar regional climatic variability [50]. Tuyuksu lost close to double the mass than the Golubin did in the last 50 years. Geodetic mass balances published in Kapitsa et al. [52] are in line with glaciological observations and reveal a mass loss for Tuyuksu of −0.39 m w.e. yr (1957/1958–1997/1998), −0.35 m w.e. yr (1997/1998–2015/2016), and −0.38 m w.e. yr (1957/1958–2015/2016). Hagg et al. [55] reported a geodetic mass balance of −0.32 m w.e. yr (1958–1997/1998) and a glaciological mass balance of −0.42 m w.e. yr (1957/1958–1997/1998) for the Tuyuksu. We calculated mass losses of −0.20 m w.e. yr (1957/1958–1997/1998), −0.31 m w.e. yr (1997/1998–2015/2016), and −0.24 m w.e. yr (1957/1958–2015/2016) for Golubin. Mean mass balances for monitored Kyrgyz glaciers Batysh Sook (−0.56 m w.e. yr from 2010/2011 to 2019/2020), No. 354 (−0.49 m w.e. yr from 2010/2011 to 2019/2020), Sary Tor (−0.73 m w.e. yr from 2014/2015 to 2019/2020), Bordu (−0.77 m w.e. yr from 2015/2016 to 2019/2020), Karabatkak (−0.43 m w.e. yr from 1957/1958 to 1997/1998), and Abramov (−0.70 m w.e. yr from 2013/2014 to 2019/202020) range between −0.45 m w.e. yr from 1967/1968 to 1997/ 1998 and −0.20 m w.e. yr from 2011/12 to 2019/2020 [25].
Van Tricht et al. [43] reconstructed the mean specific mass balance of Bordu, Kara-Batkak, and Sary-Tor by using a strongly parameterized surface energy mass balance model from 1750 until present. Similarly, their results suggest more positive mass balance at the beginning of the 20th century followed by increasingly negative mass balances, especially from the 1970s onward. In contrast with the here present study, Van Tricht et al. [43] adjusted not only the glacier area but also the thickness over the study period. They showed that initial geometry and considerations for the glacier retreat had a strong influence on glacier mass balance. Their results show more positive mass balance prior to 1900 when using a constant glacier outline and ice thickness (dating from 2017) than when the geometry is adjusted over time. This is expected, given the initial imbalance of the glacier with the climate. This suggests that our results underestimate the mass balance for the first half of the modeled period.
5.5. Limitations
A main limitation of this study is the lack of glacier thickness adjustment over the calculation time. Recent observations and new datasets documenting glacier thickness changes for this region (e.g., [32]) in combination with reinvestigated historical datasets (e.g., [56,57]) are valuable to improve glacier mass balance change assessments over long periods of time in the future.
A dominant source of uncertainty for regional glacier mass balance modeling regards meteorological forcing. The lack of direct calibration data for the mass balance model renders the calculated mass balance time series—prior to 1968/1969—strongly dependent on the input reanalysis data. Reanalyses produced by atmospheric models—with spatial resolutions typically in the range of 10–50 km—represent an essential data source for long-term mass balance modeling and to correct potential biases in future simulations (e.g., [58,59]). Mostly, this requires preliminary downscaling to increase representativeness of local-scale patterns—using ground station data (e.g., [60])—challenged by the lack of in situ meteorological data [4,19]. Among the climate drivers required for mass balance models, precipitation is particularly variable [35,61]. Obtaining accurate precipitation fields for data-sparse regions, such as Tien Shan and Pamir, remains a challenge [62]. Available reanalysis products are thus still connected to high uncertainties for the recent past. These uncertainties increase for earlier time periods, when systematic observations of atmospheric conditions are lacking [63].
More detailed and physical-based models are useful to understand and quantify the role of individual processes linking atmosphere, cryosphere, and hydrosphere (e.g., [64,65]). The downside of such models is the need for high-quality input data and detailed observational data needed for sound calibration and validation. A temperature index melt model is a simple approach able to simulate glacier melt based on few input data. This can be both an advantage and a disadvantage depending on the modeling purpose. To calculate regional glacier response to climate, simple routines are suitable (e.g., [66,67]). Yet, these computationally and data-efficient models suffer from insufficient representation of small-scale processes, using derived empirical or statistical relationships with fixed parameters (e.g., [68]). A weakness of simple approaches for long-term modeling is holding model parameters—such as the degree day factors—constant over a long period of time (1900/1901 to 1968/1969) and space. Modeling glacier mass balance for a long period of time therefore assumes an unchanged relationship between melt factors and atmospheric conditions. Furthermore, simple models often neglect relevant processes (e.g., sublimation and refreezing of meltwater in firn) which can contribute significantly to glacier mass budget [39].
We believe that our chosen simple approach in combination with other observational datasets, such as secular length change observations, are extremely valuable for data-sparse regions and times, such as Golubin, in Kyrgyzstan. For data-sparse regions, a simple model approach is necessary to overcome the hurdle of low-quality input data and lack of data calibration and validation. Finding alternative validation datasets based on historical and modern length change observations allowed us to provide, for the first time, an estimate of long-term glacier mass balance evolution for Golubin within an acceptable uncertainty range.
6. Conclusions
This study provides a unique over 100-year annual mass balance time series for Golubin, integrating repeated meteorological analyses, current and historical glaciological measurements, and observations of length change. Golubin has lost mass substantially over the past century; a mean negative mass balance of −0.16 ± 0.45 m w.e. a for the entire period from 1900/1901 to 2010/21 was reconstructed. Mass loss increased slightly in the second half of the century, with an average mass balance of −0.20 ± 0.42 m w.e. yr from 1949/50 to 2010/21—most negative values were simulated for 2008 and measured positive mass balances since 2018/2019. We found a parallel shift accompanied by a rotation of the mass balance gradients, indicating increasing ablation and less pronounced accumulation. This tendency is believed to intensify in the future, affecting glaciers’ mass balance sensitivity to changes in atmospheric conditions and year-to-year variability. Such changes will result in irregular melt water release feeding the rivers of Ala Archa basin acting as a water tower for the capital city Bishkek. This study provides evidence, for the first time, of changes in the glacier regime of Golubin. However, a lack of suitable direct observations for detailed and process-based understanding of the ongoing adjustment to climate change are still limited.
Author Contributions
Under the supervision of M.B., E.A. performed the mass balance modeling and the data analysis, validation, and interpretation. M.B. conceived the presented idea. M.H., M.B. and R.U. conceived the monitoring network and proposed the methods. M.B., R.U., E.A. and M.H. led the field measurements and capacity-building programs. S.V. provided the reanalysis time series. T.S. supervised M.E.u. when computing secular mass balances from length change. E.A. and M.B. wrote this manuscript with the help of M.H., T.S. and S.V. All authors have read and agreed to the published version of the manuscript.
Funding
This study is supported by Snowline4DailyWater. The project Snowline4DailyWater has received funding from the Autonomous Province of Bozen/Bolzano—Department for Innovation, Research, and University in the frame of the Seal of Excellence Programme. We thank the Federal Office of Meteorology and Climatology MeteoSwiss for financing the project Capacity Building and Twinning for Climate Observing Systems (CATCOS), contract no. 7F-08114.1, between the Swiss Agency for Development and Cooperation and MeteoSwiss; the project Cryospheric Climate Services for improved Adaptation (CICADA), contract no. 81049674; and the project Cryospheric Observation and Modelling for Improved Adaptation in Central Asia (CROMO-ADAPT), contract no. 81072443, between Swiss Agency for Development and Cooperation and the University of Fribourg. The Central Asian Water (CAWa) project was supported by the German Federal Foreign Office, contract no. AA7090002, as part of the Berlin Process. This study was also supported by the Swiss National Science Foundation (SNSF) through the following two projects: Snowline observations to remotely derive seasonal to sub-seasonal glacier mass balance in the Tien Shan and Pamir Mountains, grant 155903, and Changing glacier firn in Central Asia and its impact on glacier mass balance, grant 169453.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Glacier mass balance point measurements and lenght change observations are openly available at the World glacier monitoring https://wgms.ch/ (accessed on 21 April 2022). Landsat imagery and SRTM is available at https://earthexplorer.usgs.gov/ (accessed on 21 April 2022). ASTER imagery is available at https://earthdata.nasa.gov/ (last access: 11 December 2020). Meteorological data from Alplager were obtained from Kyrgyz Hydromet http://meteo.kg (accessed on 21 April 2022). Due to the hydromet institutions’ data policies, the data are not readily available for download from the respective websites but can be requested through the contact links. For modelled annual mass balance time-series please contact the authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aizen, V.B.; Kuzmichenok, V.A.; Surazakov, A.B.; Aizen, E.M. Glacier changes in the central and northern Tien Shan during the last 140 years based on surface and remote-sensing data. Ann. Glaciol. 2006, 43, 202–213. [Google Scholar] [CrossRef]
- Sorg, A.; Huss, M.; Rohrer, M.; Stoffel, M. The days of plenty might soon be over in glacierized Central Asian catchments. Environ. Res. Lett. 2014, 9, 4018. [Google Scholar] [CrossRef]
- Farinotti, D.; Longuevergne, L.; Moholdt, G.; Duethmann, D.; Mölg, T.; Bolch, T.; Vorogushyn, S.; Güntner, A. Substantial glacier mass loss in the Tien Shan over the past 50 years. Nat. Geosci. 2015, 8, 716–722. [Google Scholar] [CrossRef]
- Barandun, M.; Fiddes, J.; Scherler, M.; Mathys, T.; Saks, T.; Petrakov, D.; Hoelzle, M. The state and future of the cryosphere in Central Asia. Water Secur. 2020, 11, 100072. [Google Scholar] [CrossRef]
- Saks, T.; Pohl, E.; Machguth, H.; Dehecq, A.; Barandun, M.; Kenzhebaev, R.; Kalashnikova, O.; Hoelzle, M. Glacier Runoff Variation Since 1981 in the Upper Naryn River Catchments, Central Tien Shan. Front. Environ. Sci. 2022, 9. [Google Scholar] [CrossRef]
- Varis, O. Resources: Curb vast water use in central Asia. Nat. News 2014, 514, 27. [Google Scholar] [CrossRef]
- Kaser, G.; Grosshauser, M. The contribution potential of glaciers to Himalaya river runoff. EGU Gen. Assem. Conf. Abstr. 2010, 12, 10962. [Google Scholar]
- Huss, M.; Hock, R. Global-scale hydrological response to future glacier mass loss. Nat. Clim. Change 2018, 8, 1. [Google Scholar] [CrossRef]
- Zemp, M.; Huss, M.; Thibert, E.; Eckert, N.; McNabb, R.; Huber, J.; Barandun, M.; Machguth, H.; Nussbaumer, S.U.; Gärtner-Roer, I.; et al. Global glacier mass changes and their contributions to sea-level rise from 1961 to 2016. Nature 2019, 568, 382–386. [Google Scholar] [CrossRef]
- Barandun, M.; Pohl, E.; Naegeli, K.; McNabb, R.; Huss, M.; Berthier, E.; Saks, T.; Hoelzle, M. Hot spots of glacier mass balance variability in Central Asia. Geophys. Res. Lett. 2021, 48, e2020GL092084. [Google Scholar] [CrossRef]
- Shean, D.; Bhushan, S.; Montesano, P.; Rounce, D.R.; Arendt, A.; Osmanoğlu, B. A systematic, regional assessment of high mountain Asia glacier mass balance. Front. Earth Sci. 2020, 7, 363. [Google Scholar] [CrossRef]
- Barandun, M.; Huss, M.; Sold, L.; Farinotti, D.; Azisov, E.; Salzmann, N.; Usubaliev, R.; Merkushkin, A.; Hoelzle, M. Re-analysis of seasonal mass balance at Abramov glacier 1968–2014. J. Glaciol. 2015, 61, 1103–1117. [Google Scholar] [CrossRef]
- Barandun, M.; Huss, M.; Usubaliev, R.; Azisov, E.; Berthier, E.; Kääb, A.; Bolch, T.; Hoelzle, M. Multi-decadal mass balance series of three Kyrgyz glaciers inferred from modelling constrained with repeated snow line observations. Cryosphere 2018, 12, 1899–1919. [Google Scholar] [CrossRef]
- Bolch, T. Glacier area and mass changes since 1964 in the Ala Archa Valley, Kyrgyz Ala-Too, northern Tien Shan. Lëd I Sneg 2015, 55, 28–39. [Google Scholar] [CrossRef]
- Brun, F.; Berthier, E.; Wagnon, P.; Kääb, A.; Treichler, D. A spatially resolved estimate of High Mountain Asia glacier mass balances, 2000–2016. Nat. Geosci. 2017, 10, 668. [Google Scholar] [CrossRef]
- Kenzhebaev, R.; Barandun, M.; Kronenberg, M.; Chen, Y.; Usubaliev, R.; Hoelzle, M. Mass balance observations and reconstruction for Batysh Sook Glacier, Tien Shan, from 2004 to 2016. Cold Reg. Sci. Technol. 2017, 135, 76–89. [Google Scholar] [CrossRef]
- Kronenberg, M.; Barandun, M.; Hoelzle, M.; Huss, M.; Farinotti, D.; Azisov, E.; Usubaliev, R.; Gafurov, A.; Petrakov, D.; Kääb, A. Mass-balance reconstruction for Glacier No. 354, Tien Shan, from 2003 to 2014. Ann. Glaciol. 2016, 57, 92–102. [Google Scholar] [CrossRef]
- Pritchard, H.D. Asia’s shrinking glaciers protect large populations from drought stress. Nature 2019, 569, 649–654. [Google Scholar] [CrossRef]
- Unger-Shayesteh, K.; Vorogushyn, S.; Farinotti, D.; Gafurov, A.; Duethmann, D.; Mandychev, A.; Merz, B. What do we know about past changes in the water cycle of Central Asian headwaters? A review. Glob. Planet. Chang. 2013, 110. [Google Scholar] [CrossRef]
- Hoelzle, M.; Azisov, E.; Barandun, M.; Huss, M.; Farinotti, D.; Gafurov, A.; Hagg, W.; Kenzhebaev, R.; Kronenberg, M.; Machguth, H.; et al. Re-establishing glacier monitoring in Kyrgyzstan and Uzbekistan, Central Asia. Geosci. Instrum. Methods Data Syst. 2017, 6, 397. [Google Scholar] [CrossRef]
- Hoelzle, M.; Barandun, M.; Bolch, T.; Fiddes, J.; Gafurov, A.; Muccione, V.; Saks, T.; Shahgedanova, M. The status and role of the alpine cryosphere in Central Asia. In The Aral Sea Basin; Taylor & Francis: Abingdon, UK, 2019. [Google Scholar]
- Huss, M.; Bauder, A.; Funk, M.; Hock, R. Determination of the seasonal mass balance of four Alpine glaciers since 1865. J. Geophys. Res. Earth Surf. 2008, 113. [Google Scholar] [CrossRef]
- Venukov, M. Ocherki Zailiiskogo kraya i Prichuiskoi strany [Essays of Zailiiski region and Prichuiskii country]. Izv. Russ. Geograf. Obshch. 1861, 4, 35–61. [Google Scholar]
- Aizen, V. Reconstruktiya balansa massy lednika Golubina [Golubin glacier mass balance reconstruction]. Mater. Glyatsiol. Issled 1988, 62, 119–126. [Google Scholar]
- WGMS. Fluctuations of Glaciers Database; World Glacier Monitoring Service: Zurich, Switzerland, 2021. [Google Scholar] [CrossRef]
- Schöne, T.; Zech, C.; Unger-Shayesteh, K.; Rudenko, V.; Thoss, H.; Wetzel, H.U.; Gafurov, A.; Illigner, J.; Zubovich, A. A new permanent multi-parameter monitoring network in Central Asian high mountains—From measurements to data bases. Geosci. Instrum. Methods Data Syst. 2013, 2, 97–111. [Google Scholar] [CrossRef]
- Hole-Filled SRTM for the Globe Version 4. CGIAR-CSI SRTM 90m Database. 2008. Available online: http://srtm.csi.cgiar.org/ (accessed on 12 April 2022).
- Paul, F.; Barrand, N.E.; Baumann, S.; Berthier, E.; Bolch, T.; Casey, K.; Frey, H.; Joshi, S.; Konovalov, V.; Le Bris, R.; et al. On the accuracy of glacier outlines derived from remote-sensing data. Ann. Glaciol. 2013, 54, 171–182. [Google Scholar] [CrossRef]
- Poli, P.; Hersbach, H.; Dee, D.P.; Berrisford, P.; Simmons, A.J.; Vitart, F.; Laloyaux, P.; Tan, D.G.; Peubey, C.; Thépaut, J.N.; et al. ERA-20C: An atmospheric reanalysis of the twentieth century. J. Clim. 2016, 29. [Google Scholar] [CrossRef]
- Hoelzle, M.; Haeberli, W.; Dischl, M.; Peschke, W. Secular glacier mass balances derived from cumulative glacier length changes. Glob. Planet. Chang. 2003, 36, 295–306. [Google Scholar] [CrossRef]
- Jóhannesson, T.; Raymond, C.; Waddington, E. A simple method for determining the response time of glaciers. In Glacier Fluctuations and Climatic Change; Springer: Berlin/Heidelberg, Germany, 1989; pp. 343–352. [Google Scholar]
- Van Tricht, L.; Huybrechts, P.; Van Breedam, J.; Fürst, J.J.; Rybak, O.; Satylkanov, R.; Ermenbaiev, B.; Popovnin, V.; Neyns, R.; Paice, C.M.; et al. Measuring and inferring the ice thickness distribution of four glaciers in the Tien Shan, Kyrgyzstan. J. Glaciol. 2021, 67, 269–286. [Google Scholar] [CrossRef]
- Huss, M.; Bauder, A.; Funk, M. Homogenization of long-term mass-balance time series. Ann. Glaciol. 2009, 50, 198–206. [Google Scholar] [CrossRef]
- Hock, R. A distributed temperature-index ice- and snowmelt model including potential direct solar radiation. J. Glaciol. 1999, 45. [Google Scholar] [CrossRef]
- Aizen, V.B.; Aizen, E.M.; Melack, J.M. Climate, snow cover, glaciers, and runoff in the Tien Shan, central Asia. JAWRA J. Am. Water Resour. Assoc. 1995, 31, 1113–1129. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Hodder Arnold: London, UK, 1975. [Google Scholar]
- Hagg, W.; Mayer, C.; Lambrecht, A.; Kriegel, D.; Azizov, E. Glacier changes in the Big Naryn basin, Central Tian Shan. Glob. Planet. Chang. 2013, 110, 40–50. [Google Scholar] [CrossRef]
- Kronenberg, M.; van Pelt, W.; Machguth, H.; Fiddes, J.; Hoelzle, M.; Pertziger, F. Long-term firn and mass balance modelling for Abramov glacier, Pamir Alay. Cryosphere Discuss. 2022, 1–33. [Google Scholar] [CrossRef]
- Rasmussen, L. Meteorological controls on glacier mass balance in High Asia. Ann. Glaciol. 2013, 54, 352–359. [Google Scholar] [CrossRef]
- Aizen, V.B.; Zakharov, V. Mass Balance and Ice Flow Velocity of Davydov Glacier Basing on Research in 1984–1985. Data Glaciol. Stud. 1989, 67, 197–202. [Google Scholar]
- Ushnurtsev, S. Mass balance fluctuations of the Sary-Tor glacier in inner Tien Shan and its reconstruction for the period 1930–1988. Data Glaciol. Stud 1991, 71, 70–79. [Google Scholar]
- Van Tricht, L.; Paice, C.M.; Rybak, O.; Satylkanov, R.; Popovnin, V.; Solomina, O.; Huybrechts, P. Reconstruction of the Historical (1750–2020) Mass Balance of Bordu, Kara-Batkak and Sary-Tor Glaciers in the Inner Tien Shan, Kyrgyzstan. Front. Earth Sci. 2021, 9. [Google Scholar] [CrossRef]
- Dyurgerov, M.; Dwyer, J. ABHANDLUNGEN—The steepening of glacier mass balance gradients with northern hemispere warming. With 6 figures. Z. Gletscherkunde Glazialgeol. 2000, 36, 107–118. [Google Scholar]
- Kuhn, M. Sea level, ice and climatic change: Proceedings of the symposium held 7-8 Dec. 1978. In Climate and Glaciers; Allison, I., Ed.; International Association of Hydrological Sciences: Wallingford, UK, 1980; Volume 131, pp. 3–20. [Google Scholar]
- Kuhn, M. Mass budget imbalances as criterion for a climatic classification of glaciers. Geogr. Ann. Ser. A Phys. Geogr. 1984, 66, 229–238. [Google Scholar] [CrossRef]
- Meier, M.F.; Dyurgerov, M.B.; McCabe, G.J. The health of glaciers: Recent changes in glacier regime. Clim. Chang. 2003, 59, 123–135. [Google Scholar] [CrossRef]
- Dyurgerov, M.B.; Meier, M.F. Twentieth century climate change: Evidence from small glaciers. Proc. Natl. Acad. Sci. USA 2000, 97, 1406–1411. [Google Scholar] [CrossRef] [PubMed]
- Oerlemans, J. Glaciers and Climate Change: A Meteorologist’s View; Balkema Publishers: Lisse, The Netherlands, 2001. [Google Scholar]
- Wang, R.; Liu, S.; Shangguan, D.; Radić, V.; Zhang, Y. Spatial heterogeneity in glacier mass-balance sensitivity across High Mountain Asia. Water 2019, 11, 776. [Google Scholar] [CrossRef]
- Hugonnet, R.; McNabb, R.; Berthier, E.; Menounos, B.; Nuth, C.; Girod, L.; Farinotti, D.; Huss, M.; Dussaillant, I.; Brun, F.; et al. A globally complete, spatiotemporally resolved estimate of glacier mass change from 2000 to 2019. Nature 2021, 592, 726–731. [Google Scholar] [CrossRef]
- Kapitsa, V.; Shahgedanova, M.; Severskiy, I.; Kasatkin, N.; White, K.; Usmanova, Z. Assessment of Changes in Mass Balance of the Tuyuksu Group of Glaciers, Northern Tien Shan, Between 1958 and 2016 Using Ground-Based Observations and Pléiades Satellite Imagery. Front. Earth Sci. 2020, 8, 259. [Google Scholar] [CrossRef]
- Shea, J.; Menounos, B.; Moore, R.D.; Tennant, C. Regional estimates of glacier mass change from MODIS-derived equilibrium line altitudes. Cryosphere Discuss. 2012, 6, 3757–3780. [Google Scholar]
- Kääb, A.; Treichler, D.; Nuth, C.; Berthier, E. Brief Communication: Contending estimates of 2003–2008 glacier mass balance over the Pamir–Karakoram–Himalaya. Cryosphere 2015, 9, 557–564. [Google Scholar] [CrossRef]
- Hagg, W.J.; Braun, L.N.; Uvarov, V.N.; Makarevich, K.G. A comparison of three methods of mass-balance determination in the Tuyuksu glacier region, Tien Shan, Central Asia. J. Glaciol. 2004, 50, 505–510. [Google Scholar] [CrossRef]
- Denzinger, F.; Machguth, H.; Barandun, M.; Berthier, E.; Girod, L.; Kronenberg, M.; Usubaliev, R.; Hoelzle, M. Geodetic mass balance of Abramov Glacier from 1975 to 2015. J. Glaciol. 2021, 67, 331–342. [Google Scholar] [CrossRef]
- Kronenberg, M.; Machguth, H.; Eichler, A.; Schwikowski, M.; Hoelzle, M. Comparison of historical and recent accumulation rates on Abramov Glacier, Pamir Alay. J. Glaciol. 2021, 67, 253–268. [Google Scholar] [CrossRef]
- Maussion, F.; Scherer, D.; Mölg, T.; Collier, E.; Curio, J.; Finkelnburg, R. Precipitation seasonality and variability over the Tibetan Plateau as resolved by the High Asia Reanalysis. J. Clim. 2014, 27, 1910–1927. [Google Scholar] [CrossRef]
- Pereira-Cardenal, S.; Riegels, N.; Berry, P.; Smith, R.; Yakovlev, A.; Siegfried, T.; Bauer-Gottwein, P. Real-time remote sensing driven river basin modeling using radar altimetry. Hydrol. Earth Syst. Sci. 2011, 15, 241–254. [Google Scholar] [CrossRef]
- Fiddes, J.; Gruber, S. TopoSCALE v. 1.0: Downscaling gridded climate data in complex terrain. Geosci. Model Dev. 2014, 7, 387–405. [Google Scholar] [CrossRef]
- Roe, G.H.; Montgomery, D.R.; Hallet, B. Orographic precipitation and the relief of mountain ranges. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef]
- Shahgedanova, M.; Afzal, M.; Hagg, W.; Kapitsa, V.; Kasatkin, N.; Mayr, E.; Rybak, O.; Saidaliyeva, Z.; Severskiy, I.; Usmanova, Z.; et al. Emptying water towers? Impacts of future climate and glacier change on river discharge in the northern Tien Shan, Central Asia. Water 2020, 12, 627. [Google Scholar] [CrossRef]
- Zandler, H.; Haag, I.; Samimi, C. Evaluation needs and temporal performance differences of gridded precipitation products in peripheral mountain regions. Sci. Rep. 2019, 9, 1–15. [Google Scholar] [CrossRef]
- Mölg, T.; Maussion, F.; Scherer, D. Mid-latitude westerlies as a driver of glacier variability in monsoonal High Asia. Nat. Clim. Chang. 2014, 4, 68. [Google Scholar] [CrossRef]
- Ayala, A.; Pellicciotti, F.; MacDonell, S.; McPhee, J.; Burlando, P. Patterns of glacier ablation across North-Central Chile: Identifying the limits of empirical melt models under sublimation-favorable conditions. Water Resour. Res. 2017, 53, 5601–5625. [Google Scholar] [CrossRef]
- Lutz, A.; Immerzeel, W.; Shrestha, A.; Bierkens, M. Consistent increase in High Asia’s runoff due to increasing glacier melt and precipitation. Nat. Clim. Chang. 2014, 4, 587–592. [Google Scholar] [CrossRef]
- Immerzeel, W.; Wanders, N.; Lutz, A.; Shea, J.; Bierkens, M. Reconciling high-altitude precipitation in the upper Indus basin with glacier mass balances and runoff. Hydrol. Earth Syst. Sci. 2015, 19, 4673–4687. [Google Scholar] [CrossRef]
- Rounce, D.R.; Hock, R.; Shean, D.E. Glacier Mass Change in High Mountain Asia Through 2100 Using the Open-Source Python Glacier Evolution Model (PyGEM). Front. Earth Sci. 2020, 7, 331. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).