Triskeles and Symmetries of Mean Global Sea-Level Pressure
Abstract
:1. Introduction
2. The Singular Spectrum Analysis Method
2.1. Step 1 (Embedding Step)
2.2. Step 2 (Decomposition in Singular Values—SVD)
2.3. Step 3 (Reconstruction)
2.4. Step 4 (the Diagonal Mean, or Hankelization Step)
3. The SLP Data
4. The SSA of SLP Data
5. A Model
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lorentz, E.N. The Nature and Theory of the General Circulation of the Atmosphere; WMO 218, TP-115; World Meteorological Organization: Geneva, Switzerland, 1967; 161p. [Google Scholar]
- Lindzen, R.S.; Hou, A.V. Hadley circulations for zonally averaged heating centered off the equator. J. Atmos. Sci. 1988, 45, 2416–2427. [Google Scholar] [CrossRef]
- Hadley, G. VI. Concerning the cause of the general trade-winds. Philos. Trans. R. Soc. 1735, 39, 58–62. [Google Scholar]
- Ferrel, W. Essay on the winds and ocean currents. Nashv. J. Med. Surg. 1856, 11, 287–301. [Google Scholar]
- Jeffreys, H. On the dynamics of geostrophic winds. Q. J. R. Meteor. Soc. 1926, 52, 85–104. [Google Scholar] [CrossRef]
- Starr, V.P. An essay on the general circulation of the earth atmosphere. J. Atmos. Sci. 1948, 5, 39–43. [Google Scholar]
- Schneider, E.K. Axially symmetric steady-state models of the basic state for instability and climate studies. Part II, Nonlinear calculations. J. Atmos. Sci. 1977, 34, 280–296. [Google Scholar] [CrossRef]
- Schneider, E.K.; Lindzen, R.S. Axially symmetric steady-state models of the basic state for instability and climate studies. Part I. Linearized calculations. J. Atmos. Sci. 1977, 34, 263–279. [Google Scholar] [CrossRef]
- Usoskin, I.G.; Solanki, S.K.; Schüssler, M.; Mursula, K.; Alanko, K. Millennium-scale sunspot number reconstruction: Evidence for an unusually active Sun since the 1940s. Phys. Rev. Lett. 2003, 91, 211101. [Google Scholar] [CrossRef] [PubMed]
- Solanki, S.K.; Usoskin, I.G.; Kromer, B.; Schüssler, M.; Beer, J. Unusual activity of the Sun during recent decades compared to the previous 11,000 years. Nature 2004, 431, 1084–1087. [Google Scholar] [CrossRef]
- Lockwood, M.; Owens, M.J.; Barnard, L.; Davis, C.J.; Steinhilber, F. The persistence of solar activity indicators and the descent of the Sun into Maunder Minimum conditions. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Vieira, L.E.A.; Solanki, S.K.; Krivova, N.A.; Usoskin, I. Evolution of the solar irradiance during the Holocene. Astron. Astrophys. 2011, 531, A6. [Google Scholar] [CrossRef]
- Abreu, J.A.; Beer, J.; Ferriz-Mas, A.; McCracken, K.G.; Steinhilber, F. Is there a planetary influence on solar activity? Astron. Astrophys. 2012, 548, A88. [Google Scholar] [CrossRef]
- Kutiev, I.; Tsagouri, I.; Perrone, L.; Pancheva, D.; Mukhtarov, P.; Mikhailov, A.; Lastovicka, J.; Jakowski, N.; Buresova, D.; Blanch, E. et al. Solar activity impact on the Earth’s upper atmosphere. J. Space Weather. Space Clim. 2013, 3, A06. [Google Scholar] [CrossRef] [Green Version]
- Thuillier, G.; Bolsée, D.; Schmidtke, G.; Foujols, T.; Nikutowski, B.; Shapiro, A.I.; Brunner, R.; Weber, M.; Erhardt, C.; Hersé, M.; et al. The solar irradiance spectrum at solar activity minimum between solar cycles 23 and 24. Sol. Phys. 2014, 289, 1931–1958. [Google Scholar] [CrossRef]
- Le Mouël, J.L.; Lopes, F.; Courtillot, V. Characteristic time scales of decadal to centennial changes in global surface temperatures over the past 150 years. Earth Space Sci. 2020, 7, e2019EA000671. [Google Scholar] [CrossRef]
- Le Mouël, J.L.; Lopes, F.; Courtillot, V. Solar turbulence from sunspot records. Mon. Not. R. Astron. Soc. 2020, 492, 1416–1420. [Google Scholar] [CrossRef]
- Courtillot, V.; Lopes, F.; Le Mouël, J.L. On the prediction of solar cycles. Sol. Phys. 2021, 296, 1–23. [Google Scholar] [CrossRef]
- Barnes, R.T.H.; Hide, R.; White, A.A.; Wilson, C.A. Atmospheric angular momentum fluctuations, length-of-day changes and polar motion. Proc. R. Soc. A Math. Phys. Sci. 1983, 387, 31–73. [Google Scholar]
- Rochester, M.G. Causes of fluctuations in the rotation of the Earth. Philos. Trans. R. Soc. Ser. A Math. Phys. Sci. 1984, 313, 95–105. [Google Scholar]
- Lambeck, K. The Earth’s Variable Rotation: Geophysical Causes and Consequences; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Schindelegger, M.; Böhm, S.; Böhm, J.; Schuh, H. Atmospheric effects on Earth rotation. In Atmospheric Effects in Space Geodesy; Springer: Berlin/Heidelberg, Germany, 2013; pp. 181–231. [Google Scholar]
- Lopes, F.; Le Mouël, J.L.; Gibert, D. The mantle rotation pole position. A solar component. Comptes Rendus Geosci. 2017, 349, 159–164. [Google Scholar] [CrossRef]
- Barkin, M.Y.; Krylov, S.S.; Perepelkin, V.V. Modeling and analysis of the Earth pole motion with nonstationary perturbations. J. Phys. Conf. Ser. 2019, 1301, 012005. [Google Scholar] [CrossRef]
- Le Mouël, J.L.; Lopes, F.; Courtillot, V.; Gibert, D. On forcings of length of day changes: From 9-day to 18.6-year oscillations. Phys. Earth Planet. Inter. 2019, 292, 1–11. [Google Scholar] [CrossRef]
- Krylov, S.S.; Perepelkin, V.V.; Filippova, A.S. Long-Period Lunar Perturbations in Earth Pole Oscillatory Process: Theory. In Advances in Theory and Practice of Computational Mechanics: Proceedings of the 21st International Conference on Computational Mechanics and Modern Applied Software Systems; Springer Nature: Singapore, 2020; Volume 173, p. 315. [Google Scholar]
- Le Mouël, J.L.; Lopes, F.; Courtillot, V. Sea-Level Change at the Brest (France) Tide Gauge and the Markowitz Component of Earth’s Rotation. J. Coast. Res. 2021, 37, 683–690. [Google Scholar] [CrossRef]
- Lopes, F.; Le Mouël, J.L.; Courtillot, V.; Gibert, D. On the shoulders of Laplace. Phys. Earth Planet. Inter. 2021, 316, 106693. [Google Scholar] [CrossRef]
- Mörth, H.T.; Schlamminger, L. Planetary motion, sunspots and climate. In Solar-Terrestrial Influences on Weather and Climate; Springer: Dordrecht, The Netherlands, 1979; pp. 193–207. [Google Scholar]
- Lindzen, R.S. Climate dynamics and global change. Annu. Rev. Fluid Mech. 1994, 26, 353–378. [Google Scholar] [CrossRef]
- Gray, L.J.; Beer, J.; Geller, M.; Haigh, J.D.; Lockwood, M.; Matthes, K.; Cubasch, U.; Fleitmann, D.; Harrison, G.; Hood, L.; et al. Solar influences on climate. Rev. Geophys. 2010, 48. [Google Scholar] [CrossRef]
- Gray, L.J.; Scaife, A.A.; Mitchell, D.M.; Osprey, S.; Ineson, S.; Hardiman, S.; Butchart, N.; Knight, J.; Sutton, R.; Kodera, K. A lagged response to the 11 year solar cycle in observed winter Atlantic/European weather patterns. J. Geophys. Res. Atmos. 2013, 118, 13–405. [Google Scholar] [CrossRef]
- Roy, I.; Haigh, J.D. Solar cycle signals in sea level pressure and sea surface temperature. Atmos. Chem. Phys. 2010, 10, 3147–3153. [Google Scholar] [CrossRef]
- Johnstone, J.A.; Mantua, N.J. Atmospheric controls on northeast Pacific temperature variability and change, 1900–2012. Proc. Natl. Acad. Sci. USA 2014, 111, 14360–14365. [Google Scholar] [CrossRef]
- Le Mouël, J.L.; Lopes, F.; Courtillot, V. A solar signature in many climate indices. J. Geophys. Res. Atmos. 2019, 124, 2600–2619. [Google Scholar] [CrossRef]
- Gruzdev, A.N.; Bezverkhnii, V.A. Manifestation of the 11-year solar cycle in the North Atlantic climate. In Proceedings of the IOP Conference Series: Earth and Environmental Science—Climate Change: Causes, Risks, Consequences, Problems of Adaptation and Management, Moscow, Russia, 26–28 November 2019; Volume 606, p. 012018. [Google Scholar]
- Cionco, R.G.; Kudryavtsev, S.M.; Soon, W.H. Possible Origin of Some Periodicities Detected in Solar-Terrestrial Studies: Earth’s Orbital Movements. Earth Space Sci. 2021, 8, e2021EA001805. [Google Scholar] [CrossRef]
- Connolly, R.; Soon, W.; Connolly, M.; Baliunas, S.; Berglund, J.; Butler, C.J.; Cionco, R.G.; Elias, A.G.; Fedorov, V.M.; Harde, H.; et al. How much has the Sun influenced Northern Hemisphere temperature trends? An ongoing debate. Res. Astron. Astrophys. 2021, 21, 131. [Google Scholar] [CrossRef]
- Drews, A.; Huo, W.; Matthes, K.; Kodera, K.; Kruschke, T. The Sun’s Role for Decadal Climate Predictability in the North Atlantic. Atmos. Chem. Phys. Discuss. 2021, 22, 7893–7904. [Google Scholar] [CrossRef]
- Sonechkin, D.M.; Vakulenko, N.V. Polyphony of Short-Term Climatic Variations. Atmosphere 2021, 12, 1145. [Google Scholar] [CrossRef]
- Lindzen, R.S. On a calculation of the symmetric circulation and its implications for the role of eddies. Gen. Circ.-Theory Model. Obs. 1978, 257–281. [Google Scholar]
- Chang, E.K. The influence of Hadley circulation intensity changes on extratropical climate in an idealized model. J. Atmos. Sci. 1995, 52, 2006–2024. [Google Scholar] [CrossRef]
- Dima, I.M.; Wallace, J.M. On the seasonality of the Hadley cell. J. Atmos. Sci. 2003, 60, 1522–1527. [Google Scholar] [CrossRef]
- Frierson, D.M.; Lu, J.; Chen, G. Width of the Hadley cell in simple and comprehensive general circulation models. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Hu, Y.; Fu, Q. Observed poleward expansion of the Hadley circulation since 1979. Atmos. Chem. Phys. 2007, 7, 5229–5236. [Google Scholar] [CrossRef]
- Kharin, V.V.; Zwiers, F.W.; Zhang, X.; Hegerl, G.C. Changes in temperature and precipitation extremes in the IPCC ensemble of global coupled model simulations. J. Clim. 2017, 20, 1419–1444. [Google Scholar] [CrossRef]
- Lu, J.; Vecchi, G.A.; Reichler, T. Expansion of the Hadley cell under global warming. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Tandon, N.F.; Gerber, E.P.; Sobel, A.H.; Polvani, L.M. Understanding Hadley cell expansion versus contraction: Insights from simplified models and implications for recent observations. J. Clim. 2013, 26, 4304–4321. [Google Scholar] [CrossRef]
- Shepherd, T.G. Atmospheric circulation as a source of uncertainty in climate change projections. Nat. Geosci. 2014, 7, 703–708. [Google Scholar] [CrossRef]
- Tao, L.; Hu, Y.; Liu, J. Anthropogenic forcing on the Hadley circulation in CMIP5 simulations. Clim. Dyn. 2016, 46, 3337–3350. [Google Scholar] [CrossRef]
- Grise, K.M.; Davis, S.M. Hadley cell expansion in CMIP6 models. Atmos. Chem. Phys. 2020, 20, 5249–5268. [Google Scholar] [CrossRef]
- Schaeffer, M.; Selten, F.M.; Opsteegh, J.D. Shifts of means are not a proxy for changes in extreme winter temperatures in climate projections. Clim. Dyn. 2005, 25, 51–63. [Google Scholar] [CrossRef]
- Stott, P.A.; Gillett, N.P.; Hegerl, G.C.; Karoly, D.J.; Stone, D.A.; Zhang, X.; Zwiers, F. Detection and attribution of climate change: A regional perspective. Wiley Interdiscip. Rev. Clim. Chang. 2010, 1, 192–211. [Google Scholar] [CrossRef]
- Rahmstorf, S.; Coumou, D. Increase of extreme events in a warming world. Proc. Natl. Acad. Sci. USA 2011, 108, 17905–17909. [Google Scholar] [CrossRef]
- Rummukainen, M. Changes in climate and weather extremes in the 21st century. Wiley Interdiscip. Rev. Clim. Chang. 2012, 3, 115–129. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T.; Shepherd, T.G. Attribution of climate extreme events. Nat. Clim. Chang. 2015, 5, 725–730. [Google Scholar] [CrossRef]
- Vaideanu, P.; Dima, M.; Pirloaga, R.; Ionita, M. Disentangling and quantifying contributions of distinct forcing factors to the observed global sea level pressure field. Clim. Dyn. 2020, 54, 1453–1467. [Google Scholar] [CrossRef]
- Golyandina, N.; Zhigljavsky, A. Singular Spectrum Analysis for Time Series; Springer: Berlin/Heidelberg, Germany, 2013; Volume 120. [Google Scholar]
- Vautard, R.; Ghil, M. Singular spectrum analysis in nonlinear dynamics, with applications to paleoclimatic time series. Phys. D Nonlinear Phenom. 1989, 35, 395–424. [Google Scholar] [CrossRef]
- Ghil, M.; Vautard, R. Interdecadal oscillations and the warming trend in global temperature time series. Nature 1991, 350, 324–327. [Google Scholar] [CrossRef]
- Vautard, R.; Yiou, P.; Ghil, M. Singular-spectrum analysis: A toolkit for short, noisy chaotic signals. Phys. D Nonlinear Phenom. 1992, 58, 95–126. [Google Scholar] [CrossRef]
- Mañé, R. On the dimension of the compact invariant sets of certain non-linear maps. In Dynamical Systems and Turbulence; Warwick: St. Charles, IL, USA, 1980; Springer: Berlin/Heidelberg, Germany, 1981; pp. 230–242. [Google Scholar]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence; Warwick: St. Charles, IL, USA, 1980; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Lemmerling, P.; Van Huffel, S. Analysis of the structured total least squares problem for Hankel/Toeplitz matrices. Numer. Algorithms 2001, 27, 89–114. [Google Scholar] [CrossRef]
- Golub, G.H.; Reinsch, C. Singular value decomposition and least squares solutions. In Linear Algebra; Springer: Berlin/Heidelberg, Germany, 1971; pp. 134–151. [Google Scholar]
- Allan, R.; Ansell, T. A new globally complete monthly historical gridded mean sea level pressure dataset (HadSLP2): 1850–2004. J. Clim. 2006, 19, 5816–5842. [Google Scholar] [CrossRef] [Green Version]
- Marshall, G.J. Trends in the Southern Annular Mode from observations and reanalyses. J. Clim. 2003, 16, 4134–4143. [Google Scholar] [CrossRef]
- Gillett, N.P.; Kell, T.D.; Jones, P.D. Regional climate impacts of the Southern Annular Mode. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Jose, P.D. Sun’s motion and sunspots. Astron. J. 1965, 70, 193–200. [Google Scholar] [CrossRef]
- Gleissberg, W. A long-periodic fluctuation of the sunspot numbers. Observatory 1939, 62, 158. [Google Scholar]
- Le Mouël, J.L.; Lopes, F.; Courtillot, V. Identification of Gleissberg cycles and a rising trend in a 315-year-long series of sunspot numbers. Sol. Phys. 2017, 292, 43. [Google Scholar] [CrossRef]
- Usoskin, I.G. A history of solar activity over millennia. Living Reviews. Sol. Phys. 2017, 14, 1–97. [Google Scholar]
- Schwabe, H. Sonnen-Beobachtungen im Jahre 1843. Astron. Nachr. 1844, 21, 233–236. [Google Scholar] [CrossRef]
- Courtillot, V.; Le Mouël, J.-L.; Lopes, F.; Gibert, D. On the Nature and Origin of Atmospheric Annual and Semi-Annual Oscillations. arXiv 2022, arXiv:2206.12133. [Google Scholar]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Oxford University Press: Oxford, UK, 1961. [Google Scholar]
- Frisch, U.; Kolmogorov, A.N. Turbulence: The Legacy of AN Kolmogorov; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Taylor, G.I. VIII. Stability of a viscous liquid contained between two rotating cylinders. Philos. Trans. R. Soc. Ser. A Contain. Pap. Math. Phys. Character 1923, 223, 289–343. [Google Scholar]
- Schrauf, G. The first instability in spherical Taylor–Couette flow. J. Fluid Mech. 1986, 166, 287–303. [Google Scholar] [CrossRef]
- Mamun, C.K.; Tuckerman, L.S. Asymmetry and Hopf bifurcation in spherical Couette flow. Phys. Fluids 1995, 7, 80–91. [Google Scholar] [CrossRef]
- Nakabayashi, K.; Tsuchida, Y. Flow-history effect on higher modes in the spherical Couette system. J. Fluid Mech. 1995, 295, 43–60. [Google Scholar] [CrossRef]
- Hollerbach, R.; Junk, M.; Egbers, C. Non-axisymmetric instabilities in basic state spherical Couette flow. Fluid Dyn. Res. 2006, 38, 257. [Google Scholar] [CrossRef]
- Mahloul, M.; Mahamdia, A.; Kristiawan, M. The spherical Taylor–Couette flow. Eur. J. Mech. B Fluids 2016, 59, 1–6. [Google Scholar] [CrossRef]
- Garcia, F.; Seilmayer, M.; Giesecke, A.; Stefani, F. Modulated rotating waves in the magnetised spherical Couette system. J. Nonlinear Sci. 2019, 29, 2735–2759. [Google Scholar] [CrossRef]
- Mannix, P.M.; Mestel, A.J. Bistability and hysteresis of axisymmetric thermal convection between differentially rotating spheres. J. Fluid Mech. 2021, 911, A12. [Google Scholar] [CrossRef]
- Forbes, L.K.; Bassom, A.P. Interfacial behaviour in two-fluid Taylor–Couette flow. Q. J. Mech. Appl. Math. 2018, 71, 79–97. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Gubbins, D.; Bloxham, J. Morphology of the geomagnetic field and implications for the geodynamo. Nature 1987, 325, 509–511. [Google Scholar] [CrossRef]
- Gubbins, D.; Kelly, P. Persistent patterns in the geomagnetic field over the past 2.5 Myr. Gubbins 1993, 365, 829–832. [Google Scholar] [CrossRef]
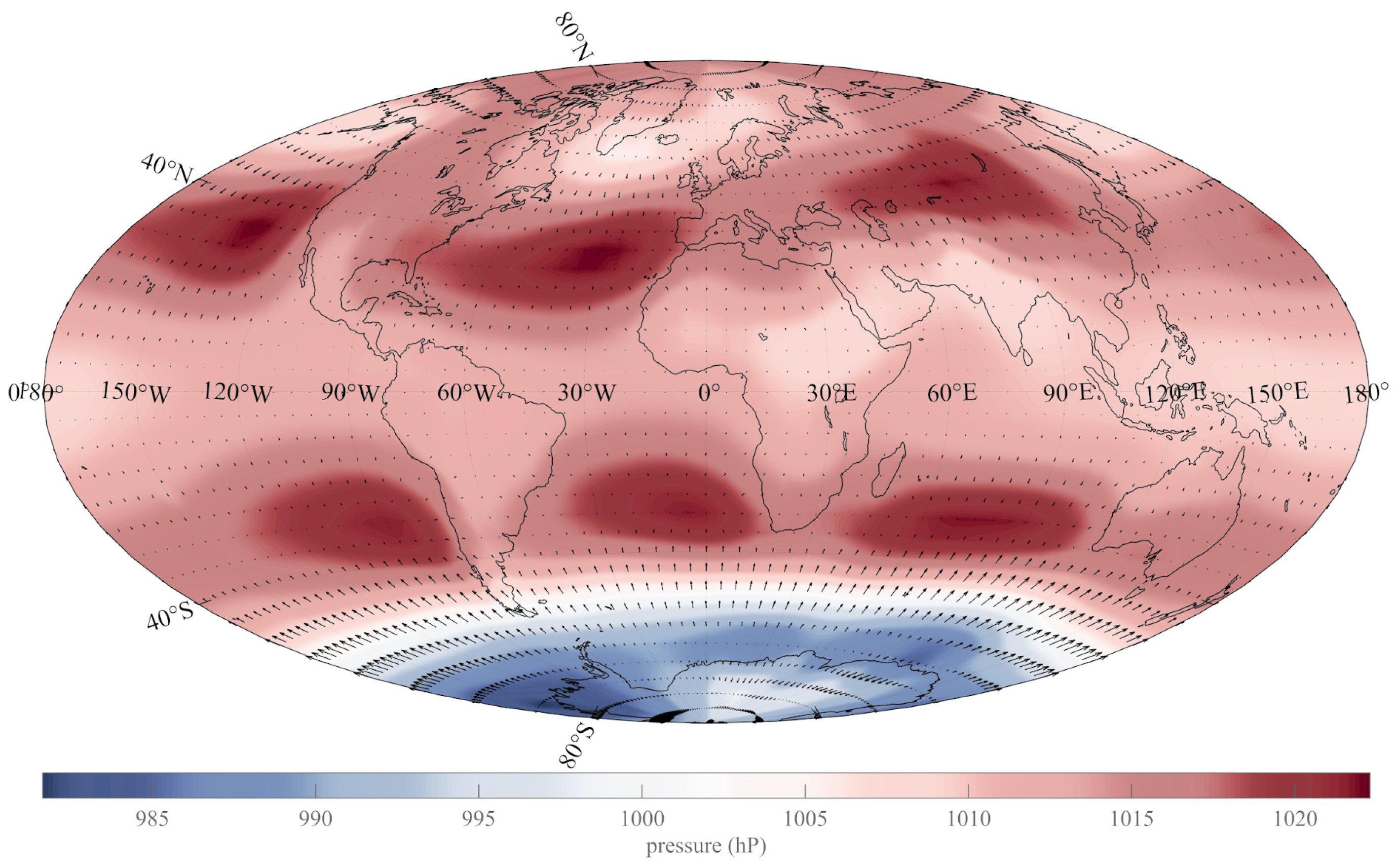
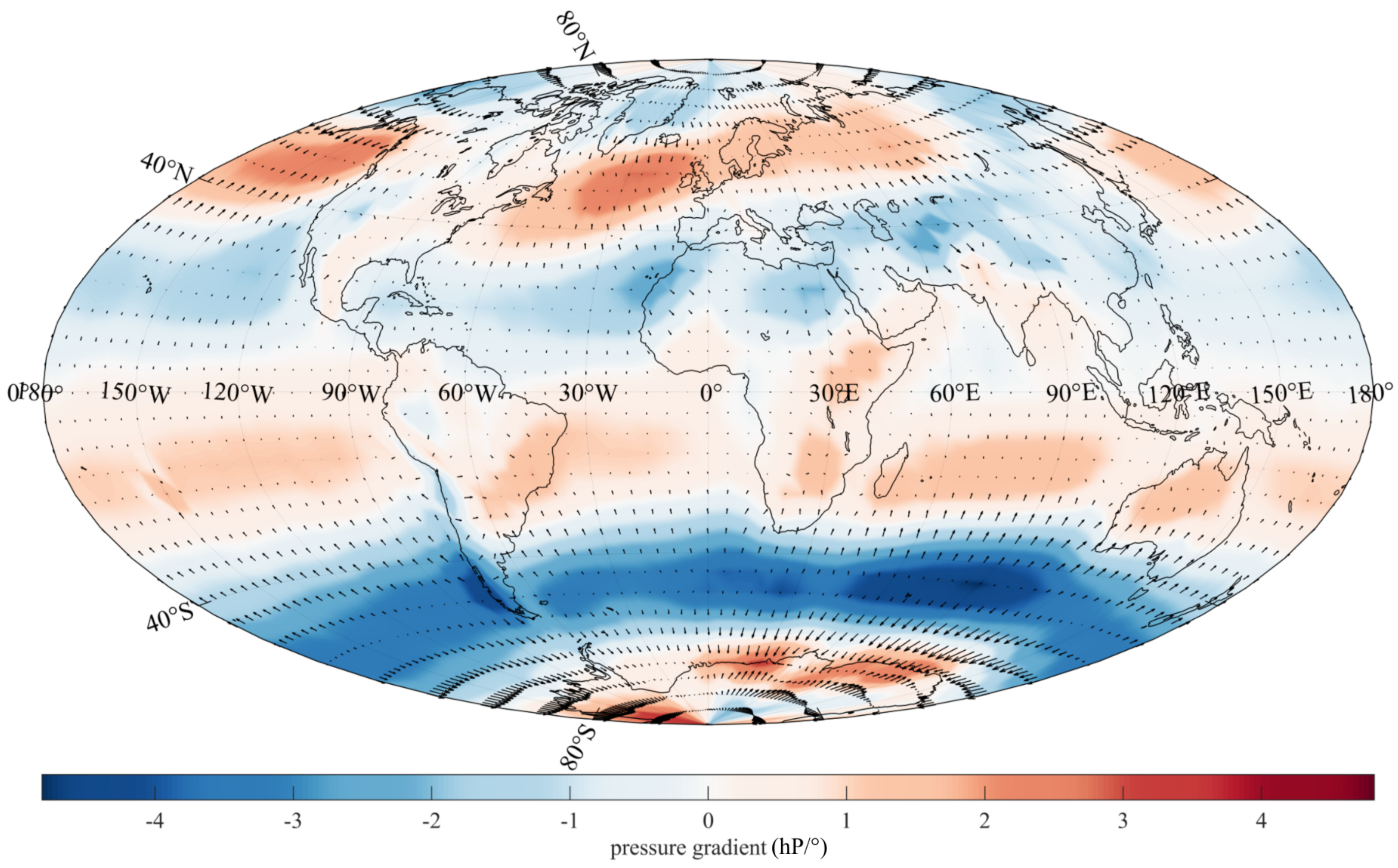
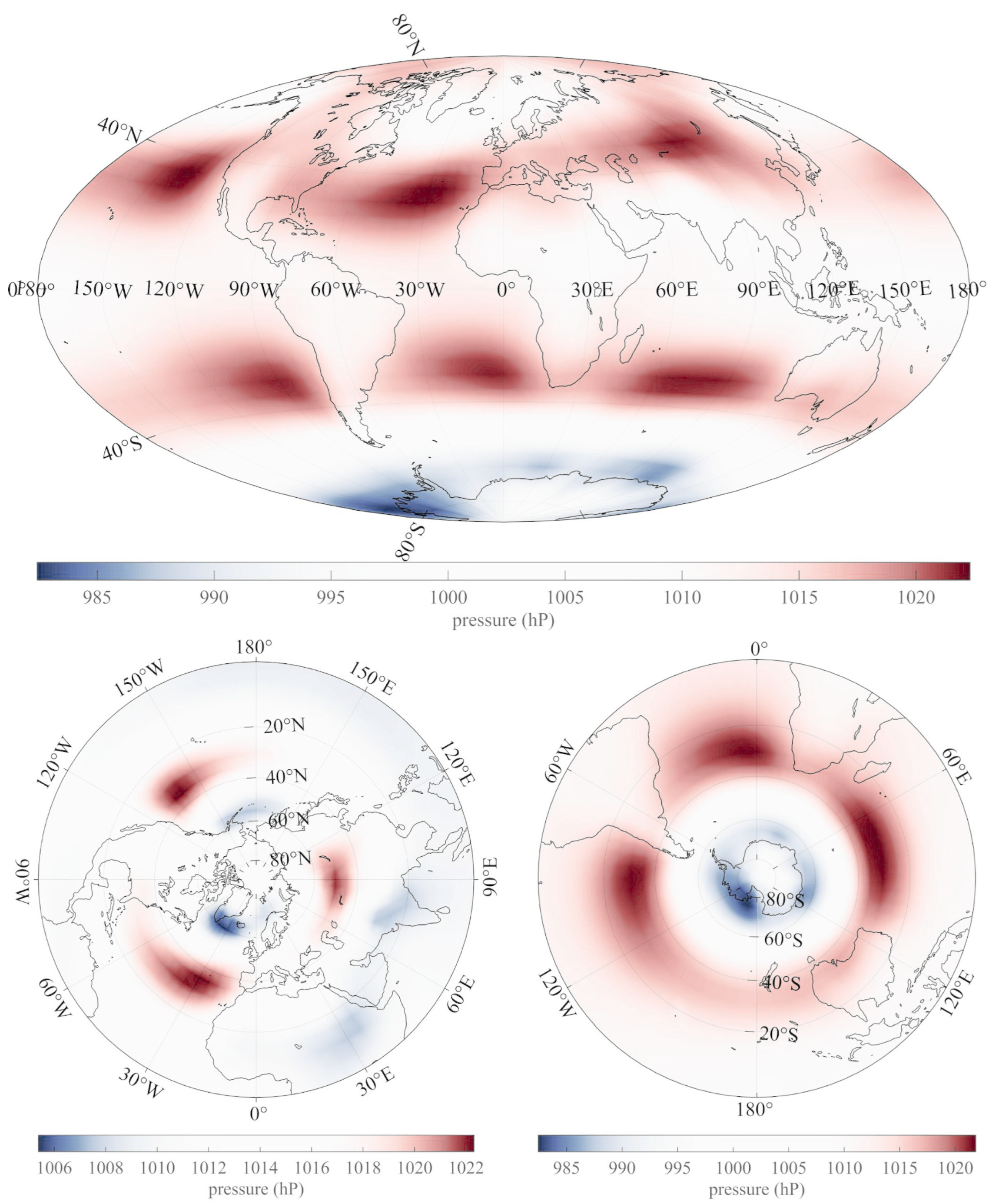
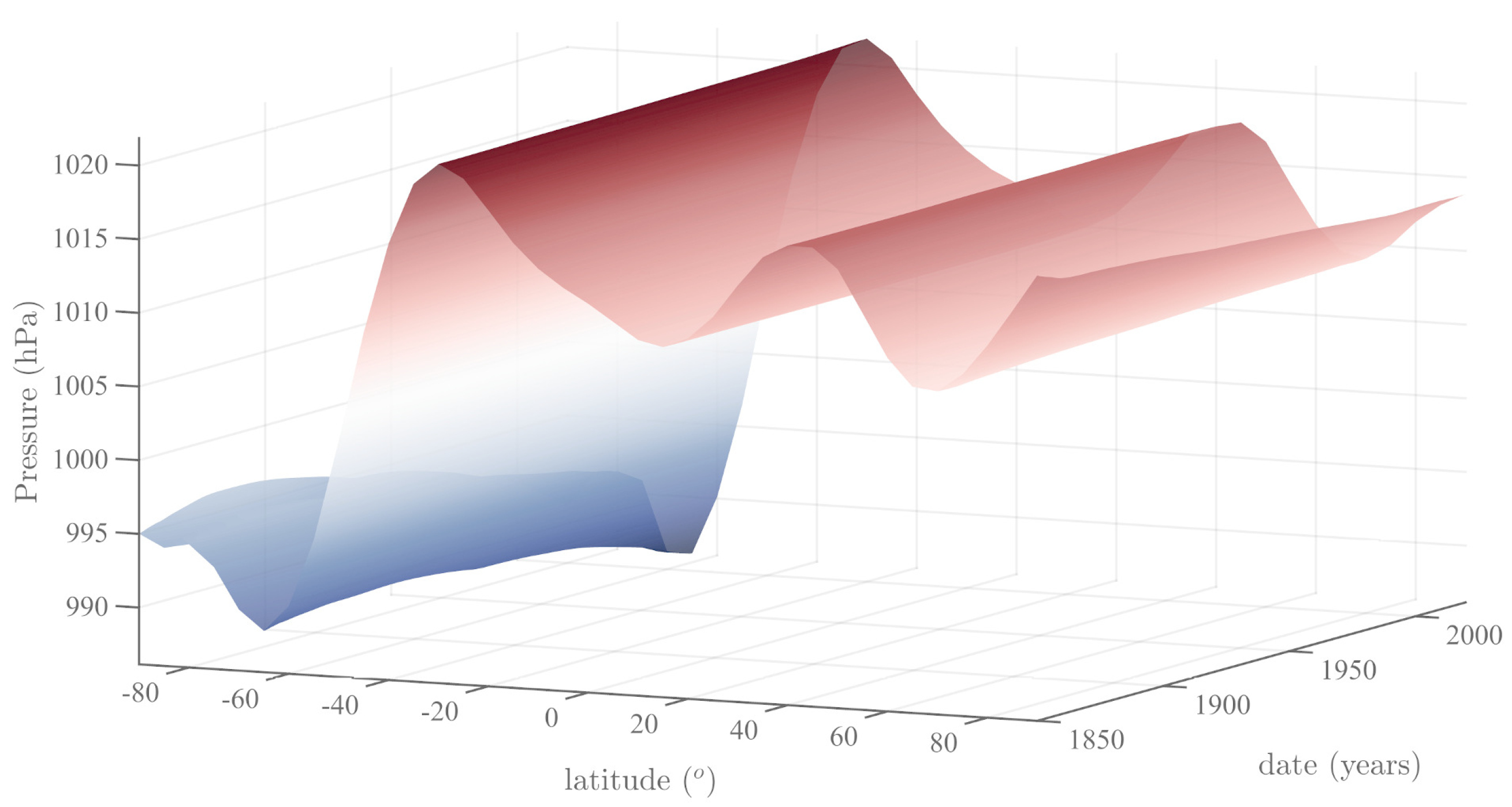

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopes, F.; Courtillot, V.; Le Mouël, J.-L. Triskeles and Symmetries of Mean Global Sea-Level Pressure. Atmosphere 2022, 13, 1354. https://doi.org/10.3390/atmos13091354
Lopes F, Courtillot V, Le Mouël J-L. Triskeles and Symmetries of Mean Global Sea-Level Pressure. Atmosphere. 2022; 13(9):1354. https://doi.org/10.3390/atmos13091354
Chicago/Turabian StyleLopes, Fernando, Vincent Courtillot, and Jean-Louis Le Mouël. 2022. "Triskeles and Symmetries of Mean Global Sea-Level Pressure" Atmosphere 13, no. 9: 1354. https://doi.org/10.3390/atmos13091354
APA StyleLopes, F., Courtillot, V., & Le Mouël, J.-L. (2022). Triskeles and Symmetries of Mean Global Sea-Level Pressure. Atmosphere, 13(9), 1354. https://doi.org/10.3390/atmos13091354




