Sensitivity of Land Surface Processes and Its Variation during Contrasting Seasons over India
Abstract
:1. Introduction
2. Methodology and Data Used
2.1. Model Description
2.2. Methodology
3. Results and Discussion
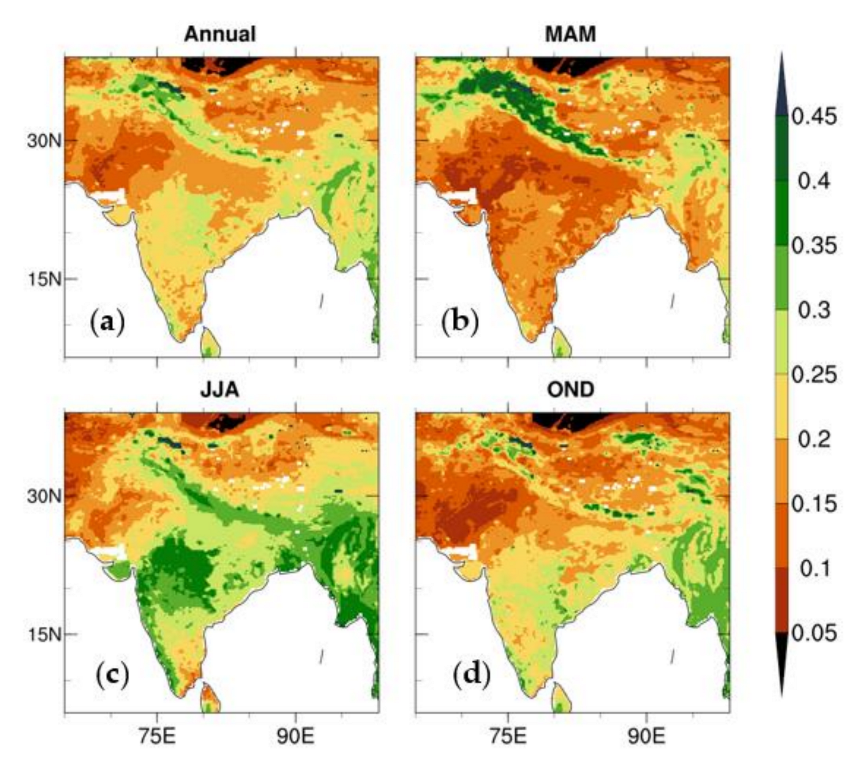
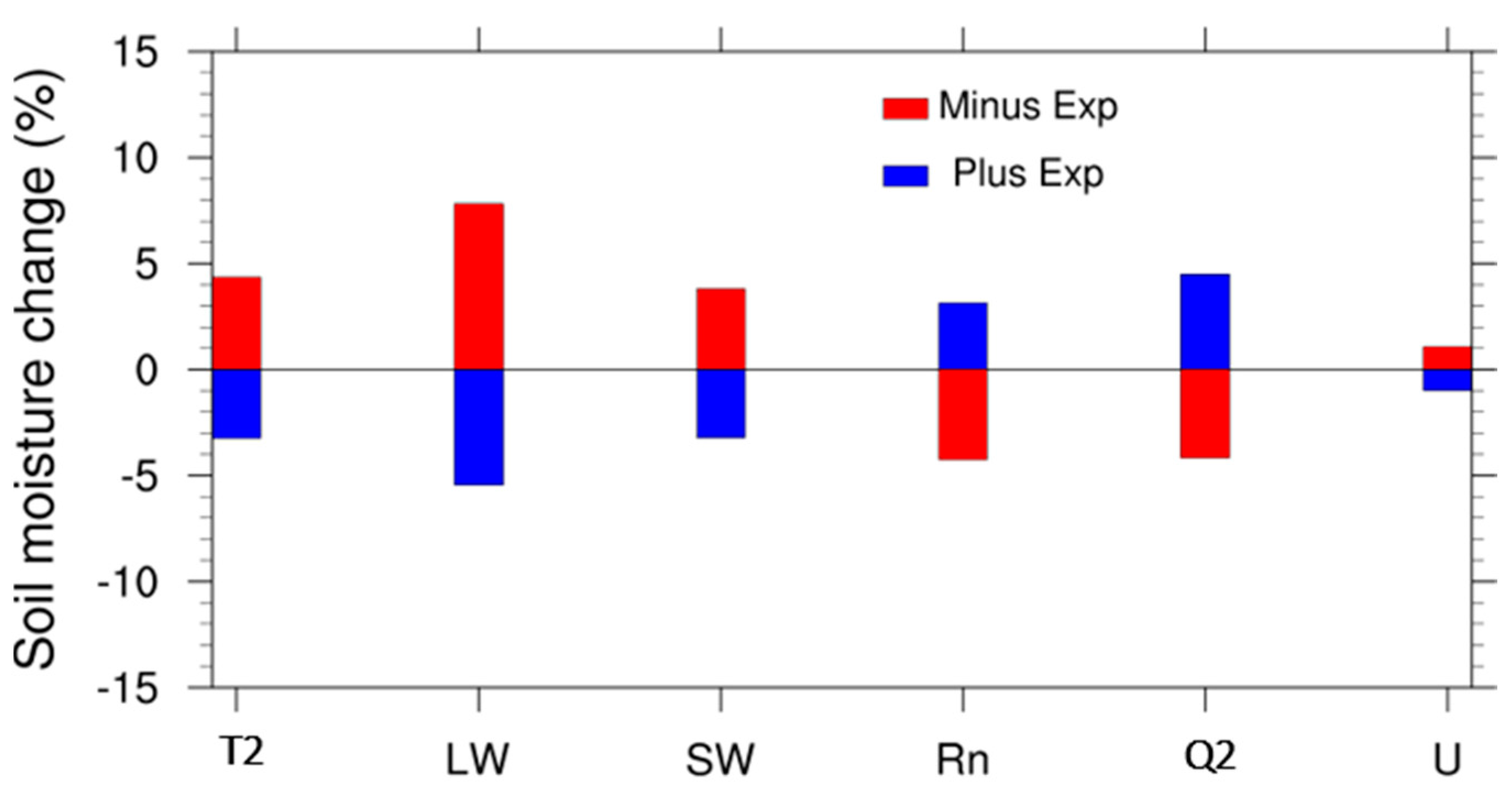
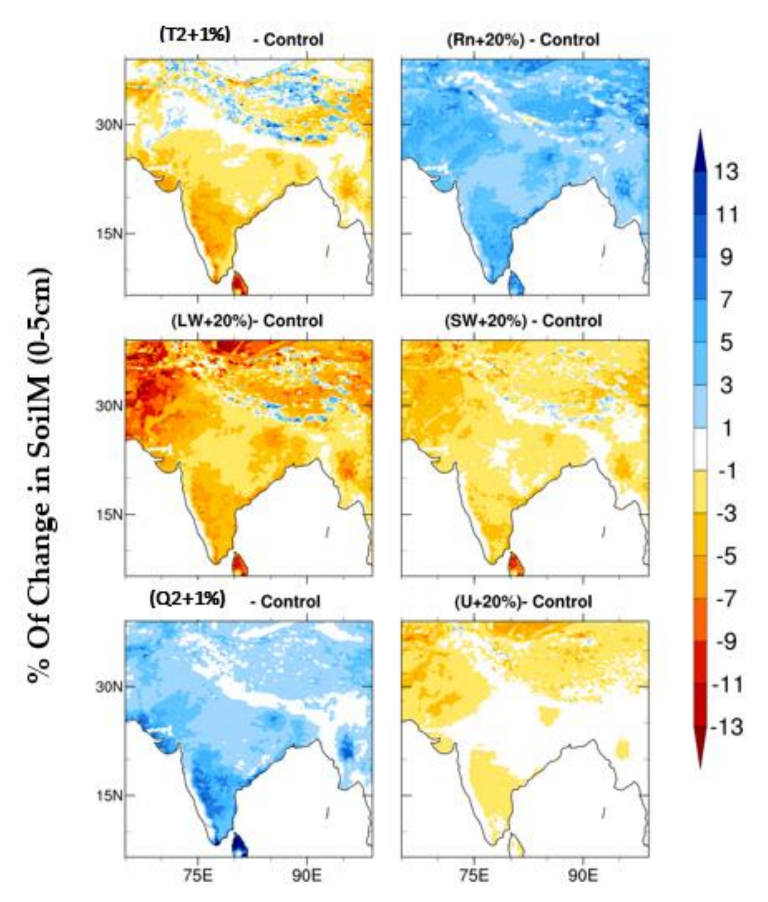
3.1. Sensitivity of Soil Moisture
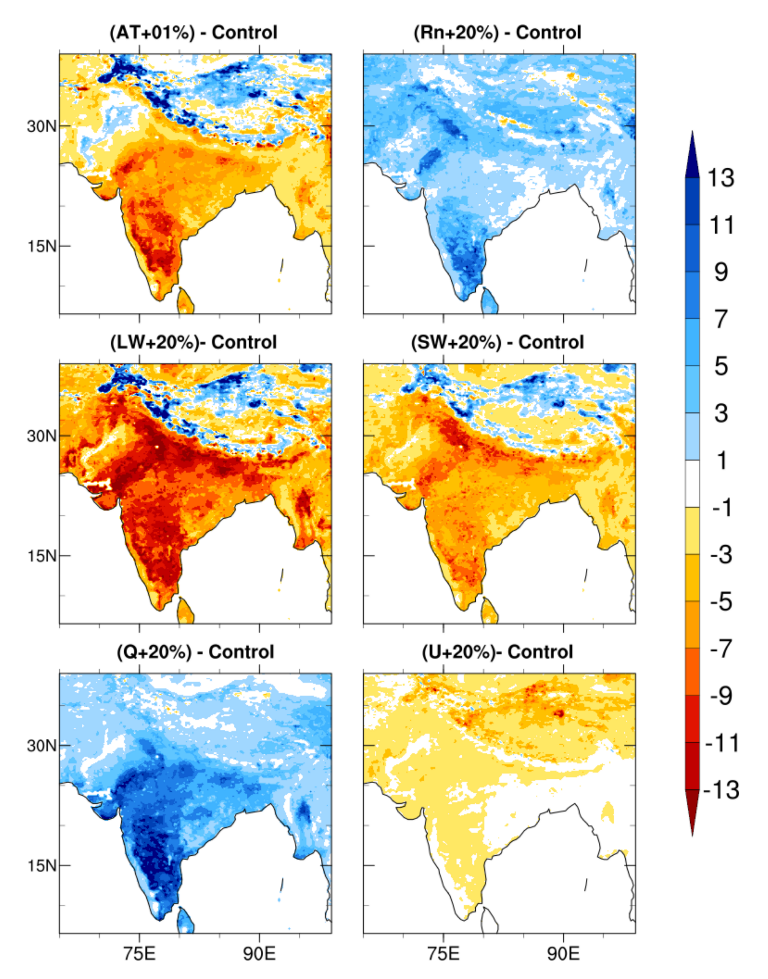
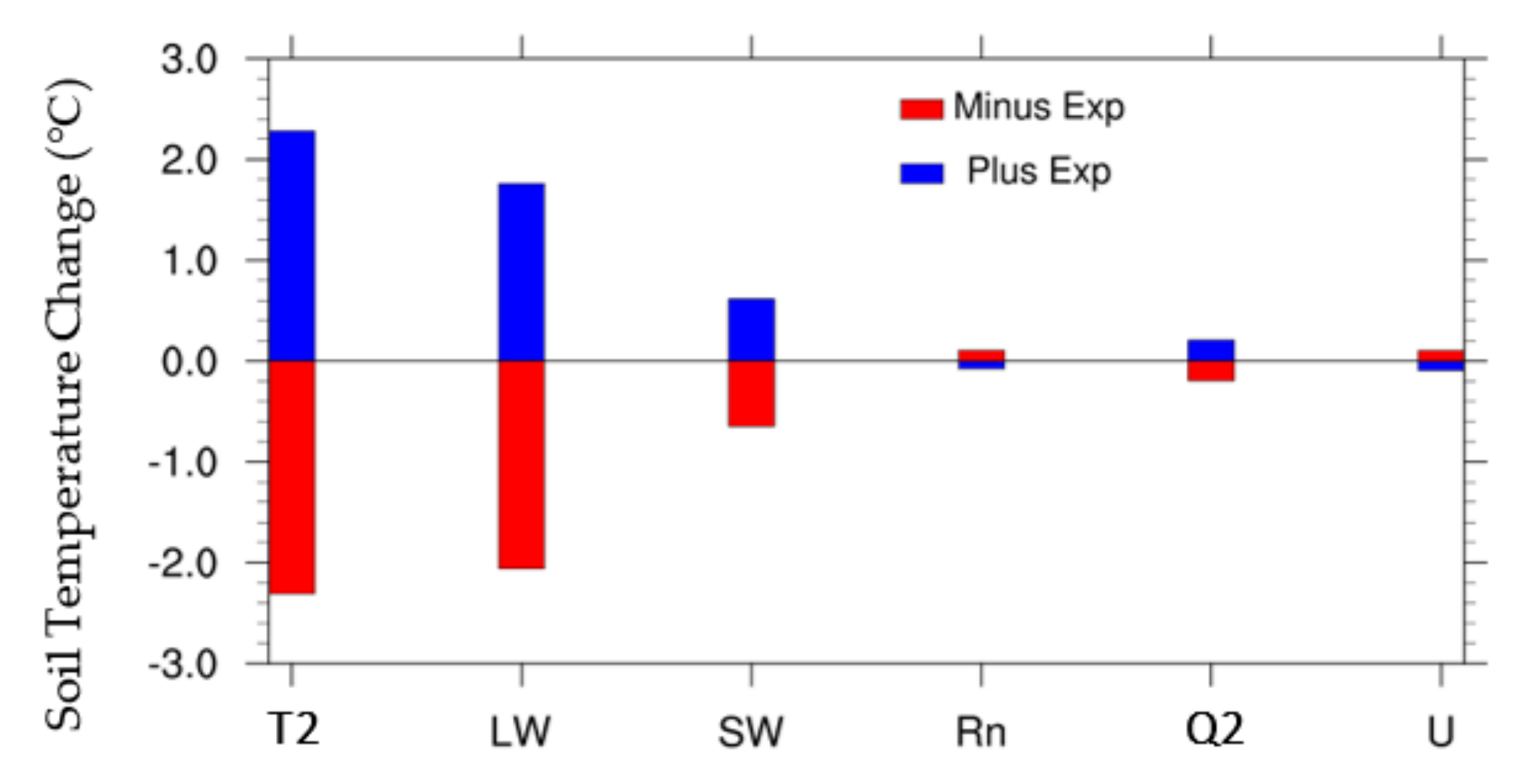
3.2. Sensitivity of Soil Temperature
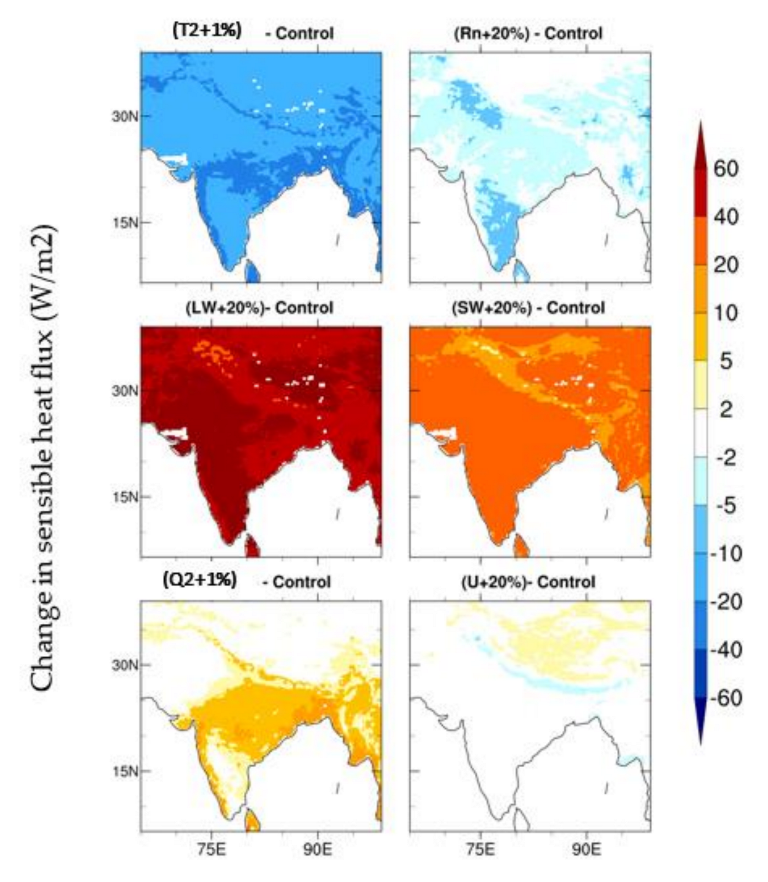
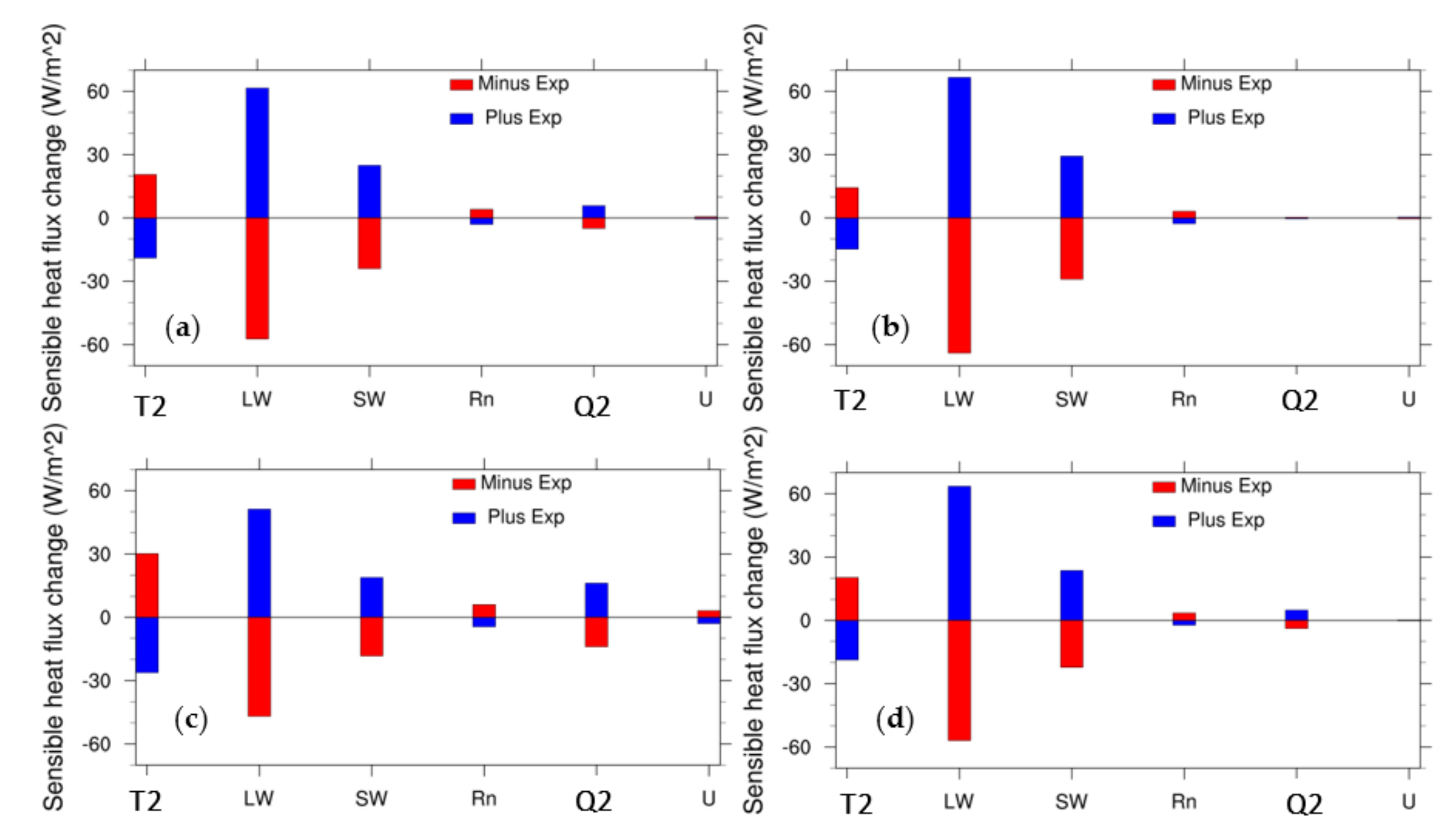
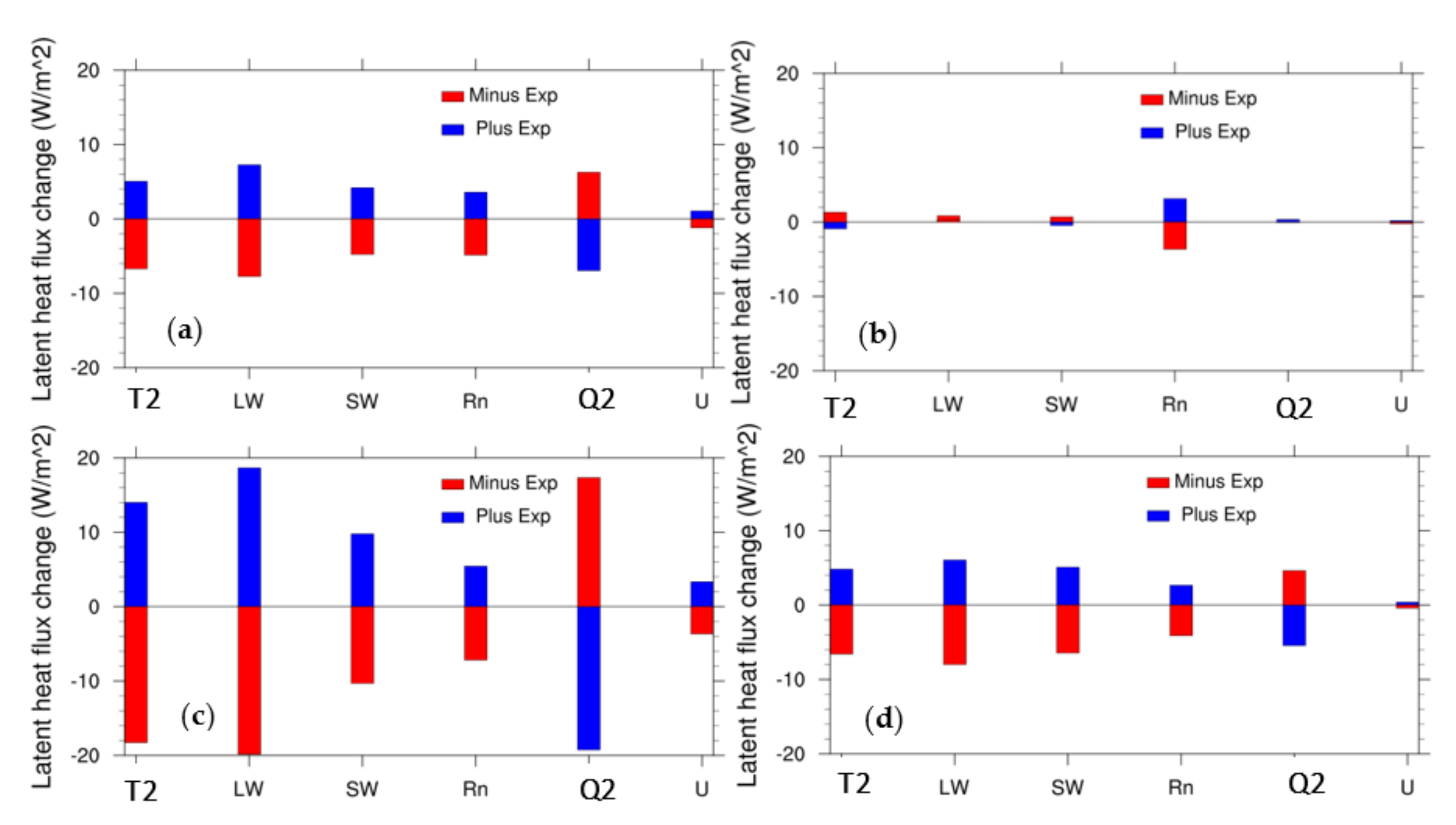
3.3. Sensitivity of Surface Fluxes
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Betts, A.K.; Ball, J.H.; Beljaars, A.C.M.; Miller, M.J.; Viterbo, P. The land surface–atmosphere interaction: A review based on observational and global modeling perspectives. J. Geophys. Res. 1996, 101, 7209–7225. [Google Scholar] [CrossRef]
- Koster, R.D.; Sud, Y.C.; Guo, Z.; Dirmeyer, P.A.; Bonan, G.; Oleson, K.W.; Chan, E.; Verseghy, D.; Cox, P.; Davies, H.; et al. GLACE: The Global Land–Atmosphere Coupling Experiment. Part I: Overview. J. Hydrometeorol. 2006, 7, 590–610. [Google Scholar] [CrossRef]
- Mintz, Y. The sensitivity of numerically simulated climates to land surface boundary conditions. In JSC Study Conf. on Land Surface Processes in Atmospheric Gen. Circulation Models; GCM: Greenbelt, MD, USA, 1982; pp. 1–50. [Google Scholar]
- Rowntree, P.R.; Bolton, J.R. Simulations of the atmospheric response to soil moisture anomalies over Europe. Q. J. R. Meteorol. Soc. 1983, 109, 501–526. [Google Scholar] [CrossRef]
- Mahfouf, J.F.; Richard, E.; Mascart, P. The influence of soil and vegetation on the development of mesoscale circulations. J. Clim. Appl. Meteorol. 1987, 26, 1483–1495. [Google Scholar] [CrossRef]
- Avissar, R.; Pielke, R.A. A parameterization of heterogeneous land surfaces for atmospheric numerical models and its impact on regional meteorology. Mon. Weather. Rev. 1989, 117, 2113–2136. [Google Scholar] [CrossRef]
- Chen, F.; Avissar, R. Impact of land-surface moisture variability on local shallow convective cumulus and precipitation in large-scale models. J. Appl. Meteorol. 1994, 33, 1382–1401. [Google Scholar] [CrossRef]
- Ament, F.; Simmer, C. Improved representation of land-surface heterogeneity in a non-hydrostatic numerical weather prediction model. Bound. Layer Meteorol. 2006, 121, 153–174. [Google Scholar] [CrossRef]
- Ozdogan, M.; Rodell, M.; Beaudoing, H.K.; Toll, D.L. Simulating the effects of irrigation over the United States in a land surface model based on satellite-derived agricultural data. J. Hydrometeorol. 2010, 11, 171–184. [Google Scholar] [CrossRef]
- Nayak, S.; Mandal, M.; Maity, S. Customization of regional climate model (RegCM4) over Indian region. Theor. Appl. Climatol. 2017, 127, 153–168. [Google Scholar] [CrossRef]
- Maity, S.; Satyanarayana, A.N.V.; Mandal, M.; Nayak, S. Performance evaluation of land surface models and cumulus convection schemes in the simulation of Indian summer monsoon using a regional climate model. Atmos. Res. 2017, 197, 21–41. [Google Scholar] [CrossRef]
- Nayak, S.; Mandal, M.; Maity, S. RegCM4 simulation with AVHRR land use data towards temperature and precipitation climatology over Indian region. Atmos. Res. 2018, 214, 163–173. [Google Scholar] [CrossRef]
- Mishra, P.; Kannan, S.R.; Radhakrishnan, C. The Effect of Anthropogenic Heat and Moisture on Local Weather at Industrial Heat Islands: A Numerical Experiment. Atmosphere 2022, 13, 357. [Google Scholar] [CrossRef]
- Nayak, H.P.; Osuri, K.K.; Sinha, P.; Nadimpalli, R.; Mohanty, U.C.; Chen, F.; Rajeevan, M.; Niyogi, D. High-resolution gridded soil moisture and soil temperature datasets for the Indian monsoon region. Nature Sci. Data 2018, 5, 180264. [Google Scholar] [CrossRef]
- Nayak, S.; Mandal, M.; Maity, S. Assessing the impact of Land-use and Land-cover changes on the climate over India using a Regional Climate Model (RegCM4). Clim. Res. 2021, 85, 1–20. [Google Scholar] [CrossRef]
- Henderson-Sellers, A. Assessing the sensitivity of a land surface scheme to parameters used in tropical deforestation experiments. Quart. J. Roy. Meteor. Soc. 1992, 118, 11. [Google Scholar] [CrossRef]
- Qu, W.A.; Henderson-Sellers, A.; Pitman, J.; Chen, T.H.; Abramopolous, F.; Beljaars, A.C.M.; Boone, A.; Chang, S.; Chen, F.; Dai, Y.; et al. Sensitivity of latent heat fluxes from PILPS land-surface schemes to perturbations of surface air temperature. J. Atmos. Sci. 1998, 55, 1909–1927. [Google Scholar] [CrossRef]
- Chen, F.; Manning, K.W.; LeMone, M.A.; Trier, S.B.; Alfieri, J.G.; Roberts, R.; Tewari, M.; Niyogi, D.; Horst, T.W.; Oncley, S.P.; et al. Description and evaluation of the characteristics of the NCAR high-resolution land data assimilation system. J. Appl. Meteorol. Climatol. 2007, 46, 649–713. [Google Scholar] [CrossRef]
- Lim, Y.-J.; Byun, K.-Y.; Lee, T.-Y.; Kwon, H.; Hong, J.; Kim, J. A land data assimilation system using the MODIS-derived land data and its application to numerical weather prediction in East Asia. Asia-Pac. J. Atmos. Sci. 2012, 481, 83–95. [Google Scholar] [CrossRef]
- Unnikrishnan, C.K.; Rajeevan, M.; Rao, S.V.B.; Kumar, M. Development of a high-resolution land surface dataset for the South Asian monsoon region. Curr. Sci. 2013, 1059, 1235–1246. [Google Scholar]
- Wilson, M.F.; Henderson-Sellers, A.; Dickinson, R.E.; Ken nedy, P.J. Sensitivity of the Biosphere-Atmosphere Transfer Scheme (BATS) to the inclusion of variable soil characteristics. J. Climate Appl. Meteor. 1987, 26, 3. [Google Scholar] [CrossRef]
- Pitman, A.; Yang, Z.-L.; Henderson-Sellers, A. Sub-grid scale precipitation in AGCMS: Re-assessing the land surface sensitivity using a single column model. Clim. Dyn. 1993, 9, 33–41. [Google Scholar] [CrossRef]
- Nayak, H.P.; Sinha, P.; Satyanarayana, A.N.V.; Bhattacharya, A.; Mohanty, U.C. Performance Evaluation of High-Resolution Land Data Assimilation System (HRLDAS) Over Indian Region. Pure Appl. Geophys. 2019, 176, 389–407. [Google Scholar] [CrossRef]
- Nayak, S.; Maity, S.; Singh, K.S.; Nayak, H.P.; Dutta, S. Influence of the Changes in Land-Use and Land Cover on Temperature over Northern and North-Eastern India. Land 2021, 10, 52. [Google Scholar] [CrossRef]
- Nayak, S.; Maity, S.; Sahu, N.; Saini, A.; Singh, K.S.; Nayak, H.P.; Dutta, S. Application of “Observation Minus Reanalysis” Method towards LULC Change Impact over Southern India. ISPRS Int. J. Geo. Inf. 2022, 11, 94. [Google Scholar] [CrossRef]
- Berg, A.A.; Famiglietti, J.S.; Walker, J.P.; Houser, P.R. Impact of bias correction to reanalysis products on simulations of North American soil moisture and hydrological fluxes. J. Geophys. Res. 2003, 108, 4490. [Google Scholar] [CrossRef]
- Stoyanova, J.; Georgiev, C.; Neytchev, P.; Kulishev, A. Spatial-Temporal Variability of Land Surface Dry Anomalies in Climatic Aspect: Biogeophysical Insight by Meteosat Observations and SVAT Modeling. Atmosphere 2019, 10, 636. [Google Scholar] [CrossRef]
- Vousdoukas, M.; Mentaschi, L.; Voukouvalas, E.; Verlaan, M.; Jevrejeva, S.; Jackson, L.; Feyen, L. Validation of the North American Land Data Assimilation System (NLDAS) retrospective forcing over the southern Great Plains. J. Geophys. Res. 2003, 108, 8843. [Google Scholar]
- Maurer, E.P.; O’Donnell, G.M.; Lettenmaier, D.P.; Roads, J.O. Evaluation of the land surface water budget in NCEP/NCAR and NCEP/DOE reanalyses using an off-line hydrologic model. J. Geophys. Res. 2001, 106, 17841–17862. [Google Scholar] [CrossRef]
- Maity, S.; Nayak, S.; Singh, K.S.; Nayak, H.P.; Dutta, S. Impact of Soil Moisture Initialization in the Simulation of Indian Summer Monsoon Using RegCM4. Atmosphere 2021, 12, 1148. [Google Scholar] [CrossRef]
- Chen, F.; Mitchell, K.; Schaake, J.; Xue, Y.; Pan, H.-L.; Koren, V.; Duan, Q.; Ek, M.; Betts, A. Modeling of land–surface evaporation by four schemes and comparison with FIFE observations. J. Geophys. Res. 1996, 101, 7251–7268. [Google Scholar] [CrossRef]
- Ek, M.B.; Mitchell, K.E.; Lin, Y.; Rogers, E.; Grunmann, P.; Koren, V.; Gayno, G.; Tarpley, J.D. Implementation of Noah land surface model advances in the National Centers for Environmental Prediction operational mesoscale Eta model. J. Geophys. Res. 2003, 108, 8851. [Google Scholar] [CrossRef]
- Mahrt, L.; Ek, M. The influence of atmospheric stability on potential evaporation. J. Appl. Meteorol. Climatol. 1984, 23, 222–234. [Google Scholar] [CrossRef]
- Mahrt, L.; Pan, H.L. A two-layer model of soil hydrology. Bound. Layer Meteorol. 1984, 29, 1–20. [Google Scholar] [CrossRef]
- Pan, H.L.; Mahrt, L. Interaction between soil hydrology and boundary-layer development. Bound. Layer Meteorol. 1987, 38, 185–202. [Google Scholar] [CrossRef]
- Koren, V.; Schaake, J.; Mitchell, K.; Duan, Q.Y.; Chen, F. A parameterization of snowpack and frozen ground intended for NCEP weather and climate models. J. Geophys. Res. 1999, 104, 19569–19585. [Google Scholar] [CrossRef]
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.; Bonan, G.; Chan, E.; Cox, P.; Gordon, C.T.; Kanae, S.; Kowalczyk, E.; Lawrence, D.; et al. Regions of strong coupling between soil moisture and precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef]
- Nayak, H.P.; Sinha, P.; Mohanty, U.C. Incorporation of surface observations in the LDAS and application to mesoscale simulation of pre-monsoon thunderstorms. Pure Appl. Geophys. 2021, 178, 565–582. [Google Scholar] [CrossRef]
- Vergopolan, N.; Sheffield, J.; Chaney, N.W.; Pan, M.; Beck, H.E.; Ferguson, C.R.; Torres-Rojas, L.; Eigenbrod, F.; Crow, W.; Wood, E.F. High-resolution soil moisture data reveal complex multi-scale spatial variability across the United States. Geophys. Res. Lett. 2022, 49, e2022GL098586. [Google Scholar] [CrossRef]
- Budyko, M.I. Climate and Life; Academic: Orlando, FL, USA, 1974. [Google Scholar]
- Seneviratne, S.I.; Koster, R.; Guo, Z.; Dirmeyer, P.; Kowalczyk, E.; Lawrence, D.; Liu, P.; Mocko, D.; Lu, C.-H.; Oleson, K.W.; et al. Soil moisture memory in AGCM simulations: Analysis of Global Land–Atmosphere Coupling Experiment (GLACE) data. J. Hydrometeor. 2006, 7, 1090–1112. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture−climate interactions in a changing climate:a review. Earth Sci Rev. 2010, 99, 125−161. [Google Scholar] [CrossRef]
- Li, M.; Ma, Z. Sensible and Latent Heat Flux Variability and Response to Dry–Wet Soil Moisture Zones Across China. Bound. Layer Meteorol. 2015, 154, 157–170. [Google Scholar] [CrossRef]
- Webb, E.K.; Pearman, G.I.; Leuning, R. Correction of flux measurements for density effects due to heat and water-vapor transfer. Q J R Meteorol Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Fuehrer, P.L.; Friehe, C.A. Flux corrections revisited. Bound. Layer Meteorol. 2002, 102, 415–457. [Google Scholar] [CrossRef]
- Kara, A.B.; Rochford, P.A.; Hurlburt, H.E. Air-sea flux estimates and the 1997-1998 ENSO event. Bound. Layer Meteorol. 2002, 103, 439–458. [Google Scholar] [CrossRef]



| Data | Sources |
|---|---|
| Land use | 20 category 30 s resolution MODIS land use |
| Green vegetation fraction | MODIS fpar 0.00833º resolution green vegetation fraction |
| Atmospheric forcing | MERRA hourly data at (1/2° × 2/3°) resolution (air temperature, specific humidity, pressure, U wind, V wind) |
| Precipitation | TRMM hourly precipitation at 0.25° resolution |
| Radiation | ECMWF 3 hourly solar radiation at 0.25° resolution |
| Numerical Experiment | Perturbed Parameter | Other Forcing Parameters |
|---|---|---|
| Control experiment | The forcing parameters used are as provided in Table 1. (No parameters are perturbed) | |
| T2 + 1% | 2 m temperature increased by 1% | Other forcing parameters remained the same as in the control experiment. |
| T2 − 1% | 2 m temperature decreased by 1% | |
| Rn + 20% | Rainrate increased by 20% | |
| Rn − 20% | Rainrate decreased by 20% | |
| SW + 20% | SW radiation increased by 20% | |
| SW − 20% | SW radiation decreased by 20% | |
| LW + 20% | LW radiation increased by 20% | |
| LW − 20% | LW radiation decreased by 20% | |
| U + 20% | 10 m wind speed increased by 20% | |
| U − 20% | 10 m wind speed decreased by 20% | |
| Q2 + 20% | 2 m specific humidity increased by 20% | |
| Q2 − 20% | 2 m specific humidity decreased by 20% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nayak, H.P.; Nayak, S.; Maity, S.; Patra, N.; Singh, K.S.; Dutta, S. Sensitivity of Land Surface Processes and Its Variation during Contrasting Seasons over India. Atmosphere 2022, 13, 1382. https://doi.org/10.3390/atmos13091382
Nayak HP, Nayak S, Maity S, Patra N, Singh KS, Dutta S. Sensitivity of Land Surface Processes and Its Variation during Contrasting Seasons over India. Atmosphere. 2022; 13(9):1382. https://doi.org/10.3390/atmos13091382
Chicago/Turabian StyleNayak, Hara Prasad, Sridhara Nayak, Suman Maity, Nibedita Patra, Kuvar Satya Singh, and Soma Dutta. 2022. "Sensitivity of Land Surface Processes and Its Variation during Contrasting Seasons over India" Atmosphere 13, no. 9: 1382. https://doi.org/10.3390/atmos13091382
APA StyleNayak, H. P., Nayak, S., Maity, S., Patra, N., Singh, K. S., & Dutta, S. (2022). Sensitivity of Land Surface Processes and Its Variation during Contrasting Seasons over India. Atmosphere, 13(9), 1382. https://doi.org/10.3390/atmos13091382










