Tuning ANN Hyperparameters by CPSOCGSA, MPA, and SMA for Short-Term SPI Drought Forecasting
Abstract
:1. Introduction
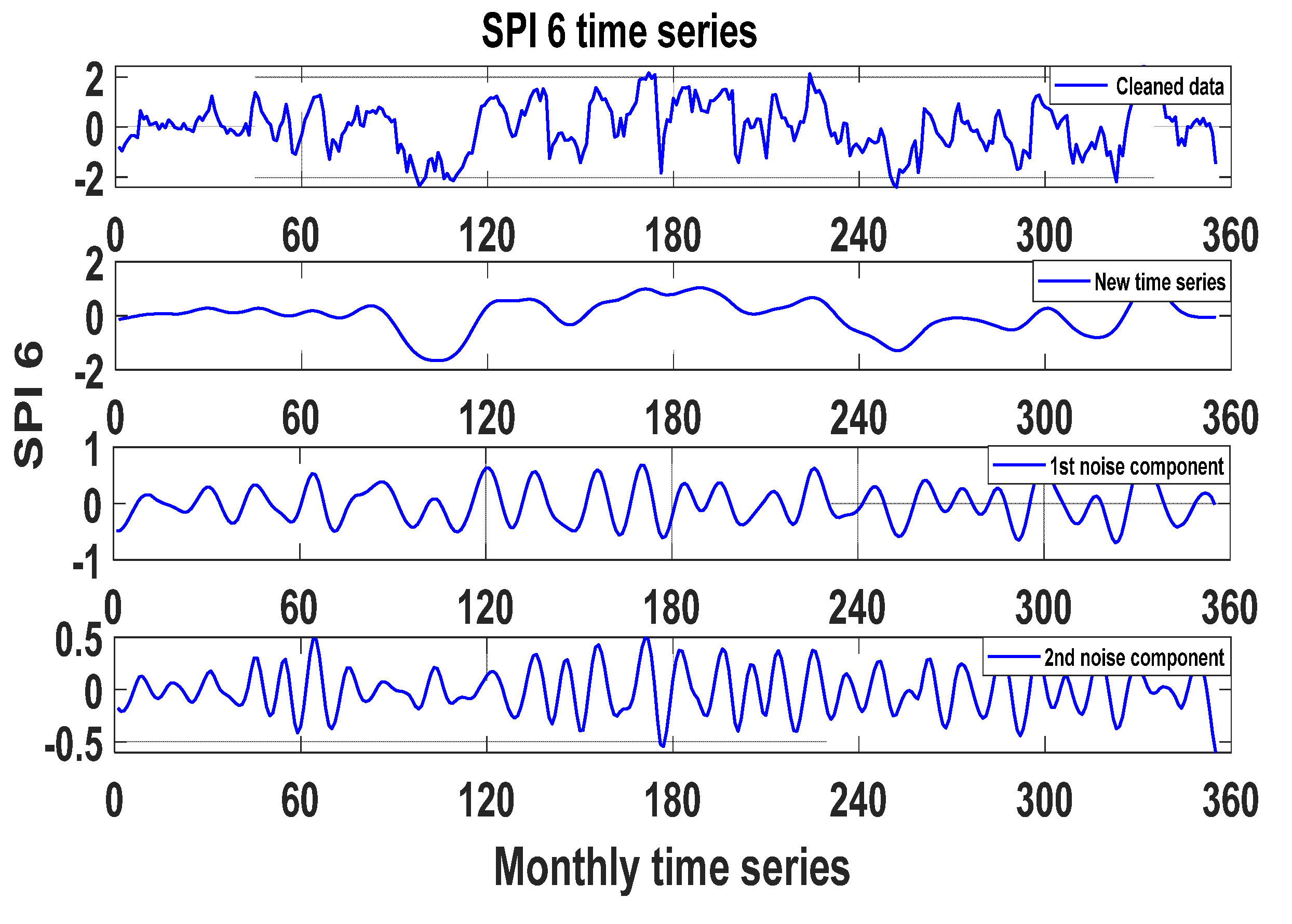
- Employing singular spectrum analysis (SSA) as a data pretreatment technique;
- Using a multivariate strategy;
- Applying the hybridisation of preprocessing-based with parameter optimisation-based hybrid models.
- Investigate 14 climate factors over thirty years to determine to what extent climate factors drive drought indices;
- Enhance raw data quality and identify the optimal predictor scenario;
- Integrate the ANN model with the recent CPSOCGSA algorithm to choose the optimal ANN hyperparameters;
- Evaluate the CPSOCGSA-ANN technique’s performance by comparing it with the updated MPA-ANN and SMA-ANN algorithms;
- Provide a scientific view of drought to the local stakeholders because this province has the highest production and marketing of wheat in Iraq.
2. Materials and Methods
2.1. Study Area and Data Collection
2.2. Methodology
2.2.1. Standardised Precipitation Index (SPI)
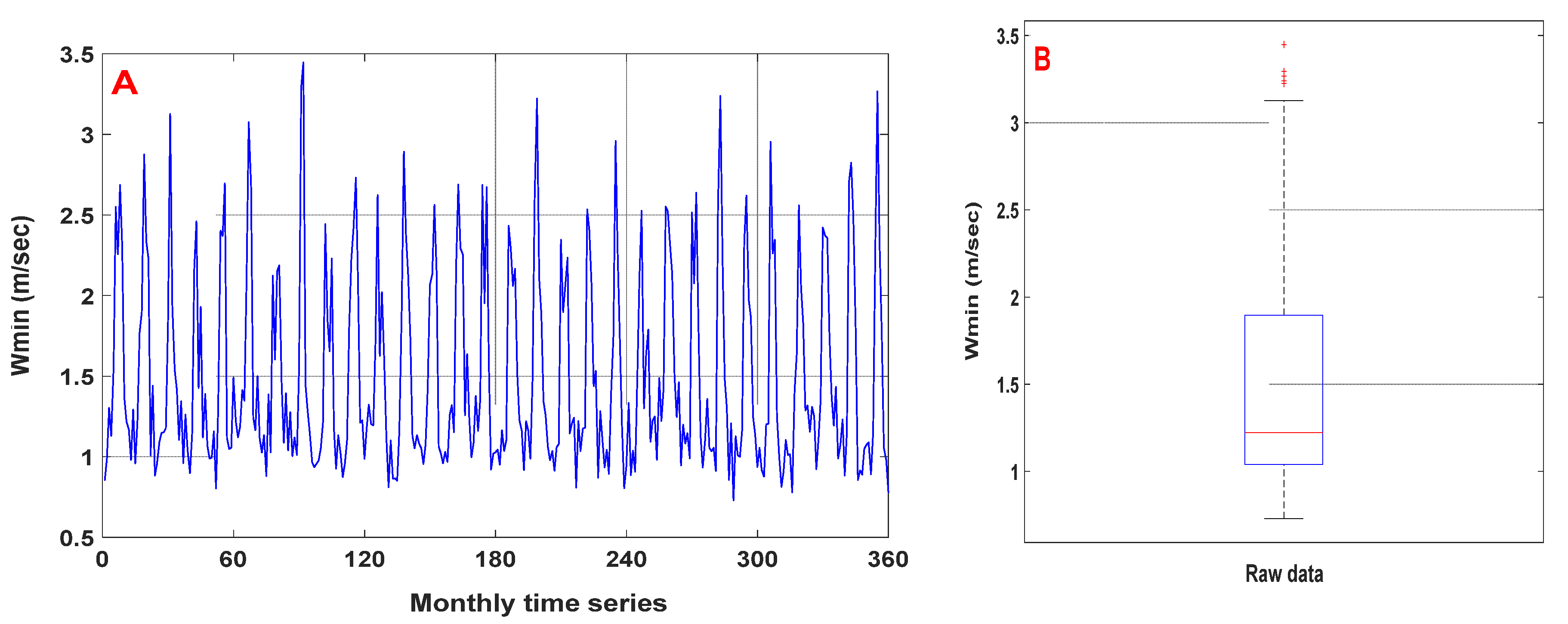
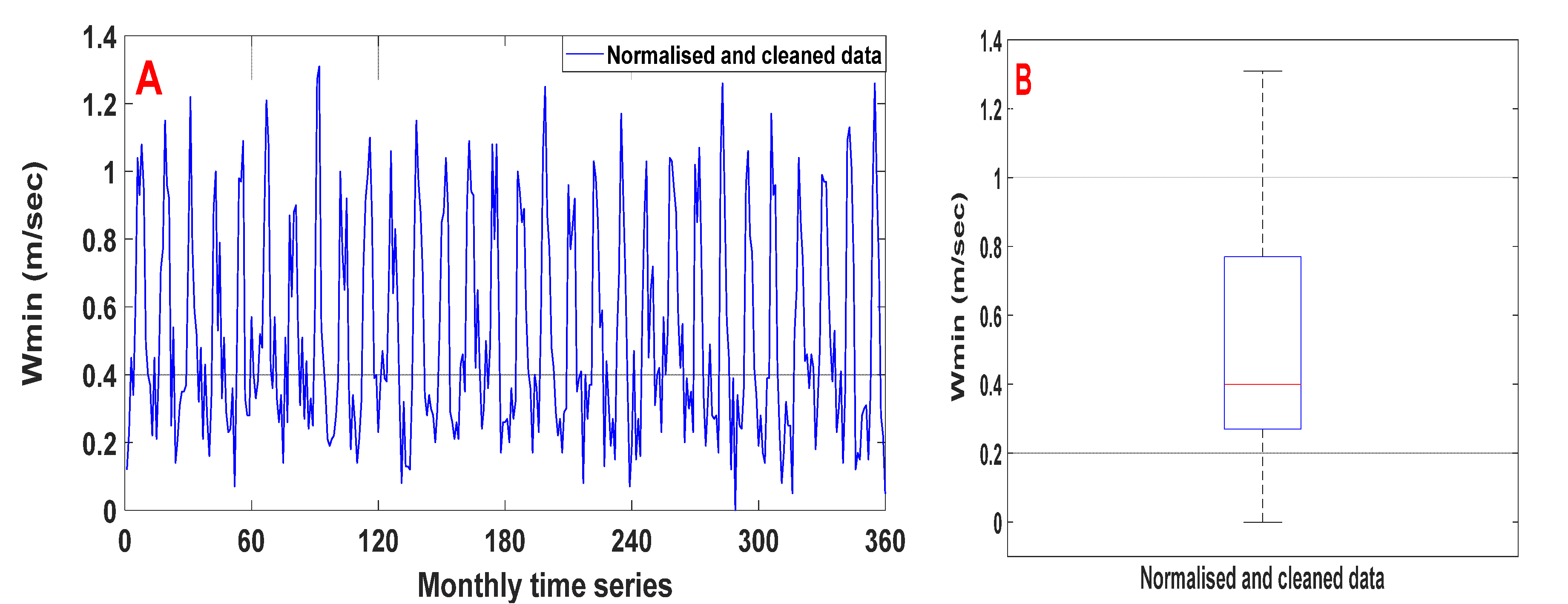
2.2.2. Data Preprocessing
Normalisation
Cleaning
Selection of the Best Model Input
2.2.3. Constriction Coefficient-Based Particle Swarm Optimisation and Chaotic Gravitational Search Algorithm (CCPSOCGSA)
- a.
- Constriction Coefficient-Based Particle Swarm Optimisation (CCPSO)
- b.
- Chaotic Gravitational Search Algorithm CGSA
- c.
- Combination of CCPSO and CGSA
2.2.4. Artificial Neural Network (ANN)
2.3. Prediction Accuracy Criteria
3. Results
3.1. Input Data Analysis
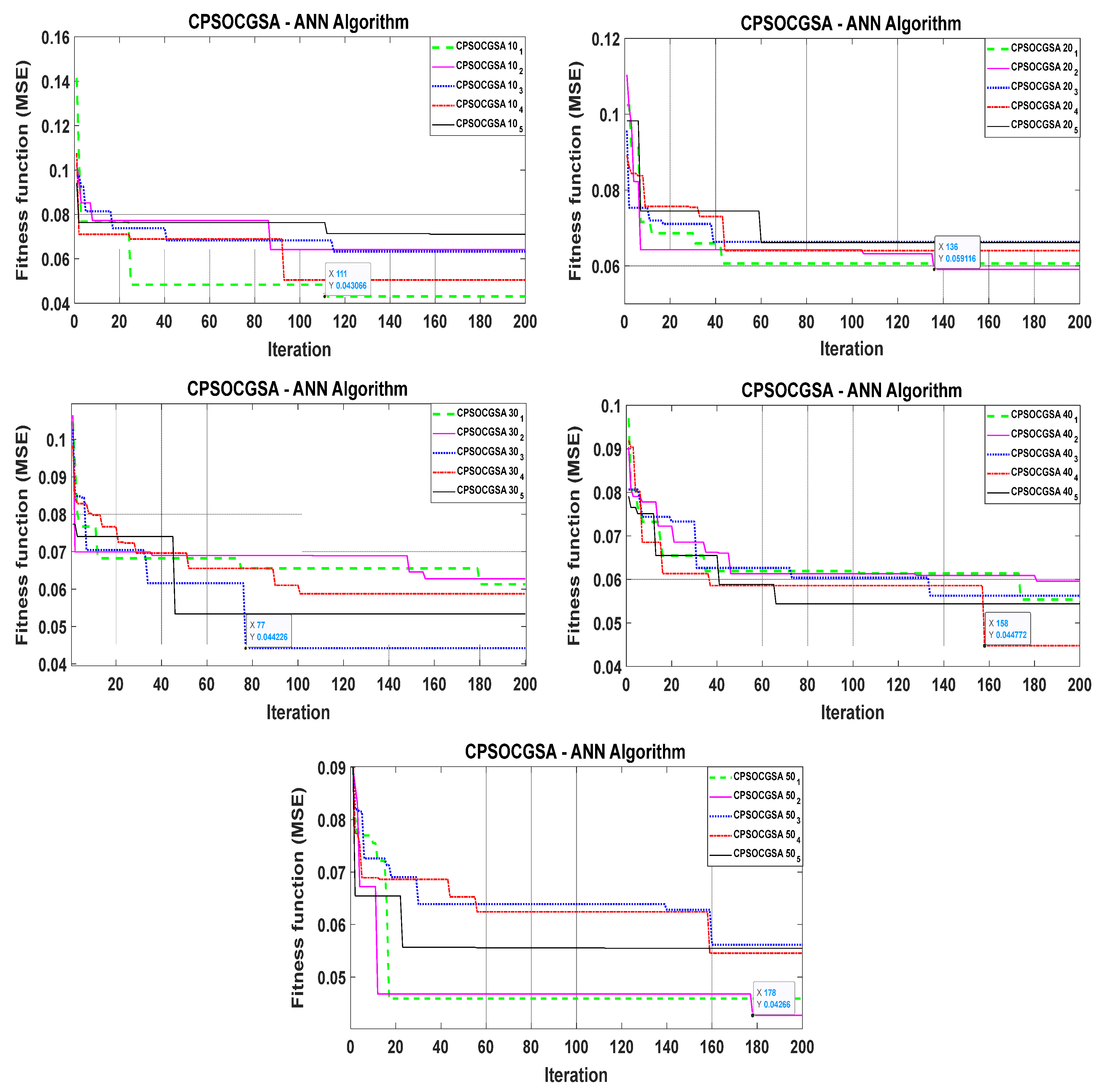
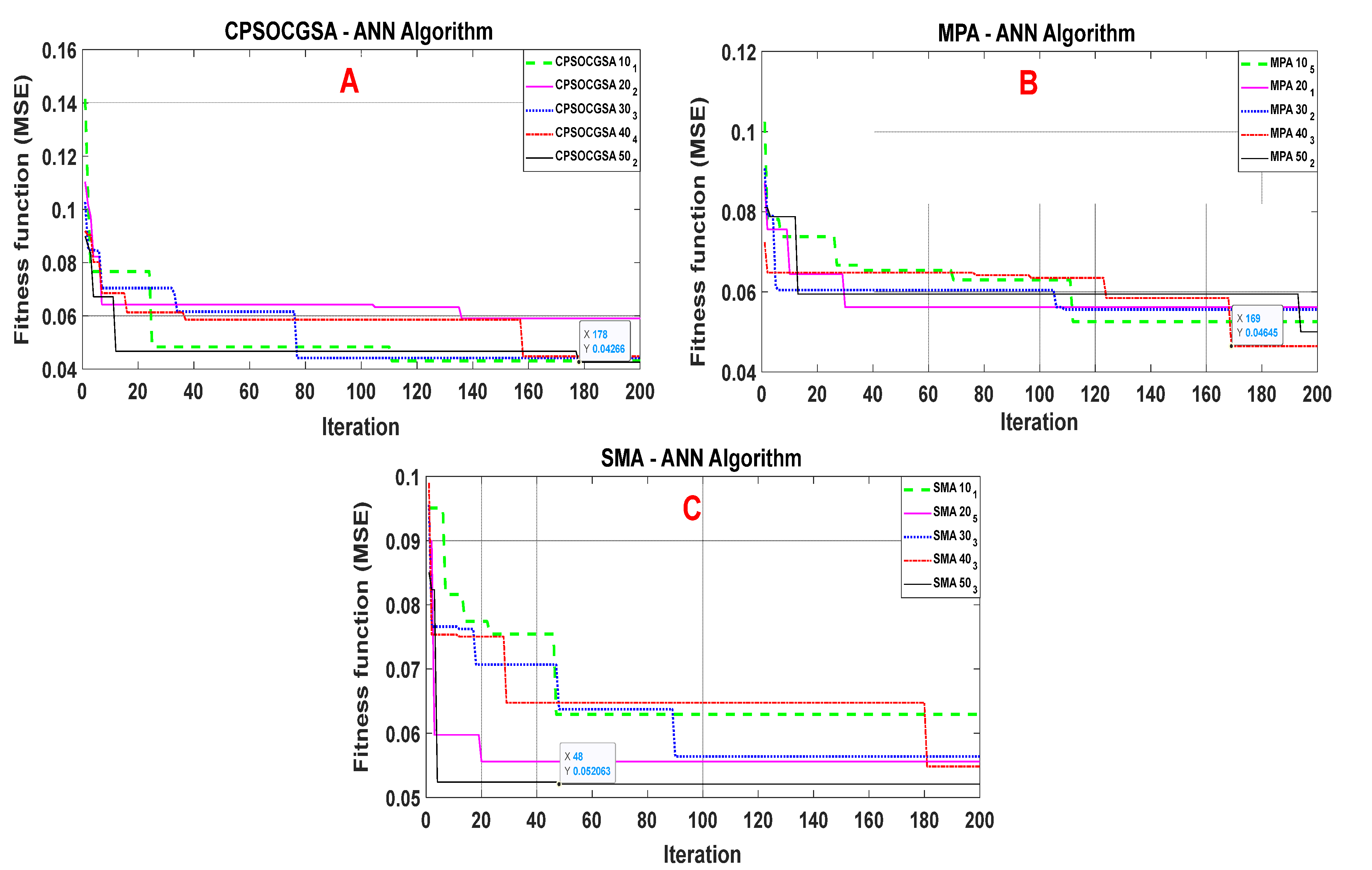
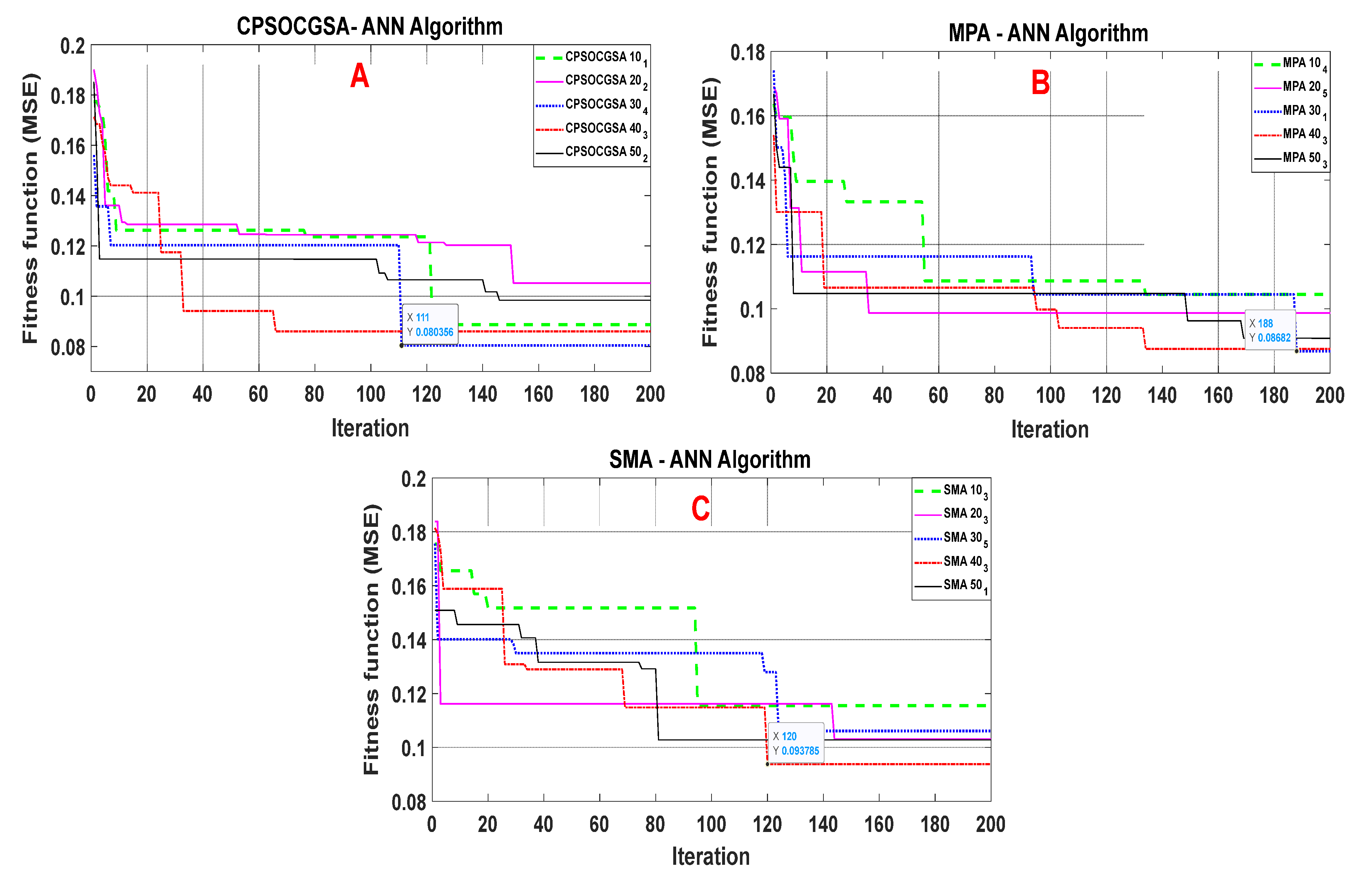
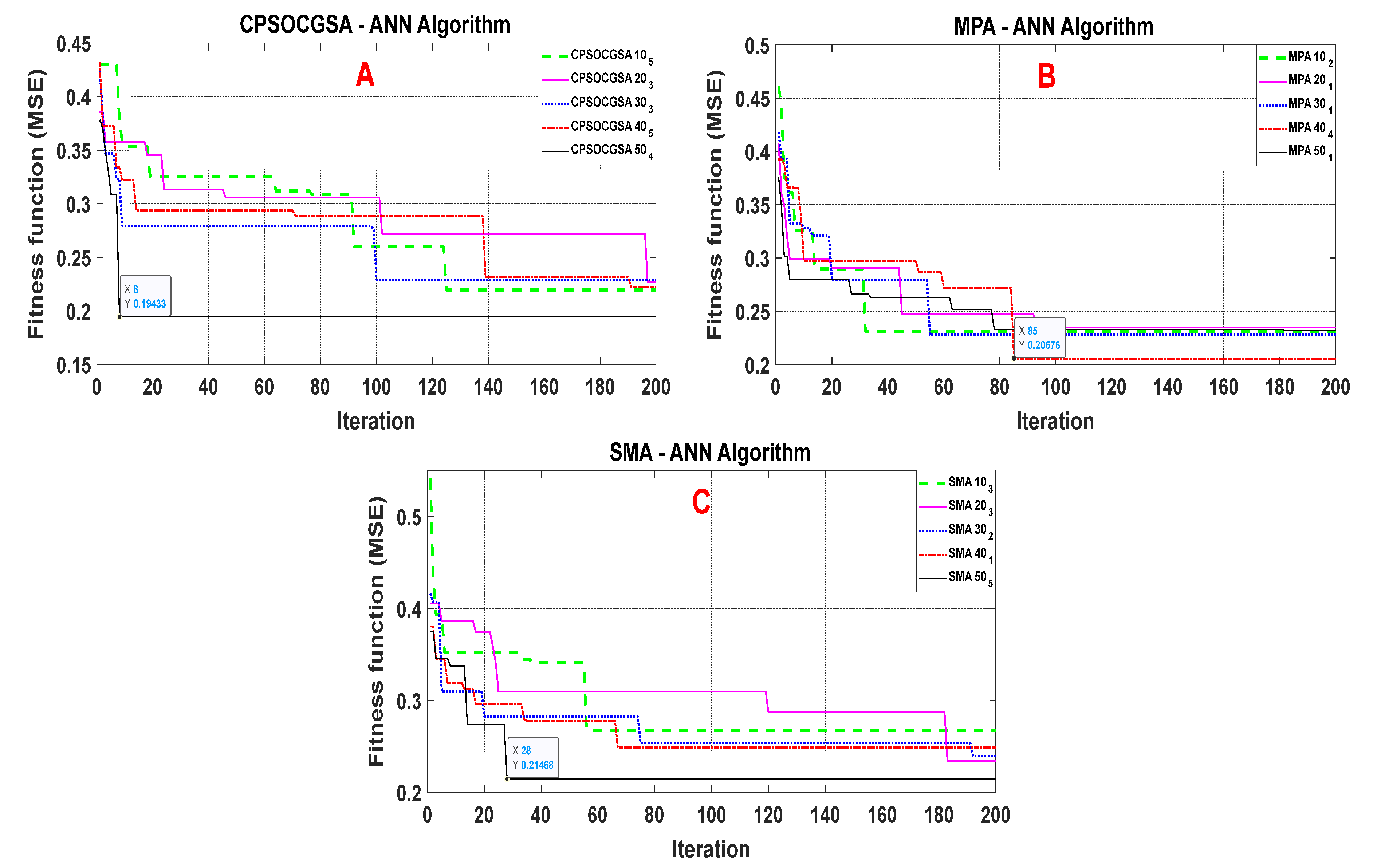
3.2. Application of the Hybrid Heuristic Algorithms—ANN Approach
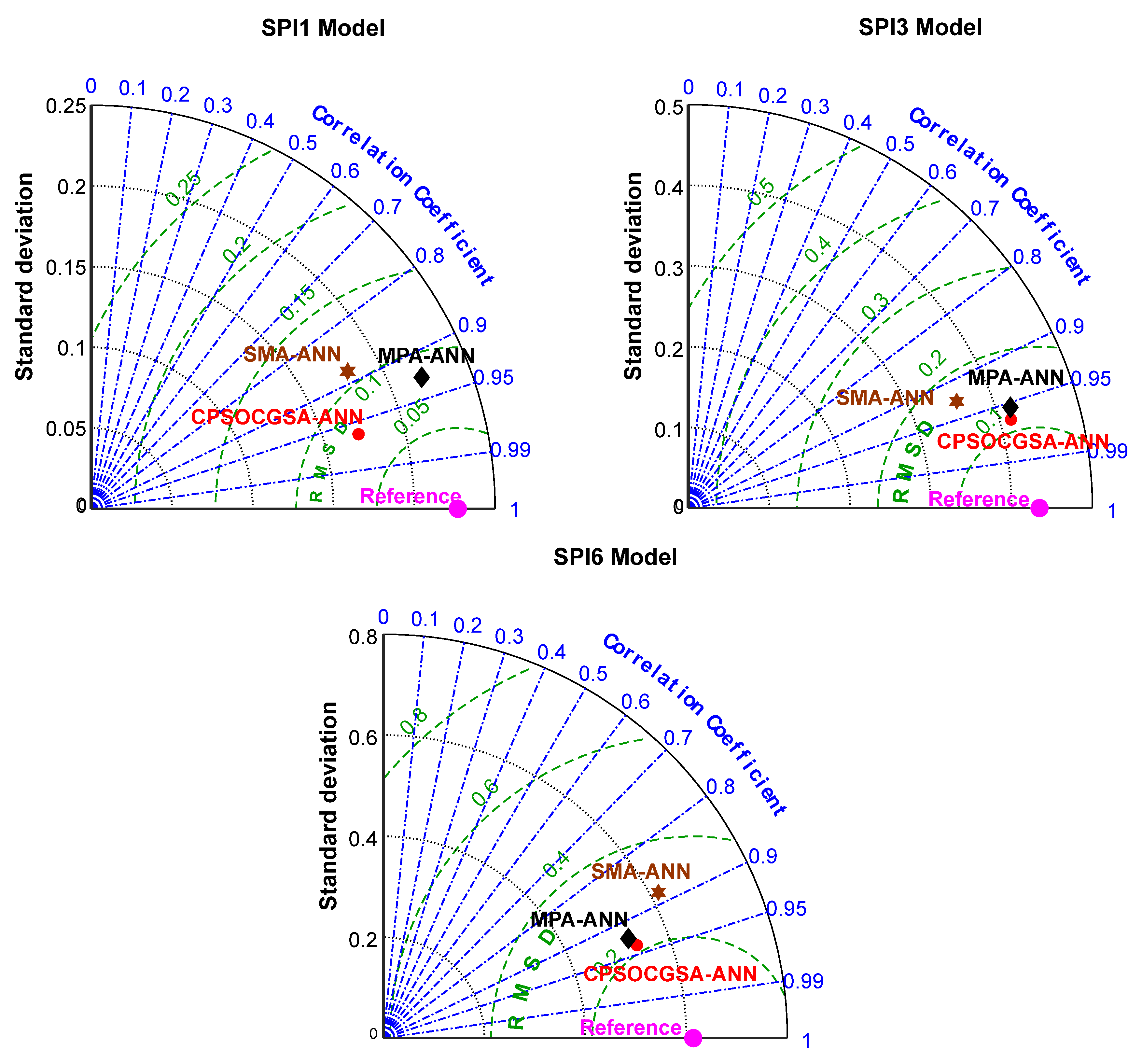
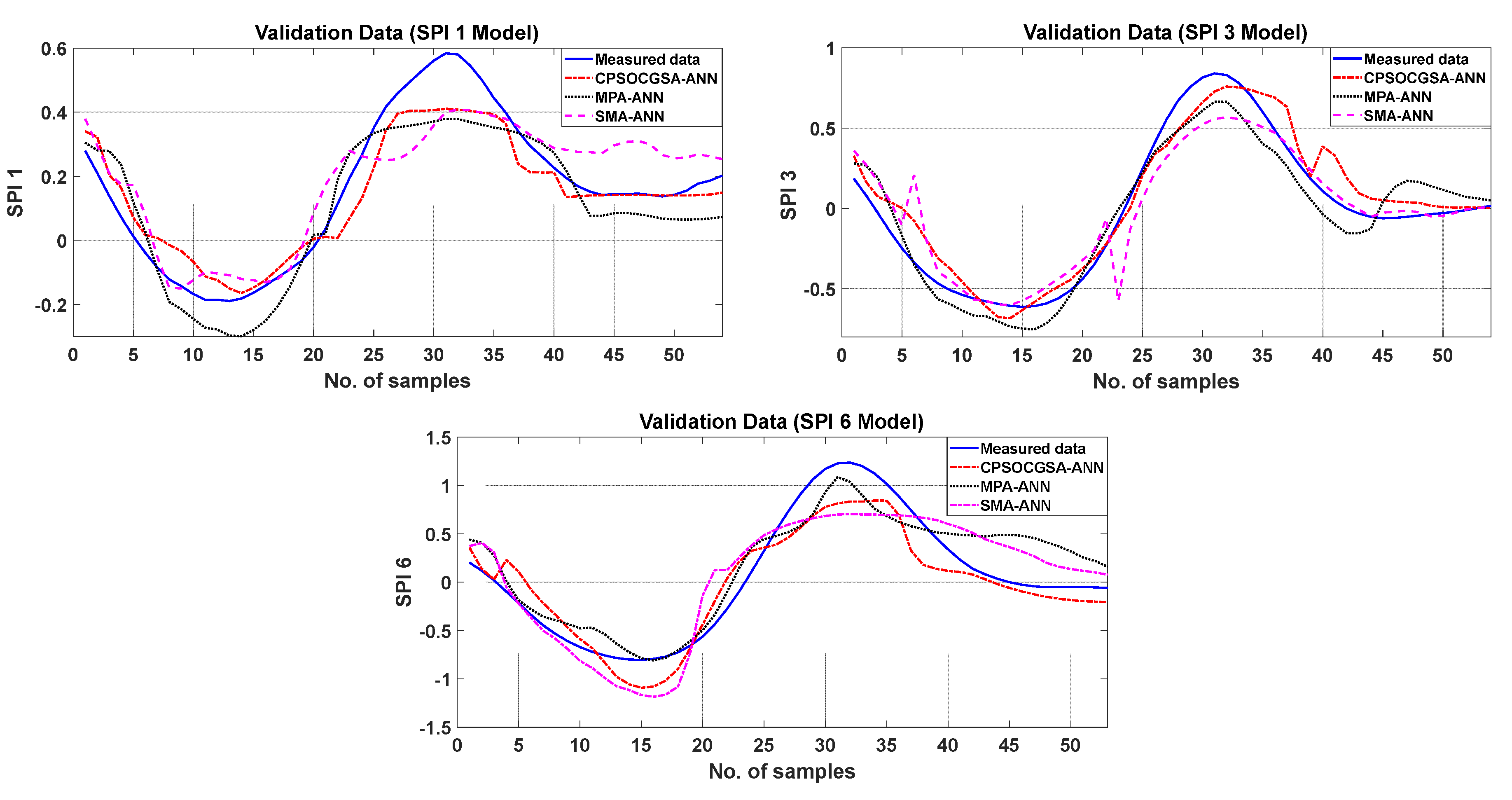
3.3. Evaluating and Comparing the Performance of the Algorithms with ANN
- (1)
- These results show the ability of SSA and tolerance strategies to enhance the quality of raw data and choose the optimal predictors scenario without transgressing the multicollinearity supposition.
- (2)
- Rain, RH, Twet, and Wmin emerged as reliable predictors of SPI 1, SPI 3, and SPI 6.
- (3)
- The CPSOCGSA-ANN method is a reliable model that can accurately predict the short-term drought index, outperforming the MPA-ANN and SMA-ANN models.
- (4)
- The proposed methodology (i.e., hybridisation of preprocessing-based with parameter optimisation-based hybrid models) accurately predicted monthly drought according to various statistical criteria.
- (5)
- The findings reveal a strong relationship between drought and climatic factors.
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, D.; Zhang, Q.; Ding, Y.; Zhang, D. Application of a hybrid ARIMA-LSTM model based on the SPEI for drought forecasting. Environ. Sci. Pollut. Res. Int. 2022, 29, 4128–4144. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J.; Khalil, B.; Ozga-Zielinski, B. Long-term SPI drought forecasting in the Awash River Basin in Ethiopia using wavelet neural network and wavelet support vector regression models. J. Hydrol. 2014, 508, 418–429. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, W.; Chen, Q.; Pu, X.; Xiang, L. Multi-models for SPI drought forecasting in the north of Haihe River Basin, China. Stoch. Environ. Res. Risk Assess. 2017, 31, 2471–2481. [Google Scholar] [CrossRef]
- Pham, Q.B.; Yang, T.-C.; Kuo, C.-M.; Tseng, H.-W.; Yu, P.-S. Coupling Singular Spectrum Analysis with Least Square Support Vector Machine to Improve Accuracy of SPI Drought Forecasting. Water Resour. Manag. 2021, 35, 847–868. [Google Scholar] [CrossRef]
- Banadkooki, F.B.; Singh, V.P.; Ehteram, M. Multi-timescale drought prediction using new hybrid artificial neural network models. Nat. Hazards 2021, 106, 2461–2478. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993. [Google Scholar]
- Anshuka, A.; van Ogtrop, F.F.; Willem Vervoort, R. Drought forecasting through statistical models using standardised precipitation index: A systematic review and meta-regression analysis. Nat. Hazards 2019, 97, 955–977. [Google Scholar] [CrossRef]
- Gumus, V.; Algin, H.M. Meteorological and hydrological drought analysis of the Seyhan−Ceyhan River Basins, Turkey. Meteorol. Appl. 2017, 24, 62–73. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Dooley, J.; Alkhaddar, R.M.; Abdellatif, M.; Al-Bugharbee, H.; Ortega-Martorell, S. A Novel approach for predicting monthly water demand by combining singular spectrum analysis with neural networks. J. Hydrol. 2018, 561, 136–145. [Google Scholar] [CrossRef]
- Sa’adi, Z.; Shahid, S.; Ismail, T.; Chung, E.-S.; Wang, X.-J. Distributional changes in rainfall and river flow in Sarawak, Malaysia. Asia Pac. J. Atmos. Sci. 2017, 53, 489–500. [Google Scholar] [CrossRef]
- Salman, S.A.; Shahid, S.; Ismail, T.; Ahmed, K.; Chung, E.-S.; Wang, X.-J. Characteristics of Annual and Seasonal Trends of Rainfall and Temperature in Iraq. Asia Pac. J. Atmos. Sci. 2019, 55, 429–438. [Google Scholar] [CrossRef]
- Salman, S.A.; Shahid, S.; Ismail, T.; Chung, E.-S.; Al-Abadi, A.M. Long-term trends in daily temperature extremes in Iraq. Atmos. Res. 2017, 198, 97–107. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Shahid, S.; Abd Rahim, N. Unidirectional trends in annual and seasonal climate and extremes in Egypt. Theor. Appl. Climatol. 2018, 136, 457–473. [Google Scholar] [CrossRef]
- Ethaib, S.; Zubaidi, S.L.; Al-Ansari, N.; Fegade, S.L. Evaluation water scarcity based on GIS estimation and climate-change effects: A case study of Thi-Qar Governorate, Iraq. Cogent Eng. 2022, 9, 2075301. [Google Scholar] [CrossRef]
- Aljanabi, A.A.; Mays, L.W.; Fox, P. A Reclaimed Wastewater Allocation Optimization Model for Agricultural Irrigation. Environ. Nat. Resour. Res. 2018, 8, 55. [Google Scholar] [CrossRef]
- Salman, S.A.; Shahid, S.; Ismail, T.; Rahman, N.b.A.; Wang, X.; Chung, E.-S. Unidirectional trends in daily rainfall extremes of Iraq. Theor. Appl. Climatol. 2017, 134, 1165–1177. [Google Scholar] [CrossRef]
- Osman, Y.; Abdellatif, M.; Al-Ansari, N.; Knutsson, S.; Jawad, S. Climate change and future precipitation in an arid environment of the middle east: Case study of Iraq. J. Environ. Hydrol. 2017, 25, 3. [Google Scholar]
- Bandyopadhyay, N.; Bhuiyan, C.; Saha, A.K. Drought mitigation: Critical analysis and proposal for a new drought policy with special reference to Gujarat (India). Prog. Disaster Sci. 2020, 5, 100049. [Google Scholar] [CrossRef]
- Adnan, S.; Ullah, K.; Shuanglin, L.; Gao, S.; Khan, A.H.; Mahmood, R. Comparison of various drought indices to monitor drought status in Pakistan. Clim. Dyn. 2017, 51, 1885–1899. [Google Scholar] [CrossRef]
- Adede, C.; Oboko, R.; Wagacha, P.W.; Atzberger, C. A Mixed Model Approach to Vegetation Condition Prediction Using Artificial Neural Networks (ANN): Case of Kenya’s Operational Drought Monitoring. Remote Sens. 2019, 11, 1099. [Google Scholar] [CrossRef]
- Elbeltagi, A.; AlThobiani, F.; Kamruzzaman, M.; Shaid, S.; Roy, D.K.; Deb, L.; Islam, M.M.; Kundu, P.K.; Rahman, M.M. Estimating the Standardized Precipitation Evapotranspiration Index Using Data-Driven Techniques: A Regional Study of Bangladesh. Water 2022, 14, 1764. [Google Scholar] [CrossRef]
- Xu, L.; Chen, N.; Zhang, X.; Chen, Z. An evaluation of statistical, NMME and hybrid models for drought prediction in China. J. Hydrol. 2018, 566, 235–249. [Google Scholar] [CrossRef] [Green Version]
- Soh, Y.W.; Koo, C.H.; Huang, Y.F.; Fung, K.F. Application of artificial intelligence models for the prediction of standardized precipitation evapotranspiration index (SPEI) at Langat River Basin, Malaysia. Comput. Electron. Agric. 2018, 144, 164–173. [Google Scholar] [CrossRef]
- Agana, N.A.; Homaifar, A. EMD-Based Predictive Deep Belief Network for Time Series Prediction: An Application to Drought Forecasting. Hydrology 2018, 5, 18. [Google Scholar] [CrossRef]
- Nabipour, N.; Dehghani, M.; Mosavi, A.; Shamshirband, S. Short-Term Hydrological Drought Forecasting Based on Different Nature-Inspired Optimization Algorithms Hybridized With Artificial Neural Networks. IEEE Access 2020, 8, 15210–15222. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J.; Khalil, B. Short-term SPI drought forecasting in the Awash River Basin in Ethiopia using wavelet transforms and machine learning methods. Sustain. Water Resour. Manag. 2015, 2, 87–101. [Google Scholar] [CrossRef]
- Altunkaynak, A.; Jalilzadnezamabad, A. Extended lead time accurate forecasting of palmer drought severity index using hybrid wavelet-fuzzy and machine learning techniques. J. Hydrol. 2021, 601, 126619. [Google Scholar] [CrossRef]
- Başakın, E.E.; Ekmekcioğlu, Ö.; Özger, M. Drought prediction using hybrid soft-computing methods for semi-arid region. Modeling Earth Syst. Environ. 2020, 7, 2363–2371. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J. Standard Precipitation Index Drought Forecasting Using Neural Networks, Wavelet Neural Networks, and Support Vector Regression. Appl. Comput. Intell. Soft Comput. 2012, 2012, 794061. [Google Scholar] [CrossRef]
- Dikshit, A.; Pradhan, B.; Alamri, A.M. Short-Term Spatio-Temporal Drought Forecasting Using Random Forests Model at New South Wales, Australia. Appl. Sci. 2020, 10, 4254. [Google Scholar] [CrossRef]
- Park, H.; Kim, K.; Lee, D.k. Prediction of Severe Drought Area Based on Random Forest: Using Satellite Image and Topography Data. Water 2019, 11, 705. [Google Scholar] [CrossRef]
- Ali, Z.; Hussain, I.; Faisal, M.; Nazir, H.M.; Hussain, T.; Shad, M.Y.; Mohamd Shoukry, A.; Hussain Gani, S. Forecasting Drought Using Multilayer Perceptron Artificial Neural Network Model. Adv. Meteorol. 2017, 2017, 5681308. [Google Scholar] [CrossRef] [Green Version]
- Dikshit, A.; Pradhan, B.; Alamri, A.M. Temporal Hydrological Drought Index Forecasting for New South Wales, Australia Using Machine Learning Approaches. Atmosphere 2020, 11, 585. [Google Scholar] [CrossRef]
- Das, P.; Naganna, S.R.; Deka, P.C.; Pushparaj, J. Hybrid wavelet packet machine learning approaches for drought modeling. Environ. Earth Sci. 2020, 79, 221. [Google Scholar] [CrossRef]
- Bari Abarghouei, H.; Kousari, M.R.; Asadi Zarch, M.A. Prediction of drought in dry lands through feedforward artificial neural network abilities. Arab. J. Geosci. 2011, 6, 1417–1433. [Google Scholar] [CrossRef]
- Apaydin, H.; Taghi Sattari, M.; Falsafian, K.; Prasad, R. Artificial intelligence modelling integrated with Singular Spectral analysis and Seasonal-Trend decomposition using Loess approaches for streamflow predictions. J. Hydrol. 2021, 600, 126506. [Google Scholar] [CrossRef]
- Ren, T.; Liu, X.; Niu, J.; Lei, X.; Zhang, Z. Real-time water level prediction of cascaded channels based on multilayer perception and recurrent neural network. J. Hydrol. 2020, 585, 124783. [Google Scholar] [CrossRef]
- Ömer Faruk, D. A hybrid neural network and ARIMA model for water quality time series prediction. Eng. Appl. Artif. Intell. 2010, 23, 586–594. [Google Scholar] [CrossRef]
- Seo, I.w.; Yun, S.H.; Choi, S.Y. Forecasting Water Quality Parameters by ANN Model Using Pre-processing Technique at the Downstream of Cheongpyeong Dam. Procedia Eng. 2016, 154, 1110–1115. [Google Scholar] [CrossRef]
- Tiu, E.S.K.; Huang, Y.F.; Ng, J.L.; AlDahoul, N.; Ahmed, A.N.; Elshafie, A. An evaluation of various data pre-processing techniques with machine learning models for water level prediction. Nat. Hazards 2022, 110, 121–153. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Ortega-Martorell, S.; Kot, P.; Alkhaddar, R.M.; Abdellatif, M.; Gharghan, S.K.; Ahmed, M.S.; Hashim, K. A Method for Predicting Long-Term Municipal Water Demands Under Climate Change. Water Resour. Manag. 2020, 34, 1265–1279. [Google Scholar] [CrossRef]
- Khan, M.M.H.; Muhammad, N.S.; El-Shafie, A. Wavelet based hybrid ANN-ARIMA models for meteorological drought forecasting. J. Hydrol. 2020, 590, 125380. [Google Scholar] [CrossRef]
- Adnan, R.M.; Mostafa, R.R.; Islam, A.R.M.T.; Gorgij, A.D.; Kuriqi, A.; Kisi, O. Improving Drought Modeling Using Hybrid Random Vector Functional Link Methods. Water 2021, 13, 3379. [Google Scholar] [CrossRef]
- Alawsi, M.A.; Zubaidi, S.L.; Al-Bdairi, N.S.S.; Al-Ansari, N.; Hashim, K. Drought Forecasting: A Review and Assessment of the Hybrid Techniques and Data Pre-Processing. Hydrology 2022, 9, 115. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Mohamed, A.; Khatib, T.; Shareef, H.; Homod, R.Z.; Ali, J.A. Real time optimal schedule controller for home energy management system using new binary backtracking search algorithm. Energy Build. 2017, 138, 215–227. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Abdulkareem, I.H.; Hashim, K.S.; Al-Bugharbee, H.; Ridha, H.M.; Gharghan, S.K.; Al-Qaim, F.F.; Muradov, M.; Kot, P.; Al-Khaddar, R. Hybridised Artificial Neural Network Model with Slime Mould Algorithm: A Novel Methodology for Prediction of Urban Stochastic Water Demand. Water 2020, 12, 2692. [Google Scholar] [CrossRef]
- Ghafil, H.N.; Jármai, K. Dynamic differential annealed optimization: New metaheuristic optimization algorithm for engineering applications. Appl. Soft Comput. 2020, 93, 106392. [Google Scholar] [CrossRef]
- Jiao, S.; Chong, G.; Huang, C.; Hu, H.; Wang, M.; Heidari, A.A.; Chen, H.; Zhao, X. Orthogonally adapted Harris hawks optimization for parameter estimation of photovoltaic models. Energy 2020, 203, 117804. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Yousri, D.; Babu, T.S.; Beshr, E.; Eteiba, M.B.; Allam, D. A Robust Strategy Based on Marine Predators Algorithm for Large Scale Photovoltaic Array Reconfiguration to Mitigate the Partial Shading Effect on the Performance of PV System. IEEE Access 2020, 8, 112407–112426. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Shehabeldeen, T.A.; Elsheikh, A.H.; Zhou, J.; Ewees, A.A.; Al-qaness, M.A.A. Utilization of Random Vector Functional Link integrated with Marine Predators Algorithm for tensile behavior prediction of dissimilar friction stir welded aluminum alloy joints. J. Mater. Res. Technol. 2020, 9, 11370–11381. [Google Scholar] [CrossRef]
- Eid, A.; Kamel, S.; Abualigah, L. Marine predators algorithm for optimal allocation of active and reactive power resources in distribution networks. Neural Comput. Appl. 2021, 33, 14327–14355. [Google Scholar] [CrossRef]
- Unnikrishnan, P.; Jothiprakash, V. Daily rainfall forecasting for one year in a single run using Singular Spectrum Analysis. J. Hydrol. 2018, 561, 609–621. [Google Scholar] [CrossRef]
- Jothiprakash, V.; Unnikrishnan, P. Data-driven multi-time-step ahead daily rainfall forecasting using singular spectrum analysis-based data pre-processing. J. Hydroinformatics 2018, 20, 645–667. [Google Scholar] [CrossRef]
- Balket, S.F.; Asmael, N.M. Study the Characteristics of Public Bus Routes in Al Kut City. J. Eng. Sustain. Dev. 2021, 25, 3-186–3-194. [Google Scholar] [CrossRef]
- Edan, M.H.; Maarouf, R.M.; Hasson, J. Predicting the impacts of land use/land cover change on land surface temperature using remote sensing approach in Al Kut, Iraq. Phys. Chem. Earth Parts A/B/C 2021, 123, 103012. [Google Scholar] [CrossRef]
- Muter, S.A.; Nassif, W.G.; Al-Ramahy, Z.A.; Al-Taai, O.T. Analysis of Seasonal and Annual Relative Humidity Using GIS for Selected Stations over Iraq during the Period (1980–2017). J. Green Eng. 2020, 10, 9121–9135. [Google Scholar]
- Ahmad, H.Q.; Kamaruddin, S.A.; Harun, S.B.; Al-Ansari, N.; Shahid, S.; Jasim, R.M. Assessment of Spatiotemporal Variability of Meteorological Droughts in Northern Iraq Using Satellite Rainfall Data. KSCE J. Civ. Eng. 2021, 25, 4481–4493. [Google Scholar] [CrossRef]
- Capt, T.; Mirchi, A.; Kumar, S.; Walker, W.S. Urban Water Demand: Statistical Optimization Approach to Modeling Daily Demand. J. Water Resour. Plan. Manag. 2021, 147, 4020105. [Google Scholar] [CrossRef]
- NOAA. National Oceanic and Atmospheric Administration. Data Tools: Find a Station. Available online: https://www.ncdc.noaa.gov/cdo-web/datatools/findstation (accessed on 1 December 2021).
- Aghelpour, P.; Bahrami-Pichaghchi, H.; Kisi, O. Comparison of three different bio-inspired algorithms to improve ability of neuro fuzzy approach in prediction of agricultural drought, based on three different indexes. Comput. Electron. Agric. 2020, 170, 105279. [Google Scholar] [CrossRef]
- Alquraish, M.; Abuhasel, K.A.; Alqahtani, A.S.; Khadr, M. SPI-Based Hybrid Hidden Markov–GA, ARIMA–GA, and ARIMA–GA–ANN Models for Meteorological Drought Forecasting. Sustainability 2021, 13, 12576. [Google Scholar] [CrossRef]
- Islam, A.R.M.T.; Salam, R.; Yeasmin, N.; Kamruzzaman, M.; Shahid, S.; Fattah, M.A.; Uddin, A.S.M.S.; Shahariar, M.H.; Mondol, M.A.H.; Jhajharia, D.; et al. Spatiotemporal distribution of drought and its possible associations with ENSO indices in Bangladesh. Arab. J. Geosci. 2021, 14, 2681. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Salih, S.Q.; Kim, S.; Kim, N.W.; Yaseen, Z.M.; Singh, V.P. Drought index prediction using advanced fuzzy logic model: Regional case study over Kumaon in India. PLoS ONE 2020, 15, e0233280. [Google Scholar] [CrossRef] [PubMed]
- Djerbouai, S.; Souag-Gamane, D. Drought Forecasting Using Neural Networks, Wavelet Neural Networks, and Stochastic Models: Case of the Algerois Basin in North Algeria. Water Resour. Manag. 2016, 30, 2445–2464. [Google Scholar] [CrossRef]
- Evkaya, O.O.; Kurnaz, F.S. Forecasting drought using neural network approaches with transformed time series data. J. Appl. Stat. 2020, 48, 2591–2606. [Google Scholar] [CrossRef]
- Thom, H.C.S. A note on the gamma distribution. Mon. Weather. Rev. 1958, 86, 117–122. [Google Scholar] [CrossRef]
- Sönmez, F.K.; Kömüscü, A.Ü.; Erkan, A.; Turgu, E. An Analysis of Spatial and Temporal Dimension of Drought Vulnerability in Turkey Using the Standardized Precipitation Index. Nat. Hazards 2005, 35, 243–264. [Google Scholar] [CrossRef]
- Tigkas, D.; Vangelis, H.; Tsakiris, G. DrinC: A software for drought analysis based on drought indices. Earth Sci. Inform. 2014, 8, 697–709. [Google Scholar] [CrossRef]
- Fung, K.F.; Huang, Y.F.; Koo, C.H.; Soh, Y.W. Drought forecasting: A review of modelling approaches 2007–2017. J. Water Clim. Change 2020, 11, 771–799. [Google Scholar] [CrossRef]
- Freitas, A.A.; Drumond, A.; Carvalho, V.S.B.; Reboita, M.S.; Silva, B.C.; Uvo, C.B. Drought Assessment in São Francisco River Basin, Brazil: Characterization through SPI and Associated Anomalous Climate Patterns. Atmosphere 2021, 13, 41. [Google Scholar] [CrossRef]
- Tabachnick, B.G.; Fidell, L.S. Using Multivariate Statistics; Pearson: Boston, MA, USA, 2013. [Google Scholar]
- Kossieris, P.; Makropoulos, C. Exploring the Statistical and Distributional Properties of Residential Water Demand at Fine Time Scales. Water 2018, 10, 1481. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Ortega-Martorell, S.; Al-Bugharbee, H.; Olier, I.; Hashim, K.S.; Gharghan, S.K.; Kot, P.; Al-Khaddar, R. Urban Water Demand Prediction for a City That Suffers from Climate Change and Population Growth: Gauteng Province Case Study. Water 2020, 12, 1885. [Google Scholar] [CrossRef]
- Karami, F.; Dariane, A.B. Melody Search Algorithm Using Online Evolving Artificial Neural Network Coupled with Singular Spectrum Analysis for Multireservoir System Management. Iran. J. Sci. Technol. Trans. Civ. Eng. 2021, 46, 1445–1457. [Google Scholar] [CrossRef]
- Hassani, H.; Mahmoudvand, R. Multivariate Singular Spectrum Analysis: A General View and New Vector Forecasting Approach. Int. J. Energy Stat. 2013, 1, 55–83. [Google Scholar] [CrossRef]
- Golyandina, N.; Zhigljavsky, A. Singular Spectrum Analysis for Time Series, 2nd ed.; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Al-Bugharbee, H.; Trendafilova, I. A fault diagnosis methodology for rolling element bearings based on advanced signal pretreatment and autoregressive modelling. J. Sound Vib. 2016, 369, 246–265. [Google Scholar] [CrossRef]
- Saayman, A.; de Klerk, J. Forecasting tourist arrivals using multivariate singular spectrum analysis. Tour. Econ. 2019, 25, 330–354. [Google Scholar] [CrossRef]
- Ouyang, Q.; Lu, W. Monthly Rainfall Forecasting Using Echo State Networks Coupled with Data Preprocessing Methods. Water Resour. Manag. 2017, 32, 659–674. [Google Scholar] [CrossRef]
- Khan, M.A.R.; Poskitt, D.S. Forecasting stochastic processes using singular spectrum analysis: Aspects of the theory and application. Int. J. Forecast. 2017, 33, 199–213. [Google Scholar] [CrossRef]
- Zubaidi, S.; Al-Bugharbee, H.; Ortega-Martorell, S.; Gharghan, S.; Olier, I.; Hashim, K.; Al-Bdairi, N.; Kot, P. A Novel Methodology for Prediction Urban Water Demand by Wavelet Denoising and Adaptive Neuro-Fuzzy Inference System Approach. Water 2020, 12, 1628. [Google Scholar] [CrossRef]
- Sundararajan, K.; Garg, L.; Srinivasan, K.; Kashif Bashir, A.; Kaliappan, J.; Pattukandan Ganapathy, G.; Kumaran Selvaraj, S.; Meena, T. A Contemporary Review on Drought Modeling Using Machine Learning Approaches. Comput. Modeling Eng. Sci. 2021, 128, 447–487. [Google Scholar] [CrossRef]
- Pallant, J. SPSS Survival Manual: A Step by Step Guide to Data Analysis Using IBM SPSS, 6th ed.; McGraw-Hill Education: New York, NY, USA, 2016. [Google Scholar]
- Clerc, M.; Kennedy, J. The particle swarm—Explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Rather, S.A.; Bala, P.S. Hybridization of Constriction Coefficient-Based Particle Swarm Optimization and Chaotic Gravitational Search Algorithm for Solving Engineering Design Problems. In Applied Soft Computing and Communication Networks; Springer: Singapore, 2020; Volume 125, pp. 95–115. [Google Scholar]
- Zubaidi, S.L.; Gharghan, S.K.; Dooley, J.; Alkhaddar, R.M.; Abdellatif, M. Short-Term Urban Water Demand Prediction Considering Weather Factors. Water Resour. Manag. 2018, 32, 4527–4542. [Google Scholar] [CrossRef]
- Mokhtarzad, M.; Eskandari, F.; Jamshidi Vanjani, N.; Arabasadi, A. Drought forecasting by ANN, ANFIS, and SVM and comparison of the models. Environ. Earth Sci. 2017, 76, 729. [Google Scholar] [CrossRef]
- Morid, S.; Smakhtin, V.; Bagherzadeh, K. Drought forecasting using artificial neural networks and time series of drought indices. Int. J. Climatol. 2007, 27, 2103–2111. [Google Scholar] [CrossRef]
- Payal, A.; Rai, C.S.; Reddy, B.V.R. Analysis of Some Feedforward Artificial Neural Network Training Algorithms for Developing Localization Framework in Wireless Sensor Networks. Wirel. Pers. Commun. 2015, 82, 2519–2536. [Google Scholar] [CrossRef]
- Mohammadi, B.; Mehdizadeh, S. Modeling daily reference evapotranspiration via a novel approach based on support vector regression coupled with whale optimization algorithm. Agric. Water Manag. 2020, 237, 106145. [Google Scholar] [CrossRef]
- Mohammadi, B.; Linh, N.T.T.; Pham, Q.B.; Ahmed, A.N.; Vojteková, J.; Guan, Y.; Abba, S.I.; El-Shafie, A. Adaptive neuro-fuzzy inference system coupled with shuffled frog leaping algorithm for predicting river streamflow time series. Hydrol. Sci. J. 2020, 65, 1738–1751. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Dawson, C.W.; Abrahart, R.J.; See, L.M. HydroTest: A web-based toolbox of evaluation metrics for the standardised assessment of hydrological forecasts. Environ. Model. Softw. 2007, 22, 1034–1052. [Google Scholar] [CrossRef]
- Valentini, M.; dos Santos, G.B.; Muller Vieira, B. Multiple linear regression analysis (MLR) applied for modeling a new WQI equation for monitoring the water quality of Mirim Lagoon, in the state of Rio Grande do Sul—Brazil. SN Appl. Sci. 2021, 3, 70. [Google Scholar] [CrossRef]
- Nourani, V.; Molajou, A.; Uzelaltinbulat, S.; Sadikoglu, F. Emotional artificial neural networks (EANNs) for multi-step ahead prediction of monthly precipitation. A case study: Northern Cyprus. Theor. Appl. Climatol. 2019, 138, 1419–1434. [Google Scholar] [CrossRef]
- Khan, M.; Muhammad, N.; El-Shafie, A. Wavelet-ANN versus ANN-Based Model for Hydrometeorological Drought Forecasting. Water 2018, 10, 998. [Google Scholar] [CrossRef] [Green Version]
- Ahmadi, F.; Mehdizadeh, S.; Mohammadi, B. Development of Bio-Inspired- and Wavelet-Based Hybrid Models for Reconnaissance Drought Index Modeling. Water Resour. Manag. 2021, 35, 4127–4147. [Google Scholar] [CrossRef]

| Variable (Monthly) | Mean | Max. | Min. | Std. Dev. |
|---|---|---|---|---|
| SPI 1 | 0.191 | 2.53 | −2.85 | 0.898 |
| SPI 3 | 0.0182 | 2.58 | −2.98 | 0.98 |
| SPI 6 | 0.0007 | 2.43 | −3.06 | 1.002 |
| SPI Values | Class |
|---|---|
| >2 | Extremely wet |
| 1.5 to 1.99 | Very wet |
| 1.0 to 1.49 | Moderately wet |
| −0.99 to 0.99 | Near normal |
| −1 to −1.49 | Moderately dry |
| −1.5 to −1.99 | Severely dry |
| <−2 | Extremely dry |
| Target | Climatic Variables | Tolerance Value |
|---|---|---|
| SPI 1 | Rain | 0.292 |
| RH | 0.240 | |
| Twet | 0.577 | |
| Wmin | 0.678 | |
| SPI 3 | Rain | 0.292 |
| RH | 0.241 | |
| Twet | 0.578 | |
| Wmin | 0.682 | |
| SPI 6 | Rain | 0.291 |
| RH | 0.242 | |
| Twet | 0.579 | |
| Wmin | 0.686 |
| Model | Parameter | CPSOCGSA | MPA | SMA |
|---|---|---|---|---|
| SPI 1 | N1 | 3 | 5 | 7 |
| N2 | 7 | 5 | 13 | |
| Lr | 0.3686 | 0.0010 | 0.4192 | |
| SPI 3 | N1 | 4 | 10 | 3 |
| N2 | 5 | 1 | 14 | |
| Lr | 0.5841 | 0.1115 | 0.6413 | |
| SPI 6 | N1 | 5 | 9 | 3 |
| N2 | 3 | 1 | 4 | |
| Lr | 0.2747 | 0.0013 | 0.2570 |
| Target | Model | R2 | MAE | RMSE |
|---|---|---|---|---|
| SPI 1 | CPSOCGSA-ANN | 0.93 | 0.0635 | 0.0791 |
| MPA-ANN | 0.86 | 0.0840 | 0.0976 | |
| SMA-ANN | 0.78 | 0.0961 | 0.1127 | |
| SPI 3 | CPSOCGSA-ANN | 0.93 | 0.1020 | 0.1270 |
| MPA-ANN | 0.91 | 0.1172 | 0.1344 | |
| SMA-ANN | 0.86 | 0.1220 | 0.1676 | |
| SPI 6 | CPSOCGSA-ANN | 0.88 | 0.2004 | 0.2334 |
| MPA-ANN | 0.86 | 0.2186 | 0.2589 | |
| SMA-ANN | 0.78 | 0.2618 | 0.3001 |
| Target | Kolmogorov–Smirnova (K–S) | Shapiro–Wilk (S–W) |
|---|---|---|
| SPI 1 | 0.200 | 0.224 |
| SPI 3 | 0.200 | 0.545 |
| SPI 6 | 0.200 | 0.340 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alawsi, M.A.; Zubaidi, S.L.; Al-Ansari, N.; Al-Bugharbee, H.; Ridha, H.M. Tuning ANN Hyperparameters by CPSOCGSA, MPA, and SMA for Short-Term SPI Drought Forecasting. Atmosphere 2022, 13, 1436. https://doi.org/10.3390/atmos13091436
Alawsi MA, Zubaidi SL, Al-Ansari N, Al-Bugharbee H, Ridha HM. Tuning ANN Hyperparameters by CPSOCGSA, MPA, and SMA for Short-Term SPI Drought Forecasting. Atmosphere. 2022; 13(9):1436. https://doi.org/10.3390/atmos13091436
Chicago/Turabian StyleAlawsi, Mustafa A., Salah L. Zubaidi, Nadhir Al-Ansari, Hussein Al-Bugharbee, and Hussein Mohammed Ridha. 2022. "Tuning ANN Hyperparameters by CPSOCGSA, MPA, and SMA for Short-Term SPI Drought Forecasting" Atmosphere 13, no. 9: 1436. https://doi.org/10.3390/atmos13091436
APA StyleAlawsi, M. A., Zubaidi, S. L., Al-Ansari, N., Al-Bugharbee, H., & Ridha, H. M. (2022). Tuning ANN Hyperparameters by CPSOCGSA, MPA, and SMA for Short-Term SPI Drought Forecasting. Atmosphere, 13(9), 1436. https://doi.org/10.3390/atmos13091436










