Estimation of Potential Evapotranspiration in the Yellow River Basin Using Machine Learning Models
Abstract
:1. Introduction
2. Materials and Methods
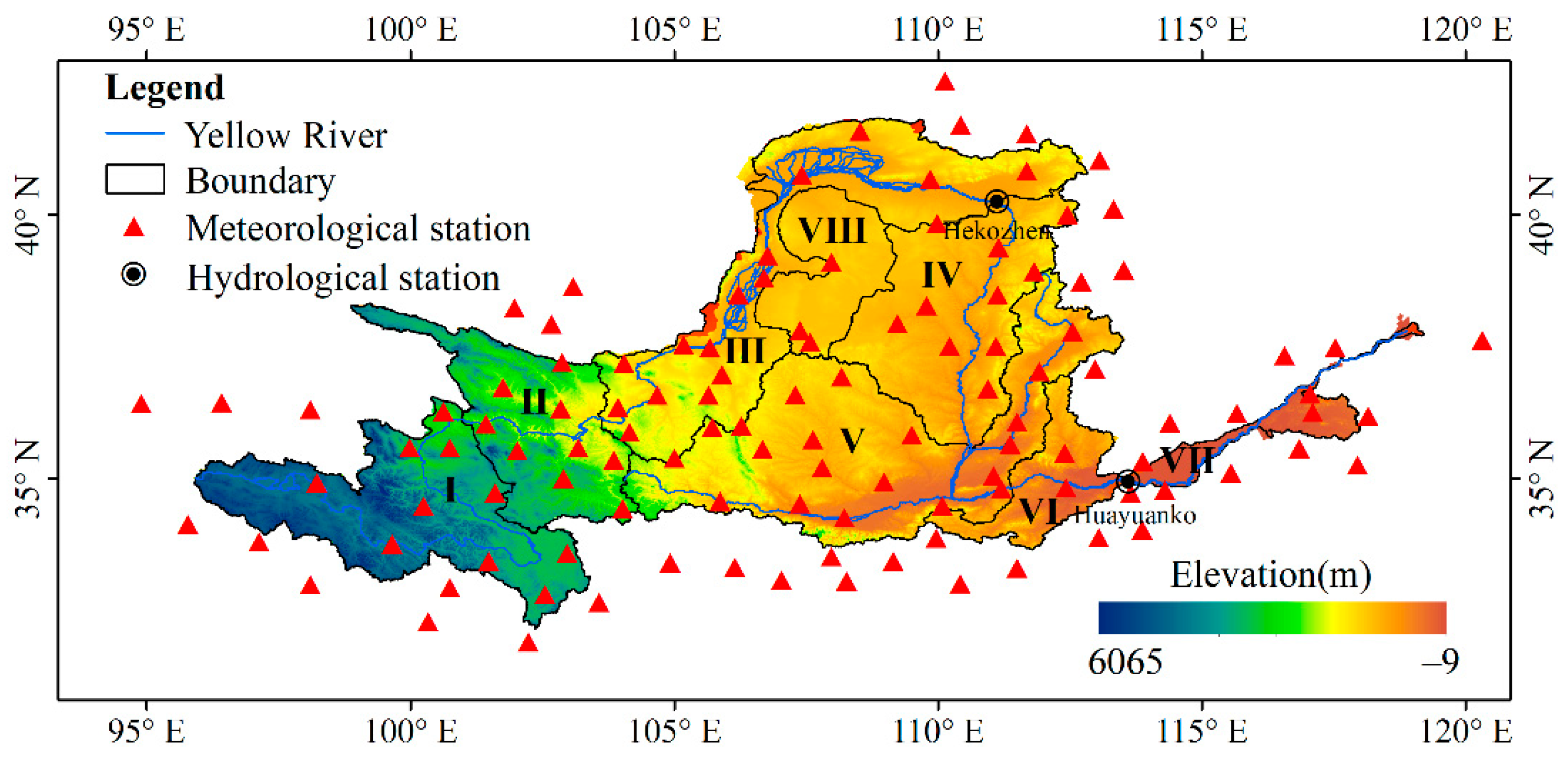
2.1. Study Area
2.2. Empirical Models for Estimation of PET
2.3. Machine Learning Algorithms
2.4. Evaluation Indicators
3. Results
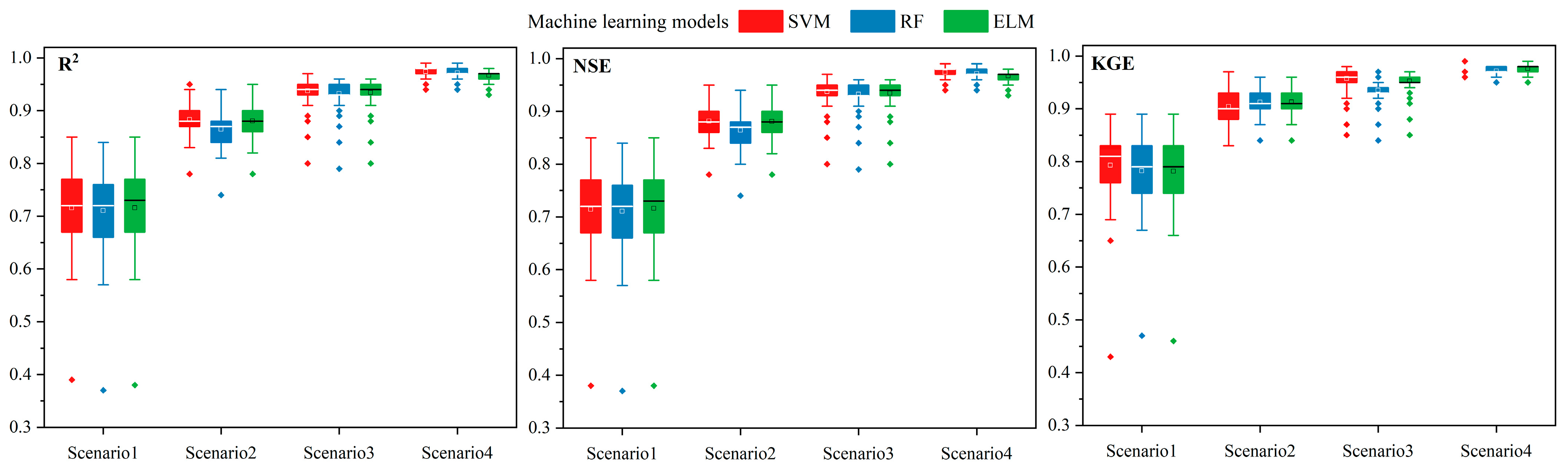
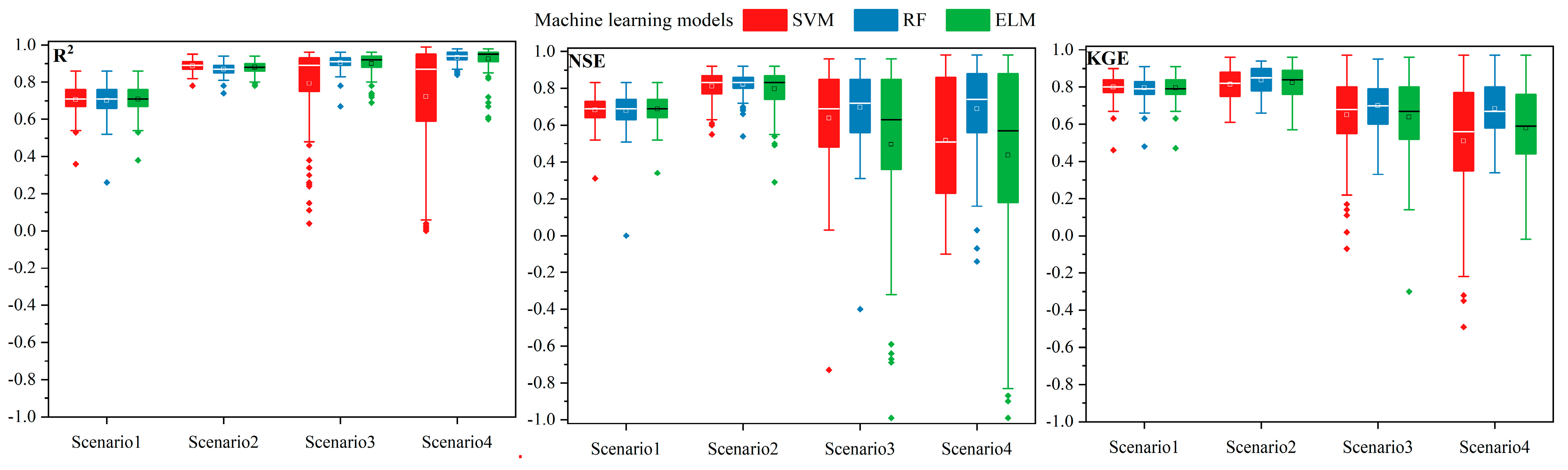
3.1. Performance Evaluation of Machine Learning Models
3.1.1. Machine Learning Model Input Scenario
3.1.2. Performance of the Machine Learning Model during Training and Testing Periods
3.1.3. Stability Evaluation of Machine Learning Models
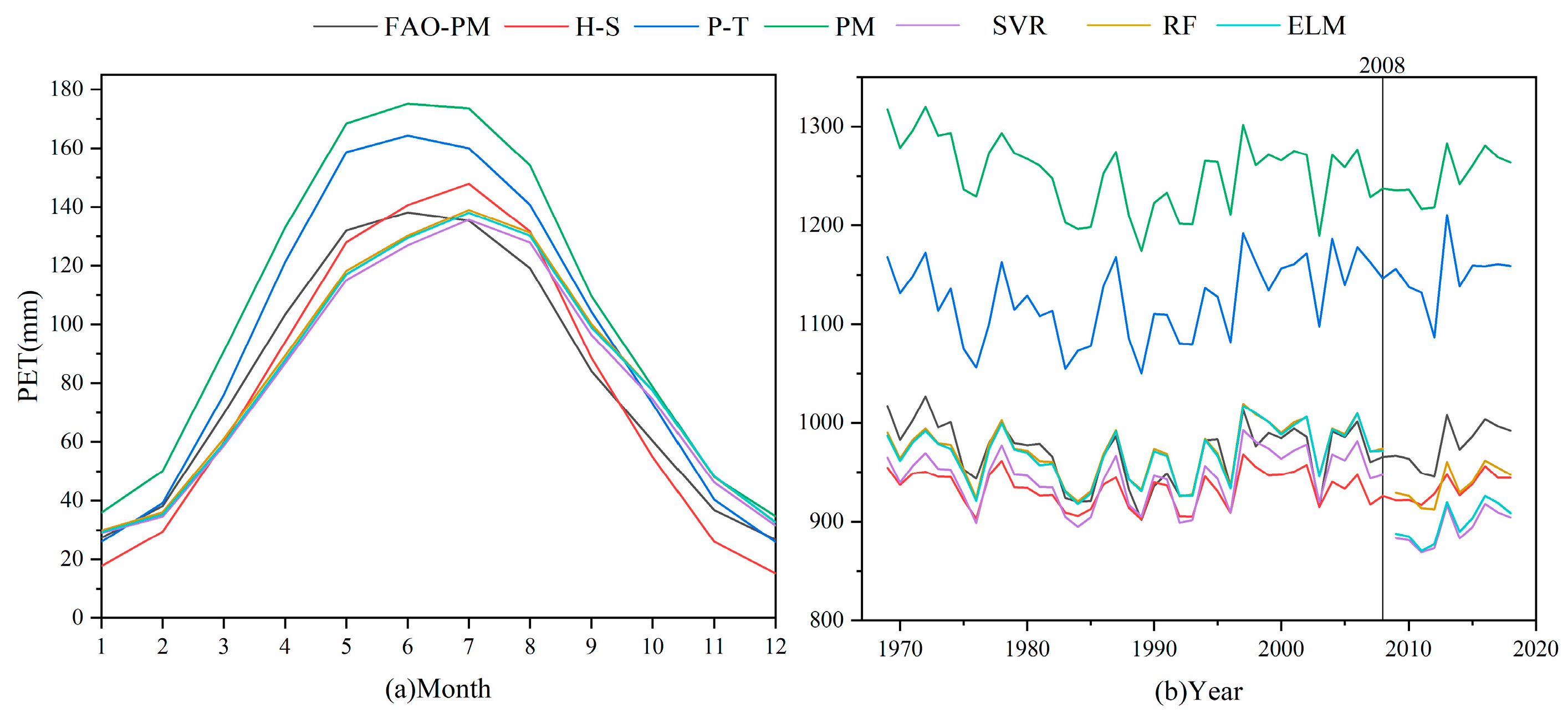
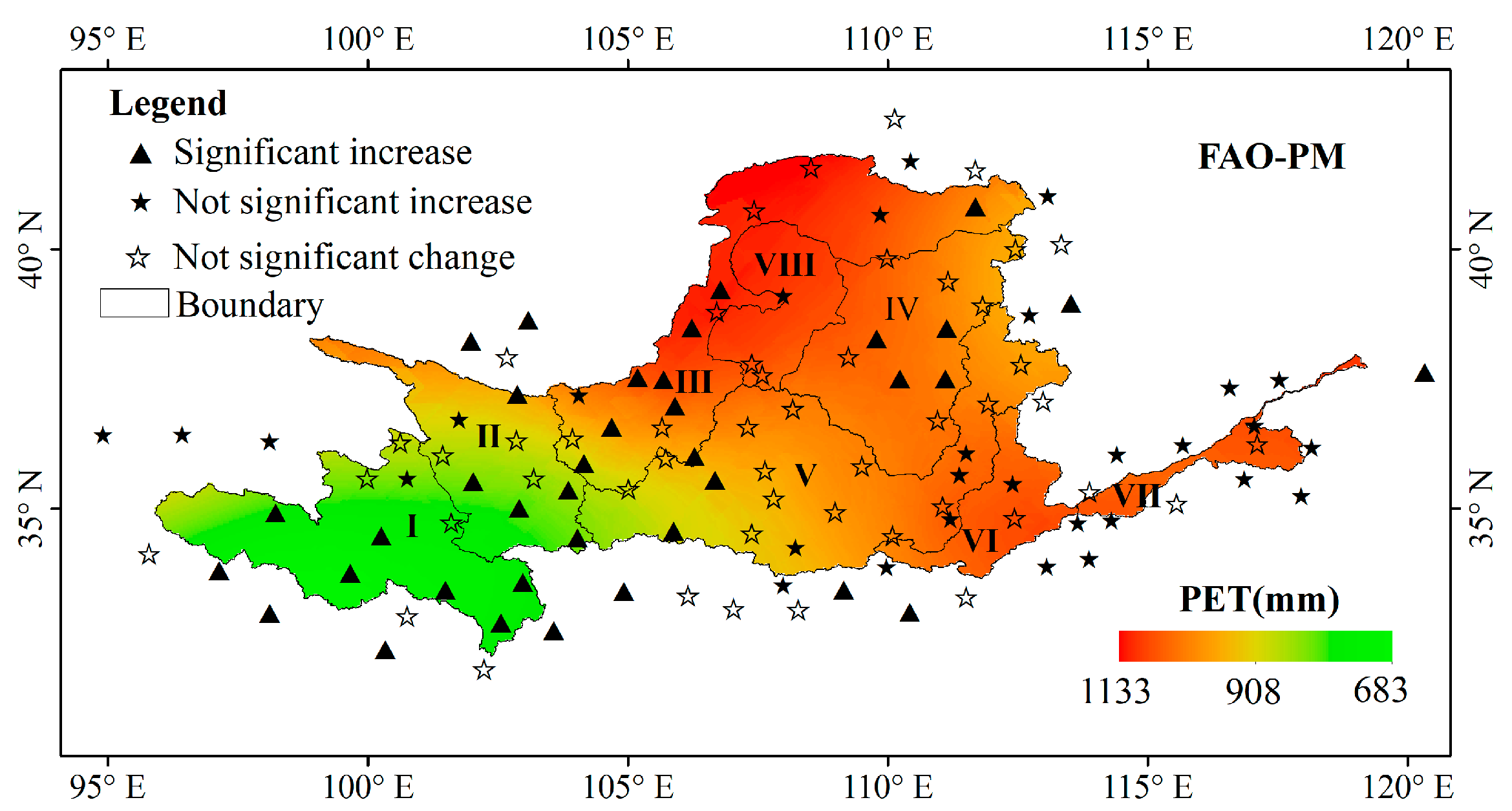
3.2. Spatiotemporal Variation of PET
3.3. Comparative Analysis of Machine Learning Models and Empirical Models
4. Discussion
4.1. Comparative Analysis of PET Calculation Models
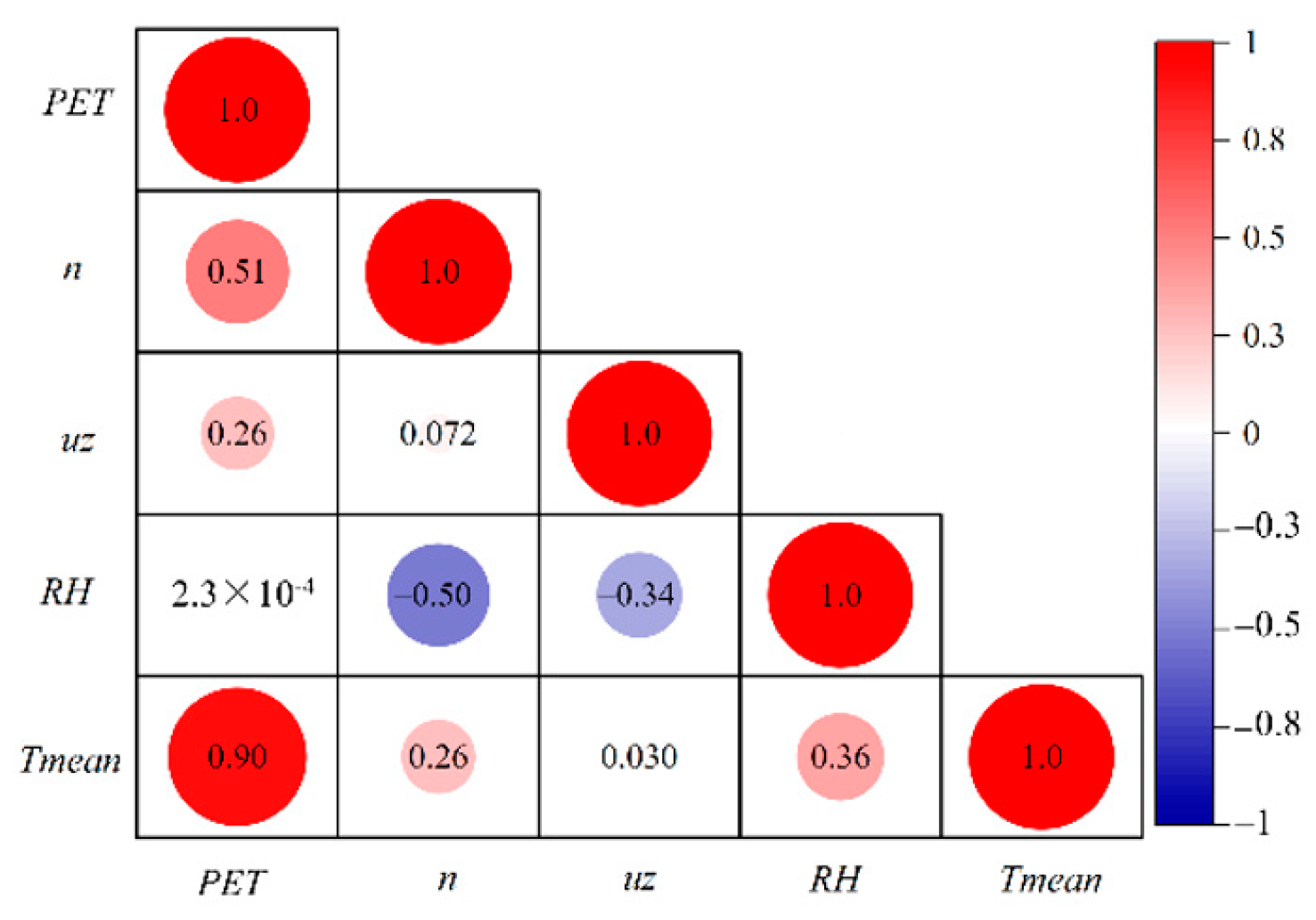
4.2. Factors Affecting the Accuracy of Machine Learning Estimation
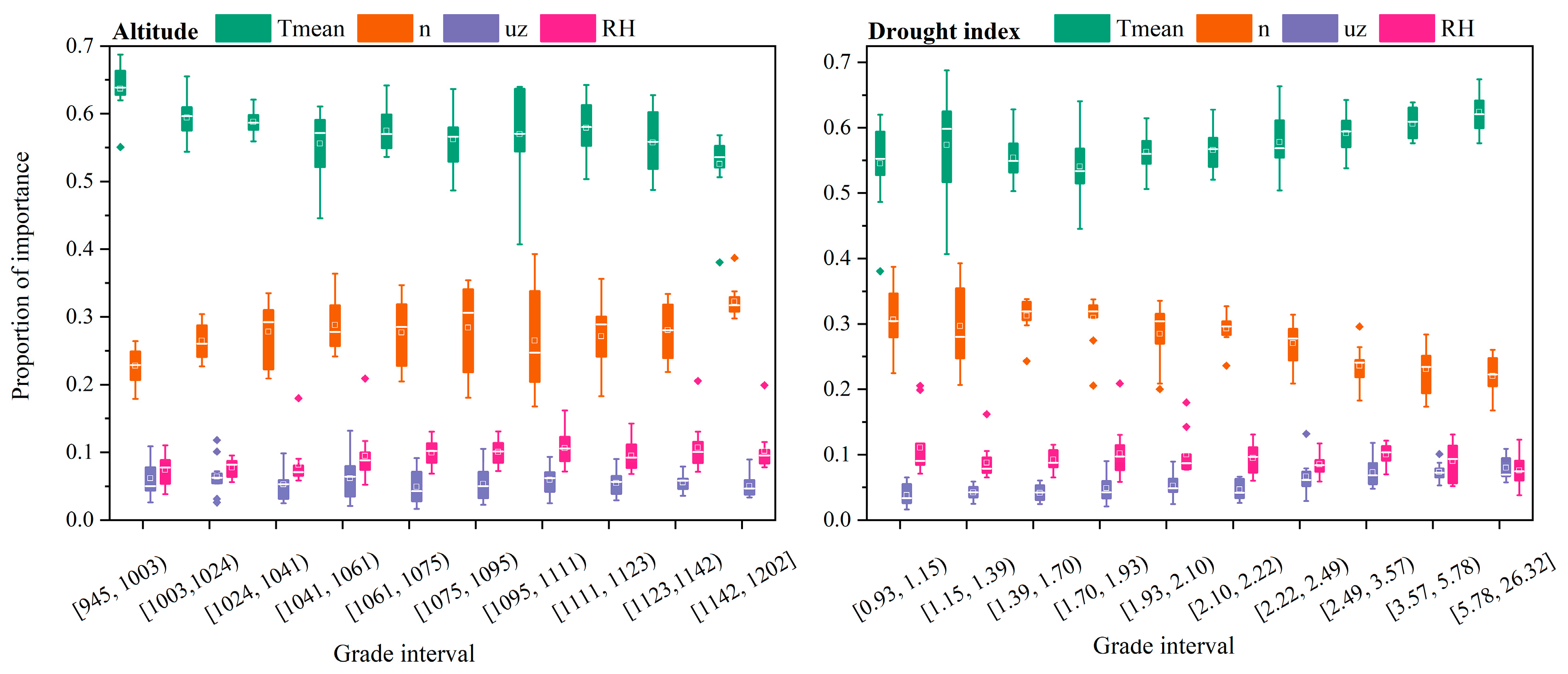
4.3. Importance of Meteorological Factors of Altitude and Drought Index for PET Predictions
5. Conclusions
- (1)
- Average temperature (Tmean) and sunshine hours (n) can be used as input combinations of the model to obtain satisfactory daily potential evapotranspiration (PET) predictions when lacking complete meteorological variables and using machine learning to estimate PET in the Yellow River basin (YRB).
- (2)
- A comparison of the selected machine learning and empirical models shows that machine learning models limited to two input variables generally perform better than empirical models, and the empirical models usually overestimate or underestimate. Among the six models, random forest (RF) performs best in general, followed by extreme learning machine; none of the six methods selected in this study are optimal for prediction in all watersheds.
- (3)
- Analysis of variance results show that the accuracy of PET simulation in the YRB depends on the input scenario of different meteorological factors at the significance level of 0.05 relative to machine learning models.
- (4)
- According to the importance index provided by RF simulation, Tmean is the most important factor, followed by n. However, the influence of Tmean on PET gradually decreases with increased altitude and gradually increases with a drier climate, whereas the influence of n shows the opposite trend. The importance of relative humidity is higher than that of wind speed, in contrast to the ranking calculated by the Spearman correlation coefficient with PET, indicating that the simulation of PET is a complex, nonlinear calculation process.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, J.; Wang, Y.; Su, B.; Wang, A.; Tao, H.; Zhai, J.; Kundzewicz, Z.W.; Jiang, T. Choice of potential evapotranspiration formulas influences drought assessment: A case study in China. Atmos. Res. 2020, 242, 104979. [Google Scholar] [CrossRef]
- Wang, W.; Shao, Q.; Peng, S.; Xing, W.; Yang, T.; Luo, Y.; Yong, B.; Xu, J. Reference evapotranspiration change and the causes across the Yellow River Basin during 1957–2008 and their spatial and seasonal differences. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Zhang, B.; Xu, D.; Liu, Y.; Chen, H. Review of multi-scale evapotranspiration estimation and spatio-temporal scale expansion. Trans. Chin. Soc. Agric. Eng. 2015, 31, 8–16. (In Chinese) [Google Scholar]
- Kim, D.; Chun, J.A.; Ko, J. A hybrid approach combining the FAO-56 method and the complementary principle for predicting daily evapotranspiration on a rainfed crop field. J. Hydrol. 2019, 577, 123941. [Google Scholar] [CrossRef]
- Liu, X.; Yang, W.; Zhao, H.; Wang, Y.; Wang, G. Effects of the freeze-thaw cycle on potential evapotranspiration in the permafrost regions of the Qinghai-Tibet Plateau, China. Sci. Total Environ. 2019, 687, 257–266. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Sun, G.; McNulty, S.G.; Amatya, D.M. A Comparison of Six Potential Evapotranspiration Methods for Regional Use in the Southeastern United States. J. Am. Water Resour. As. 2005, 41, 621–633. [Google Scholar] [CrossRef]
- Bai, P.; Liu, X.; Yang, T.; Li, F.; Liang, K.; Hu, S.; Liu, C.J.J. Assessment of the influences of different potential evapotranspiration inputs on the performance of monthly hydrological models under different climatic conditions. J. Hydrometeorol. 2016, 17, 2259–2274. [Google Scholar] [CrossRef]
- Band, L.E.; Mackay, D.S.; Creed, I.F.; Semkin, R.; Jeffries, D. Ecosystem processes at the watershed scale: Sensitivity to potential climate change. Limnol. Oceanogr. 1996, 41, 928–938. [Google Scholar] [CrossRef]
- Hay, L.E.; McCabe, G.J. Spatial Variability in Water-Balance Model Performance in the Conterminous United States. J. Am. Water Resour. Assoc. 2002, 38, 847–860. [Google Scholar] [CrossRef]
- Xiang, K.; Li, Y.; Horton, R.; Feng, H. Similarity and difference of potential evapotranspiration and reference crop evapotranspiration—A review. Agr. Water Manag. 2020, 232, 106043. [Google Scholar] [CrossRef]
- Li, S.; Kang, S.; Zhang, L.; Zhang, J.; Du, T.; Tong, L.; Ding, R. Evaluation of six potential evapotranspiration models for estimating crop potential and actual evapotranspiration in arid regions. J. Hydrol. 2016, 543, 450–461. [Google Scholar] [CrossRef]
- Um, M.J.; Kim, Y.; Park, D.; Jung, K.; Wang, Z.; Kim, M.M.; Shin, H. Impacts of potential evapotranspiration on drought phenomena in different regions and climate zones. Sci. Total Environ. 2020, 703, 135590. [Google Scholar] [CrossRef] [PubMed]
- Lang, D.; Zheng, J.; Shi, J.; Liao, F.; Ma, X.; Wang, W.; Chen, X.; Zhang, M. A Comparative Study of Potential Evapotranspiration Estimation by Eight Methods with FAO Penman–Monteith Method in Southwestern China. Water 2017, 9, 734. [Google Scholar] [CrossRef]
- Grismer, M.E.; Orang, M.; Snyder, R.; Matyac, R. Pan Evaporation to Reference Evapotranspiration Conversion Methods. J. Irrig. Drain Eng. 2002, 128, 180–184. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, R.; Han, C.; Liu, Z. Evaluation of 18 models for calculating potential evapotranspiration in different climatic zones of China. Agr. Water Manag. 2021, 244, 106545. [Google Scholar] [CrossRef]
- Bormann, H. Sensitivity analysis of 18 different potential evapotranspiration models to observed climatic change at German climate stations. Clim. Chang. 2010, 104, 729–753. [Google Scholar] [CrossRef]
- Allan, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration-Guidelines for computing crop water requirements—FAO Irrigation and drainage paper 56. FAO Rome 1998, 300, D05109. [Google Scholar]
- Xu, C.-y.; Gong, L.; Jiang, T.; Chen, D.; Singh, V.P. Analysis of spatial distribution and temporal trend of reference evapotranspiration and pan evaporation in Changjiang (Yangtze River) catchment. J. Hydrol. 2006, 327, 81–93. [Google Scholar] [CrossRef]
- Fan, J.; Wang, X.; Wu, L.; Zhou, H.; Zhang, F.; Yu, X.; Lu, X.; Xiang, Y. Comparison of Support Vector Machine and Extreme Gradient Boosting for predicting daily global solar radiation using temperature and precipitation in humid subtropical climates: A case study in China. Energ. Convers. Manag. 2018, 164, 102–111. [Google Scholar] [CrossRef]
- Mattar, M.A. Using gene expression programming in monthly reference evapotranspiration modeling: A case study in Egypt. Agr. Water Manag. 2018, 198, 28–38. [Google Scholar] [CrossRef]
- Taormina, R.; Chau, K.-W. Data-driven input variable selection for rainfall–runoff modeling using binary-coded particle swarm optimization and Extreme Learning Machines. J. Hydrol. 2015, 529, 1617–1632. [Google Scholar] [CrossRef]
- Acharya, N.; Shrivastava, N.A.; Panigrahi, B.K.; Mohanty, U.C. Development of an artificial neural network based multi-model ensemble to estimate the northeast monsoon rainfall over south peninsular India: An application of extreme learning machine. Clim. Dynam. 2013, 43, 1303–1310. [Google Scholar] [CrossRef]
- Deo, R.C.; Tiwari, M.K.; Adamowski, J.F.; Quilty, J.M. Forecasting effective drought index using a wavelet extreme learning machine (W-ELM) model. Stoch. Env. Res. Risk A 2016, 31, 1211–1240. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.; Zhao, L.; Hu, X.; Gong, D. Comparison of ELM, GANN, WNN and empirical models for estimating reference evapotranspiration in humid region of Southwest China. J. Hydrol. 2016, 536, 376–383. [Google Scholar] [CrossRef]
- Tabari, H.; Kisi, O.; Ezani, A.; Hosseinzadeh Talaee, P. SVM, ANFIS, regression and climate based models for reference evapotranspiration modeling using limited climatic data in a semi-arid highland environment. J. Hydrol. 2012, 444–445, 78–89. [Google Scholar] [CrossRef]
- Antonopoulos, V.Z.; Antonopoulos, A.V. Daily reference evapotranspiration estimates by artificial neural networks technique and empirical equations using limited input climate variables. Comput. Electron. Agric. 2017, 132, 86–96. [Google Scholar] [CrossRef]
- Huang, G.; Wu, L.; Ma, X.; Zhang, W.; Fan, J.; Yu, X.; Zeng, W.; Zhou, H.J.J. Evaluation of CatBoost method for prediction of reference evapotranspiration in humid regions. J. Hydrol. 2019, 574, 1029–1041. [Google Scholar] [CrossRef]
- Salam, R.; Islam, A.R.M.T. Potential of RT, bagging and RS ensemble learning algorithms for reference evapotranspiration prediction using climatic data-limited humid region in Bangladesh. J. Hydrol. 2020, 590, 125241. [Google Scholar] [CrossRef]
- Wen, X.; Si, J.; He, Z.; Wu, J.; Shao, H.; Yu, H. Support-Vector-Machine-Based Models for Modeling Daily Reference Evapotranspiration with Limited Climatic Data in Extreme Arid Regions. Water Resour. Manag. 2015, 29, 3195–3209. [Google Scholar] [CrossRef]
- Yamaç, S.S.; Todorovic, M. Estimation of daily potato crop evapotranspiration using three different machine learning algorithms and four scenarios of available meteorological data. Agr. Water Manag. 2020, 228, 105875. [Google Scholar] [CrossRef]
- AR6 Climate Change 2021: The Physical Science Basis Intergovernmental Panel. 2021. Available online: https://www.ipcc.ch/report/ar6/wg1/ (accessed on 17 May 2022).
- Jia, L.; Yu, K.; Li, Z.; Li, P.; Zhang, J.; Wang, A.; Ma, L.; Xu, G.; Zhang, X. Temporal and spatial variation of rainfall erosivity in the Loess Plateau of China and its impact on sediment load. CATENA 2022, 210, 0341–8162. [Google Scholar] [CrossRef]
- Ullah, I.; Ma, X.; Ren, G.; Yin, J.; Iyakaremye, V.; Syed, S.; Lu, K.; Xing, Y.; Singh, V.P. Recent Changes in Drought Events over South Asia and Their Possible Linkages with Climatic and Dynamic Factors. Remote Sens. 2022, 14, 3219. [Google Scholar] [CrossRef]
- Ullah, I.; Saleem, F.; Iyakaremye, V.; Yin, J.; Ma, X.; Syed, S.; Hina, S.; Asfaw, T.G.; Omer, A. Projected Changes in Socioeconomic Exposure to Heatwaves in South Asia Under Changing Climate. Earth’s Future 2022, 10, e2021EF002240. [Google Scholar] [CrossRef]
- Ullah, I.; Ma, X.; Yin, J.; Omer, A.; Habtemicheal, B.A.; Saleem, F.; Iyakaremye, V.; Syed, S.; Arshad, M.; Liu, M. Spatiotemporal characteristics of meteorological drought variability and trends (1981–2020) over South Asia and the associated large-scale circulation patterns. Clim. Dyn. 2022, 1–24. [Google Scholar] [CrossRef]
- Xi, J. Speech at the symposium on ecological protection and quality development in Speech at the symposium on ecological protection and quality development in the Yellow River Basin. Water Resour. Dev. Manag. 2019, 1–4. (In Chinese) [Google Scholar] [CrossRef]
- Guo, H. Sustainable development and ecological environment protection in high-quality development of the Yellow River Basin. J. Humanit. 2020, 17–21. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, W.; Ji, X.; Liu, H. Progresses in Evapotranspiration Research and Prospect in Desert Oasis Evapotranspiration Research. Arid Zone Res. 2011, 28, 463–470. (In Chinese) [Google Scholar]
- Zhao, Y.; He, F.; He, G.; Li, H.; Wang, L.; Chang, H.; Zhu, Y. Review the Phenomenon of Yellow River Cutoff from a Whole Perspective and ldentification of Current Water Shortage. Yellow River 2020, 42, 42–46. (In Chinese) [Google Scholar]
- Wang, W.; Zhang, Y.; Tang, Q. Impact assessment of climate change and human activities on streamflow signatures in the Yellow River Basin using the Budyko hypothesis and derived differential equation. J. Hydrol. 2020, 591, 125460. [Google Scholar] [CrossRef]
- Liu, F.; Chen, S.; Dong, P.; Peng, J. Temporal and spatial variation of runoff in the Yellow River Basin in the past 60 years. J. Geogr. Sci. 2012, 22, 1013–1033. [Google Scholar] [CrossRef]
- Ringler, C.; Cai, X.; Wang, J.; Ahmed, A.; Xue, Y.; Xu, Z.; Yang, E.; Jianshi, Z.; Zhu, T.; Cheng, L.; et al. Yellow River basin: Living with scarcity. Water Int. 2010, 35, 681–701. [Google Scholar] [CrossRef]
- Miao, C.; Ni, J.; Borthwick, A.G.L.; Yang, L. A preliminary estimate of human and natural contributions to the changes in water discharge and sediment load in the Yellow River. Glob. Planet Chang. 2011, 76, 196–205. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, A.Z. Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Priestley, C.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large Scale Parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Penman, H.L. Vegtation and Hydrology. Soil Sci. 1963, 96, 357. [Google Scholar] [CrossRef]
- Douglas, E.M.; Jacobs, J.M.; Sumner, D.M.; Ray, R.L. A comparison of models for estimating potential evapotranspiration for Florida land cover types. J. Hydrol. 2009, 373, 366–376. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Chen, J.T.; Zhong, J.; Xie, Y.C.; Cai, C.Y. Text Classification Using SVM with Exponential Kernel. Appl. Mech. Mater. 2014, 519–520, 807–810. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wang, S.; Lian, J.; Peng, Y.; Hu, B.; Chen, H. Generalized reference evapotranspiration models with limited climatic data based on random forest and gene expression programming in Guangxi, China. Agr. Water Manag. 2019, 221, 220–230. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Dou, X.; Yang, Y. Applications of Machine Learning Methods in Modeling Carbon and Water Fluxes of Terrestrial Ecosystems. Ph.D. Thesis, China University of Mining University, Beijing, China, 2018. [Google Scholar]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Meles, M.B.; Goodrich, D.C.; Gupta, H.V.; Shea Burns, I.; Unkrich, C.L.; Razavi, S.; Guertin, D.P. Multi-criteria, time dependent sensitivity analysis of an event-oriented, physically-based, distributed sediment and runoff model. J. Hydrol. 2021, 598, 126268. [Google Scholar] [CrossRef]
- Yu, K.-x.; Zhang, X.; Xu, B.; Li, P.; Zhang, X.; Li, Z.; Zhao, Y. Evaluating the impact of ecological construction measures on water balance in the Loess Plateau region of China within the Budyko framework. J. Hydrol. 2021, 601, 126596. [Google Scholar] [CrossRef]
- Moral, F.J.; Paniagua, L.L.; Rebollo, F.J.; García-Martín, A. Spatial analysis of the annual and seasonal aridity trends in Extremadura, southwestern Spain. Theor. Appl. Climatol. 2017, 130, 917–932. [Google Scholar] [CrossRef]
- Dong, J.; Zhu, Y.; Jia, X.; Shao, M.a.; Han, X.; Qiao, J.; Bai, C.; Tang, X. Nation-scale reference evapotranspiration estimation by using deep learning and classical machine learning models in China. J. Hydrol. 2022, 604, 127207. [Google Scholar] [CrossRef]
- Martínez-Cob, A.; Tejero-Juste, M. A wind-based qualitative calibration of the Hargreaves ET0 estimation equation in semiarid regions. Agr. Water Manag. 2004, 64, 251–264. [Google Scholar] [CrossRef]
- Khoob, R.A. Comparative study of Hargreaves’s and artificial neural network’s methodologies in estimating reference evapotranspiration in a semiarid environment. Irrig. Sci. 2008, 26, 253–259. [Google Scholar] [CrossRef]
- Granata, F. Evapotranspiration evaluation models based on machine learning algorithms—A comparative study. Agr. Water Manag. 2019, 217, 303–315. [Google Scholar] [CrossRef]
- Fernández Delgado, M.; Cernadas García, E.; Barro Ameneiro, S.; Amorim, D.G. Do we need hundreds of classifiers to solve real world classification problems. J. Mach. Learn. Res. 2014, 15, 3133–3181. [Google Scholar] [CrossRef]
- Abdullah, S.S.; Malek, M.A.; Abdullah, N.S.; Kisi, O.; Yap, K.S. Extreme Learning Machines: A new approach for prediction of reference evapotranspiration. J. Hydrol. 2015, 527, 184–195. [Google Scholar] [CrossRef]
- Laaboudi, A.; Mouhouche, B.; Draoui, B. Neural network approach to reference evapotranspiration modeling from limited climatic data in arid regions. Int. J. Biometeorol. 2012, 56, 831–841. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Yue, W.; Wu, L.; Zhang, F.; Cai, H.; Wang, X.; Lu, X.; Xiang, Y. Evaluation of SVM, ELM and four tree-based ensemble models for predicting daily reference evapotranspiration using limited meteorological data in different climates of China. Agr. Forest Meteorol. 2018, 263, 225–241. [Google Scholar] [CrossRef]
- Chen, H.; Huang, J.J.; McBean, E. Partitioning of daily evapotranspiration using a modified shuttleworth-wallace model, random Forest and support vector regression, for a cabbage farmland. Agr. Water Manag. 2020, 228, 105923. [Google Scholar] [CrossRef]
- Mohammadi, B.; Mehdizadeh, S. Modeling daily reference evapotranspiration via a novel approach based on support vector regression coupled with whale optimization algorithm. Agr. Water Manag. 2020, 237, 106145. [Google Scholar] [CrossRef]
- Feng, Y.; Jia, Y.; Zhang, Q.; Gong, D.; Cui, N. National-scale assessment of pan evaporation models across different climatic zones of China. J. Hydrol. 2018, 564, 314–328. [Google Scholar] [CrossRef]
- Wu, L.; Huang, G.; Fan, J.; Ma, X.; Zhou, H.; Zeng, W. Hybrid extreme learning machine with meta-heuristic algorithms for monthly pan evaporation prediction. Comput. Electron. Agric. 2020, 168, 105115. [Google Scholar] [CrossRef]
- Zhao, L.; Zhao, X.; Pan, X.; Shi, Y.; Qiu, Z.; Li, X.; Xing, X.; Bai, J. Prediction of daily reference crop evapotranspiration in different Chinese climate zones: Combined application of key meteorological factors and Elman algorithm. J. Hydrol. 2022, 610, 127822. [Google Scholar] [CrossRef]
- Li, Y.; Qin, Y.; Rong, P. Evolution of potential evapotranspiration and its sensitivity to climate change based on the Thornthwaite, Hargreaves, and Penman–Monteith equation in environmental sensitive areas of China. Atmos. Res. 2022, 273, 106178. [Google Scholar] [CrossRef]
- Ma, T.; Liang, Y.; Lau, M.K.; Liu, B.; Wu, M.M.; He, H.S. Quantifying the relative importance of potential evapotranspiration and timescale selection in assessing extreme drought frequency in conterminous China. Atmos. Res. 2021, 263, 105797. [Google Scholar] [CrossRef]
- Shi, L.; Feng, P.; Wang, B.; Liu, D.L.; Yu, Q. Quantifying future drought change and associated uncertainty in southeastern Australia with multiple potential evapotranspiration models. J. Hydrol. 2020, 590, 125394. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, S.; Zhao, W.; Liu, Y. The increasing contribution of potential evapotranspiration to severe droughts in the Yellow River basin. J. Hydrol. 2022, 605, 127310. [Google Scholar] [CrossRef]
- Wu, L.; Fan, J. Comparison of neuron-based, kernel-based, tree-based and curve-based machine learning models for predicting daily reference evapotranspiration. PLoS ONE 2019, 14, e0217520. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| Method | Category | Abbreviation | Formulation | |
|---|---|---|---|---|
| Hargreaves–Samani | Temperature-based method | H-S | (2) | |
| Priestley–Taylor | Radiation-based method | P-T | (3) | |
| Penman | Combination method | PM | (4) |
| Input Scenario | Model Input Factor(s) |
|---|---|
| Scenario 1 | Tmean |
| Scenario 2 | Tmean + n |
| Scenario 3 | Tmean + n + uz |
| Scenario 4 | Tmean + n + uz + RH |
| Sub-Basin | Evaluation Indicator | SVR | RF | ELM | H-S | P-T | PM |
|---|---|---|---|---|---|---|---|
| I | PBIAS | −1.95 | −1.05 | −1.30 | 5.90 | 29.90 | 35.90 |
| AICc | −2.17 | −2.13 | −2.16 | 0.51 | 1.77 | 0.59 | |
| II | PBIAS | −4.80 | −2.90 | −3.80 | −0.25 | 32.80 | 31.70 |
| AICc | −1.47 | −1.53 | −1.35 | 3.32 | 2.15 | 0.72 | |
| III | PBIAS | −4.90 | −1.00 | −1.80 | −13.70 | 3.80 | 26.10 |
| AICc | −1.13 | −1.02 | −1.21 | 0.63 | 1.59 | 0.81 | |
| IV | PBIAS | −6.15 | −1.50 | −2.10 | −8.30 | 14.55 | 26.30 |
| AICc | −1.07 | −1.17 | −1.18 | 0.38 | 1.98 | 0.76 | |
| V | PBIAS | −5.00 | −1.80 | −3.10 | 0.40 | 27.00 | 29.00 |
| AICc | −1.33 | −1.40 | −1.36 | 0.17 | 1.74 | 0.74 | |
| VI | PBIAS | −7.7 | −3.6 | −6.1 | −0.60 | 16.20 | 26.70 |
| AICc | −0.54 | −0.97 | −0.25 | 0.28 | 1.60 | 0.78 | |
| VII | PBIAS | −2.95 | 0.60 | 0.40 | 0.15 | 7.55 | 28.30 |
| AICc | −1.41 | −1.42 | −1.43 | 0.25 | 1.13 | 0.88 | |
| VIII | PBIAS | −5.80 | −1.10 | −2.2 | −15.55 | 8.20 | 24.60 |
| AICc | −1.06 | −1.08 | −1.16 | 0.80 | 1.92 | 0.76 |
| SS | df | MS | F Value | p-Value | F Crit | |
|---|---|---|---|---|---|---|
| Scenarios | 0.1654 | 3 | 0.0551 | 31.0516 | 6.15 × 10−6 | 3.4903 |
| Models | 0.0131 | 2 | 0.0065 | 3.6784 | 0.0568 | 3.8853 |
| Scenarios and models | 0.0219 | 6 | 0.0036 | 2.0540 | 0.1360 | 2.9961 |
| Inside | 0.0213 | 12 | 0.0018 | |||
| Total | 0.2217 | 23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Yu, K.; Li, P.; Jia, L.; Zhang, X.; Yang, Z.; Zhao, Y. Estimation of Potential Evapotranspiration in the Yellow River Basin Using Machine Learning Models. Atmosphere 2022, 13, 1467. https://doi.org/10.3390/atmos13091467
Liu J, Yu K, Li P, Jia L, Zhang X, Yang Z, Zhao Y. Estimation of Potential Evapotranspiration in the Yellow River Basin Using Machine Learning Models. Atmosphere. 2022; 13(9):1467. https://doi.org/10.3390/atmos13091467
Chicago/Turabian StyleLiu, Jie, Kunxia Yu, Peng Li, Lu Jia, Xiaoming Zhang, Zhi Yang, and Yang Zhao. 2022. "Estimation of Potential Evapotranspiration in the Yellow River Basin Using Machine Learning Models" Atmosphere 13, no. 9: 1467. https://doi.org/10.3390/atmos13091467
APA StyleLiu, J., Yu, K., Li, P., Jia, L., Zhang, X., Yang, Z., & Zhao, Y. (2022). Estimation of Potential Evapotranspiration in the Yellow River Basin Using Machine Learning Models. Atmosphere, 13(9), 1467. https://doi.org/10.3390/atmos13091467







