Convolutional Neural Networks for Automated ULF Wave Classification in Swarm Time Series
Abstract
:1. Introduction
2. Materials and Methods
2.1. Image Classification
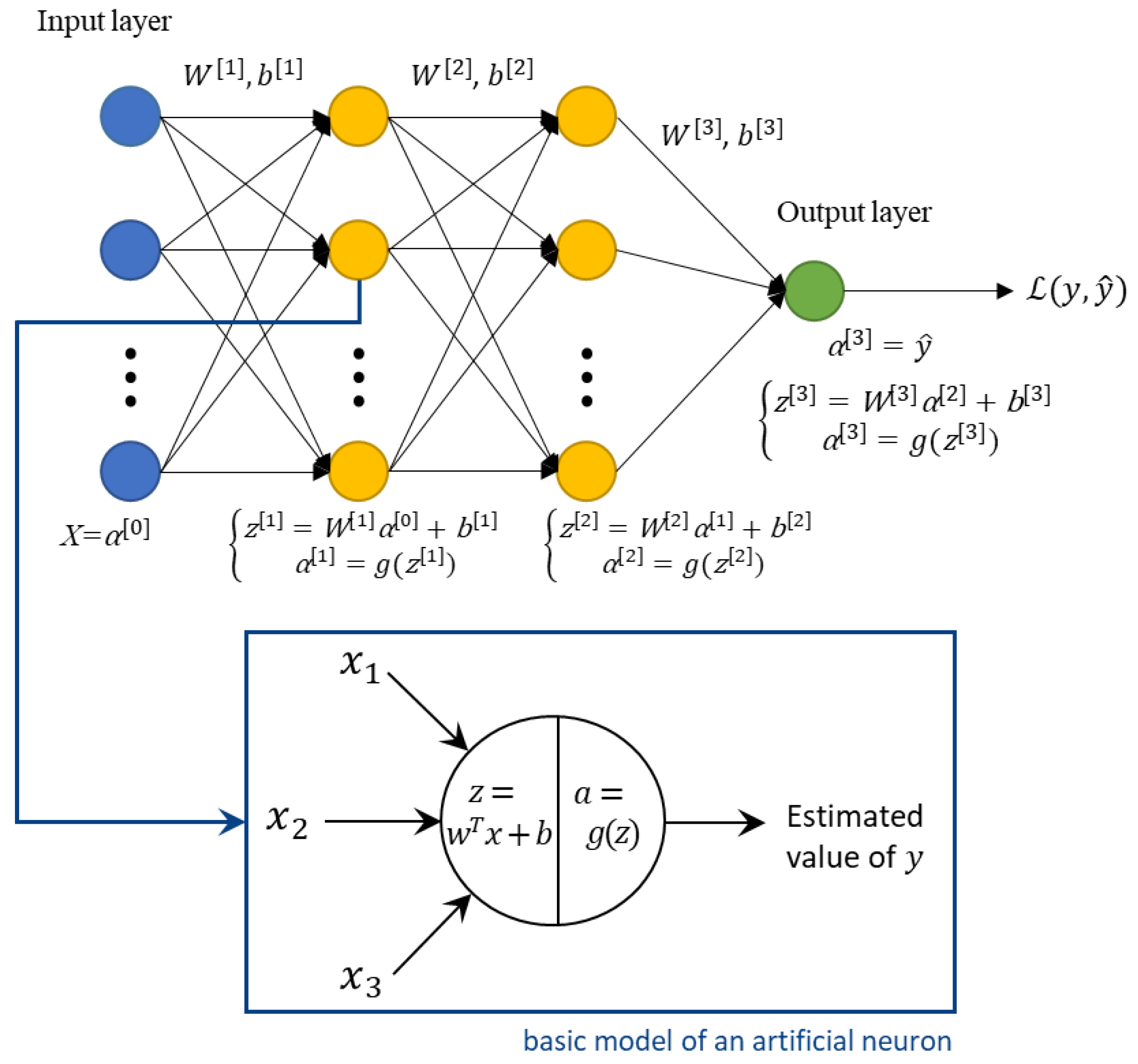
2.2. Artificial Neural Networks (ANNs)
2.3. Convolutional Neural Networks (ConvNets)
2.4. Layers Used to Build ConvNets
2.5. The k-Nearest Neighbors (k-NN) and the Support Vector Machines (SVM) Classification Algorithms
2.6. Swarm-Tailored Methodology
- Pc3 ULF Wave Events, detected in the frequency range 20–100 mHz,
- Background Noise, i.e., tracks without significant wave activity,
- False Positives (FP’s), i.e., signals that exhibit wave power in the Pc3 range but are not true ULF pulsations, containing measurements contaminated by short lived anomalies, such as spikes or abrupt discontinuities due to instrument errors, and
- Plasma Instabilities (PI’s), attributed primarily to ESF events which are predominantly present in the nightside tracks and have similar characteristics to Pc3 waves even though they are not true ULF pulsations [7].
- it must exhibit a duration of at least 2 times its peak period,
- it must have an amplitude that does not exceed certain limits (10 nT),
- and it must be smooth enough to constitute a continuous pulsation, so its difference series must always be smaller than 1 nT.
2.7. Data & Training of the Network
- Divide the training dataset into k subsets and perform training k times in total. Each time use subsets for training and the remaining one for testing.
- For each one of the k’ times, compute the accuracy on the training and the test set (i.e., ).
- Finally, compute the mean () and standard deviation () values of the accuracies of the training subsets and the test subsets .
- Data used: total magnitude, Swarm VFM, NEC local Cartesian coordinate frame, 1 Hz sampling rate (MAGX_LR_1B Product), for February, March and April of the year 2015.
- Number of total samples: 2620 samples, manually annotated with 4 labels.
- Input: pairs of wavelet power spectra images with their annotation (class label)
- Training set—Test set split: 80% (2096 samples)–20% (524 samples) of total sample
- Layers: 2 convolutional, 2 max-pooling, 1 fully connected.
- Parameter initializer: Xavier Initialization [57]
- Activation functions: ReLU, Softmax [58]
- Cost function: Cross-entropy (Log Loss) [59]
- Optimizer: Adam Optimization
- Extra: Dropout Regularization.
3. Results
4. Conclusions & Discussion
- Accuracy on the training set (2096 samples) = 98.3%
- Accuracy on the test set (524 samples) = 97.3%
- Heidke Skill Score (HSS) = 96.2%
- Comparing with the well-known kNN & the very competitive SVM classification methods: kNN (k = 5) = 57.5%, SVM = 88.1%, ConvNet gives the best results achieving the highest accuracy.
- This new methodology could be applied to investigate:
- other frequency ranges (Pc1/EMIC, Pc2, Pc4, Pc5)
- observations from other satellite missions
- ground-based observations.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McPherron, R.L. Magnetic Pulsations: Their Sources and Relation to Solar Wind and Geomagnetic Activity. Surv. Geophys. 2005, 26, 545–592. [Google Scholar] [CrossRef]
- Jacobs, J.A.; Kato, Y.; Matsushita, S.; Troitskaya, V.A. Classification of geomagnetic micropulsations. J. Geoph. Res. 1964, 69, 180–181. [Google Scholar] [CrossRef]
- Mann, I.R. Waves, particles, and storms in geospace: An introduction. In Waves, Particles, and Storms in Geospace; Balasis, G., Daglis, I.A., Mann, I.R., Eds.; Oxford University Press: Oxford, UK, 2016; pp. 1–14. [Google Scholar]
- Daglis, I.A.; Katsavrias, C.; Georgiou, M. From solar sneezing to killer electrons: Outer radiation belt response to solar eruptions. Philos. Trans. R. Soc. A 2019, 377, 20180097. [Google Scholar] [CrossRef] [PubMed]
- Balasis, G.; Daglis, I.A.; Georgiou, M.; Papadimitriou, C.; Haagmans, R. Magnetospheric ULF wave studies in the frame of Swarm mission: A time-frequency analysis tool for automated detection of pulsations in magnetic and electric field observations. Earth Planets Space 2013, 65, 18. [Google Scholar] [CrossRef]
- Balasis, G.; Aminalragia-Giamini, S.; Papadimitriou, C.; Daglis, I.A.; Anastasiadis, A.; Haagmans, R. A machine learning approach for automated ULF wave recognition. J. Space Weather Space Clim. 2019, 9, A13. [Google Scholar] [CrossRef]
- Balasis, G.; Papadimitriou, C.; Daglis, I.A.; Pilipenko, V. ULF wave power features in the topside ionosphere revealed by Swarm observations. Geophys. Res. Lett. 2015, 42, 6922–6930. [Google Scholar] [CrossRef]
- Olsen, N.; Finlay, C.C.; Kotsiaros, S.; Tøffner-Clausen, L. A model of Earth’s magnetic field derived from 2 years of Swarm satellite constellation data. Earth Planets Space 2016, 68, 124. [Google Scholar] [CrossRef]
- Leger, J.-M.; Bertrand, F.; Jager, T.; Le Prado, M.; Fratter, I.; Lalaurie, J.-C. Swarm Absolute Scalar and Vector Magnetometer Based on Helium 4 Optical Pumping. Procedia Chem. 2009, 1, 634–637. [Google Scholar] [CrossRef]
- Stolle, C.; Lühr, H.; Rother, M.; Balasis, G. Magnetic signatures of equatorial spread F as observed by the CHAMP satellite. J. Geophys. Res. 2006, 111, A02304. [Google Scholar] [CrossRef]
- Park, J.; Stolle, C.; Noja, M.; Stolle, C.; Lühr, H. The Ionospheric Bubble Index deduced from magnetic field and plasma observations onboard Swarm. Earth Planet Space 2013, 65, 13. [Google Scholar] [CrossRef] [Green Version]
- Baker, D.N. Linear prediction filter analysis of relativistic electron properties at 6.6 RE. J. Geophys. Res. Space Phys. 1990, 95, 15133–15140. [Google Scholar] [CrossRef]
- Valdivia, J.A.; Sharma, A.S.; Papadopoulos, K. Prediction of magnetic storms by nonlinear models. Geophys. Res. Lett. 1996, 23, 2899–2902. [Google Scholar] [CrossRef]
- Sutcliffe, P.R. Substorm onset identification using neural networks and Pi2 pulsations. Ann. Geophys. 1997, 15, 1257–1264. [Google Scholar] [CrossRef]
- Lundstedt, H. AI techniques in geomagnetic storm forecasting. In Magnetic Storms; Tsurutani, B.T., Gonzalez, W.D., Kamide, Y., Arballo, J.K., Eds.; American Geophysical Union: Washington, DC, USA, 1997. [Google Scholar]
- Lundstedt, H. Progress in space weather predictions and applications. Adv. Space Res. 2005, 36, 2516–2523. [Google Scholar] [CrossRef]
- Boberg, F.; Wintoft, P.; Lundstedt, H. Real time Kp predictions from solar wind data using neural networks. Phys. Chem. Earth Part C 2000, 25, 275–280. [Google Scholar] [CrossRef]
- Vassiliadis, D. System identification, modeling, and prediction for space weather environments. IEEE Trans. Plasma Sci. 2000, 28, 1944–1955. [Google Scholar] [CrossRef]
- Gleisner, H.; Lundstedt, H. A neural network-based local model for prediction of geomagnetic disturbances. J. Geophys. Res. Space Phys. 2001, 106, 8425–8433. [Google Scholar] [CrossRef]
- Li, X. Quantitative prediction of radiation belt electrons at geostationary orbit based on solar wind measurements. Geophys. Res. Lett. 2001, 28, 1887–1890. [Google Scholar] [CrossRef]
- Vandegriff, J. Forecasting space weather: Predicting interplanetary shocks using neural networks. Adv. Space Res. 2005, 36, 2323–2327. [Google Scholar] [CrossRef]
- Wing, S.; Johnson, J.; Jen, J.; Meng, C.-I.; Sibeck, D.; Bechtold, K.; Carr, S.; Costello, K.; Freeman, J.; Balikhin, M.; et al. Kp forecast models. J. Geophys. Res. 2005, 110, A04203. [Google Scholar] [CrossRef]
- Cesaroni, C.; Spogli, L.; Aragon-Angel, A.; Fiocca, M.; Dear, V.; De Franceschi1, G.; Romano, V. Neural network based model for global Total Electron Content forecasting. J. Space Weather Space Clim. 2020, 10, 11. [Google Scholar] [CrossRef]
- Park, W.; Lee, J.; Kim, K.-C.; Lee, J.; Park, K.; Miyashita, Y.; Sohn, J.; Park, J.; Kwak, Y.; Hwang, J.; et al. Operational Dst index prediction model based on combination of artificial neural network and empirical model. J. Space Weather Space Clim. 2021, 11, 38. [Google Scholar] [CrossRef]
- Chakraborty, S.; Morley, S. Probabilistic prediction of geomagnetic storms and the Kp index. J. Space Weather Space Clim. 2020, 10, 36. [Google Scholar] [CrossRef]
- Arregui, I. Recent Applications of Bayesian Methods to the Solar Corona. Front. Astron. Space Sci. 2022, 9, 826947. [Google Scholar] [CrossRef]
- Georgoulis, M.K.; Bloomfield, D.S.; Piana, M.; Massone, A.M.; Soldati, M.; Gallagher, P.T.; Pariat, E.; Vilmer, N.; Buchlin, E.; Baudin, F.; et al. The flare likelihood and region eruption forecasting (FLARECAST) project: Flare forecasting in the big data & machine learning era. J. Space Weather Space Clim. 2021, 11, 39. [Google Scholar] [CrossRef]
- Lavasa, E.; Giannopoulos, G.; Papaioannou, A.; Anastasiadis, A.; Daglis, I.A.; Aran, A.; Pacheco, D.; Sanahuja, B. Assessing the Predictability of Solar Energetic Particles with the Use of Machine Learning Techniques. Sol. Phys. 2021, 296, 107. [Google Scholar] [CrossRef]
- Aminalragia-Giamini, S.; Raptis, S.; Anastasiadis, A.; Tsigkanos, A.; Sandberg, I.; Papaioannou, A.; Papadimitriou, C.; Jiggens, P.; Aran, A.; Daglis, I.A. Solar Energetic Particle Event occurrence prediction using Solar Flare Soft X-ray measurements and Machine Learning. J. Space Weather Space Clim. 2021, 11, 59. [Google Scholar] [CrossRef]
- Blandin, M.; Connor, H.K.; Öztürk, D.S.; Keesee, A.M.; Pinto, V.; Mahmud, M.S.; Ngwira, C.; Priyadarshi, S. Multi-Variate LSTM Prediction of Alaska Magnetometer Chain Utilizing a Coupled Model Approach. Front. Astron. Space Sci. 2022, 9, 846291. [Google Scholar] [CrossRef]
- Capannolo, L.; Li, W.; Huang, S. Identification and Classification of Relativistic Electron Precipitation at Earth Using Supervised Deep Learning. Front. Astron. Space Sci. 2022, 9, 858990. [Google Scholar] [CrossRef]
- Pinto, V.A.; Keesee, A.M.; Coughlan, M.; Mukundan, R.; Johnson, W.; Ngwira, C.M.; Connor, H.K. Revisiting the Ground Magnetic Field Perturbations Challenge: A Machine Learning Perspective. Front. Astron. Space Sci. 2022, 9, 869740. [Google Scholar] [CrossRef]
- Yeakel, K.L.; Vandegriff, J.D.; Garton, T.M.; Jackman, C.M.; Clark, G.; Vines, S.K.; Smith, A.W.; Kollmann, P. Classification of Cassini’s Orbit Regions as Magnetosphere, Magnetosheath, and Solar Wind via Machine Learning. Front. Astron. Space Sci. 2022, 9, 875985. [Google Scholar] [CrossRef]
- Camporeale, E.; Wing, S.; Johnson, J. Machine Learning Techniques for Space Weather; Elsevier: Amsterdam, The Netherlands, 2008; p. 454. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet classification with deep convolutional neural networks. In Proceedings, Advances in Neural Information Processing Systems 25 (NIPS 2012); Pereira, F., Burges, C.J., Bottou, L., Weinberger, K.Q., Eds.; Curran Associates, Inc.: New York, NY, USA, 2012; pp. 1090–1098. [Google Scholar]
- Collobert, R.; Weston, J. A Unified Architecture for Natural Language Processing: Deep Neural Networks with Multitask Learning. In Proceedings of the Twenty-Fifth International Conference on Machine Learning (ICML 2008), Helsinki, Finland, 5–9 June 2008; pp. 160–167. [Google Scholar]
- Narock, T.; Narock, A.; Dos Santos, L.F.G.; Nieves-Chinchilla, T. Identification of Flux Rope Orientation via Neural Networks. Front. Astron. Space Sci. 2022, 9, 838442. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- CS231n: Deep Learning for Computer Vision, Stanford, Spring 2022. Available online: http://cs231n.stanford.edu/ (accessed on 21 May 2022).
- Alom, M.Z.; Taha, T.; Yakopcic, C.; Westberg, S.; Hasan, M.; Esesn, B.; Awwal, A.; Asari, V. The History Began from AlexNet: A Comprehensive Survey on Deep Learning Approaches. arXiv 2018, arXiv:1803.01164. [Google Scholar]
- Theodoridis, S.; Koutroumbas, K. Pattern Recognition, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2003; p. 689. ISBN 0-12-685875-6. [Google Scholar]
- Imandoust, S.B.; Bolandraftar, M. Application of K-nearest neighbor (KNN) approach for predicting economic events theoretical background. Int. J. Eng. Res. Appl. 2013, 3, 605–610. [Google Scholar]
- Güvenç, E.; Çetin, G.; Koçak, H. Comparison of KNN and DNN Classifiers Performance in Predicting Mobile Phone Price Ranges. Adv. Artif. Intell. Res. 2021, 1, 19–28. [Google Scholar]
- Cunningha, P.; Delany, S.J. k-Nearest Neighbour Classifiers; Technical Report UCD-CSI-2007-4; University College Dublin: Dublin, Ireland, 2007. [Google Scholar]
- Cai, Y.; Ji, D.; Cai, D. A KNN Research Paper Classification Method Based on Shared Nearest Neighbor. In Proceedings of the NTCIR-8 Workshop Meeting, Tokyo, Japan, 15–18 June 2010. [Google Scholar]
- Chamasemani, F.F.; Singh, Y.P. Multi-class Support Vector Machine (SVM) classifiers—An Application in Hypothyroid detection and Classification. In Proceedings of the Sixth International Conference on Bio-Inspired Computing: Theories and Applications, Penang, Malaysia, 27–29 September 2011. [Google Scholar] [CrossRef]
- Applied Machine Learning—INFO-4604. University of Colorado Boulder. 2018. Available online: https://cmci.colorado.edu/classes/INFO-4604/ (accessed on 24 June 2022).
- Haasdonk, B. Feature Space Interpretation of SVMs with Indefinite Kernels. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 4. [Google Scholar] [CrossRef]
- Finlay, C.C.; Olsen, N.; Kotsiaros, S.; Gillet, N.; Tøffner-Clausen, L. Recent geomagnetic secular variation from Swarm and ground observatories as estimated in the CHAOS-6 geomagnetic field model. Earth Planet Space 2016, 68, 112. [Google Scholar] [CrossRef]
- Ritter, P.; Lühr, H.; Rauberg, J. Determining field-aligned currents with the Swarm constellation mission. Earth Planet Space 2013, 65, 1285–1294. [Google Scholar] [CrossRef] [Green Version]
- Swarm Data Access. Available online: https://swarm-diss.eo.esa.int/ (accessed on 27 May 2022).
- Papadimitriou, C.; Balasis, G.; Daglis, I.A.; Giannakis, O. An initial ULF wave index derived from 2 years of Swarm observations. Ann. Geophys. 2018, 36, 287–299. [Google Scholar] [CrossRef]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. arXiv 2012, arXiv:207.0580v1. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Chia Laguna Resort, Sardinia, Italy, 13–15 May 2010; pp. 249–256. Available online: https://proceedings.mlr.press/v9/glorot10a.html (accessed on 14 July 2022).
- Nwankpa, C.E.; Ijomah, W.; Gachagan, A.; Marshall, S. Activation Functions: Comparison of trends in Practice and Research for Deep Learning. arXiv 2018, arXiv:1811.03378v1. [Google Scholar] [CrossRef]
- Good, I.J. Rational Decisions. J. R. Stat. Soc. Ser. B 1952, 14, 107–114. [Google Scholar] [CrossRef]
- Papadimitriou, C.; Balasis, B.; Boutsi, A.Z.; Daglis, I.A.; Giannakis, O.; Anastasiadis, A.; De Michelis, P.; Consolini, G. Dynamical Complexity of the 2015 St. Patrick’s Day Magnetic Storm at Swarm Altitudes Using Entropy Measures. Entropy 2020, 22, 574. [Google Scholar] [CrossRef]
- Balasis, G.; Papadimitriou, C.; Boutsi, A.Z.; Daglis, I.A.; Giannakis, O.; Anastasiadis, A.; De Michelis, P.; Consolini, G. Dynamical complexity in Swarm electron density time series using Block entropy. EPL 2020, 131, 69001. [Google Scholar] [CrossRef]
- De Michelis, P.; Pignalberi, A.; Consolini, G.; Coco, I.; Tozzi, R.; Pezzopane, M.; Giannattasio, F.; Balasis, G. On the 2015 St. Patrick’s Storm Turbulent State of the Ionosphere: Hints From the Swarm Mission. J. Geophys. Res. Space Phys. 2020, 125, e2020JA027934. [Google Scholar] [CrossRef]
- Balasis, G.; Daglis, I.A.; Contoyiannis, Y.; Potirakis, S.M.; Papadimitriou, C.; Melis, N.S.; Giannakis, O.; Papaioannou, A.; Anastasiadis, A.; Kontoes, C. Observation of intermittency-induced critical dynamics in geomagnetic field time series prior to the intense magnetic storms of March, June, and December 2015. J. Geophys. Res. Space Phys. 2018, 123, 4594–4613. [Google Scholar] [CrossRef]
- Forecast Verification Methods Across Time and Space Scales—Heidke Skill Score (Cohen’s k). In Proceedings of the 7th International Verification Methods Workshop; Berlin, Germany, 8–11 May 2017. Available online: https://cawcr.gov.au/projects/verification/ (accessed on 24 May 2022).
- Tsagouri, I.; Borries, C.; Perry, C.; Dierckxsens, M.; Georgoulis, M.; Bloomfield, D.S. Guidelines for Common Validation in the SSA SWE Network; Technical Note ssa-swe-escdef-tn-5401; European Space Agency: Paris, France, 2019. [Google Scholar]
- Goutte, C.; Gaussier, E. A Probabilistic Interpretation of Precision, Recall and F-Score, with Implication for Evaluation. Adv. Inf. Retr. 2005, 3408, 345–359. [Google Scholar] [CrossRef]
- Raghavan, V.; Bollmann, P.; Jung, G.S. A critical investigation of recall and precision as measures of retrieval system performance. ACM Trans. Inf. Syst. 1989, 7, 205–229. [Google Scholar] [CrossRef]









| Layers | Details |
|---|---|
| Convolutional layer 1 | 8 filters, , |
| Max-Pooling layer 1 | , |
| Convolutional layer 2 | 16 filters, , |
| Max-Pooling layer 2 | , |
| Fully Connected layer | 4-neuron output |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antonopoulou, A.; Balasis, G.; Papadimitriou, C.; Boutsi, A.Z.; Rontogiannis, A.; Koutroumbas, K.; Daglis, I.A.; Giannakis, O. Convolutional Neural Networks for Automated ULF Wave Classification in Swarm Time Series. Atmosphere 2022, 13, 1488. https://doi.org/10.3390/atmos13091488
Antonopoulou A, Balasis G, Papadimitriou C, Boutsi AZ, Rontogiannis A, Koutroumbas K, Daglis IA, Giannakis O. Convolutional Neural Networks for Automated ULF Wave Classification in Swarm Time Series. Atmosphere. 2022; 13(9):1488. https://doi.org/10.3390/atmos13091488
Chicago/Turabian StyleAntonopoulou, Alexandra, Georgios Balasis, Constantinos Papadimitriou, Adamantia Zoe Boutsi, Athanasios Rontogiannis, Konstantinos Koutroumbas, Ioannis A. Daglis, and Omiros Giannakis. 2022. "Convolutional Neural Networks for Automated ULF Wave Classification in Swarm Time Series" Atmosphere 13, no. 9: 1488. https://doi.org/10.3390/atmos13091488
APA StyleAntonopoulou, A., Balasis, G., Papadimitriou, C., Boutsi, A. Z., Rontogiannis, A., Koutroumbas, K., Daglis, I. A., & Giannakis, O. (2022). Convolutional Neural Networks for Automated ULF Wave Classification in Swarm Time Series. Atmosphere, 13(9), 1488. https://doi.org/10.3390/atmos13091488








