Retrieval of Road Surface (Bridge Deck) Temperature near 0 °C Based on Random Forest Model
Abstract
1. Introduction
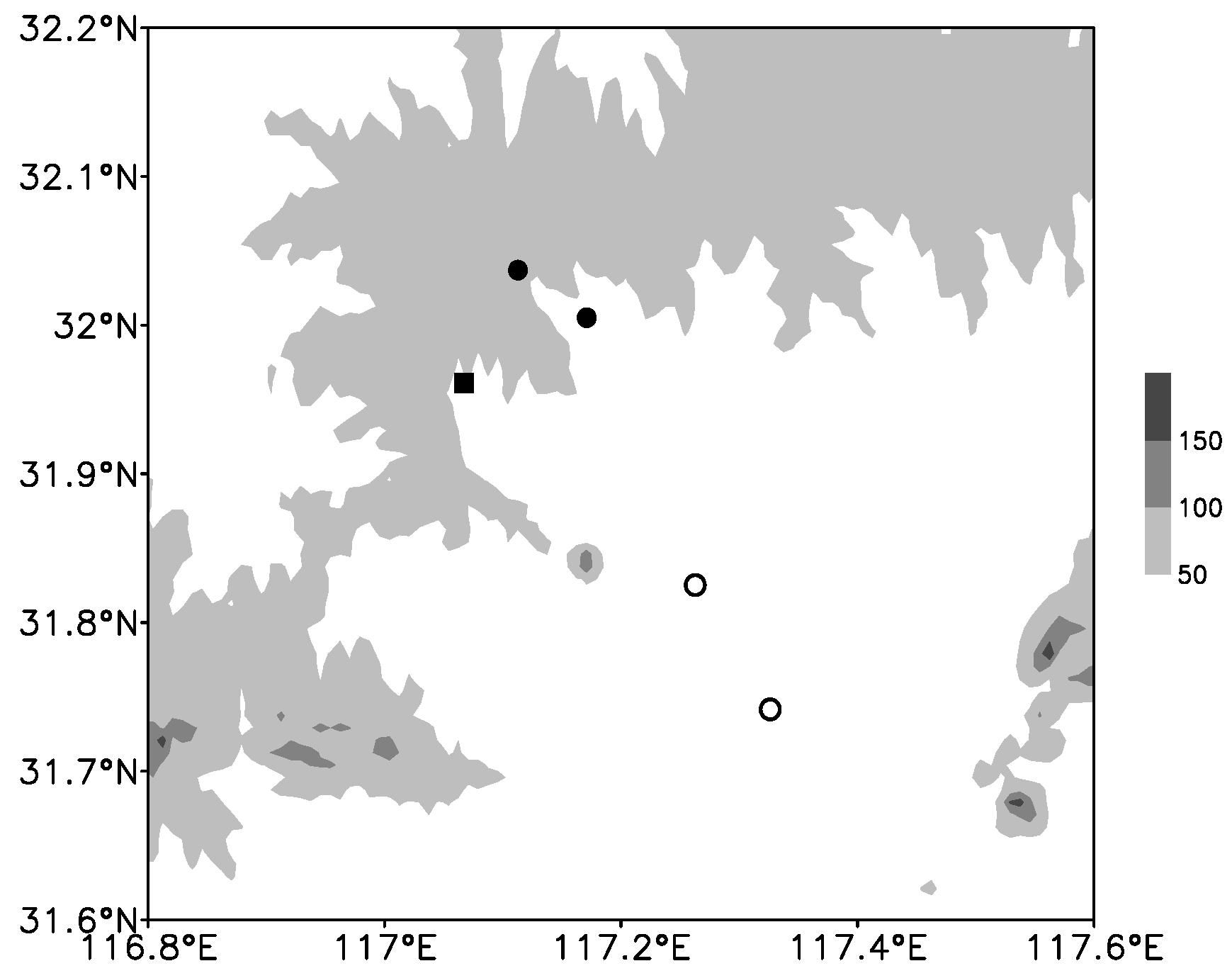
2. Data and Methods
3. Relations between Surface Temperature and Meteorological Factors
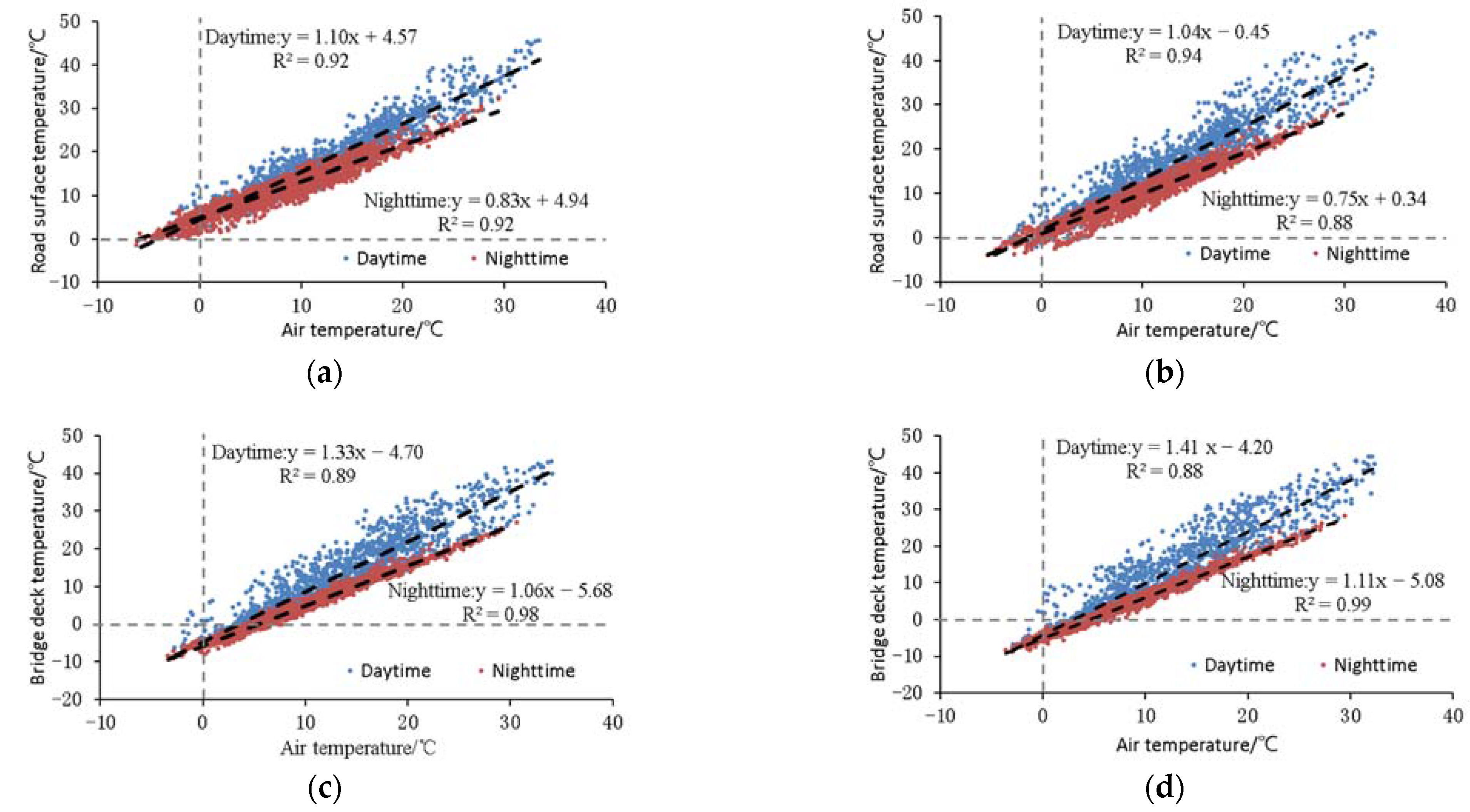
3.1. Relations between Surface Temperature and Air Temperature
3.2. Relationship of Surface Temperature with Other Meteorological Factors
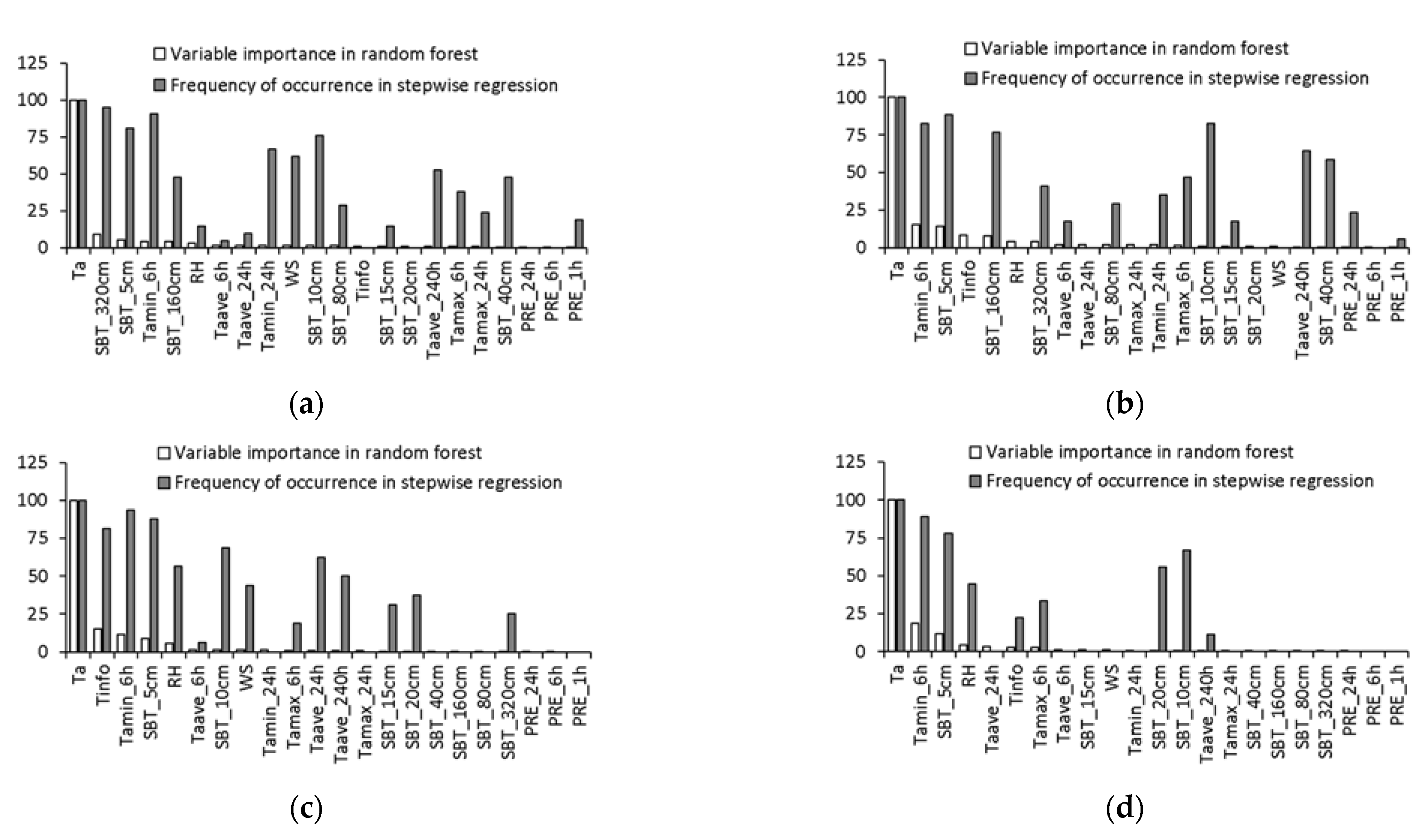
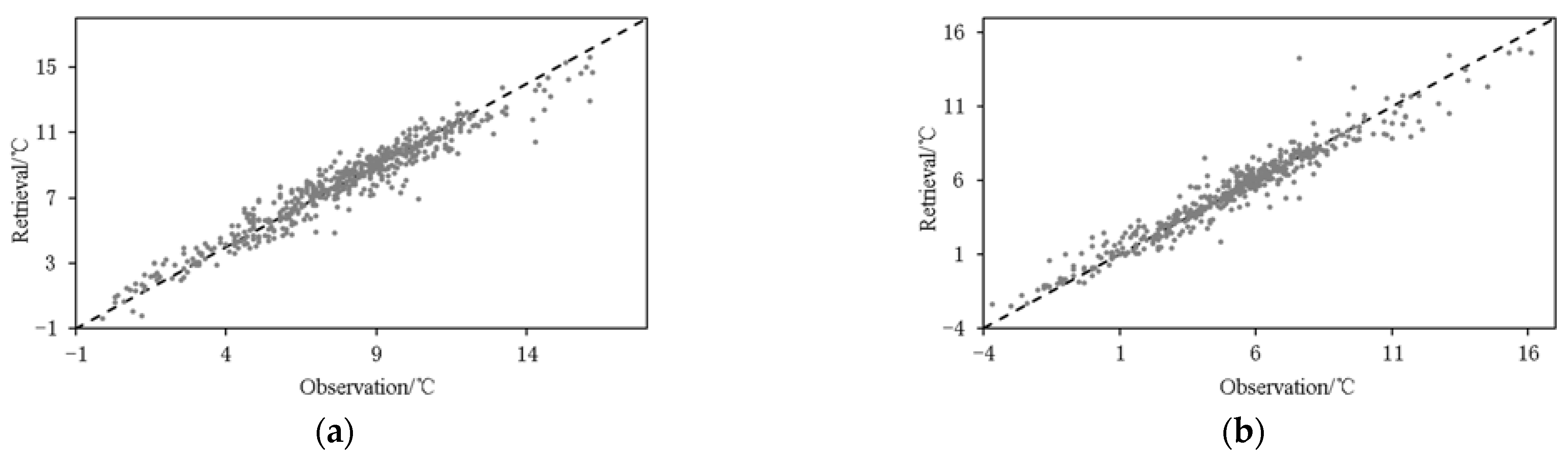
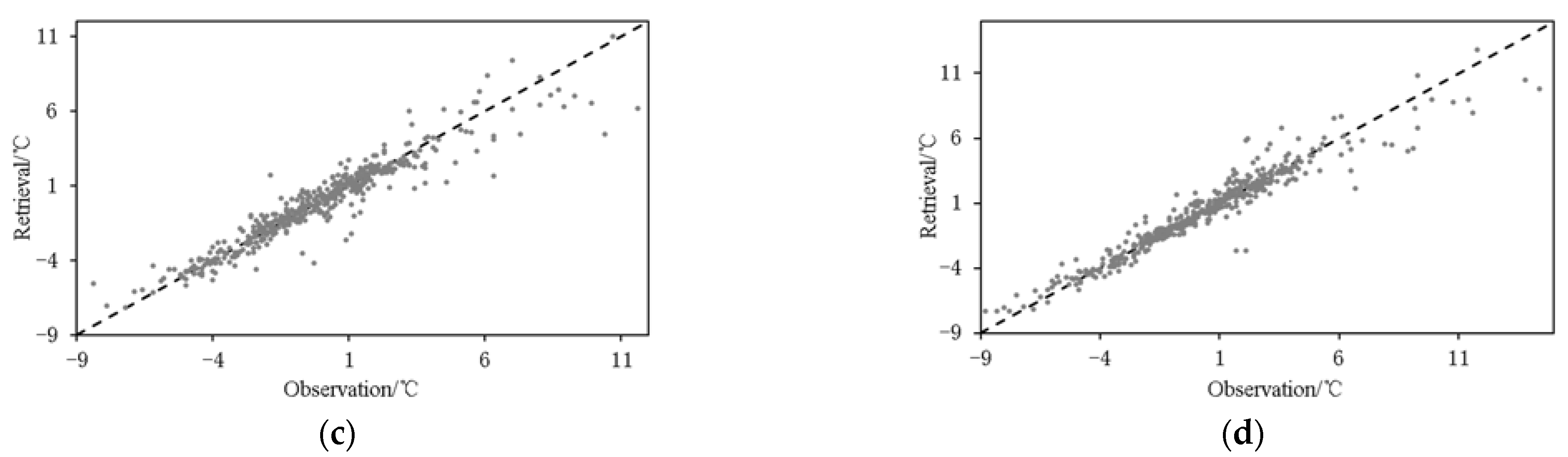
4. Surface Temperature Retrieving Model
5. Conclusions and Discussion
- (1)
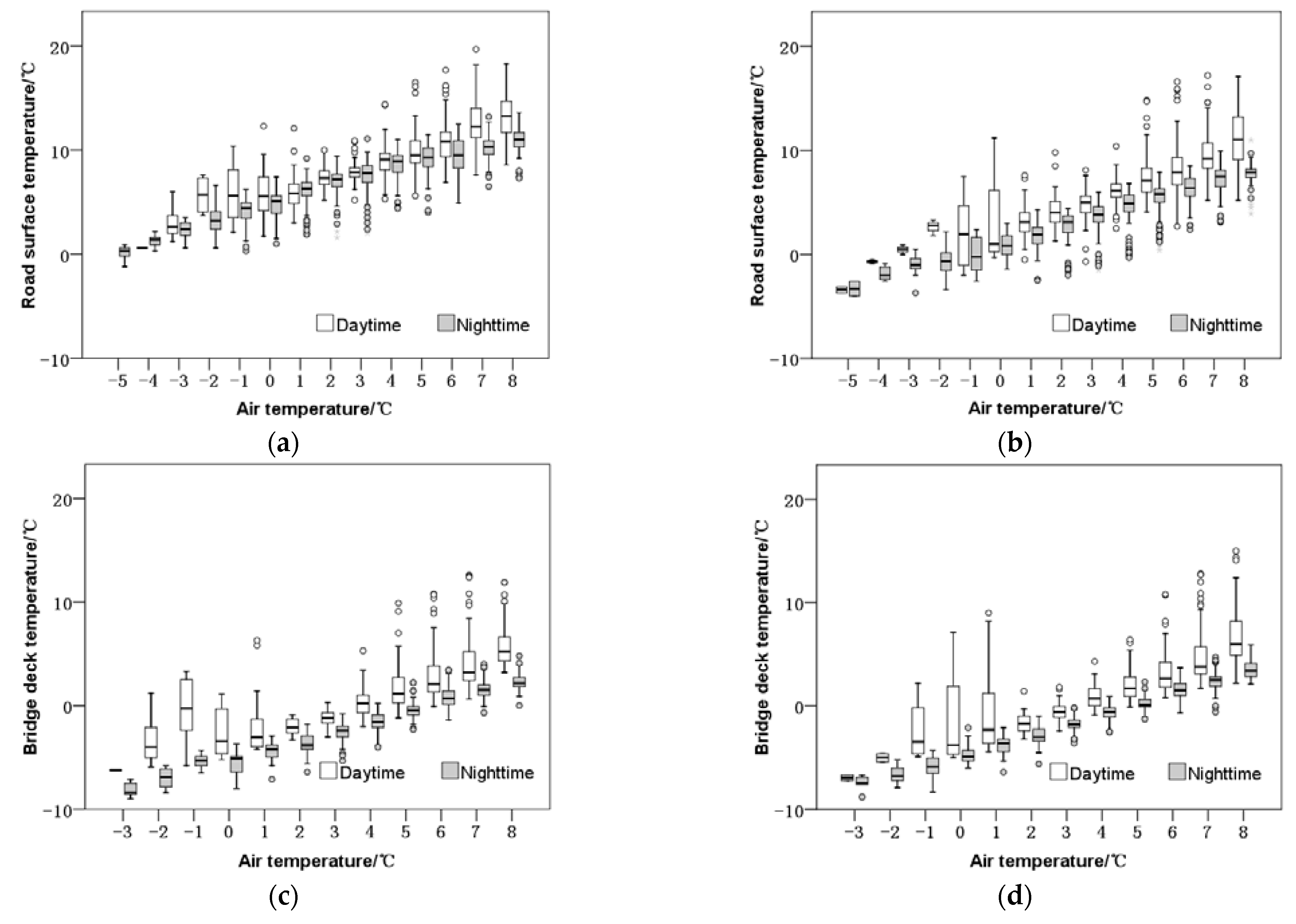
- The road surface (bridge deck) temperature linearly correlates with air temperature. The correlation coefficient at night is higher than that during the day, and is higher at the road surface. Under low temperature conditions (air temperature ≤ 8 °C), the road surface temperature is higher than air temperature, and the bridge deck temperature is lower than the air temperature. When the air temperature is between −4 °C and −2 °C, the median value of road surface temperature falls below 0 °C; when the air temperature is between 3 °C and 5 °C, the median value of bridge deck temperature falls below 0 °C.
- (2)
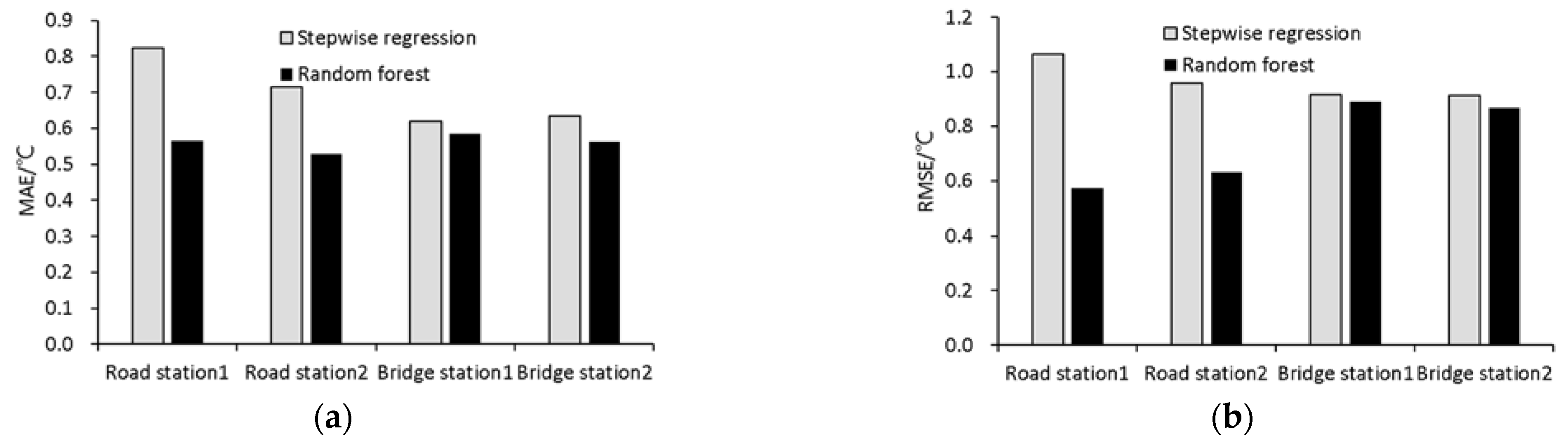
- The retrieving errors of the random forest model are smaller than those of stepwise regression for both road surface and bridge deck, and the improvement on road surface is more obvious using the random forest model. Compared with stepwise regression, MAE of road surface temperature based on the random forest model are reduced by 0.19 °C and 0.26 °C, respectively, and RMSE are reduced by 0.33 °C and 0.49 °C, respectively. The bias in the retrievals can be originated from the model itself as well as the error in the observations.
- (3)
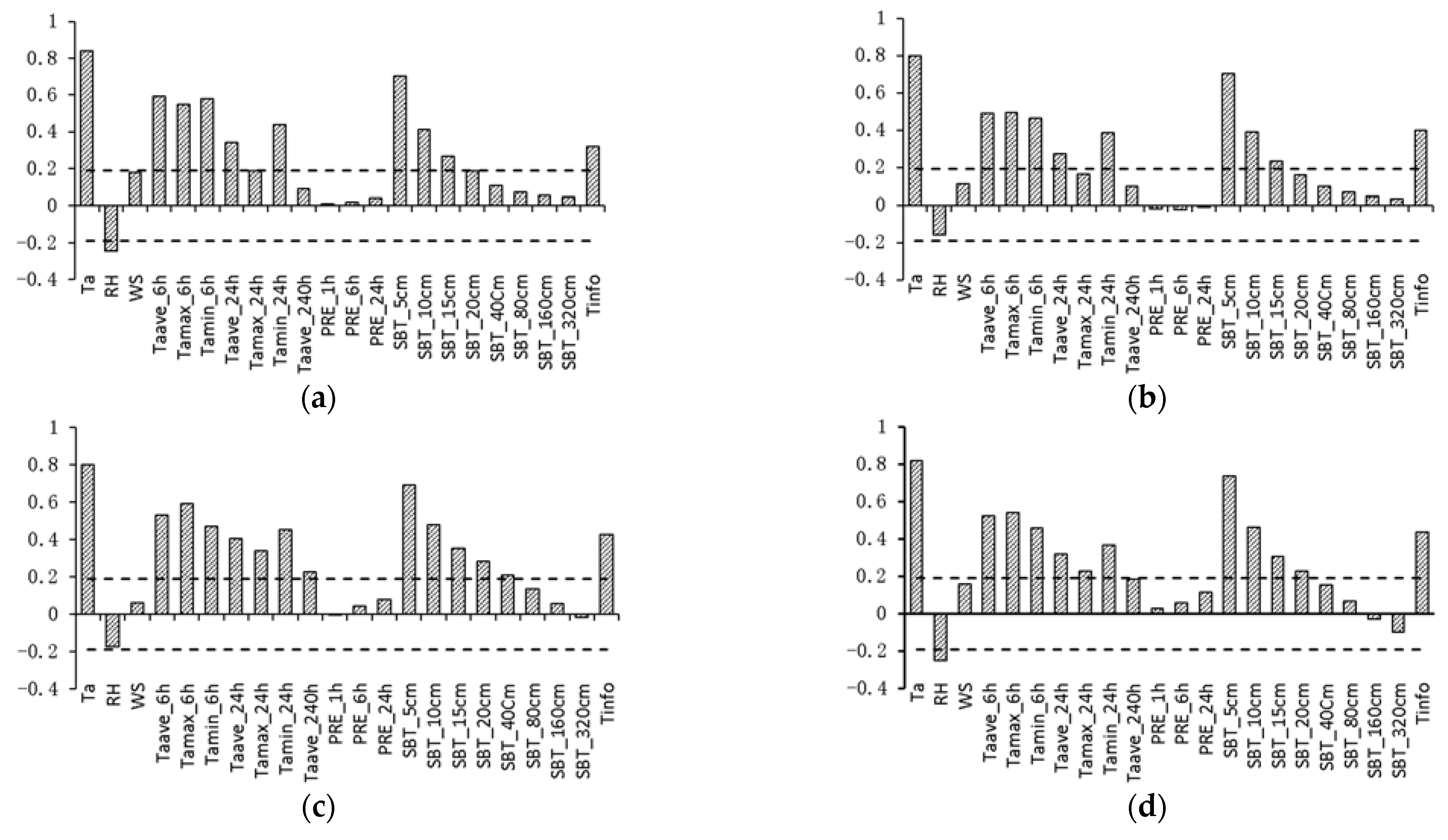
- Among the factors selected by the random forest model, temperature is the most important. Meanwhile, the importance of each factor is different in the retrieval of road surface and bridge deck temperature. Ground temperature is more important in road surface temperature retrieval, while humidity and wind speed are generally more important in bridge deck temperature retrieval. The precipitation factors are least important in both models.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gultepe, I.; Heymsfield, A.J.; Gallagher, M.; Ickes, L.; Baumgardner, D. Ice Fog: The current state of knowledge and future challenges. Meteorol. Monogr. 2017, 58, 4.1–4.24. [Google Scholar] [CrossRef]
- Juga, I.; Nurmi, P.; Hippi, M. Statistical modelling of wintertime road surface friction. Meteor. Appl. 2013, 20, 318–329. [Google Scholar] [CrossRef]
- Toms, B.A.; Basara, J.B.; Hong, Y. Usage of existing meteorological data networks for parameterized road ice formation modeling. J. Appl. Meteor. Climatol. 2017, 56, 1959–1976. [Google Scholar] [CrossRef]
- Gultepe, I.; Isaac, G.A.; Rasmussen, R.M.; Ungar, K. A Freezing Fog/Drizzle Event during the FRAM-S Project; SAE Technical Papers; SAE International: Warrendale, PA, USA, 2011. [Google Scholar] [CrossRef]
- Gultepe, I.; Pavolonis, M.; Zhou, B.; Ware, R.; Rabin, R.; Burrows, W.; Milbrandt, J.; Garand, L. Freezing Fog and Drizzle Observations; SAE Technical Papers; SAE International: Warrendale, PA, USA, 2015. [Google Scholar]
- Kangas, M.; Heikinheimo, M.; Hippi, M. Roadsurf: A modelling system for predicting road weather and road surface conditions. Meteor. Appl. 2015, 22, 544–553. [Google Scholar] [CrossRef]
- Jacobs, W.; Raatz, W.E. Forecasting road-surface temperatures for different site characteristics. Meteor. Appl. 1996, 3, 243–256. [Google Scholar] [CrossRef]
- Postgård, U.; Lindqvist, S. Air and road surface temperature variations during weather change. Meteorol. Appl. 2001, 8, 71–84. [Google Scholar] [CrossRef]
- Yang, C.; Yun, D.-G.; Sung, J. Validation of a road surface temperature prediction model using real-time weather forecasts. KSCE J. Civ. Eng. 2012, 16, 1289–1294. [Google Scholar] [CrossRef]
- Kim, Y.-J.; Jee, J.-B.; Kim, G.-T.; Nam, H.-G.; Lee, J.-S.; Kim, B.-J. Diurnal Variations of Surface and Air Temperatures on the Urban Streets in Seoul, Korea: An Observational Analysis during BBMEX Campaign. Atmosphere 2020, 11, 60. [Google Scholar] [CrossRef]
- Jörgen, B.; Torbjörn, G.; Maria, K. Temperature differences in the air layer close to a road surface. Meteorol. Appl. 2001, 8, 385–395. [Google Scholar]
- Monforte, P.; Ragusa, M.A. Temperature Trend Analysis and Investigation on a Case of Variability Climate. Mathematics 2022, 10, 2202. [Google Scholar] [CrossRef]
- Cheshmehzangi, A. The analysis of global warming patterns from 1970s to 2010s. Atmos. Clim. Sci. 2020, 10, 392–404. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E.; Sirangelo, B. Trend analysis of monthly mean values and extreme indices of daily temperature in a region of southern Italy. Int. J. Clim. 2017, 37, 284–297. [Google Scholar] [CrossRef]
- Chapman, L.; E Thornes, J.; Bradley, A.V. Modelling of road surface temperature from a geographical parameter database. Part 2: Numerical. Meteorol. Appl. 2001, 8, 421–436. [Google Scholar] [CrossRef]
- Crevier, L.-P.; Delage, Y. METRo: A New Model for Road-Condition Forecasting in Canada. J. Appl. Meteorol. 2001, 40, 2026–2037. [Google Scholar] [CrossRef]
- Xia, X.A.; Wang, P.C.; Chen, H.B.; Liang, F. Analysis of downwelling surface solar radiation in China from National Centers for Environmental Prediction reanalysis, satellite estimates, and surface observations. J. Geophys. Res. 2006, 111, D09103. [Google Scholar] [CrossRef]
- Chapman, L.; Thornes, J.E. The influence of traffic on road surface temperatures: Implications for thermal mapping studies. Meteorol. Appl. 2005, 12, 371–380. [Google Scholar] [CrossRef]
- Marchetti, M.; Chapman, L.; Khalifa, A. New role of thermal mapping in winter maintenance with principal components analysis. Adv. Meteorol. 2014, 2014, 254795. [Google Scholar] [CrossRef]
- Asefzadeh, A.; Hashemian, L.; Bayat, A. Development of statistical temperature prediction models for a test road in Edmonton, Alberta, Canada. Int. J. Pavement Res. Technol. 2017, 10, 369–382. Available online: http://creativecommons.org/licenses/by-nc-nd/4.0/ (accessed on 24 May 2017). [CrossRef]
- Chen, J.; Wang, H.; Xie, P. Pavement temperature prediction: Theoretical models and critical affecting factors. Appl. Therm. Eng. 2019, 158, 113755. [Google Scholar] [CrossRef]
- Ahijevych, D.; Pinto, J.O.; Williams, J.K. Probabilistic forecasts of mesoscale convective system initiation using the random forest data mining technique. Weather Forecast. 2016, 31, 581–599. [Google Scholar] [CrossRef]
- Liu, N.; Yan, Z.; Tong, X.; Jiang, J.; Li, H.; Xia, J.; Lou, X.; Ren, R.; Fang, Y. Meshless Surface Wind Speed Field Reconstruction Based on Machine Learning. Adv. Atmos. Sci. 2022, 39, 1721–1733. [Google Scholar] [CrossRef]
- Jonsson, P.; Riehm, M. Infrared thermometry in winter road maintenance. J. Atmos. Ocean. Technol. 2012, 29, 846–856. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hertl, S.; Schaffar, G. An autonomous approach to road temperature prediction. Meteor. Appl. 1998, 5, 227–238. [Google Scholar] [CrossRef]
- Bouilloud, L.; Martin, E.; Habete, F.; Boone, A.; Le Moigne, P.; Livet, J.; Marchetti, M.; Foidart, A.; Franchistéguy, L.; Morel, S.; et al. Road surface condition forecasting in France. J. Appl. Meteor. Climatol. 2009, 48, 2513–2527. [Google Scholar] [CrossRef]
- Gultepe, I.; Feltz, W.F. Aviation meteorology: Observations and models. Introduction. Pure Appl. Geophys. 2019, 176, 1863–1867. [Google Scholar] [CrossRef]
- Gultepe, I.; Isaac, G.A.; Joe, P.; Kucera, P.A.; Theriault, J.M.; Fisico, T. Roundhouse (RND) Mountain Top Research Site: Measurements and Uncertainties for Winter Alpine Weather Conditions. Pure Appl. Geophys. 2014, 171, 59–85. [Google Scholar] [CrossRef]
- Handler, S.L.; Reeves, H.D.; McGovern, A. Development of a Probabilistic Subfreezing Road Temperature Nowcast and Forecast Using Machine Learning. Weather Forecast. 2020, 35, 1845–1863. [Google Scholar] [CrossRef]
- Lohmann, U.; Humble, J.; Leaitch, W.R. Simulations of ice clouds during FIRE ACE using the CCCMA single-column model. J. Geophys. Res. 2001, 106, 15123–15138. [Google Scholar] [CrossRef]
- Gultepe, I.; Heymsfield, A.J. Ice fog, ice clouds, and remote sensing. Pure Appl. Geophys. 2016, 173, 2977–2982. [Google Scholar] [CrossRef][Green Version]



| Order Number | Variable | Unit | Abbreviation |
|---|---|---|---|
| 1 | air temperature | °C | Ta |
| 2 | relative humidity | % | RH |
| 3 | wind speed at 10 m | m⋅s−1 | WS |
| 4 | mean air temperature during the past 6 h | °C | Taave_6 h |
| 5 | maximum temperature during the past 6 h | °C | Tamax_6 h |
| 6 | minimum temperature during the past 6 h | °C | Tamin_6 h |
| 7 | mean air temperature during the past 24 h | °C | Taave_24 h |
| 8 | maximum temperature during the past 24 h | °C | Tamax_24 h |
| 9 | minimum temperature during the past 24 h | °C | Tamin_24 h |
| 10 | mean air temperature during the past 240 h | °C | Taave_240 h |
| 11 | 1 h accumulated precipitation | mm | PRE_1 h |
| 12 | 6 h accumulated precipitation | mm | PRE_6 h |
| 13 | 24 h accumulated precipitation | mm | PRE_24 h |
| 14 | subsurface temperature at 5 cm | °C | SBT_5 cm |
| 15 | subsurface temperature at 10 cm | °C | SBT_10 cm |
| 16 | subsurface temperature at 15 cm | °C | SBT_15 cm |
| 17 | subsurface temperature at 20 m | °C | SBT_20 cm |
| 18 | subsurface temperature at 40 cm | °C | SBT_40 Cm |
| 19 | subsurface temperature at 80 cm | °C | SBT_80 cm |
| 20 | subsurface temperature at 160 cm | °C | SBT_160 cm |
| 21 | subsurface temperature at 320 cm | °C | SBT_320 cm |
| 22 | time coefficient | -- | Tinfo (1 and 0 represent day and night) |
| Station | Regression |
|---|---|
| road station 1 | −5.788 + 0.537 × Ta + 0.664 × SBT_320 cm − 0.128 × Tamin_6 h + 2.114 × SBT_5 cm − 3.129 × SBT_10 cm + 0.108 × Tamin_24 h − 0.342 × WS + 1.486 × SBT_15 cm − 0.107 × Taave_240 h |
| road station 2 | −10.548 + 0.620 × Ta − 0.192 × Tamin_6 h + 2.221 × SBT_5 cm − 2.515 × SBT_10 cm − 1.652 × SBT_160 cm − 0.571 × Taave_240 h + 0.870 × SBT_40 cm + 0.124 × Tamax_6 h+ 0.994 × SBT_320 cm + 0.147×Tamin_24 h + 1.708 × SBT_80 cm − 0.021 × PRE_24 h |
| bridge station 1 | −5.292 + 1.411 × Ta − 0.788 × Tamin_6 h + 1.531 × SBT_5 cm + 0.332 × Tinfo + 0.106 × Taave_24 h − 2.656 × SBT_10 cm + 1.582 × SBT_15 cm − 0.014 × RH |
| bridge station 2 | −4.493 + 1.090 × Ta − 0.626 × Tamin_6 h + 2.04 × SBT_5 cm − 2.737 × SBT_10 cm + 1.274 × SBT_20 cm − 0.016 × RH + 0.165 × Tamax_6 h |
| Station | Road Station 1 | Road Station 2 | Bridge Station 1 | Bridge Station 2 |
|---|---|---|---|---|
| Ta | 0.511 | 0.496 | 1.013 | 0.761 |
| RH | / | / | −0.081 | −0.076 |
| WS | 0.079 | / | / | / |
| Taave_6 h | / | / | / | / |
| Tamax_6 h | / | 0.125 | / | 0.139 |
| Tamin_6 h | −0.128 | 0.163 | −0.588 | −0.465 |
| Taave_24 h | / | / | / | / |
| Tamax_24 h | / | / | / | / |
| Tamin_24 h | 0.109 | 0.123 | 0.092 | / |
| Taave_240 h | −0.126 | −0.551 | 0.080 | / |
| PRE_1 h | / | / | / | / |
| PRE_6 h | / | / | / | / |
| PRE_24 h | / | −0.046 | / | / |
| SBT_5 cm | 1.666 | 1.480 | 1.043 | 1.243 |
| SBT_10 cm | −2.394 | −1.549 | −1.569 | −1.424 |
| SBT_15 cm | 1.161 | / | 0.944 | / |
| SBT_20 cm | / | / | / | 0.660 |
| SBT_40 cm | / | 0.558 | / | / |
| SBT_80 cm | / | 1.117 | / | / |
| SBT_160 cm | / | −1.032 | / | / |
| SBT_320 cm | 0.309 | 0.409 | / | / |
| Tinfo (1 and 0 represent day and night) | / | / | 0.048 | / |
| Station | Parameters |
|---|---|
| road station 1 | n_estimators = 100, max_depth = 13 |
| road station 2 | n_estimators = 100, max_depth = 15 |
| bridge station 1 | n_estimators = 100, max_depth = 10 |
| bridge station 2 | n_estimators = 100, max_depth = 13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Jia, B.; Zhou, J.; Feng, L.; Chen, J. Retrieval of Road Surface (Bridge Deck) Temperature near 0 °C Based on Random Forest Model. Atmosphere 2022, 13, 1491. https://doi.org/10.3390/atmos13091491
Wang C, Jia B, Zhou J, Feng L, Chen J. Retrieval of Road Surface (Bridge Deck) Temperature near 0 °C Based on Random Forest Model. Atmosphere. 2022; 13(9):1491. https://doi.org/10.3390/atmos13091491
Chicago/Turabian StyleWang, Chuanhui, Beixi Jia, Jianping Zhou, Lei Feng, and Jian Chen. 2022. "Retrieval of Road Surface (Bridge Deck) Temperature near 0 °C Based on Random Forest Model" Atmosphere 13, no. 9: 1491. https://doi.org/10.3390/atmos13091491
APA StyleWang, C., Jia, B., Zhou, J., Feng, L., & Chen, J. (2022). Retrieval of Road Surface (Bridge Deck) Temperature near 0 °C Based on Random Forest Model. Atmosphere, 13(9), 1491. https://doi.org/10.3390/atmos13091491





