Heterogenous Canopy in a Lagrangian-Stochastic Dispersion Model for Particulate Matter from Multiple Sources over the Haifa Bay Area
Abstract
:1. Introduction
2. Methods
2.1. Modelling Approach
2.2. The IIBR Lagrangian Stochastic Model
2.3. Inertia Effects
2.4. Canopy Layer Model and Surface Layer Parametrizations
2.5. Input Fields
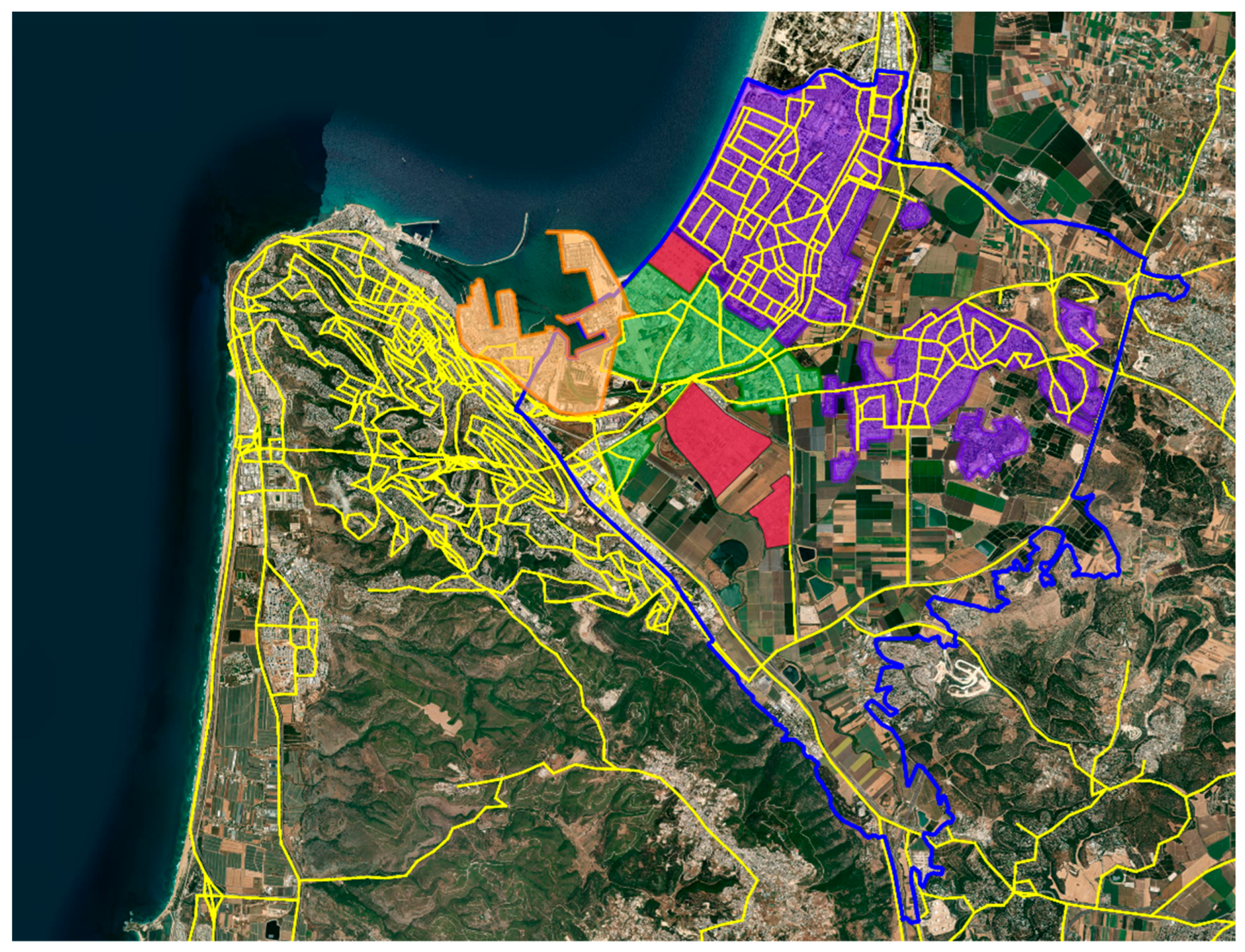
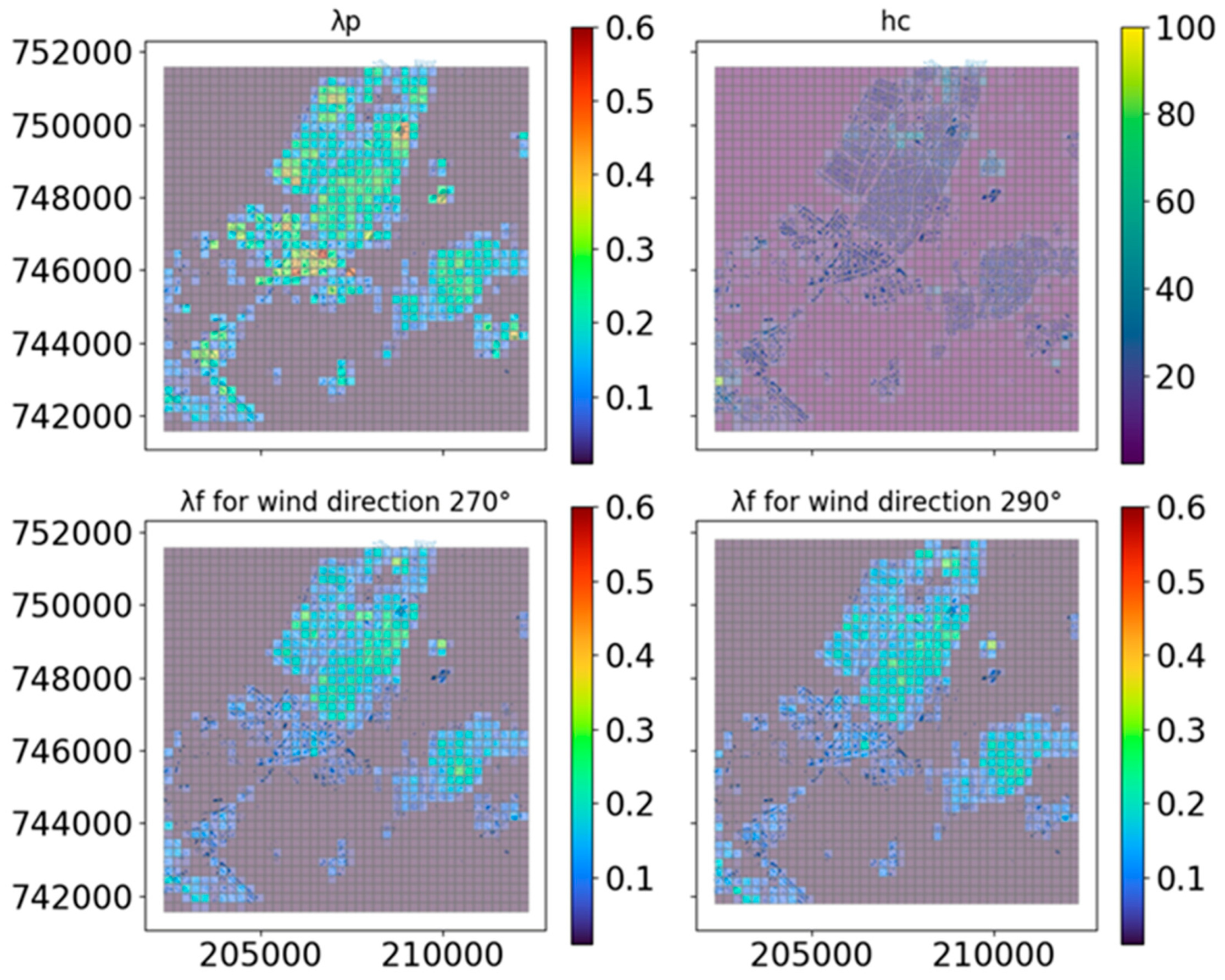
2.5.1. Canopy Model Parameters for Inhomogeneous Urban Area
2.5.2. Pollutant Sources
3. Results
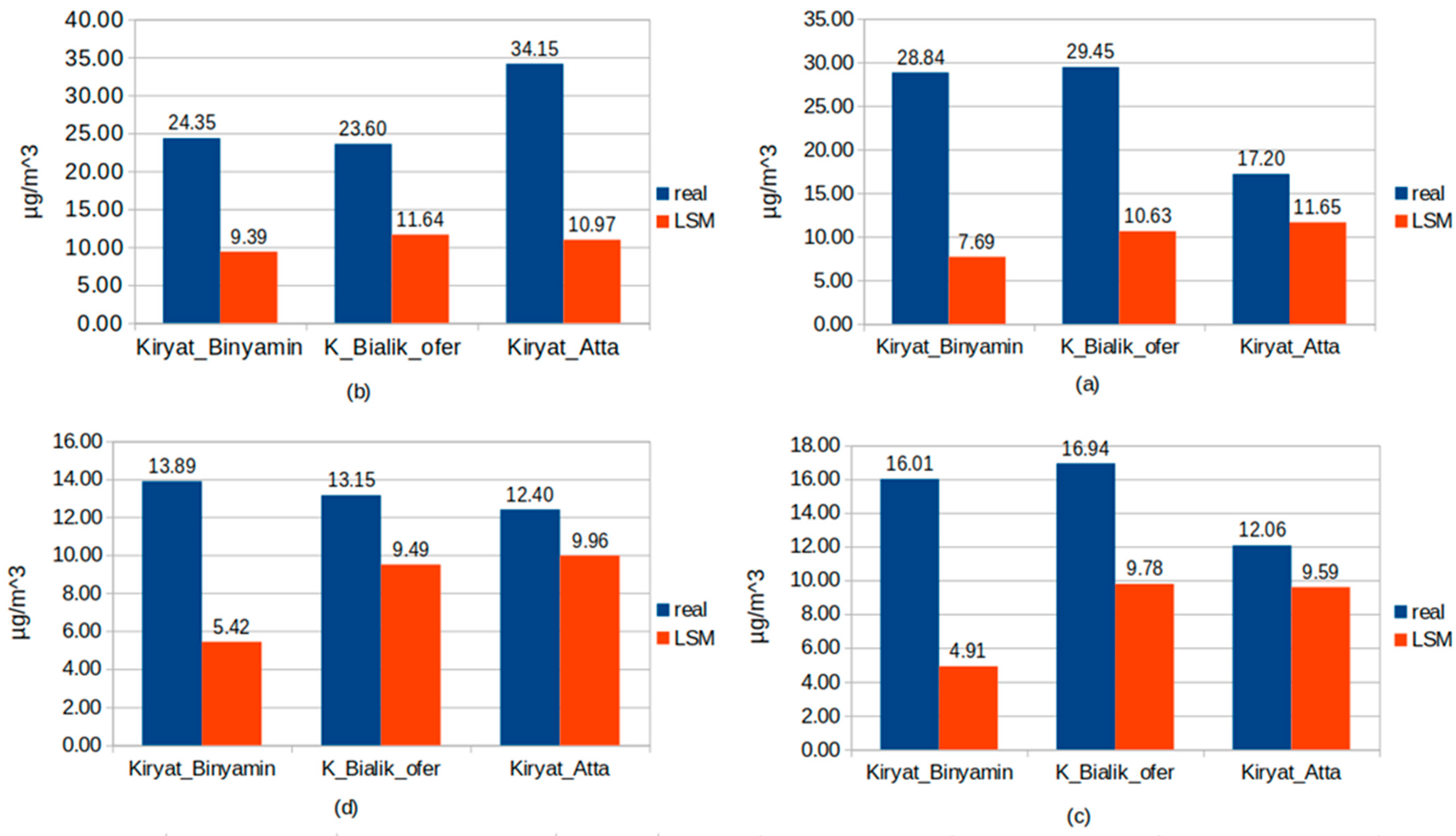
3.1. Comparison of the PM Concentration Estimated by the LSM Model to Measurements
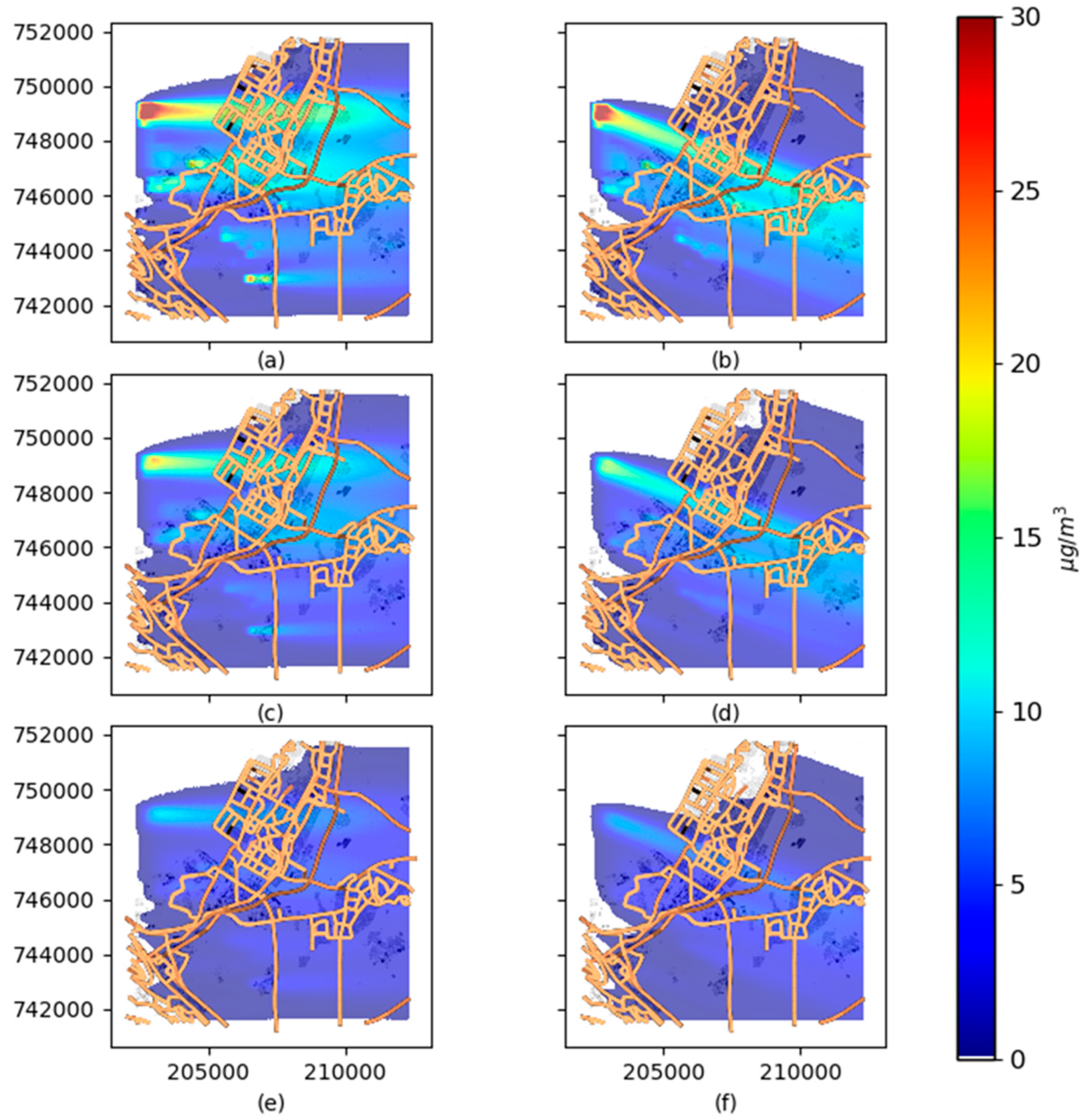
3.2. Modelled Three-Dimensional PM Fields in the HBA
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Federman, R.; Mendelson, A.; Romem, E.; Mor-Federman, T.; Lahav, C.; Ron, M.; Ramon, U. Zevulun Survey—Survey, Analysis and Evaluation of Nature, Landscape and Human Heritage; The Open Landscape Institute (OLI): Tel Aviv, Israel, 2015. [Google Scholar]
- Raz, R.; Yuval; Bar-Or, R.L.; Kark, J.D.; Sinnreich, R.; Broday, D.M.; Harari-Kremer, R.; Bentur, L.; Gileles-Hillel, A.; Keinan-Boker, L.; et al. Associations between Exposure to Industrial Air Pollution and Prevalence of Asthma and Atopic Diseases in Haifa Bay Area. Atmosphere 2021, 12, 516. [Google Scholar] [CrossRef]
- Yuval; Tritscher, T.; Raz, R.; Levi, Y.; Levy, I.; Broday, D.M. Emissions vs. Turbulence and Atmospheric Stability: A Study of Their Relative Importance in Determining Air Pollutant Concentrations. Sci. Total Environ. 2020, 733, 139300. [Google Scholar] [CrossRef] [PubMed]
- Klausner, Z.; Ben-Efraim, M.; Arav, Y.; Tas, E.; Fattal, E. The Micrometeorology of the Haifa Bay Area and Mount Carmel during the Summer. Atmosphere 2021, 12, 354. [Google Scholar] [CrossRef]
- Saaroni, H.; Levi, E.; Ziv, B. Particulate Matter in the Summer Season and Its Relation to Synoptic Conditions and Regional Climatic Stress—The Case of Haifa, Israel. Water. Air. Soil Pollut. 2018, 229, 313. [Google Scholar] [CrossRef]
- Karimi, A.; Shirmardi, M.; Hadei, M.; Birgani, Y.T.; Neisi, A.; Takdastan, A.; Goudarzi, G. Concentrations and Health Effects of Short- and Long-Term Exposure to PM2.5, NO2, and O3 in Ambient Air of Ahvaz City, Iran (2014–2017). Ecotoxicol. Environ. Saf. 2019, 180, 542–548. [Google Scholar] [CrossRef]
- Yunesian, M.; Rostami, R.; Zarei, A.; Fazlzadeh, M.; Janjani, H. Exposure to High Levels of PM2.5 and PM10 in the Metropolis of Tehran and the Associated Health Risks during 2016–2017. Microchem. J. 2019, 150, 104174. [Google Scholar] [CrossRef]
- Khreis, H.; Kelly, C.; Tate, J.; Parslow, R.; Lucas, K.; Nieuwenhuijsen, M. Exposure to Traffic-Related Air Pollution and Risk of Development of Childhood Asthma: A Systematic Review and Meta-Analysis. Environ. Int. 2017, 100, 1–31. [Google Scholar] [CrossRef] [Green Version]
- Meier-Girard, D.; Delgado-Eckert, E.; Schaffner, E.; Schindler, C.; Künzli, N.; Adam, M.; Pichot, V.; Kronenberg, F.; Imboden, M.; Frey, U.; et al. Association of Long-Term Exposure to Traffic-Related PM10 with Heart Rate Variability and Heart Rate Dynamics in Healthy Subjects. Environ. Int. 2019, 125, 107–116. [Google Scholar] [CrossRef]
- Eitan, O.; Yuval; Barchana, M.; Dubnov, J.; Linn, S.; Carmel, Y.; Broday, D.M. Spatial Analysis of Air Pollution and Cancer Incidence Rates in Haifa Bay, Israel. Sci. Total Environ. 2010, 408, 4429–4439. [Google Scholar] [CrossRef]
- Petrov, A.; Valente, J.; Bauman-Stantzer, K.; Batchvarova, E. Applicability of Gaussian Dispersion Models for Accidental Releases in Urban Environment-Results of the “Michelstadt” Test Case in Cost Action ES1006. Bulg. J. Meteorol. Hydrol. 2017, 22, 87–102. [Google Scholar]
- Pirhalla, M.; Heist, D.; Perry, S.; Tang, W.; Brouwer, L. Simulations of Dispersion through an Irregular Urban Building Array. Atmos. Environ. 2021, 258, 118500. [Google Scholar] [CrossRef] [PubMed]
- Efthimiou, G.C.; Bartzis, J.G.; Berbekar, E.; Hertwig, D.; Harms, F.; Leitl, B. Modelling Short-Term Maximum Individual Exposure from Airborne Hazardous Releases in Urban Environments. Part II: Validation of a Deterministic Model with Wind Tunnel Experimental Data. Toxics 2015, 3, 259–267. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hanna, S.R.; Britter, R.E. Wind Flow and Vapor Cloud Dispersion at Industrial and Urban Sites; Center for Chemical Process Safety/AIChE: New York, NY, USA, 2002; ISBN 0-8169-0863-X. [Google Scholar]
- Hanna, S.R.; Brown, M.J.; Camelli, F.E.; Chan, S.T.; Coirier, W.J.; Hansen, O.R.; Huber, A.H.; Kim, S.; Reynolds, R.M. Detailed Simulations of Atmospheric Flow and Dispersion in Downtown Manhattan: An Application of Five Computational Fluid Dynamics Models. Bull. Am. Meteorol. Soc. 2006, 87, 1713–1726. [Google Scholar] [CrossRef] [Green Version]
- Neophytou, M.; Gowardhan, A.; Brown, M. An Inter-Comparison of Three Urban Wind Models Using Oklahoma City Joint Urban 2003 Wind Field Measurements. J. Wind Eng. Ind. Aerodyn. 2011, 99, 357–368. [Google Scholar] [CrossRef]
- Hanna, S.; White, J.; Trolier, J.; Vernot, R.; Brown, M.; Gowardhan, A.; Kaplan, H.; Alexander, Y.; Moussafir, J.; Wang, Y.; et al. Comparisons of JU2003 Observations with Four Diagnostic Urban Wind Flow and Lagrangian Particle Dispersion Models. Atmos. Environ. 2011, 45, 4073–4081. [Google Scholar] [CrossRef]
- Thomson, D.J. Criteria for the Selection of Stochastic Models of Particle Trajectories in Turbulent Flows. J. Fluid Mech. 1987, 180, 529–556. [Google Scholar] [CrossRef]
- Wilson, J.D.; Sawford, B.L. Review of Lagrangian Stochastic Models for Trajectories in the Turbulent Atmosphere. Bound.-Layer Meteorol. 1996, 78, 191–210. [Google Scholar] [CrossRef]
- Gavze, E.; Fattal, E. A Semi-Analytical Model for Short-Range Near-Ground Continuous Dispersion. Bound.-Layer Meteorol. 2018, 169, 297–326. [Google Scholar] [CrossRef]
- Wilson, J. Turbulent Transport within the Plant Canopy. In Estimationn of Areal Evapotranspiration; Black, T.A., Spittlehouse, D., Novak, M., Price, D.T., Eds.; International Association of Hydrological Sciences (IAHS): Wallingford, UK, 1989; pp. 43–80. [Google Scholar]
- Wilson, J.D.; Yee, E.; Ek, N.; D’Amours, R. Lagrangian Simulation of Wind Transport in the Urban Environment. Q. J. R. Meteorol. Soc. 2009, 135, 1586–1602. [Google Scholar] [CrossRef]
- Wang, C.; Li, Q.; Wang, Z.H. Quantifying the Impact of Urban Trees on Passive Pollutant Dispersion Using a Coupled Large-Eddy Simulation–Lagrangian Stochastic Model. Build. Environ. 2018, 145, 33–49. [Google Scholar] [CrossRef]
- Röckle, R. Bestimmung Der Stomungsver-Haltnisse Im Bereich Komplexer Bebauugsstruk-Turen Darmstadt. Ph.D. Thesis, Technischen Hochschule Darmstadt, Darmstadt, Germany, 1990. [Google Scholar]
- Kaplan, H.; Dinar, N. A Lagrangian Dispersion Model for Calculating Concentration Distribution within a Built-up Domain. Atmos. Environ. 1996, 30, 4197–4207. [Google Scholar] [CrossRef]
- Oldrini, O.; Armand, P.; Duchenne, C.; Olry, C.; Moussafir, J.; Tinarelli, G. Description and Preliminary Validation of the PMSS Fast Response Parallel Atmospheric Flow and Dispersion Solver in Complex Built-up Areas. Environ. Fluid Mech. 2017, 17, 997–1014. [Google Scholar] [CrossRef]
- Brown, M.J.; Gowardhan, A.; Nelson, M.; Williams, M.; Pardyjak, E.R. Evaluation of the Quic Wind and Dispersion Models Using the Joint Urban 2003 Field Experiment Dataset. AMS 8th Symp. Urban Environ. 2009, J19.4. [Google Scholar]
- Raupach, M.R.; Finnigan, J.J.; Brunei, Y. Coherent Eddies and Turbulence in Vegetation Canopies: The Mixing-Layer Analogy; Springer: Berlin/Heidelberg, Germany, 1996; Volume 78, pp. 351–382. [Google Scholar]
- Finnigan, J.J. Turbulence in Plant Canopies. Annu. Rev. Fluid Mech. 2000, 32, 519–571. [Google Scholar] [CrossRef]
- Shnapp, R.; Bohbot-Raviv, Y.; Liberzon, A.; Fattal, E. Turbulence-Obstacle Interactions in the Lagrangian Framework: Applications for Stochastic Modeling in Canopy Flows. Phys. Rev. Fluids 2020, 5, 094601. [Google Scholar] [CrossRef]
- Fattal, E. A Non-Homogenous Non-Gaussian Lagrangian Stochastic Model for Pollutant Dispersion in Complex Topography—Comparison to Haifa 2009 Urban Tracer Campaign; IIBR Sci. Report 2014/56/53/5614; Israel Institute for Biological Research: Ness Ziona, Israel, 2014. (In Hebrew) [Google Scholar]
- Hanna, S.; Chang, J. Acceptance Criteria for Urban Dispersion Model Evaluation. Meteorol. Atmos. Phys. 2012, 116, 133–146. [Google Scholar] [CrossRef]
- Fattal, E.; David-Saroussi, H.; Klausner, Z.; Buchman, O. An Urban Lagrangian Stochastic Dispersion Model for Simulating Traffic Particulate-Matter Concentration Fields. Atmosphere 2021, 12, 580. [Google Scholar] [CrossRef]
- Thomson, D.J.; Wilson, J.D. History of Lagrangian Stochastic Models for Turbulent Dispersion. In Lagrangian Modeling of the Atmosphere; Lin, J., Brunner, D., Gerbig, C., Stohl, A., Luhar, A., Webley, P., Eds.; American Geophysical Union: Washington, DC, USA, 2012; pp. 19–36. ISBN 978-0-87590-490-0. [Google Scholar]
- Pope, S.B. Turbulent Flows, 1st ed.; Cambridge University Press: London, UK, 2000; ISBN 0521598869. [Google Scholar]
- Obukhov, A.M. Description of Turbulence in Terms of Lagrangian Variables. In Advances in Geophysics, Volume 6; Frenkiel, F.N., Sheppard, P.A., Eds.; Academic Press: New York, NY, USA, 1959; pp. 113–116. ISBN 0120188066. [Google Scholar]
- Tutkun, M. Markovian Properties of Velocity Increments in Boundary Layer Turbulence. Phys. D Nonlinear Phenom. 2017, 351–352, 53–61. [Google Scholar] [CrossRef]
- Novikov, E.A. Relation between the Lagrangian and Eulerian Descriptions of Turbulence. J. Appl. Math. Mech. 1969, 33, 862–864. [Google Scholar] [CrossRef]
- Pope, S.B. Consistency Conditions for Random-Walk Models of Turbulent Dispersion. Phys. Fluids 1987, 30, 2374–2379. [Google Scholar] [CrossRef]
- Sawford, B.L. Rotation of Trajectories in Lagrangian Stochastic Models of Turbulent Dispersion. Bound. -Layer Meteorol. 1999, 93, 411–424. [Google Scholar] [CrossRef]
- Wilson, J.D.; Flesch, T.K. Trajectory Curvature as a Selection Criterion for Valid Lagrangian Stochastic Dispersion Models. Bound.-Layer Meteorol. 1997, 84, 411–425. [Google Scholar] [CrossRef]
- Brouwers, J.J.H. Statistical Description of Turbulent Dispersion. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2012, 86, 1–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Faranda, D.; Pons, F.M.E.; Dubrulle, B.; Daviaud, F.; Saint-Michel, B.; Herbert, É.; Cortet, P.P. Modelling and Analysis of Turbulent Datasets Using Auto Regressive Moving Average Processes. Phys. Fluids 2014, 26, 105101. [Google Scholar] [CrossRef] [Green Version]
- Pope, S.B. The Vanishing Effect of Molecular Diffusivity on Turbulent Dispersion: Implications for Turbulent Mixing and the Scalar Flux. J. Fluid Mech. 1998, 359, 299–312. [Google Scholar] [CrossRef] [Green Version]
- Gardiner, C.W. Stochastic Methods: A Handbook for the Natural and Social Sciences, 4th ed.; Springer-Verlang: Berlin, Germany, 1997; ISBN 3-540-61634-9. [Google Scholar]
- Shnapp, R.; Shapira, E.; Peri, D.; Bohbot-Raviv, Y.; Fattal, E.; Liberzon, A. Extended 3D-PTV for Direct Measurements of Lagrangian Statistics of Canopy Turbulence in a Wind Tunnel. Sci. Rep. 2019, 9, 7405. [Google Scholar] [CrossRef] [Green Version]
- Shnapp, R. On Small-Scale and Large-Scale Intermittency of Lagrangian Statistics in Canopy Flow. J. Fluid Mech. 2021, 913, 1–13. [Google Scholar] [CrossRef]
- Poggi, D.; Katul, G.G.; Cassiani, M. On the Anomalous Behavior of the Lagrangian Structure Function Similarity Constant inside Dense Canopies. Atmos. Environ. 2008, 42, 4212–4231. [Google Scholar] [CrossRef]
- Du, S. Universality of the Lagrangian Velocity Structure Function Constant (C0) across Different Kinds of Turbulence. Bound.-Layer Meteorol. 1997, 83, 207–219. [Google Scholar] [CrossRef]
- Rizza, U.; Degrazia, G.A.; Mangia, C.; Filho, E.P.M. Estimation of the Kolmogorov Constant for the Lagrangian Velocity Spectrum and Structure Function under Different PBL Stability Regimes Generated by Les. Phys. A Stat. Mech. Appl. 2010, 389, 4009–4017. [Google Scholar] [CrossRef]
- Christen, A.; Vogt, R.; Rotach, M.W. Profile Measurements of Selected Turbulence Characteristics over Different Urban Surfaces. In Proceedings of the 4th International Conference on Urban Air Quality, Prague, Czech Republic, 22–24 July 2003; Volume 1, pp. 408–411. [Google Scholar]
- Flesch, T.K.; Wilson, J.D. A Two-Dimensional Trajectory-Simulation Model for Non-Gaussian, Inhomogeneous Turbulence within Plant Canopies. Bound.-Layer Meteorol. 1992, 61, 349–374. [Google Scholar] [CrossRef]
- Gloster, J.; Williams, P.; Doel, C.; Esteves, I.; Coe, H.; Valarcher, J.-F. Foot-and-Mouth Disease—Quantification and Size Distribution of Airborne Particles Emitted by Healthy and Infected Pigs. Vet. J. 2007, 174, 42–53. [Google Scholar] [CrossRef] [PubMed]
- Mayer, D.; Reiczigel, J.; Rubel, F. A Lagrangian Particle Model to Predict the Airborne Spread of Foot-and-Mouth Disease Virus. Atmos. Environ. 2008, 42, 466–479. [Google Scholar] [CrossRef]
- Garner, M.G.; Hess, G.D.; Yang, X. An Integrated Modelling Approach to Assess the Risk of Wind-Borne Spread of Foot-and-Mouth Disease Virus from Infected Premises. Environ. Model. Assess. 2006, 11, 195–207. [Google Scholar] [CrossRef]
- Klausner, Z.; Klement, E.; Fattal, E. Modeling Long Distance Dispersal of Airborne Foot-and-Mouth Disease Virus as a Polydisperse Aerosol—Application to the Emergence of a New Strain from Egypt to Israel. Atmos. Environ. 2015, 122, 332–342. [Google Scholar] [CrossRef]
- Pozorski, J. Models of Turbulent Flows and Particle Dynamics. In Particles in Wall-Bounded Turbulent Flows: Deposition, Re-Suspension and Agglomeration; Minier, J.-P., Pozorski, J., Eds.; Springer: Cham, Germany, 2017; pp. 97–150. ISBN 978-3-319-41566-6. [Google Scholar]
- Minier, J.P. On Lagrangian Stochastic Methods for Turbulent Polydisperse Two-Phase Reactive Flows. Prog. Energy Combust. Sci. 2015, 50, 1–62. [Google Scholar] [CrossRef]
- Wilson, J.D. Trajectory Models for Heavy Particles in Atmospheric Turbulence: Comparison with Observations. J. Appl. Meteorol. 2000, 39, 1894–1912. [Google Scholar] [CrossRef]
- Mamun, A.A.; Cheng, I.; Zhang, L.; Dabek-Zlotorzynska, E.; Charland, J.-P. Overview of Size Distribution, Concentration, and Dry Deposition of Airborne Particulate Elements Measured Worldwide. Environ. Rev. 2020, 28, 77–88. [Google Scholar] [CrossRef]
- Casal, J.; Planas-Cuchi, E.; Moresob, J.M.; Casal, J. Forecasting Virus Atmospherical Dispersion. Studies with Foot-and-Mouth Disease. J. Hazard. Mater. 1995, 43, 229–244. [Google Scholar] [CrossRef]
- Yuval; Broday, D.M. High-Resolution Spatial Patterns of Long-Term Mean Concentrations of Air Pollutants in Haifa Bay Area. Atmos. Environ. 2006, 40, 3653–3664. [Google Scholar] [CrossRef]
- Shi, J.P.; Mark, D.; Harrison, R.M. Characterization of Particles from a Current Technology Heavy-Duty Diesel Engine. Environ. Sci. Technol. 2000, 34, 748–755. [Google Scholar] [CrossRef]
- Yuval; Broday, D.M.; Alpert, P. Exploring the Applicability of Future Air Quality Predictions Based on Synoptic System Forecasts. Environ. Pollut. 2012, 166, 65–74. [Google Scholar] [CrossRef] [PubMed]
- Hazi, Y.; Heikkinen, M.S.A.; Cohen, B.S. Size Distribution of Acidic Sulfate Ions in Fine Ambient Particulate Matter and Assessment of Source Region Effect. Atmos. Environ. 2003, 37, 5403–5413. [Google Scholar] [CrossRef]
- Mehlmann, A.; Warneck, P. Atmospheric Gaseous HNO3, Particulate Nitrate, and Aerosol Size Distributions of Major Ionic Species at a Rural Site in Western Germany. Atmos. Environ. 1995, 29, 2359–2373. [Google Scholar] [CrossRef]
- Csanady, G.T. Turbulent Diffusion of Heavy Particles in the Atmosphere. J. Atmos. Sci. 1963, 20, 201–208. [Google Scholar] [CrossRef]
- Belcher, S.E.; Jerram, N.; Hunt, J.C.R. Adjustment of a Turbulent Boundary Layer to a Canopy of Roughness Elements. J. Fluid Mech. 2003, 488, 369–398. [Google Scholar] [CrossRef] [Green Version]
- Raupach, M.R.; Shaw, R.H. Averaging Procedures for Flow Canopies. Bound. -Layer Meteorol. 1982, 22, 79–90. [Google Scholar] [CrossRef]
- Coceal, O.; Belcher, S.E. A Canopy Model of Mean Winds through Urban Areas. Q. J. R. Meteorol. Soc. 2004, 130, 1349–1372. [Google Scholar] [CrossRef] [Green Version]
- Grimmond, C.S.B.; Oke, T.R. Aerodynamic Properties of Urban Areas Derived from Analysis of Surface Form. J. Appl. Meteorol. Clim. 1999, 38, 1262–1292. [Google Scholar] [CrossRef]
- Coceal, O.; Belcher, S.E. Mean Winds through an Inhomogeneous Urban Canopy. Bound.-Layer Meteorol. 2005, 115, 47–68. [Google Scholar] [CrossRef]
- Inoue, E. On the Turbulent Structure of Airflow within Crop Canopies. J. Meteorol. Soc. Japan. Ser. II 1963, 41, 317–326. [Google Scholar] [CrossRef] [Green Version]
- Finnigan, J.; Harman, I.; Ross, A.; Belcher, S. First-Order Turbulence Closure for Modelling Complex Canopy Flows. Q. J. R. Meteorol. Soc. 2015, 141, 2907–2916. [Google Scholar] [CrossRef]
- Harman, I.N.; Finnigan, J.J. A Simple Unified Theory for Flow in the Canopy and Roughness Sublayer. Bound.-Layer Meteorol. 2007, 123, 339–363. [Google Scholar] [CrossRef]
- Hicks, B.B.; Pendergrass, W.R.; Vogel, C.A.; Keener, R.N.; Leyton, S.M. On the Micrometeorology of the Southern Great Plains 1: Legacy Relationships Revisited. Bound.-Layer Meteorol. 2014, 151, 389–405. [Google Scholar] [CrossRef]
- Wilson, J.D. Monin-Obukhov Functions for Standard Deviations of Velocity. Bound.-Layer Meteorol. 2008, 129, 353–369. [Google Scholar] [CrossRef]
- Hanna, S.R. Applications in Air Pollution Modeling. In Atmospheric Turbulence and Air Pollution Modelling; Nieuwstadt, F.T.M., van Dop, H., Eds.; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1982; pp. 275–310. ISBN 978-90-277-1807-5. [Google Scholar]
- Kastner-Klein, P.; Rotach, M.W. Mean Flow and Turbulence Characteristics in an Urban Roughness Sublayer. Bound.-Layer Meteorol. 2004, 111, 55–84. [Google Scholar] [CrossRef]
- Mortarini, L.; Ferrero, E.; Richiardone, R.; Falabino, S.; Anfossi, D.; Trini Castelli, S.; Carretto, E. Assessment of Dispersion Parameterizations through Wind Data Measured by Three Sonic Anemometers in a Urban Canopy. Adv. Sci. Res. 2009, 3, 91–98. [Google Scholar] [CrossRef] [Green Version]
- Israel Ministry of Environmental Protection. Israel’s Hourly Inventory of Traffic Air Pollutants by Road Sections for 2019; Received by Authors Request; Israel Ministry of Environmental Protection: Jerusalem, Israel, 2020.
- Israel Ministry of Environmental Protection. Israel’s Hourly Inventory of Air Pollutants, Point Sources and Other Source Types for 2018; Received by Authors Request; Israel Ministry of Environmental Protection: Jerusalem, Israel, 2020.
- Klausner, Z.; Fattal, E. An Objective and Automatic Method for Identification of Pattern Changes in Wind Direction Time Series. Int. J. Climatol. 2011, 31, 783–790. [Google Scholar] [CrossRef]
- Dayan, U.; Levy, I. The Influence of Meteorological Conditions and Atmospheric Circulation Types on PM 10 and Visibility in Tel Aviv. J. Appl. Meteorol. 2005, 44, 606–619. [Google Scholar] [CrossRef]
- Erel, Y.; Kalderon-Asael, B.; Dayan, U.; Sandler, A. European Atmospheric Pollution Imported by Cooler Air Masses to the Eastern Mediterranean during the Summer. Environ. Sci. Technol. 2007, 41, 5198–5203. [Google Scholar] [CrossRef]
- Kalderon-Asael, B.; Erel, Y.; Sandler, A.; Dayan, U. Mineralogical and Chemical Characterization of Suspended Atmospheric Particles over the East Mediterranean Based on Synoptic-Scale Circulation Patterns. Atmos. Environ. 2009, 43, 3963–3970. [Google Scholar] [CrossRef]
- Ganor, E.; Levin, Z.; Van Grieken, R. Composition of Individual Aerosol Particles above the Israelian Mediterranean Coast during the Summer Time. Atmos. Environ. 1998, 32, 1631–1642. [Google Scholar] [CrossRef]
- Freiman, M.T.; Hirshel, N.; Broday, D.M. Urban-Scale Variability of Ambient Particulate Matter Attributes. Atmos. Environ. 2006, 40, 5670–5684. [Google Scholar] [CrossRef]
- Meng, Z.; Seinfeld, J.H. Time Scales to Achieve Atmospheric Gas-Aerosol Equilibrium for Volatile Species. Atmos. Environ. 1996, 30, 2889–2900. [Google Scholar] [CrossRef]
- Levin, Z.; Teller, A.; Ganor, E. On the Interactions of Mineral Dust, Sea-Salt Particles, and Clouds: A Measurement and Modeling Study from the Mediterranean Israeli Dust Experiment Campaign. J. Geophys. Res. 2005, 110, D20202. [Google Scholar] [CrossRef] [Green Version]
- Athanasopoulou, E.; Tombrou, M.; Pandis, S.N.; Russell, A.G. The Role of Sea-Salt Emissions and Heterogeneous Chemistry in the Air Quality of Polluted Coastal Areas. Atmos. Chem. Phys. 2008, 8, 5755–5769. [Google Scholar] [CrossRef] [Green Version]
- Carvalho, A.R.; Gama, C.; Monteiro, A. Investigating the Contribution of Sea Salt to PM10 Concentration Values on the Coast of Portugal. Air Qual. Atmos. Health 2021, 14, 1697–1708. [Google Scholar] [CrossRef]
- Chow, J.C.; Watson, J.G.; Lowenthal, D.H.; Countess, R.J. Sources and Chemistry of PM10 Aerosol in Santa Barbara County, CA. Atmos. Environ. 1996, 30, 1489–1499. [Google Scholar] [CrossRef]
- Mkoma, S.L.; Maenhaut, W.; Chi, X.; Wang, W.; Raes, N. Characterisation of PM10 Atmospheric Aerosols for the Wet Season 2005 at Two Sites in East Africa. Atmos. Environ. 2009, 43, 631–639. [Google Scholar] [CrossRef]
- Herut, B.; Nimmo, M.; Medway, A.; Chester, R.; Krom, M.D. Dry Atmospheric Inputs of Trace Metals at the Mediterranean Coast of Israel (SE Mediterranean): Sources and Fluxes. Atmos. Environ. 2001, 35, 803–813. [Google Scholar] [CrossRef]
- Dayan, U.; Erel, Y.; Shpund, J.; Kordova, L.; Wanger, A.; Schauer, J.J. The Impact of Local Sources and Meteorological Factors on Nitrogen Oxide and Particulate Matter Concentrations: A Case Study of the Day of Atonement in Israel. Atmos. Environ. 2011, 45, 3325–3332. [Google Scholar] [CrossRef]
- Ganor, E.; Stupp, A.; Alpert, P. A Method to Determine the Effect of Mineral Dust Aerosols on Air Quality. Atmos. Environ. 2009, 43, 5463–5468. [Google Scholar] [CrossRef]
- Chang, J.C.; Hanna, S.R. Air Quality Model Performance Evaluation. Meteorol. Atmos. Phys. 2004, 87, 167–196. [Google Scholar] [CrossRef]
- Elbir, T. Comparison of Model Predictions with the Data of an Urban Air Quality Monitoring Network in Izmir, Turkey. Atmos. Environ. 2003, 37, 2149–2157. [Google Scholar] [CrossRef]
- Heist, D.; Isakov, V.; Perry, S.; Snyder, M.; Venkatram, A.; Hood, C.; Stocker, J.; Carruthers, D.; Arunachalam, S.; Owen, R.C. Estimating Near-Road Pollutant Dispersion: A Model Inter-Comparison. Transp. Res. Part D Transp. Environ. 2013, 25, 93–105. [Google Scholar] [CrossRef]

| Particle Type | Rush Hour Period | NMSE | FAC2 | NAD | |
|---|---|---|---|---|---|
| PM10 | Morning | 0.88 | 1.03 | 0.33 | 0.44 |
| Evening | 0.86 | 1.1 | 0.33 | 0.43 | |
| PM2.5 | Morning | 0.45 | 0.28 | 0.67 | 0.23 |
| Evening | 0.6 | 0.5 | 0.67 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fattal, E.; David-Saroussi, H.; Buchman, O.; Tas, E.; Klausner, Z. Heterogenous Canopy in a Lagrangian-Stochastic Dispersion Model for Particulate Matter from Multiple Sources over the Haifa Bay Area. Atmosphere 2023, 14, 144. https://doi.org/10.3390/atmos14010144
Fattal E, David-Saroussi H, Buchman O, Tas E, Klausner Z. Heterogenous Canopy in a Lagrangian-Stochastic Dispersion Model for Particulate Matter from Multiple Sources over the Haifa Bay Area. Atmosphere. 2023; 14(1):144. https://doi.org/10.3390/atmos14010144
Chicago/Turabian StyleFattal, Eyal, Hadas David-Saroussi, Omri Buchman, Eran Tas, and Ziv Klausner. 2023. "Heterogenous Canopy in a Lagrangian-Stochastic Dispersion Model for Particulate Matter from Multiple Sources over the Haifa Bay Area" Atmosphere 14, no. 1: 144. https://doi.org/10.3390/atmos14010144
APA StyleFattal, E., David-Saroussi, H., Buchman, O., Tas, E., & Klausner, Z. (2023). Heterogenous Canopy in a Lagrangian-Stochastic Dispersion Model for Particulate Matter from Multiple Sources over the Haifa Bay Area. Atmosphere, 14(1), 144. https://doi.org/10.3390/atmos14010144








