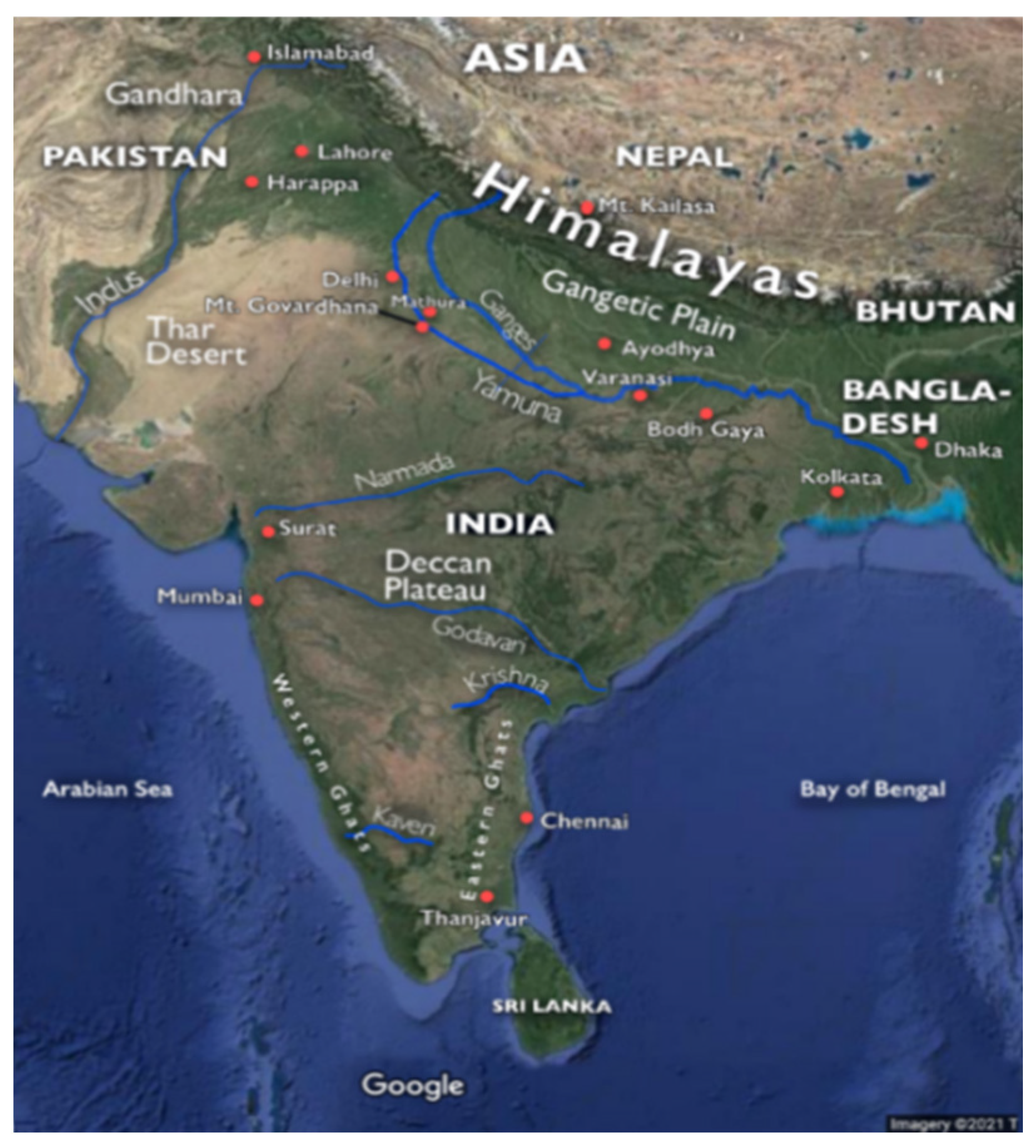
Figure 1.
Topographic Map of South Asia.
Figure 1.
Topographic Map of South Asia.
Figure 2.
The first row shows mean annual SU indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); The second row shows annual trend of SU indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 2.
The first row shows mean annual SU indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); The second row shows annual trend of SU indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 3.
The first row shows mean annual WSDI indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows annual trend of WSDI indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 3.
The first row shows mean annual WSDI indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows annual trend of WSDI indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 4.
The first row shows mean annual TXx indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows annual trend of TXx indices under four scenarios: historical, SSP245, SSP585, and G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 4.
The first row shows mean annual TXx indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows annual trend of TXx indices under four scenarios: historical, SSP245, SSP585, and G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 5.
The first row shows mean annual TNx indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows annual trend of TNx indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 5.
The first row shows mean annual TNx indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows annual trend of TNx indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 6.
The first row shows mean annual ID indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows annual trend of ID indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 6.
The first row shows mean annual ID indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows annual trend of ID indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 7.
The first row shows mean annual CSDI indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows annual trend of CSDI indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 7.
The first row shows mean annual CSDI indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows annual trend of CSDI indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 8.
The first row shows mean annual TNn indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows annual trend of TNn indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 8.
The first row shows mean annual TNn indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows annual trend of TNn indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 9.
The first row shows mean annual TXn indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows annual trend of TXn indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 9.
The first row shows mean annual TXn indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows annual trend of TXn indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 10.
The first row shows mean annual CDD indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows annual trend of CDD indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 10.
The first row shows mean annual CDD indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows annual trend of CDD indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 11.
The first row shows mean annual CWD indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows annual trend of CWD indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 11.
The first row shows mean annual CWD indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows annual trend of CWD indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 12.
The first row shows mean annual RX1day indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows annual trend of RX1day indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 12.
The first row shows mean annual RX1day indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows annual trend of RX1day indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 13.
The first row shows mean summer RX1day indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows Trend of summer RX1day indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 13.
The first row shows mean summer RX1day indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows Trend of summer RX1day indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 14.
Pearson correlation coefficients between annual RX1day indices and annual precipitation under four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059).
Figure 14.
Pearson correlation coefficients between annual RX1day indices and annual precipitation under four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059).
Figure 15.
The first row shows the mean annual RX5day indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows annual trend of RX5day indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Figure 15.
The first row shows the mean annual RX5day indices under the four scenarios: historical (1985–2014), SSP245 (2030–2059), SSP585 (2030–2059), G6sulfur (2030–2059); the second row shows annual trend of RX5day indices under four scenarios: historical, SSP245, SSP585, G6sulfur, where stippling indicates statistically significant trends at a level p < 0.05.
Table 1.
Climate models used in this study.
Table 1.
Climate models used in this study.
| Model | Institution | Resolution |
|---|
| CNRM-ESM2-1 [19] | CNRM-CERFACS, Toulouse, France | h: 256 × 128, v: 91 |
| IPSL-CM6A-LR [20] | IPSL, Paris 75252, France | h: 144 × 143, v: 79 |
| MPI-ESM1-2-LR [21] | MPI-M, Hamburg 20146, Germany | h: 192 × 96, v: 47 |
| UKESM1-0-LL [22] | MOHC, Exeter, Devon, EX1 3PB, UK | h: 192 × 144, v: 85 |
Table 2.
Definition of climate extreme indices.
Table 2.
Definition of climate extreme indices.
| Category | Index | Description | Definition | Unit |
|---|
| Warm Temperature Extremes | SU | Summer days | Annual number of days when TX > 25 °C | Days |
| TXx | Highest Tmax | Annual maximum value of daily maximum temperature | °C |
| TNx | Highest Tmin | Annual maximum value of daily minimum temperature | °C |
| WSDI | Thermal endurance index | Annual count of days with at least six consecutive days
when TX > 90th percentile | Days |
| Cold Temperature Extremes | ID | Ice days | Annual number of days when
TX < 0 °C | Days |
| TXn | Lowest Tmax | Annual maximum value of daily maximum temperature | °C |
| TNn | Lowest Tmin | Annual minimum value of daily minimum temperature | °C |
| CSDI | Cold persistence index | Annual count of days with at least six consecutive days
when TN < 10th percentile | Days |
| Precipitation Extremes | CDD | Consecutive dry days | Maximum number of consecutive days when precipitation < 1 mm | Days |
| CWD | Consecutive wet days | Maximum number of consecutive days when precipitation ≥ 1 mm | Days |
| Rx1day | Wettest consecutive one day | Maximum daily precipitation | mm |
| Rx5day | Wettest consecutive five days | Maximum of consecutive 5-day (cumulative) precipitation amount | mm |
Table 3.
Trend difference in SU index among four scenarios (Unit: days/decade).
Table 3.
Trend difference in SU index among four scenarios (Unit: days/decade).
| | Difference | SSP245-Historical | G6sulfur-Historical | G6sulfur-SSP245 | G6sulfur-SSP585 |
|---|
| Region | |
|---|
| Northern Afghanistan | −3 to −1 | −2 to 0 | −3 to 1 | −5 to −2 |
| Ganges River Plain | 1 to 6 | 1 to 4 | −4 to 1 | −8 to 0 |
| Interior of the Deccan Plateau | −3 to 0 | −4 to −1 | −4 to 1 | −4 to 0 |
| Thar desert | 1 to 4 | −1 to 2 | −4 to 0 | −7 to −2 |
Table 4.
Trend difference in WSDI index among four scenarios (Unit: days/decade).
Table 4.
Trend difference in WSDI index among four scenarios (Unit: days/decade).
| | Difference | SSP245-Historical | G6sulfur-Historical | G6sulfur-SSP245 | G6sulfur-SSP585 |
|---|
| Region | |
|---|
| Afghanistan | 1 to 10 | 1 to 7 | −5 to 2 | −18 to −11 |
| Western Ganges River Plain | 8 to 19 | 8 to 14 | −4 to −1 | −16 to −8 |
| Deccan Plateau | 24 to 54 | 18 to 52 | −10 to −1 | −21 to −11 |
| Kashmir | 1 to 6 | −2 to 5 | −3 to 2 | −14 to −7 |
Table 5.
Trend difference in TXx index among four scenarios (Unit: °C/decade).
Table 5.
Trend difference in TXx index among four scenarios (Unit: °C/decade).
| | Difference | SSP245-Historical | G6sulfur-Historical | G6sulfur-SSP245 | G6sulfur-SSP585 |
|---|
| Region | |
|---|
| Eastern Afghanistan | −0.2 to 0.1 | −0.3 to −0.1 | −0.1 to 0 | −0.2 to −0.1 |
| The southern slope of the Himalayas | 0.1 to 0.4 | 0 to 0.3 | −0.3 to 0.4 | −0.6 to 0 |
| Western Deccan Platea | −0.2 to 0.2 | −0.1 to 0.2 | −0.4 to 0.1 | −0.6 to −0.2 |
| Western Indus River Plain | 0 to 0.2 | 0.1 to 0.3 | −0.3 to 0.4 | 0 to 0.2 |
Table 6.
Trend difference in TNx index among four scenarios (Unit: °C/decade).
Table 6.
Trend difference in TNx index among four scenarios (Unit: °C/decade).
| | Difference | SSP245-Historical | G6sulfur-Historical | G6sulfur-SSP245 | G6sulfur-SSP585 |
|---|
| Region | |
|---|
| Western Afghanistan | −0.3 to −0.1 | −0.3 to 0 | −0.2 to 0.1 | −0.4 to −0.1 |
| Western Deccan Plateau | 0 to 0.2 | −0.1 to 0.2 | −0.3 to −0.1 | −0.4 to 0 |
| Thar desert | 0.1 to 0.2 | −0.2 to 0.1 | −0.2 to 0.1 | −0.6 to −0.2 |
| The southern slope of the Himalayas | 0.1 to 0.2 | 0.1 to 0.3 | −0.1 to 0.3 | −0.4 to −0.1 |
Table 7.
Trend difference in ID index among four scenarios (Unit: °C/decade).
Table 7.
Trend difference in ID index among four scenarios (Unit: °C/decade).
| | Difference | SSP245-Historical | G6sulfur-Historical | G6sulfur-SSP245 | G6sulfur-SSP585 |
|---|
| Region | |
|---|
| Afghanistan | 0 to 3 | 0 to 3 | −1 to 2 | 0 to 5 |
| Deccan Plateau | −1 to 0 | −1 to 0 | −1 to 1 | 0 to 1 |
| The southern slope of the Himalayas | −1 to 1 | −1 to 1 | −1 to 3 | 0 to 5 |
| Kashmir | −1 to 1 | −3 to 1 | −2 to 1 | 0 to 4 |
Table 8.
Trend difference in CSDI index among four scenarios (Unit: days/decade).
Table 8.
Trend difference in CSDI index among four scenarios (Unit: days/decade).
| | Difference | SSP245-Historical | G6sulfur-Historical | G6sulfur-SSP245 | G6sulfur-SSP585 |
|---|
| Region | |
|---|
| Southern Afghanista | 2 to 4 | 2 to 4 | −1 to 1 | 0 to 1 |
| Southern Deccan Plateau | 4 to 5 | 3 to 5 | 0 to 1 | 0 to 1 |
| Thar desert | 2 to 4 | 2 to 4 | −1 to 1 | 0 to 1 |
| Middle Deccan Plateau | 2 to 4 | 3 to 4 | 0 to 1 | 0 to 1 |
Table 9.
Trend difference in TNn index among four scenarios (Unit: °C/decade).
Table 9.
Trend difference in TNn index among four scenarios (Unit: °C/decade).
| | Difference | SSP245-Historical | G6sulfur-Historical | G6sulfur-SSP245 | G6sulfur-SSP585 |
|---|
| Region | |
|---|
| Afghanistan | −0.9 to −0.2 | −0.6 to −0.1 | −0.1 to 0.6 | −1.8 to −0.5 |
| The southern slope of the Himalayas | −0.7 to −0.1 | −0.5 to 0.6 | −0.3 to 1.2 | −1.4 to −0.1 |
| Western Deccan Plateau | 0.1 to 0.6 | −0.2 to 0.2 | −0.4 to −0.1 | 0 to 0.4 |
| Marva Plateau | 0 to 0.5 | −0.2 to 0.3 | −0.1 to 0 | 0.1 to 0.3 |
Table 10.
Trend difference in TXn index among four scenarios (Unit: °C/decade).
Table 10.
Trend difference in TXn index among four scenarios (Unit: °C/decade).
| | Difference | SSP245-Historical | G6sulfur-Historical | G6sulfur-SSP245 | G6sulfur-SSP585 |
|---|
| Region | |
|---|
| Eastern Afghanistan | −0.8 to 0 | −0.7 to 0 | −0.5 to 0 | −0.7 to −0.4 |
| Middle Deccan Plateau | −0.3 to 0.3 | −0.2 to 0.3 | −0.4 to 0.3 | −0.3 to −0.1 |
| Thar Desert | 0 to 0.4 | −0.4 to 0 | −0.5 to −0.1 | −0.6 to 0 |
| The southern slope of the Himalayas | −0.2 to 0.3 | −0.2 to 0.4 | −0.4 to 0.2 | −0.6 to −0.1 |
Table 11.
Trend difference in CDD index among four scenarios (Unit: days/decade).
Table 11.
Trend difference in CDD index among four scenarios (Unit: days/decade).
| | Difference | SSP245-Historical | G6sulfur-Historical | G6sulfur-SSP245 | G6sulfur-SSP585 |
|---|
| Region | |
|---|
| Western Afghanistan | 1 to 4 | 1 to 3 | −4 to 0 | −5 to 1 |
| Ganges Delta | −3 to −1 | −4 to 0 | −2 to 2 | −4 to 1 |
| Western Deccan Plateau | −1 to 7 | −2 to 5 | −4 to 3 | 4 to 7 |
| Southwestern Indus River Plain | 3 to 6 | −4 to 4 | −8 to −1 | −7 to −1 |
Table 12.
Trend difference in CWD index among four scenarios (Unit: days/decade).
Table 12.
Trend difference in CWD index among four scenarios (Unit: days/decade).
| | Difference | SSP245-Historical | G6sulfur-Historical | G6sulfur-SSP245 | G6sulfur-SSP585 |
|---|
| Region | |
|---|
| Afghanistan | −1 to 0 | −1 to 0 | −1 to 1 | −1 to 1 |
| Southern Deccan Plateau | 2 to 6 | 1 to 4 | −4 to 0 | 0 to 2 |
| Southern Indus River Plain | −1 to 0 | −1 to 0 | −1 to 1 | 0 to 1 |
| The southern slope of the Himalayas | −3 to 0 | −5 to 1 | −4 to 1 | −5 to 2 |
Table 13.
Trend difference in RX1day index among four scenarios (Unit: mm/decade).
Table 13.
Trend difference in RX1day index among four scenarios (Unit: mm/decade).
| | Difference | SSP245-Historical | G6sulfur-Historical | G6sulfur-SSP245 | G6sulfur-SSP585 |
|---|
| Region | |
|---|
| Ganges Delta | −2.6 to 2.5 | −4.3 to 2.1 | −6.6 to 3.4 | −5.4 to 2.3 |
| Middle Deccan Plateau | 2.1 to 7.3 | −6.9 to 6.4 | −5.8 to −0.3 | −5.3 to −0.2 |
| Indus River Plain | −4.6 to 1.2 | −2.2 to 1.5 | −2.6 to 4.5 | −1.6 to 5.2 |
| Marva Plateau | −2.1 to 1.1 | −2.3 to 6.4 | 3.3 to 8.1 | 2.4 to 7.9 |
Table 14.
Trend difference in RX5day index among four scenarios (Unit: mm/decade).
Table 14.
Trend difference in RX5day index among four scenarios (Unit: mm/decade).
| | Difference | SSP245-Historical | G6sulfur-Historical | G6sulfur-SSP245 | G6sulfur-SSP585 |
|---|
| Region | |
|---|
| Ganges Delta | −10.9 to 17.8 | −7.1 to 8.9 | −20.1 to 29.8 | −19.4 to 4.2 |
| Middle Deccan Plateau | 5.3 to 21.6 | −10.4 to 17.4 | −28.6 to 7.6 | −11.3 to 16.7 |
| Indus river plain | −11.9 to 2.1 | −7.2 to 3.5 | −7.2 to 13.4 | −3.1 to 9.4 |
| Marwa Plateau | −16.9 to −4.3 | −13.4 to 17.4 | 1.2 to 33.8 | 0.8 to 16.7 |