Study on Spatial and Temporal Distribution Characteristics of the Cooking Oil Fume Particulate and Carbon Dioxide Based on CFD and Experimental Analyses
Abstract
:1. Introduction
2. Experimental Testing
2.1. Experimental Kitchen Layout and Test Parameters
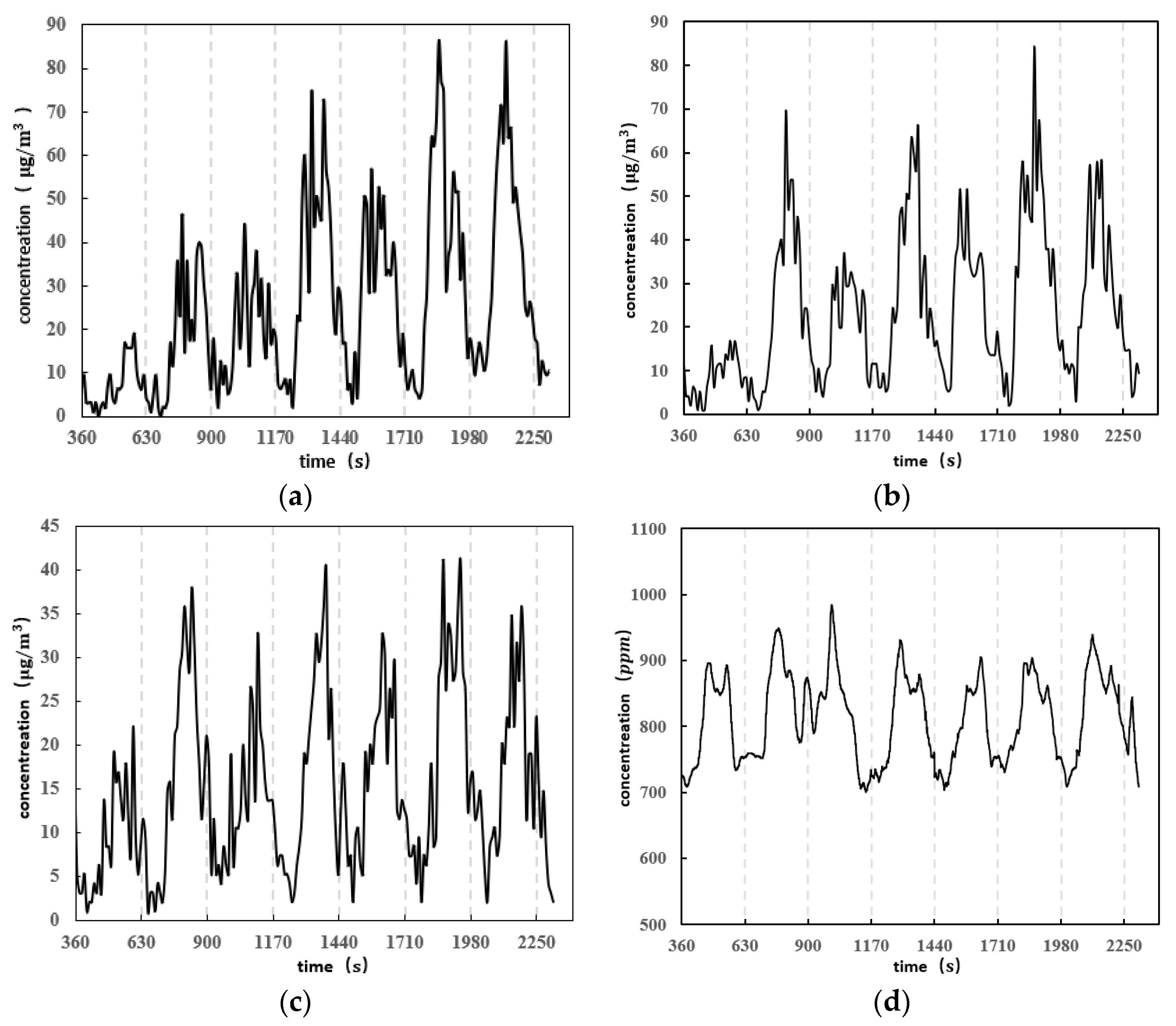
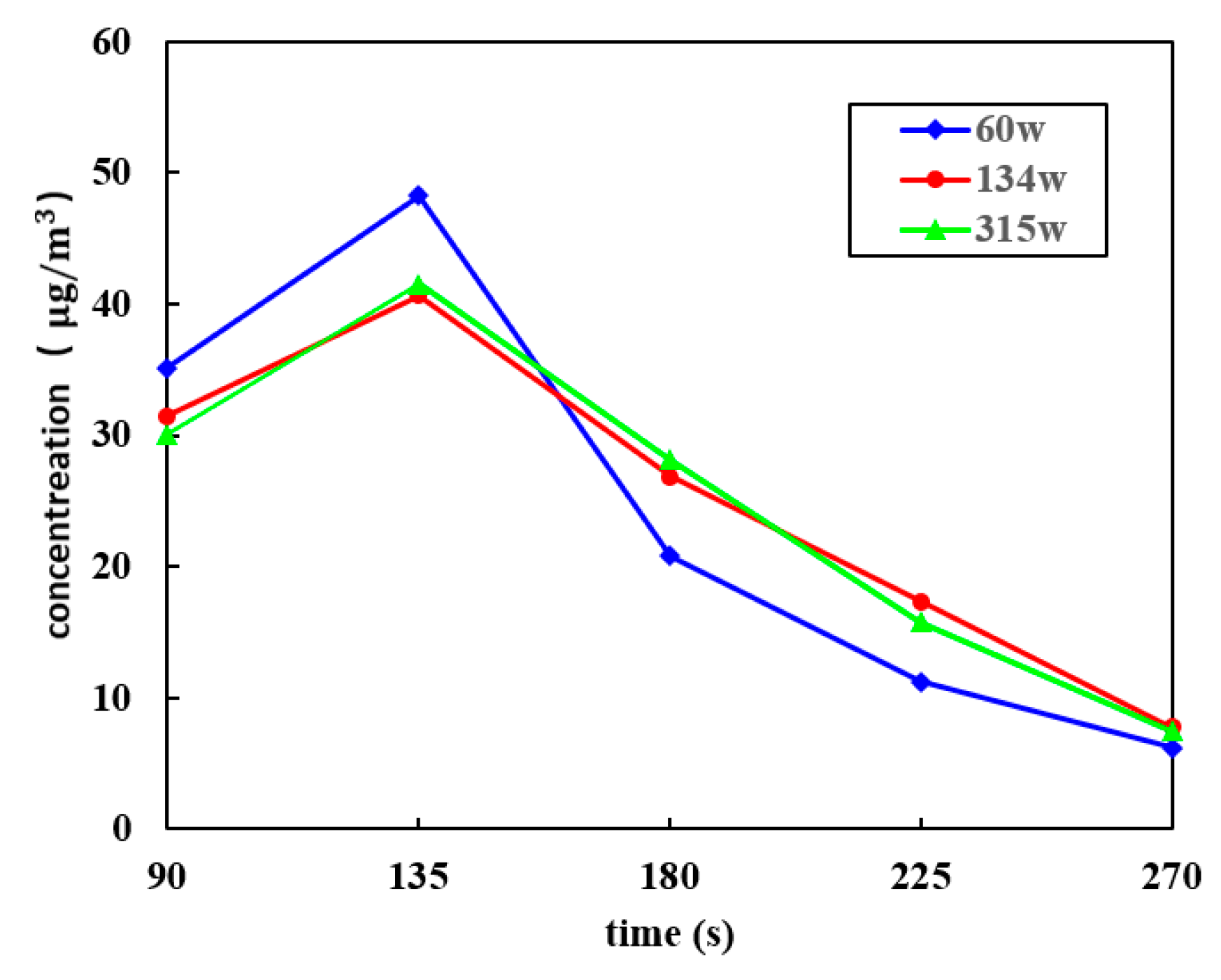
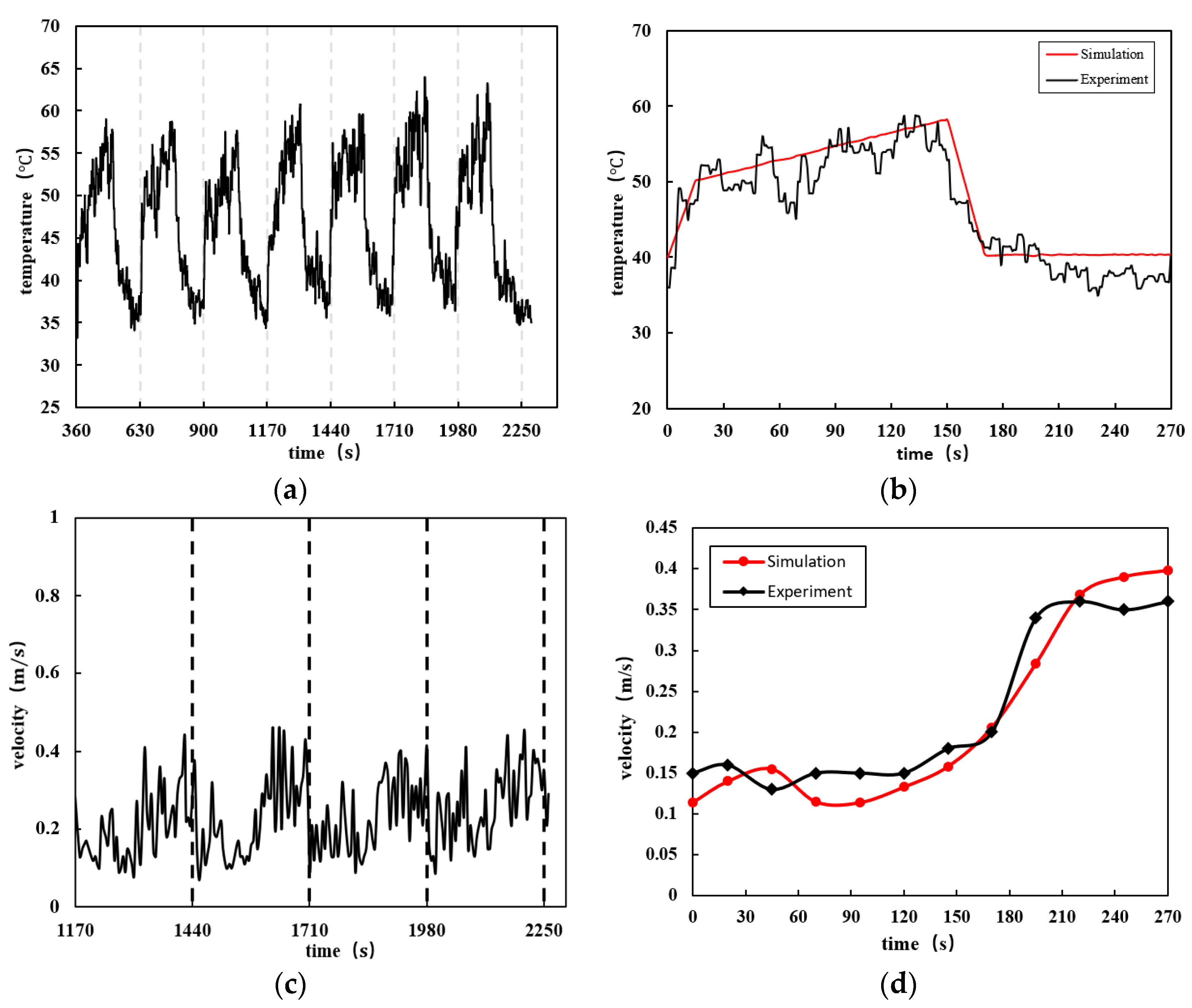
2.2. Test Results and Analysis
3. Numerical Calculation
3.1. Numerical Method
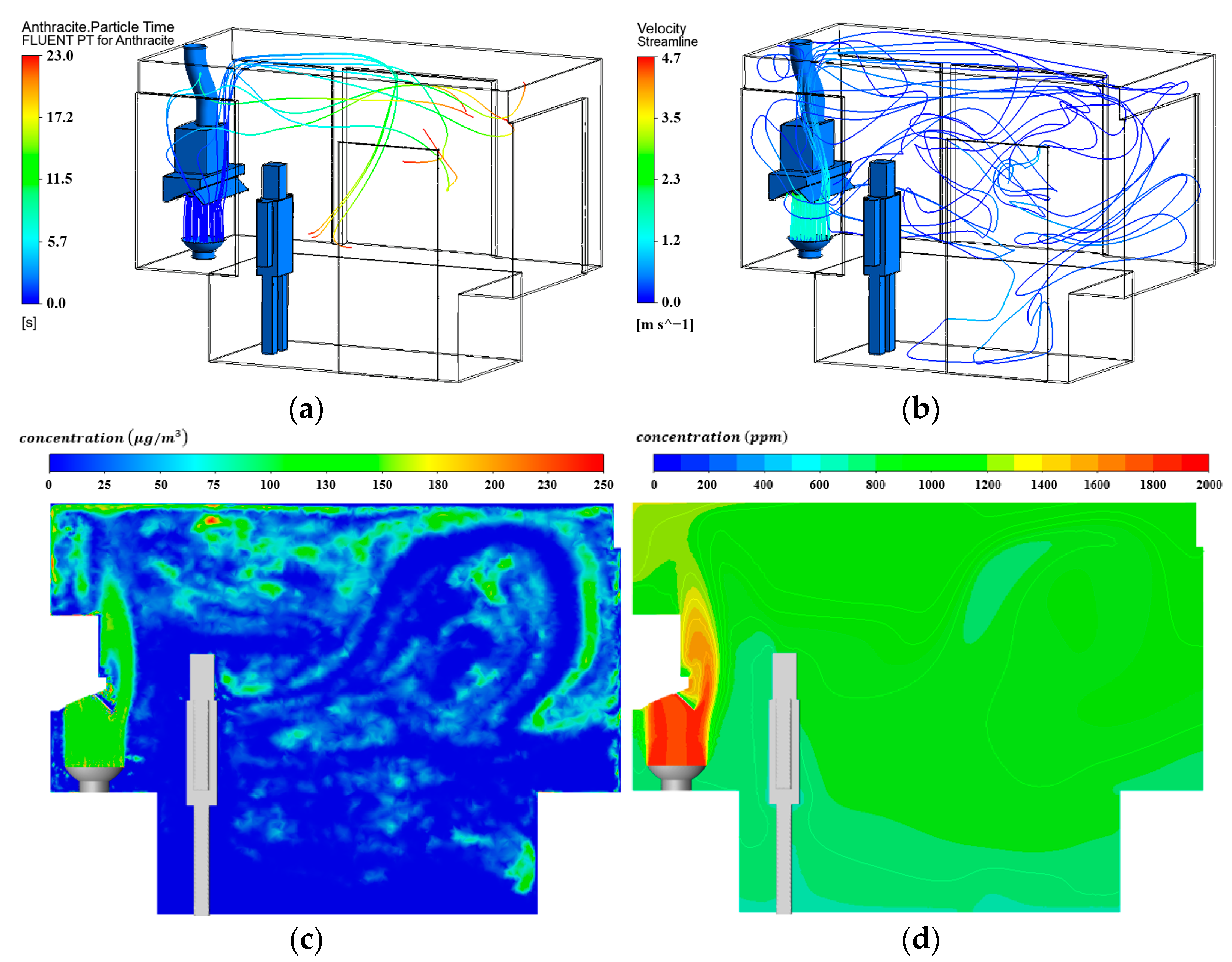
3.2. Simulation Process of COFP and CO2
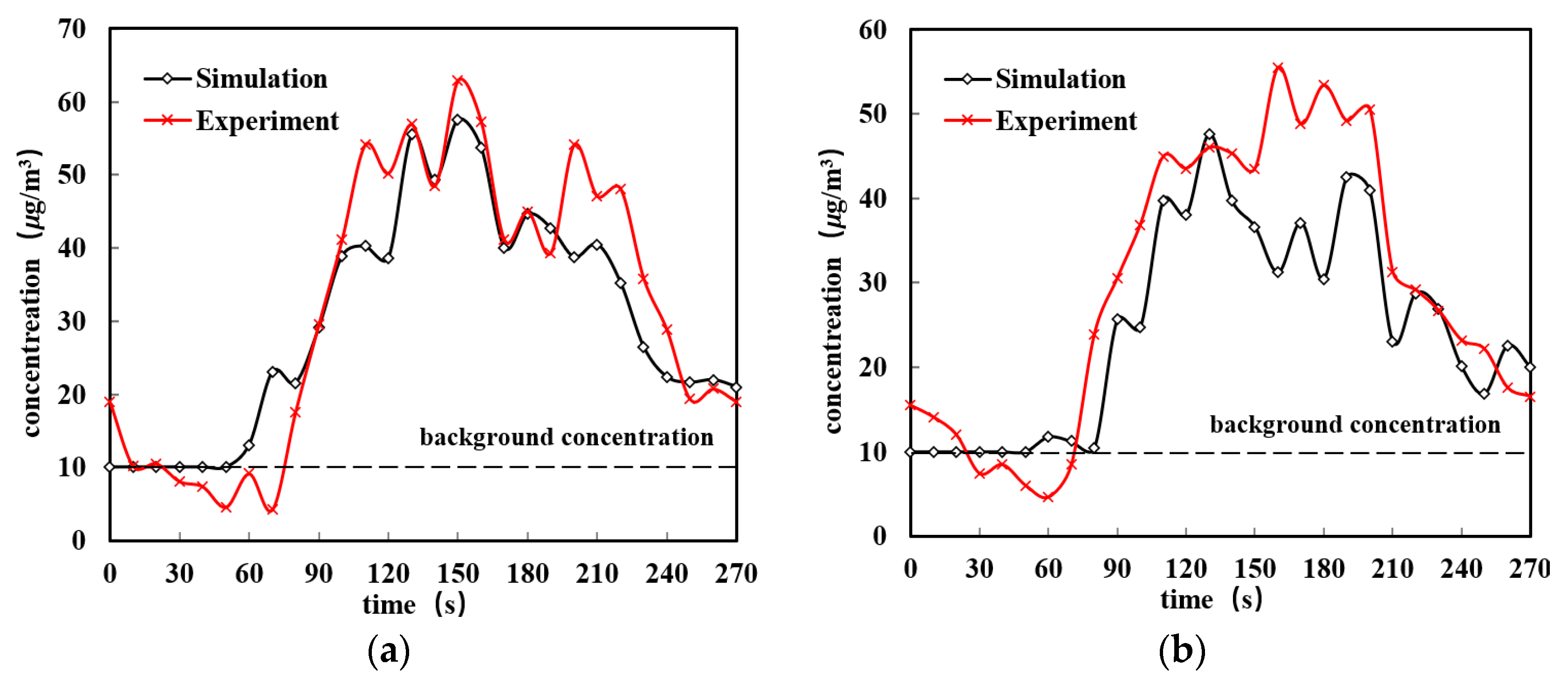
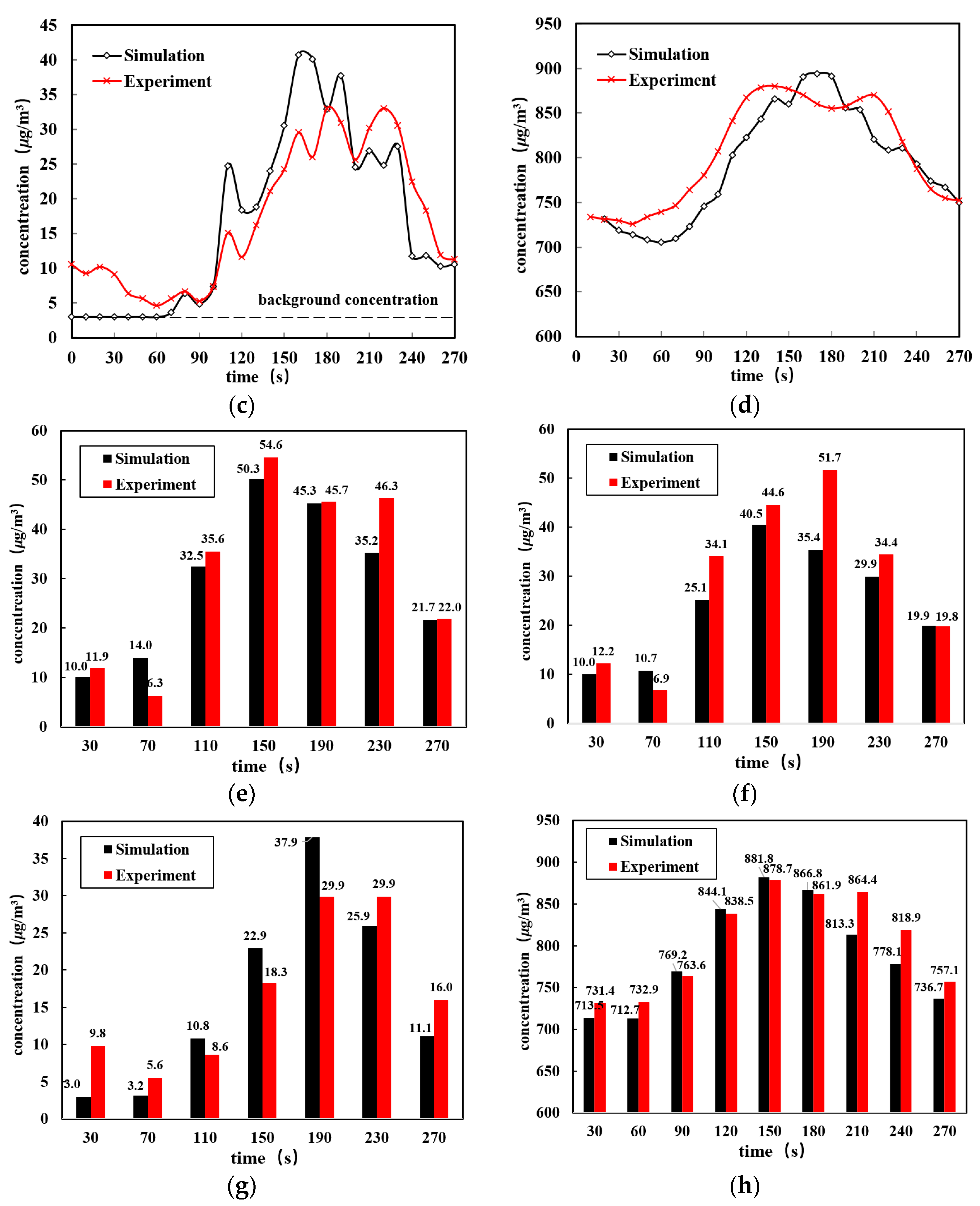
4. Comparison and Analysis of Simulation and Testing
5. Study on the Substitutability of COFP
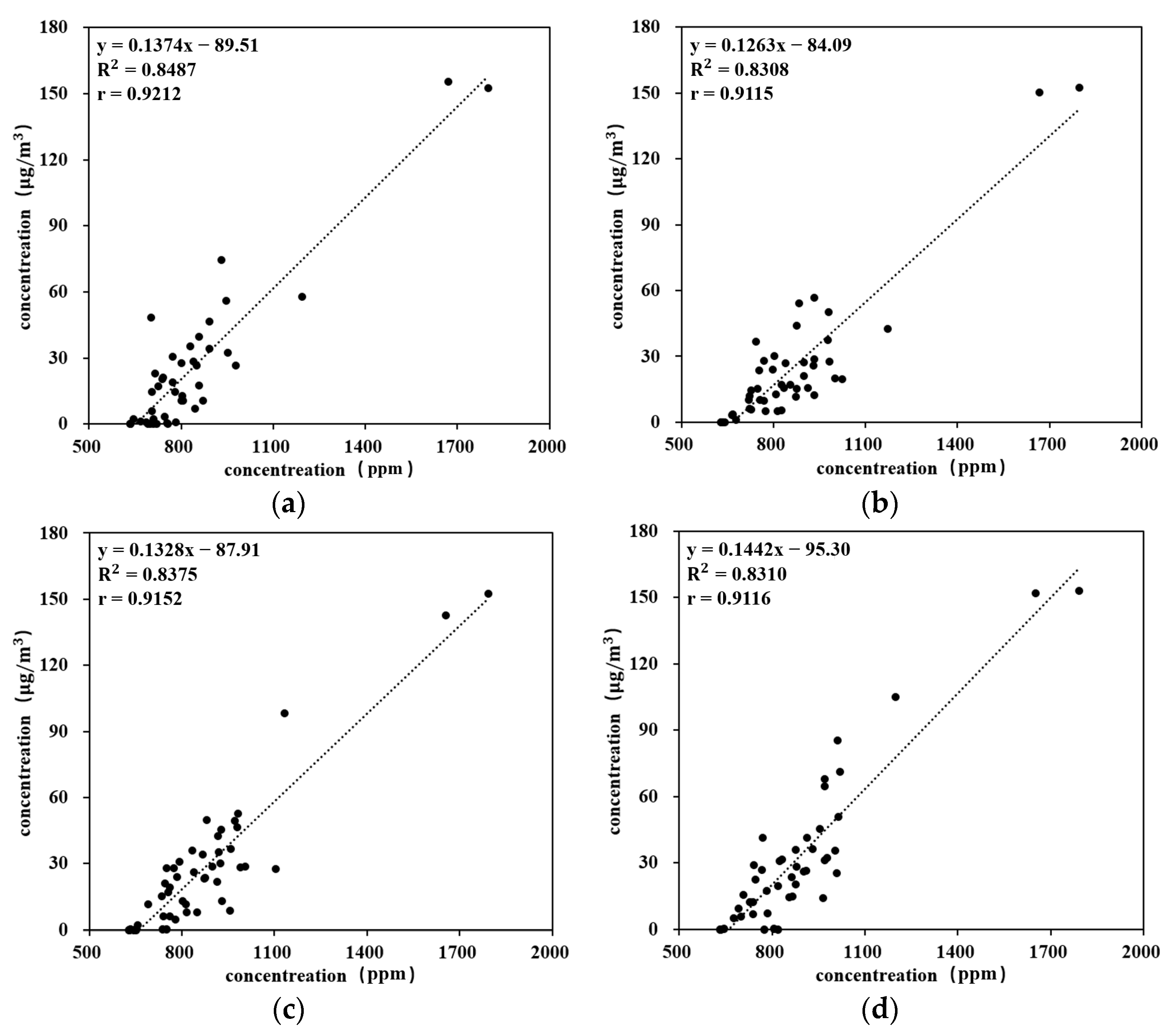
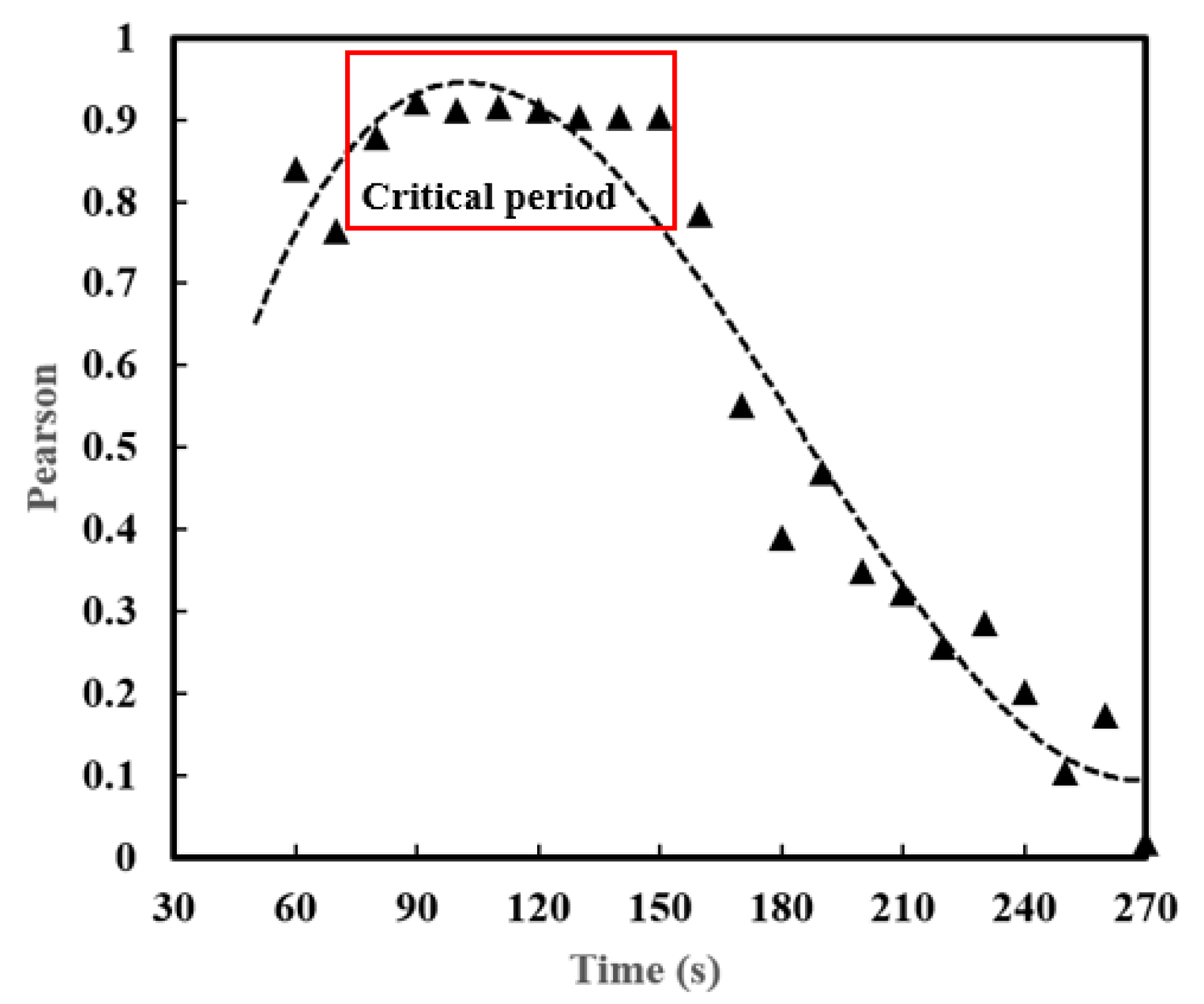
5.1. Analysis of the Correlation between COFP and CO2
5.2. Correlation Analysis Results
5.3. The Relationship Functions
6. Conclusions
- (1)
- A kitchen experiment testing platform was set up to monitor and collect the concentrations of COFP and CO2 during multiple identical cooking processes. By organizing and analyzing the experimental data, it was found that the concentrations of COFP and CO2 would sharply increase after 90 s of cooking and reach their peak at the end of the cooking process (150 s). Moreover, the time of concentration peak was observed to be delayed with the decrease in spatial height.
- (2)
- We utilized the same kitchen grid model and developed simulation processes for COFP and CO2 during cooking through the discrete phase model and the species transport model. The boundary conditions were built by using UDF to simulate the movement and diffusion of COFP and CO2 under the same operating conditions. The reliability of the numerical simulation process was validated by comparing the simulation results with experimental data.
- (3)
- We propose a method for evaluating and controlling COFP concentration using low-cost CO2 analysis and monitoring technology. Firstly, Pearson correlation theory and the linear fitting method were used to analyze and organize the data. The results showed that there was a strong correlation (r > 0.9) between the concentration of COFP and CO2 concentration during the critical cooking period (90~150 s), and more than 80% of the variability could be explained by the linear model. Based on this, the coefficient-weighted averaging method was used to construct a relationship function between COFP concentration and CO2 concentration. The CO2 simulation correction result obtained from this can replace the COFP simulation result with an accuracy of over 90%, leading to an increased computation efficiency of 70%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Leikauf, G.D.; Kim, S.H.; Jang, A.S. Mechanisms of ultrafine particle-induced respiratory health effects. Exp. Mol. Med. 2020, 52, 329–337. [Google Scholar] [CrossRef] [PubMed]
- Xue, T.; Han, Y.; Fan, Y.; Zheng, Y.; Geng, G.; Zhang, Q.; Zhu, T. Association between a Rapid Reduction in Air Particle Pollution and Improved Lung Function in Adults. Ann. Am. Thorac Soc. 2021, 18, 247–256. [Google Scholar] [CrossRef] [PubMed]
- Wong, Y.J.; Shiu, H.Y.; Chang, J.H.; Ooi, M.C.G.; Li, H.H.; Homma, R.; Nik Sulaiman, N.M. Spatiotemporal impact of COVID-19 on Taiwan air quality in the absence of a lockdown: Influence of urban public transportation use and meteorological conditions. J. Clean. Prod. 2022, 365, 132893. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Jain, M.K. Interrelationship of Indoor Particulate Matter and Respiratory Dust Depositions of Women in the Residence of Dhanbad City, India. Environ. Sci. Pollut. Res. Int. 2022, 29, 4668–4689. [Google Scholar] [CrossRef]
- Tong, X.; Ho, J.M.W.; Li, Z.; Lui, K.H.; Kwok, T.C.Y.; Tsoi, K.K.F.; Ho, K.F. Prediction model for air particulate matter levels in the households of elderly individuals in Hong Kong. Sci. Total Environ. 2020, 717, 135323. [Google Scholar] [CrossRef] [PubMed]
- Shupler, M.; Hystad, P.; Birch, A.; Chu, Y.L.; Jeronimo, M.; Miller-Lionberg, D.; Brauer, M. Multinational prediction of household and personal exposure to fine particulate matter (PM2.5) in the PURE cohort study. Environ. Int. 2022, 159, 107021. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Shin, D.; Hong, K.J.; Lee, G.; Kim, S.B.; Park, I.; Hwang, J. Prediction of indoor PM2.5 concentrations and reduction strategies for cooking events through various IAQ management methods in an apartment of South Korea. Indoor Air 2022, 32, e13173. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Li, Q.; Shen, G.; Deng, J.; Zhou, W.; Hao, J.; Jiang, J. Significant ultrafine particle emissions from residential solid fuel combustion. Sci. Total Environ. 2020, 715, 136992. [Google Scholar] [CrossRef]
- Xiang, J.; Hao, J.; Austin, E.; Shirai, J.; Seto, E. Characterization of cooking-related ultrafine particles in a US residence and impacts of various intervention strategies. Sci. Total Environ. 2021, 798, 149236. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, G. A predictive model of indoor PM2.5 considering occupancy level in a hospital outpatient hall. Sci. Total Environ. 2022, 844, 157233. [Google Scholar] [CrossRef]
- Lai, A.C.K.; Chen, F.Z. Comparison of a new Eulerian model with a modified Lagrangian approach for particle distribution and deposition indoors. Atmos. Environ. 2007, 41, 5249–5256. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Kang, K.; Kim, T. CFD Simulation Analysis on Make-up Air Supply by Distance from Cookstove for Cooking-Generated Particle. Int. J. Environ. Res. Public Health 2020, 17, 7799. [Google Scholar] [CrossRef]
- Zhao, B.; Yang, C.; Yang, X.; Liu, S. Particle dispersion and deposition in ventilated rooms: Testing and evaluation of different Eulerian and Lagrangian models. J. Build. Environ. 2007, 43, 388–397. [Google Scholar] [CrossRef]
- Gao, N.P.; Niu, J.L.; Perino, M.; Heiselberg, P. The airborne transmission of infection between flats in high-rise residential buildings: Particle simulation. Build. Environ. 2009, 44, 402–410. [Google Scholar] [CrossRef] [PubMed]
- Hong, B.; Qin, H.; Jiang, R.; Xu, M.; Niu, J. How Outdoor Trees Affect Indoor Particulate Matter Dispersion: CFD Simulations in a Naturally Ventilated Auditorium. Int. J. Environ. Res. Public Health 2018, 15, 2862. [Google Scholar] [CrossRef]
- Tan, H.; Wong, K.Y.; Othman, M.H.D.; Kek, H.Y.; Wahab, R.A.; Ern, G.K.P.; Lee, K.Q. Current and potential approaches on assessing airflow and particle dispersion in healthcare facilities: A systematic review. Environ. Sci. Pollut. Res. Int. 2022, 29, 80137–80160. [Google Scholar] [CrossRef] [PubMed]
- Abdolzadeh, M.; Alimolaei, E.; Pustelnik, M. Numerical simulation of airflow and particle distributions with floor circular swirl diffuser for underfloor air distribution system in an office environment. Environ. Sci. Pollut. Res. Int. 2019, 26, 24552–24569. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; You, X.Y. Effects of chef operation on oil fume particle collection of household range hood. Environ. Sci. Pollut. Res. Int. 2020, 27, 23824–23836. [Google Scholar] [CrossRef]
- Chen, Z.; Xin, J.; Liu, P. Air quality and thermal comfort analysis of kitchen environment with CFD simulation and experimental calibration. J. Build. Environ. 2020, 172, 106691. [Google Scholar] [CrossRef]
- Wong, K.Y.; Tan, H.; Nyakuma, B.B.; Kamar, H.M.; Tey, W.Y.; Hashim, H.; Kuan, G. Effects of medical staff’s turning movement on dispersion of airborne particles under large air supply diffuser during operative surgeries. Environ. Sci. Pollut. Res. Int. 2022, 29, 82492–82511. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, B. Emissions of air pollutants from Chinese cooking: A literature review. Build. Simul. 2018, 11, 977–995. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, C.; Zhao, B. Emission characteristics of PM2.5-bound chemicals from residential Chinese cooking. Build. Environ. 2019, 149, 623–629. [Google Scholar] [CrossRef]
- Lai, A.C.K.; Ho, Y.W. Spatial concentration variation of cooking-emitted particles in a residential kitchen. J. Build. Environ. 2008, 43, 871–876. [Google Scholar] [CrossRef]
- Chang, T.J.; Hsieh, Y.F.; Kao, H.M. Numerical investigation of airflow pattern and particulate matter transport in naturally ventilated multi-room buildings. Indoor Air 2006, 16, 136–152. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.; Hou, W.; Zhu, Y.; Zheng, S.; Ainiwaer, S.; Shen, G.; Tao, S. Temporal and spatial variation of PM2.5 in indoor air monitored by low-cost sensors. Sci. Total Environ. 2021, 770, 145304. [Google Scholar] [CrossRef] [PubMed]
- Jung, C.C.; Lin, W.Y.; Hsu, N.Y.; Wu, C.D.; Chang, H.T.; Su, H.J. Development of Hourly Indoor PM2.5 Concentration Prediction Model: The Role of Outdoor Air, Ventilation, Building Characteristic, and Human Activity. Int. J. Environ. Res. Public Health 2020, 17, 5906. [Google Scholar] [CrossRef] [PubMed]
- Cho, S.; Lee, G.; Park, D.; Kim, M. Study on Characteristics of Particulate Matter Resuspension in School Classroom through Experiments Using a Simulation Chamber: Influence of Humidity. Int. J. Environ. Res. Public Health 2021, 18, 2856. [Google Scholar] [CrossRef]

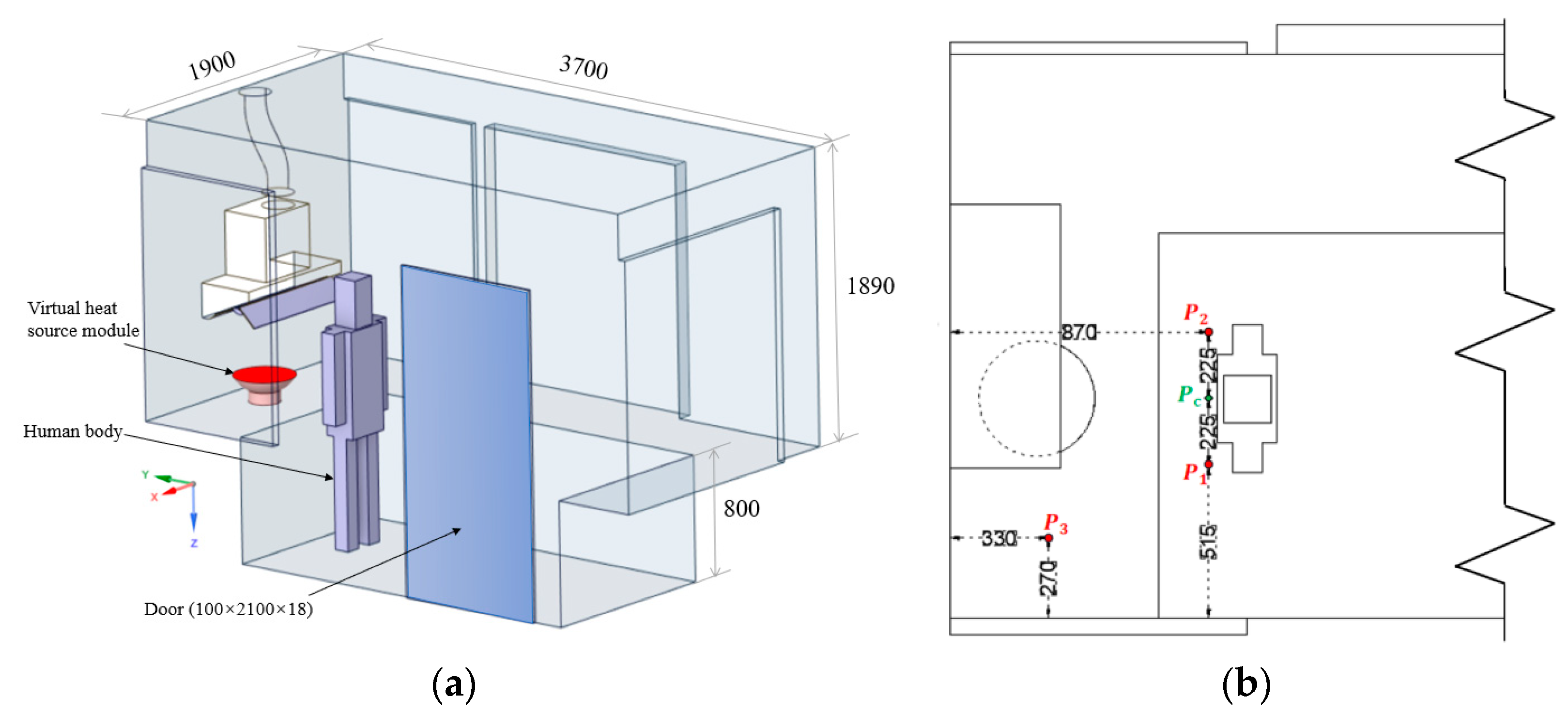

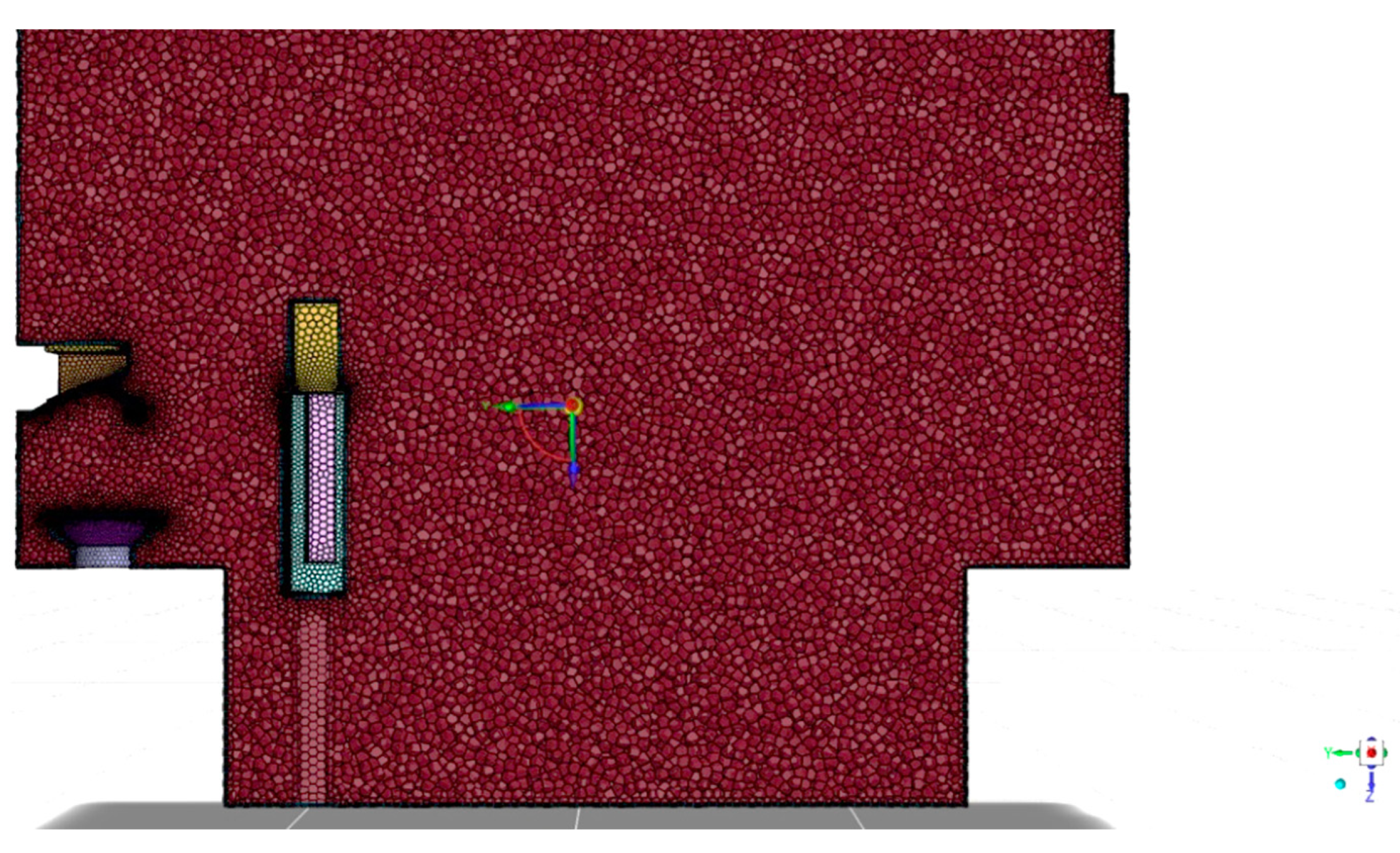




| Parameters | |
|---|---|
| Initial temperature at the center of the pot surface (°C) | 200 |
| Heating time (s) | 30 |
| Temperature to which the center of the pot surface is heated (°C) | 230~240 |
| Weight of potatoes (g) | 300 ± 2 |
| Weight of sunflower oil (g) | 14.5 ± 0.5 |
| Stirring method | lower right, down, left (clockwise) |
| Interval between stirring (s) | 1 |
| Cooking time (s) | 120 |
| Cooling time (s) | 120 |
| Testing cycle (s) | 270 |
| Testing time (s) | 2250 – 270 – 90 = 1890 |
| 1.225 | |
| 0.0242 | |
| 1.7894 × 10−5 | |
| 1.7878 | |
| 0.0145 | |
| 1.37 × 10−5 | |
| 950 | |
| 0.33 | |
| 1 × 10−5 | |
| Boundary | Boundary Condition | Value |
|---|---|---|
| Virtual heat source module | Velocity inlet | |
| Range hood outlet | Pressure outlet | Surface temperature: 293 K |
| Pressure: −5.7 Pa | ||
| Door gap | Pressure inlet | Surface temperature: 298 K |
| Pressure: 0.0 Pa | ||
| Human body | Wall (heat source) | Heat: 16 W/m2 |
| Computer Parameter | |
|---|---|
| Processor | Dual-core processor |
| CPU core | 48 |
| Thread | 96 |
| Calculation parameter | |
| Calculation Method | Parallel Computing |
| Thread | 36 |
| Simulated Cooking COFP Time | 240 h |
| Simulated Cooking CO2 Time | 72 h |
| Work Condition | COFP () | () | Absolute Error () | Relative Error |
|---|---|---|---|---|
| 95 s | 23.98 | 24.29 | 0.31 | 1.29% |
| 105 s | 28.92 | 27.15 | −1.77 | −6.12% |
| 115 s | 27.50 | 29.34 | 1.84 | 6.69% |
| 125 s | 33.69 | 30.61 | −3.08 | −9.14% |
| 135 s | 31.08 | 31.71 | 0.63 | 2.01% |
| 145 s | 34.39 | 33.55 | −0.85 | −2.46% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, M.; Zhang, S.; Wang, J.; Ye, F.; Chen, Z. Study on Spatial and Temporal Distribution Characteristics of the Cooking Oil Fume Particulate and Carbon Dioxide Based on CFD and Experimental Analyses. Atmosphere 2023, 14, 1522. https://doi.org/10.3390/atmos14101522
Ding M, Zhang S, Wang J, Ye F, Chen Z. Study on Spatial and Temporal Distribution Characteristics of the Cooking Oil Fume Particulate and Carbon Dioxide Based on CFD and Experimental Analyses. Atmosphere. 2023; 14(10):1522. https://doi.org/10.3390/atmos14101522
Chicago/Turabian StyleDing, Minting, Shunyu Zhang, Jiahua Wang, Feng Ye, and Zhenlei Chen. 2023. "Study on Spatial and Temporal Distribution Characteristics of the Cooking Oil Fume Particulate and Carbon Dioxide Based on CFD and Experimental Analyses" Atmosphere 14, no. 10: 1522. https://doi.org/10.3390/atmos14101522
APA StyleDing, M., Zhang, S., Wang, J., Ye, F., & Chen, Z. (2023). Study on Spatial and Temporal Distribution Characteristics of the Cooking Oil Fume Particulate and Carbon Dioxide Based on CFD and Experimental Analyses. Atmosphere, 14(10), 1522. https://doi.org/10.3390/atmos14101522




