Performance-Based Evaluation of CMIP5 and CMIP6 Global Climate Models and Their Multi-Model Ensembles to Simulate and Project Seasonal and Annual Climate Variables in the Chungcheong Region of South Korea
Abstract
:1. Introduction
2. Materials and Methods
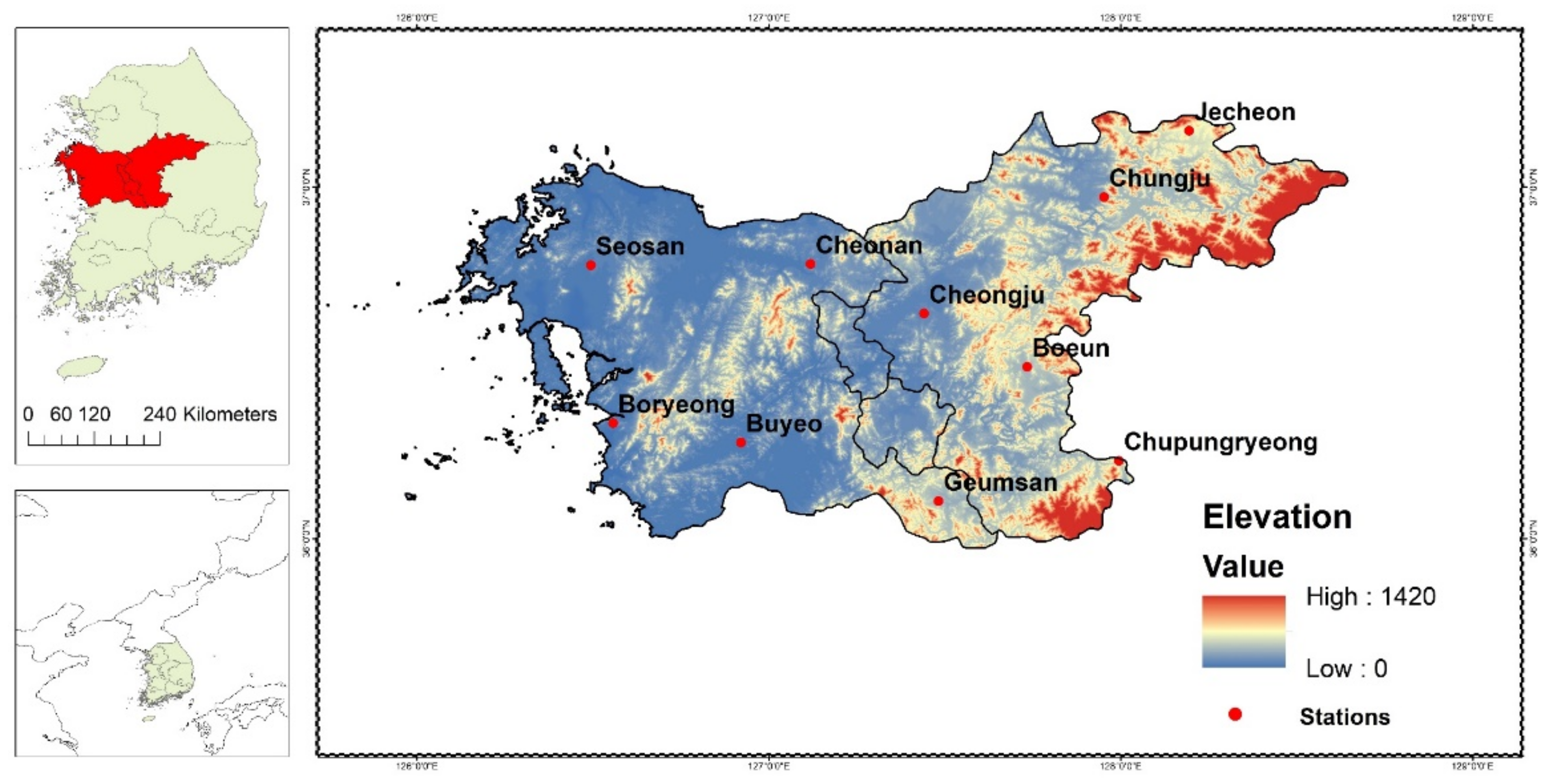
2.1. Study Area
2.2. Datasets and Sources
2.3. Methods
2.3.1. Bias Correction
2.3.2. Evaluation Metrics and GCM Ranking
2.3.3. Multi-Model Ensemble Development
2.3.4. Trend Analysis
3. Results
3.1. Performance Evaluation and Ranking of GCMs
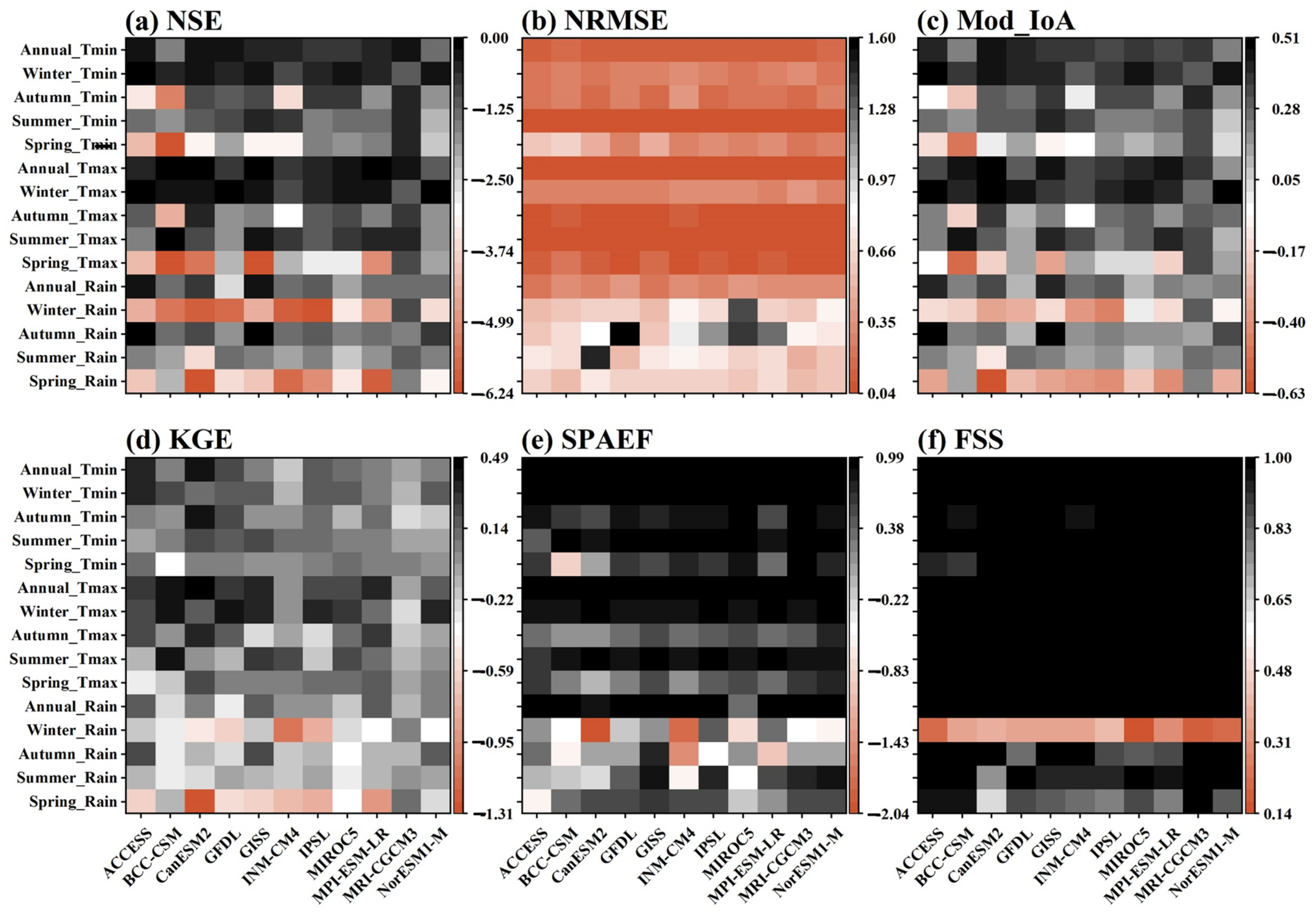
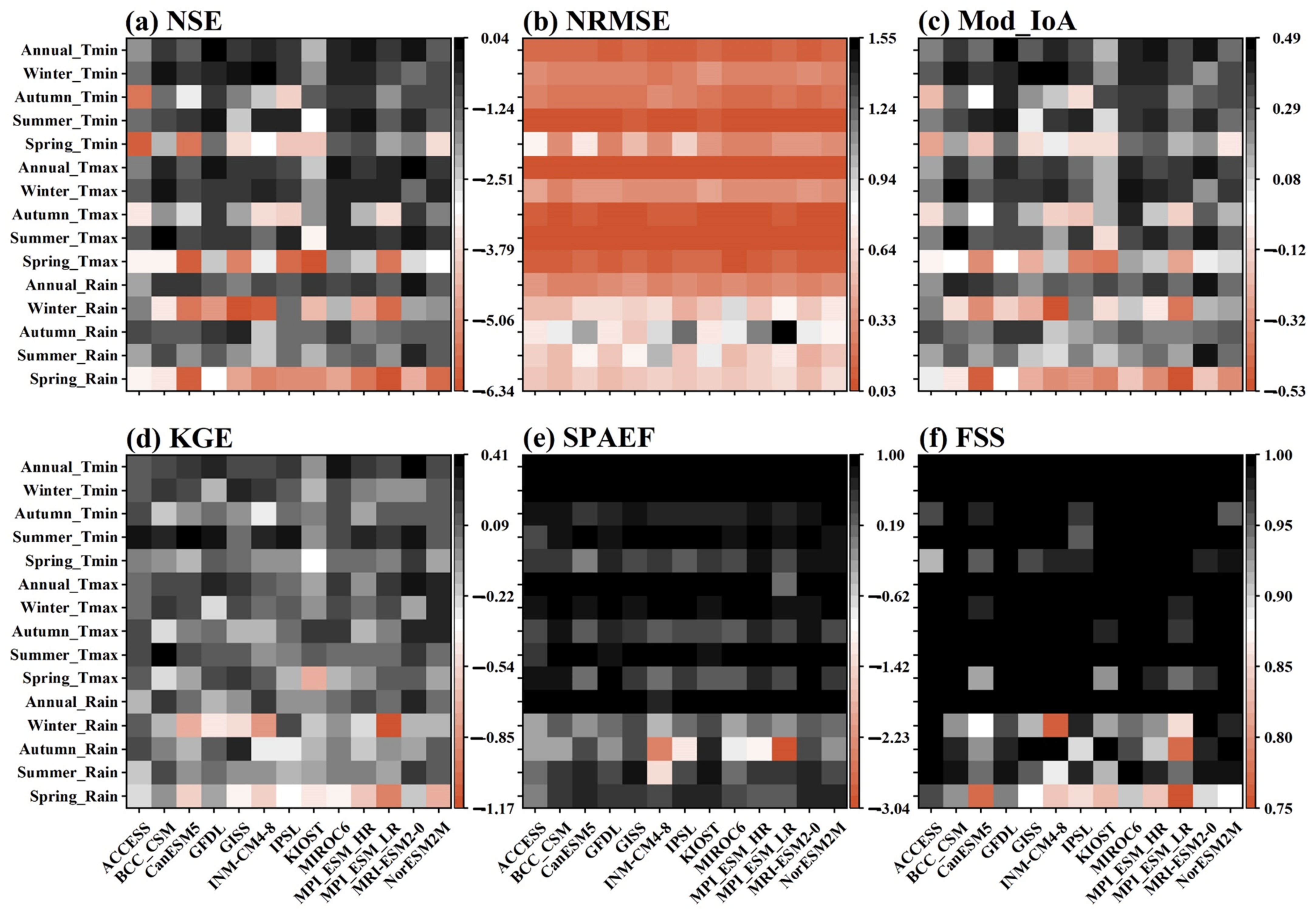
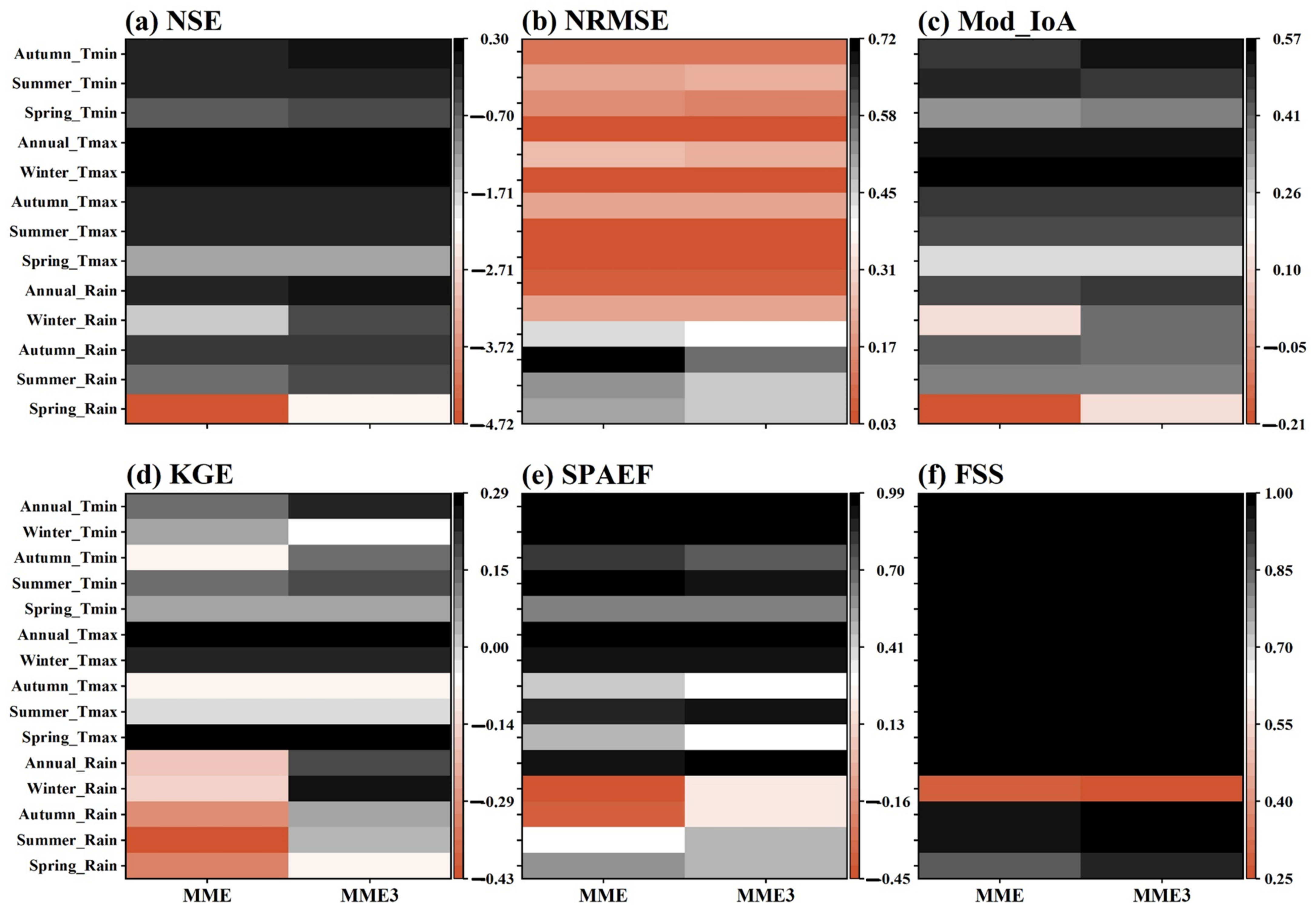
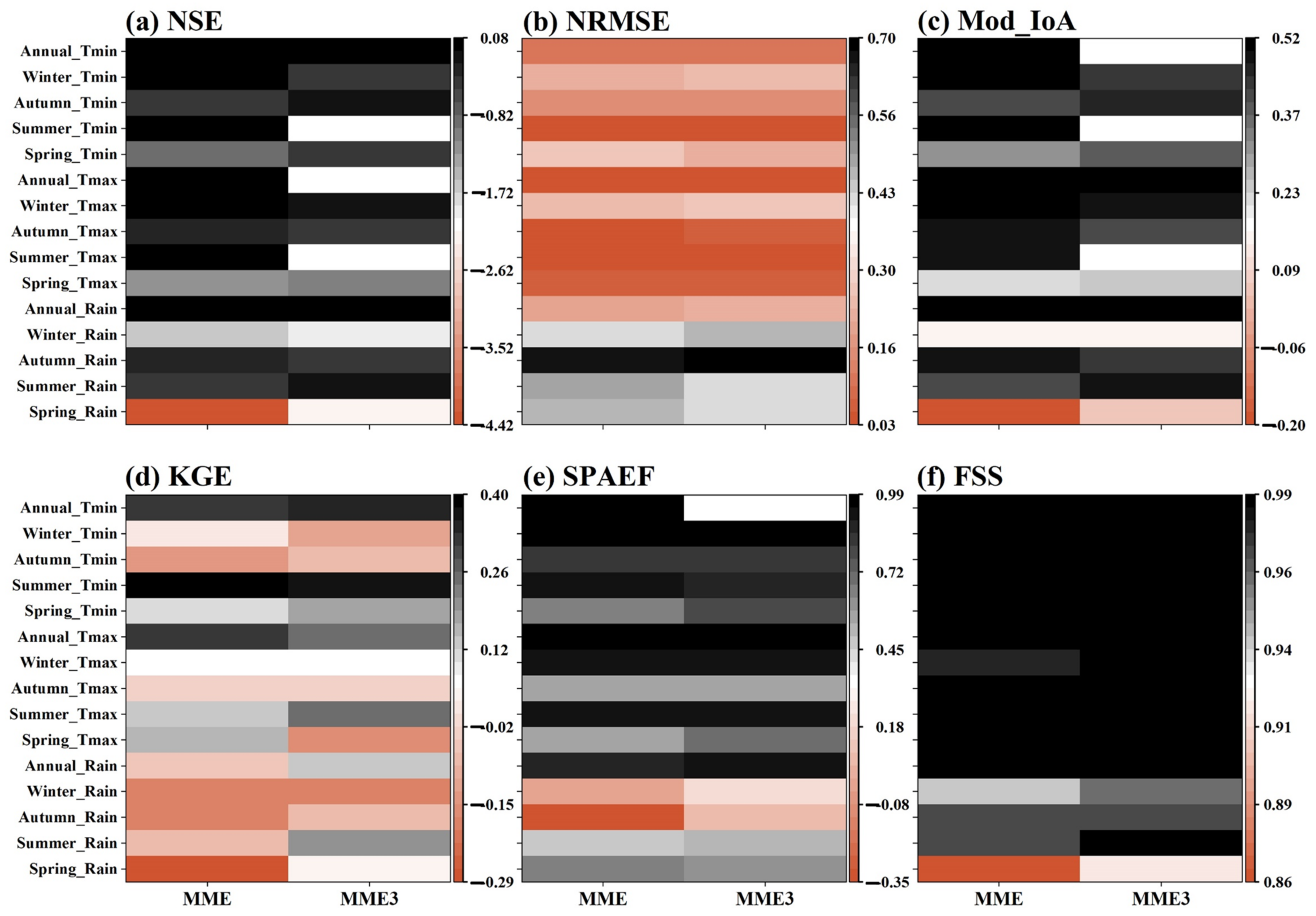
3.1.1. Performance Evaluation of GCMs
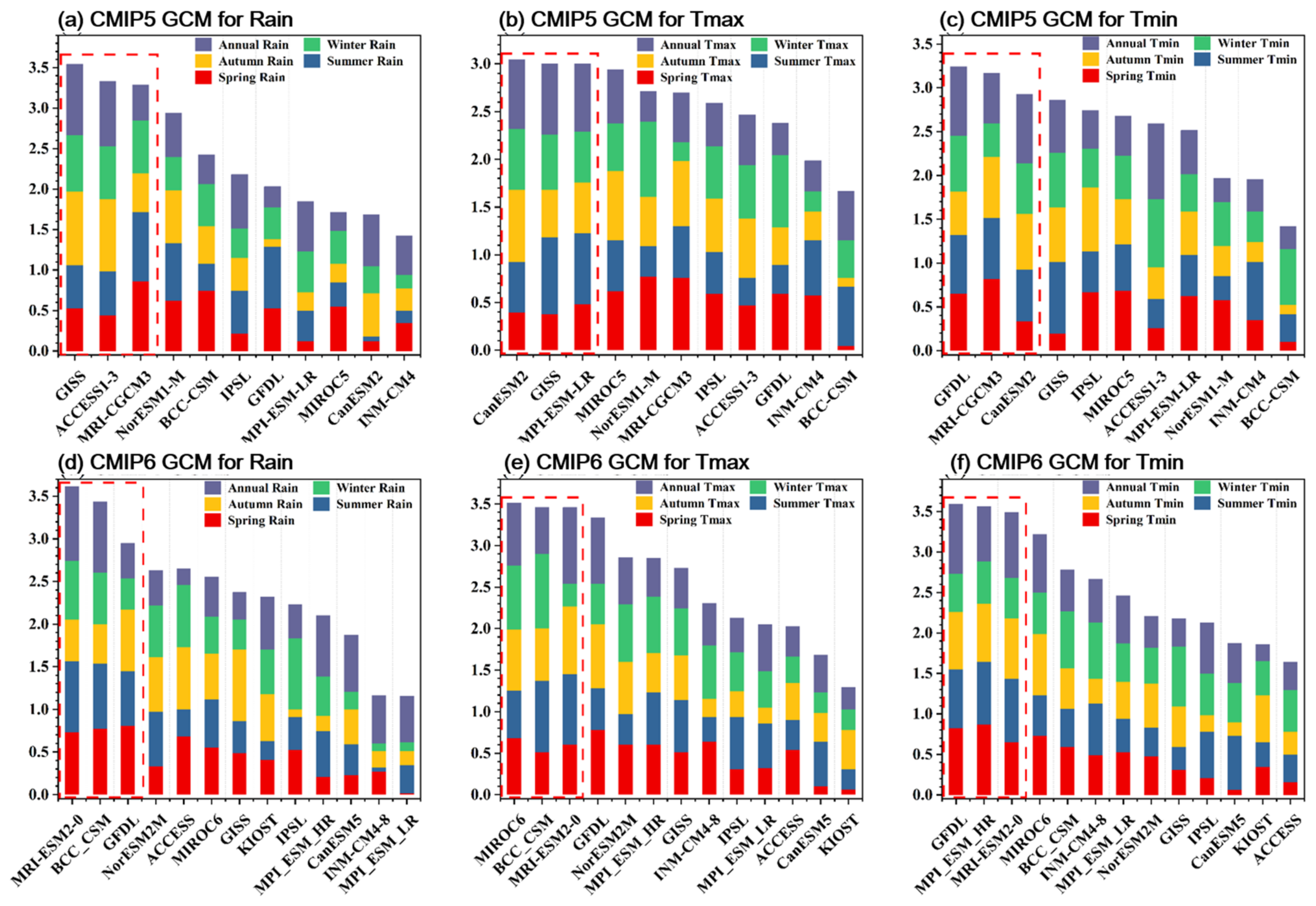
3.1.2. Comprehensive Ranking of CMIP5 and CMIP6 GCMs
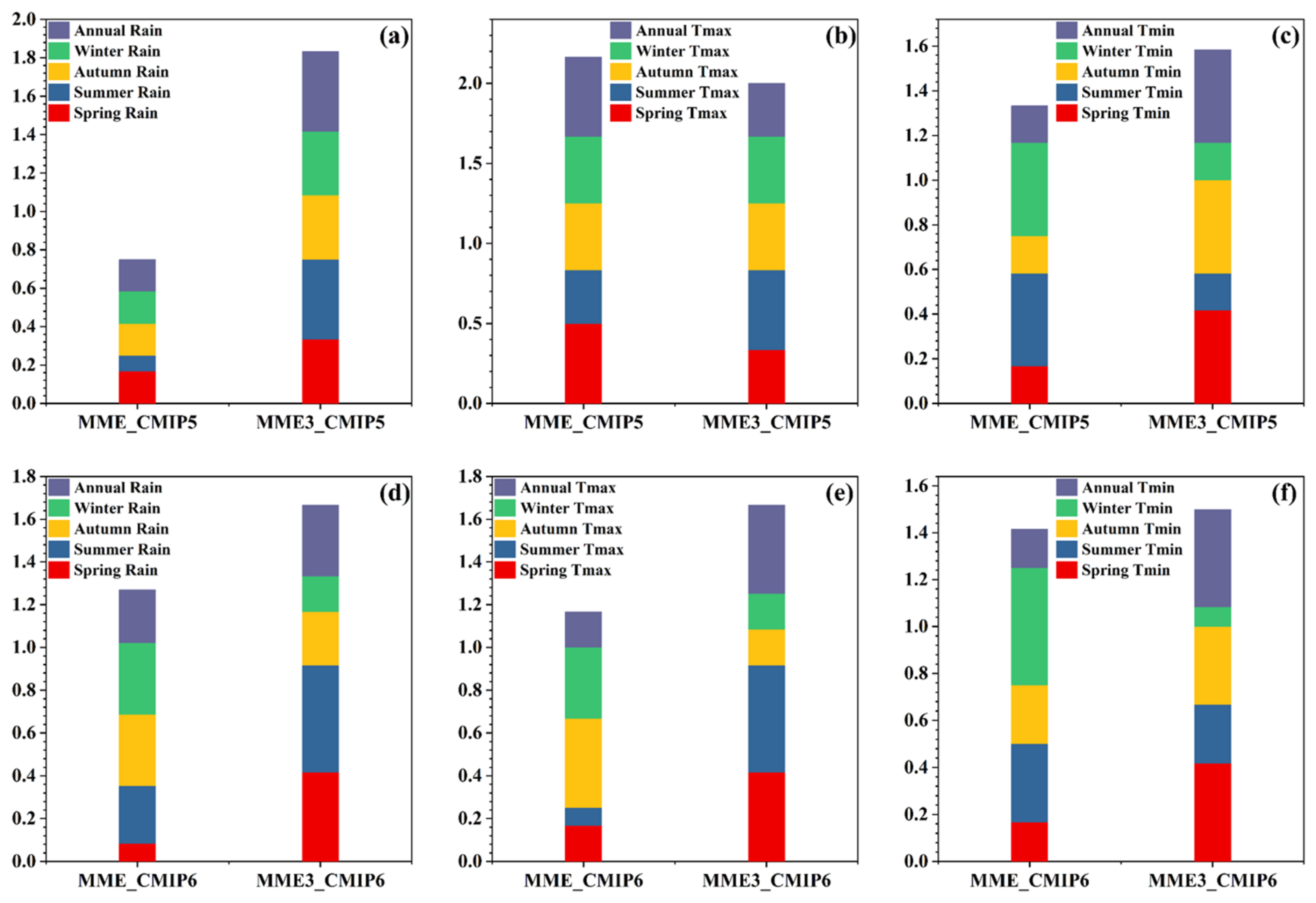
3.2. Selection of Multi-Model Ensemble Members
Performance of the Multi-Model Ensembles
3.3. Analysis of Future Precipitation and Temperature Changes
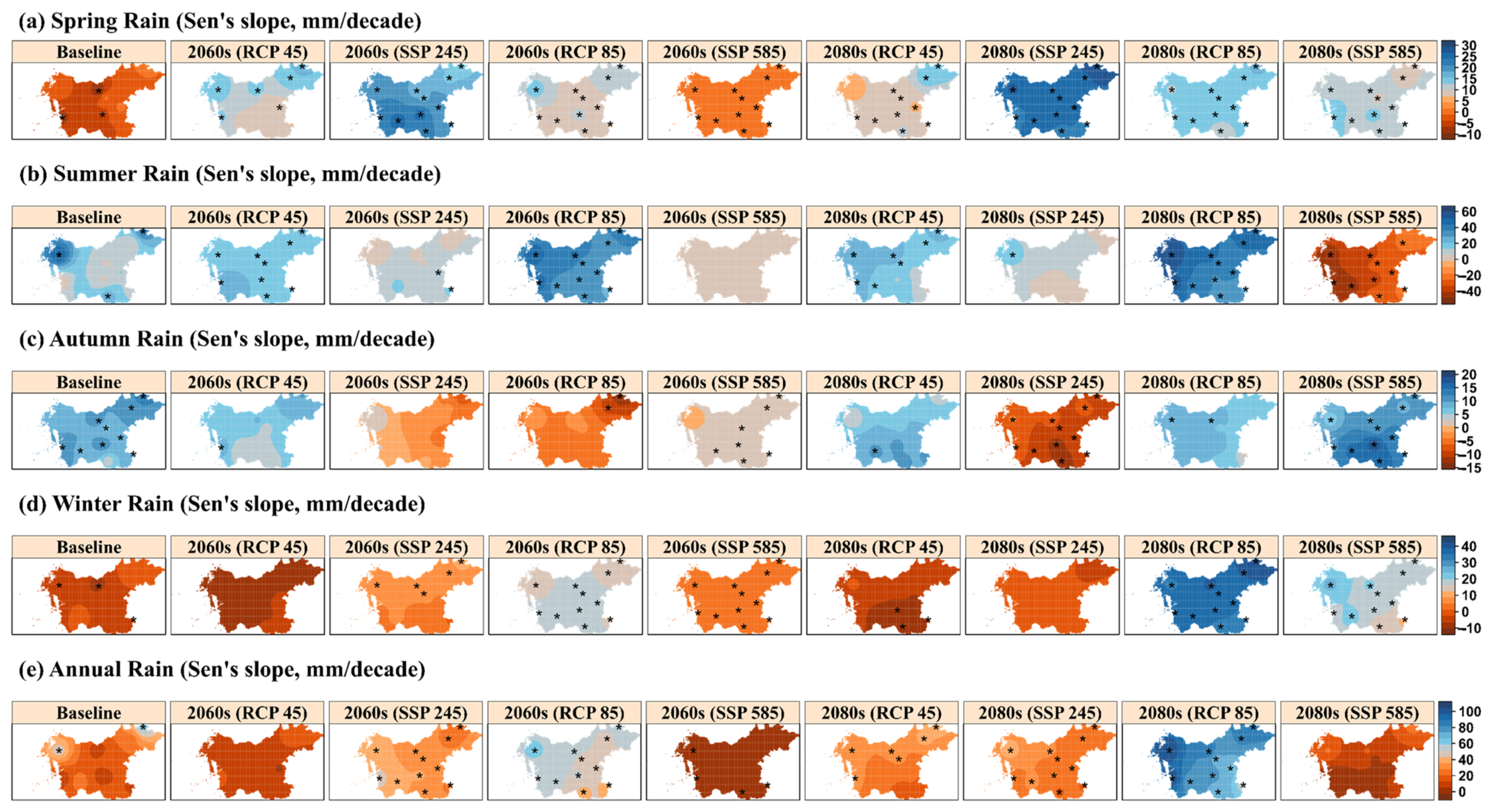
3.3.1. Spatial–Temporal Analysis and Trends in Seasonal and Annual Precipitation
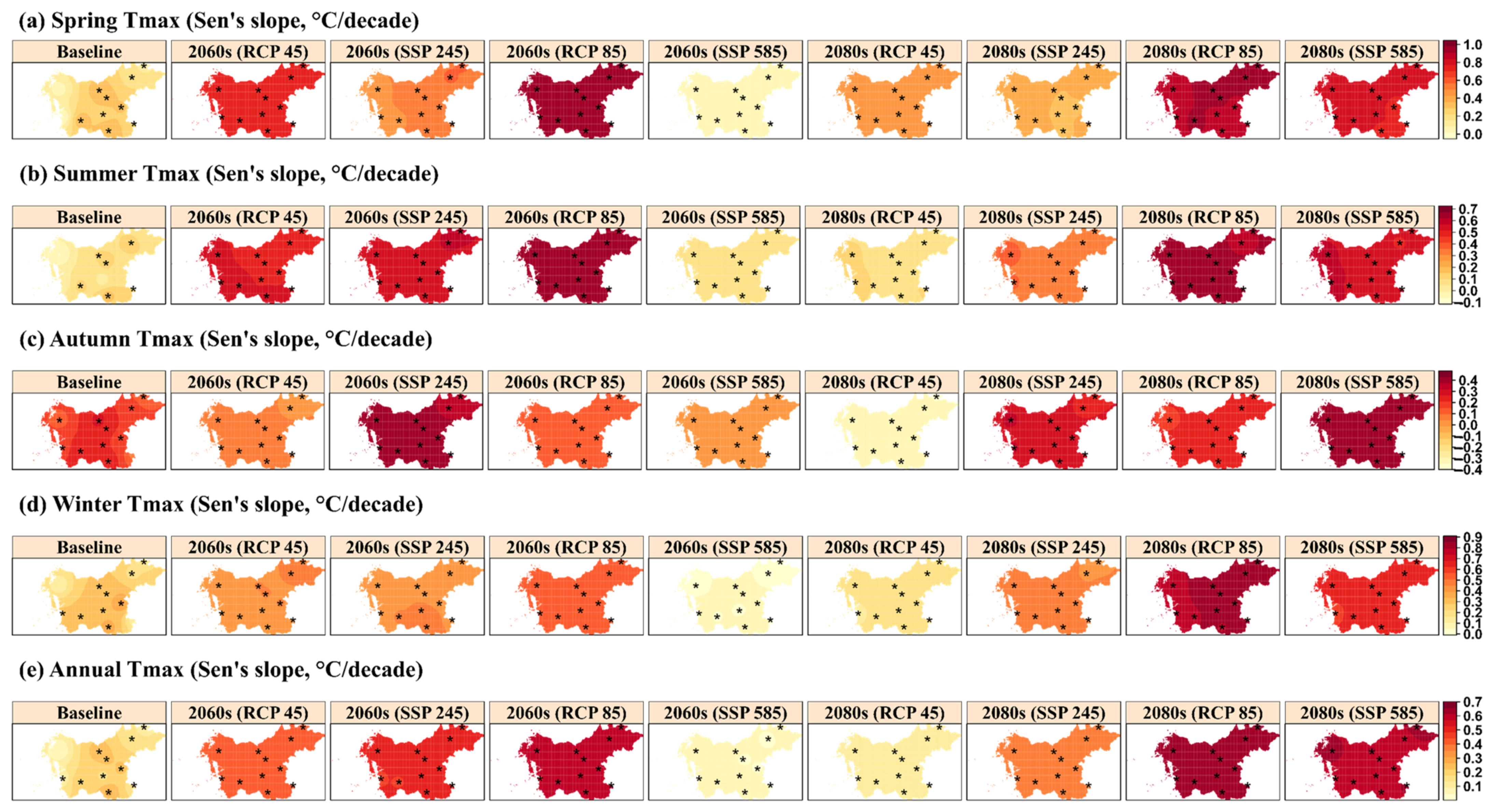
3.3.2. Spatial–Temporal Trends in Seasonal and Annual Tmax
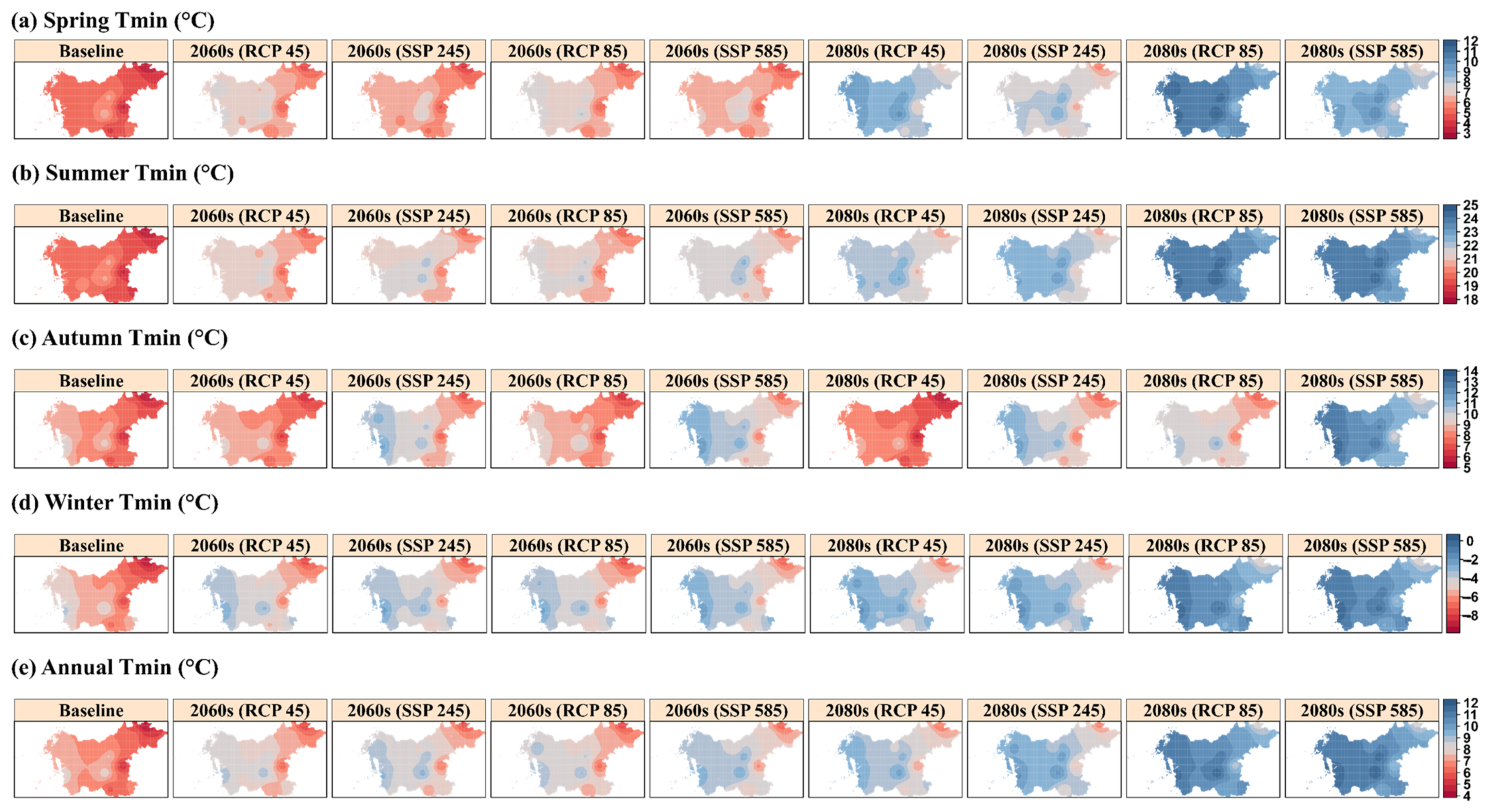
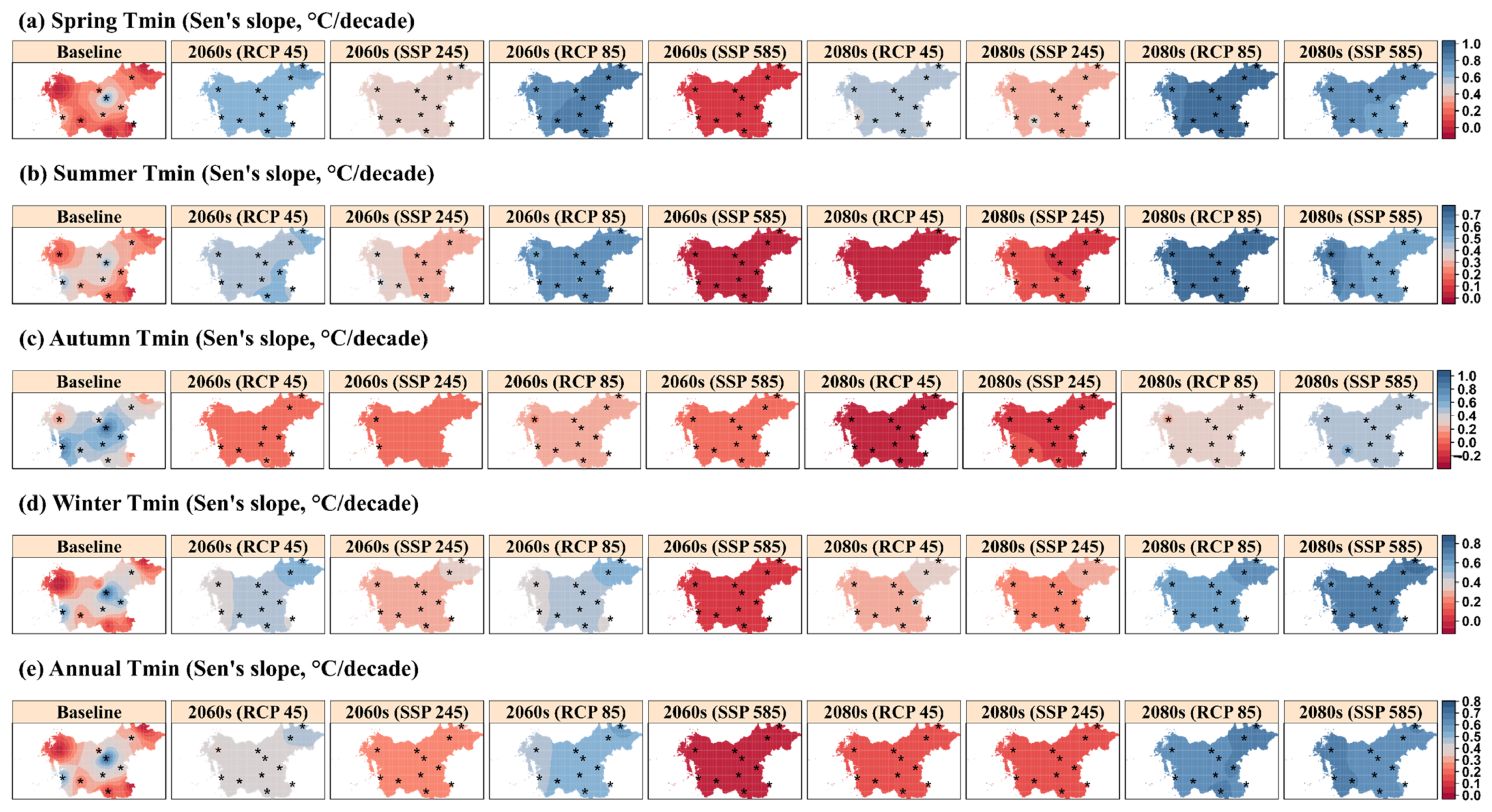
3.3.3. Spatial–Temporal Trends in Seasonal and Annual Tmin
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alexander, L.V. Global observed long-term changes in temperature and precipitation extremes: A review of progress and limitations in IPCC assessments and beyond. Weather Clim. Extrem. 2016, 11, 4–16. [Google Scholar] [CrossRef]
- IPCC. Intergovernmental Panel on Climate Change. Climate Change 2022—Impacts, Adaptation and Vulnerability; Cambridge University Press: Cambridge, UK, 2022; ISBN 9781009325844. [Google Scholar]
- Huang, Y.; Ren, H.L.; Kug, J.S.; Wang, R.; Li, J. Projected change of East-Asian winter precipitation related to strong El Niño under the future emission scenarios. Clim. Change 2023, 176, 81. [Google Scholar] [CrossRef]
- Adelodun, B.; Odey, G.; Lee, S.; Choi, K.S. Investigating the causal impacts relationship between economic flood damage and extreme precipitation indices based on ARDL-ECM framework: A case study of Chungcheong region in South Korea. Sustain. Cities Soc. 2023, 95, 104606. [Google Scholar] [CrossRef]
- Jiang, W.; Tan, Y. Overview on failures of urban underground infrastructures in complex geological conditions due to heavy rainfall in China during 1994–2018. Sustain. Cities Soc. 2022, 76, 103509. [Google Scholar] [CrossRef]
- An, S.; Park, G.; Jung, H.; Jang, D. Assessment of Future Drought Index Using SSP Scenario in Rep. of Korea. Sustainability 2022, 14, 4252. [Google Scholar] [CrossRef]
- Ahmad, M.J.; Choi, K.S. Spatial-temporal evolution and projection of climate extremes in South Korea based on multi-GCM ensemble data. Atmos. Res. 2023, 289, 106772. [Google Scholar] [CrossRef]
- Bae, G.; Yeung, J. Record Rainfall Kills at Least 9 in Seoul as Water Floods Buildings, Submerges Cars. Cable News Netw. Seoul Flooding: Record Rainfall Kills at Least 9 in South Korean Capital as Water Floods Buildings, Submerges Cars | CNN. 2022. Available online: https://www.cnnphilippines.com/world/2022/8/9/Seoul-South-Korea-rain-flood.html (accessed on 31 August 2023).
- Im, E.S.; Thanh, N.X.; Kim, Y.H.; Ahn, J.B. 2018 summer extreme temperatures in South Korea and their intensification under 3 C global warming. Environ. Res. Lett. 2019, 14, 094020. [Google Scholar] [CrossRef]
- Suk, L.Y.; Baker, J.A. South Korea Grapples with One of Its Worst Water Scarcity Crises. Channelnewsasia. 2023. Available online: https://www.channelnewsasia.com/asia/south-korea-water-scarcity-drought-water-tanks-seafood-supply-affected-3385501 (accessed on 31 August 2023).
- Van Doi, M.; Kim, J. Future Projections and Uncertainties of CMIP6 for Hydrological Indicators and Their Discrepancies from CMIP5 over South Korea. Water 2022, 14, 2926. [Google Scholar] [CrossRef]
- Shiru, M.S.; Chung, E.S. Performance evaluation of CMIP6 global climate models for selecting models for climate projection over Nigeria. Theor. Appl. Climatol. 2021, 146, 599–615. [Google Scholar] [CrossRef]
- Du, Y.; Wang, D.; Zhu, J.; Wang, D.; Qi, X.; Cai, J. Comprehensive assessment of CMIP5 and CMIP6 models in simulating and projecting precipitation over the global land. Int. J. Climatol. 2022, 42, 6859–6875. [Google Scholar] [CrossRef]
- Das, S.; Kamruzzaman, M.; Islam, A.R.M.T. Assessment of characteristic changes of regional estimation of extreme rainfall under climate change: A case study in a tropical monsoon region with the climate projections from CMIP6 model. J. Hydrol. 2022, 610, 128002. [Google Scholar] [CrossRef]
- Song, Y.H.; Shahid, S.; Chung, E. Differences in multi-model ensembles of CMIP5 and CMIP6 projections for future droughts in South Korea. Int. J. Climatol. 2022, 42, 2688–2716. [Google Scholar] [CrossRef]
- Song, Y.H.; Chung, E.-S.; Shahid, S. Uncertainties in evapotranspiration projections associated with estimation methods and CMIP6 GCMs for South Korea. Sci. Total Environ. 2022, 825, 153953. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Wang, X.; Fan, Y.; Liang, X.; Jia, H.; Liu, L. How Extreme Events in China Would Be Affected by Global Warming—Insights From a Bias-Corrected CMIP6 Ensemble. Earths Future 2023, 11, e2022EF003347. [Google Scholar] [CrossRef]
- Adelodun, B.; Odey, G.; Cho, H.; Lee, S.; Adeyemi, K.A.; Choi, K.S. Spatial-temporal variability of climate indices in Chungcheong provinces of Korea: Application of graphical innovative methods for trend analysis. Atmos. Res. 2022, 280, 106420. [Google Scholar] [CrossRef]
- KOSIS. Ministry of Land Infrastructure and Transport Statistics System. Available online: https://kosis.kr/index/index.do (accessed on 25 April 2022).
- Shiru, M.S.; Kim, J.H.; Chung, E.S. Variations in Projections of Precipitations of CMIP6 Global Climate Models under SSP 2–45 and SSP 5–85. KSCE J. Civ. Eng. 2022, 26, 5404–5416. [Google Scholar] [CrossRef]
- Adelodun, B.; Odey, G.; Lee, S.; Choi, K.S. Analysis of Spatial-temporal Variability and Trends of Extreme Precipitation Indices over Chungcheong Province, South Korea. J. Korean Soc. Agric. Eng. 2022, 64, 101–112. [Google Scholar] [CrossRef]
- KMA. Korea Meteorological Administration. Available online: https://www.kma.go.kr/eng/index.jsp (accessed on 1 May 2022).
- KWRC. Korean Water Resources Corporation: Overview, K-Water. Available online: https://www.kwater.or.kr/eng/about/sub02/kwaterPage.do?s_mid=1099 (accessed on 1 May 2022).
- Soriano, E.; Mediero, L.; Garijo, C. Selection of Bias Correction Methods to Assess the Impact of Climate Change on Flood Frequency Curves. Water 2019, 11, 2266. [Google Scholar] [CrossRef]
- Zhao, Y.; Xiao, D.; Bai, H.; Tang, J.; Liu, D.L.; Luo, J. Future projection for climate extremes in the North China plain using multi-model ensemble of CMIP5. Meteorol. Atmos. Phys. 2022, 134, 90. [Google Scholar] [CrossRef]
- Cannon, A.J.; Sobie, S.R.; Murdock, T.Q. Bias correction of GCM precipitation by quantile mapping: How well do methods preserve changes in quantiles and extremes? J. Clim. 2015, 28, 6938–6959. [Google Scholar] [CrossRef]
- Xavier, A.C.F.; Martins, L.L.; Rudke, A.P.; de Morais, M.V.B.; Martins, J.A.; Blain, G.C. Evaluation of Quantile Delta Mapping as a bias-correction method in maximum rainfall dataset from downscaled models in São Paulo state (Brazil). Int. J. Climatol. 2022, 42, 175–190. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” Measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Demirel, M.C.; Mai, J.; Mendiguren, G.; Koch, J.; Samaniego, L.; Stisen, S. Combining satellite data and appropriate objective functions for improved spatial pattern performance of a distributed hydrologic model. Hydrol. Earth Syst. Sci. 2018, 22, 1299–1315. [Google Scholar] [CrossRef]
- Roberts, N.M.; Lean, H.W. Scale-selective verification of rainfall accumulations from high-resolution forecasts of convective events. Mon. Weather Rev. 2008, 136, 78–97. [Google Scholar] [CrossRef]
- Gaur, S.; Singh, R.; Bandyopadhyay, A.; Singh, R. Diagnosis of GCM-RCM-driven rainfall patterns under changing climate through the robust selection of multi-model ensemble and sub-ensembles. Clim. Change 2023, 176, 13. [Google Scholar] [CrossRef]
- Koch, J.; Demirel, M.C.; Stisen, S. The SPAtial EFficiency metric (SPAEF): Multiple-component evaluation of spatial patterns for optimization of hydrological models. Geosci. Model Dev. 2018, 11, 1873–1886. [Google Scholar] [CrossRef]
- Ahmed, K.; Sachindra, D.A.; Shahid, S.; Demirel, M.C.; Chung, E.-S. Selection of multi-model ensemble of general circulation models for the simulation of precipitation and maximum and minimum temperature based on spatial assessment metrics. Hydrol. Earth Syst. Sci. 2019, 23, 4803–4824. [Google Scholar] [CrossRef]
- Zhang, Y.; You, Q.; Chen, C.; Ge, J.; Adnan, M. Evaluation of downscaled CMIP5 Coupled with VIC model for flash drought simulation in a humid subtropical basin, China. J. Clim. 2018, 31, 1075–1090. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C. The Mann-Kendall test modified by effective sample size to detect trend in serially correlated hydrological series. Water Resour. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Bock, L.; Lauer, A.; Schlund, M.; Barreiro, M.; Bellouin, N.; Jones, C.; Meehl, G.A.; Predoi, V.; Roberts, M.J.; Eyring, V. Quantifying Progress Across Different CMIP Phases With the ESMValTool. J. Geophys. Res. Atmos. 2020, 125, e2019JD032321. [Google Scholar] [CrossRef]
- Cannon, A.J. Reductions in daily continental-scale atmospheric circulation biases between generations of global climate models: CMIP5 to CMIP6. Environ. Res. Lett. 2020, 15, 064006. [Google Scholar] [CrossRef]
- Jia, Q.; Jia, H.; Li, Y.; Yin, D. Applicability of CMIP5 and CMIP6 models in China: Reproducibility of historical simulation and uncertainty of future projection. J. Clim. 2023, 6, 5809–5824. [Google Scholar] [CrossRef]
- Song, Y.H.; Chung, E.S.; Shahid, S. Spatiotemporal differences and uncertainties in projections of precipitation and temperature in South Korea from CMIP6 and CMIP5 general circulation models. Int. J. Climatol. 2021, 41, 5899–5919. [Google Scholar] [CrossRef]
- Hamed, M.M.; Nashwan, M.S.; Shiru, M.S.; Shahid, S. Comparison between CMIP5 and CMIP6 Models over MENA Region Using Historical Simulations and Future Projections. Sustainability 2022, 14, 10375. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, T.; Zhang, L.; Chen, X.; Zhang, W.; Jiang, J. Global Land Monsoon Precipitation Changes in CMIP6 Projections. Geophys. Res. Lett. 2020, 47, e2019GL086902. [Google Scholar] [CrossRef]
- Hong, J.; Javan, K.; Shin, Y.; Park, J.S. Future projections and uncertainty assessment of precipitation extremes in iran from the cmip6 ensemble. Atmosphere 2021, 12, 1052. [Google Scholar] [CrossRef]
- Song, Y.H.; Nashwan, M.S.; Chung, E.S.; Shahid, S. Advances in CMIP6 INM-CM5 over CMIP5 INM-CM4 for precipitation simulation in South Korea. Atmos. Res. 2021, 247, 105261. [Google Scholar] [CrossRef]
- Xin, X.; Zhang, L.; Zhang, J.; Wu, T.; Fang, Y. Climate change projections over east asia with BBC_CSM1.1 climate model under RCP scenarios. J. Meteorol. Soc. Jpn. 2013, 91, 413–429. [Google Scholar] [CrossRef]
- O’Neill, B.C.; Tebaldi, C.; Van Vuuren, D.P.; Eyring, V.; Friedlingstein, P.; Hurtt, G.; Knutti, R.; Kriegler, E.; Lamarque, J.F.; Lowe, J.; et al. The Scenario Model Intercomparison Project (ScenarioMIP) for CMIP6. Geosci. Model Dev. 2016, 9, 3461–3482. [Google Scholar] [CrossRef]
- Horinouchi, T.; Kawatani, Y.; Sato, N. Inter-model variability of the CMIP5 future projection of Baiu, Meiyu, and Changma precipitation. Clim. Dyn. 2023, 60, 1849–1864. [Google Scholar] [CrossRef]


| Models | Modeling Institute | Country | Resolution (Lat. × Long.) | |
|---|---|---|---|---|
| CMIP5 | ACCESS1-3 | Commonwealth Scientific and Industrial | Australia | 1.875° × 1.25° |
| CMIP6 | ACCESS-ESM1-5 | Research Organization and Bureau of Meteorology | Australia | 1.875° × 1.25° |
| CMIP5 | BCC-CSM1-1 | Beijing Climate Center, China Meteorological Administration | China | 2.8° × 2.8° |
| CMIP6 | BCC-CSM2-MR | Beijing Climate Center, China Meteorological Administration | China | 1.125° × 1.125° |
| CMIP5 | CanESM2 | Canadian Centre for Climate Modelling and Analysis | Canada | 2.8° × 2.8° |
| CMIP6 | CanESM5 | Canadian Centre for Climate Modelling and Analysis | Canada | 2.8° × 2.8° |
| CMIP5 | GFDL-ESM2M | NOAA/Geophysical Fluid Dynamics Laboratory Earth System Model | USA | 2.5° × 2.0° |
| CMIP6 | GFDL-ESM4 | NOAA/Geophysical Fluid Dynamics Laboratory Earth System Model | USA | 1.25° × 1.00° |
| CMIP5 | GISS-E2-R | NASA Goddard Institute for Space Studies | USA | 2.5° × 1.875° |
| CMIP6 | GISS-E2-2-G | NASA Goddard Institute for Space Studies | USA | 2.5° × 1.875° |
| CMIP5 | INM-CM4 | Institute for Numerical Mathematics, Russian Academy of Science | Russia | 1.5° × 2.0° |
| CMIP6 | INM-CM4-8 | Institute for Numerical Mathematics, Russian Academy of Science | Russia | 1.5° × 2.0° |
| CMIP5 | IPSL-CM5A-LR | Institut Pierre-Simon Laplace | France | 3.75° × 1.875° |
| CMIP6 | IPSL-CM6A-LR | Institut Pierre-Simon Laplace | France | 2.5° × 1.26° |
| CMIP5 | MIROC5 | National Institute for Environmental Studies, Japan Agency for Marine-Earth Science and Technology, and Atmosphere and Ocean Research Institute (The University of Tokyo) | Japan | 1.4° × 1.4° |
| CMIP6 | MIROC6 | National Institute for Environmental Studies, Japan Agency for Marine-Earth Science and Technology, and Atmosphere and Ocean Research Institute (The University of Tokyo) | Japan | 1.4° × 1.4° |
| CMIP5 | MPI-ESM-LR | Max Planck Institute for Meteorology | Germany | 1.875° × 1.875° |
| CMIP6 | MPI-ESM-1-2-HR | Max Planck Institute for Meteorology | Germany | 0.94° × 0.94° |
| CMIP6 | MPI-ESM-1-2-LR | Max Planck Institute for Meteorology | Germany | 1.875° × 1.875° |
| CMIP5 | MRI-CGCM3 | Meteorological Research Institute | Japan | 1.125° × 1.125° |
| CMIP6 | MRI-ESM2-0 | Meteorological Research Institute | Japan | 1.125° × 1.125° |
| CMIP5 | NorESM1-M | Norwegian Climate Centre | Norway | 2.50° × 1.88° |
| CMIP6 | NorESM2-MM | Norwegian Climate Centre | Norway | 0.94° × 1.25° |
| CMIP6 | KIOST-ESM | Korea Institute of Ocean Science and Technology Earth System Model | South Korea | 1.87° × 1.87° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adelodun, B.; Ahmad, M.J.; Odey, G.; Adeyi, Q.; Choi, K.S. Performance-Based Evaluation of CMIP5 and CMIP6 Global Climate Models and Their Multi-Model Ensembles to Simulate and Project Seasonal and Annual Climate Variables in the Chungcheong Region of South Korea. Atmosphere 2023, 14, 1569. https://doi.org/10.3390/atmos14101569
Adelodun B, Ahmad MJ, Odey G, Adeyi Q, Choi KS. Performance-Based Evaluation of CMIP5 and CMIP6 Global Climate Models and Their Multi-Model Ensembles to Simulate and Project Seasonal and Annual Climate Variables in the Chungcheong Region of South Korea. Atmosphere. 2023; 14(10):1569. https://doi.org/10.3390/atmos14101569
Chicago/Turabian StyleAdelodun, Bashir, Mirza Junaid Ahmad, Golden Odey, Qudus Adeyi, and Kyung Sook Choi. 2023. "Performance-Based Evaluation of CMIP5 and CMIP6 Global Climate Models and Their Multi-Model Ensembles to Simulate and Project Seasonal and Annual Climate Variables in the Chungcheong Region of South Korea" Atmosphere 14, no. 10: 1569. https://doi.org/10.3390/atmos14101569
APA StyleAdelodun, B., Ahmad, M. J., Odey, G., Adeyi, Q., & Choi, K. S. (2023). Performance-Based Evaluation of CMIP5 and CMIP6 Global Climate Models and Their Multi-Model Ensembles to Simulate and Project Seasonal and Annual Climate Variables in the Chungcheong Region of South Korea. Atmosphere, 14(10), 1569. https://doi.org/10.3390/atmos14101569









