Data-Driven Global Subseasonal Forecast for Intraseasonal Oscillation Components
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.2. Methods
2.2.1. Filtering Method
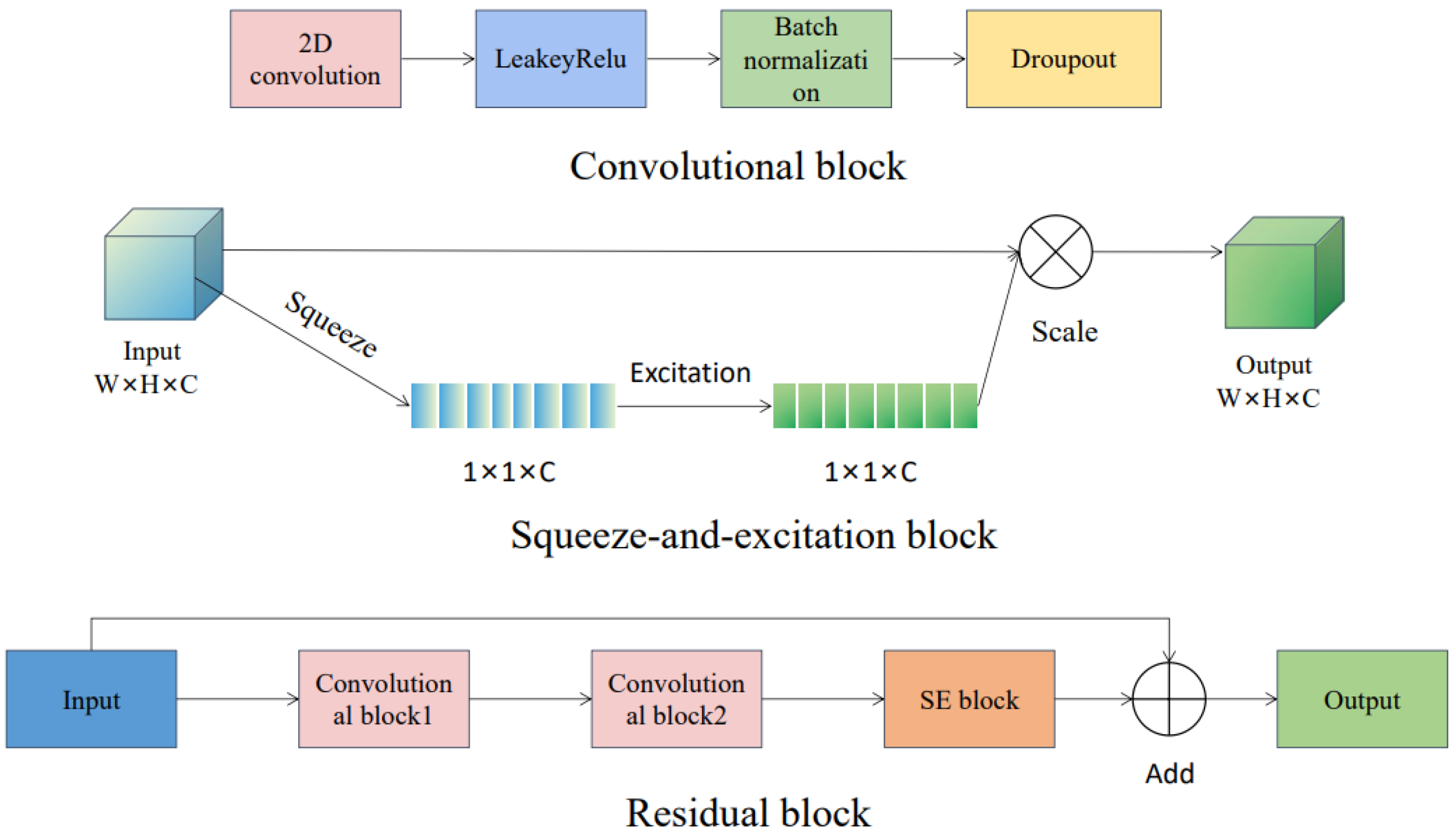
2.2.2. Forecast Model
2.2.3. Forecast Effect Evaluation Methods
3. Model Forecast Results
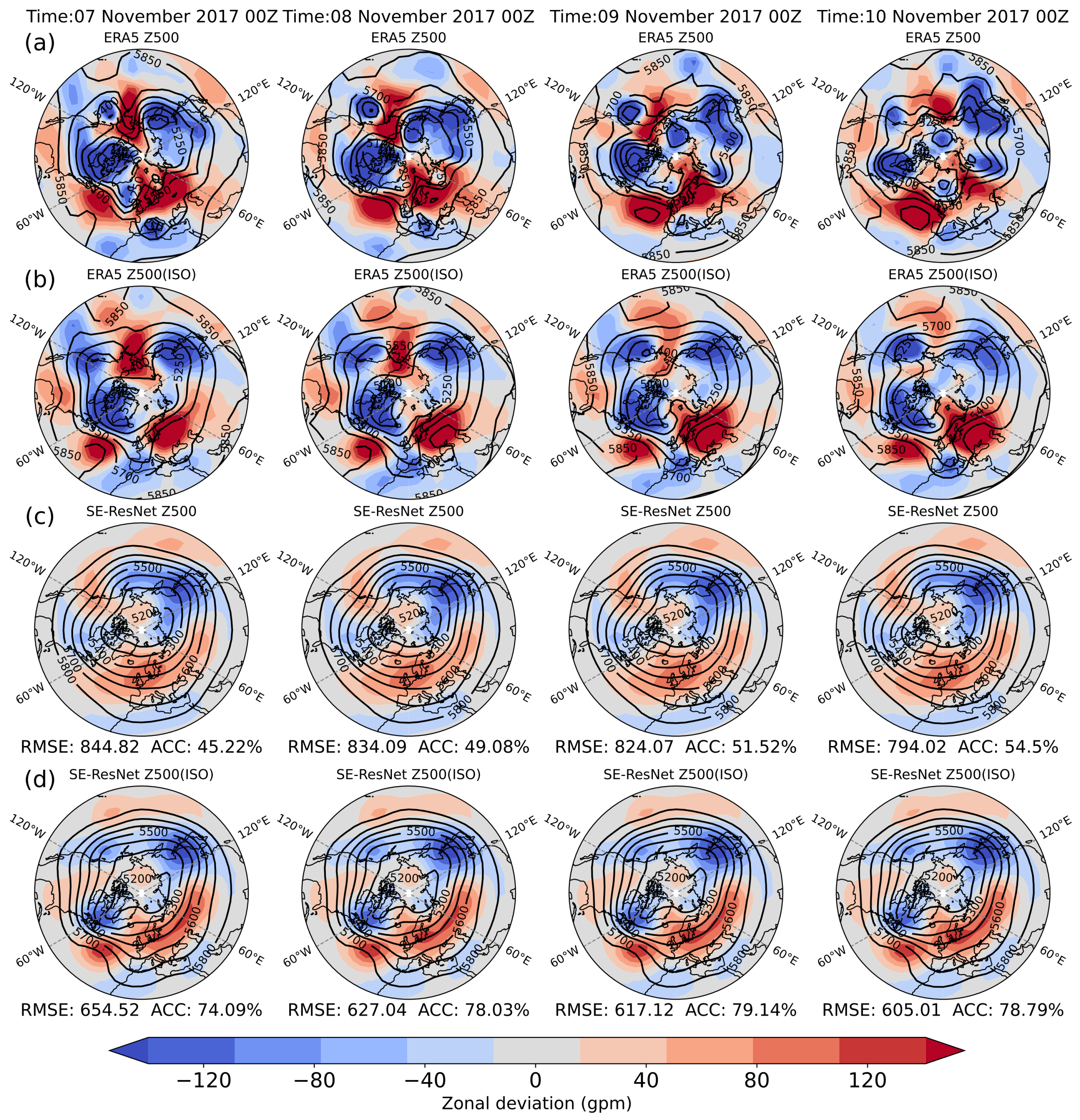
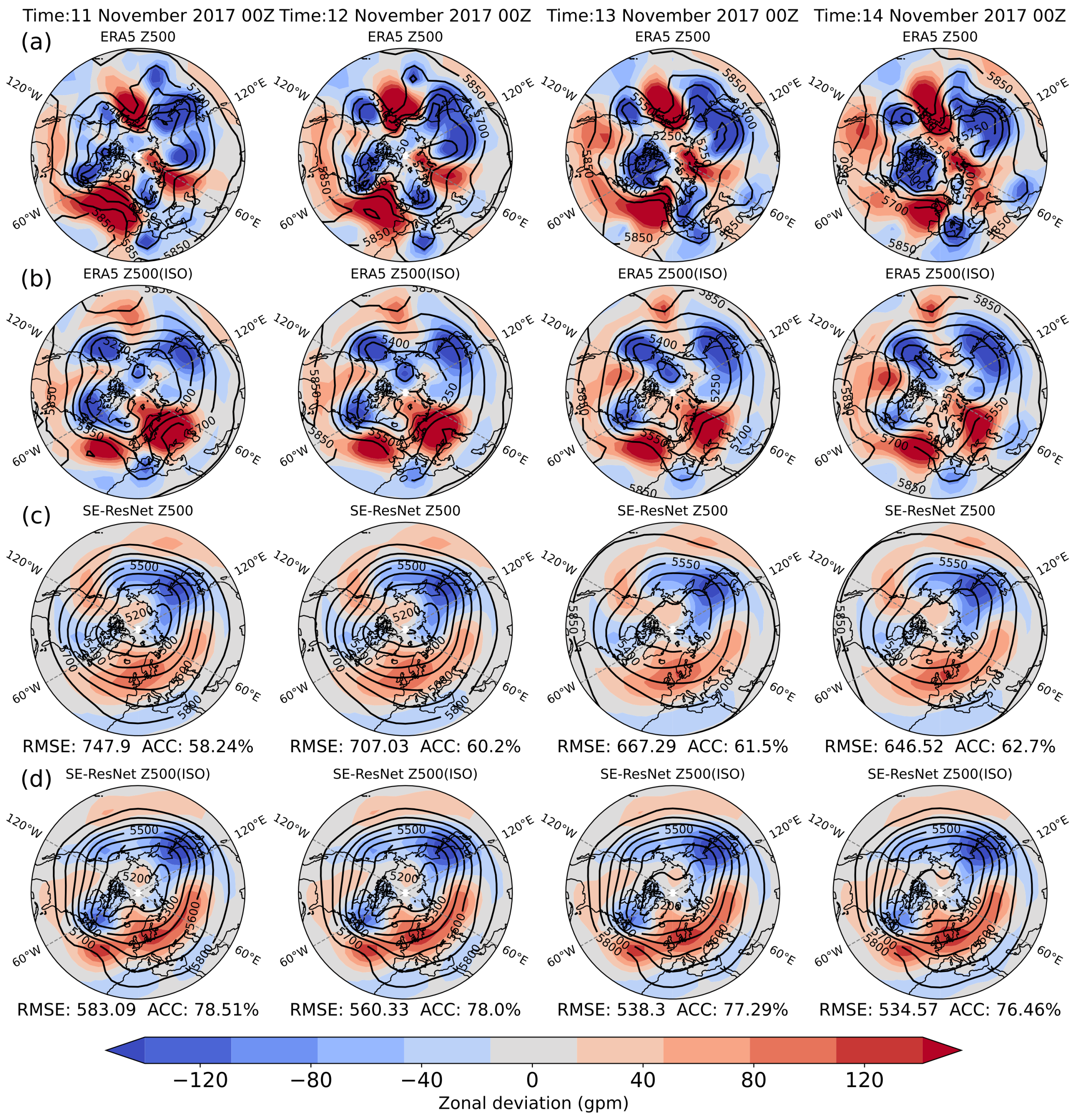
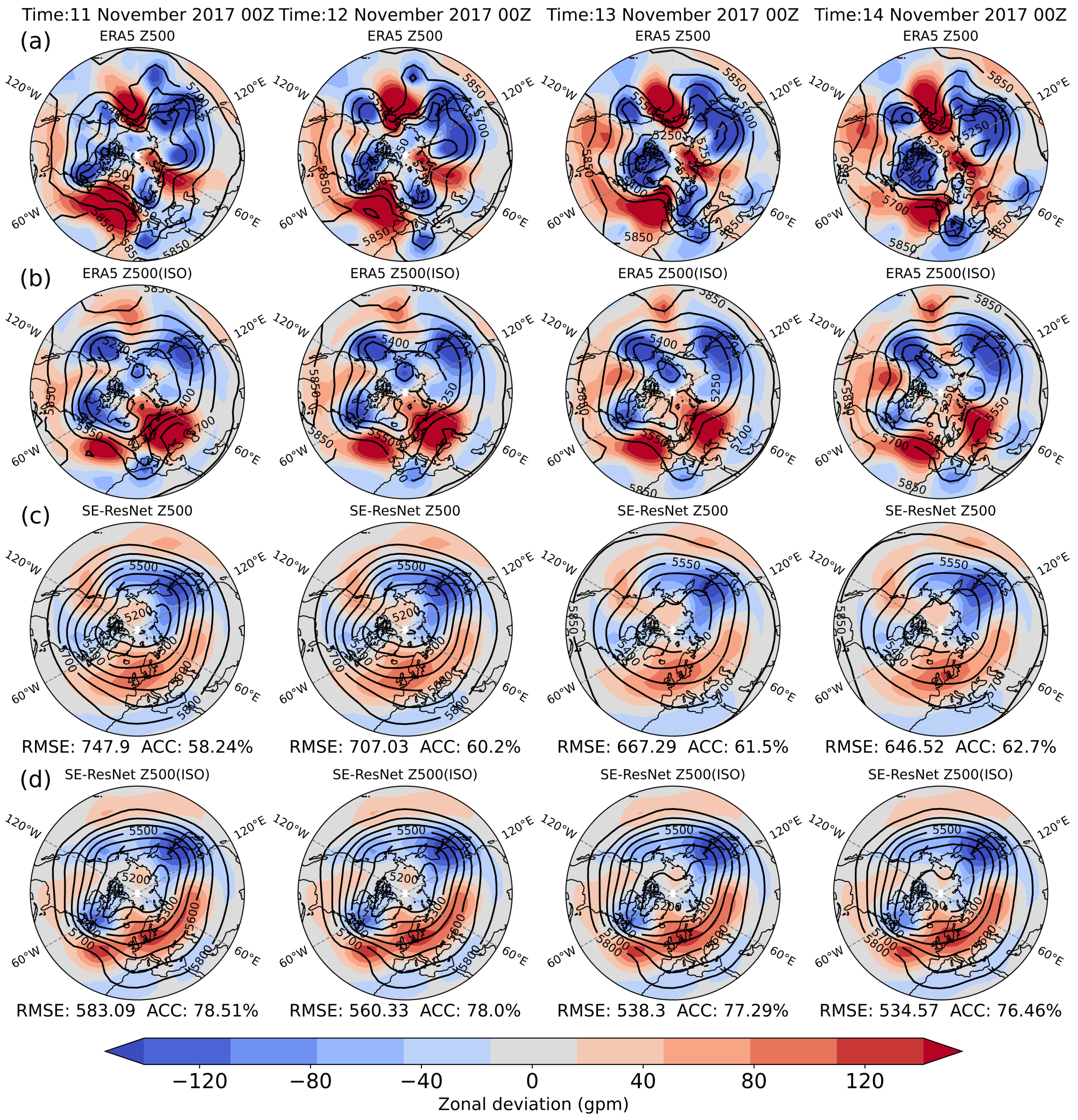
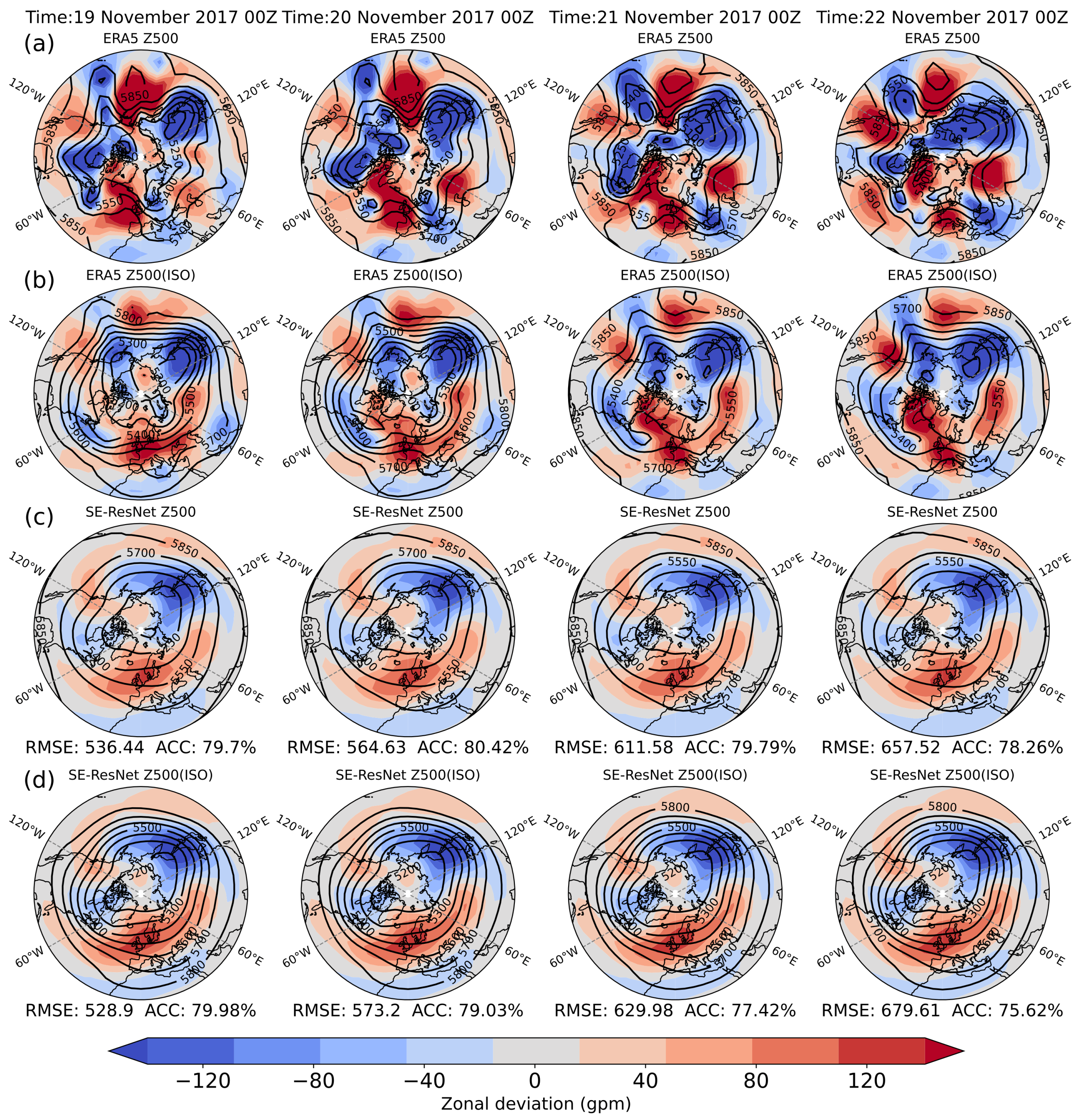
3.1. Prediction Case Analysis: Original Data vs. ISO Component
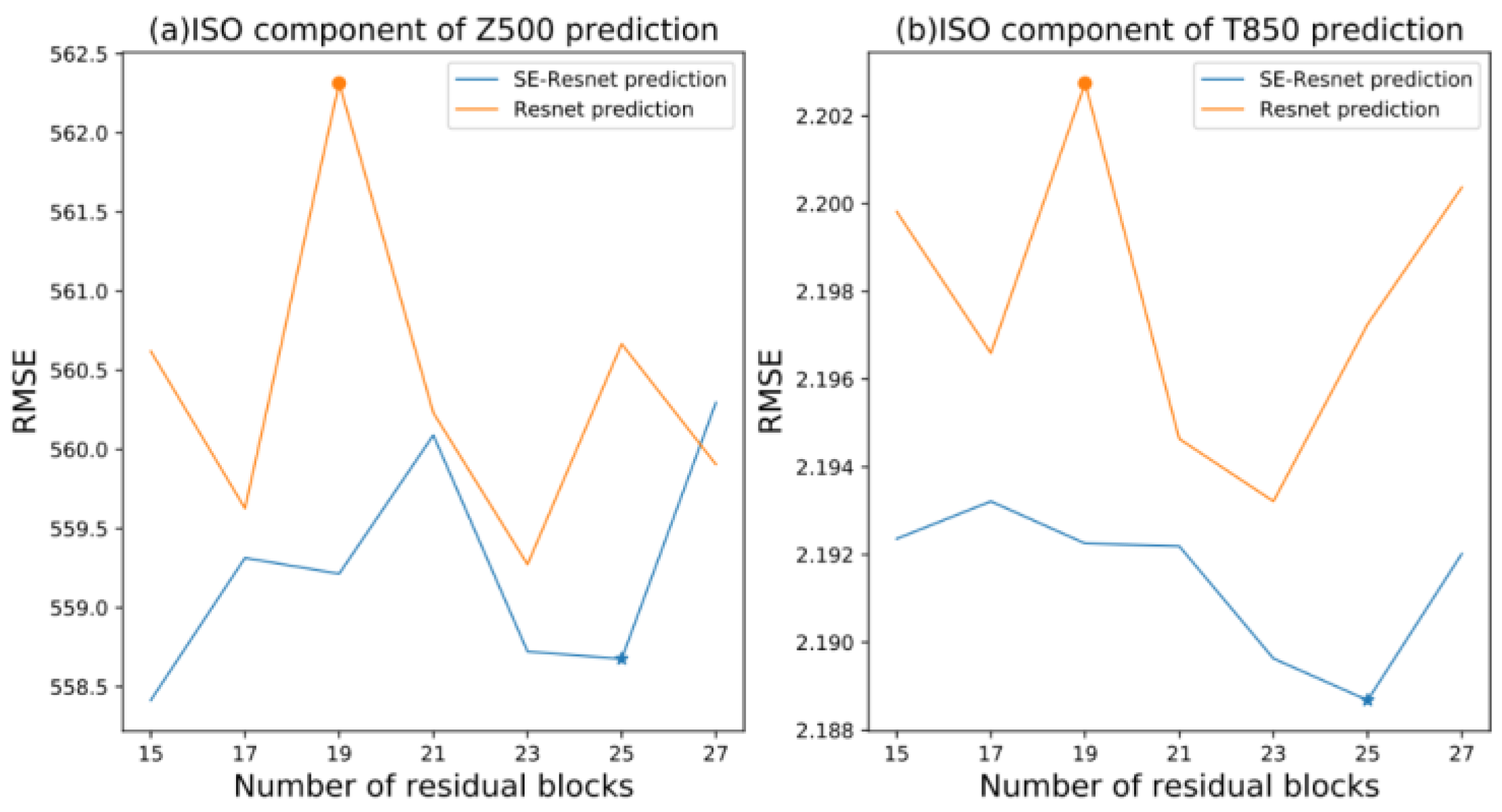
3.2. Overall Evaluation of the Model
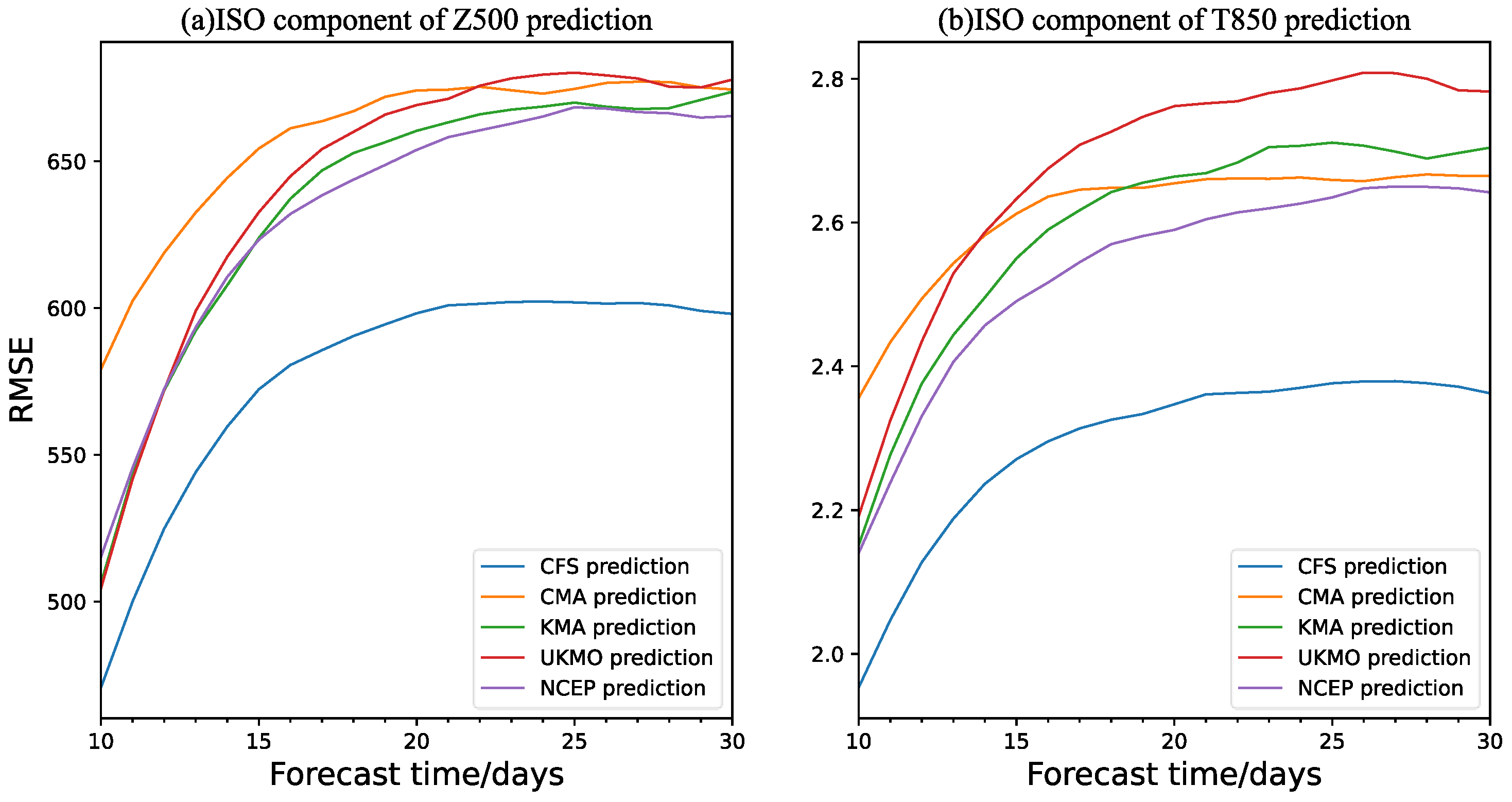
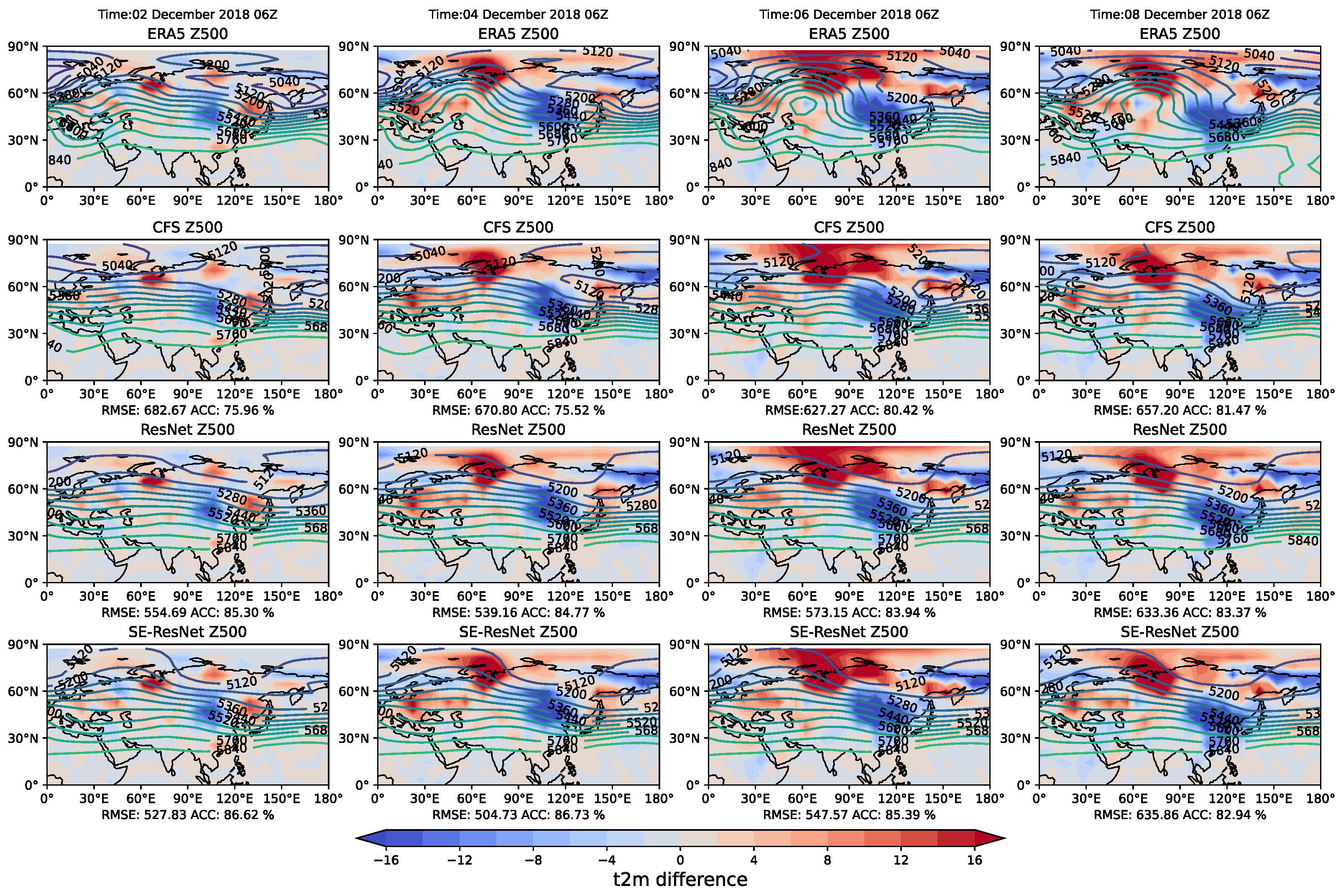
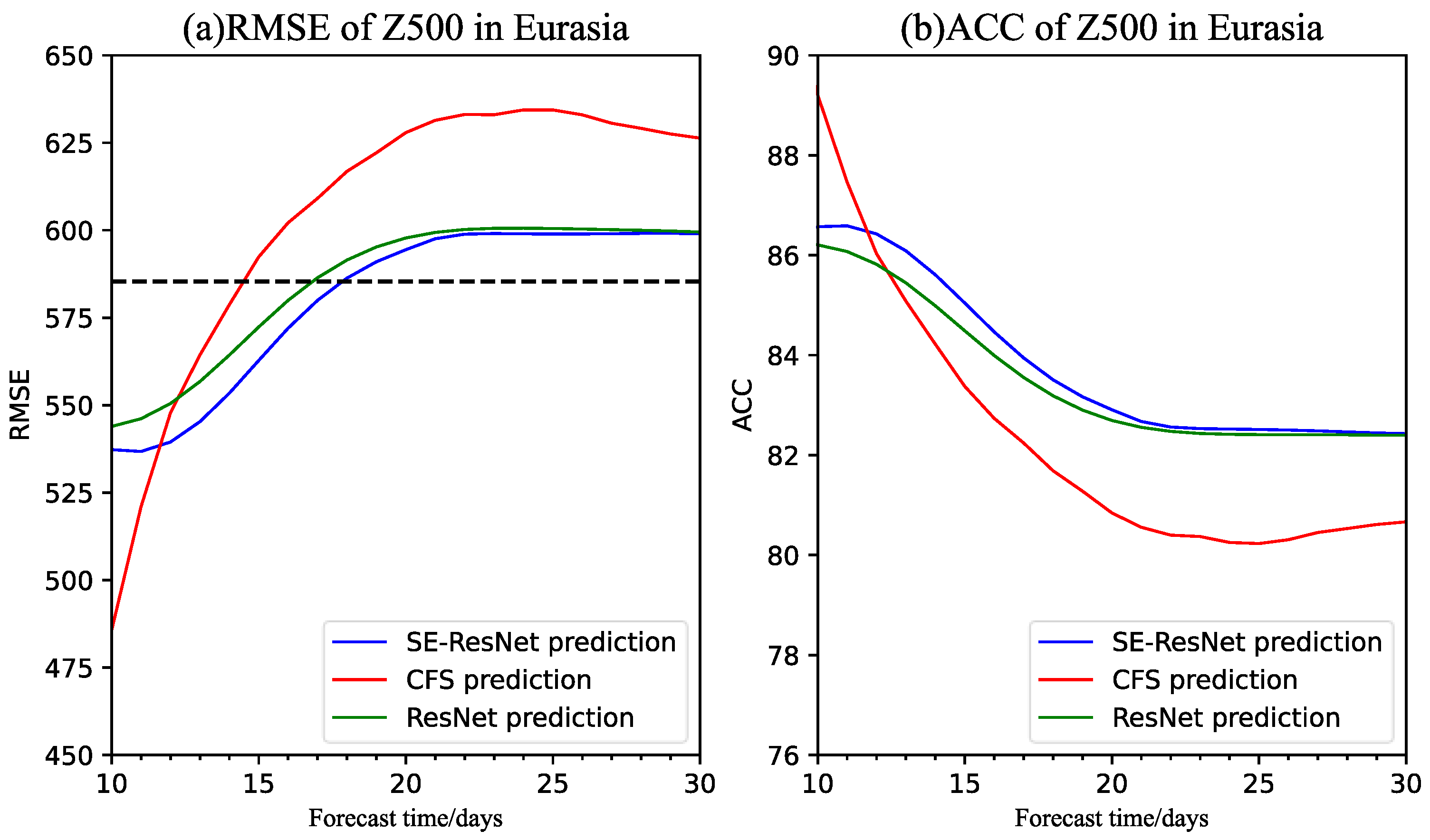
3.3. Prediction and Evaluation of the 500 hPa Circulation Situation in the Eurasian Region
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Jin, R.; Ma, J.; Ren, H.; Yin, S.; Cai, X.; Huang, W. Advances and development countermeasures of 10~30 days extended-range forecasting technology in China. Adv. Earth Sci. 2019, 34, 814–825. (In Chinese) [Google Scholar] [CrossRef]
- Hoskins, B.J. The potential for skill across the range of the seamless weather-climate prediction problem: A stimulus for our science. Q. J. R. Meteorol. Soc. 2013, 139, 573–584. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Mayer, K.J.; Barnes, E.A. Subseasonal Forecasts of Opportunity Identified by an Explainable Neural Network. Geophys. Res. Lett. 2021, 48, e2020GL092092. [Google Scholar] [CrossRef]
- Srinivasan, V.; Khim, J.; Banerjee, A.; Ravikumar, P. Subseasonal climate prediction in the western US using Bayesian spatial models. In Proceedings of the 37th Conference on Uncertainty in Artificial Intelligence, Virtual, Online, 27–30 July 2021; Available online: https://auai.org/uai2021/pdf/uai2021.361.pdf (accessed on 12 December 2021).
- Vitart, F.; Ardilouze, C.; Bonet, A.; Brookshaw, A.; Chen, M.; Codorean, C.; Déqué, M.; Ferranti, L.; Fucile, E.; Fuentes, M.; et al. The Subseasonal to Seasonal (S2S) Prediction Project Database. Bull. Amer. Meteor. Soc. 2017, 98, 163–173. [Google Scholar] [CrossRef]
- Mariotti, A.; Ruti, P.M.; Rixen, M. Progress in subseasonal to seasonal prediction through a joint weather and climate community effort. NPJ Clim. Atmos. Sci. 2018, 1, 4. [Google Scholar] [CrossRef]
- Robertson, A.W.; Kumar, A.; Peña, M.; Vitart, F. Improving and Promoting Subseasonal to Seasonal Prediction. Bull. Amer. Meteor. Soc. 2015, 96, ES49–ES53. [Google Scholar] [CrossRef]
- Li, W.; Hsu, P.C.; He, J.; Zhu, Z.; Zhang, W. Extended-range forecast of spring rainfall in southern china based on the madden–julian oscillation. Meteor. Atmos. Phys. 2016, 128, 331–345. [Google Scholar] [CrossRef]
- Zhu, Z.; Li, T.; Bai, L.; Gao, J. Extended-range forecast for the temporal distribution of clustering tropical cyclogenesis over the western north pacific. Theor. Appl. Climatol. 2017, 130, 865–877. [Google Scholar] [CrossRef]
- Mouatadid, S.; Orenstein, P.; Flaspohler, G.; Cohen, J.; Oprescu, M.; Fraenkel, E.; Mackey, L. Adaptive bias correction for improved subseasonal forecasting. Nat. Commun. 2023, 14, 3482. [Google Scholar] [CrossRef]
- van Straaten, C.; Whan, K.; Coumou, D.; van den Hurk, B.; Schmeits, M. Using Explainable Machine Learning Forecasts to Discover Subseasonal Drivers of High Summer Temperatures in Western and Central Europe. Mon. Weather Rev. 2022, 150, 1115–1134. [Google Scholar] [CrossRef]
- Zhu, H.; Wheeler, M.C.; Sobel, A.H.; Hudson, D. Seamless precipitation prediction skill in the tropics and extratropics from a global model. Mon. Weather Rev. 2014, 142, 1556–1569. [Google Scholar] [CrossRef]
- Zhang, D.; Zheng, Z.; Chen, L.; Zhang, P. Advances on the Predictability and Prediction Methods of 10-30 d Extended Range Forecast. J. Appl. Meteor. Sci. 2019, 30, 416–430. (In Chinese) [Google Scholar] [CrossRef]
- Hsu, P.C.; Li, T.; You, L.; Gao, J.; Ren, H.L. A spatial–temporal projection model for 10–30 day rainfall forecast in south China. Clim. Dyn. 2015, 44, 1227–1244. [Google Scholar] [CrossRef]
- Wang, Q.; Chou, J.; Feng, G. Extracting predictable components and forecasting techniques in extended-range numerical weather prediction. Sci. China Earth Sci. 2014, 57, 1525–1537. [Google Scholar] [CrossRef]
- Lu, C.; Kong, Y.; Guan, Z. A mask R-CNN model for reidentifying extratropical cyclones based on quasi-supervised thought. Sci. Rep. 2020, 10, 15011. [Google Scholar] [CrossRef] [PubMed]
- Lagerquist, R.; Mcgovern, A.; Gagne, D.J. Deep learning for spatially explicit prediction of synoptic-scale fronts. Wea. Forecast. 2019, 34, 1137–1160. [Google Scholar] [CrossRef]
- Lagerquist, R.; Allen, J.T.; McGovern, A. Climatology and Variability of Warm and Cold Fronts over North America from 1979 to 2018. J. Clim. 2020, 33, 6531–6554. [Google Scholar] [CrossRef]
- Ravuri, S.; Lenc, K.; Willson, M.; Kangin, D.; Lam, R.; Mirowski, P.; Fitzsimons, M.; Athanassiadou, M.; Kashem, S.; Madge, S.; et al. Skilful precipitation nowcasting using deep generative models of radar. Nature 2021, 597, 672–677. [Google Scholar] [CrossRef]
- Bi, K.; Xie, L.; Zhang, H.; Chen, X.; Gu, X.; Tian, Q. Accurate medium-range global weather forecasting with 3D neural networks. Nature 2023, 619, 533–538. [Google Scholar] [CrossRef]
- Chen, K.; Han, T.; Gong, J.; Bai, L.; Ling, F.; Luo, J.J.; Chen, X.; Ma, L.; Zhang, T.; Su, R.; et al. FengWu: Pushing the Skillful Global Medium-range Weather Forecast beyond 10 Days Lead. arXiv 2023, arXiv:2304.02948. [Google Scholar]
- Song, K.; Yu, X.; Gu, Z.; Zhang, W.; Yang, G.; Wang, Q.; Xu, C.; Liu, J.; Liu, W.; Shi, C.; et al. Deep Learning Prediction of Incoming Rainfalls: An Operational Service for the City of Beijing China. In Proceedings of the 2019 International Conference on Data Mining Workshops (ICDMW), Beijing, China, 8–11 November 2019. [Google Scholar] [CrossRef]
- Sønderby, C.K.; Espeholt, L.; Heek, J.; Dehghani, M.; Oliver, A.; Salimans, T.; Agrawal, S.; Hickey, J.; Kalchbrenner, N. MetNet: A Neural Weather Model for Precipitation Forecasting. arXiv 2020, arXiv:2003.12140. [Google Scholar]
- Weyn, J.A.; Durran, D.R.; Caruana, R.; Cresswell-Clay, N. Sub-seasonal forecasting with a large ensemble of deep-learning weather prediction models. J. Adv. Model. Earth Syst. 2021, 13, e2021MS002502. [Google Scholar] [CrossRef]
- Rasp, S.; Thuerey, N. Data-driven medium-range weather prediction with a resnet pretrained on climate simulations: A new model for weatherbench. J. Adv. Model. Earth Syst. 2021, 13, e2020MS002405. [Google Scholar] [CrossRef]
- Jin, W.; Zhang, W.; Hu, J.; Weng, B.; Huang, T.; Chen, J. Using the Residual Network Module to Correct the Sub-Seasonal High Temperature Forecast. Front. Earth Sci. 2021, 9, 760766. [Google Scholar] [CrossRef]
- Rasp, S.; Dueben, P.D.; Scher, S.; Weyn, J.A.; Thuerey, N. Weatherbench: A benchmark data set for data-driven weather forecasting. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002203. [Google Scholar] [CrossRef]
- Mathieu, M.; Couprie, C.; LeCun, Y. Deep multi-scale video prediction beyond mean square error. arXiv 2015, arXiv:1511.05440. [Google Scholar]
- Slingo, J.M.; Bates, K.R.; Nikiforakis, N.; Piggott, M.D.; Roberts, M.J.; Shaffrey, L.C.; Stevens, I.T.; Vidale, P.L.; Weller, H. Developing the next-generation climate system models: Challenges and achievements. Phil. Trans. R. Soc. A 2008, 367, 815–831. [Google Scholar] [CrossRef]
- Kashinath, K.; Mustafa, M.; Albert, A.; Wu, J.L.; Jiang, C.; Esmaeilzadeh, S.; Azizzadenesheli, K.; Wang, R.; Chattopadhyay, A.; Singh, A.; et al. Physics-informed machine learning: Case studies for weather and climate modelling. Phil. Trans. R. Soc. A 2021, 379, 20200093. [Google Scholar] [CrossRef]
- Wu, J.; Kashinath, K.; Albert, A.; Chirila, D.B.; Prabhat; Xiao, H. Enforcing statistical constraints in generative adversarial networks for modeling chaotic dynamical systems. J. Comput. Phys. 2020, 406, 109209. [Google Scholar] [CrossRef]
- Mohan, A.; Livescu, D.; Chertkov, M. Wavelet-powered neural networks for turbulence. In Proceedings of the ICLR 2020 Workshop on Climate Change AI, Virtual, Online, 26–30 April 2020; Available online: https://www.climatechange.ai/papers/iclr2020/16 (accessed on 12 December 2021).
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-Excitation Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.T.; Chuang, H.Y.; Iredell, M.; et al. The NCEP Climate Forecast System Version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar] [CrossRef]
- Rasp, S.; Thuerey, N. Data-Driven Medium-Range Weather Prediction with a Resnet Pretrained on Climate Simulations: A New Model for Weatherbench. Available online: https://github.com/raspstephan/WeatherBench (accessed on 12 December 2021).
- Qi, X.; Yang, J.; Gao, M.; Yang, H.; Liu, H. Roles of the Tropical/Extratropical Intraseasonal Oscillations on Generating the Heat Wave Over Yangtze River Valley: A Numerical Study. J. Geophys. Res. Atmos. 2019, 124, 3110–3123. [Google Scholar] [CrossRef]
- Petoukhov, V.; Rahmstorf, S.; Petri, S.; Schellnhuber, H.J. Quasiresonant amplification of planetary waves and recent Northern Hemisphere weather extremes. Proc. Natl. Acad. Sci. USA 2013, 110, 5336–5341. [Google Scholar] [CrossRef]
- Screen, J.A.; Simmonds, I. Amplified mid-latitude planetary waves favour particular regional weather extremes. Nat. Clim. Chang. 2014, 4, 704–709. [Google Scholar] [CrossRef]
- Weyn, J.A.; Durran, D.R.; Caruana, R. Improving data-driven global weather prediction using deep convolutional neural networks on a cubed sphere. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002109. [Google Scholar] [CrossRef]
- Pawar, S.; San, O.; Nair, A.G.; Rasheed, A.; Kvamsdal, T. Model fusion with physics-guided machine learning: Projection-based reduced-order modeling. Phys. Fluids 2021, 33, 067123. [Google Scholar] [CrossRef]
- Karra, S.; Ahmmed, B.; Mudunuru, M.K. AdjointNet: Constraining machine learning models with physics-based codes. arXiv 2021, arXiv:2109.03956. [Google Scholar]
- He, S.; Li, X.; Trenary, L.; Cash, B.A.; DelSole, T.; Banerjee, A. Learning and dynamical models for sub-seasonal climate forecasting: Comparison and collaboration. arXiv 2021, arXiv:2110.05196. [Google Scholar] [CrossRef]
- Clare, M.C.; Jamil, O.; Morcrette, C.J. Combining distribution-based neural networks to predict weather forecast probabilities. Q. J. R. Meteorol. Soc. 2021, 147, 4337–4357. [Google Scholar] [CrossRef]
- Rasp, S.; Dueben, P.D.; Scher, S.; Weyn, J.A.; Thuerey, N. Weatherbenh: A Benchmark Data Set for Data-Driven Weather Forecasting. Available online: https://mediatum.ub.tum.de/1524895 (accessed on 12 December 2021).

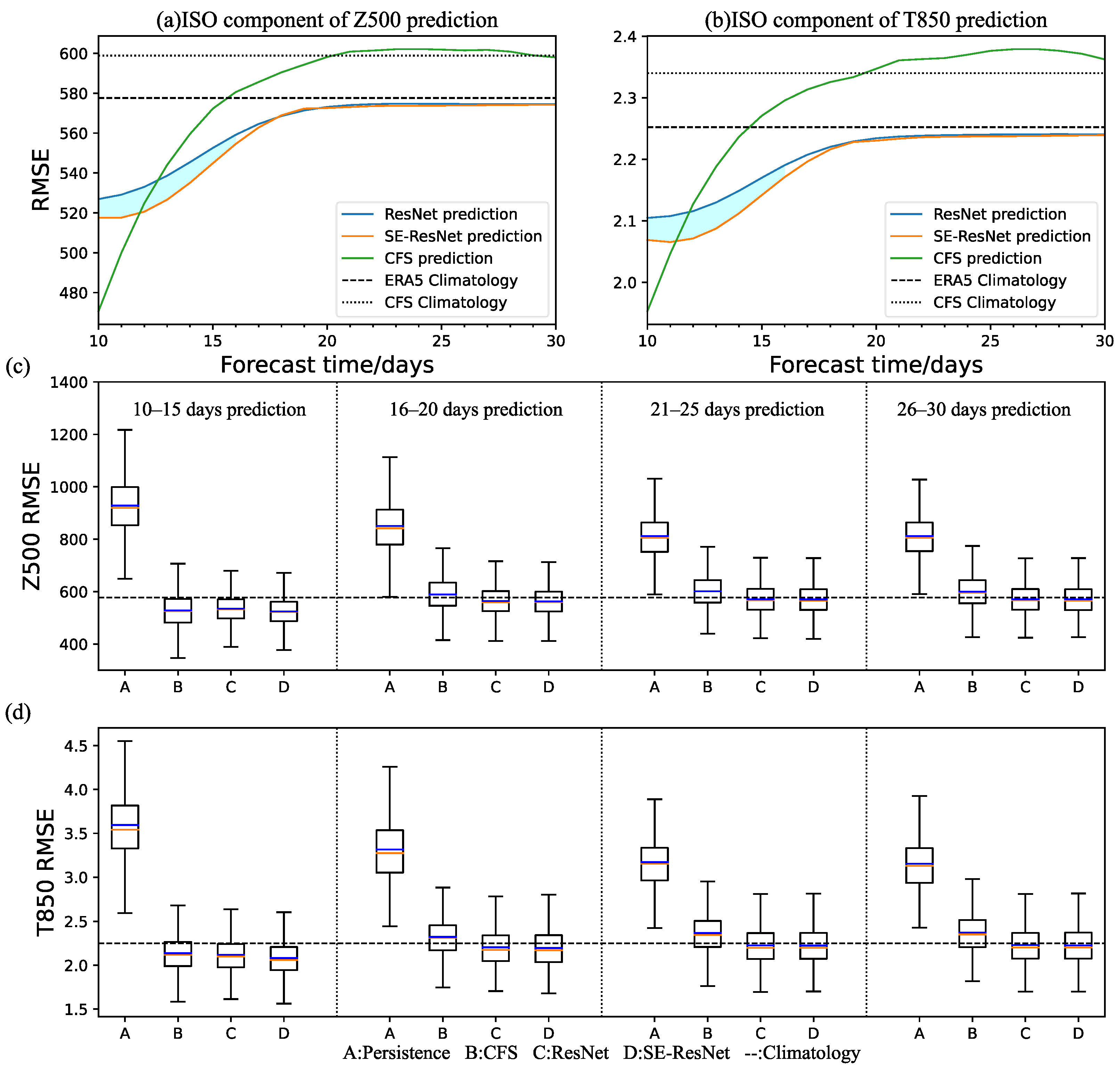
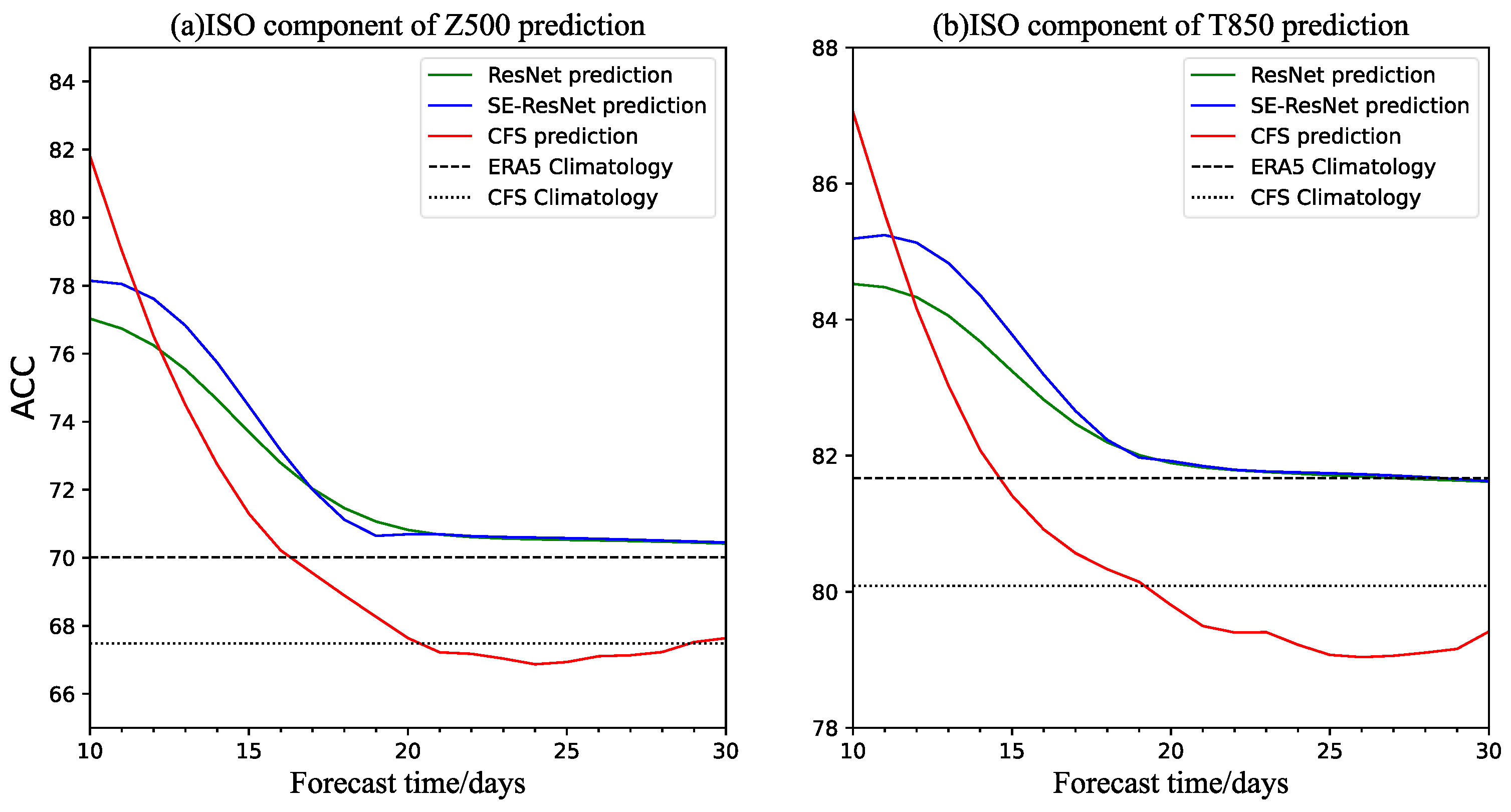
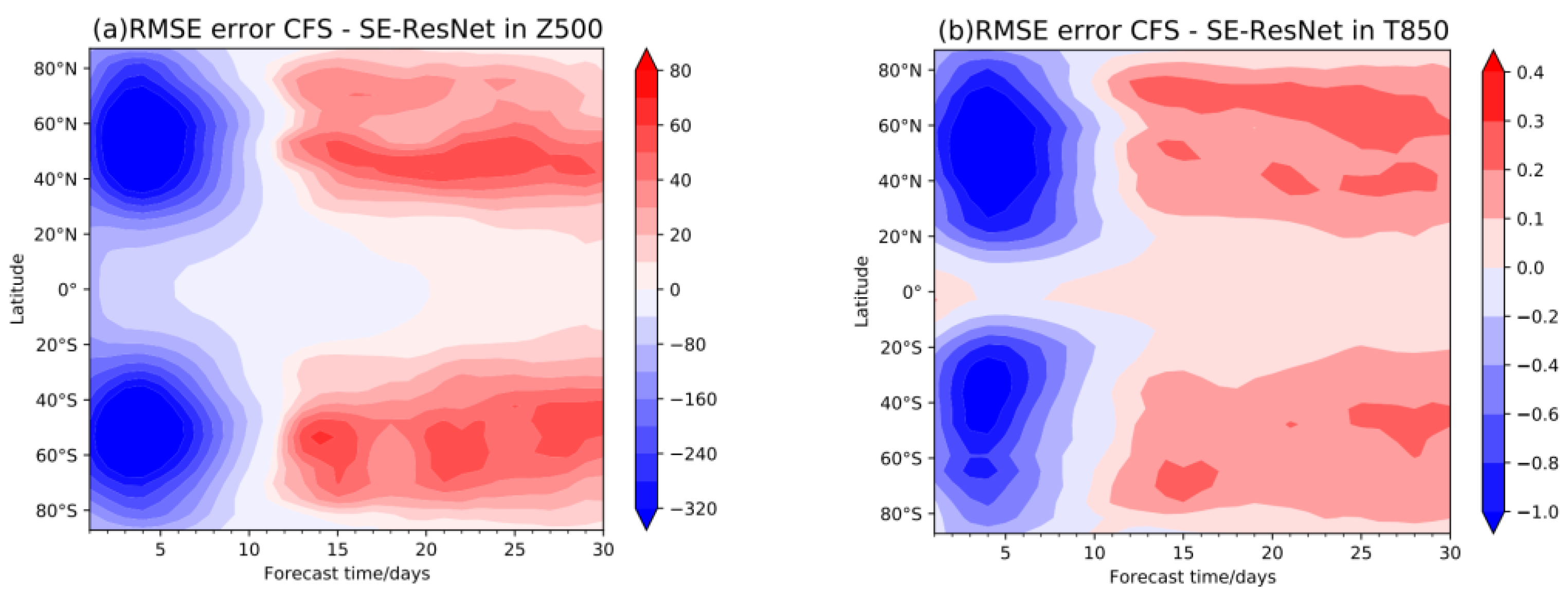
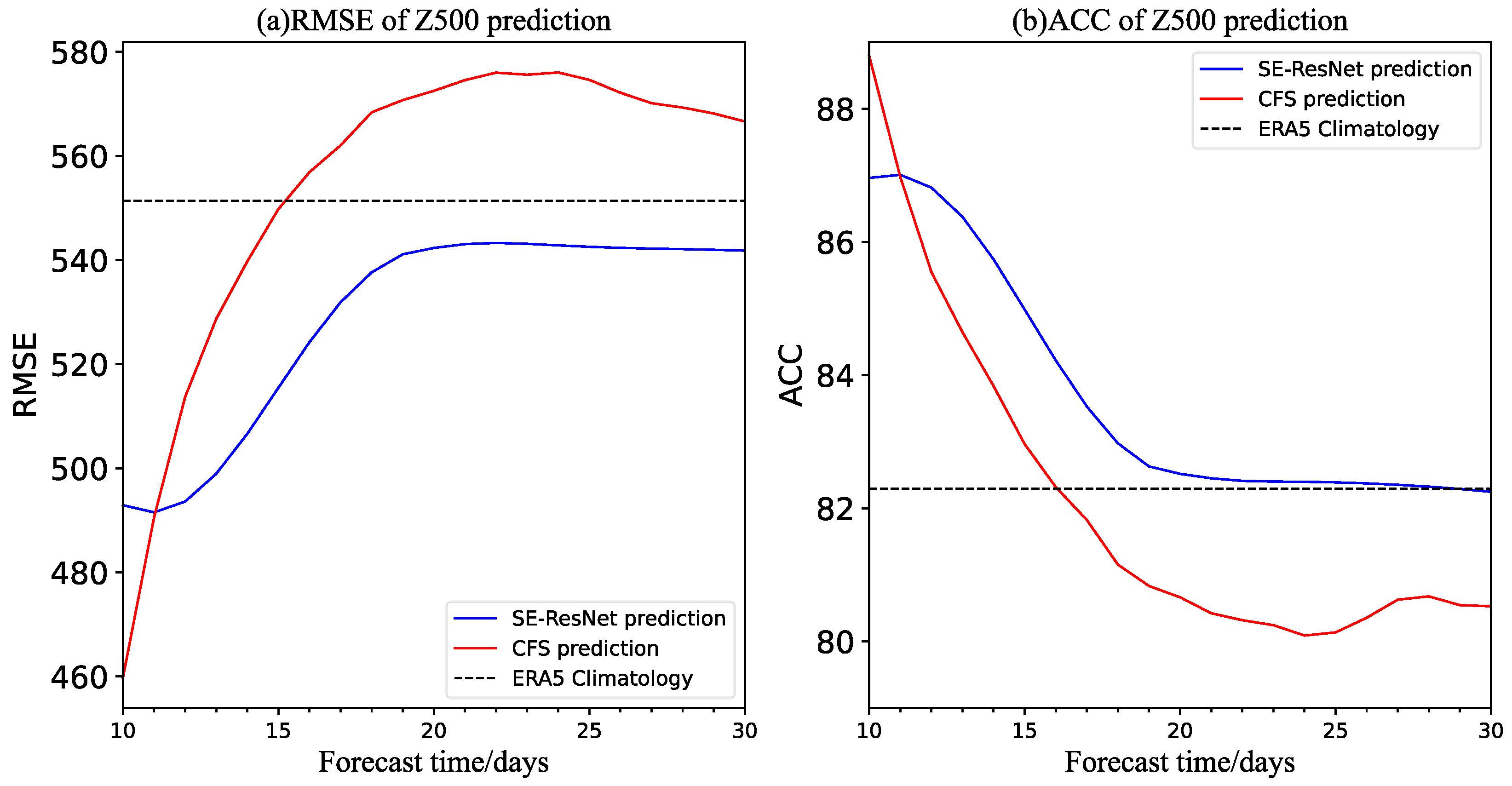
| Test Year | Z500 (Units: m2 s−2) | T850 (Units: K) |
|---|---|---|
| (2007, 2008) | 561.14/565.21 | 2.19/2.20 |
| (2009, 2010) | 567.92/572.66 | 2.24/2.26 |
| (2011, 2012) | 570.70/574.64 | 2.18/2.20 |
| (2013, 2014) | 556.41/560.09 | 2.20/2.21 |
| (2015, 2016) | 567.05/571.18 | 2.19/2.20 |
| (2017, 2018) | 558.68/562.31 | 2.19/2.20 |
| Model | Z500 (Units: m2 s−2) | T850 (Units: K) | ||||
|---|---|---|---|---|---|---|
| 10–20 | 21–30 | 10–30 | 10–20 | 21–30 | 10–30 | |
| CFSv2 | 556.44 * | 600.98 * | 577.65 * | 2.22 * | 2.37 * | 2.29 * |
| ResNet | 551.15 * | 574.59 | 562.31 * | 2.17 * | 2.24 | 2.20 * |
| SE-ResNet | 544.89 | 573.84 | 558.68 | 2.14 | 2.24 | 2.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Y.; Lu, C.; Wang, Y.; Huang, D.; Xin, F. Data-Driven Global Subseasonal Forecast for Intraseasonal Oscillation Components. Atmosphere 2023, 14, 1682. https://doi.org/10.3390/atmos14111682
Shen Y, Lu C, Wang Y, Huang D, Xin F. Data-Driven Global Subseasonal Forecast for Intraseasonal Oscillation Components. Atmosphere. 2023; 14(11):1682. https://doi.org/10.3390/atmos14111682
Chicago/Turabian StyleShen, Yichen, Chuhan Lu, Yihan Wang, Dingan Huang, and Fei Xin. 2023. "Data-Driven Global Subseasonal Forecast for Intraseasonal Oscillation Components" Atmosphere 14, no. 11: 1682. https://doi.org/10.3390/atmos14111682
APA StyleShen, Y., Lu, C., Wang, Y., Huang, D., & Xin, F. (2023). Data-Driven Global Subseasonal Forecast for Intraseasonal Oscillation Components. Atmosphere, 14(11), 1682. https://doi.org/10.3390/atmos14111682







